您应当知道的 MQL5 向导技术（第 28 部分）：据入门学习率重新审视 GAN

概述

我们将精力放到一个特定的超参数，来重新审视我们在早前的文章中研究过的一种神经网络形式。学习率。生成式对抗网络是一种成对运作的神经网络，其中一个网络经训练按传统辨别真相，而另一个网络经训练辨别前者据真实发生事件的预测。这种二元性意味着传统训练的网络（前者）正试图欺骗后者，这是真相，不过这两个网络在“同一个团队”，且两者并发训练，最终令生成式网络为交易者所用。至于本文，我们精力放在通过专注学习率进行训练过程。

始终如这些文章，旨在展示未预装在函数库中的信号类、尾随类、或资金管理类，但可按某种形式与交易者的现有策略兼容。特别是 MQL5 向导允许以最低的编码需求，针对智能系统的常用交易函数进行无缝组装和测试。从此处可以获取的是一个自定义类，其可作为一款组装好的智能系统独立测试，也可与其它向导类并行测试，因为向导组装能轻易这样做。对于刚接触向导组装过程的任何人，此处和此处的文章提供了该主题的有益介绍。

因此，本文中，在一个简单的生成式对抗网络（GAN）内，我们将检验学习率对性能的重要性（如果有的话）。“性能”本身是一个非常主观的术语，严格来说，运作的测试应当比我们在这些文章内研究的周期要更长。故此，就我们的目的，“性能”只是总盈利，同时考虑到恢复因子。我们将会研究若干种学习率类型（或调度），并努力据其全部进行穷尽测试，尤其是当它们与同伙明显不同时。

本文的格式将与我们之前文章中曾用过的格式有所不同。在表述每种学习率格式时，会伴随其策略测试报告。略微对照我们之前所做，其时报告通常都出现在文章的末尾，在结束语之前。故此，这是一种探索性格式，对于学习率是否潜在影响机器学习算法（或者更具体地是 GAN）性能持开放态度。由于我们正在视察多种类型和格式的学习率，故拥有统一的测试衡量值非常重要，这就是为什么我们将在所有学习率类型中采用单一品种、时间帧、和测试区间的原因。

基于此，我们贯穿全程采用的品种将是 EURJPY、时间帧将是日线数据、测试区间将是 2023 年。我们正在 GAN 上进行测试，其默认架构肯定是一个因素。始终会有争辩，即精心设计每层的数量和规模才是首要重点，不过尽管这些都是考虑重点，但在此我们专注于学习率。为此，我们的 GAN 将相对简单，只有 3 层，包括一个隐藏层。每层的总体规模从输入到输出依次为 5-8-1。这些设置在随附的代码中均有所指示，如果读者希望使用替代设置，能轻易修改。

为了生成做多和做空条件，我们按前述文章中所做的相同方式实现所有不同的学习率格式，前文探讨了在 MQL5 中运用 GAN 作为自定义信号类。一如既往地附上源代码，不过为了完整起见，它如下所示：

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalCGAN::LongCondition(void)
{  int result = 0;
   double _gen_out = 0.0;
   bool _dis_out = false;
   GetOutput(_gen_out, _dis_out);
   _gen_out *= 100.0;
   if(_dis_out && _gen_out > 50.0)
   {  result = int(_gen_out);
   }
   //printf(__FUNCSIG__ + " generator output is: %.5f, which is backed by discriminator as: %s", _gen_out, string(_dis_out));return(0);
   return(result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalCGAN::ShortCondition(void)
{  int result = 0;
   double _gen_out = 0.0;
   bool _dis_out = false;
   GetOutput(_gen_out, _dis_out);
   _gen_out *= 100.0;
   if(_dis_out && _gen_out < 50.0)
   {  result = int(fabs(_gen_out));
   }
   //printf(__FUNCSIG__ + " generator output is: %.5f, which is backed by discriminator as: %s", _gen_out, string(_dis_out));return(0);
   return(result);
}

固定学习率

为启事，固定学习率大概是大多数机器学习算法新用户所用，因为它是最简单的。算法的权重和乖离的标准衡量在每次学习迭代中进行调整，若经由不同的训练局次则根本不会改变。

固定汇率的优势根源于其简单性。它很容易实现，因为您有一个浮点值可经由所有局次所用，这也令训练动态更加可预测，这都有助于更好地理解整个过程，以及调试它。此外，这提高了可复现性。尤其是在许多神经网络中，那些使用随机权重初始化的神经网络，给出的测试运行结果不一定是可复现的。在我们的例子中，经由所有不同学习率格式，我们正在采用标准初始权重 0.1，和初始乖离 0.01。按这些固定值，我们可以更好地复现测试运行结果。

还有，固定学习率在早期训练过程中带来了稳定性，因为学习率不会像大多数其它学习率格式那样在后期降低、或暴跌。稍后在测试运行中遇到的数据，可认为与最旧数据的程度类似。当您依据另一个非学习率的超参数优调网络时，这令基准测试和比较变得更加容易。举例来说这可能是神经网络所用的初始权重。按固定学习率，这种优化搜索可以更快捷地达至有意义的结果。

固定学习率的主要问题是次优收敛。在训练时会有担忧，梯度下降可能会卡在局部最小值，而非最优收敛。在建立理想的固定学习率之前，这一点尤其重要。此外，还有适应性差的论点，它遵循一个普遍的共识，即当遇到连续的训练局次时，“学习”的需求不会一成不变。普遍的看法是它会降低。

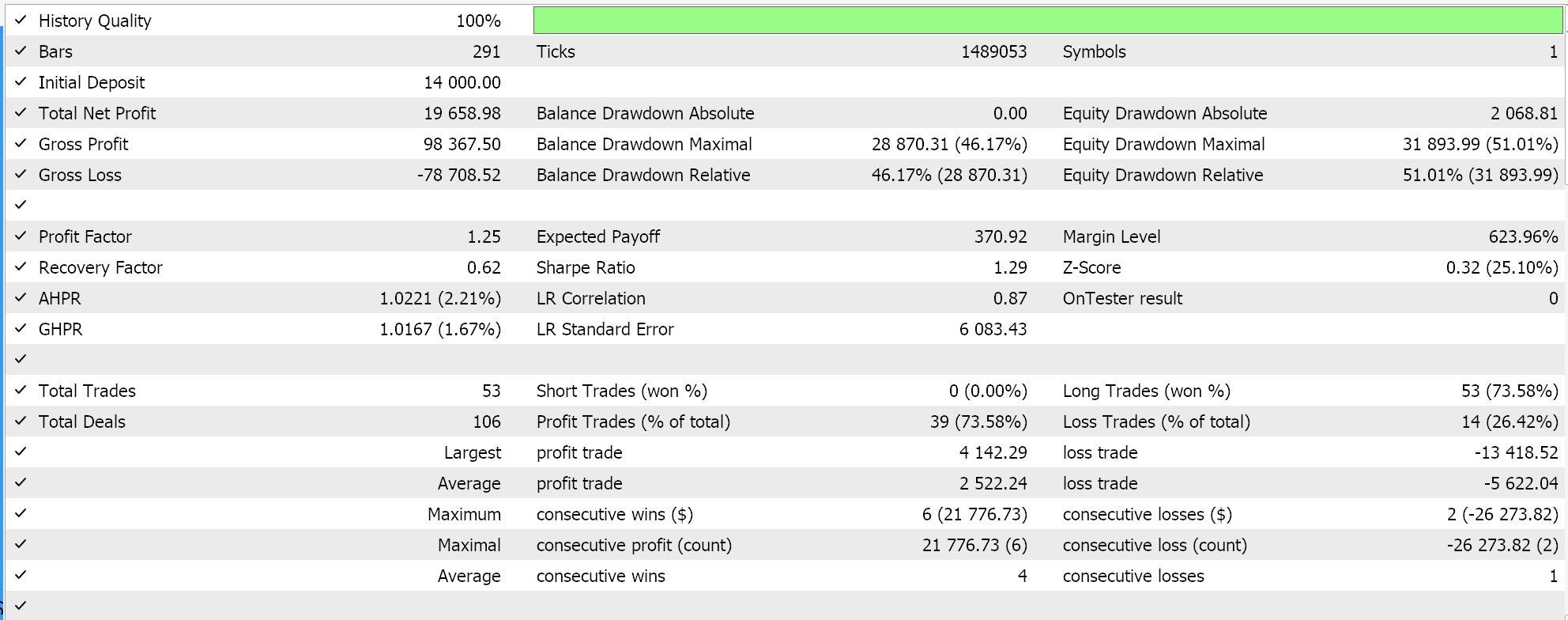
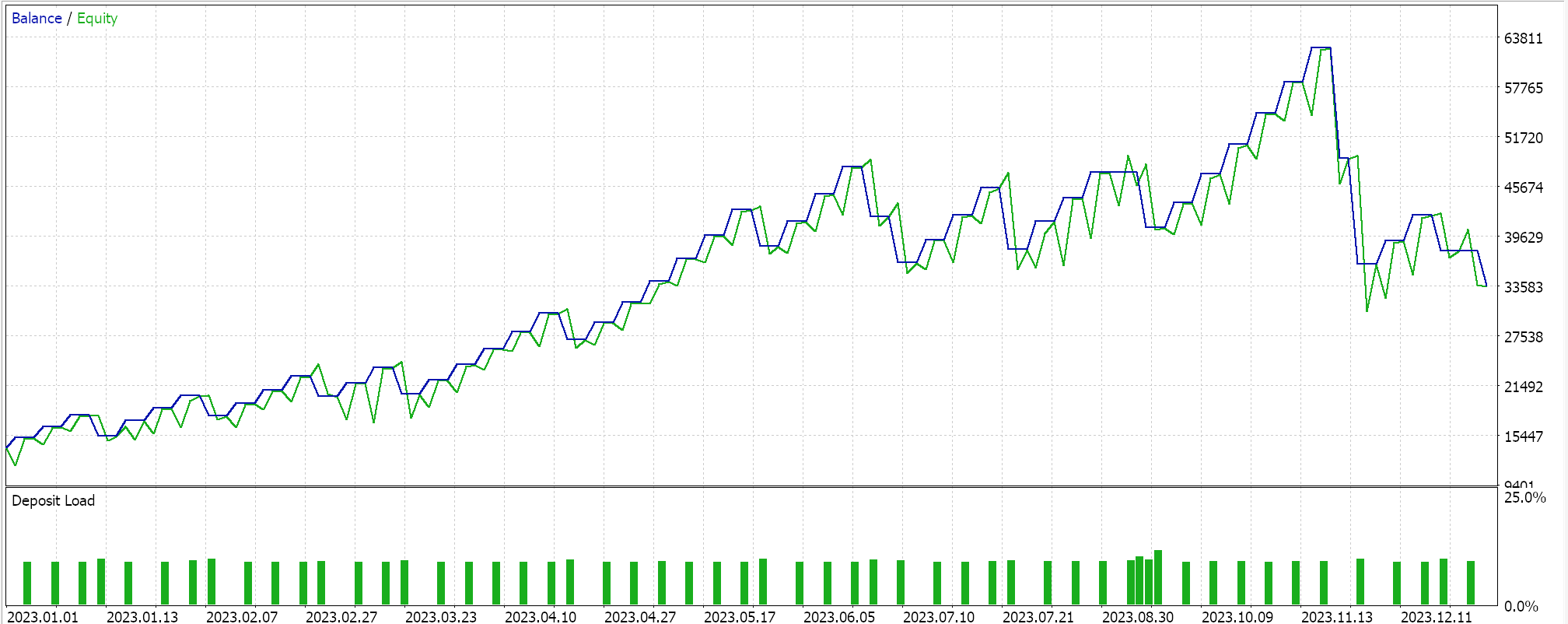
尽然，即便有这些优点和缺点，当据 EURJPY 货币对、2023 年日线时间帧进行试运行时，我们得到以下图片：

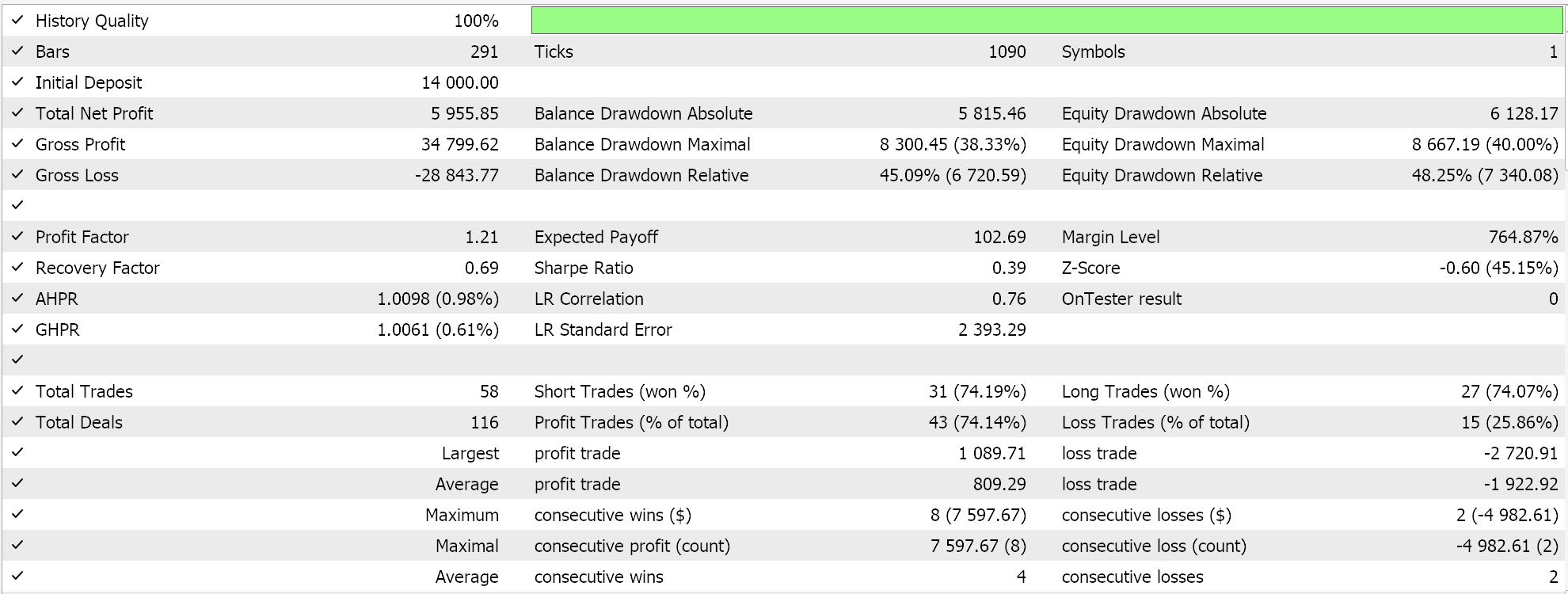
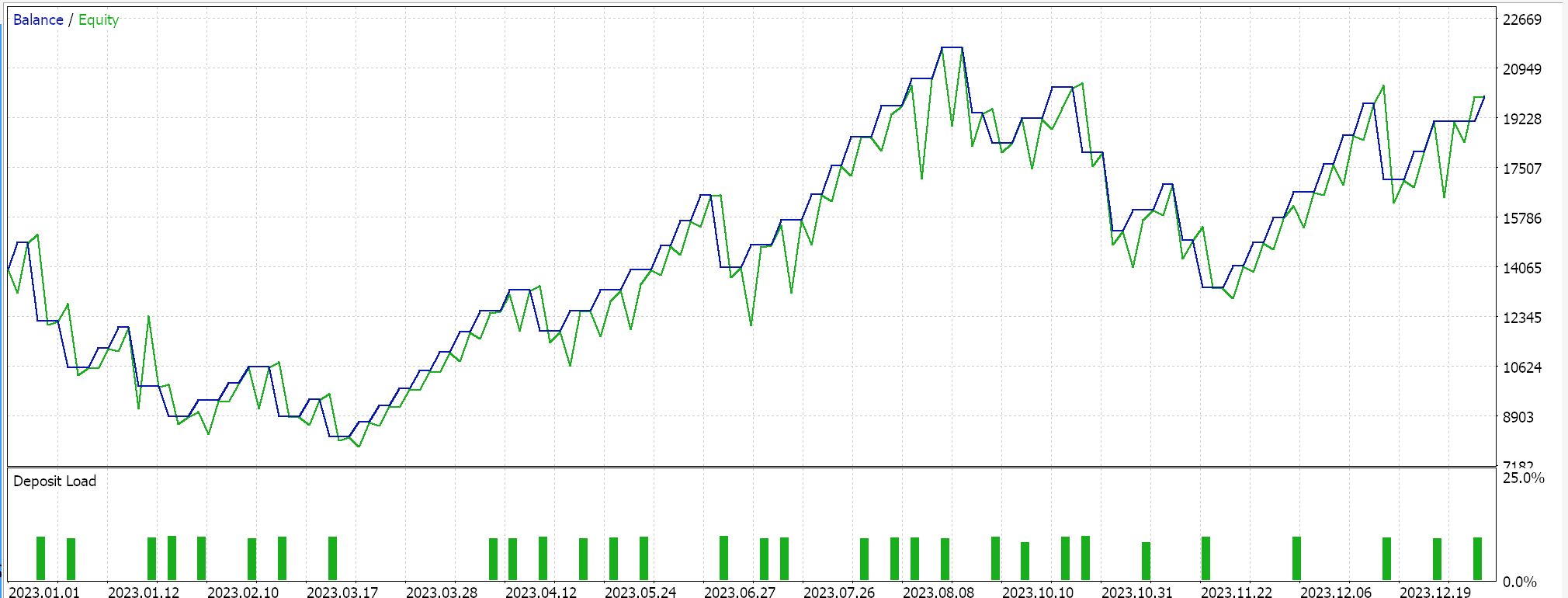
步进衰减

接下来是步进衰减学习率，它实际上是一个固定学习率，只搭配两个额外的参数，监管初始固定学习率如何随每个后续局次而降低。MQL5 的实现如下：

      if(m_learning_type == LEARNING_STEP_DECAY)
      {  int _epoch_index = int(MathFloor((m_epochs - i) / m_decay_epoch_steps));
         _learning_rate = m_learning_rate * pow(m_decay_rate, _epoch_index);
      }

故此，判定每个局次的学习率是一个两步过程。首先，我们需要获取局次索引。这只是一个索引，衡量我们在训练会话期间经由每个局次的进展有多远。其值深受第二个输入参数 'm_decay_epoch_steps' 的影响。我们的 for 循环是倒计数，而非像典型情况那样向上计数，故我们从局次总数中减去当前 i 值，除以第二个输入之后，执行数学向下取整。由此得出的四舍五入整数结果用作局次索引，我们用它来量化我们需要在当前局次降低初始学习率的程度。如果我们的步长（第 2 个输入值）为 5，那么我们始终等待，且仅在每 5 个局次后降低学习率。如果步长为 10，则在 10 个局次之后降低，依此类推。

步进衰减的总体策略是渐次降低这个学习率，如此这般免于“超过”最小值，并有效地抵达最优解。它在快速初始学习、与之后的优调之间提供平衡，并为之自豪。它可有助于逃避损失地貌中的局部最小值和鞍型点，并常常因降低学习率（与固定率不同）导致更佳的普适，这能有助于避免过度拟合。

如果我们据 EURJPY 的 2023 年日线，按上述方式运行，我们作为会所得如下：

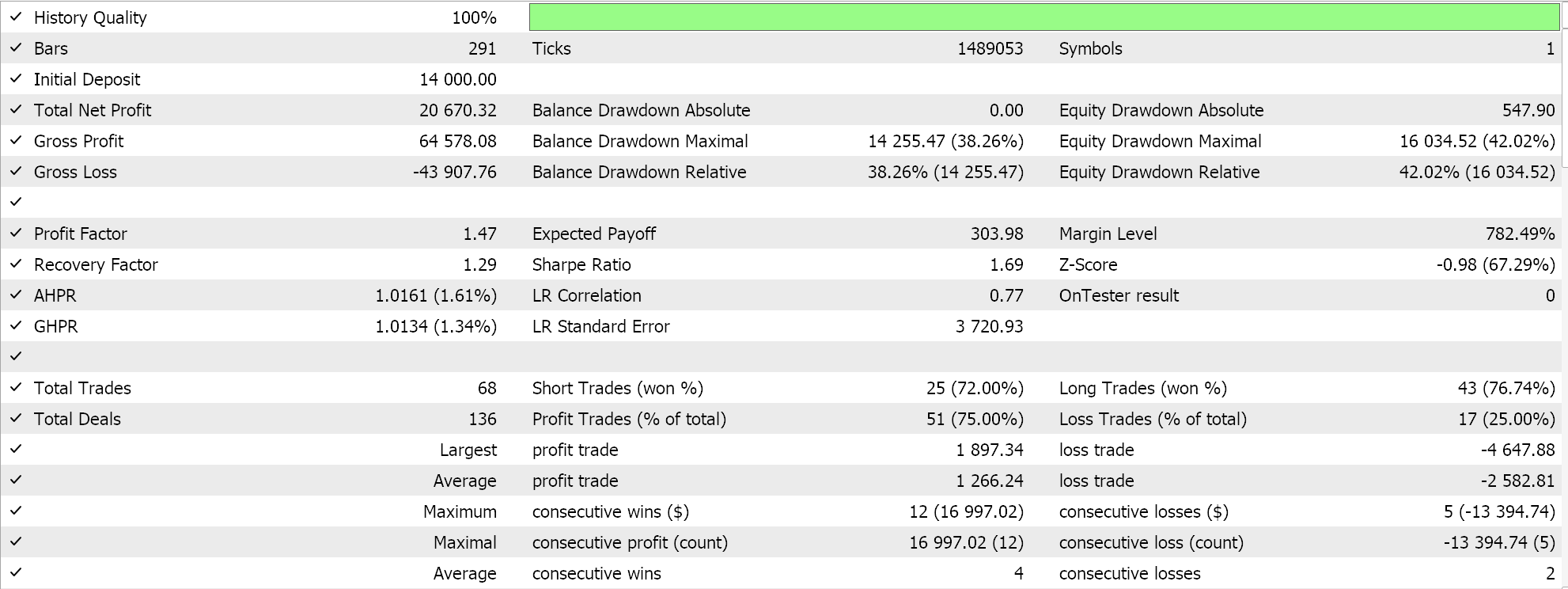
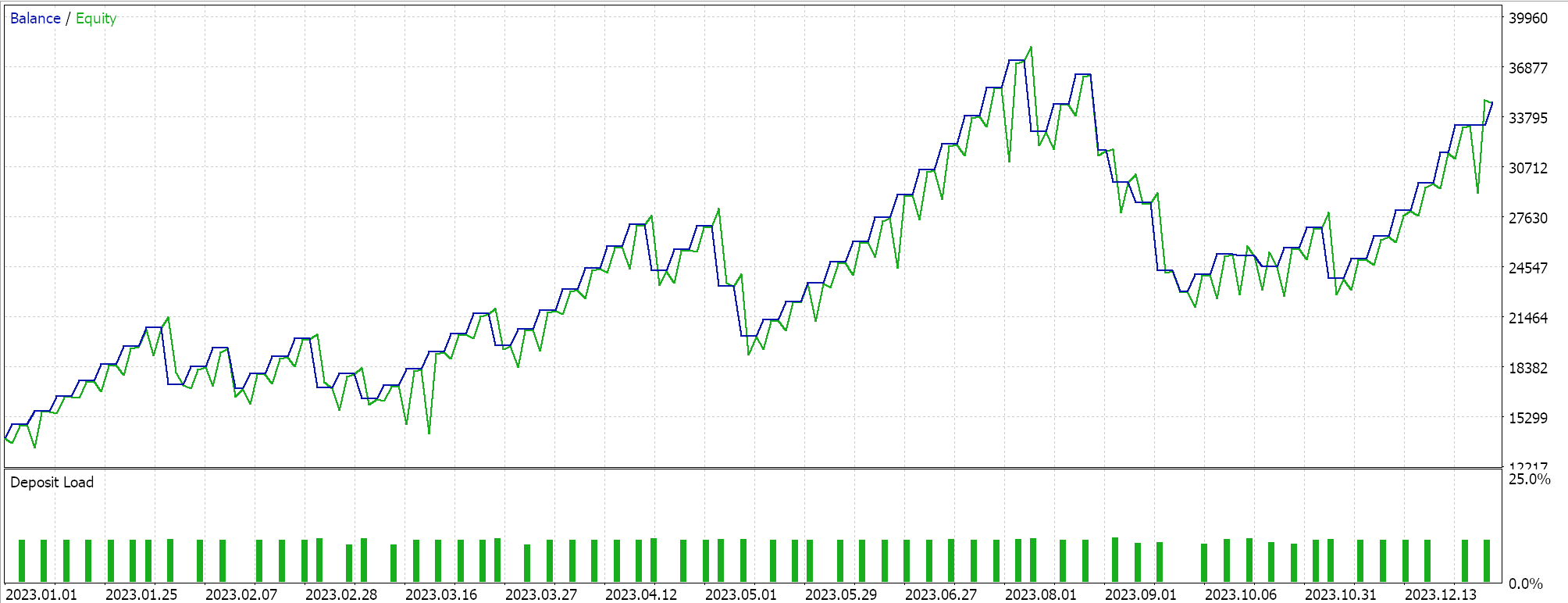
指数衰减

指数衰减学习率与步进衰减率不同，它在降低学习率方面更平滑。回想我们在上面所见，只有当局次索引增加、或在预定义的局次步数之后，步进衰减学习率才会降低。而据指数衰减，学习率的降低总是在每个新局次中发生。这由以下公式表示：

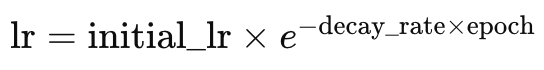
其中

• lr 是学习率
• initial_lr 是初始学习率
• e 是欧拉（Euler）常数
• decay_rate 和 epoch 分别名如其义

MQL5 的代码如下：

      else if(m_learning_type == LEARNING_EXPONENTIAL_DECAY)
      {  _learning_rate = m_learning_rate * exp(-1.0 * m_decay_rate * (m_epochs - i + 1));
      }

指数衰减能够通过在每个新局次的处乘以衰减因子来降低学习率。与上述步进方式相比，这可确保学习率更加渐次降低。渐次方式的优势偏重更符合降低学习率的普遍方式。这些已在上面与步进衰减方法共享。指数衰减能够提供步进衰减所缺少的，避免学习率突降，这可能令训练过程不稳定。

如果我们据 EURJPY 的 2023 年日线时间帧执行上述测试运行，我们会得到以下结果：

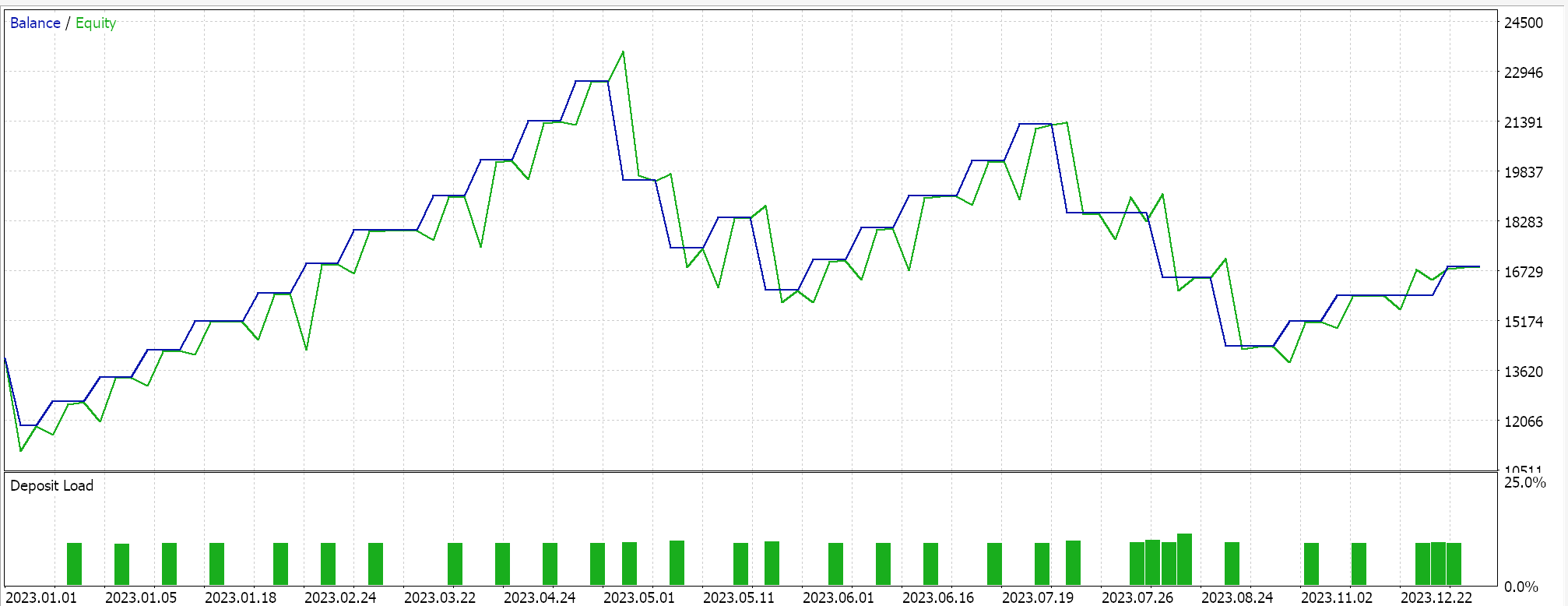
尽管指数衰减允许更平滑、及渐次降低学习率，通过修正每个局次的学习率，并非所有降低步数都相同。在训练初启，学习率的降幅明显更大，且随着训练进度迈向最后一个局次，这些值会减小。

多项式衰减

这像指数衰减，也会随着训练进度而降低学习率。与指数衰减的主要区别在于，多项式衰减一开始降低学习率很缓慢。随着训练接近该过程的后期局次，降低率最终会提升。这可用如下方程表示：

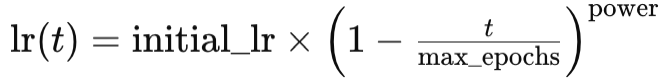
其中

• lr(t) 是局次 t 处的学习率
• initial_lr 是初始学习率
• t 是局次索引
• max_epochs 和 power 分别名如其义

因此，实现如下：

      else if(m_learning_type == LEARNING_POLYNOMIAL_DECAY)
      {  _learning_rate = m_learning_rate * pow(1.0 - ((m_epochs - i) / m_epochs), m_polynomial_power);
      }

多项式衰减引入 'power' 输入参数至我们的信号类。所有学习率格式都被合并到单一信号类文件之中，其中输入参数允许选择特定的学习率。该代码文件附于文章底部。多项式 'power' 输入是一个常量指数，我们用来根据局次降低学习率的因子，如上公式中所示。

多项式衰减如同指数衰减、以及步进衰减，都会降低它们的学习率。如上所述，多项式衰减与同伙的相异之处在于，在训练迈向结束时，学习率急速降低。后一种急速降低往往允许“优调”训练过程，即学习率会尽可能长时间里保持尽可能高，且仅在局次耗尽时才会降低。这种“优调”是通过判定各种训练局次的最优多项式幂来达成的，一旦确定了这一点，就能期待一个更优化的学习过程。

多项式衰减的优点类似于我们上面提到的其它学习率格式，主要以渐次降低为中心，这在总体上提供了一个更平滑的过程。如前所述，学习率的优调除了判定经由局次的理想学习率外，它还允许控制训练过程所需的时间。较大的多项式幂可以理解为加快训练过程，而较低的幂应该会减慢训练过程。

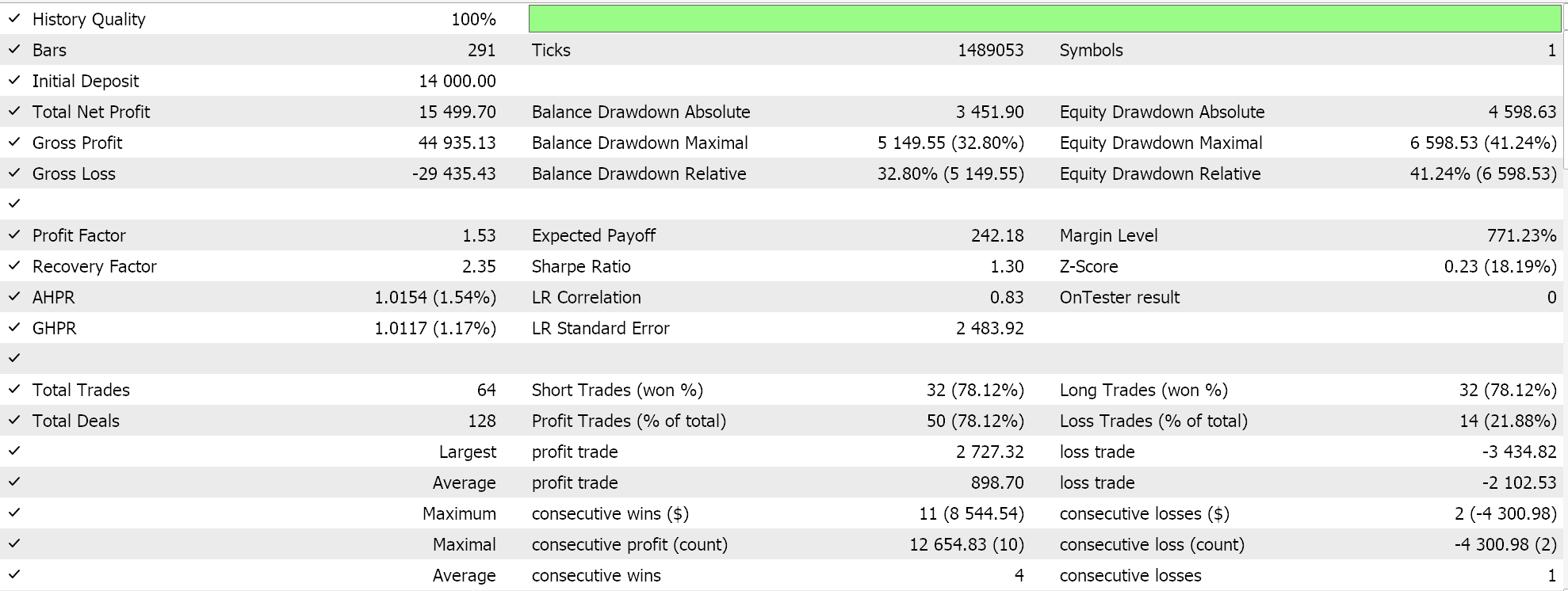
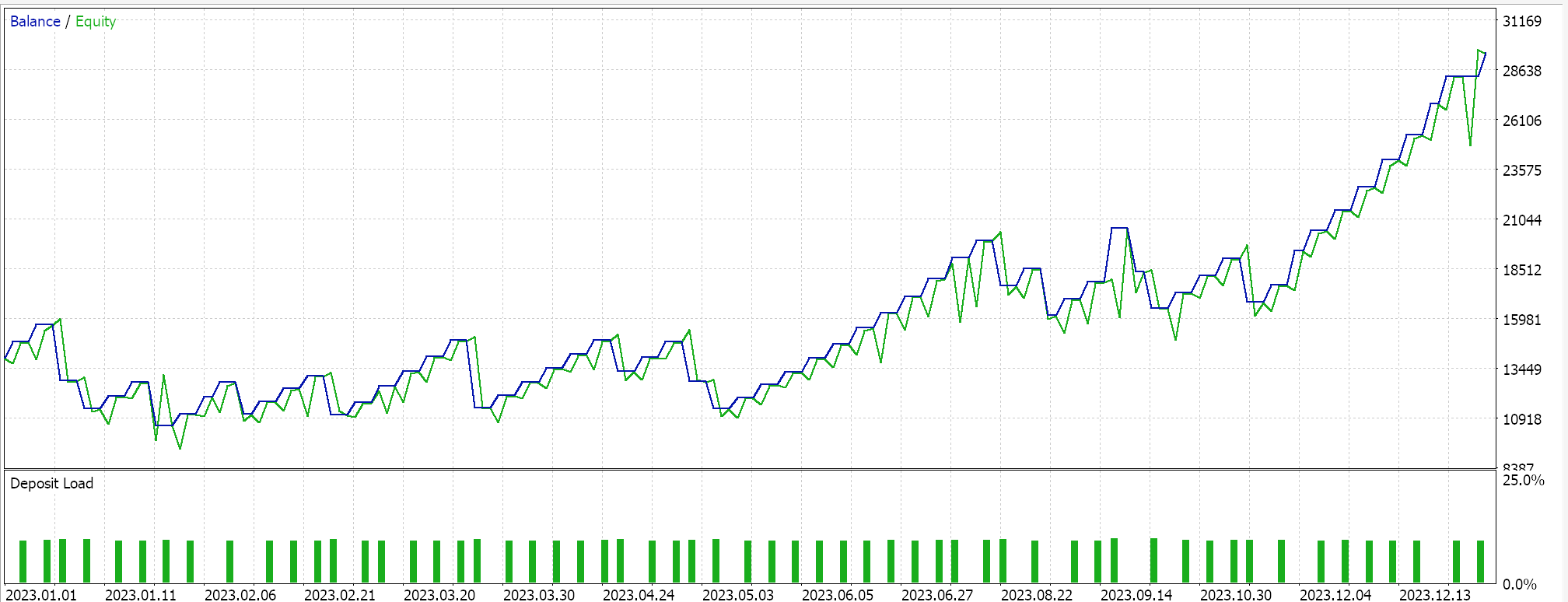
据 EURJPY 的 2023 年日线时间帧测试运行，为我们给出以下结果：

逆时衰减

逆时也会在每个局次按参考时间衰减来降低学习率。上面我们研究了指数衰减初始阶段的学习率快速降低，及多项式衰减的学习率缓慢降低，而时间衰减允许学习率的降低速度更慢，故其在处理非常大的训练数据集时，甚至比多项式衰减更适合。

逆时衰减公式为：

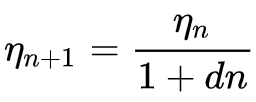
其中

• ηn+1  是局次 n + 1 处的学习率
• ηn  是局次 n 处的先验学习率
• d 是衰减率
• 而 n 是局次索引。

我们所做的 MQL5 实现如下所示：

      else if(m_learning_type == LEARNING_INVERSE_TIME_DECAY)
      {  _learning_rate = m_prior_learning_rate / (1.0 + (m_decay_rate * (m_epochs - i)));
         m_prior_learning_rate = _learning_rate;
      }

该算法对于非常大的训练数据集很理想，给定方式确实减缓了学习速度的降低。它共享了前述其它学习率格式的大部分优势。此处包含它作为研究示例，看看在相同交易品种、时间帧、和测试区间上测试时，它相较于其它学习率会如何。完整的源代码附于文后，故用户可进行更改，以便执行更复杂的测试。然而，若我们遵照我们至今一直采用的设置进行测试运行，我们会得到以下结果：

余弦退火

余弦退火率调度器也能降低学习率，遵循余弦函数，渐次地迈向预设的最小值。学习率降低意向，类似于上面提到的格式，不过配以余弦退火，有一个目标最小值，并且每当达到最小学习率时，该过程就会不断重启，直至全部局次耗尽。

其公式可以表示如下：

其中

• lr(t) 是局次 t 处的学习率
• initial_lr 是初始学习率
• t 是局次索引
• T 是局次总数
• min_lr 是最小学习率

MQL5 实现如下：

      else if(m_learning_type == LEARNING_COSINE_ANNEALING)
      {  _learning_rate = m_min_learning_rate + (0.5 * (m_learning_rate - m_min_learning_rate) * (1.0 + MathCos(((m_epochs - i) * M_PI) / m_epochs)));
      }

余弦退火更适合大型数据集，甚至超过逆时衰减。这是因为，虽然逆时衰减足以将学习率的大幅下降推迟到迈向一个训练局次，但余弦退火允许一旦触发预设最小学习率，则将其恢复为初始值，从而“重置”学习。这与另一种称为“热重启”的技术类似，但略有不同，其在预设的训练循环内，学习率会恢复到其初始值。

热重启适用于采用批次/轮次的非常大的训练场景，如此每个批次都被切分成局次，而相较于单批次方式，我们已在迄今所有学习率格式中加以研究。当采用批次时，在给定批次结束时，会自动执行将学习率重置、或恢复到其原始值。

余弦退火的单批次格式的测试结果，为我们给出以下报告：

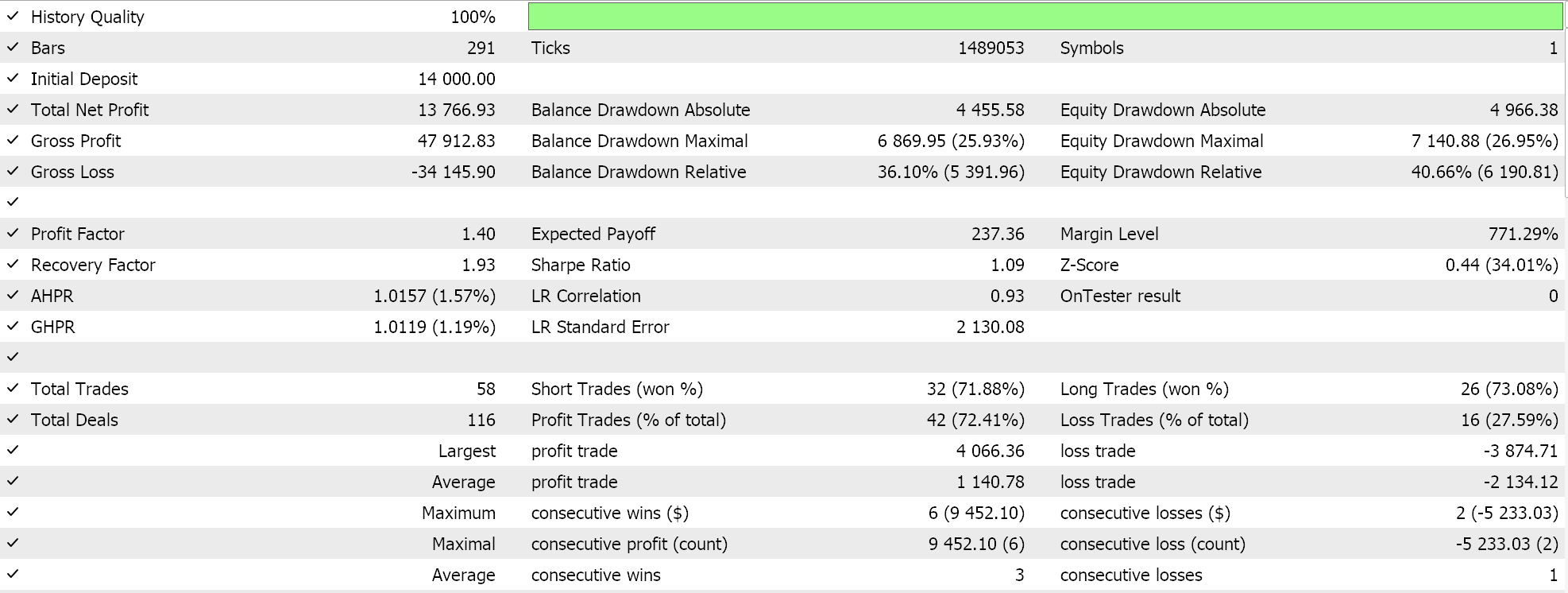
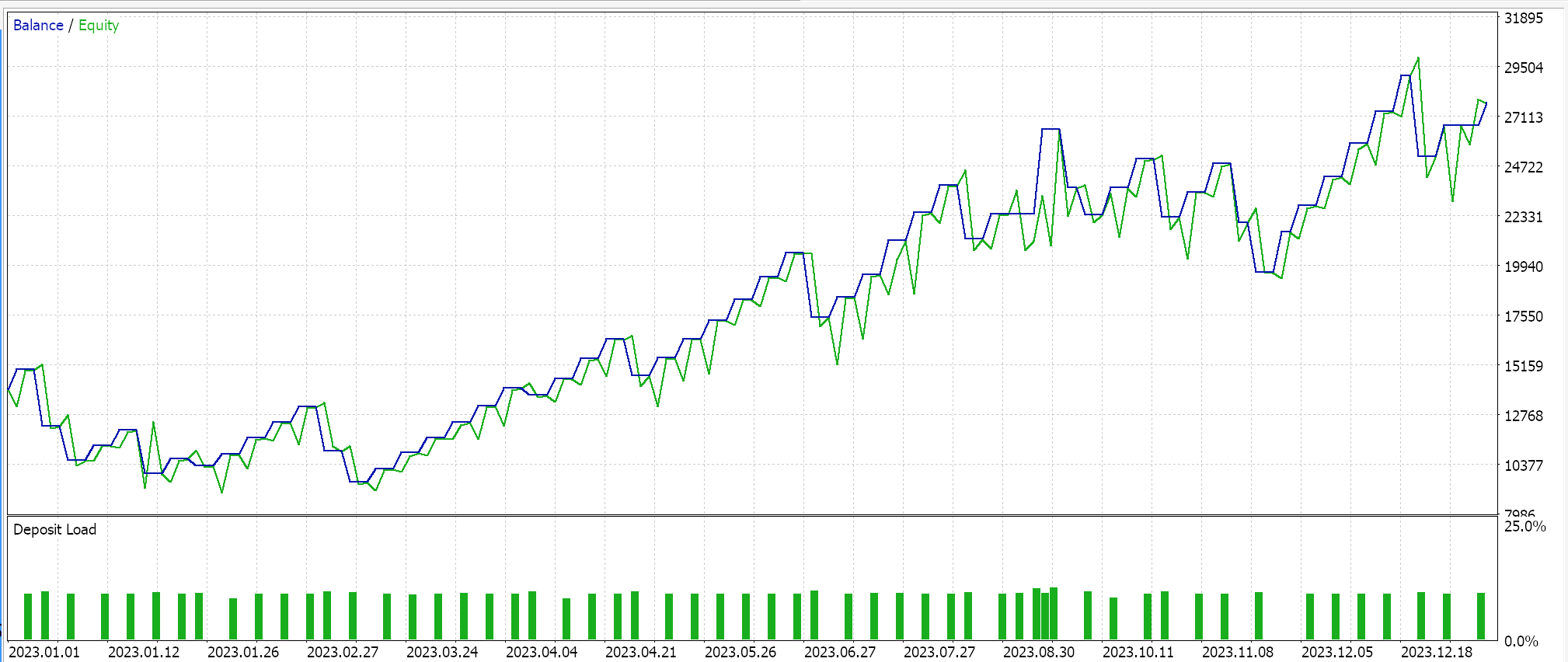
此外，余弦退火也可进行优调，因为我们有一个额外的输入参数，即最小学习率。根据我们分配给这个速率的值，我们不仅可以完全把控训练过程的品质，还能判定所有局次的训练持续多久。故此，根据所面临的训练数据的大小，这可能极其显要。

终究，经常有争论余弦退火在探索和利用之间提供了平衡。探索是寻找理想的学习率，尤其是经由调整和优调最低学习率；而利用则指遵照已知最佳学习率收获最佳网络权重和乖离。鉴于双管齐下的优化，这往往会导致模型的普适提升。

轮转学习率

与我们目前看到的格式不同，轮转学习率在最终将其降低至最小值之前，先从提升学习率开始。这以轮转形态发生。因此，训练总是从每个轮转的最小学习率开始。它由以下公式指导：

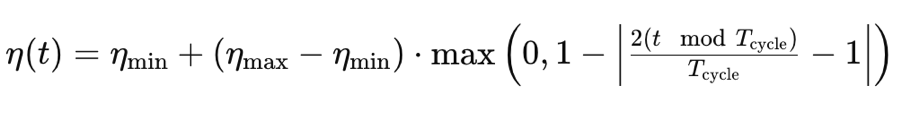
其中

• η(t) 是局次 t 处的学习率
• ηmin 是最小学习率
• ηmax 是最大学习率
• Tcycle 是给定批次、或轮转中的局次总数（我们仅用单轮转进行测试）
• (t modTcycle) 是轮转中局次总数除以局次索引的余数。我们将该值乘以 2

我们作为的 MQL5 如下：

      else if(m_learning_type == LEARNING_CYCLICAL)
      {  double _x = fabs(((2.0 * fmod(m_epochs - i, m_epochs))/m_epochs) - 1.0);
         _learning_rate = m_min_learning_rate + ((m_learning_rate - m_min_learning_rate) * fmax(0.0, (1.0 - _x)));
      }

依据该学习率执行测试运行，同时坚持采用我们上面的相同品种、时间帧、和测试区间设置，为我们给出这些结果：

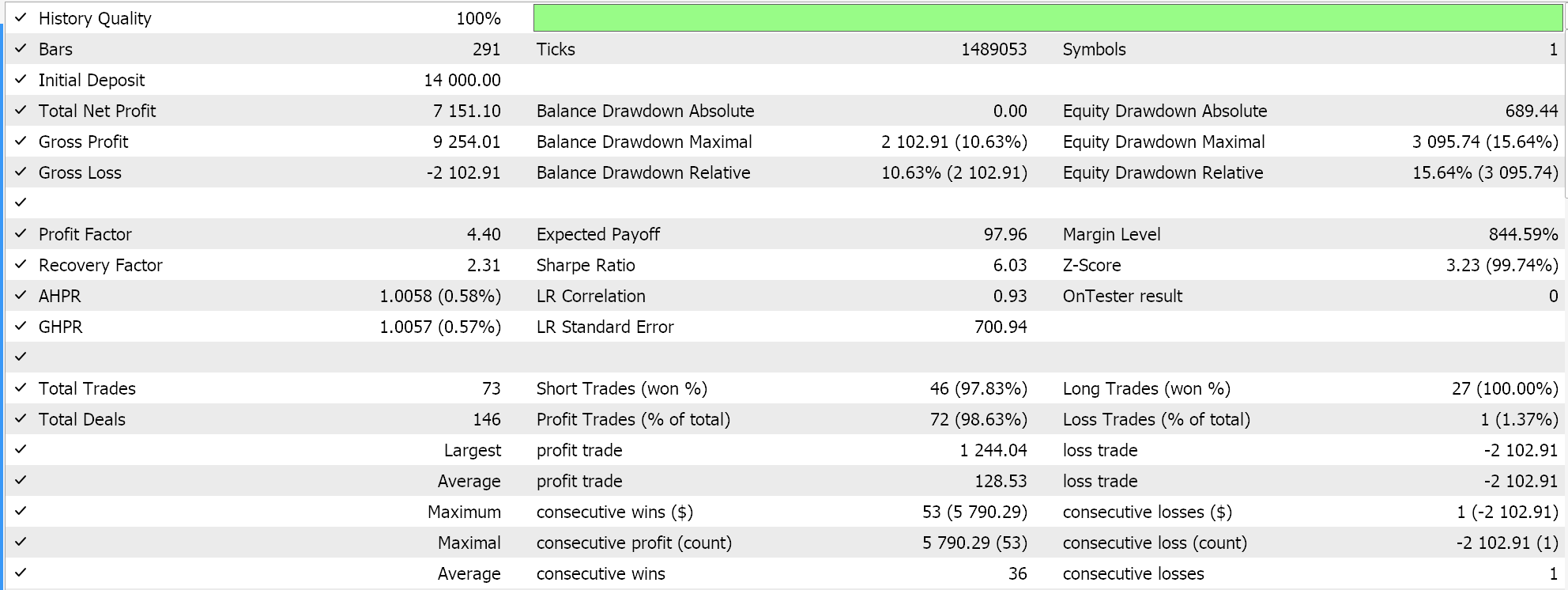
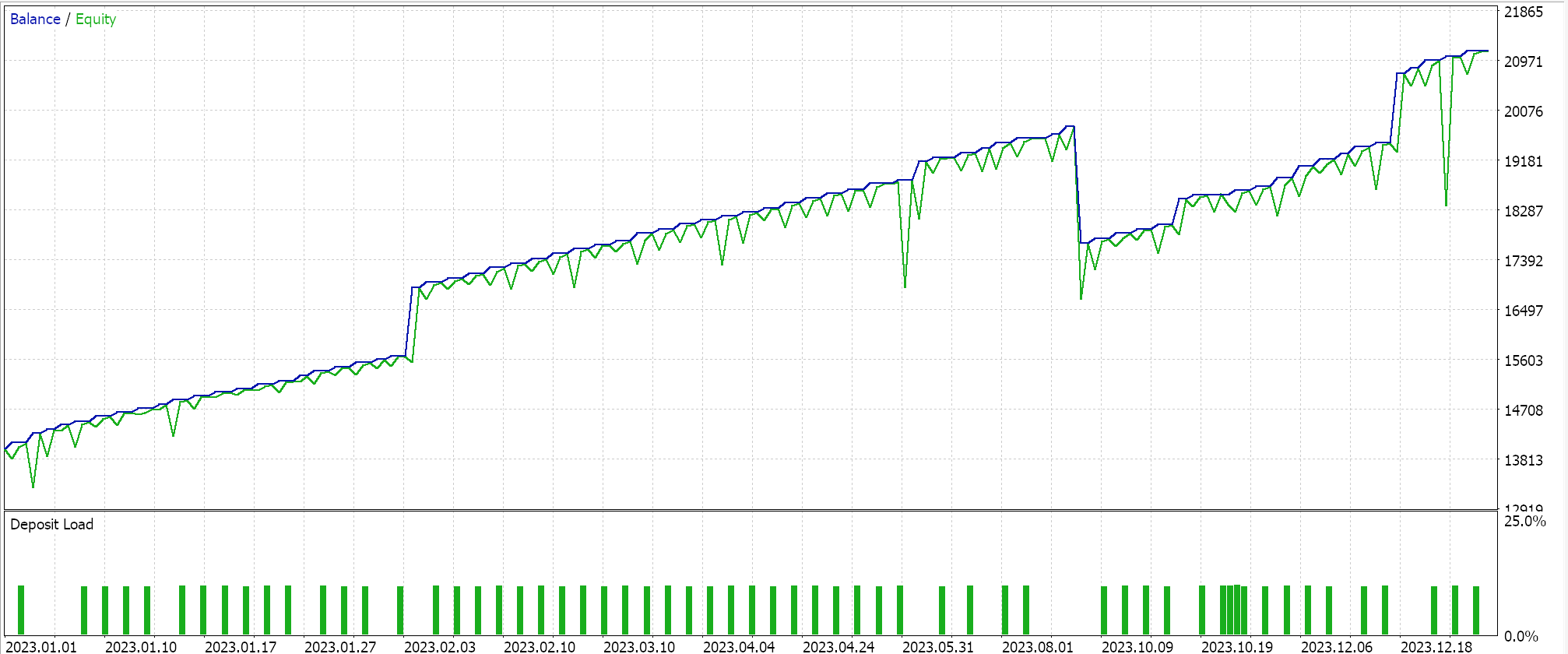
轮转学习率还有另一种实现方式，称为 'triangular-2'，在其降至最低值之后，再次初始学习率。然而，与我们上面看到的不同之处在于，学习率所能提至的最大值，在每次轮转中不断降低。

我们将研究该学习率格式，以及其它格式，包括自适应学习率，它本身相对较宽，因为它具有不同的格式；热重启，以及下一篇文章的单轮转率。

结束语

总而言之，我们已见识到在机器学习算法，诸如生成式对抗网络，仅替换学习率如何产生无数不同的结果。显然，学习率是一个非常敏感的超参数。有些东西看似很空泛，如学习率，其主要目的是得到更具体、及更受欢迎的网络权重和乖离，但很明显，在固定的时间和资源内进行测试时，选择达至这些权重和乖离的路径，可能会因所用学习率而有很大变数。