Características del Wizard MQL5 que debe conocer (Parte 24): Medias móviles

Introducción

En esta continuación de la serie sobre el Asistente de MQL5, analizamos el indicador de media móvil y exploramos cómo podría añadirse a la biblioteca de herramientas disponibles, de maneras que podrían resultar innovadoras para algunos traders. La Media móvil tiene muchísimas variantes como serie temporal única acoplable a un gráfico, pero también otras variantes como oscilador e incluso otras como indicador de envolventes.

Exploraremos estas múltiples aplicaciones o variantes dentro de una categoría especial de 3 Medias Móviles (MAs, Moving Averages), denominadas Medias pitagóricas. Las 3 MAs con este nombre son Media aritmética (AM, Arithmetic Mean), Media geométrica (GM, Geometric Mean) y Media armónica (HM, Harmonic Mean). La primera de ellas, la media aritmética, es en la que primero piensa todo el mundo cuando se menciona la MA. Es simplemente la media de cualquier número de valores de un conjunto. Wikipedia tiene un resumen muy interesante de estos 3 tipos de medios en un diagrama. Lo compartimos a continuación:

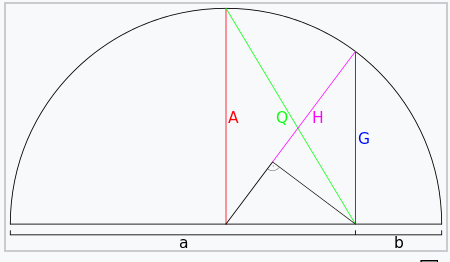
Lo que se presenta arriba es un semicírculo cuyo diámetro se divide de forma desigual en dos valores a y b. La media aritmética de estos dos valores está marcada como A en rojo en el diagrama, lo que equivale al radio del semicírculo, como cabría esperar. A efectos de exhaustividad, la fórmula de la media aritmética se comparte a continuación como:

Donde:

• AM : Es la media aritmética.
• x : Son los valores del conjunto cuya media se calcula.
• n : Es el tamaño del conjunto.

Ahora bien, la media geométrica viene dada por la fórmula:

Donde:

• GM : Es la media geométrica.
• x y n : Representan lo mismo que en el caso anterior de AM.

El valor de GM en el semicírculo de arriba es equivalente en longitud a la cuerda azul marcada con G, lo que hace que tenga más peso el valor menor de b que el mayor de a. Además, cabe destacar que el GM siempre será positivo aunque todos los valores sean negativos. Esta situación podría solucionarse asignando un valor negativo al GM calculado si el conjunto tuviera números totalmente negativos, pero en el caso de que fuera una mezcla de valores negativos y positivos, la obtención del GM real sería problemática.

Para la media armónica, la representación semicircular es la línea marcada con H cuya longitud equivale a la media de a y b. Su fórmula está representada por:

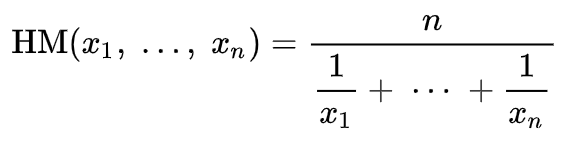
Donde:

• HM : Es, por supuesto, la media armónica.
• x y n : Representan lo mismo que arriba.

Si por alguna razón el valor b, fuera cero, como puede verse en el diagrama de semicírculo, tanto la media geométrica como la armónica serían cero. (Esto a pesar de obtener una «división por cero» al calcular la media armónica). Curiosamente, esto sería cierto independientemente del recuento (es decir, si son más de 2) de los números cuyas medias se calculan; mientras alguno de esos números sea un cero, entonces la media geométrica y la media armónica de todos los valores es cero.

En esencia, esta propiedad mide hasta qué punto el valor más pequeño de un conjunto se aproxima a cero. ¿Qué significa esto para los comerciantes? Podría significar una serie de cosas, dependiendo de los datos de la media móvil se está considerando.

Si sólo se trata del precio de los valores, la media móvil podría ser un buen indicador del soporte. ¿Por qué? GM y HM dan mayor peso a los precios bajos. Esto podría significar, por ejemplo, que una ruptura del precio por debajo de estas medias tendría mayor importancia que una ruptura por debajo de una media móvil normal. Así pues, GM y HM podrían ser ingeniosos en el extremo de soporte de la mayoría de las acciones del precio. ¿Qué pasa con la resistencia? Podríamos obtener un equivalente especular tanto de GM como de HM a partir de las siguientes fórmulas:

HM’ = AM + (AM - HM)

GM’ = AM + (AM - GM)

Donde:

• HM' : Es la media armónica reflejada.
• GM' : Es el reflejo geométrico medio.
• AM, GM y HM : Son iguales que los anteriores.

Al introducir equivalentes especulares o reflejos de GM y HM, en cierto sentido estamos añadiendo un equilibrio a las medias, ya que las ponderaciones de estos reflejos se inclinarán hacia los valores más grandes en cualquier conjunto de valores cuya media se esté calculando. Esto también significa que, para responder a la pregunta sobre la resistencia, ahora podemos utilizar GM' o HM' como medias ponderadas de precios más altos para que sirvan como sustitutos más eficaces a la hora de definir el nivel de resistencia.

Para nosotros, la diferencia entre GM y HM es sólo de grado. Esto se debe a que ambos se ponderan hacia los valores más pequeños, con la diferencia principal de que HM tiene una mayor ponderación hacia cero que GM.

Implementaciones personalizadas

Ahora veremos cómo se pueden utilizar estas medias simples en MQL5 para aprovechar sus propiedades únicas. En primer lugar, la media aritmética básica. De estos 3 este es el más ordinario ya que toma los fundamentos mismos de los promedios sin ninguna modificación y la manera más simple de usar este promedio debería ser monitoreando los cruces de precios. Existen muchas aplicaciones de las medias móviles a la hora de seguir la estructura de los precios, y ésta es posiblemente la más sencilla y común. Así pues, esta aplicación se presenta aquí principalmente a efectos comparativos con los otros medios no tan comunes de MG y MH ya presentados anteriormente.

El análisis comparativo es una función esencial de los expertos configurados en el asistente de MQL5, especialmente en lo referente a las clases de señales. Cada clase de señal seleccionada en el asistente puede recibir una ponderación o "voto" que contribuye a definir las condiciones de compra y venta de un activo negociado. Gracias a los tipos de datos vectoriales, obtenemos fácilmente el búfer AM de esta función:

//+------------------------------------------------------------------+
//| Arithmetic Mean                                                  |
//+------------------------------------------------------------------+
double CSignalAM::AM(int Index, int Mask = 8)
{  vector _am;
   _am.CopyRates(m_symbol.Name(), m_period, Mask, Index, m_fast);
   return(_am.Mean());
}

Y también, podemos medir la brecha de precio actual, que es clave en el seguimiento de cruce de medias móviles, con esta función a continuación:

   double            CrossOver(int Index)
   {                 m_close.Refresh(-1);
      return(AM(Index) - m_close.GetData(Index));
   }

Normalmente, en los casos en los que se opera manualmente, tendría más sentido tener esto, así como el GM y HM codificados como un indicador personalizado. No estamos operando manualmente ya que esto es para un Asesor Experto, y por lo tanto una función que accede a los búferes de precios de clase incorporados estará bien.

La media HM, al igual que la GM, está ponderada hacia los valores más pequeños y, como hemos visto anteriormente, puede reflejarse para crear otra media, HM', que está ponderada hacia los valores más altos. Así pues, al ser medios ponderados hacia los extremos, HM y HM' se prestan a la capacidad de captar divergencias. Ahora bien, cuando se piensa en divergencias, lo primero que podría venir a la mente sería una diferencia de tendencia entre un oscilador y el precio de su valor. Estos combates se producen en periodos muy cortos y hay que estar atento para pillarlos. Alternativamente, podría ser una divergencia totalmente en los precios de un valor pero en diferentes marcos temporales, como una caída del precio en el marco temporal de una hora cuando en el marco temporal semanal existe una fuerte tendencia alcista.

Sin embargo, para sacar partido de los «sesgos» de la media armónica, nos fijaremos en las divergencias en los precios máximos y mínimos. Específicamente, buscaremos abrir posiciones sólo cuando el cambio en los precios altos sea diferente en dirección al cambio en los precios bajos. Esto, sin embargo, aún podría explorarse de dos maneras. O bien abriríamos una posición en máximos decrecientes y mínimos crecientes, o bien abriríamos en máximos crecientes y mínimos decrecientes. Para este artículo estamos explorando este último, pero como toda la fuente se adjunta al final de este artículo el lector puede personalizar esto y tratar de explotar la divergencia engulf más popular que no hemos mirado.

Por lo tanto, buscaremos una subida de la media armónica de los máximos que coincida con una caída de la media armónica de los mínimos para abrir posiciones. Un indicador de seguimiento para ayudar a guiar en la apertura de una posición larga o corta se puede personalizar aquí, pero lo que vamos a utilizar como seguimiento es simplemente el cambio en el precio de cierre. Si tenemos una subida en el precio de cierre, siguiendo una divergencia en la barra anterior, entonces vamos en largo y viceversa.

El código para ponerlo en práctica, como vimos con AM, también es doble. En primer lugar, tenemos la función HM y su espejo, que se presenta a continuación:

//+------------------------------------------------------------------+
//| Harmonic Mean                                                    |
//+------------------------------------------------------------------+
double CSignalHM::HM(int Index, int Mask = 8)
{  vector _hm, _hm_i;
   _hm_i.CopyRates(m_symbol.Name(), m_period, Mask, Index, m_slow);
   _hm = (1.0 / _hm_i);
   return(m_slow / _hm.Sum());
}
//+------------------------------------------------------------------+
//| Inverse Harmonic Mean                                            |
//+------------------------------------------------------------------+
double CSignalHM::HM_(int Index, int Mask = 8)
{  double _am = AM(Index, Mask);
   double _hm = HM(Index, Mask);
   return(_am + (_am - _hm));
}

Luego tenemos la función de divergencia, y esta es la siguiente:

   double            Divergence(int Index)
   {                 return((HM_(Index, 2) - HM_(Index + 1, 2)) - (HM(Index, 4) - HM(Index + 1, 4)));
   }

Al utilizar los vectores para copiar y cargar datos, el índice 'rates mask' es indispensable, ya que nos permite cambiar rápidamente entre varios precios (OHLC) y, al mismo tiempo, el uso de las funciones estadísticas incorporadas en el tipo de datos vectorial ahorra mucho código. Además, nuestras funciones de prueba para estas medias pitagóricas utilizan dos periodos de media móvil, un periodo rápido y un periodo lento. Esta es una práctica común, especialmente cuando se utiliza la estrategia de cruce para determinar los puntos de entrada y salida. Tanto para la media armónica como para la media geométrica, nos basamos en el periodo lento para calcular nuestros valores. Los periodos rápidos sólo se utilizan para el búfer de la media aritmética.

Esto, por supuesto, puede modificarse o ajustarse para adaptarse mejor a la estrategia y el enfoque de cada uno, pero aquí nos ceñimos a ello únicamente a efectos de prueba.

Por último, la media geométrica que al igual que la armónica se aplicará de forma similar a las Bandas de Bollinger. Es como si el armónico se inclinara más hacia los valores pequeños y en mayor medida. Es esta ponderación la que lo haría ideal para derivar un indicador similar a las Bandas de Bollinger ya que, como es bien sabido, las Bandas de Bollinger son una media móvil más 2 desviaciones estándar. Pero antes de llegar a la implementación, el código para obtener una media geométrica y su espejo (equivalente ponderado de alto valor) sería el indicado a continuación:

//+------------------------------------------------------------------+
//| Geometric Mean                                                   |
//+------------------------------------------------------------------+
double CSignalGM::GM(int Index, int Mask = 8)
{  vector _gm;
   _gm.CopyRates(m_symbol.Name(), m_period, Mask, Index, m_slow);
   return(pow(_gm.Prod(), 1.0 / m_slow));
}
//+------------------------------------------------------------------+
//| Inverse Geometric Mean                                           |
//+------------------------------------------------------------------+
double CSignalGM::GM_(int Index, int Mask = 8)
{  double _am = AM(Index, Mask);
   double _gm = GM(Index, Mask);
   return(_am + (_am - _gm));
}

Una vez más, estamos utilizando los tipos de datos vectoriales y sus funciones incorporadas para agilizar nuestro proceso de codificación. Los buffers de las bandas son dos, formados por una banda superior y otra inferior. Estos también se recuperan de las dos funciones que se indican a continuación:

   double            BandsUp(int Index)
   {  vector _bu;
      _bu.CopyRates(m_symbol.Name(), m_period, 2, Index, m_slow);
      return(GM_(Index, 2) + (2.0 * _bu.Std()));
   }

   double            BandsDn(int Index)
   {  vector _bd;
      _bd.CopyRates(m_symbol.Name(), m_period, 4, Index, m_slow);
      return(GM(Index, 4) - (2.0 * _bd.Std()));
   }

Las dos funciones simplemente devuelven el precio de la banda superior y el precio de la banda inferior para las funciones 'BandsUp' y 'BandsDn' respectivamente. Estos valores devueltos pueden reconstituirse fácilmente en búferes paralelos para analizarlos de varias formas. Simplemente los estamos utilizando de forma cruzada para establecer si potencialmente tenemos aperturas para posiciones largas o cortas. Para comprobar una posición larga, necesitaríamos la confirmación de que el precio ha cruzado la banda inferior desde abajo, es decir, que estaba por debajo de la banda inferior pero ahora está por encima. Del mismo modo, para comprobar si hay posiciones cortas, necesitaríamos confirmar un cruce de precios de la banda superior desde arriba, donde el precio había estado por encima de la banda superior pero en una barra de precios posterior ahora está por debajo.

Clases de señales personalizadas

Los tres promedios móviles pitagóricos (MAs) pueden integrarse en una sola clase con un parámetro adicional que permite seleccionar uno de ellos para utilizarlo en un Asesor Experto. Sin embargo, las implementamos como clases de señales separadas porque vamos a explorar la configuración del peso de las clases de señales mediante la realización de una optimización para la ponderación ideal de cada promedio con el fin de tener una idea de cuál de estas señales y, por extensión, cuál de los promedios, es más útil en la predicción y la colocación de órdenes con nuestro Asesor Experto.

Sin embargo, antes de hacernos una idea de la importancia relativa, puede ser diligente realizar primero pruebas independientes de cada clase de señal por su cuenta, de forma que los pesos relativos que obtengamos al final puedan servir como validación (o refutación) de estas primeras pruebas que habríamos realizado. Por lo tanto, comenzaremos desarrollando un Asesor Experto para cada uno de los 3 promedios y los probaremos de forma independiente para evaluar su propio rendimiento. Una vez que tengamos estos resultados, haríamos pruebas en un Asesor Experto que combine las tres medias que optimizaremos para las ponderaciones relativas de cada una de estas medias.

Para desarrollar una condición larga y corta para la clase de señal media aritmética, simplemente comprobaremos si hay un cambio en el valor de cruce devuelto por la función 'Crossover', cuyo código se comparte más arriba. Nuestro código de condición largo y corto son bastante breves, y ambos los compartimos a continuación:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalAM::LongCondition(void)
{  int result = 0;
   if(CrossOver(StartIndex()) > 0.0 && CrossOver(StartIndex()+1) < 0.0)
   {  result = int(round(100.0 * ((CrossOver(StartIndex()) - CrossOver(StartIndex()+1))/fmax(fabs(CrossOver(StartIndex()))+fabs(CrossOver(StartIndex()+1)),fabs(CrossOver(StartIndex()+1))+fabs(CrossOver(StartIndex()+2))))));
   }
   return(result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalAM::ShortCondition(void)
{  int result = 0;
   if(CrossOver(StartIndex()) < 0.0 && CrossOver(StartIndex()+1) > 0.0)
   {  result = int(round(100.0 * ((CrossOver(StartIndex()+1) - CrossOver(StartIndex()))/fmax(fabs(CrossOver(StartIndex()))+fabs(CrossOver(StartIndex()+1)),fabs(CrossOver(StartIndex()+1))+fabs(CrossOver(StartIndex()+2))))));
   }
   return(result);
}

Como siempre, parece que el quid viene a la hora de normalizar el valor del resultado en el caso de que tengas una señal potencial. Para AM utilizamos el cambio actual en los valores de cruce dividido por el mayor en magnitud de los valores de cruce anteriores. Evidentemente, esta es un área que se puede personalizar mucho y el lector es bienvenido a su propia implementación, esta elegida, sin embargo, tiende a sacar provecho de la media aritmética y por lo tanto se utiliza.

La condición de media armónica larga y corta utilizará a su vez las funciones de «Divergence» para filtrar posibles aperturas de posiciones largas y cortas. Tenemos las condiciones cortas y largas que se indican a continuación:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalHM::LongCondition(void)
{  int result = 0;
   m_close.Refresh(-1);
   if(Divergence(StartIndex()+1) > 0.0 && m_close.GetData(StartIndex()) > m_close.GetData(StartIndex()+1))
   {  result = int(round(100.0 * (Divergence(StartIndex()+1)/(fabs(Divergence(StartIndex()))+fabs(Divergence(StartIndex()+1))))));
   }
   return(result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalHM::ShortCondition(void)
{  int result = 0;
   m_close.Refresh(-1);
   if(Divergence(StartIndex()+1) > 0.0 && m_close.GetData(StartIndex()) < m_close.GetData(StartIndex()+1))
   {  result = int(round(100.0 * (Divergence(StartIndex()+1)/(fabs(Divergence(StartIndex()))+fabs(Divergence(StartIndex()+1))))));
   }
   return(result);
}

Con la media armónica, buscamos cualquier divergencia positiva en la que los máximos suben y los mínimos bajan, y esto va seguido de una subida del precio de cierre para una apertura alcista o de una bajada del precio de cierre para una apertura bajista. Estos dos acontecimientos se producen secuencialmente y no en la misma barra. Esta divergencia es, en muchos sentidos, lo contrario de la pauta envolvente más popular que presenta, por lo general, máximos decrecientes y mínimos crecientes.

Una vez que tenemos una apertura, ya sea larga o corta, la siguiente cuestión es determinar el valor entero del resultado que es siempre la salida para las condiciones larga y corta de estas funciones de clase de señal. Una vez más, hay varios enfoques que pueden adoptarse aquí para cuantificar el resultado y varios de estos enfoques podrían relacionarse con otros indicadores además de la media armónica. Sin embargo, para nuestros propósitos queremos apoyarnos aún más en la media armónica para establecer la cantidad del resultado, por lo que utilizamos una relación entre la divergencia actual y la magnitud de los valores anteriores para llegar a un valor entero en el rango de 0 a 100.

Por lo tanto, este resultado significa simplemente que cuanto mayor sea la divergencia actual, más alcistas o bajistas seremos. En el denominador de este resultado ratio (que normalizamos al rango 0 – 100 mediante porcentaje) están los valores de divergencia actuales y anteriores. Esto nos lleva a aplicar la media geométrica.

GM se implementa calculando los valores de las Bandas de Bollinger superior e inferior que se basan en los buffers del GM, como se compartió anteriormente. Para convertir esto en una señal de acción, buscaríamos un cruce de precios de banda inferior y un cruce de precios de banda superior para configuraciones alcistas y bajistas respectivamente, como se mencionó anteriormente. Esto se codifica de la siguiente manera en las condiciones largas y cortas:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalGM::LongCondition(void)
{  int result = 0;
   m_close.Refresh(-1);
   if(m_close.GetData(StartIndex()) > m_close.GetData(StartIndex() + 1) && m_close.GetData(StartIndex()) > BandsDn(StartIndex()) && m_close.GetData(StartIndex() + 1) < BandsDn(StartIndex() + 1))
   {  result = int(round(100.0 * ((m_close.GetData(StartIndex()) - m_close.GetData(StartIndex()+1))/(fabs(m_close.GetData(StartIndex()) - m_close.GetData(StartIndex()+1)) + fabs(BandsUp(StartIndex()) - BandsDn(StartIndex()))))));
   }
   return(result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalGM::ShortCondition(void)
{  int result = 0;
   m_close.Refresh(-1);
   if(m_close.GetData(StartIndex()) < m_close.GetData(StartIndex() + 1) && m_close.GetData(StartIndex()) < BandsUp(StartIndex()) && m_close.GetData(StartIndex() + 1) > BandsUp(StartIndex() + 1))
   {  result = int(round(100.0 * ((m_close.GetData(StartIndex()+1) - m_close.GetData(StartIndex()))/(fabs(m_close.GetData(StartIndex()) - m_close.GetData(StartIndex()+1)) + fabs(BandsUp(StartIndex()) - BandsDn(StartIndex()))))));
   }
   return(result);
}

El tamaño del resultado como hemos seguido con la media aritmética y la media armónica también se inclinará más por la media geométrica y no utilizar algún otro indicador. Así que, para ello, con GM, el resultado es una relación entre el cambio en el precio de cierre y la brecha entre las bandas superior e inferior de nuestras bandas de Bollinger derivadas. Una vez más, este resultado significa que un mayor movimiento del precio en relación con la compresión de la brecha de las bandas, debería indicar una mayor señal de entrada o cierre. Señal de cierre porque la condición larga y corta no sólo fijan los umbrales de apertura, sino que también determinan el umbral al que se cierran sus posiciones inversas. Así, en los ajustes de entrada, siempre tenemos un umbral de apertura y un umbral de cierre. Esta última debería ser inferior a la primera, ya que se desea cerrar las posiciones largas antes de tomar posiciones cortas y viceversa.

Además, las posibles implementaciones alternativas de las Bandas de Bollinger derivadas de GM para establecer una señal podrían considerar opciones que rastreen el tamaño de la brecha entre las bandas superior e inferior con la pendiente del promedio de referencia y algunas otras iteraciones. Nuestra aplicación aquí no es la única forma en que podríamos utilizar o mirar las Bandas de Bollinger.

Probador de estrategias y evaluación de resultados

Por lo tanto, primero vamos a realizar pruebas independientes con cada media móvil pitagórica por su cuenta en un Asesor Experto y una vez que tenemos los resultados independientes de cada uno hacemos una prueba de un Asesor Experto que se ensambla con las 3 señales de medias pitagóricas, y optimizamos este Asesor Experto para encontrar la ponderación relativa de cada una de nuestras medias.

Por uniformidad, realizaremos pruebas con un símbolo EURJPY en el marco temporal de 20 minutos para el año 2023. Para la media aritmética, obtenemos los siguientes resultados:

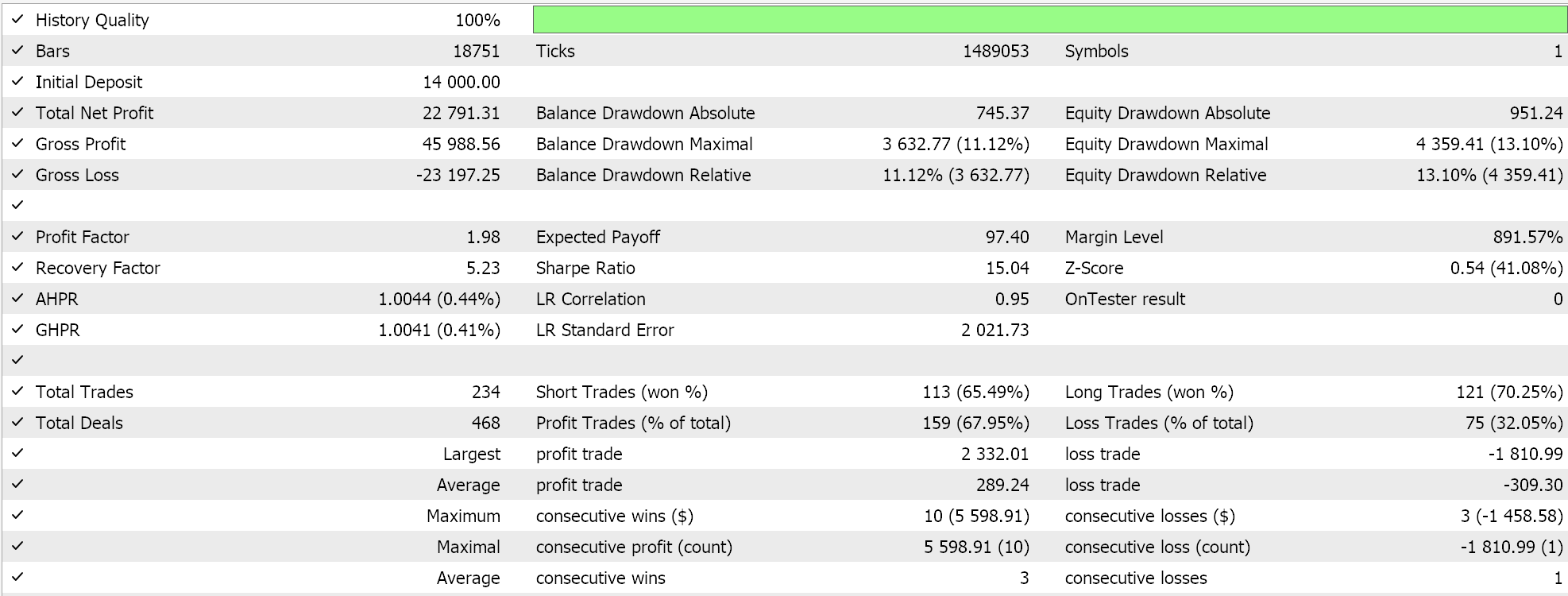
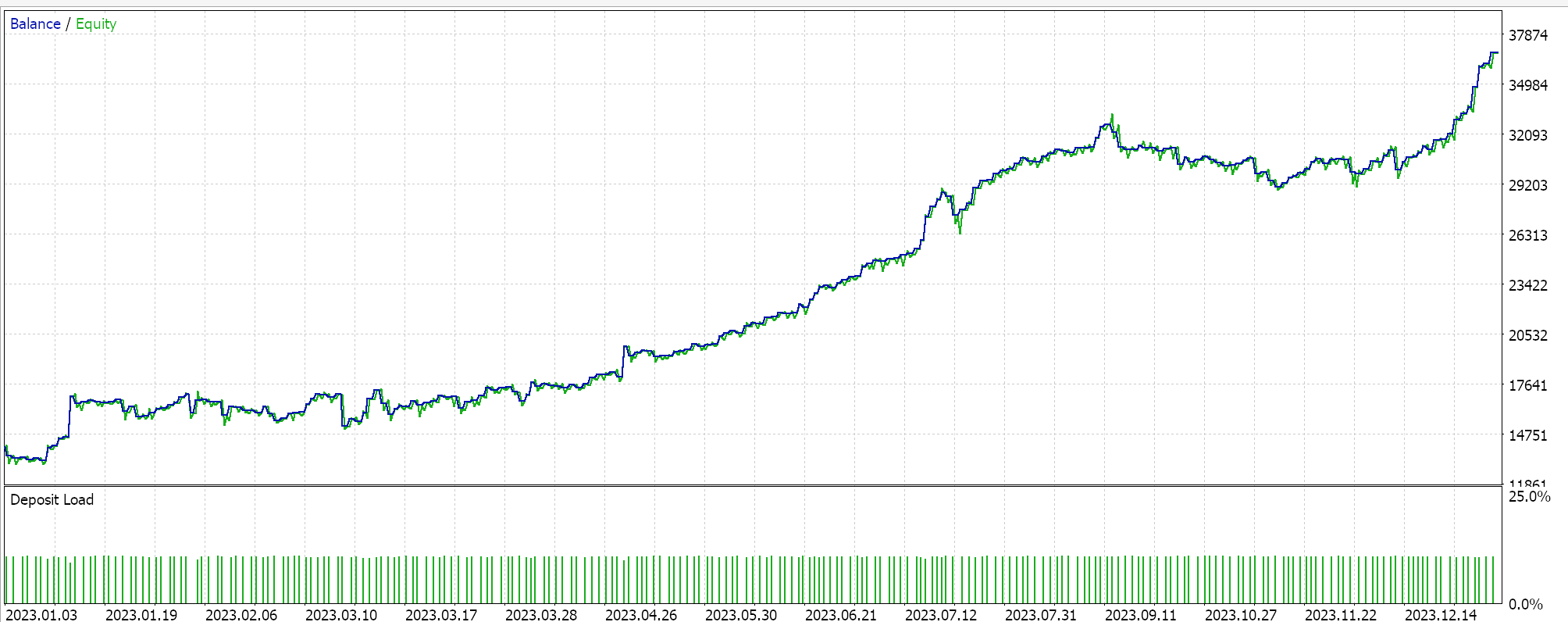
Para la media armónica, obtenemos lo siguiente:

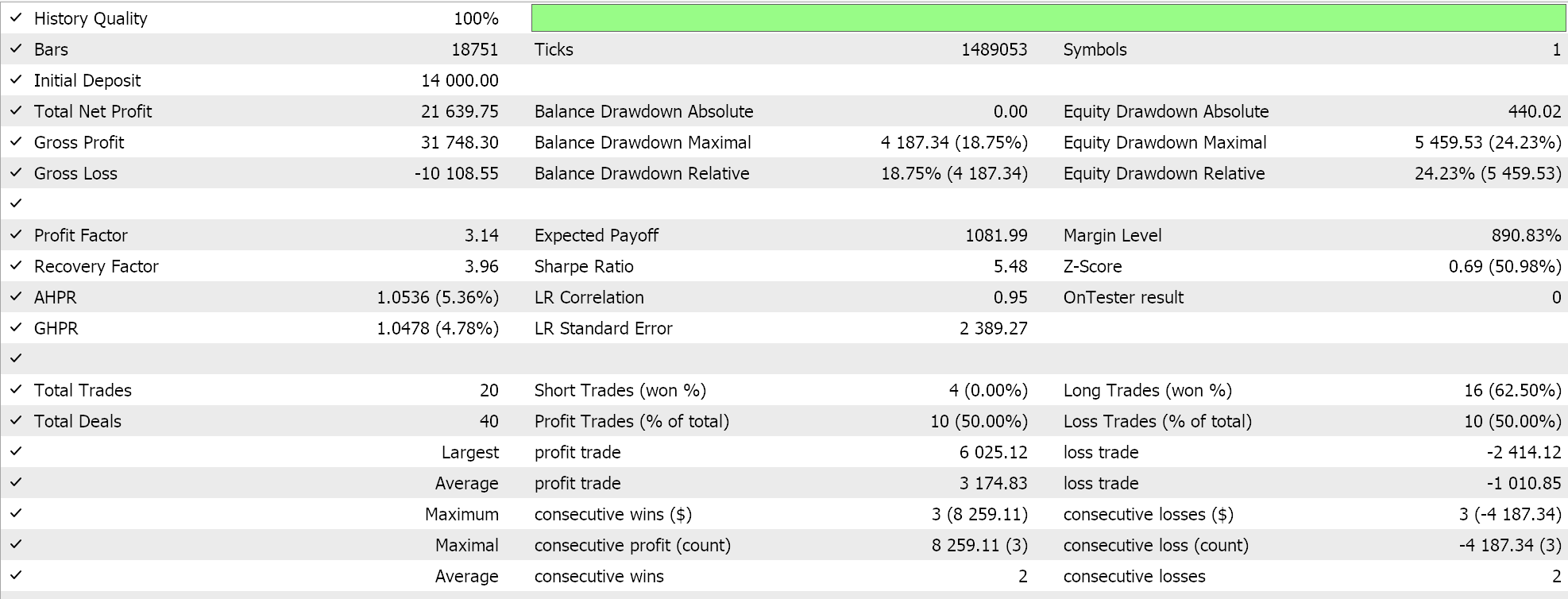
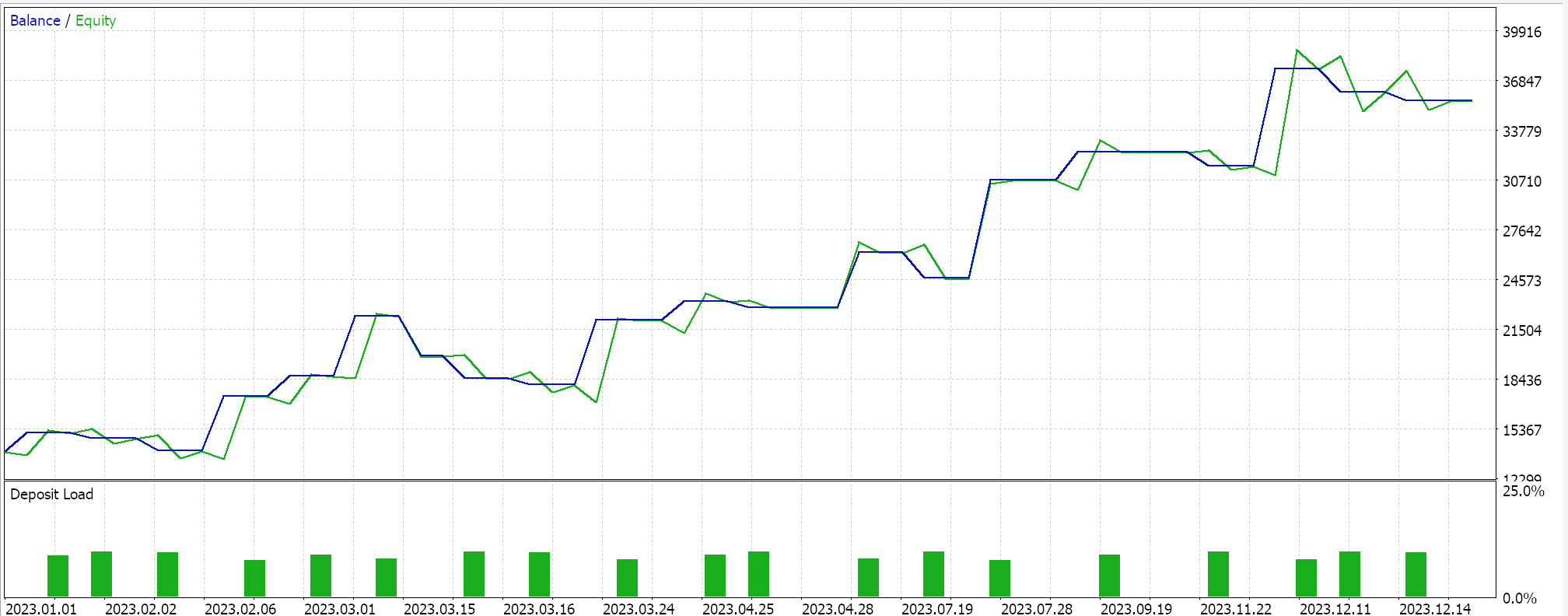
Y finalmente, para la media geométrica, tenemos:

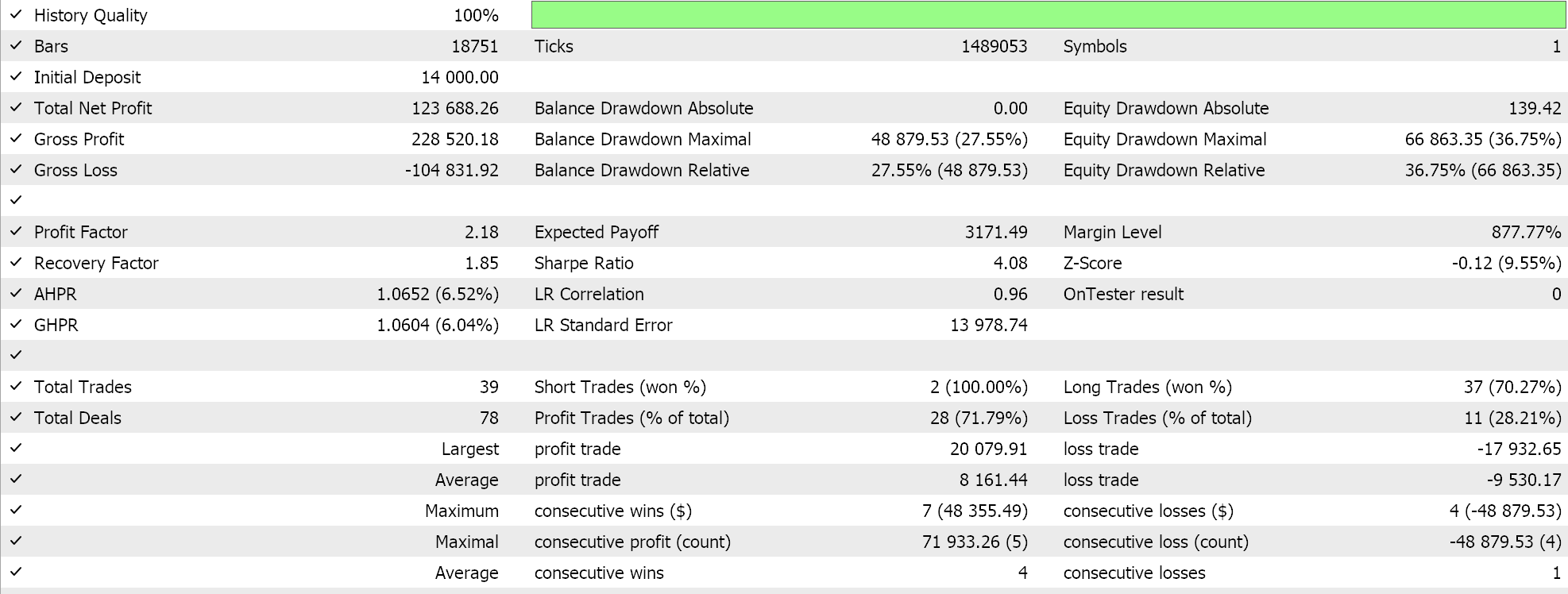
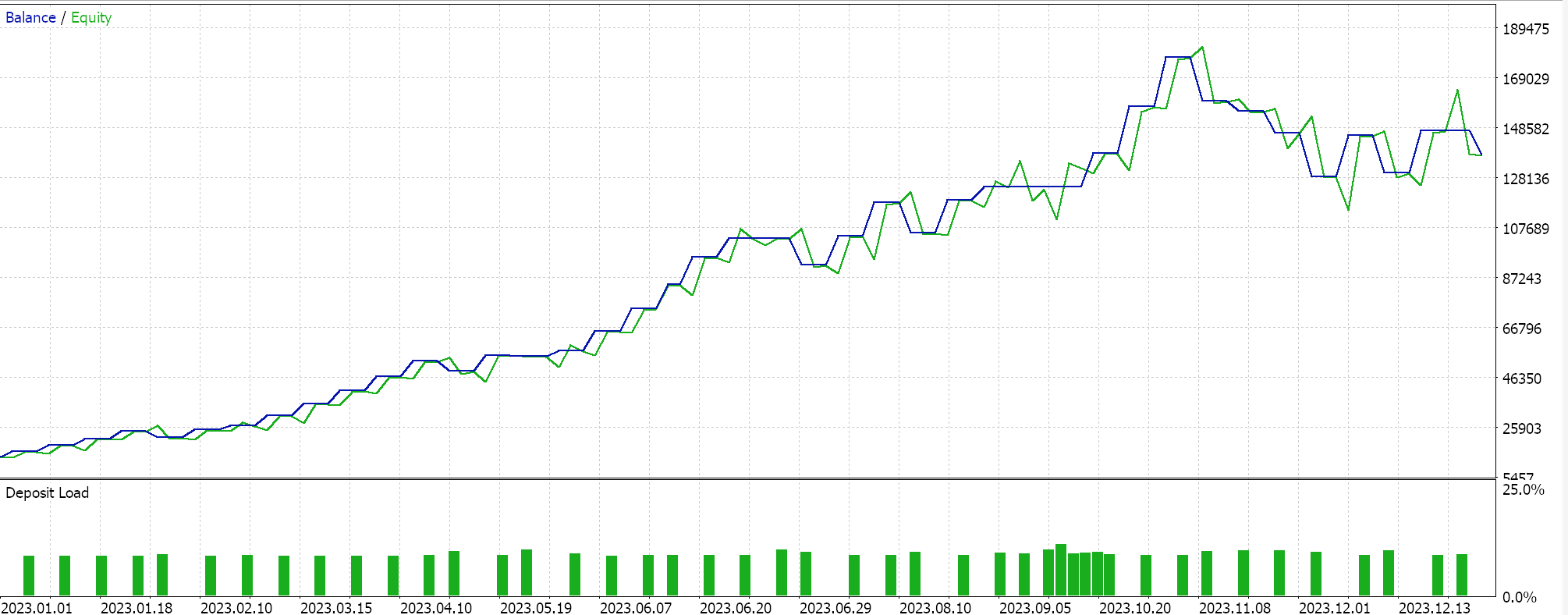
De los resultados independientes se desprende que la media geométrica tiene una gran influencia, seguida de la media aritmética cruzada simple y la divergencia armónica media. Por supuesto, nuestros resultados se ven influidos por el hecho de que estamos realizando pruebas en una ventana muy pequeña y hemos realizado personalizaciones específicas sobre cómo interpretamos e implementamos las señales de entrada para cada uno de los medios. Es evidente que se necesitan más pruebas para sacar conclusiones sobre el rendimiento relativo, pero lo que esto indica es una variabilidad relativamente amplia del rendimiento, lo que puede ser una señal prometedora en las pruebas preliminares.

Si ahora realizamos pruebas con las tres medias e intentamos optimizarlas para obtener una ponderación relativa, obtenemos como uno de nuestros mejores resultados el siguiente:

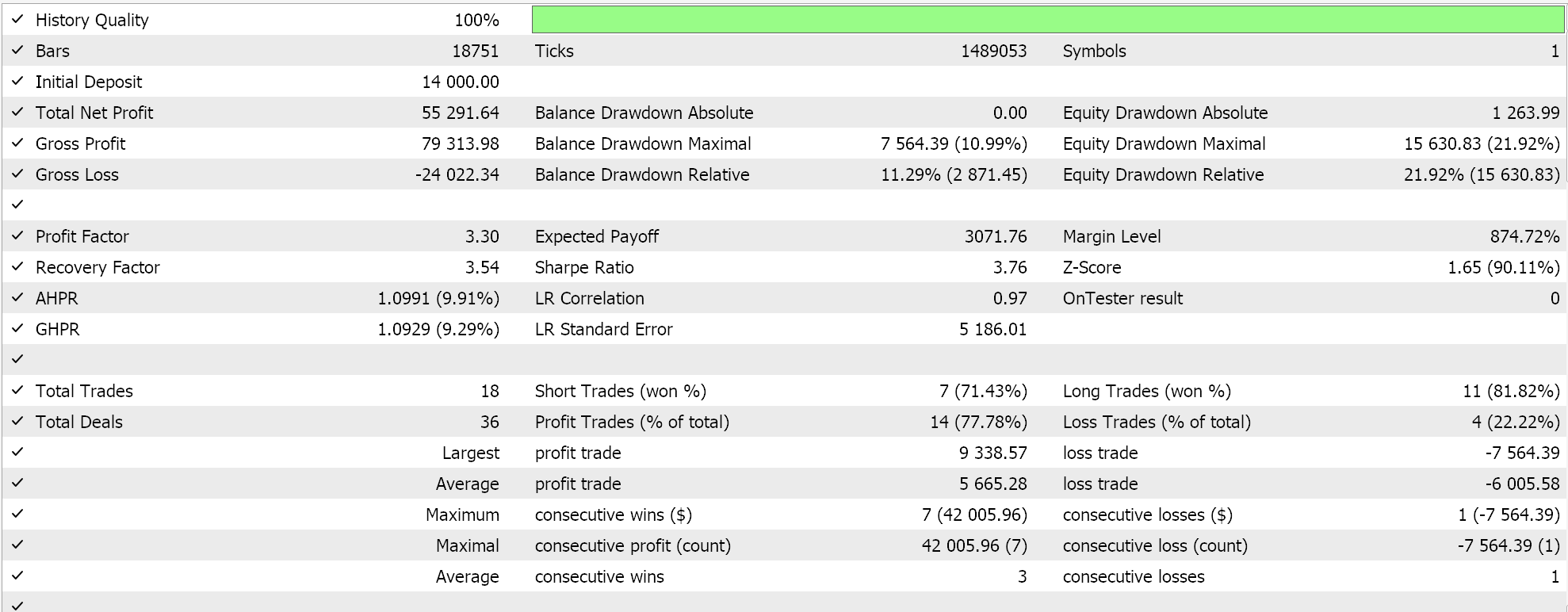
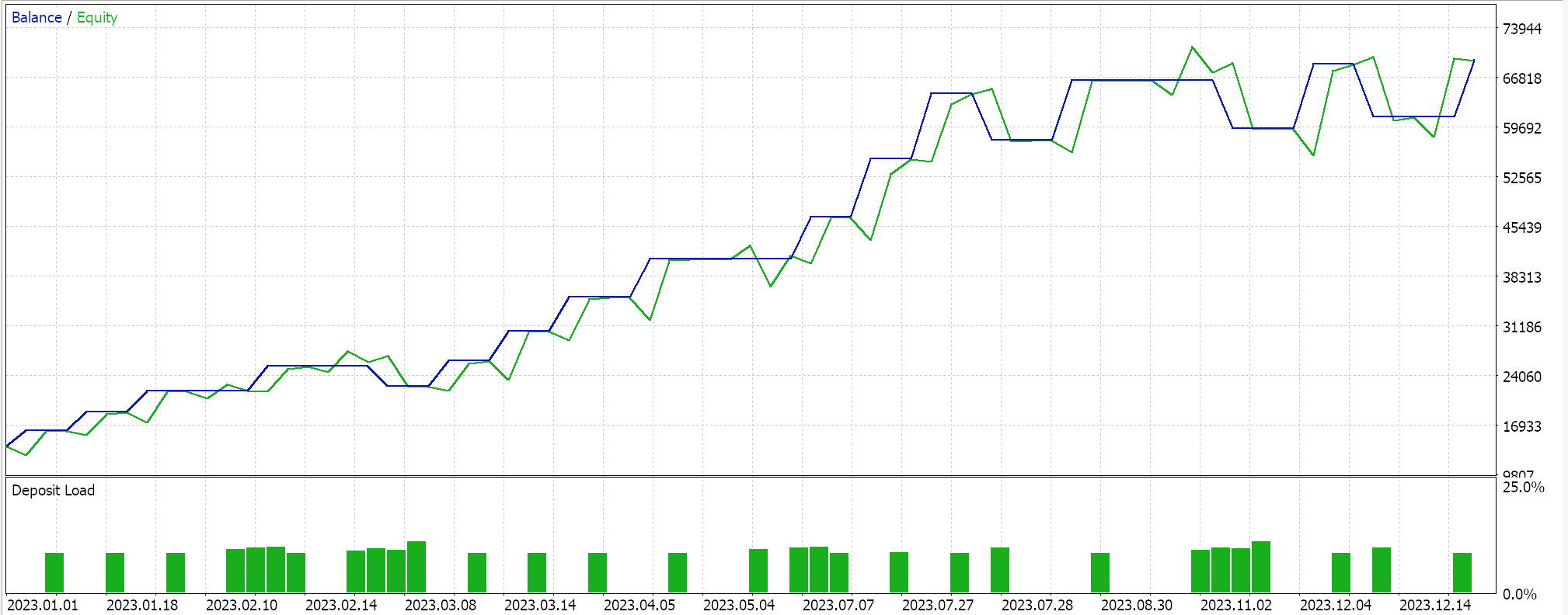
Evidentemente, los resultados independientes de la media geométrica siguen siendo el tiempo de la campana, por supuesto sujetos a pruebas durante periodos más largos. Curiosamente, o irónicamente, para que las 3 señales funcionen juntas, la que mejor funciona de forma independiente debe recibir la ponderación mínima de 0,4. Las medias armónica y aritmética tienen una ponderación mayor (1,0 y 0,9), lo que podría explicar por qué el rendimiento global de las tres medias combinadas no sólo es inferior al rendimiento independiente de la media geométrica, sino que el rendimiento del GM sigue siendo mejor incluso si se suman los rendimientos independientes de las medias aritmética y armónica. Los ajustes para la combinación del Asesor Experto se comparten a continuación:

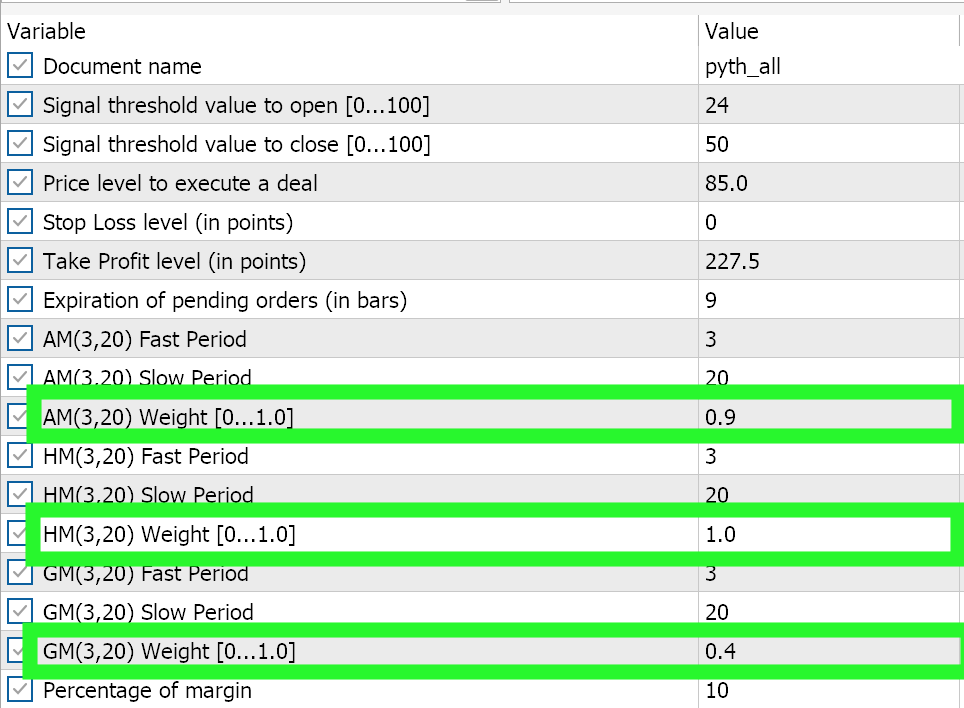
Conclusión

El rendimiento pasado no garantiza los resultados futuros y, como ya se ha mencionado, siempre está justificado realizar pruebas exhaustivas, preferiblemente durante periodos más largos, y es más seguro que hacerlo con pocas pruebas, como las de un año que tenemos aquí. Como siempre, montamos el código adjunto para estas señales siguiendo las pautas compartidas en los artículos aquí y aquí. La media geométrica que está más ponderada a valores más pequeños de las tres medias consideradas en este artículo se muestra prometedora en el entorno de las Bandas de Bollinger, sin embargo no hemos examinado la media armónica en un entorno de bandas similar para tener conclusiones más definitivas sobre este rendimiento relativo. Y también, además de las Bandas de Bollinger, el cruce AM o la divergencia HM existen otras implementaciones de medias móviles en forma de oscilador como la OSMA o la TRIX que no hemos explorado. Estos y otros métodos pueden tenerse en cuenta a la hora de sopesar el potencial relativo de las medias pitagóricas.