Rede neural na prática: Grafico da Rectifier

Introdução

No artigo anterior Rede neural na prática: Surgimento de C_Neuron, começamos a fazer as coisas de uma forma um tanto quanto mais organizadas. Visto que começamos a construir uma classe, cujo objetivo é conter tudo que será preciso colocar dentro de um neurônio. Isto para que no futuro, possamos ligar diversos neurônios em uma arquitetura. Cujo intuito será de fato construir uma pequena rede neural simples. Nada do estilo ChatGPT ou coisa do gênero. O objetivo aqui, é apresentar e mostrar para entusiastas de redes neurais. Como elas funcionam por debaixo dos panos. Sem usar nenhum artifício extra. Programando as coisas nos mesmos.

Pois bem, nosso primeiro neurônio básico, já consegue fazer algumas coisas. Visto que ele consegue convergir em muitas das situações simples nas quais podemos experimentar ele. Como ele já nos permite mudar de forma extremamente simples e rápida, a quantidade de entradas. Isto o torna bem mais interessante, para que pensemos em diversas possíveis aplicações para ele. No entanto, ele ainda se encontra em sua fase mais inicial. Não tendo em seu modelo, nenhum tipo de função de ativação, e tão pouco um formato que nos permita colocar os neurônios em cascata. Formando assim uma fila de neurônios, e por consequência uma pequena rede neural.

Mas antes de vermos isto, precisamos falar de um outro tema. Então aqui vamos começar a falar um pouco sobre funções de ativação. Estas funções, muitas das vezes são muito mal utilizadas por grande parte dos iniciantes. Isto quanto o tema envolvido é rede neural. E o motivo para serem mal utilizadas, se deve ao fato, de que elas são mal compreendidas. E muitas das vezes muito mal explicadas em termos gerais.

Algumas pessoas, simplesmente dizem para se usar esta ou aquela função de ativação. O que já é algo errado de se fazer. Mas o pior, é o fato de quem está usando tais funções, não tem se quer o mínimo conhecimento matemático da coisa. E ao ver que sua rede neural, parou de aprender, não consegue entender por que. E acaba tomando más decisões justamente pela falta do conhecimento matemático envolvido.

O que irei explicar neste artigo, e muito provavelmente serão necessários outros. É justamente o que acontece dentro da função de ativação. Isto de maneira que você, meu caro leitor, consiga compreender. Quando, por que e como usar e selecionar a função de ativação mais adequada. Pois cada caso é um caso. Não existe uma receita de bolo. Algo que você deverá sempre fazer, ou sempre utilizar. Mas para conseguir fazer as melhores escolhas, é preciso que você compreenda como cada uma das funções de ativação funcionam. E qual o impacto dela em toda a rede neural. Isto de uma forma geral.

Muito bem, como existem dezenas, e isto literalmente, de funções de ativação. Irei mostrar apenas algumas. Pelo menos as mais populares, ou as que são usadas na maior parte dos casos. Então, não fique pensando que existem apenas as que forem mostradas e explicadas. Procure se informar sobre expressões, ou equações matemáticas que podem ser usadas como funções de ativação. Mas irei pelo menos lhe dar uma base, para que você consiga compreender pelo menos o básico sobre este assunto. Do qual muitos gostam de falar, mas poucos de fato entendem como realmente funciona.

Entendendo o problema

Existe um problema em se tentar explicar certas coisas. Não por ser complicado. Longe disto. Muitas das vezes, o problema é o fato de que precisamos entender diversas coisas aparentemente isoladas, mas que fazem parte de um todo. E esta questão sobre funções de ativação, assim como a propagação reversa, que irei falar mais para frente. É um destes temas. É muito complicado explicar como funciona, sem que entremos em alguns assuntos que talvez ainda não foram devidamente abordados.

Então de forma bem resumida, a função de ativação, serve para recortar e modificar a reta secante que estará sendo construída pela função de custo. Basicamente é isto. Parece maluquice dizer tal coisa. Mas a função de ativação não tem outra finalidade, se não está que acabo de falar. E não, a função de custo não usa a reta tangente, ela usa a reta secante, já expliquei isto em outros artigos. Mas esta é a parte fácil da explicação. A parte complicada é mostrar como ela, a função de ativação faz este tipo de coisa. E por que em alguns casos você de fato irá precisar da função de ativação. Enquanto em outros casos, ela pode ser perfeitamente ignorada. Diferente do que muitos dizem, que é o fato de você sempre precisar usar alguma em uma rede neural.

Ok. me parece bastante razoável que a explicação fique focada em mostrar este tipo de coisa acontecendo. Mas existe um outro problema. E este surge pelo fato de estarmos usando o gradiente descendente, no lugar do mínimo quadrado. Este problema será um tanto melhor abordado quando formos ver a questão da propagação reversa. Mas ele já nos traz algum tipo de cuidado a ser tomado já na função de ativação. E que problema é este? Bem, a origem do problema são as derivadas.

Mas como assim? As derivadas não servem para tornar a função de custo menos dispendiosa em termos de custo computacional? Sim, meu caro leitor. Porém, quando usamos derivadas na função de custo, precisamos nos preocupar com os efeitos dela na função de ativação. Mas como eu falei a pouco, este problema nos atinge mais fortemente é na propagação reversa. Ali é onde o uso das derivadas realmente pega. Isto por que se você fizer a escolha errada da função de ativação. Chegará um momento em que o neurônio, ou melhor dizendo a rede neural, simplesmente irá estagnar. Não conseguindo mais convergir devido a uma falha matemática. Ou seja, você acha que sabe o que está fazendo. E sua rede neural, simplesmente para de funcionar. Justamente por conta da falta de conhecimento matemático sobre o assunto.

Então, o que irei explicar aqui, apenas se aplica, quando usamos derivadas na função de custo. Se você não estiver usando derivadas, grande parte do que será explicando não se aplicará na sua rede neural. Entendido isto, podemos começar a ver as coisas de uma forma, que tentarei ser o mais didático quanto for possível. O grande detalhe é que terá bastante matemática envolvida na explicação. Então quem não curte matemática, com toda a certeza irá odiar este tema. Mas infelizmente, redes neurais são assim. É muita matemática e quando você acha que está terminando, começa tudo de novo. Só que com ainda mais matemática envolvida.

Mas explicar as coisas usando pouca matemática é quase impossível. Mas vamos começar com uma função de ativação bem simples, cuja matemática envolvida é igualmente simples. Assim você, meu caro leitor, não fica apavorado e com medo das próximas coisas que iremos ver.

A função de ativação Rectifier

Bem, a primeira função de ativação que vamos ver é a Rectifier, mais conhecida popularmente como ReLU. Mas por que do nome ReLU? Bem, ele vem do nome completo, que seria: REctifiedLinearUnit. As letras em maiúsculo, é justamente as usadas no nome. Por isto ReLU. Ela tem um objetivo bem simples. Remover todos os valores negativos de dentro da rede neural. Simples assim. Valores negativos em alguns momentos são algo que mais atrapalha do que nos ajuda. E em outros eles são essenciais para uma perfeita convergência dos parâmetros dentro da rede neural. Se a sua rede específica estiver tendo problemas por conta de valores negativos presentes nela. Você pode usar a ReLU para os remover. Sua formula é vista logo abaixo.

Cara mais é só isto a função de ativação? Sim, meu caro leitor. Porém ela tem um problema, se você estiver usando derivadas na função de custo. Um detalhe: Toda vez em que for dito derivadas, você deverá subentender de que estou me referindo a função de custo. Salvo o fato de eu mencionar alguma outra coisa. Isto para não ficar repetindo diversas vezes o mesmo termo.

Mas voltando ao assunto. Se você entende o básico sobre derivadas sabe que não é possível criar uma derivada na posição zero. E este é um dos pontos que surge na ReLU. Todo e qualquer valor negativo, será sempre convertido automaticamente para zero. E no momento em que tivermos de calcular a derivada neste ponto, surge um problema. Novamente o problema não é gerado agora, e sim durante a propagação reversa.

Agora a derivada desta função é muito simples. Na verdade, é uma das mais simples entre as funções de ativação. A equação é mostrada abaixo.

Nesta expressão acima, temos o resultado da derivada. Mas note o seguinte, estamos definindo o valor para x menor que zero e para x maior que zero. O que acontece quando x for igual a zero? Bem, neste caso o valor seria indefinido. Mas em computação, não temos como trabalhar com isto. Então precisamos recorrer a um pequeno truque, ou trapaça. Quando o valor de x for igual a zero, dizemos qual é a derivada. Normalmente, se define ela como sendo zero. Mas isto não indica que de fato seja zero. Apenas é um truque usado na computação. Ok, esta foi a parte da explicação matemática. Mas como programadores, não nos interessa estas escritas matemáticas. Na verdade, algumas parecem hieróglifos de tão confusas e complicadas de se ler. Me desculpem os matemáticos de plantão. Mas não resistir a piada.

Muito bem, agora para tornar a coisa um tanto quanto mais didática. Vamos implementar um pequeno indicador, para que possamos estudar estas funções, de uma forma um tanto mais fácil de entender. Vendo-as sendo mostradas em um gráfico. Assim, acredito que ficará bem mais simples de entender o que estará acontecendo. Aqui poderíamos usar diversas linguagens para criar os gráficos. Mas como o propósito é fazer tudo em MQL5, vamos fazer isto em MQL5 puro. Vai ser interessante. Mas para separar um pouco as coisas, vamos ver isto em um novo tópico.

Plotando os gráficos das funções

Como muita gente, tem uma grande dificuldade em olhar uma equação ou expressão matemática e a entender. Acredito que mostrar isto em forma gráfica, fica consideravelmente mais didático. Já que você pode simplesmente estudar tanto o gráfico, como também o código usado para criar o mesmo. Os códigos que serão vistos, têm como objetivo, justamente promover esta interpretação mais simples do que a equação matemática representa.

Legal, tendo isto em mente, vamos ver o código inicial para nosso indicador. Ele é visto logo abaixo.

001. //+------------------------------------------------------------------+
002. #property copyright "Daniel Jose"
003. #property indicator_chart_window
004. #property indicator_plots 0
005. //+------------------------------------------------------------------+
006. #include <Canvas\Canvas.mqh>
007. //+------------------------------------------------------------------+
008. #define def_Limit   10.0
009. #define def_Step    0.5
010. //+------------------------------------------------------------------+
011. CCanvas *canvas;
012. //+------------------------------------------------------------------+
013. struct st_00
014. {
015.     int     x,
016.             y,
017.             maxX,
018.             maxY;
019.     double  Position;
020. }global;
021. //+------------------------------------------------------------------+
022. void PlotTextPosition(void)
023. {
024.     uint w, h;
025.     string sz0;
026. 
027.     sz0 = StringFormat("Position: [%.1f]", global.Position);
028.     TextGetSize(sz0, w, h);
029.     (*canvas).TextOut(global.x - (w / 2), global.maxY + 5, sz0, ColorToARGB(clrBlack)); 
030. }
031. //+------------------------------------------------------------------+
032. void Function_Curve(void)
033. {
034. }
035. //+------------------------------------------------------------------+
036. void UpdateGraphics(int direct)
037. {
038.     double value = global.Position + def_Step * direct;
039. 
040.     global.Position = MathAbs(value) <= def_Limit ? value : global.Position;
041. 
042.     (*canvas).Erase(ColorToARGB(clrWhite, 255));
043. 
044.     (*canvas).LineVertical(global.x, 0, global.maxY, ColorToARGB(clrRoyalBlue, 255));
045.     (*canvas).LineHorizontal(0, global.maxX, global.y, ColorToARGB(clrRoyalBlue, 255));
046. 
047.     PlotTextPosition();
048.     Function_Curve();
049. 
050.     (*canvas).Update(true);
051. }
052. //+------------------------------------------------------------------+
053. void Resize(void)
054. {
055.     uint w, h;
056.    
057.     global.maxX = (int)ChartGetInteger(0, CHART_WIDTH_IN_PIXELS, 0);
058.     global.maxY = (int)ChartGetInteger(0, CHART_HEIGHT_IN_PIXELS, 0);
059. 
060.     if (canvas != NULL)
061.     {
062.         (*canvas).Destroy();
063.         delete canvas;
064.     }
065.     canvas = new CCanvas;
066.     (*canvas).CreateBitmapLabel("BL", 0, 0, global.maxX, global.maxY, COLOR_FORMAT_ARGB_NORMALIZE);
067.     global.x = global.maxX / 2;
068.     global.y = global.maxY / 2;
069.     TextGetSize("M", w, h);
070.     global.maxY -= (int)(h * 2);
071. }
072. //+------------------------------------------------------------------+
073. int OnInit()
074. {      
075.     ZeroMemory(global);
076.     canvas = NULL;
077. 
078.     return INIT_SUCCEEDED;
079. }
080. //+------------------------------------------------------------------+
081. int OnCalculate(const int rates_total, const int prev_calculated, const int begin, const double &price[])
082. {
083.    return rates_total;
084. }
085. //+------------------------------------------------------------------+
086. void OnChartEvent(const int id, const long &lparam, const double &dparam, const string &sparam)
087. {
088.     int direct = 0;
089. 
090.     switch (id)
091.     {
092.         case CHARTEVENT_CHART_CHANGE:
093.             Resize();
094.             break;
095.         case CHARTEVENT_KEYDOWN:
096.             if (TerminalInfoInteger(TERMINAL_KEYSTATE_LEFT)) direct = -1;
097.             if (TerminalInfoInteger(TERMINAL_KEYSTATE_RIGHT)) direct = 1;
098.             break;
099.     }
100.     UpdateGraphics(direct);
101. }
102. //+------------------------------------------------------------------+
103. void OnDeinit(const int reason)
104. {
105.     (*canvas).Destroy();
106.     delete canvas;
107. }
108. //+------------------------------------------------------------------+

Este código é o esqueleto básico do que precisaremos e usaremos. No exato momento, ele não faz grandes coisas. Apenas cria o que seria a representação de um plano cartesiano no gráfico. E nos mostra um pequeno texto. Além é claro de nos permitir interagir com o gráfico de alguma forma. Coisa bem simples e básica mesmo. Mas para quem olhando este código não consegue compreender como ele funciona. Vamos dar uma rápida passada explicando os principais pontos do mesmo. Assim ficará mais simples de você, meu caro leitor, que possivelmente possa ser um entusiasta e está chegando neste artigo de paraquedas. Venha a conseguir entender o que estamos fazendo neste código mais simples.

Basicamente, em todo este código, existem dois pontos nos quais você poderá modificar, caso deseje fazer isto. Existe um outro ponto, mas isto será visto depois. Mas a princípio, você não precisará mudar nada.

Mas se for mexer, lhe oriento a mexer nos seguintes pontos: O primeiro é o valor que está sendo definido na linha oito. E o segundo, é o valor que está sendo definido na linha nove. Estes são valores usados para promover o deslocamento de um indicador que será colocado no gráfico depois. Basicamente são somente estes dois pontos que você pode pensar em mexer neste momento.

Então vamos dar uma rápida passada pra entender outros detalhes deste código. Na linha 11 defino uma variável que será usada para acessar a biblioteca padrão do MQL5. Note que estou definindo como um ponteiro, a tal variável. E isto tem um motivo. Definindo-a desta forma, consigo testar posteriormente se estamos ou não com o gráfico inicializado.

Na linha 13 definimos uma estrutura global. Cujo objetivo é promover um acesso mais controlado a determinadas variáveis. Já na linha 22, temos um procedimento, para nos permitir plotar alguma informação em forma de texto. Neste ponto, apenas iremos plotar o valor da posição atual. Na linha 32, temos um procedimento que será visto depois. Porém ele irá ser dependente do que iremos colocar no gráfico. Já na linha 36, temos um procedimento para atualização do gráfico conforme efetuamos algum tipo de mudança no mesmo. Algo bem simples e que não exige tantas explicações.

Agora na linha 53, temos um procedimento um tanto quanto curioso. Basicamente ele serve para ajustar as dimensões do objeto bitmap que estamos usando. Isto via biblioteca padrão. Todo o procedimento é bastante simples. Porém na linha 60, fazemos um teste. Isto para checar se a classe CCanvas está ou não sendo instanciada pela aplicação. Caso esteja, iremos remover ela do gráfico, e logo depois na linha 65, inicializar o ponteiro, para poder instanciar a classe. Este é o motivo pelo qual estou usando um ponteiro, na declaração da linha 11. Mas por que estou fazendo isto? Bem, para entender é preciso entender como o indicador é de fato lançando pelo MetaTrader 5.

Ao dizer ao MetaTrader 5, que queremos adicionar o indicador no gráfico. O MetaTrader 5, irá começar a executar o código pela função OnInit. Esta está presente na linha 73. Nesta função iniciamos as coisas. Como na linha 75, onde iniciamos os valores globais, garantindo que todos estarão em zero. E na linha 76, dizemos que o ponteiro está como nulo. Ou seja, não está sendo instanciado. Uma vez feito isto, o MetaTrader 5, irá disparar um novo evento, este será capturado pela função da linha 86. O primeiro evento, é um CHARTEVENT_CHART_CHANGE, que diz a todas aplicações presentes no gráfico, de que algo mudou. Como este evento está sendo capturado pela nossa aplicação, iremos na linha 93, chamar o procedimento da linha 53. E é neste momento em que iremos começar a instanciar a classe CCanvas da biblioteca padrão. Já que na linha 65 iremos fazer a construção da mesma.

Ok, mas precisava de toda esta complicação? Na verdade, isto não se trata de uma complicação. Já que se você mudar as dimensões do gráfico. O MetaTrader 5 irá novamente disparar o evento CHARTEVENT_CHART_CHANGE, com isto, conseguimos manter sempre um dimensionamento correto. Sem precisar ficar testando as coisas a todo momento. Mas voltando as explicações, na linha 81 temos o tratador de eventos OnCalculate. Ele não fará nada, mas é necessário declaramos ele por conta de estarmos usando uma aplicação do tipo indicador. Na linha 86, temos o tratador de eventos de OnChartEvent. Como já vimos ele é usado na inicialização ou mudança no gráfico. Mas também é usado para capturar as setas para a direita e para a esquerda. Mudando assim a posição que será vista em breve.

Já na linha 103 temos o procedimento cujo objetivo é tratar o evento Deinit, que removerá qualquer coisa que foi colocada pela aplicação e que não deverá permanecer no gráfico. Se você compilar este código e o lançar em algum gráfico. Irá ver a animação abaixo, quando pressionar as setas para a direita e esquerda.

Muito legal esta ideia. Já que agora tudo que precisaremos fazer, será definir a expressão ou equação a ser mostrada no gráfico. Daí podemos sem mudar basicamente nada no código. Visualizar a equação. Mas existe uma questão interessante neste ponto. Precisamos descrever a equação em termos de código. Não na forma matemática. Apesar de que se fizermos uma programação voltada para isto. Poderemos sim, escrever a formula como ela se apresenta normalmente em livros e literatura matemática. Mas como o objetivo aqui, é apenas mostrar certos detalhes, não vamos ir tão longe assim. Vamos ficar em um nível mais básico da coisa toda.

Bem, agora precisamos pensar em como vamos apresentar as curvas no gráfico. Ou seja, devemos colocar algum código dentro do procedimento da linha 32. Esta talvez seja a parte realmente interessante. Já que podemos fazer isto de diversas maneiras diferentes. Mas como quero usar o mínimo possível de código. Iremos fazer isto usando um mecanismo, que eu usava lá no início de minha vida como programador. É um mecanismo relativamente simples, porém nos permite fazer diversas coisas com um mínimo de esforço. Mesmo em equipamentos mais modestos.

Vamos então ver como será feito a plotagem das curvas, que não serão tão suáveis no começo. Mas você verá que podemos ir muito além, tudo irá depender do que se deseja fazer. Lembrando que para tornar as curvas mais suáveis, bastará que você mude os valores presentes nas linhas oito e nove. Mas logo você entenderá melhor isto. Vamos então ao código. E como apenas e somente ele será diferente, para cada uma das funções de ativação, que serão mostradas. Irei separar isto em blocos, ou tópicos. Assim vamos ver a primeira das funções no tópico abaixo.

Plotando a ReLU e sua derivada

O código para plotar tanto a função de ativação ReLU, quanto a sua derivada é visto logo abaixo.

31. //+------------------------------------------------------------------+
32. void Function_Curve(void)
33. {
34.     int x[], y[], d[];
35.     uint p;
36.     double fx, step;
37.     
38.     ArrayResize(x, (int)(((def_Limit * 2) / def_Step) + 1));
39.     ArrayResize(y, x.Size());
40.     ArrayResize(d, x.Size());
41. 
42.     step = MathMin(global.maxY, global.maxX) / (x.Size() * 1.0) / def_Step;
43. 
44.     fx = -def_Limit;
45.     for (uint c = 0, m = x.Size(); c < m; c++, fx += def_Step)
46.     {
47.         p = (fx <= global.Position ? c : p);
48.         x[c] = global.x + (int)(step * fx);
49.         y[c] = global.y - (int)(step * MathMax(0, fx));
50.         d[c] = global.y - (int)(step * (fx <= 0 ? 0 : 1));
51.     }
52. 
53.     (*canvas).PolylineThick(x, y, ColorToARGB(clrIndigo, 255), 3, STYLE_SOLID, LINE_END_ROUND);
54.     (*canvas).PolylineThick(x, d, ColorToARGB(clrDarkOrange, 255), 3, STYLE_SOLID, LINE_END_ROUND);
55. 
56.     (*canvas).FillCircle(x[p], y[p], 5, ColorToARGB(clrForestGreen, 255));
57.     (*canvas).FillCircle(x[p], d[p], 5, ColorToARGB(clrFireBrick, 255));
58. 
59.     ArrayFree(d);
60.     ArrayFree(y);
61.     ArrayFree(x);
62. }
63. //+------------------------------------------------------------------+

Muito bem, aí está um lindo e magnifico código. Parece até mesmo algo divino. Já que ele está de fato fazendo as coisas com muito pouco código precisando realmente ser criado. E tudo isto de maneira super simples e fácil de entender. Mas principalmente fácil de ser explicado, sendo assim bastante didático. Mesmo que não seja tão eficiente em termos de execução. Então vamos ver o que está sendo feito aqui. Mas antes que tão ver o resultado da execução. Esta pode ser vista na animação logo abaixo.

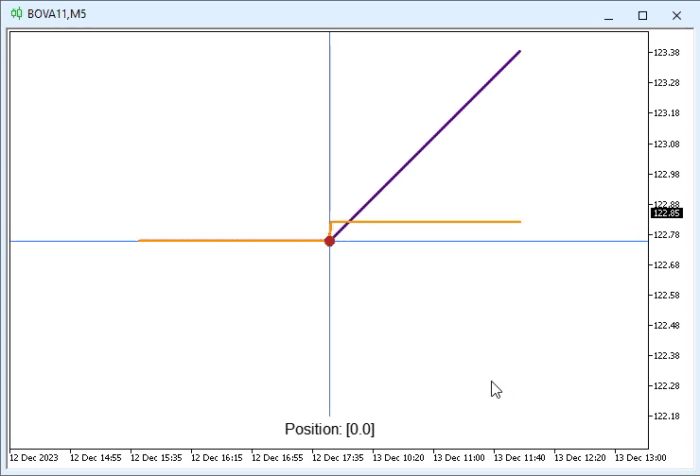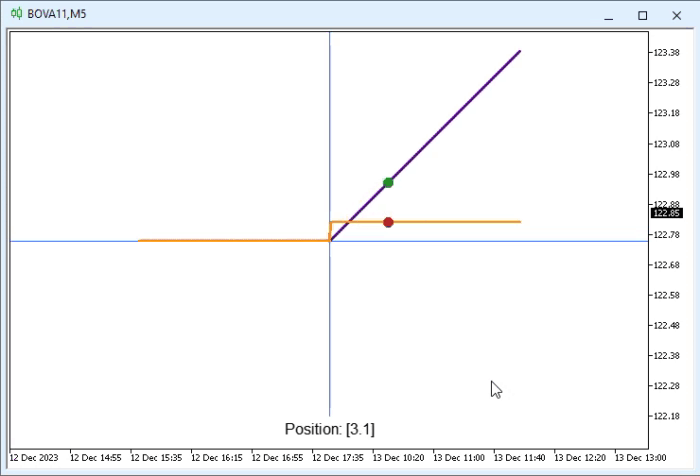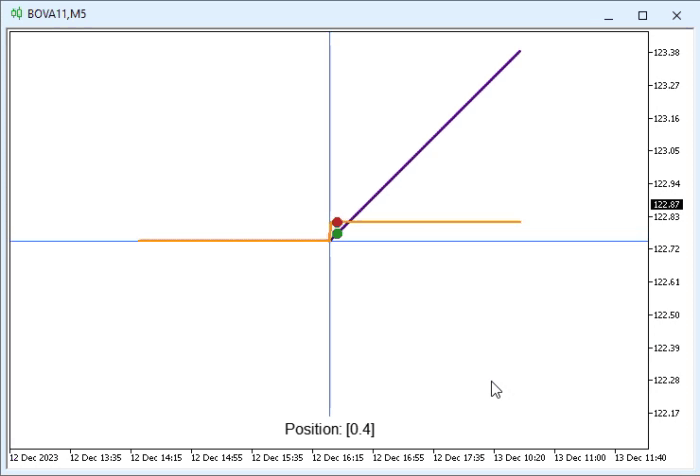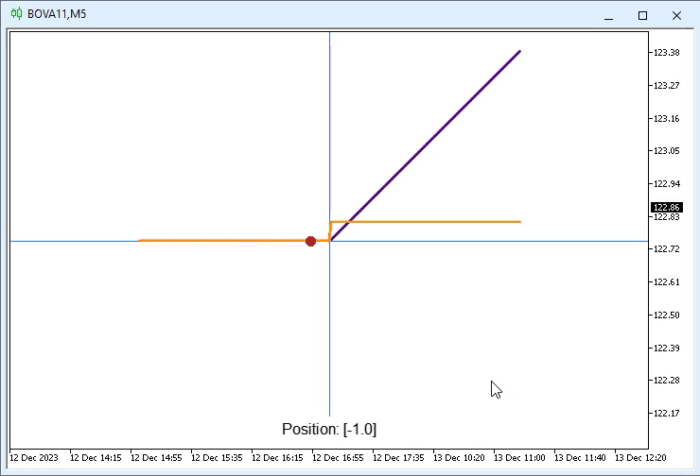
É algo realmente impressionante o que podemos fazer, quando estamos dispostos em fazer. Bem, mas vamos entender o que é esta animação vista acima. Mas para isto, temos que voltar nossa atenção ao fragmento mostrado no começo do tópico. Sendo assim, vamos aos detalhes. Na animação você pode notar que temos dois segmentos de reta. Um em índigo, que seria um tom de azul, outro em laranja. Assim como duas figuras circulares. Uma em verde e outra em vermelho. Pois objetos são criados pelas seguintes linhas respectivamente, 53 a linha em índigo; 54 a linha em laranja; 56 o círculo verde e finalmente na linha 57 o círculo vermelho.

Note que todas estas linhas tem algo em comum. Todas estão de alguma forma utilizando os arrays, que estão declarados na linha 34. Então vamos entender como as coisas estão sendo desenhadas na tela. Isto por que grande parte deste código mostrado no fragmento, não irá mudar. Apenas precisaremos mudar duas linhas, no mesmo para que possamos desenhar as demais funções de ativação.

Ok, nas linhas 38 a 40, alocamos espaço suficiente para comportar todos os valores dentro do limite que foi estabelecido lá na linha oito. Já na linha 42, calculamos qual será o tamanho dos passos, ou melhor dizendo, qual a granulação das retas a serem criadas. Como este valor irá depender tanto do tamanho da janela gráfica, quanto dos valores definidos nas linhas oito e nove do código. Podemos ter a necessidade de mudar ligeiramente as coisas para que tenhamos uma curva sendo plotada. Caso a granulação esteja alta, você irá ver o desenho da curva bem cheio de irregularidades. Como a ReLU, é praticamente uma reta, não notamos isto neste momento. Mas depois você verá isto acontecendo.

Como esta parte do código não mudará, você precisará apenas mudar o valor da linha nove, para deixar a granulação mais fina. Assim a curva será desenhada de forma mais suave. De qualquer maneira, na linha 44, inicializamos o valor de fx. Este será o valor usado no cálculo. Agora entramos no laço for, isto na linha 45. Este laço é que faz todo o trabalho para nós. Já que ele irá criar as curvas ou linhas, dependendo do caso específico.

Na linha 47, fazemos uma pequena pesquisa a fim de saber qual o index dentro do array. Este index, servirá para que plotemos os círculos no gráfico. Mas por que fazer assim? Bem, a motivação para fazer isto é bem simples. Evitar repetir de forma desnecessária o cálculo a ser feito. Já que sem esta linha 47, seriamos obrigados a executar o cálculo duas vezes. Uma para desenhar a curva da função e da derivada. E uma outra para sabermos onde colocar os pontos na curva. A fim de podermos ver onde está sendo feito a amostragem. Já na linha 48, temos o cálculo cujo objetivo é determinar onde estarão os pontos no eixo X. Estes pontos dependem do limite e do número de divisões. Ambos valores são declarados nas linhas oito e nove do código.

Maravilha, agora vamos ver as duas únicas linhas que precisarão ser modificadas. Isto para que possamos plotar gráficos e funções diferentes. Quero que você meu caro leitor, preste muita atenção a linha 49 e 50. Veja que elas são praticamente iguais. Salvo pelo final de cada uma das linhas. Você sabe o que isto significa? Bem, se você prestou atenção ao artigo. Irá notar que o final da linha 49 é exatamente o cálculo que foi mencionado como sendo o da ReLU. Já o final da linha 50 é o cálculo da derivada da equação ReLU. Parece sinistro que tais cálculos sejam tão simples de serem colocados em código. Mas é assim mesmo. Tanto que todo e absolutamente todo o código permanecerá inalterado em qualquer tipo de situação. A única coisa que irá mudar é justamente o conteúdo final desta linha 49 e 50.

Muito bem, isto foi lindo. Para finalizar, usamos a linha 53 para plotar a curva da função que foi calculada. E na linha 54 plotamos a curva da derivada da função. Na linha 56 posicionamos um pequeno círculo, na curva da função. E na linha 57 posicionamos um outro círculo na curva da derivada. Isto sim é algo surpreendente. Pois sem precisar fazer grandes malabarismos, em termos de código, conseguimos produzir algo que plota a curva de uma função e de sua derivada. Isto de maneira que podemos analisar por meio de interação, onde a curva faz determinada coisa. Simplesmente maravilhoso.

Considerações finais

Neste artigo, basicamente apenas construímos um código em MQL5 puro, de forma a poder estudar com mais calma a questão das derivadas e de suas funções. Entender o que acontece, em termos de resultado de uma derivada ou de sua função. Será extremamente importante, para entender como as funções de ativação de fato funcionam. Mas principalmente entender quando e por que usar uma ou outra função de ativação.

Como este artigo teve em sua maior parte do tempo, sendo focado em mostrar o indicador que iremos usar. Isto para conseguir visualizar a curva da derivada e da função de ativação. No anexo, você terá apenas e somente a função de ativação ReLU estando disponível. Mas em breve iremos ver outras funções de ativação. Porém se você, meu caro leitor, já souber qual é a equação a ser utilizada poderá fazer isto diretamente no código. Mas se este não é o seu caso, meu caro leitor. Não se preocupe. Pois iremos ver uma a uma, pelo menos as mais populares ou mais usadas funções de ativação. Assim você poderá estudar com calma cada uma. Testando e aprendendo como elas variam conforme os valores vão sendo ajustados.

De qualquer maneira, aproveite o conhecimento mostrado neste artigo. E como tarefa de casa, que tão criar uma grade no plano cartesiano? Não é algo complicado de ser feito. Porém vou deixar como algo para que cada um tente fazer da melhor forma possível. Isto a fim de visualizar valores no eixo X e eixo Y, enquanto move os pequenos círculos no gráfico.