Indicadores alternativos de risco e rentabilidade em MQL5

Introdução

Todos os traders buscam maximizar o percentual do retorno de seus investimentos; no entanto, um retorno mais alto geralmente está associado a um risco maior. É por isso que a rentabilidade ajustada ao risco é o principal indicador de desempenho na indústria de investimentos. Existem muitos indicadores de rentabilidade ajustada ao risco diferentes, cada um com seu conjunto de vantagens e desvantagens. O índice de Sharpe é um indicador popular de risco e rentabilidade, conhecido por impor condições prévias irrealistas na distribuição dos retornos analisados. Isso inevitavelmente levou ao desenvolvimento de indicadores de desempenho alternativos, sem as desvantagens do índice de Sharpe. Neste artigo, consideraremos não só como implementar indicadores alternativos de risco e rentabilidade como também como criar e analisar curvas de patrimônio líquido hipotéticas.

Modelagem de curvas patrimônio líquido

Para garantir interpretabilidade, usaremos dados do SP500 como base para a estratégia de negociação modelada. Não utilizaremos nenhuma regra de negociação específica; em vez disso, usaremos números aleatórios para criar curvas de patrimônio líquido e as respectivas séries de retornos. O capital inicial será padronizado para um montante personalizável. E um número inicial (seed) definirá os números aleatórios, para que qualquer pessoa que deseje reproduzir os experimentos possa fazê-lo.

Visualização das curvas de patrimônio líquido

A figura abaixo mostra um complemento do MetaTrader 5 (MT5), implementado como um robô investidor (EA), que exibe três curvas de patrimônio líquido. A curva de patrimônio vermelha serve como referência. As curvas de patrimônio azul e verde são construídas com base nela. A referência pode ser alterada, ajustando o patrimônio inicial, configurado a partir do complemento.  

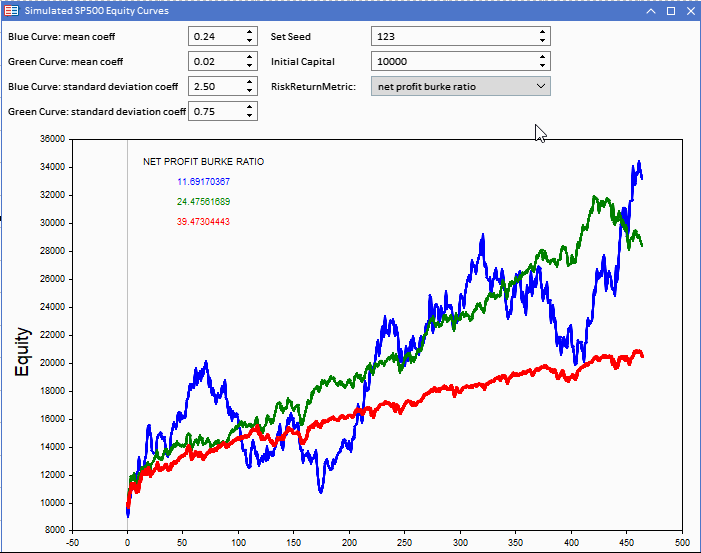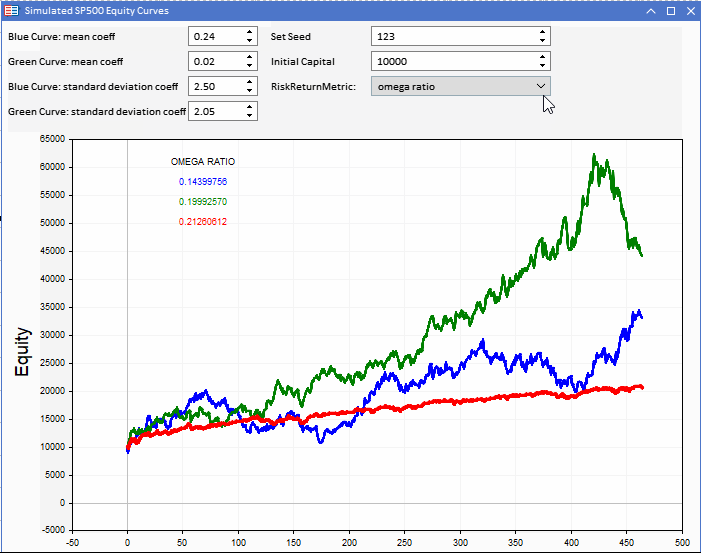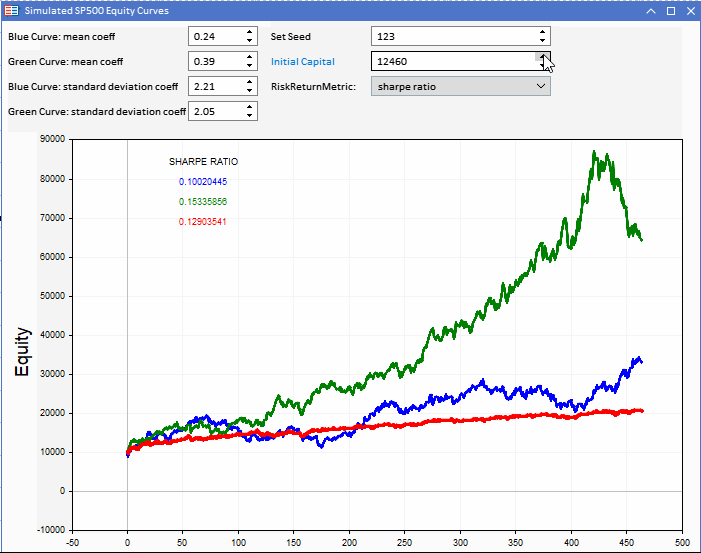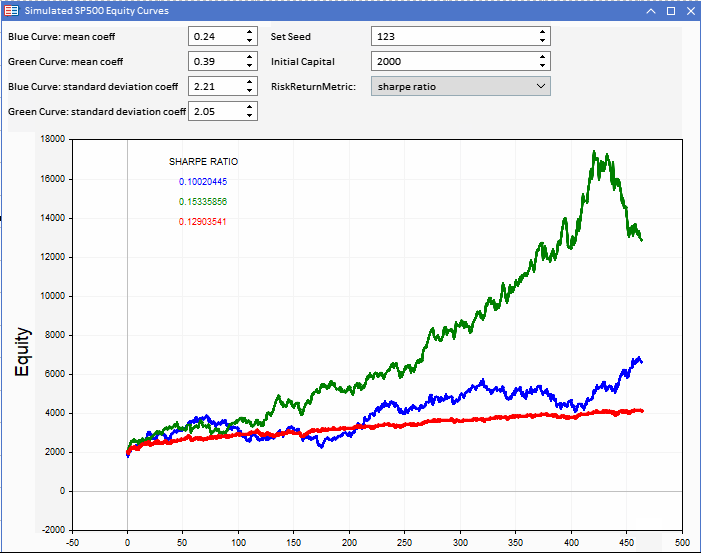
As curvas de patrimônio líquido serão construídas com base na série de referência. Cada uma delas é definida por um componente aleatório, que pode ser controlado por meio de duas constantes ajustáveis, que são o coeficiente médio e o coeficiente de desvio padrão. Em combinação com o desvio padrão do retorno de referência, eles determinam os parâmetros dos números aleatórios normalmente distribuídos, usados ​​para criar duas curvas de patrimônio líquido hipotéticas.   

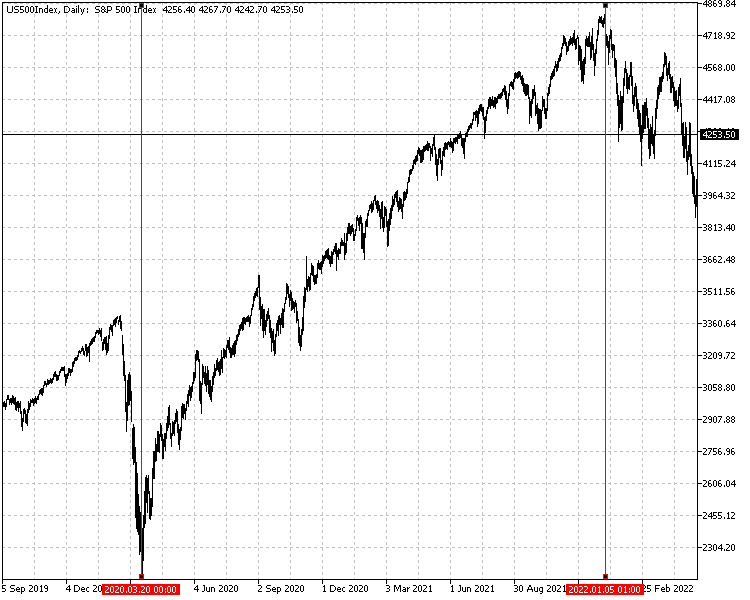
Primeiramente, calculamos a rentabilidade usando os preços de fechamento diários do SP500 para o período de 20 de março de 2020 a 5 de janeiro de 2022, inclusive. A curva de patrimônio é construída a partir da série de retornos. Usamos as séries que definem o patrimônio líquido e o retorno, para comparar o desempenho calculado com base na aparência dessa curva de patrimônio líquido.

O código do complemento está anexado ao artigo.

Indicadores de rebaixamento

O rebaixamento, ou 'downdraw', representa a maior quantidade de dinheiro perdido pela estratégia entre dois pontos no tempo. Este valor traz uma noção do risco que a estratégia assumiu para alcançar seus objetivos, caso eles tenham sido atingidos. Quando uma série, que consiste em um número arbitrário dos maiores rebaixamentos, é contada e somada, o resultado pode ser usado como uma medida de variabilidade.

Razão de Burke

Em 1994, Burke escreveu um artigo intitulado "A sharper sharpe ratio" (um índice de Sharpe mais preciso), no qual introduziu a razão de Burke como uma alternativa ao popular índice de Sharpe. A razão de Burke substitui o denominador na fórmula do índice de Sharpe pelo quadrado da soma de um determinado valor dos maiores rebaixamentos absolutos. O numerador pode ser o retorno médio ou o retorno absoluto da estratégia/portfólio, ou seja, o lucro líquido. Consideramos duas variações do cálculo. Distinguimos duas versões: a razão de Burke baseada no lucro líquido e a razão de Burke baseada no retorno médio. As fórmulas são apresentadas abaixo.

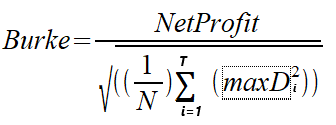
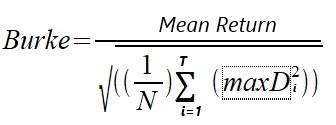
MaxD é uma série dos maiores rebaixamentos absolutos de T, série essa calculada com base em valores de patrimônio líquido. Aqui, N representa o número de valores de patrimônio líquido próprio utilizados nos cálculos.

Neste caso, a razão de Burke do lucro líquido é implementada como a função netprofit_burke(). A função requer um array de valores de patrimônio líquido que descreva a curva de patrimônio líquido e um valor inteiro que denote o número de maiores rebaixamentos a serem incluídos no cálculo.

//+------------------------------------------------------------------+
//|Net profit based Burke ratio                                      |
//+------------------------------------------------------------------+
double netprofit_burke(double &in_ec[],int n_highestdrawdowns=0)
  {
   double outdd[];
   double sumdd=0;
   int insize=ArraySize(in_ec);

   if(n_highestdrawdowns<=0)
      n_highestdrawdowns=int(insize/20);

   if(MaxNDrawdowns(n_highestdrawdowns,in_ec,outdd))
     {
      for(int i=0; i<ArraySize(outdd); i++)
        {
         sumdd+=(outdd[i]*outdd[i]);
        }
      return (in_ec[insize-1]-in_ec[0])/(MathSqrt((1.0/double(insize)) * sumdd));
     }
   else
      return 0;
  }

Caso seja especificado um valor padrão de zero, a função usará a fórmula N/20 para definir o número de rebaixamentos a serem considerados, em que N é o tamanho do array de fundos.

A função MaxNDradowns() é usada para coletar o número especificado de rebaixamentos. Ele gera uma série dos maiores rebaixamentos absolutos, organizados em ordem crescente.

//+------------------------------------------------------------------+
//|Maximum drawdowns function given equity curve                     |
//+------------------------------------------------------------------+
bool MaxNDrawdowns(const int num_drawdowns,double &in_ec[],double &out_dd[])
  {
   ZeroMemory(out_dd);

   ResetLastError();

   if(num_drawdowns<=0)
     {
      Print("Invalid function parameter for num_drawdowns ");
      return false;
     }
   double u[],v[];

   int size = ArraySize(in_ec);

   if((ArrayResize(v,(size*(size-1))/2)< int((size*(size-1))/2))||
      (ArraySize(out_dd)!=num_drawdowns && ArrayResize(out_dd,num_drawdowns)<num_drawdowns))
     {
      Print(__FUNCTION__, " resize error ", GetLastError());
      return false;
     }

   int k=0;
   for(int i=0; i<size-1; i++)
     {
      for(int j=i+1; j<size; j++)
        {
         v[k]=in_ec[i]-in_ec[j];
         k++;
        }
     }

   ArraySort(v);

   for(int i=0; i<k; i++)
     {
      if(v[i]>0)
        {
         if(i)
           {
            if(!ArrayRemove(v,0,i))
              {
               Print(__FUNCTION__, " error , ArrayRemove: ",GetLastError());
               return false;
              }
            else
               break;
           }
         else
            break;
        }
     }

   size=ArraySize(v);

   if(size && size<=num_drawdowns)
     {
      if(ArrayCopy(out_dd,v)<size)
        {
         Print(__FUNCTION__, " error ", GetLastError());
         return false;
        }
      else
         return (true);
     }


   if(ArrayCopy(out_dd,v,0,size-num_drawdowns,num_drawdowns)<num_drawdowns)
     {
      Print(__FUNCTION__, " error ", GetLastError());
      return false;
     }


   return(true);

  }

A razão de Burke, que usa o retorno médio como numerador, é implementada como a função meanreturns_burke e tem parâmetros de entrada semelhantes.

//+------------------------------------------------------------------+
//|Mean return based Burke ratio                                     |
//+------------------------------------------------------------------+
double meanreturns_burke(double &in_ec[],int n_highestdrawdowns=0)
  {
   double outdd[];
   double rets[];

   double sumdd=0;
   int insize=ArraySize(in_ec);

   if(ArrayResize(rets,insize-1)<insize-1)
     {
      Print(__FUNCTION__," Memory allocation error ",GetLastError());
      return 0;
     }

   for(int i=1; i<insize; i++)
      rets[i-1] = (in_ec[i]/in_ec[i-1]) - 1.0;

   if(n_highestdrawdowns<=0)
      n_highestdrawdowns=int(insize/20);

   if(MaxNDrawdowns(n_highestdrawdowns,in_ec,outdd))
     {
      for(int i=0; i<ArraySize(outdd); i++)
         sumdd+=(outdd[i]*outdd[i]);
      return MathMean(rets)/(MathSqrt((1.0/double(insize)) * sumdd));
     }
   else
      return 0;
  }

Razão entre lucro líquido e rebaixamento máximo

A fórmula da razão de Burke, que usa o lucro líquido como numerador, é semelhante à da razão entre o lucro líquido e o rebaixamento máximo (Netprofit to Maximum Drawdown ratio, NPMD). A diferença reside no uso do único maior rebaixamento no cálculo do NPMD.

O cálculo do NPMD é implementado na forma da função netProfiMaxDD(), que requer como entrada um array de valores de patrimônio líquido.

//+------------------------------------------------------------------+
//|Net profit to maximum drawdown ratio                              |
//+------------------------------------------------------------------+
double netProfiMaxDD(double &in_ec[])
  {
   double outdd[];
   int insize=ArraySize(in_ec);

   if(MaxNDrawdowns(1,in_ec,outdd))
      return ((in_ec[insize-1]-in_ec[0])/outdd[0]);
   else
      return 0;
  }

Os índices baseados em rebaixamento foram introduzidos para abordar algumas das críticas ao índice de Sharpe. Os cálculos não penalizam por lucros anormais ou grandes e, o que é mais importante, são não paramétricos. O uso de rebaixamentos absolutos no denominador, embora seja uma vantagem, faz com que a razão de Burke e o NPMD favoreçam estratégias com saltos descendentes relativamente pequenos.

Usamos a ferramenta de visualização de curva de patrimônio líquido. A curva azul tem o retorno mais alto, mas sua pontuação é mais baixa do que as outras.

Os valores de referência para ambos os indicadores destacam o quão enganosos eles podem ser quando usados para comparar o desempenho das estratégias. Os indicadores básicos são significativamente mais altos, apesar de outras curvas gerarem maiores retornos reais.

O uso de rebaixamentos absolutos pode superestimar o risco em comparação com o uso de uma distribuição de retornos negativos, como no caso do índice de Sharpe.

Comparando os valores de Sharpe, vemos que a curva verde tem o maior indicador, com muito menos diferença entre os resultados da estratégia modelada.

Interpretação dos indicadores de rebaixamento

Quanto maior a razão de Burke ou NPMD, melhor o desempenho da estratégia de investimento ajustada ao risco. Isso significa que a estratégia gera um retorno mais alto em comparação com o risco assumido.

- Se a razão de Burke ou NPMD for maior que 0, isso indica que a estratégia de investimento oferece um retorno excedente em comparação com o risco calculado.

- Se a razão de Burke ou NPMD for menor que 0, isso indica que a estratégia de investimento não está gerando retorno excedente suficiente em relação ao risco assumido.

Indicadores de momentos parciais

Os Indicadores baseados em momentos parciais são mais uma tentativa de criar uma alternativa ao índice de Sharpe. Eles se baseiam no conceito estatístico de semivariância e oferecem uma visão de quão bem a estratégia se desempenha em termos de risco de baixa (retorno negativo) em comparação com o potencial de alta (retorno positivo). Para calcular os Indicadores de momentos parciais, primeiro precisamos identificar o ganho parcial e a perda parcial. Esses valores são obtidos determinando um retorno de referência, geralmente o retorno mínimo aceitável ou a taxa livre de risco, e calculando a diferença entre o retorno real e o retorno de referência para cada observação.

As diferenças que estão acima do limite para o momento parcial inferior ou abaixo do limite para o momento parcial superior (higher partial moment, HPM) podem ser ignoradas no cálculo. O momento parcial inferior (Lower Partial Moment, LPM) mede os desvios quadráticos dos retornos que caem abaixo de um valor de referência, enquanto o momento parcial superior (Higher Partial Moment, HPM) mede os desvios quadráticos dos retornos que excedem esse valor de referência. Os momentos parciais apresentam uma visão alternativa do risco para os indicadores de rebaixamento, concentrando-se no risco associado aos retornos que estão abaixo ou acima de um determinado limiar.

Abaixo estão as fórmulas para LPM e HPM, respectivamente:

Onde thresh é o limiar, x é o retorno observado, e max define o valor máximo entre a diferença resultante e zero antes de ser elevado ao expoente n. Aqui, n representa o expoente do momento parcial. Com n=0, LPM se torna a probabilidade de que a observação seja menor que o limiar, enquanto HPM indica a probabilidade de ser maior. N é o número de retornos observados. Examinaremos dois Indicadores de momentos parciais: o ômega generalizado e a razão de potencial de alta (Upside Potential Ratio, UPR).

Razão ômega

O ômega generalizado é definido por um termo em n graus e um valor de referência que determina o LPM utilizado no cálculo.

A função omega() implementa o cálculo da razão ômega, recebendo como entrada um array de valores de retorno. A função usa o momento parcial inferior ao quadrado, enquanto o retorno de limiar é considerado igual a zero.

//+------------------------------------------------------------------+
//|omega ratio                                                       |
//+------------------------------------------------------------------+
double omega(double &rt[])
  {
   double rb[];

   if(ArrayResize(rb,ArraySize(rt))<0)
     {
      Print(__FUNCTION__, " Resize error ",GetLastError());
      return 0;
     }

   ArrayInitialize(rb,0.0);

   double pmomentl=MathPow(partialmoment(2,rt,rb),0.5);

   if(pmomentl)
      return MathMean(rt)/pmomentl;
   else
      return 0;
  }

Potencial de alta

No UPR, dois termos são elevados ao expoente n (n1 e n2 na fórmula) e um valor de limiar. E n1 define o expoente do HPM no numerador, e n2 define o expoente do LPM no denominador.

Similar à implementação da métrica de desempenho do ômega, a função upsidePotentialRatio() calcula o UPR. O cálculo também utiliza momentos parciais ao quadrado, com os valores de referência retornados como zero.

//+------------------------------------------------------------------+
//|Upside potential ratio                                            |
//+------------------------------------------------------------------+
double upsidePotentialRatio(double &rt[])
  {
   double rb[];

   if(ArrayResize(rb,ArraySize(rt))<0)
     {
      Print(__FUNCTION__, " Resize error ",GetLastError());
      return 0;
     }

   ArrayInitialize(rb,0.0);

   double pmomentu=MathPow(partialmoment(2,rt,rb,true),0.5);
   double pmomentl=MathPow(partialmoment(2,rt,rb),0.5);
   if(pmomentl)
      return pmomentu/pmomentl;
   else
      return 0;
  }

Os cálculos de momentos parciais são implementados na função partsmoment(). Os dados de entrada necessários incluem o expoente do momento como um número inteiro sem sinal, dois arrays do tipo double e um valor booleano. O primeiro array deve conter a rentabilidade observada, enquanto o segundo deve conter a retorno de referência ou limiar usado nos cálculos. O valor booleano determina o tipo de momento parcial a ser calculado: verdadeiro para o momento parcial superior e falso para o momento parcial inferior.

//+------------------------------------------------------------------+
//|Partial Moments                                                   |
//+------------------------------------------------------------------+
double partialmoment(const uint n,double &rt[],double &rtb[],bool upper=false)
  {
   double pm[];
   int insize=ArraySize(rt);

   if(n)
     {
      if(ArrayResize(pm,insize)<insize)
        {
         Print(__FUNCTION__," resize error ", GetLastError());
         return 0;
        }

      for(int i=0; i<insize; i++)
         pm[i] = (!upper)?MathPow(MathMax(rtb[i]-rt[i],0),n):MathPow(MathMax(rt[i]-rtb[i],0),n);
      return MathMean(pm);
     }
   else
     {
      int k=0;
      for(int i=0; i<insize; i++)
        {
         if((!upper && rtb[i]>=rt[i]) || (upper && rt[i]>rtb[i]))
           {
            ArrayResize(pm,k+1,1);
            pm[k]=rt[i];
            ++k;
           }
         else
            continue;
        }

      return MathMean(pm);

     }

  }

Ao observar as razões ômega e o UPR de nossas curvas de patrimônio líquido, notamos uma semelhança na classificação com o índice de Sharpe.

Mais uma vez, a preferência é dada a curvas de patrimônio líquido menos voláteis. O ômega definitivamente parece ser uma alternativa viável ao índice de Sharpe.

Interpretação do indicador de momentos parciais

A razão ômega é muito mais direta em termos de interpretação em comparação com o UPR. Quanto maior o ômega, melhor. Valores negativos indicam estratégias deficitárias, enquanto valores positivos sugerem rentabilidade superior ao nível de risco.

Por outro lado, o UPR pode parecer um pouco mais complexo quando se trata de interpretação. Observando algumas curvas de patrimônio líquido modeladas com perfis de desempenho divergentes.

A curva de patrimônio azul mostra um retorno negativo, no entanto, o resultado do UPR é positivo. Mais estranhos ainda são os resultados das curvas de patrimônio líquido verde e vermelha. As próprias curvas são quase idênticas: a curva de patrimônio verde gera uma rentabilidade mais alta, mas o valor do UPR é menor do que o da curva vermelha.

Análise regressiva e rentabilidade – Alfa de Jensen

A regressão linear permite construir uma linha que melhor se ajusta a um conjunto de dados. Assim, os indicadores baseados em regressões medem a linearidade das curvas de patrimônio líquido. O Alfa de Jensen calcula o valor alfa na equação padrão de regressão. Ele quantifica a relação entre a retorno de referência e a rentabilidade observada.

Para calcular o valor do alfa, podemos usar o método dos mínimos quadrados. A função leastsquarefit() recebe como entrada dois arrays que definem a resposta e o preditor. Neste contexto, a resposta será um array de retornos observados, enquanto o preditor será um array de retornos de referência. A função produz valores alfa e beta, cujas referências devem ser fornecidas ao chamar a função.

//+------------------------------------------------------------------+
//|linear model using least squares fit y=a+bx                       |
//+------------------------------------------------------------------+
double leastsquaresfit(double &y[],double &x[], double &alpha,double &beta)
  {
   double esquared=0;

   int ysize=ArraySize(y);
   int xsize=ArraySize(x);

   double sumx=0,sumy=0,sumx2=0,sumxy=0;

   int insize=MathMin(ysize,xsize);

   for(int i=0; i<insize; i++)
     {
      sumx+=x[i];
      sumx2+=x[i]*x[i];
      sumy+=y[i];
      sumxy+=x[i]*y[i];
     }

   beta=((insize*sumxy)-(sumx*sumy))/((insize*sumx2)-(sumx*sumx));
   alpha=(sumy-(beta*sumx))/insize;

   double pred,error;

   for(int i=0; i<insize; i++)
     {
      pred=alpha+(beta*x[i]);
      error=pred-y[i];
      esquared+=(error*error);
     }

   return esquared;

  }

Ao aplicar o Alfa de Jensen às nossas curvas de patrimônio líquido modeladas, obtemos uma medida de linearidade das curvas de patrimônio líquido verde e azul em relação à referência (curva de patrimônio líquido vermelha).

Este é o primeiro indicador que avalia a curva de patrimônio líquido azul como a estratégia mais eficiente. Este indicador geralmente recompensa o bom desempenho quando os resultados dos indicadores de controle são ruins. O Alfa de Jensen pode indicar um retorno positivo, mesmo se o retorno absoluto for negativo. Isso pode acontecer quando os retornos absolutos de referência são simplesmente piores do que os retornos sob análise. Por isso, tenha cuidado ao usar este indicador.

Interpretação do Alfa de Jensen

O fato de o Alfa de Jensen ser positivo indica que o portfólio/estratégia gerou uma rentabilidade excedente em comparação com a referência, sinalizando a superioridade dos resultados após considerar o nível de risco. Já o fato de o Alfa de Jensen ser negativo significa que a estratégia não gerou resultados em comparação com a retorno de referência.

Além do valor alfa, o valor beta obtido pelo método dos mínimos quadrados fornece uma medida da sensibilidade dos retornos em relação à referência. Um beta igual a 1 indica que a os retornos da estratégia mudam sincronamente com o indicador de referência. Um beta menor que 1 sugere que a curva de patrimônio é menos volátil do que a curva de referência, enquanto um beta maior que 1 indica maior volatilidade.

Considerações finais

Descrevemos como implementar vários indicadores de retorno ajustado ao risco, que podem ser usados como alternativas ao índice de Sharpe. Na minha opinião, o melhor deles é a razão ômega. Ele oferece as mesmas vantagens que o índice de Sharpe, sem quaisquer expectativas de normalidade na distribuição dos retornos. No entanto, também deve ser observado que, ao tomar decisões de investimento, é melhor considerar vários indicadores de desempenho da estratégia. Nenhum indicador pode fornecer uma imagem completa do risco ou retorno esperado. Lembre-se também que a maioria dos indicadores de retorno ajustado ao risco são medidas retrospectivas, e resultados passados não garantem resultados futuros. Desse modo, ao avaliar opções de investimento, é importante considerar outros fatores, como objetivos de investimento, horizonte temporal e tolerância ao risco.

O código-fonte de todos os indicadores está contido em PerformanceRatios.mqh. Vale ressaltar que nenhuma das implementações fornece indicadores anualizados. O arquivo zip anexado também contém o código do complemento usado para visualizar nossas curvas de patrimônio líquido modeladas. O complemento é implementado usando a biblioteca EasyAndFastGUI, disponível em CodeBase no site mql5.com. O artigo inclui o código-fonte do EA e uma versão compilada pronta para uso.

Nome do arquivo	Descrição
Mql5\Files\sp500close.csv	Arquivo CSV com preços de fechamento do SP500, usado para calcular as curvas de patrimônio líquido
Mql5\Include\PerformanceRatios.mqh	Arquivo de inclusão contendo definições de todos os indicadores de desempenho descritos no artigo
Mql5\Experts\EquityCurves.mq5	Código-fonte do EA para a ferramenta de visualização. Sua compilação requer a interface gráfica simples e rápida, disponível no CodeBase
Mql5\Experts\EquityCurves.ext	Versão compilada do EA