Альтернативные показатели риска и доходности в MQL5

Введение

Все трейдеры стараются максимально увеличить процентную доходность своих инвестиций, однако более высокая доходность обычно сопряжена с более высоким риском. Именно по этой причине доходность, скорректированная на риск, является основным показателем эффективности в инвестиционной отрасли. Существует множество различных показателей доходности с поправкой на риск, каждый из которых имеет свой набор преимуществ и недостатков. Коэффициент Шарпа — популярный показатель риска и доходности, известный тем, что накладывает нереалистичные предварительные условия на распределение анализируемой доходности. Это неизбежно привело к разработке альтернативных показателей эффективности без недостатков коэффициента Шарпа. В этой статье мы рассмотрим реализацию альтернативных показателей риска и доходности и сгенерируем гипотетические кривые капитала для анализа их характеристик.

Моделирование кривых эквити

Чтобы обеспечить интерпретируемость, мы будем использовать данные SP500 в качестве основы для моделируемой торговой стратегии. Мы не будем использовать какие-либо конкретные торговые правила, вместо этого мы используем случайные числа для создания кривых капитала и соответствующих рядов доходности. Первоначальный капитал будет стандартизирован до настраиваемой суммы. Случайные числа будут определяться начальным числом (seed), чтобы любой, кто захочет воспроизвести эксперименты, мог это сделать.

Визуализация кривых эквити

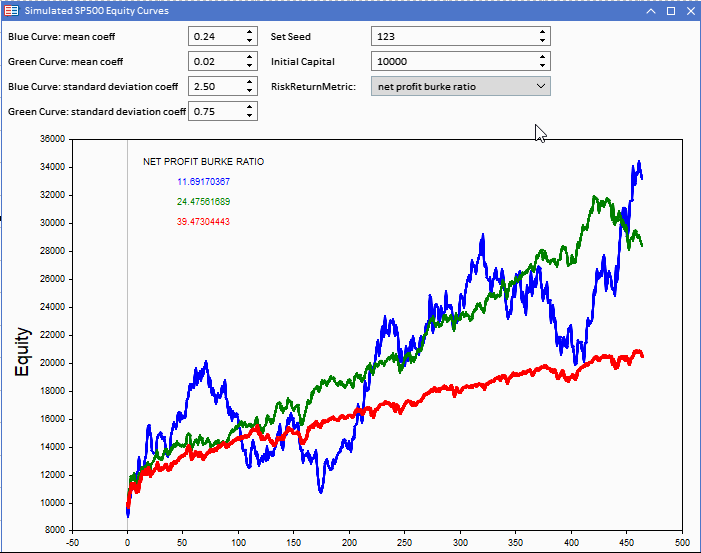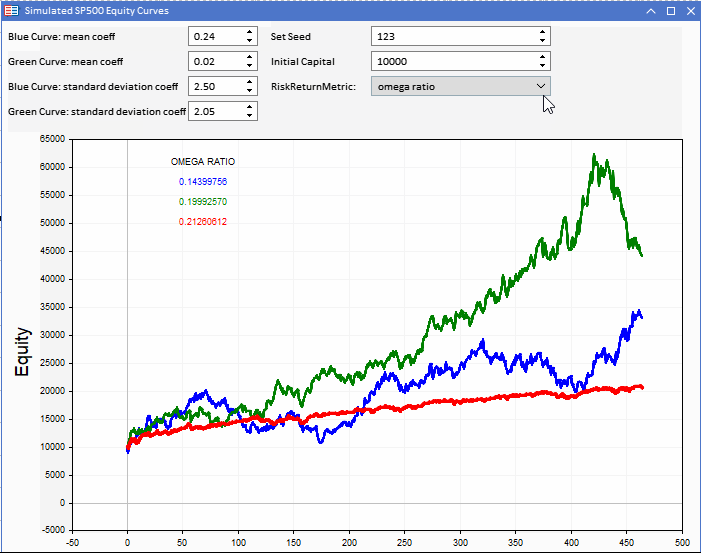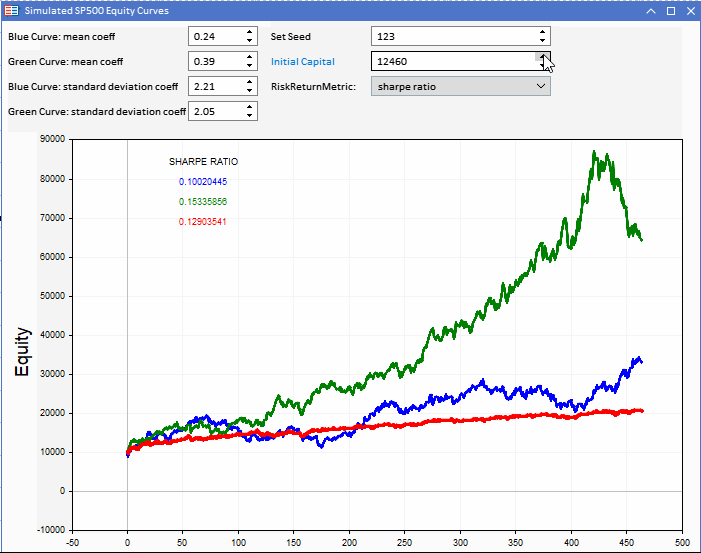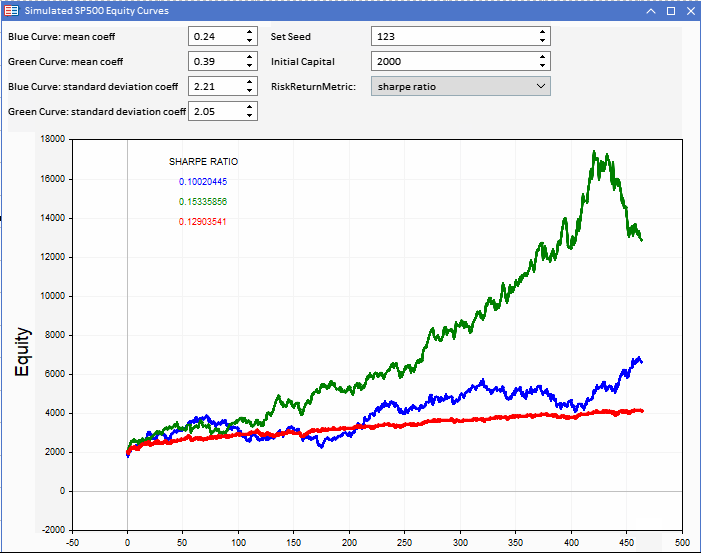
На рисунке ниже показано приложение MetaTrader 5 (MT5), реализованное в виде советника (EA), которое отображает три кривые эквити. Красная кривая эквити является эталоном, на основе которого построены синяя и зеленая кривые капитала. Эталон можно изменить, настроив начальный капитал. Настраивается из приложения.  

Кривые эквити будут построены на основе эталонной серии. Каждый из них определяется случайной составляющей, которой можно управлять с помощью двух регулируемых констант - среднего коэффициента и коэффициента стандартного отклонения. В сочетании со стандартным отклонением эталонной доходности они определяют параметры нормально распределенных случайных чисел, используемых для создания двух гипотетических кривых эквити.   

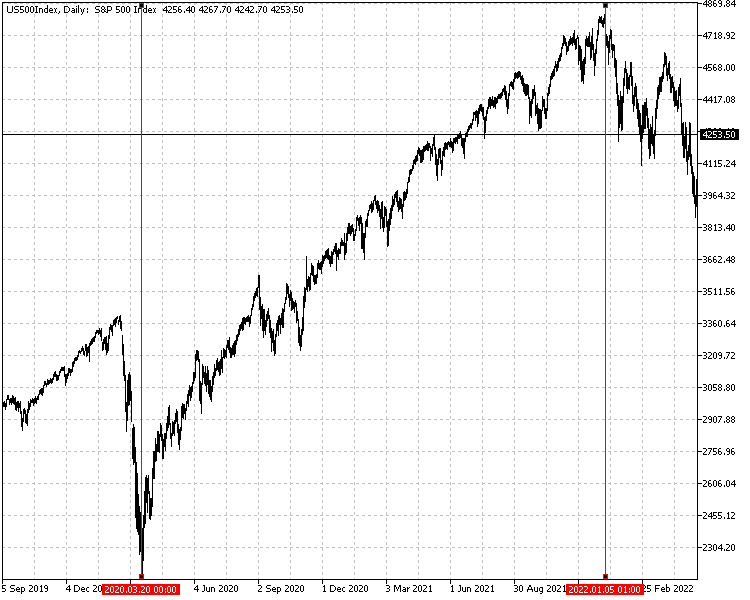
Сначала мы рассчитываем доходность, используя дневные цены закрытия SP500 за период с 20 марта 2020 года по 5 января 2022 года включительно. Кривая эквити строится из серии доходностей. С помощью рядов, определяющих капитал и доходность, мы сравним результаты деятельности, рассчитанные с учетом внешнего вида данной кривой эквити.

Код приложения приложен к статье.

Коэффициенты просадки

Просадка представляет собой наибольшую сумму средств, потерянную стратегией между любыми двумя моментами времени. Это значение дает представление о риске, который стратегия взяла на себя для достижения своих целей, если таковые были достигнуты. Когда ряд, состоящий из произвольного числа самых высоких просадок, подсчитывается и агрегируется, результат можно использовать в качестве меры изменчивости.

Коэффициент Берка

В 1994 году Берк написал статью под названием "A sharper sharpe ratio" (более точный коэффициент Шарпа), в которой представил коэффициент Берка как альтернативу популярному коэффициенту Шарпа. Коэффициент Берка заменяет знаменатель в формуле коэффициента Шарпа квадратом суммы определенного значения самых высоких абсолютных просадок. Числителем может быть либо средняя доходность, либо абсолютная денежная доходность стратегии/портфеля, то есть чистая прибыль. Рассмотрим два варианта расчета. Мы различаем две версии: коэффициент Берка, основанный на чистой прибыли, и коэффициент Берка средней доходности. Формулы приведены ниже.

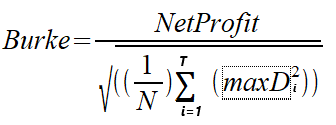
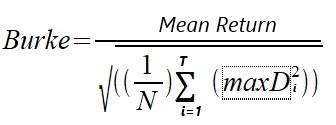
MaxD — это серия крупнейших абсолютных просадок T, рассчитанная на основе значений эквити. N представляет собой количество значений собственного капитала, использованных в расчетах.

Коэффициент Берка чистой прибыли реализован как функция netprofit_burke(). Для функции требуется массив значений капитала, описывающий кривую капитала, а также целое значение, обозначающее количество наибольших просадок, которые следует учитывать при расчете.

//+------------------------------------------------------------------+
//|Net profit based Burke ratio                                      |
//+------------------------------------------------------------------+
double netprofit_burke(double &in_ec[],int n_highestdrawdowns=0)
  {
   double outdd[];
   double sumdd=0;
   int insize=ArraySize(in_ec);

   if(n_highestdrawdowns<=0)
      n_highestdrawdowns=int(insize/20);

   if(MaxNDrawdowns(n_highestdrawdowns,in_ec,outdd))
     {
      for(int i=0; i<ArraySize(outdd); i++)
        {
         sumdd+=(outdd[i]*outdd[i]);
        }
      return (in_ec[insize-1]-in_ec[0])/(MathSqrt((1.0/double(insize)) * sumdd));
     }
   else
      return 0;
  }

Если указано нулевое значение по умолчанию, функция использует формулу N/20 для установки количества учитываемых просадок, где N — размер массива средств.

Для сбора заданного количества просадок подключается функция MaxNDradowns(). Она выводит серию самых высоких абсолютных просадок, расположенных в порядке возрастания.

//+------------------------------------------------------------------+
//|Maximum drawdowns function given equity curve                     |
//+------------------------------------------------------------------+
bool MaxNDrawdowns(const int num_drawdowns,double &in_ec[],double &out_dd[])
  {
   ZeroMemory(out_dd);

   ResetLastError();

   if(num_drawdowns<=0)
     {
      Print("Invalid function parameter for num_drawdowns ");
      return false;
     }
   double u[],v[];

   int size = ArraySize(in_ec);

   if((ArrayResize(v,(size*(size-1))/2)< int((size*(size-1))/2))||
      (ArraySize(out_dd)!=num_drawdowns && ArrayResize(out_dd,num_drawdowns)<num_drawdowns))
     {
      Print(__FUNCTION__, " resize error ", GetLastError());
      return false;
     }

   int k=0;
   for(int i=0; i<size-1; i++)
     {
      for(int j=i+1; j<size; j++)
        {
         v[k]=in_ec[i]-in_ec[j];
         k++;
        }
     }

   ArraySort(v);

   for(int i=0; i<k; i++)
     {
      if(v[i]>0)
        {
         if(i)
           {
            if(!ArrayRemove(v,0,i))
              {
               Print(__FUNCTION__, " error , ArrayRemove: ",GetLastError());
               return false;
              }
            else
               break;
           }
         else
            break;
        }
     }

   size=ArraySize(v);

   if(size && size<=num_drawdowns)
     {
      if(ArrayCopy(out_dd,v)<size)
        {
         Print(__FUNCTION__, " error ", GetLastError());
         return false;
        }
      else
         return (true);
     }


   if(ArrayCopy(out_dd,v,0,size-num_drawdowns,num_drawdowns)<num_drawdowns)
     {
      Print(__FUNCTION__, " error ", GetLastError());
      return false;
     }


   return(true);

  }

Вычисление коэффициента Берка, в котором в качестве числителя используется средняя доходность, реализовано в виде функции meanreturns_burke и имеет аналогичные входные параметры.

//+------------------------------------------------------------------+
//|Mean return based Burke ratio                                     |
//+------------------------------------------------------------------+
double meanreturns_burke(double &in_ec[],int n_highestdrawdowns=0)
  {
   double outdd[];
   double rets[];

   double sumdd=0;
   int insize=ArraySize(in_ec);

   if(ArrayResize(rets,insize-1)<insize-1)
     {
      Print(__FUNCTION__," Memory allocation error ",GetLastError());
      return 0;
     }

   for(int i=1; i<insize; i++)
      rets[i-1] = (in_ec[i]/in_ec[i-1]) - 1.0;

   if(n_highestdrawdowns<=0)
      n_highestdrawdowns=int(insize/20);

   if(MaxNDrawdowns(n_highestdrawdowns,in_ec,outdd))
     {
      for(int i=0; i<ArraySize(outdd); i++)
         sumdd+=(outdd[i]*outdd[i]);
      return MathMean(rets)/(MathSqrt((1.0/double(insize)) * sumdd));
     }
   else
      return 0;
  }

Коэффициент чистой прибыли к максимальной просадке

Формула коэффициента Берка, в которой в качестве числителя используется чистая прибыль, аналогична соотношению чистой прибыли к максимальной просадке (Netprofit to Maximum Drawdown ratio, NPMD). Разница заключается в использовании единственной наибольшей просадки при расчете коэффициента NPMD.

Расчет NPMD реализован в виде функции netProfiMaxDD(), требующей в качестве входных данных массив значений эквити.

//+------------------------------------------------------------------+
//|Net profit to maximum drawdown ratio                              |
//+------------------------------------------------------------------+
double netProfiMaxDD(double &in_ec[])
  {
   double outdd[];
   int insize=ArraySize(in_ec);

   if(MaxNDrawdowns(1,in_ec,outdd))
      return ((in_ec[insize-1]-in_ec[0])/outdd[0]);
   else
      return 0;
  }

Коэффициенты, основанные на просадке, были введены для устранения некоторых критических замечаний в адрес коэффициента Шарпа. Расчеты не наказывают за аномальную или большую прибыль и, что наиболее важно, являются непараметрическими. Использование абсолютных просадок в знаменателе, хотя и является преимуществом, приводит к тому, что коэффициенты Берка и NPMD отдают предпочтение стратегиям с относительно небольшими нисходящими скачками.

Обращение к инструменту визуализации кривой эквити. Синяя кривая имеет самую высокую доходность, но ее балл ниже, чем у остальных.

Контрольные значения для обоих коэффициентов подчеркивают, насколько обманчивыми могут быть показатели, когда они используются для сравнения эффективности стратегий. Базовые коэффициенты значительно выше, несмотря на то, что другие кривые приносят большую реальную доходность.

Использование абсолютных просадок может переоценить риск по сравнению с использованием распределения отрицательной доходности, как в случае с коэффициентом Шарпа.

Сравнивая значения Шарпа, мы видим, что зеленая кривая имеет самый высокий показатель с гораздо меньшей разницей между результатами смоделированной стратегии.

Интерпретация коэффициентов просадки

Чем выше коэффициент Берка или NPMD, тем лучше эффективность инвестиционной стратегии с поправкой на риск. Это означает, что стратегия приносит более высокую прибыль по сравнению с принятым риском.

- Если коэффициент Берка или NPMD больше 0, это говорит о том, что инвестиционная стратегия обеспечивает избыточную доходность по сравнению с расчетным риском.

- Если коэффициент Берка или NPMD меньше 0, это указывает на то, что инвестиционная стратегия не приносит достаточной избыточной прибыли по сравнению с принятым риском.

Коэффициенты частичных моментов

Коэффициенты, основанные на частичном моменте, являются еще одной попыткой создать альтернативу коэффициенту Шарпа. Они основаны на статистической концепции полудисперсии и дают представление о том, насколько хорошо стратегия работает с точки зрения риска снижения (отрицательная доходность) по сравнению с потенциалом роста (положительная доходность). Чтобы рассчитать частичные коэффициенты моментов, нам сначала необходимо определить частичную прибыль и частичный убыток. Эти значения получаются путем определения порогового уровня доходности, обычно минимально приемлемой доходности или безрисковой ставки, и расчета разницы между фактической доходностью и пороговой доходностью для каждого наблюдения.

При расчете можно игнорировать различия, которые либо превышают порог для нижнего частичного момента, либо ниже порога для более высокого частичного момента (higher partial moment, HPM). Нижний частичный момент (lower partial moment, LPM) измеряет квадратичные отклонения доходности, которая падает ниже порогового значения, тогда как более высокий частичный момент (HPM) измеряет квадратичные отклонения доходности, превышающей пороговое значение. Частичные моменты представляют альтернативный взгляд на риск по сравнению с коэффициентами просадки, сосредоточив внимание на риске, связанном с доходностью, которая либо ниже, либо выше определенного порога.

Ниже приведены формулы для LPM и HPM соответственно:

Где thresh — это порог, x — это наблюдаемая доходность, а max определяет максимальное значение между результирующей разницей и нулем перед возведением в степень n. n определяет степень частичного момента. При n=0 LPM становится вероятностью того, что наблюдение меньше порога, а HPM дает вероятность того, что оно выше. N — количество наблюдаемых доходов. Мы рассмотрим два коэффициента частичных моментов — обобщенную Омегу и коэффициент потенциала роста (Upside Potential Ratio, UPR).

Омега

Обобщенная омега определяется одним термином в n градусах и пороговым значением, которое определяет LPM, используемый в расчете.

Функция omega() реализует вычисление коэффициента Омега, принимая в качестве входных данных массив возвращаемых значений. Функция использует нижний частичный момент в степени 2, при этом пороговая доходность принимается равной нулю.

//+------------------------------------------------------------------+
//|omega ratio                                                       |
//+------------------------------------------------------------------+
double omega(double &rt[])
  {
   double rb[];

   if(ArrayResize(rb,ArraySize(rt))<0)
     {
      Print(__FUNCTION__, " Resize error ",GetLastError());
      return 0;
     }

   ArrayInitialize(rb,0.0);

   double pmomentl=MathPow(partialmoment(2,rt,rb),0.5);

   if(pmomentl)
      return MathMean(rt)/pmomentl;
   else
      return 0;
  }

Потенциал роста

В UPR используются два члена в степени n (n1 и n2 в формуле) и пороговое значение. n1 определяет степень HPM в числителе, а n2 определяет степень LPM в знаменателе.

Подобно реализации метрики производительности Омеги, функция upsidePotentialRatio() вычисляет коэффициент UPR. В вычислении также используются частичные моменты в степени 2, а пороговые значения возвращаются как ноль.

//+------------------------------------------------------------------+
//|Upside potential ratio                                            |
//+------------------------------------------------------------------+
double upsidePotentialRatio(double &rt[])
  {
   double rb[];

   if(ArrayResize(rb,ArraySize(rt))<0)
     {
      Print(__FUNCTION__, " Resize error ",GetLastError());
      return 0;
     }

   ArrayInitialize(rb,0.0);

   double pmomentu=MathPow(partialmoment(2,rt,rb,true),0.5);
   double pmomentl=MathPow(partialmoment(2,rt,rb),0.5);
   if(pmomentl)
      return pmomentu/pmomentl;
   else
      return 0;
  }

Расчеты частичных моментов реализованы в функции partsmoment(). В качестве входных данных требуются степень момента в виде целого числа без знака, два массива типа double и логическое значение. Первый массив должен содержать наблюдаемую доходность, а второй — пороговую или эталонную доходность, использованную в расчетах. Логическое значение определяет тип вычисляемого частичного момента: true для высокого частичного момента и false для низкого частичного момента.

//+------------------------------------------------------------------+
//|Partial Moments                                                   |
//+------------------------------------------------------------------+
double partialmoment(const uint n,double &rt[],double &rtb[],bool upper=false)
  {
   double pm[];
   int insize=ArraySize(rt);

   if(n)
     {
      if(ArrayResize(pm,insize)<insize)
        {
         Print(__FUNCTION__," resize error ", GetLastError());
         return 0;
        }

      for(int i=0; i<insize; i++)
         pm[i] = (!upper)?MathPow(MathMax(rtb[i]-rt[i],0),n):MathPow(MathMax(rt[i]-rtb[i],0),n);
      return MathMean(pm);
     }
   else
     {
      int k=0;
      for(int i=0; i<insize; i++)
        {
         if((!upper && rtb[i]>=rt[i]) || (upper && rt[i]>rtb[i]))
           {
            ArrayResize(pm,k+1,1);
            pm[k]=rt[i];
            ++k;
           }
         else
            continue;
        }

      return MathMean(pm);

     }

  }

Глядя на коэффициенты Омега и UPR наших кривых эквити, мы замечаем сходство рейтинга с коэффициентом Шарпа.

Опять же, последовательность предпочтительнее более волатильных кривых эквити. Омега определенно выглядит как жизнеспособная альтернатива коэффициенту Шарпа.

Интерпретация соотношения частичных моментов

Омега гораздо более прямолинейна, когда дело доходит до интерпретации по сравнению с UPR. Чем выше омега, тем лучше. Отрицательные значения указывают на убыточные стратегии, а положительные значения предполагают доходность, превышающую уровень риска.

С другой стороны, UPR может показаться немного странным, когда дело доходит до интерпретации. Взгляните на некоторые смоделированные кривые эквити с расходящимися профилями производительности.

Синяя кривая эквити показывает отрицательную доходность, однако результат UPR положительный. Еще более странными выглядят результаты зеленой и красной кривых эквити. Сами кривые почти аналогичны: зеленая кривая капитала дает более высокую доходность, но значение UPR меньше, чем у красной кривой.

Регрессионный анализ доходности – Альфа Дженсена

Линейная регрессия позволяет построить линию, которая лучше всего соответствует набору данных. Таким образом, показатели, основанные на регрессии, измеряют линейность кривых капитала. Альфа Дженсена вычисляет значение альфа в стандартном уравнении регрессии. Он количественно определяет взаимосвязь между эталонной и наблюдаемой доходностью.

Чтобы вычислить значение альфы, мы можем использовать метод наименьших квадратов. Функция leastsquarefit() принимает в качестве входных данных два массива, которые определяют ответ и предиктор. В этом контексте ответом будет массив наблюдаемых доходностей, а предиктором — массив эталонных доходностей. Функция выводит альфа- и бета-значения, ссылки на которые должны быть предоставлены при вызове функции.

//+------------------------------------------------------------------+
//|linear model using least squares fit y=a+bx                       |
//+------------------------------------------------------------------+
double leastsquaresfit(double &y[],double &x[], double &alpha,double &beta)
  {
   double esquared=0;

   int ysize=ArraySize(y);
   int xsize=ArraySize(x);

   double sumx=0,sumy=0,sumx2=0,sumxy=0;

   int insize=MathMin(ysize,xsize);

   for(int i=0; i<insize; i++)
     {
      sumx+=x[i];
      sumx2+=x[i]*x[i];
      sumy+=y[i];
      sumxy+=x[i]*y[i];
     }

   beta=((insize*sumxy)-(sumx*sumy))/((insize*sumx2)-(sumx*sumx));
   alpha=(sumy-(beta*sumx))/insize;

   double pred,error;

   for(int i=0; i<insize; i++)
     {
      pred=alpha+(beta*x[i]);
      error=pred-y[i];
      esquared+=(error*error);
     }

   return esquared;

  }

Применяя Альфа Дженсена к нашим смоделированным кривым капитала, мы получаем меру линейности зеленой и синей кривых капитала относительно эталона (красная кривая эквити).

Это первый показатель, который оценивает синюю кривую эквити как наиболее эффективную стратегию. Этот показатель обычно вознаграждает за хорошую производительность, когда результаты контрольных показателей плохие. Альфа Дженсена может указывать на положительную доходность, даже если абсолютная доходность отрицательна. Это может произойти, когда абсолютная эталонная доходность просто хуже, чем изучаемая доходность. Поэтому будьте осторожны при использовании этого показателя.

Интерпретация Альфы Дженсена

Если Альфа Дженсена положительна, это говорит о том, что портфель/стратегия принесла избыточную доходность по сравнению с контрольным показателем, что указывает на превосходство результатов после рассмотрения уровня риска. Если Альфа Дженсена отрицательна, это означает, что стратегия не принесла результатов по сравнению с эталонной доходностью.

Помимо значения альфа, значение бета, полученное методом наименьших квадратов, обеспечивает меру чувствительности доходности по отношению к эталону. Бета, равная 1, указывает на то, что доходность стратегии меняется синхронно с эталонным показателем. Бета меньше 1 предполагает, что кривая капитала менее волатильна, чем кривая эталона, тогда как бета больше 1 указывает на более высокую волатильность.

Заключение

Мы описали реализацию нескольких показателей доходности с поправкой на риск, которые можно использовать в качестве альтернативы коэффициенту Шарпа. На мой взгляд, лучший кандидат — это показатель омега. Он обеспечивает те же преимущества, что и коэффициент Шарпа, без каких-либо ожиданий нормальности распределения доходов. Однако следует также отметить, что при принятии инвестиционных решений лучше учитывать несколько показателей эффективности стратегии. Ни один показатель не сможет дать полную картину ожидаемого риска или доходности. Также помните, что большинство показателей доходности риска представляют собой ретроспективные измерения, и прошлые результаты не гарантируют будущих результатов. Поэтому при оценке вариантов инвестирования важно учитывать другие факторы, такие как инвестиционные цели, временной горизонт и толерантность к риску.

Исходный код всех показателей содержится в PerformanceRatios.mqh. Следует отметить, что ни одна из реализаций не дает годовых показателей. Прикрепленный zip-файл также содержит код приложения, используемого для визуализации наших смоделированных кривых капитала. Приложение реализовано с помощью библиотеки EasyAndFastGUI, доступной в CodeBase на сайте mql5.com. К статье приложены исходный код советника и рабочая скомпилированная версия.

Имя файла	Описание
Mql5\Files\sp500close.csv	CSV-файл с ценами закрытия SP500, используемый при расчете кривых эквити
Mql5\Include\PerformanceRatios.mqh	Включаемый файл, содержащий определения всех показателей производительности, описанных в статье
Mql5\Experts\EquityCurves.mq5	Исходный код советника для инструмента визуализации. Для его компиляции требуется простой и быстрый графический интерфейс, доступный в CodeBase
Mql5\Experts\EquityCurves.ext	Скомпилированная версия советника