MQL5における代替リスクリターン指標

はじめに

すべてのトレーダーは、投資に対するリターンの割合を可能な限り最大化したいと願っていますが、高いリターンは通常、高いリスクを伴います。これが、投資業界においてリスク調整後リターンがパフォーマンスの主な尺度となっている理由です。リスク調整後リターンの尺度にはさまざまなものがあり、それぞれに長所と短所があります。シャープレシオは、分析対象のリターン分布に非現実的な前提条件を課すことで有名な、一般的なリスクリターン指標です。これは、必然的に、シャープレシオの欠点なしに、同じような普遍性を提供しようとする代替的なパフォーマンス指標の開発につながりました。本稿では、代替的なリスクリターン指標の実装を提供し、仮想資本曲線を作成してその特性を分析します。

模擬資本曲線

解釈のしやすさを確保するため、SP500のデータを模擬取引戦略の基礎として使用します。特定の売買ルールは用いず、乱数を用いて資本曲線とそれに対応する一連のリターンを生成します。初期資本金は設定可能な金額に統一されます。乱数はシードによって定義されるので、実験を再現したい人は誰でもできます。

資本曲線の視覚化

下の図は、エキスパートアドバイザー(EA)として実装されたMetatrader 5 (MT5)アプリケーションで、3つの資本曲線を表示しています。赤の資本曲線は、青と緑の資本曲線の元となるベンチマークです。ベンチマークは、初期資本を設定することで変更できます。アプリケーションから調整可能です。 

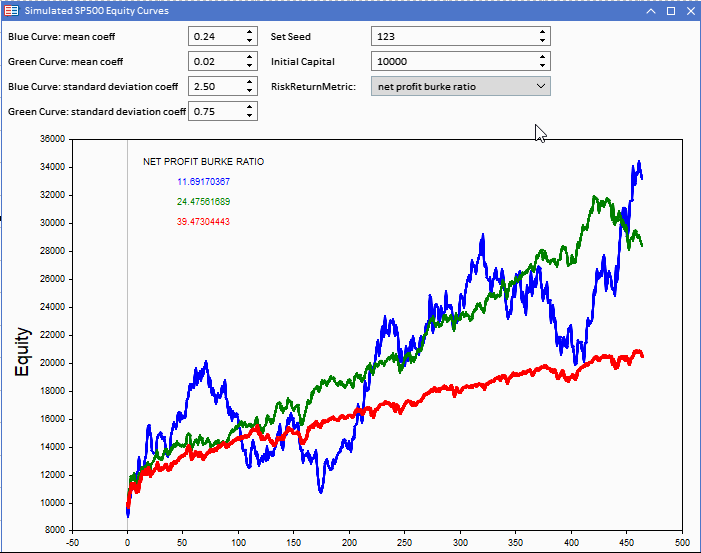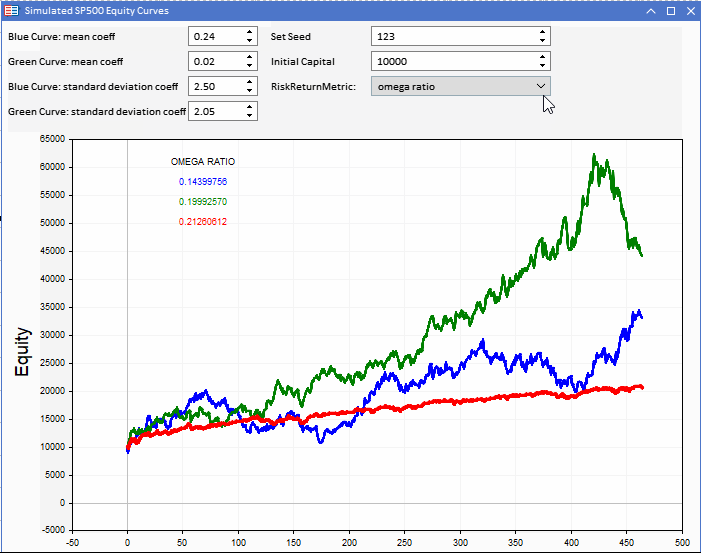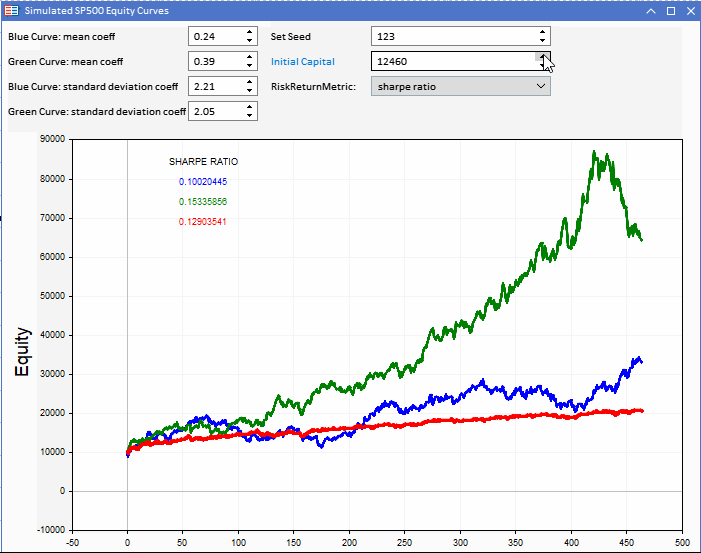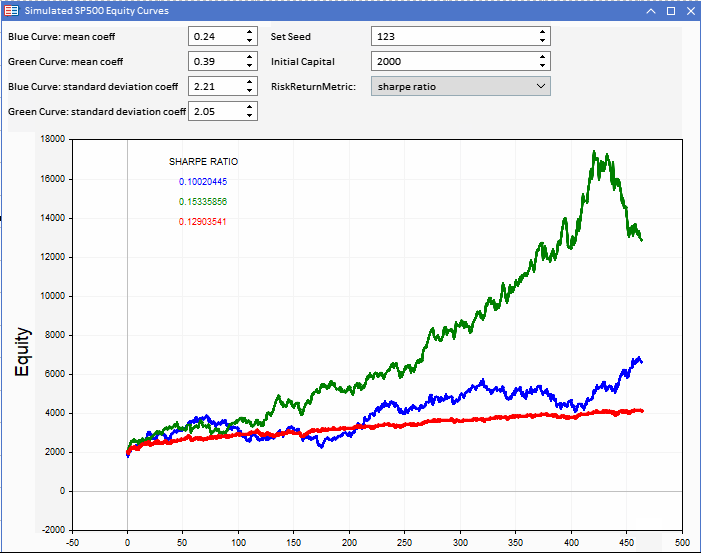
資本曲線はベンチマークシリーズに基づいて作成されます。それぞれは、2つの調整可能な定数によって制御できるランダムな構成要素によって定義されます。平均係数と標準偏差係数です。これらとベンチマークリターンの標準偏差を組み合わせて、2つの仮想資本曲線を生成するために使用される正規分布乱数のパラメータを決定します。   

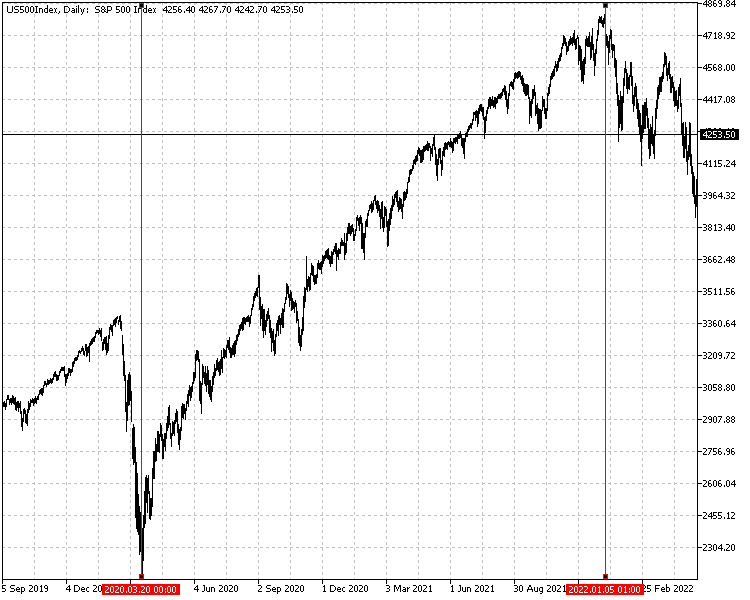
まず、SP500の2020年3月20日から2022年1月5日までの日次終値を使用してリターンを計算します。資本曲線は一連のリターンから作られます。エクイティとリターンを定義するシリーズを使って、所定の資本曲線の外観とともに計算されたパフォーマンス結果を比較します。

アプリケーションのコードは記事に添付されています。

ドローダウン比

ドローダウンは、ストラテジーがある2つの時点の間に失ったエクイティの最大量を示します。この値は、利益が得られたとしても、その利益を達成するために戦略が負うリスクを示すものです。任意の数の最高ドローダウンからなるシリーズを集計すると、その結果を変動性の尺度として使用することができます。

バークレシオ

1994年、バークは「A sharper sharpe ratio」と題する論文を執筆し、おなじみのシャープレシオに代わるものとしてバークレシオを紹介しました。バークレシオは、シャープレシオの計算式の分母を、指定された最高絶対ドローダウンの数の二乗和に置き換えたものです。分子は、平均リターンか、戦略/ポートフォリオの絶対的な金銭的リターン、すなわち純利益のいずれかとすることができます。2つのバージョンの計算を見てみましょう。純利益ベースのバークレシオと平均リターンのバークレシオとして2つのバージョンを区別します。計算式を以下に示します。

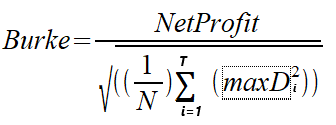
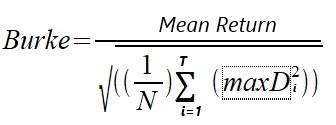
MaxDは、株式価値から計算された最大のT絶対ドローダウンの系列です。Nは、計算に使用される資産価値の数を表します。

純利益バークレシオはnetprofit_burke()関数として実装されています。この関数は、資本曲線を記述するエクイティ値の配列と、計算で考慮する最高ドローダウンの数を示す整数値を必要とします。

//+------------------------------------------------------------------+
//|Net profit based Burke ratio                                      |
//+------------------------------------------------------------------+
double netprofit_burke(double &in_ec[],int n_highestdrawdowns=0)
  {
   double outdd[];
   double sumdd=0;
   int insize=ArraySize(in_ec);

   if(n_highestdrawdowns<=0)
      n_highestdrawdowns=int(insize/20);

   if(MaxNDrawdowns(n_highestdrawdowns,in_ec,outdd))
     {
      for(int i=0; i<ArraySize(outdd); i++)
        {
         sumdd+=(outdd[i]*outdd[i]);
        }
      return (in_ec[insize-1]-in_ec[0])/(MathSqrt((1.0/double(insize)) * sumdd));
     }
   else
      return 0;
  }

デフォルト値であるゼロが指定された場合、この関数は考慮すべきドローダウンの回数を設定するためにN/20という式を使用します。

指定された回数のドローダウンを収集するために、MaxNDradowns()関数が使用されます。絶対ドローダウンの値が最も大きいものを昇順に並べて出力します。

//+------------------------------------------------------------------+
//|Maximum drawdowns function given equity curve                     |
//+------------------------------------------------------------------+
bool MaxNDrawdowns(const int num_drawdowns,double &in_ec[],double &out_dd[])
  {
   ZeroMemory(out_dd);

   ResetLastError();

   if(num_drawdowns<=0)
     {
      Print("Invalid function parameter for num_drawdowns ");
      return false;
     }
   double u[],v[];

   int size = ArraySize(in_ec);

   if((ArrayResize(v,(size*(size-1))/2)< int((size*(size-1))/2))||
      (ArraySize(out_dd)!=num_drawdowns && ArrayResize(out_dd,num_drawdowns)<num_drawdowns))
     {
      Print(__FUNCTION__, " resize error ", GetLastError());
      return false;
     }

   int k=0;
   for(int i=0; i<size-1; i++)
     {
      for(int j=i+1; j<size; j++)
        {
         v[k]=in_ec[i]-in_ec[j];
         k++;
        }
     }

   ArraySort(v);

   for(int i=0; i<k; i++)
     {
      if(v[i]>0)
        {
         if(i)
           {
            if(!ArrayRemove(v,0,i))
              {
               Print(__FUNCTION__, " error , ArrayRemove: ",GetLastError());
               return false;
              }
            else
               break;
           }
         else
            break;
        }
     }

   size=ArraySize(v);

   if(size && size<=num_drawdowns)
     {
      if(ArrayCopy(out_dd,v)<size)
        {
         Print(__FUNCTION__, " error ", GetLastError());
         return false;
        }
      else
         return (true);
     }


   if(ArrayCopy(out_dd,v,0,size-num_drawdowns,num_drawdowns)<num_drawdowns)
     {
      Print(__FUNCTION__, " error ", GetLastError());
      return false;
     }


   return(true);

  }

平均リターンを分子とするバークレシオ計算は、meanreturns_burke関数として実装されており、同様の入力パラメータを持っています。

//+------------------------------------------------------------------+
//|Mean return based Burke ratio                                     |
//+------------------------------------------------------------------+
double meanreturns_burke(double &in_ec[],int n_highestdrawdowns=0)
  {
   double outdd[];
   double rets[];

   double sumdd=0;
   int insize=ArraySize(in_ec);

   if(ArrayResize(rets,insize-1)<insize-1)
     {
      Print(__FUNCTION__," Memory allocation error ",GetLastError());
      return 0;
     }

   for(int i=1; i<insize; i++)
      rets[i-1] = (in_ec[i]/in_ec[i-1]) - 1.0;

   if(n_highestdrawdowns<=0)
      n_highestdrawdowns=int(insize/20);

   if(MaxNDrawdowns(n_highestdrawdowns,in_ec,outdd))
     {
      for(int i=0; i<ArraySize(outdd); i++)
         sumdd+=(outdd[i]*outdd[i]);
      return MathMean(rets)/(MathSqrt((1.0/double(insize)) * sumdd));
     }
   else
      return 0;
  }

純利益対最大ドローダウン比

純利益を分子とするバークレシオの計算式は、純利益対最大ドローダウン比(NPMD)に似ています。この違いは、NPMD比の計算において、最も高いドローダウン1回分を使用する点にあります。

NPMDの計算はnetProfiMaxDD()関数として実装され、株式価値の配列を入力として必要とします。

//+------------------------------------------------------------------+
//|Net profit to maximum drawdown ratio                              |
//+------------------------------------------------------------------+
double netProfiMaxDD(double &in_ec[])
  {
   double outdd[];
   int insize=ArraySize(in_ec);

   if(MaxNDrawdowns(1,in_ec,outdd))
      return ((in_ec[insize-1]-in_ec[0])/outdd[0]);
   else
      return 0;
  }

ドローダウンに基づく比率は、シャープレシオに対する批判のいくつかに対処するために導入されました。この計算では、異常なゲインや大きなゲインにペナルティが課されることはなく、最も重要なのはノンパラメトリックであることです。有利ではありますが、分母にドローダウンの絶対値を使うため、バークレシオもNPMD比も、下降スパイクが比較的穏やかな戦略が有利になります。

資本曲線の視覚化ツールを指します。青い曲線は最もリターンが高いが、他の曲線よりスコアは低くなります。

両レシオのベンチマーク値は、戦略のパフォーマンスを比較するために使用する場合、この指標がいかに誤解を招きやすいかを強調しています。ベンチマークレシオは、他の曲線の方が実質リターンが高いにもかかわらず、かなり高くなっています。

絶対ドローダウンを用いると、シャープレシオのように負のリターンの分布を用いる場合と比べて、リスクが過度に強調される可能性があります。

シャープスコアを比較すると、緑色の曲線が最も高く、模擬戦略の結果との差がかなり少ないことがわかります。

ドローダウン比の解釈

バークレシオまたはNPMDレシオが高いほど、投資戦略のリスク調整後パフォーマンスが優れていることになります。これは、その戦略が取ったリスクに比べ高いリターンを生み出していることを意味します。

-バークレシオまたはNPMDレシオが0より大きい場合、その投資戦略は計算されたリスクと比較して超過リターンを提供していることが示されます。

-バークレシオまたはNPMDレシオが0より小さい場合、投資戦略が取ったリスクに比べ十分な超過リターンを生み出していないことが示されます。

部分モーメント比

部分モーメントに基づく比率は、シャープレシオに代わるもう一つの試みです。これらは、半分散の統計概念に基づいており、上向きの可能性（正のリターン）と比較して、下向きのリスク（負のリターン）の観点から戦略がどの程度うまく機能しているかについての洞察を提供します。部分モーメント比を計算するには、まず部分的な利益と部分的な損失を決定する必要があります。これらの値は、しきい値リターンレベル（通常は許容可能な最小リターンまたはリスクフリーレート）を特定し、各オブザベーションについて実際のリターンとしきい値リターンとの差を計算することによって導き出されます。

この計算では、下位部分モーメント(LPM)の閾値以上、または上位部分モーメント(HPM)の閾値未満の差は無視することができます。LPMは、しきい値を下回るリターンの2乗偏差を測定し、HPMは、しきい値を上回るリターンの2乗偏差を測定します。部分モーメントは、特定の閾値を下回ったり上回ったりするリターンに関連するリスクに焦点を当てることで、ドローダウン比と比較してリスクに関する別の視点を提示します。

以下は、LPMとHPMそれぞれの計算式です。

ここで、threshは閾値、xは観測されたリターン、maxは結果の差とn乗される前のゼロとの間の最大値を決定します。nは部分モーメントの次数を定義します。n=0のとき、LPMはオブザベーションが閾値より小さい確率となり、HPMは閾値より大きい確率となります。Nは観測されたリターンの数です。ここでは、一般化オメガとアップサイドポテンシャル比(UPR)の2つの部分モーメント比を取り上げます。

オメガ

一般化オメガは、n次の項と、計算に使用するLPMを定義する閾値によって定義されます。

omega()関数は、リターンの配列を入力としてオメガ比の計算をおこないます。この関数は次数2の下位部分モーメントを使用し、閾値の戻りはゼロとします。

//+------------------------------------------------------------------+
//|omega ratio                                                       |
//+------------------------------------------------------------------+
double omega(double &rt[])
  {
   double rb[];

   if(ArrayResize(rb,ArraySize(rt))<0)
     {
      Print(__FUNCTION__, " Resize error ",GetLastError());
      return 0;
     }

   ArrayInitialize(rb,0.0);

   double pmomentl=MathPow(partialmoment(2,rt,rb),0.5);

   if(pmomentl)
      return MathMean(rt)/pmomentl;
   else
      return 0;
  }

アップサイドポテンシャル比

UPRでは、2 つのn次項（式のn1とn2）としきい値が使用されます。n1は分子のHPM次数を決定し、n2は分母のLPM次数を指定します。

オメガのパフォーマンス指標の実装と同様に、upsidePotentialRatio()関数はUPRレシオを計算します。この計算には次数2の部分モーメントも使用し、閾値はゼロと定義されています。

//+------------------------------------------------------------------+
//|Upside potential ratio                                            |
//+------------------------------------------------------------------+
double upsidePotentialRatio(double &rt[])
  {
   double rb[];

   if(ArrayResize(rb,ArraySize(rt))<0)
     {
      Print(__FUNCTION__, " Resize error ",GetLastError());
      return 0;
     }

   ArrayInitialize(rb,0.0);

   double pmomentu=MathPow(partialmoment(2,rt,rb,true),0.5);
   double pmomentl=MathPow(partialmoment(2,rt,rb),0.5);
   if(pmomentl)
      return pmomentu/pmomentl;
   else
      return 0;
  }

部分モーメント計算はpartialmoment()関数で実装されています。入力として、符号なし整数としてのモーメントの次数、double型の2つの配列、およびブール値を必要とします。最初の配列には観測されたリターンを、2番目の配列には計算で使用したしきい値またはベンチマークのリターンを入れます。ブーリアン値は、計算される部分モーメントのタイプを決定し、高い部分モーメントの場合はtrue、低い部分モーメントの場合はfalseとなります。

//+------------------------------------------------------------------+
//|Partial Moments                                                   |
//+------------------------------------------------------------------+
double partialmoment(const uint n,double &rt[],double &rtb[],bool upper=false)
  {
   double pm[];
   int insize=ArraySize(rt);

   if(n)
     {
      if(ArrayResize(pm,insize)<insize)
        {
         Print(__FUNCTION__," resize error ", GetLastError());
         return 0;
        }

      for(int i=0; i<insize; i++)
         pm[i] = (!upper)?MathPow(MathMax(rtb[i]-rt[i],0),n):MathPow(MathMax(rt[i]-rtb[i],0),n);
      return MathMean(pm);
     }
   else
     {
      int k=0;
      for(int i=0; i<insize; i++)
        {
         if((!upper && rtb[i]>=rt[i]) || (upper && rt[i]>rtb[i]))
           {
            ArrayResize(pm,k+1,1);
            pm[k]=rt[i];
            ++k;
           }
         else
            continue;
        }

      return MathMean(pm);

     }

  }

資本曲線のオメガレシオとUPRレシオを見ると、シャープレシオの格付けと類似していることに気づきます。

ここでも、ボラティリティの高い資本曲線よりも一貫性が好まれます。オメガは特に、シャープレシオに代わる有効な選択肢のように見えます。

部分モーメント比の解釈

オメガは、UPRとの関連で言えば、その解釈はもっと単純明快です。オメガは高ければ高いほどよくなります。負の数値は損をする戦略を示し、正の数値はリスクに比して超過リターンをもたらすパフォーマンスを示唆します。

一方、UPRの解釈に関しては、少し変わり種である可能性があります。発散するパフォーマンスプロファイルを持つ模擬資本曲線をいくつかご覧ください。

青い資産は負のリターンを示していますが、UPRの結果は正です。さらに奇妙なのは、緑と赤の資本曲線の結果です。曲線自体はほぼ類似しており、緑色の資本曲線の方が優れたリターンを上げていますが、UPRの値は赤色の曲線より小さくなっています。

リターンの回帰分析 - ジェンセンのアルファ

線形回帰は，データ集合に最もよく適合する直線の構築を可能にします。したがって、回帰に基づく指標は、資本曲線の直線性を測定します。ジェンセンのアルファは、標準回帰式におけるアルファの値を計算します。これは、ベンチマークリターンと観測リターンとの関係を定量化したものです。

アルファ値を計算するには、最小二乗法を使うことができます。関数leastsquarefit()は，応答と予測変数を定義する2つの配列を入力としてとります。この文脈では、応答は観察されたリターンの配列であり、予測変数はベンチマークのリターンの配列です。この関数は、関数を呼び出すときに参照を指定する必要があるアルファ値とベータ値を出力します。

//+------------------------------------------------------------------+
//|linear model using least squares fit y=a+bx                       |
//+------------------------------------------------------------------+
double leastsquaresfit(double &y[],double &x[], double &alpha,double &beta)
  {
   double esquared=0;

   int ysize=ArraySize(y);
   int xsize=ArraySize(x);

   double sumx=0,sumy=0,sumx2=0,sumxy=0;

   int insize=MathMin(ysize,xsize);

   for(int i=0; i<insize; i++)
     {
      sumx+=x[i];
      sumx2+=x[i]*x[i];
      sumy+=y[i];
      sumxy+=x[i]*y[i];
     }

   beta=((insize*sumxy)-(sumx*sumy))/((insize*sumx2)-(sumx*sumx));
   alpha=(sumy-(beta*sumx))/insize;

   double pred,error;

   for(int i=0; i<insize; i++)
     {
      pred=alpha+(beta*x[i]);
      error=pred-y[i];
      esquared+=(error*error);
     }

   return esquared;

  }

模擬資本曲線にジェンセンのアルファを適用すると、ベンチマーク（赤の資本曲線）に対する緑と青の資本曲線の直線性の尺度が得られます。

これは、青い資本曲線を最高のパフォーマンス戦略として評価した最初の指標です。この指標は通常、ベンチマークリターンが悪いときに、良いパフォーマンスに報いるものです。絶対リターンが負であっても、ジェンセンのアルファが正のリターンを示すことは可能です。これは、ベンチマークの絶対リターンが調査対象のリターンより単純に悪い場合に起こり得ます。この指標を使うときには注意が必要です。

ジェンセンのアルファの解釈

ジェンセンのアルファが正の場合、そのポートフォリオ/戦略はベンチマークと比較して超過リターンを生み出していることを示唆し、リスクレベルを考慮した上でアウトパフォームを示しています。そうでない場合、ジェンセンのアルファが負であれば、その戦略はベンチマークのリターンに比べてパフォーマンスを下回っています。

アルファ値の他に、最小二乗計算によるベータ値もベンチマークに対するリターンの感応度を測る指標となります。ベータが1であれば、戦略のリターンがベンチマークと同調して動くことを示します。ベータが1未満は、資本曲線がベンチマークのそれよりもボラティリティが低いことを示唆し、ベータが1より大きい場合はボラティリティが高いことを示す。

結論

ここまで、シャープレシオに代わるリスク調整後リターンの指標をいくつか紹介してきました。私の考えでは、最有力候補はオメガ指標です。リターンの分布に正規性を期待することなく、シャープレシオと同じ利点が提供されます。しかし、投資判断を下す際には、複数の戦略パフォーマンス指標を考慮した方が良いということにも留意すべきです。期待されるリスクやリターンの全体像を提供することは決してできません。また、ほとんどのリスクリターン指標は遡及的な指標であり、過去の実績が将来の結果を保証するものではないことを忘れないでください。したがって、投資オプションを評価する際には、投資目的、時間軸、リスク許容度など、他の要素も考慮することが重要です。

すべての指標のソースコードは、PerformanceRatios.mqhに含まれています。注意すべきなのは、どの実装も年率換算した数字を出していないことです。添付のZIPファイルには、模擬資本曲線を可視化するためのアプリケーションのコードも含まれています。これは、mql5.comコードベースで利用可能なEasyAndFastGUIライブラリを使用して実装されています。ライブラリは記事には添付されていません。添付されているのは、EAのソースコードとコンパイル済みバージョンです。

ファイル名	詳細
Mql5\Files\sp500close.csv	資本曲線の計算に使用したSP500終値のcsvファイル
Mql5IncludePerformanceRatios.mqh	記事で説明したすべてのパフォーマンス指標の定義が含まれているインクルードファイル
Mql5\Experts\EquityCurves.mq5	可視化ツールのEAソースコード（コンパイルするにはコードベースにある簡単で高速なGUIが必要です）
Mql5\Experts\EquityCurves.ext	EAのコンパイル済みバージョン