私はBayesianOptimisationで実験しました。
あなたは最適化可能な9つのパラメータの最大のセットを持っていました。そして、計算に時間がかかるとおっしゃいました。
10個の最初のランダムセットで最適化する20個のパラメータセットを試してみました。NS自体の計算時間を考慮せずに、BayesianOptimisationで組み合わせを計算するのに1.5時間かかりました(NSを実験のための簡単な数式に置き換えました)。
また、50や100のパラメータを最適化したい場合、1セットの計算に24時間かかるでしょう。ランダムな組み合わせを何十通りも生成してNSで計算し、Accuracyで最適なものを選択した方が早いと思います。
パッケージのディスカッションでこの問題について述べられている。1年前に著者は、もしもっと高速な計算パッケージが見つかったらそれを使うつもりだが、今のところは今のままだ、と書いている。
bigGp - 例題のSN2011feデータセットが見つからない(どうやらインターネットからダウンロードしたようで、ページが利用できない)。私はその例を試すことができなかった。
laGP - 適性関数に紛らわしい式があり、その呼び出しが数百回行われ、NSの計算が数百回行われる。例えば100のうち10。つまり、100の集合を最適化することはできない。
遺伝的アルゴリズムも フィットネス関数(NS計算)を何百回も呼び出すので、適していない。
一般的に、類似の方法はありませんし、BayesianOptimisation自体も長すぎます。
私はBayesianOptimisationで実験しました。
あなたは最適化可能な9つのパラメーターの最大のセットを持っていました。そして、あなたは計算に時間がかかったと言いました。
私は10個の最初のランダムセットで最適化する20個のパラメータセットを試しました。BayesianOptimisationで組み合わせそのものを計算するのに1.5時間かかりましたが、NSそのものを計算する時間は考慮に入れていません(NSを実験のための簡単な数式に置き換えました)。
また、50個や100個のパラメータを最適化する場合、1セットの計算に24時間かかるでしょう。ランダムな組み合わせを何十通りも生成してNSで計算し、精度で最適なものを選んだ方が早いと思います。
パッケージのディスカッションでこの問題について述べられている。1年前、著者は、もしもっと高速な計算パッケージが見つかったら、それを使うつもりだが、今のところは-現状のままだ、と書いている。
bigGp - 例題のSN2011feデータセットが見つからない(インターネットからダウンロードしたものらしく、ページがない)。私はその例を試すことができなかった。
laGP - 適性関数に紛らわしい式があり、その呼び出しが数百回行われ、NSの計算が数百回行われる。例えば100のうち10。つまり、100の集合を最適化することはできない。
遺伝的アルゴリズムも、フィットネス関数の呼び出し(NS計算)が何百回も発生するため、適していない。
一般に、類似のものはなく、BayesianOptimisation自体が長すぎる。
このような問題がある。それは、このパッケージが純粋なRで書かれているという事実と関係している。しかし、私個人としては、このパッケージを使う利点は時間的コストを上回る。hyperopt(Python)というパッケージがあります。
でも、誰かがこのパッケージをC++で書き直すと思う。もちろん、自分で計算の一部をGPUに移すこともできるが、それにはかなりの時間がかかる。本当に切羽詰まったときだけだ。
今のところ、私は今あるものを使うつもりだ。
幸運を祈る。
また、GPfitパッケージ自体の例でも実験してみました。
頂点が2つの曲線を記述する1つのパラメータを最適化する例です(GPfit f-yaはもっと頂点があるので、2つのままにしました):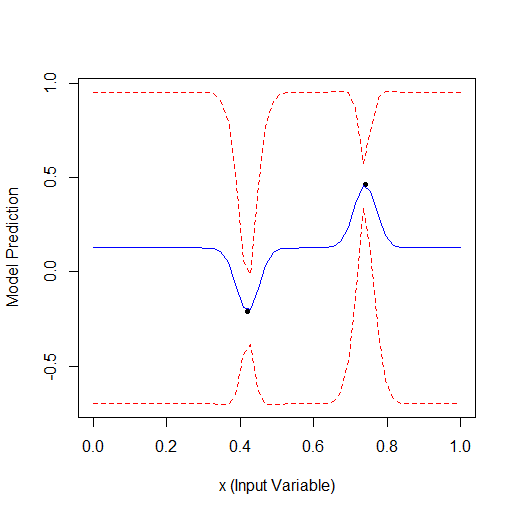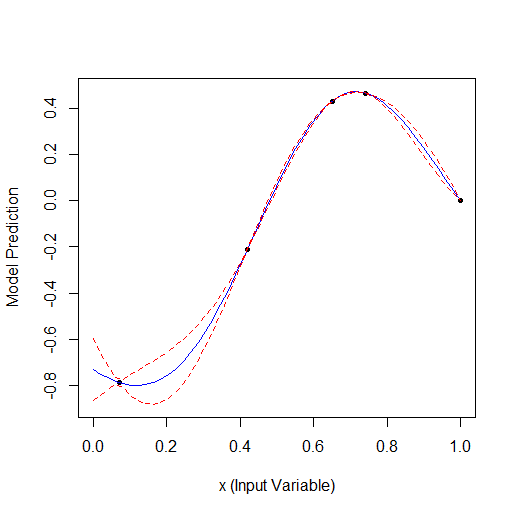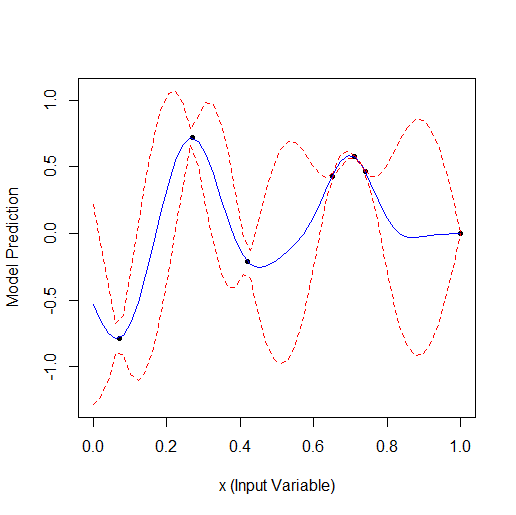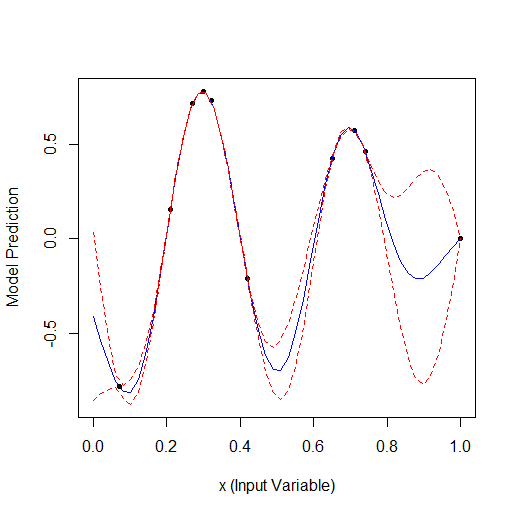
ランダムに2点を取り、最適化します。まず小さい頂点が見つかり、次に大きい頂点が見つかるのがわかります。合計9回の計算-ランダム2回と最適化7回。
2Dでのもう一つの例-2つのパラメータを最適化する。元のf-yは次のようになる: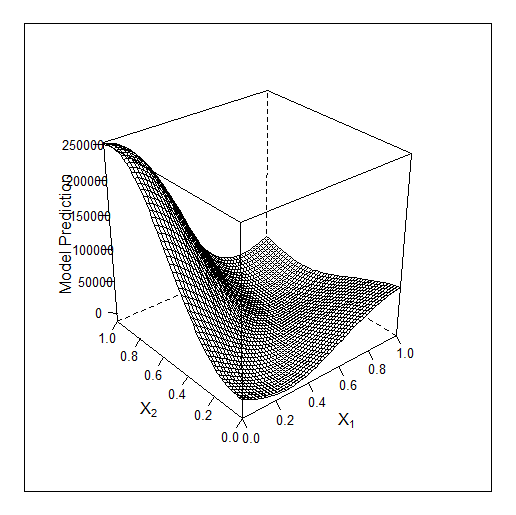
19点に最適化:

これらの2つの例を比較すると、1つのパラメータを追加した場合、最大値を求めるのに必要な反復回数が2倍になることがわかります。
つまり、10個のパラメータを最適化する場合、9 * 2^10 = 9000回の計算が必要になります。
14点でアルゴリズムはほぼ最大値を見つけたが、これは計算回数の約1.5倍である。また、許容できる計算時間にしては多い。
記事で得られた20~30点の結果は、実際の最大値からはかけ離れているかもしれない。
遺伝的アルゴリズムでは、このような単純な例であっても、計算にはもっと多くのポイントが必要になると思います。ですから、これ以上の選択肢はないでしょう。
また、GPfitパッケージ自体の例でも実験してみました。
以下は、頂点が2つの曲線を記述する1つのパラメータを最適化する例です(GPfit f-yaはもっと頂点が多いので、2つのままにしました):
ランダムに2点を取り、最適化します。まず小さい頂点が見つかり、次に大きい頂点が見つかるのがわかります。合計9回の計算-ランダム2回と最適化7回。
2Dの別の例-2つのパラメータを最適化。元のf-yaは次のようになる:
19点まで最適化する:
これらの2つの例を比較すると、1つのパラメータを追加した場合、最大値を求めるのに必要な反復回数が2倍になることがわかります。
つまり、10個のパラメータを最適化する場合、9 * 2^10 = 9000回の計算が必要になります。
14点でアルゴリズムはほぼ最大値を見つけたが、これは計算回数の約1.5倍である。また、許容できる計算時間の割には多い。
1.この記事で得られた20~30点の結果は、実際の最大値からはかけ離れているかもしれない。
遺伝的アルゴリズムでは、このような単純な例でも、もっと多くのポイントを計算する必要があると思います。結局のところ、これ以上の選択肢はないのだろう。
ブラボー。
素晴らしい。
YouTubeには、ベイズ最適化の仕組みを説明した講義がたくさんあります。まだ見たことがなければ、ぜひ見てほしい。とても参考になる。
どうやってアニメーションを挿入したのですか?
可能な限りベイズ法を使うようにしています。結果はとてもいい。
1.私は逐次最適化を行っている。最初にランダムな10点を初期化し、10~20点の計算を行い、次に前回の最適化で得られた最良の10点を初期化し、10~20点の計算を行う。通常、2回目の反復の後、結果は意味のある改善には至りません。
幸運を祈る
YouTubeにベイズ最適化の仕組みを説明する講義が多数アップされている。まだご覧になったことがない方は、ぜひご覧になることをお勧めする。とても参考になる。
私はコードと結果を写真で見た(そしてあなたに見せた)。一番重要なのはGPfitのガウシアンプロセスです。そして、最適化は最も一般的なもので、標準的なRのオプティマイザを使い、GPfitが2点、3点などで出した曲線/形状の最大値を探すだけです。GPfitが導き出したものは、上のアニメーションで見ることができます。このオプティマイザーは、上位100点のランダムな点を取り出そうとしているだけなのだ。
将来、時間があるときに講義を見るかもしれないが、今はGPfitをブラックボックスとして使うことにしよう。
どうやってアニメーションを挿入したのですか?
GPfit::plot.GP(GP、surf_check = TRUE)の結果をステップバイステップで表示し、それをPhotoshopに貼り付けてアニメーションGIFとして保存しただけです。
次のように、前回の最適化で得られたベスト10の 結果を初期化し、10-20点の計算を行いました。
私の実験によると、今後の計算のために、既知の点はすべて残しておいたほうがよいようです。なぜなら、低い点が削除されると、GPfitは面白い点があると考え、その点を計算したがるかもしれないからです。また、これらの低いポイントでは、GPfitはこれらの低い領域には探すべきものがないことを知ることになる。
しかし、もし結果があまり改善されないのであれば、それは小さな揺らぎを持つ広範なプラトーが存在することを意味します。
インストールと起動方法
).

- 2016.04.26
- Vladimir Perervenko
- www.mql5.com
最適パラメータによるモデルのフォワードテスト
DNNの最適パラメータが、"将来の "相場値のテストにおいて、どれくらいの期間、許容できる品質の結果を生み出すかをチェックしてみよう。テストは、前の最適化とテストの後に残った環境で、以下のように実行される。
1350バーの移動ウィンドウを使用し、train = 1000、test = 350 (検証用-最初の250サンプル、テスト用-最後の100サンプル)、ステップ100で、プレトレーニングに使用した最初の(4000 + 100)バーの後のデータを通過する。10ステップを "前進 "させる。各ステップでは、2つのモデルがトレーニングされ、テストされる:
- すなわち、各ステップで新しいレンジで微調整を行う;
- 2つ目は、微調整段階での最適化後に得られたDNN.optを新しいレンジで追加学習する 。
#---prepare----
evalq({
step <- 1:10
dt <- PrepareData(Data, Open, High, Low, Close, Volume)
DTforv <- foreach(i = step, .packages = "dplyr" ) %do% {
SplitData(dt, 4000, 1000, 350, 10, start = i*100) %>%
CappingData(., impute = T, fill = T, dither = F, pre.outl = pre.outl)%>%
NormData(., preproc = preproc) -> DTn
foreach(i = 1:4) %do% {
DTn[[i]] %>% dplyr::select(-c(v.rstl, v.pcci))
} -> DTn
list(pretrain = DTn[[1]],
train = DTn[[2]],
val = DTn[[3]],
test = DTn[[4]]) -> DTn
list(
pretrain = list(
x = DTn$pretrain %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTn$pretrain$Class %>% as.data.frame()
),
train = list(
x = DTn$train %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTn$train$Class %>% as.data.frame()
),
test = list(
x = DTn$val %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTn$val$Class %>% as.data.frame()
),
test1 = list(
x = DTn$test %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTn$test$Class %>% as.vector()
)
)
}
}, env)
SRBM+上位層+BPの訓練で得られた事前訓練済みDNNと最適ハイパーパラメータを使用して、フォワードテストの第1段階を実行する。
#----#---SRBM + upperLayer + BP---- evalq({ #--BestParams-------------------------- best.par <- OPT_Res3$Best_Par %>% unname # n1, n2, fact1, fact2, dr1, dr2, Lr.rbm , Lr.top, Lr.fine n1 = best.par[1]; n2 = best.par[2] fact1 = best.par[3]; fact2 = best.par[4] dr1 = best.par[5]; dr2 = best.par[6] Lr.rbm = best.par[7] Lr.top = best.par[8] Lr.fine = best.par[9] Ln <- c(0, 2*n1, 2*n2, 0) foreach(i = step, .packages = "darch" ) %do% { DTforv[[i]] -> X if(i==1) Res3$Dnn -> Dnn #----train/test------- fineTuneBP(Ln, fact1, fact2, dr1, dr2, Dnn, Lr.fine) -> Dnn.opt predict(Dnn.opt, newdata = X$test$x %>% tail(100) , type = "class") -> Ypred yTest <- X$test$y[ ,1] %>% tail(100) #numIncorrect <- sum(Ypred != yTest) #Score <- 1 - round(numIncorrect/nrow(xTest), 2) Evaluate(actual = yTest, predicted = Ypred)$Metrics[ ,2:5] %>% round(3) } -> Score3_dnn }, env)
最適化中に 得られた Dnn.optを 使用してフォワードテストの第2段階:
evalq({
foreach(i = step, .packages = "darch" ) %do% {
DTforv[[i]] -> X
if(i==1) {Res3$Dnn.opt -> Dnn}
#----train/test-------
fineTuneBP(Ln, fact1, fact2, dr1, dr2, Dnn, Lr.fine) -> Dnn.opt
predict(Dnn.opt, newdata = X$test$x %>% tail(100) , type = "class") -> Ypred
yTest <- X$test$y[ ,1] %>% tail(100)
#numIncorrect <- sum(Ypred != yTest)
#Score <- 1 - round(numIncorrect/nrow(xTest), 2)
Evaluate(actual = yTest, predicted = Ypred)$Metrics[ ,2:5] %>%
round(3)
} -> Score3_dnnOpt
}, env)
テスト結果を表にして比較する:
env$Score3_dnn env$Score3_dnnOpt
| イター | Score3_dnn | Score3_dnnOpt |
|---|---|---|
| 精度 リコール F1 | 精度 リコール F1 | |
| 1 | -1 0.76 0.737 0.667 0.7 1 0.76 0.774 0.828 0.8 | -1 0.77 0.732 0.714 0.723 1 0.77 0.797 0.810 0.803 |
| 2 | -1 0.79 0.88 0.746 0.807 1 0.79 0.70 0.854 0.769 | -1 0.78 0.836 0.78 0.807 1 0.78 0.711 0.78 0.744 |
| 3 | -1 0.69 0.807 0.697 0.748 1 0.69 0.535 0.676 0.597 | -1 0.67 0.824 0.636 0.718 1 0.67 0.510 0.735 0.602 |
| 4 | -1 0.71 0.738 0.633 0.681 1 0.71 0.690 0.784 0.734 | -1 0.68 0.681 0.653 0.667 1 0.68 0.679 0.706 0.692 |
| 5 | -1 0.56 0.595 0.481 0.532 1 0.56 0.534 0.646 0.585 | -1 0.55 0.578 0.500 0.536 1 0.55 0.527 0.604 0.563 |
| 6 | -1 0.61 0.515 0.829 0.636 1 0.61 0.794 0.458 0.581 | -1 0.66 0.564 0.756 0.646 1 0.66 0.778 0.593 0.673 |
| 7 | -1 0.67 0.55 0.595 0.571 1 0.67 0.75 0.714 0.732 | -1 0.73 0.679 0.514 0.585 1 0.73 0.750 0.857 0.800 |
| 8 | -1 0.65 0.889 0.623 0.733 1 0.65 0.370 0.739 0.493 | -1 0.68 0.869 0.688 0.768 1 0.68 0.385 0.652 0.484 |
| 9 | -1 0.55 0.818 0.562 0.667 1 0.55 0.222 0.500 0.308 | -1 0.54 0.815 0.55 0.657 1 0.54 0.217 0.50 0.303 |
| 10 | -1 0.71 0.786 0.797 0.791 1 0.71 0.533 0.516 0.525 | -1 0.71 0.786 0.797 0.791 1 0.71 0.533 0.516 0.525 |
この表は、最初の2つのステップが良い結果を出していることを示している。実際には、両変種とも最初の2ステップでは品質は同じで、その後低下する。したがって、最適化とテストの後、DNNは、少なくとも200~250の次のバーで、テスト・セットのレベルの分類の品質を維持すると仮定できる。
前の記事で 述べたフォワードテストでのモデルの追加訓練のための他の多くの組み合わせと、 多くの調整可能なハイパーパラメータがある。
質問は何ですか?
こんにちは、ウラジミール、
なぜNSがトレーニングデータでトレーニングされ、テストデータで評価されるのかがよく理解できません(もし私が間違っていなければ、あなたはそれを検証データとして使っていますね)。
Score <- Evaluate(actual = yTest, predicted = Ypred)$Metrics[ ,2:5] %>% round(3)
この場合、テストプロットへの適合は得られないのでしょうか、つまり、テストプロットで最もよく機能したモデルを選択するのでしょうか?
また、テストプロットはかなり小さく、時間的な規則性の1つにフィットする可能性があり、すぐに機能しなくなる可能性があることも考慮する必要があります。
たぶん、トレーニングプロット、またはプロットの合計、またはDarchのように(検証データが提出されている場合)Err = (ErrLeran * 0.37 + ErrValid * 0.63)で推定する方が良いでしょう - これらの係数はデフォルトですが、変更することができます。
多くのオプションがあり、どれが最良かは明らかではありません。テストプロットを支持するあなたの議論は興味深い。
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索
新しい記事 ディープニューラルネットワーク(その5)DNNハイパーパラメータのベイズ最適化 はパブリッシュされました:
本稿では、様々な訓練の変形によって得られたディープニューラルネットワークのハイパーパラメータにベイズ最適化を適用する可能性について検討します。様々な訓練の変形における最適なハイパーパラメータを有するDNNの分類の質が比較されます。DNN最適ハイパーパラメータの有効性の深さは、フォワードテストで確認されています。分類の質を向上させるための方向性が特定されています。
結果は良好です。訓練履歴のグラフをプロットしましょう。
plot(env$Res1$Dnn.opt, type = "class")図2 SRBM + RP変形によるDNN訓練の履歴
図からわかるように、検証セットのエラーは訓練セットのエラーよりも小さいものです。これは、モデルが過剰適合されておらず、一般化能力が良好であることを意味します。赤い縦線は、最良と見なされ、訓練後に結果として返されるモデルの結果を示します。
他の3つの訓練変形については、詳細な計算を行わずに計算結果と履歴グラフのみを提供します。すべてが同様に計算されます。
作者: Vladimir Perervenko