ミニマーケットエミュレータまたは手動ストラテジーテスター

はじめに

外国為替取引は、収益戦略、データ分析手法、勝ち取引モデルといった理論的基礎の研究から始まります。すべての初心者トレーダーは、収益を得るという同じ考えによって導かれていますが、優先順位、言葉、機会、目標などは自分自分で定義します。

初心者トレーダーの行動にはいくつかのシナリオがあります。

• 「一度にすべて」オプション：ほとんどの初心者は、多額の収益を素早く得たいものです。彼らは、少額または無料で使用できる、魔法のように完璧な戦略の魅力的な宣伝に屈します。これらは確かに迅速かつ簡単に思えますが、資金を失うのも迅速かつ簡単です。
  
• 「教育、教育、また教育」オプション：おとぎ話を信じることなく責任を持って訓練を受ける初心者もいます。彼らは市場と取引システムの法律を徹底的に研究します。しかし、本当の口座での取引が始まると、得られるのは教科書通りの予想よりも少ない利益です。これは何故で、次に何をすべきなのでしょうか。

1番目の状況では、ほとんどの初心者は金融市場で取引することに永遠的に失望しています。第2のシナリオでは、初心者は理論とその実践戦略を研究し続けます。

本稿は主に、デモ口座での取引や戦略のテストをしたくてたまらない初心者を対象としています。ここにも選択肢は2つあります。

• 1グループは、研究した短期的戦略を試してみたいと考えます。しかし、メンバーがフルタイムで働くと、週末に市場が閉鎖されているので、夜間のみが残されます。
  
• 2番目のグループは、中期戦略または長期戦略を使用します。デモ口座で戦略を洗練するのに一年間かけることは、間違えなく、彼らの望みではありません。

当然のことながら、戦略を迅速かつ効果的にテストできる履歴チャートがある場合、そのような難儀はなぜ必要かという疑問が出るでしょう。これは実際には必ずしもうまくいくわけではありません。優れたバックテスト結果を持つ戦略が何らかの理由で「ライブ」市場であまりうまく機能しないことはよくあります。いずれにしても、現実に近いシステムで取引を学ぶ方がよいでしょう。たとえば、市場エミュレータは十分で、そのようなプログラムはインターネットで購入できます。

本稿では、このようなシステムのMetaTrader 5での実装について議論したいと考えています。私はターミナルのフルバージョンと比較して機能が限定された「ミニマーケットエミュレータ」指標を書きました。これは戦略の理論的検証のために設計されています。

アプリケーションの特徴

このアプリケーションには、独自のコントロールパネルと、「親システム」（MetaTrader 5ターミナル自体）の特定のボタンがあります。

エミュレータで実行できる主要なアクションは次のとおりです。

1. 異なる方向（売りと買い）の2つの注文のみが出せます。注文とその数量を設定する前の決済逆指値と決済指値の設定もサポートされています。出された注文は修正が可能で、ストップレベルはドラッグすることができます。
   
2. モデリング速度には7段階しかありませんが、3つのグループに分けられます。最初は「ジュエリー」で、ストラテジーテスターとほぼ同じように、分足時間枠のデータからのティックの生成に基づいたモデリングが行われます。2番目は生成なしで構築された分足データを考慮します（このモードは高速ですが精度は低くなります）。3番目のモードが最速で、時間枠にかかわらず、1秒あたり1つのローソク足が構築されます。
3. 利益、ポイント数、および数量の現在の取引情報が提供されます。データは、現在および過去の注文、ならびにエミュレーションの開始からの一般的な取引について与えられます。
4. ターミナルに存在するすべての標準的なグラフィカルオブジェクトが利用できます。
5. すべての標準時間枠がサポートされています（ターミナルパネルのボタンによって切り替えられます）。

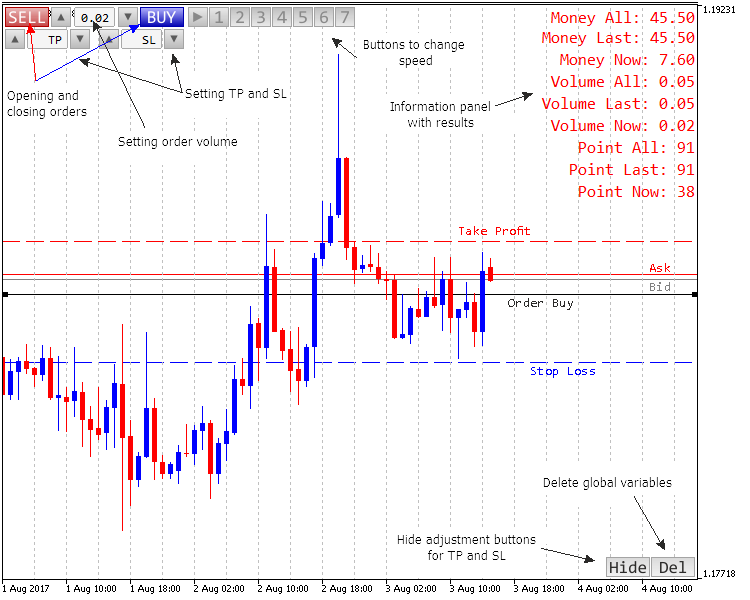
図1　アプリケーションのコントロールと外観

ティック生成システム

ティック生成の原則は「METATRADER 5 ターミナルのストラテジーテスタ内でティック作成をするアルゴリズム」からとられたもので、創造的に改訂され、代替バージョンとして提示されています。

メインと補助のティック生成は2つの関数で担当されます。

メイン関数はTick Generationで、ローソク足自体とレスポンスデータ（ティック）の配列の2つのパラメータが渡されます。次に、入力ローソク足の4つの価格レベルがすべて等しい場合、ティックの量は1ティックに等しく設定されます。これは、間違ったデータが渡された場合のゼロ除算エラーの可能性を排除するために行われました。

これに続いて新しいローソク足が形成されます。ローソク足内に1〜3ティックがある場合、ティック生成過程は前述の記事に記載されているように継続します。

3ティック以上の場合は、作業がより複雑になります。渡されたローソク足は、3つの不等な部分に分割されています（分割の原則は下記のコードで提供され、弱気と強気ローソク足のために分かれています）。そして、上下にティックがなくなると、調整が行われます。次に、ローソク足の性質に応じて制御が補助関数に移されます。

//+------------------------------------------------------------------+
//| Func Tick Generation                                             |
//+------------------------------------------------------------------+
void func_tick_generation(
MqlRates &rates,      // ローソク足のデータ
double &tick[]        // ティックの動的配列
)
{
 if(rates.open==rates.close && rates.high==rates.low && rates.open==rates.high){rates.tick_volume=1;}
 if(rates.tick_volume<4)// 4ティック未満
 {
ArrayResize(tick,int(rates.tick_volume));         // 配列サイズをティック数に合わせて変更する
if(rates.tick_volume==1)tick[0]=rates.close;      // 1ティック
if(rates.tick_volume==2)                          // 2ティック
{
 tick[0]=rates.open;
 tick[1]=rates.close;
}
if(rates.tick_volume==3)                          // 3ティック
{
 tick[0]=rates.open;
 tick[2]=rates.close;
 if(rates.open==rates.close)                      // 一方向に進んで始値のレベルに戻った
 {
if(rates.high==rates.open)tick[1]=rates.low;
if(rates.low==rates.open)tick[1]=rates.high;
 }
 if(rates.close==rates.low && rates.open!=rates.high)tick[1]=rates.high;           // 一方向に進み、ロールバックして始値のレベルを破った
 if(rates.close==rates.high && rates.open!=rates.low)tick[1]=rates.low;
 if(rates.open==rates.high && rates.close!=rates.low)tick[1]=rates.low;            // 一方向に進み、ロールバックしたが始値のレベルを破らなかった
 if(rates.open==rates.low && rates.close!=rates.high)tick[1]=rates.high;
 if((rates.open==rates.low && rates.close==rates.high) || (rates.open==rates.high && rates.close==rates.low))
 {
tick[1]=NormalizeDouble((((rates.high-rates.low)/2)+rates.low),_Digits);       // 一方向の数ポイント
 }
}
 }
 if(rates.tick_volume>3)      // 4ティック以上
 {

 // ローソク足のサイズをポイント単位で計算する
int candle_up=0;
int candle_down=0;
int candle_centre=0;
if(rates.open>rates.close)
{
 candle_up=int(MathRound((rates.high-rates.open)/_Point));
 candle_down=int(MathRound((rates.close-rates.low)/_Point));
}
if(rates.open<=rates.close)
{
 candle_up=int(MathRound((rates.high-rates.close)/_Point));
 candle_down=int(MathRound((rates.open-rates.low)/_Point));
}
candle_centre=int(MathRound((rates.high-rates.low)/_Point));
int candle_all=candle_up+candle_down+candle_centre;      // 動きの全体の長さ
int point_max=int(MathRound(double(candle_all)/2));      // ティックの最大許容数
double share_up=double(candle_up)/double(candle_all);
double share_down=double(candle_down)/double(candle_all);
double share_centre=double(candle_centre)/double(candle_all);

// 各セクションの基準点の数を計算する
char point=0;
if(rates.tick_volume<10)point=char(rates.tick_volume);
else point=10;
if(point>point_max)point=char(point_max);
char point_up=char(MathRound(point*share_up));
char point_down=char(MathRound(point*share_down));
char point_centre=char(MathRound(point*share_centre));

// 選択した範囲の基準点を確認する
if(candle_up>0 && point_up==0)
{point_up=1;point_centre=point_centre-1;}
if(candle_down>0 && point_down==0)
{point_down=1;point_centre=point_centre-1;}

// 出力配列のサイズを変更する
ArrayResize(tick,11);
char p=0;                     // ティック配列(tick[])のインデックス
tick[p]=rates.open;           // 1番目のティックは始値に等しい
if(rates.open>rates.close)    // 下向き
{
 func_tick_small(rates.high,1,candle_up,point_up,tick,p);
 func_tick_small(rates.low,-1,candle_centre,point_centre,tick,p);
 func_tick_small(rates.close,1,candle_down,point_down,tick,p);
 ArrayResize(tick,p+1);
}
if(rates.open<=rates.close)   // 上向きまたは同時
{
 func_tick_small(rates.low,-1,candle_down,point_down,tick,p);
 func_tick_small(rates.high,1,candle_centre,point_centre,tick,p);
 func_tick_small(rates.close,-1,candle_up,point_up,tick,p);
 ArrayResize(tick,p+1);
}
 }
}

名前通り、Tick Small関数はマイナーなティック生成を実行します。最後に処理されたティックの情報、移動する方向（上下）、必要なステップ数、最後の価格を受け取り、計算されたステップを上記のティック配列に渡します。結果の配列には11個以下のチックが含まれます。

//+------------------------------------------------------------------+
//| Func Tick Small                                                  |
//+------------------------------------------------------------------+
void func_tick_small(
 double end,        // 動きの終わり
 char route,        // 動きの方向
 int candle,        // 動きの距離
 char point,        // ポイント数
 double &tick[],    // ティック配列
 char&i           // 配列の現在のインデックス
 )
{
 if(point==1)
 {
i++;
if(i>10)i=10;       // 調整
tick[i]=end;
 }
 if(point>1)
 {
double wave_v=(point+1)/2;
double step_v=(candle-1)/MathFloor(wave_v)+1;
step_v=MathFloor(step_v);
for(char p_v=i+1,i_v=i; p_v<i_v+point;)
{
 i++;
 if(route==1)tick[i]=tick[i-1]+(step_v*_Point);
 if(route==-1)tick[i]=tick[i-1]-(step_v*_Point);
 p_v++;
 if(p_v<i_v+point)
 {
i++;
if(route==1)tick[i]=tick[i-1]-_Point;
if(route==-1) tick[i]=tick[i-1]+_Point;
 }
 p_v++;
}
if(NormalizeDouble(tick[i],_Digits)!=NormalizeDouble(end,_Digits))
{
 i++;
 if(i>10)i=10;    // 調整
 tick[i]=end;
}
 }
}

これは、つまり、「ジュエリー」モデリング全体の中核です（結論はこれが「ジュエリー」と呼ばれる理由を説明しています）。さて、システムの相互作用の本質に移りましょう。

相互作用とデータ交換

システムのコードは一見すると難しいです。関数は完全に一貫しているわけではなく、プログラムのさまざまな部分からの呼び出しが可能です。これは、システムがユーザだけでなくターミナルともやり取りする必要があるためです。これらの相互作用の大まかなスキームを以下に示します（図2）。

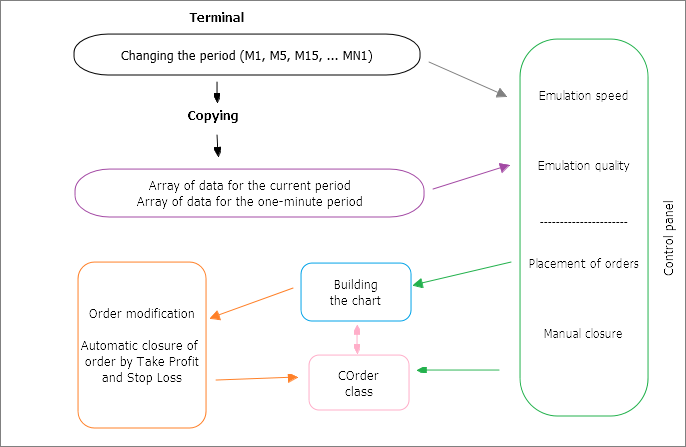
図2　アプリケーション内の相互作用のスキーマ

指標ウィンドウ内のコントロールオブジェクトの数を減らすために、期間を切り替えるためのメカニズムがターミナルシェルから借用されました。ただし、期間を切り替えるとアプリケーションが再初期化され、ローカルスコープとグローバルスコープのすべての変数が上書きされるため、切り替えが発生するたびにデータの配列がコピーされます。特に、M1と選択された期間の2つの期間のデータがコピーされます。これらのデータの後続処理のためのパラメータであるシミュレーション速度及び品質（「ジュエリー」または簡単な高速メソッド）は、パネル上で選択されます。準備が整うと、チャートのモデリングが始まります。

コントロールパネルは、発注や注文の削除に便利です。これを行うために、プログラムは "COrder"クラスを参照します。このクラスは、チャートの作成時に注文を管理するためにも使用されます。

前述のように、チャート期間が変わると指標は再起動されます。したがって、アプリケーションの構造全体にわたって通信を提供するためにはクライアントターミナルのグローバル変数が使用されます。従来のグローバル変数とは異なり、それらはより長い期間（4週間）保存され、再起動には耐性があります。唯一の欠点は、データ型がdoubleに制限されていることです。しかし、一般的に、これは、新しいファイルを作成し、毎回それを書いて読んでおくよりはるかに便利です。

相互作用要素のコードに直接移りましょう。

コードでの実装

コードの初め

まず、変数を宣言するための標準的な手順が行われます。OnInit()関数がバッファを初期化し、コントロールパネルのインターフェイスを描画し、エミュレーションの先頭からのオフセットを計算します。オフセットは、シミュレーションが空のチャートで始まらずに特定の履歴を使用してすぐに戦略の確認を開始するために必要です。

データ配列がコピーされ、メインの結合変数（time_end）が読み込まれます。これは、シミュレーションが停止した時間を示します。

//---  指標がそこまで描画された時間を設定する
 if(GlobalVariableCheck(time_end))end_time_indicator=datetime(GlobalVariableGet(time_end));

これで、指標がどこで停止したのかが常に「わかり」ます。OnInit()関数は、タイマー呼び出しで終了します。実際には、新しいティックを出力するか、または速度に応じてローソク足全体を形成するコマンドが与えられます。

タイマー関数

コントロールパネルの「再生」ボタンの状態は、関数の開始時に確認され、押されていると、さらなるコードが実行されます。

まず、シミュレーションが停止した指標バーを現在の時刻と比較して決定します。最後のシミュレーション時間 'end_time_indicator'と現在時刻を両端とします。チャートは常に移動（土曜日と日曜日を除いて）していて、時間内に同期されていないため、データが毎秒再計算されます。したがって、チャートはChartNavigate()関数によって動的に追跡され、移動されます。

その後、変数 'number_now_rates'、 'bars_now_rates'、 'all_bars_indicator'が計算されます。時間が後で確認されます。入力パラメータに従って実行されていない場合、func_merger() 関数を使用してモデリングが実行されます。 次に、グローバル変数に記録された値を用いて現在のポジションとその収益性を確認し、指標の情報ブロックに出力します。

ここでは、"COrder"クラスの、ユーザアクション(position.Delete) の結果またはストップレベルのアクティブ化 (position.Check)の結果として注文の自動削除を担当する部分が呼ばれます。

//+------------------------------------------------------------------+
//| タイマー関数                                                      |
//+------------------------------------------------------------------+
void OnTimer()
{
//---
 if(button_play)
 {
end_bar_indicator=Bars(_Symbol,_Period,end_time_indicator,TimeCurrent());      // 最も早い時点から現在までのバーの数
ChartNavigate(0,CHART_END,-end_bar_indicator);                                 // 現在のモデリングされているバーにチャート（指標）を移動する
number_now_rates=(Bars(_Symbol,_Period,real_start,end_time_indicator)-1);      // 現在モデリングに使われているバー
bars_now_rates=(Bars(_Symbol,_Period,real_start,stop)-1);                      // 現在の期間の履歴から使用されたバーの数
all_bars_indicator=(Bars(_Symbol,_Period,real_start,TimeCurrent()))-1;         // シミュレーションの開始から現在までのバーの数

if(end_time_indicator<stop)                                                    // シミュレーション時刻の確認
{
 func_merger();
 ObjectSetDouble(0,line_bid,OBJPROP_PRICE,price_bid_now);
 if(ObjectFind(0,line_ask)>=0)
 {ObjectSetDouble(0,line_ask,OBJPROP_PRICE,price_ask_now);}

 //--- 注文の現在値
 int point_now=0;
 double vol_now=0;
 double money_now=0;
 if(ObjectFind(0,order_buy)>=0 && GlobalVariableGet(order_buy)>0)             // 買い注文が存在する
 {
int p_now=int((price_bid_now-GlobalVariableGet(order_buy))*dig_pow);
double v_now=GlobalVariableGet(vol_buy);
double m_now=p_now*v_now*10;
point_now+=p_now;
vol_now+=v_now;
money_now+=m_now;
 }
 if(ObjectFind(0,order_sell)>=0 && GlobalVariableGet(order_sell)>0)           // 売り注文が存在する
 {
int p_now=int((GlobalVariableGet(order_sell)-price_ask_now)*dig_pow);
double v_now=GlobalVariableGet(vol_sell);
double m_now=p_now*v_now*10;
point_now+=p_now;
vol_now+=v_now;
money_now+=m_now;
 }
 GlobalVariableSet(info_point_now,point_now);
 GlobalVariableSet(info_vol_now,vol_now);
 GlobalVariableSet(info_money_now,money_now);
}

COrder position;    // "COrder" クラスオブジェクト
position.Delete(price_bid_now,price_ask_now,(-1));
position.Check(end_time_indicator,GlobalVariableGet(order_buy),GlobalVariableGet(tp_buy),GlobalVariableGet(sl_buy),
 GlobalVariableGet(order_sell),GlobalVariableGet(tp_sell),GlobalVariableGet(sl_sell));

func_info_print("Money All: ",info_money_all,2);
func_info_print("Money Last: ",info_money_last,2);
func_info_print("Money Now: ",info_money_now,2);
func_info_print("Volume All: ",info_vol_all,2);
func_info_print("Volume Last: ",info_vol_last,2);
func_info_print("Volume Now: ",info_vol_now,2);
func_info_print("Point All: ",info_point_all,0);
func_info_print("Point Last: ",info_point_last,0);
func_info_print("Point Now: ",info_point_now,0);

position.Modify();
 }
//--- Hideボタンの管理
 char x=char(GlobalVariableGet("hide"));
 if(x==1)
 {
ObjectSetInteger(0,"20",OBJPROP_STATE,false);
ObjectSetInteger(0,"14",OBJPROP_YDISTANCE,24);
ObjectSetInteger(0,"15",OBJPROP_YDISTANCE,24);
ObjectSetInteger(0,"16",OBJPROP_YDISTANCE,24);
ObjectSetInteger(0,"17",OBJPROP_YDISTANCE,24);
ObjectSetInteger(0,"18",OBJPROP_YDISTANCE,24);
ObjectSetInteger(0,"19",OBJPROP_YDISTANCE,24);
 }
 if(x==2)
 {
ObjectSetInteger(0,"20",OBJPROP_STATE,true);
ObjectSetInteger(0,"14",OBJPROP_YDISTANCE,-24);
ObjectSetInteger(0,"15",OBJPROP_YDISTANCE,-24);
ObjectSetInteger(0,"16",OBJPROP_YDISTANCE,-24);
ObjectSetInteger(0,"17",OBJPROP_YDISTANCE,-24);
ObjectSetInteger(0,"18",OBJPROP_YDISTANCE,-24);
ObjectSetInteger(0,"19",OBJPROP_YDISTANCE,-24);
 }
}

COrderクラス

このクラスには、ポジションの開閉、現在の注文状況の変更（決済逆指値および決済指値の管理）のための関数が含まれています。

Placedを使用して注文を出しましょう。注文の種類（買いまたは売り）はスイッチ演算子によって選択され、データはグローバル変数（order_buyまたはorder_sell）に保管されます。m_take_profitとm_stop_lossが事前に定義されている場合は、対応するグローバル変数に格納し、チャートに描画します。線は、このクラスのLine関数によって設定されます。

//+------------------------------------------------------------------+
//| COrderクラス                                                      |
//+------------------------------------------------------------------+
class COrder
{
public:
 void Placed(
 char m_type,// 注文の種類（1-買い、2-売り）
 double m_price_bid, // ビッド
 double m_price_ask, // アスク
 int m_take_profit,//決済指値
 int m_stop_loss // 決済逆指値
 )
 {
switch(m_type)
{
 case 1:
 {
GlobalVariableSet(order_buy,m_price_ask);
Line(GlobalVariableGet(order_buy),order_buy,col_buy,STYLE_SOLID,1,true);
if(m_take_profit>0)
{
 GlobalVariableSet(tp_buy,(m_price_ask+(_Point*m_take_profit)));
 Line(GlobalVariableGet(tp_buy),tp_buy,col_tp,STYLE_DASH,1,true);
}
if(m_stop_loss>0)
{
 GlobalVariableSet(sl_buy,(m_price_ask-(_Point*m_stop_loss)));
 Line(GlobalVariableGet(sl_buy),sl_buy,col_sl,STYLE_DASH,1,true);
}
 }
 break;
 case 2:
 {
GlobalVariableSet(order_sell,m_price_bid);
Line(GlobalVariableGet(order_sell),order_sell,col_sell,STYLE_SOLID,1,true);
if(m_take_profit>0)
{
 GlobalVariableSet(tp_sell,(m_price_bid-(_Point*m_take_profit)));
 Line(GlobalVariableGet(tp_sell),tp_sell,col_tp,STYLE_DASH,1,true);
}
if(m_stop_loss>0)
{
 GlobalVariableSet(sl_sell,(m_price_bid+(_Point*m_stop_loss)));
 Line(GlobalVariableGet(sl_sell),sl_sell,col_sl,STYLE_DASH,1,true);
}
 }
 break;
}
 }

次にあるのは注文を削除するためのDelete関数です。ここでも、スイッチ演算子によって自動削除、買い、売りの3つのオプションのいずれかが選択されます。ここでの自動削除とは、チャートから線を削除することによって注文を削除することです。

これは、クラスのSmall_del_buyおよびSmall_del_sell補助関数によって行われます。

 void Delete(
 double m_price_bid,      // ビッド
 double m_price_ask,      // アスク
 char m_del_manual        // 削除の種類（-1 - 自動、1 - 買い、2 - 売り）
 )
 {
switch(m_del_manual)
{
 case(-1):
if(ObjectFind(0,order_buy)<0 && GlobalVariableGet(order_buy)>0)
{Small_del_buy(m_price_bid);}
if(ObjectFind(0,order_sell)<0 && GlobalVariableGet(order_sell)>0)
{Small_del_sell(m_price_ask);}
break;
 case 1:
if(ObjectFind(0,order_buy)>=0)
{
 ObjectDelete(0,order_buy);
 Small_del_buy(m_price_bid);
}
break;
 case 2:
if(ObjectFind(0,order_sell)>=0)
{
 ObjectDelete(0,order_sell);
 Small_del_sell(m_price_ask);
}
break;
}
 }

このうちの1つであるSmall_del_sellについて考えてみましょう。

決済逆指値と決済指値の線を確認し、存在すれば削除し、order_sell global変数をゼロにします。グローバル変数を使用して注文があるかどうかを確認する場合には、これは後で必要になります。

注文の決済指値に関する情報は、グローバル変数（info_point_last、info_vol_last、info_money_last）にも格納されます。 これはsmall_concatenation（+=演算子に似ているがグローバル変数を使用）によって実行されます。 利益（数量）を要約し、グローバル変数（info_point_all、info_vol_all、info_money_all）に格納します。

void Small_del_sell(double m_price_ask)
 {
if(ObjectFind(0,tp_sell)>=0)ObjectDelete(0,tp_sell);       // 決済指値の線を削除する
 if(ObjectFind(0,sl_sell)>=0)ObjectDelete(0,sl_sell);      // 決済逆指値の線を削除する
 int point_plus=int(MathRound((GlobalVariableGet(order_sell)-m_price_ask)/_Point));      // 取引の利益を計算する
GlobalVariableSet(order_sell,0);                           // 出された注文の価格を示す変数をゼロにする
GlobalVariableSet(info_vol_last,GlobalVariableGet(vol_sell));
GlobalVariableSet(vol_sell,0);
GlobalVariableSet(info_point_last,point_plus);
GlobalVariableSet(info_money_last,(GlobalVariableGet(info_point_last)*GlobalVariableGet(info_vol_last)*10));
Small_concatenation(info_point_all,info_point_last);
Small_concatenation(info_vol_all,info_vol_last);
Small_concatenation(info_money_all,info_money_last);
 }

注文はマウスで位置を変更することによって修正されます。やり方は2つあります。1番目は、注文のオープニングラインをドラッグすることです。この場合、移動方向と注文の種類に応じて、新しい決済逆指値と決済指値の線がプロットされます。Small_mod関数もまたCOrderクラスに実装されています。その入力パラメータは、オブジェクト名、オブジェクトを移動する権限、および注文の種類です。

Small_mod関数の初めには、オブジェクトが存在することが確認されます。その後、決済逆指値と決済指値の線を移動することが許可されている場合、価格の変化はグローバル変数に格納されます。売り及び買い線の移動が禁止されている場合は、注文の種類によっては、新しい決済逆指値と決済指値の線が線の新しい位置に表示され、注文の線がその場所に戻ります。

 void Small_mod(string m_name,      // オブジェクト名とグローバル変数名
bool m_mode,                        // 位置を変える許可
char m_type                         // 1 — 買い、2 — 売り
)
 {
if(ObjectFind(0,m_name)>=0)
{
 double price_obj_double=ObjectGetDouble(0,m_name,OBJPROP_PRICE);
 int price_obj=int(price_obj_double*dig_pow);
 double price_glo_double=GlobalVariableGet(m_name);
 int price_glo=int(price_glo_double*dig_pow);
 if(price_obj!=price_glo && m_mode==true)
 {
GlobalVariableSet(m_name,(double(price_obj)/double(dig_pow)));
 }
 if(price_obj!=price_glo && m_mode==false)
 {
switch(m_type)
{
 case 1:                         // 買い注文
if(price_obj>price_glo)          // TP
{
 GlobalVariableSet(tp_buy,(double(price_obj)/double(dig_pow)));
 Line(GlobalVariableGet(tp_buy),tp_buy,col_tp,STYLE_DASH,1,true);
}
if(price_obj<price_glo)          // SL
{
 GlobalVariableSet(sl_buy,(double(price_obj)/double(dig_pow)));
 Line(GlobalVariableGet(sl_buy),sl_buy,col_sl,STYLE_DASH,1,true);
}
break;
 case 2:                        // 売り注文
if(price_obj>price_glo)         // SL
{
 GlobalVariableSet(sl_sell,(double(price_obj)/double(dig_pow)));
 Line(GlobalVariableGet(sl_sell),sl_sell,col_sl,STYLE_DASH,1,true);
}
if(price_obj<price_glo)         // TP
{
 GlobalVariableSet(tp_sell,(double(price_obj)/double(dig_pow)));
 Line(GlobalVariableGet(tp_sell),tp_sell,col_tp,STYLE_DASH,1,true);
}
break;
}
ObjectSetDouble(0,m_name,OBJPROP_PRICE,(double(price_glo)/double(dig_pow)));
 }
}
 }

チャートのモデリング中、注文は常にCOrderクラスのCheck関数によって確認されます。 この関数には、注文に関する情報を格納するすべてのグローバル変数が渡されます。 この関数には、注文に関する情報を格納するすべてのグローバル変数が渡されます。これにより、各呼び出しは、関数の最後の呼び出しと現在のチャート描画時刻の間の全間隔での価格帯（分足時間枠）を確認できます。

この期間中に価格がストップラインの1つに到達するか、それを突破すると、制御は注文を削除する関数（COrderクラスのDelete関数）に渡されます。

 void Check(
datetime m_time,
double m_price_buy,
double m_price_tp_buy,
double m_price_sl_buy,
double m_price_sell,
double m_price_tp_sell,
double m_price_sl_sell
)
 {
int start_of_z=0;
int end_of_z=0;
datetime time_end_check=datetime(GlobalVariableGet(time_end_order_check));
if(time_end_check<=0){time_end_check=m_time;}
GlobalVariableSet(time_end_order_check,m_time);
start_of_z=Bars(_Symbol,PERIOD_M1,real_start,time_end_check);
end_of_z=Bars(_Symbol,PERIOD_M1,real_start,m_time);
for(int z=start_of_z; z<end_of_z; z++)
{
 COrder del;
 double p_bid_high=period_m1[z].high;
 double p_bid_low=period_m1[z].low;
 double p_ask_high=p_bid_high+(spread*_Point);
 double p_ask_low=p_bid_low+(spread*_Point);
 if(m_price_buy>0)                                              // 買い注文がある
 {
if(ObjectFind(0,tp_buy)>=0)
{
 if(m_price_tp_buy<=p_bid_high && m_price_tp_buy>=p_bid_low)    // TPがトリガされる
 {del.Delete(m_price_tp_buy,0,1);}                              // TP価格で決済する
} 
if(ObjectFind(0,sl_buy)>=0)
{
 if(m_price_sl_buy>=p_bid_low && m_price_sl_buy<=p_bid_high)    // SLがトリガされる
 {del.Delete(m_price_sl_buy,0,1);}                              // SL価格で決済する
}
 }
 if(m_price_sell>0)                                                   // 売り注文がある
 {
if(ObjectFind(0,tp_sell)>=0)
{
 if(m_price_sl_sell<=p_ask_high && m_price_sl_sell>=p_ask_low)  // SLがトリガされる
 {del.Delete(0,m_price_sl_sell,2);}                             // SL価格で決済する
}
if(ObjectFind(0,sl_sell)>=0)
{
 if(m_price_tp_sell>=p_ask_low && m_price_tp_sell<=p_ask_high)  // TPがトリガされる
 {del.Delete(0,m_price_tp_sell,2);}                             // TP価格で決済する
}
 }
}
 }

クラスの主な関数についてはこれで終わりです。ローソク足をチャート上に描くことを直接担当する関数を調べてみましょう。

func_filling()関数

期間を切り替えると指標が再初期化されるので、チャートを再び描画し、現在のローソク足の時間（いわゆる「尾」）に至るまで過去のローソク足を配置しなければなりません。 この関数は、新しいローソク足が生成される前に使用され、チャートの「尾」を正規化して表示精度を高めることができます。

この関数には、現在の期間、現在の表示時間、ローソク足のの総数、および現在描画されているローソク足ののデータ配列が渡されます。一度実行されると、この関数は、最後に表示されたローソク足のの開始時刻とそれに続くローソク足のの開始時刻を返します。 指標配列も書き入れられ、関数完了フラグ 'work_status'が返されます。

関数は、 'for'ループを使用して、描画されたローソク足に至るまでの以前に表示された指標バッファ全体と、現在描画されているローソク足のの価格値（通常は始値に等しい）を入力します。

//+------------------------------------------------------------------+
//| Func Filling                                                     |
//+------------------------------------------------------------------+
void func_filling(MqlRates &input_rates[],                // 入力する（現在の期間の）データ
datetime input_end_time_indicator,      // 指標の現在時刻
int input_all_bars_indicator,           // 指標のバーの総数
datetime &output_time_end_filling,      // 最後のバーの開いた時刻
datetime &output_time_next_filling,     // 次のバーの開いた時刻
int input_end_bar_indicator,            // 指標の現在の（完成した）バー
double &output_o[],
double &output_h[],
double &output_l[],
double &output_c[],
double &output_col[],
char &work_status)                      // 操作の状態
{
 if(work_status==1)
 {
int stopped_rates_bar;
for(int x=input_all_bars_indicator,y=0;x>0;x--,y++)
{
 if(input_rates[y].time<input_end_time_indicator)
 {
output_o[x]=input_rates[y].open;
output_h[x]=input_rates[y].high;
output_l[x]=input_rates[y].low;
output_c[x]=input_rates[y].close;
if(output_o[x]>output_c[x])output_col[x]=0;
else output_col[x]=1;
output_time_end_filling=input_rates[y].time;
output_time_next_filling=input_rates[y+1].time;
input_end_bar_indicator=x;
stopped_rates_bar=y;
 }
 else break;
}
output_o[input_end_bar_indicator]=input_rates[stopped_rates_bar].open;
output_h[input_end_bar_indicator]=output_o[input_end_bar_indicator];
output_l[input_end_bar_indicator]=output_o[input_end_bar_indicator];
output_c[input_end_bar_indicator]=output_o[input_end_bar_indicator];
work_status=-1;
 }
}

実行されると、制御は、現在のローソク足を描くための3つの関数のうちの1つに移されます。 最速のものから順に考えてみましょう。

ローソク足を毎秒描画するfunc_candle_per_seconds()関数

他の2つの関数と異なり、ここでは、指標が再読み込みされるか、チャートの描画速度が変更される前に、他の関数に制御が移されることはありません。新しい呼び出しはタイマーによって1秒ごとに発生し、この間に現在のローソク足が描画されます（データが描かれます）。最初に、データが渡された配列から現在のローソク足にコピーされ、その後、最初のデータが次のローソク足に渡されます。関数は、最後には、最後のローソク足が形成された時を渡します。

上記の関数には、ローソク足生成の「7番目の速度」の責任があります（コントロールパネルを参照）。

//+------------------------------------------------------------------+
//| Func Candle Per Seconds                                          |
//+------------------------------------------------------------------+
void func_candle_per_seconds(MqlRates &input_rates[],
 datetime &input_end_time_indicator,
 int input_bars_now_rates,
 int input_number_now_rates,
 int &input_end_bar_indicator,
 double &output_o[],
 double &output_h[],
 double &output_l[],
 double &output_c[],
 double &output_col[],
 char &work_status)
{
 if(work_status==-1)
 {
if(input_number_now_rates<input_bars_now_rates)
{
 if(input_number_now_rates!=0)
 {
output_o[input_end_bar_indicator]=input_rates[input_number_now_rates-1].open;
output_h[input_end_bar_indicator]=input_rates[input_number_now_rates-1].high;
output_l[input_end_bar_indicator]=input_rates[input_number_now_rates-1].low;
output_c[input_end_bar_indicator]=input_rates[input_number_now_rates-1].close;
if(output_o[input_end_bar_indicator]>output_c[input_end_bar_indicator])output_col[input_end_bar_indicator]=0;
else output_col[input_end_bar_indicator]=1;
 }
 input_end_bar_indicator--;
 output_o[input_end_bar_indicator]=input_rates[input_number_now_rates].open;
 output_h[input_end_bar_indicator]=input_rates[input_number_now_rates].high;
 output_l[input_end_bar_indicator]=input_rates[input_number_now_rates].low;
 output_c[input_end_bar_indicator]=input_rates[input_number_now_rates].close;
 if(output_o[input_end_bar_indicator]>output_c[input_end_bar_indicator])output_col[input_end_bar_indicator]=0;
 else output_col[input_end_bar_indicator]=1;
 input_end_time_indicator=input_rates[input_number_now_rates+1].time;
}
 }
}

次の2つの関数は互いに非常に似ています。そのうちの1つは、ティックと関係なく、時間によってローソク足を生成します。2番目のもの（「ジュエリー」）は、市場のより完全なエミュレーションのために、本稿冒頭で説明したティック生成器を使用します。

ローソク足構築のためのfunc_of_form_candle()関数

入力パラメータは以前と同じです(OHLC)。機能に関しては、すべてが非常にシンプルです。価格は、func_filling()関数から受け取った時刻から開始して、M1時間枠データから現在のローソク足にループでコピーされます。時間を変えることによって、ローソク足が徐々に形成されることが分かります。2番目から6番目までの速度はこのようにして構築されます（コントロールパネル参照）。時間が現在の時間枠上のローソク足の完了の瞬間に達した後、 'work_status'フラグが変更され、次のタイマーの実行によってfunc_filling()関数が再び呼び出されます。

//+------------------------------------------------------------------+
//| Func Of Form Candle                                              |
//+------------------------------------------------------------------+
void func_of_form_candle(MqlRates &input_rates[],
 int input_bars,
 datetime &input_time_end_filling,
 datetime &input_end_time_indicator,
 datetime &input_time_next_filling,
 int input_end_bar_indicator,
 double &output_o[],
 double &output_h[],
 double &output_l[],
 double &output_c[],
 double &output_col[],
 char &work_status)
{
 if(work_status==-1)
 {
int start_of_z=0;
int end_of_z=0;
start_of_z=Bars(_Symbol,PERIOD_M1,real_start,input_time_end_filling);
end_of_z=Bars(_Symbol,PERIOD_M1,real_start,input_end_time_indicator);
for(int z=start_of_z; z<end_of_z; z++)
{
 output_c[input_end_bar_indicator]=input_rates[z].close;
 if(output_h[input_end_bar_indicator]<input_rates[z].high)output_h[input_end_bar_indicator]=input_rates[z].high;
 if(output_l[input_end_bar_indicator]>input_rates[z].low)output_l[input_end_bar_indicator]=input_rates[z].low;
 if(output_o[input_end_bar_indicator]>output_c[input_end_bar_indicator])output_col[input_end_bar_indicator]=0;
 else output_col[input_end_bar_indicator]=1;
}
if(input_end_time_indicator>=input_time_next_filling)work_status=1;
 }
}

次に、できる限り市場に近いローソク足のを生成する関数に移りましょう。

ローソク足の 「ジュエリー」シミュレーションのためのfunc_of_form_jeweler_candle()関数

関数の冒頭では、すべてが前のバージョンのように起こります。分足の時間枠データは、最後の1分を除いて、現在のローソク足を完全に満たします。. データはfunc_tick_generation()関数に渡され、ティックが生成されます。これについては、本稿冒頭で説明しました。関数を呼び出すたびに、受け取ったティックの配列は、「髭」の調整を考慮して、現在のローソク足の終値として徐々に渡されます。配列の「ティック」が終わると、この過程が繰り返されます。

//+------------------------------------------------------------------+
//| Func Of Form Jeweler Candle                                      |
//+------------------------------------------------------------------+
void func_of_form_jeweler_candle(MqlRates &input_rates[],  // ティック生成のための情報
 int input_bars,                             // 情報配列のサイズ
 datetime &input_time_end_filling,           // クイックフィルの終了時刻
 datetime &input_end_time_indicator,         // 指標の最後のシミュレーション時刻
 datetime &input_time_next_filling,          // 現在の時間枠の完全なバーが完全に形成されるまでの残り時間
 int input_end_bar_indicator,                // 指標の現在描画されているバー
 double &output_o[],
 double &output_h[],
 double &output_l[],
 double &output_c[],
 double &output_col[],
 char &work_status                           // 操作終了タイプ（クイックフィル関数のコマンド）
 )
{
 if(work_status==-1)
 {
int start_of_z=0;
int current_of_z=0;
start_of_z=Bars(_Symbol,PERIOD_M1,real_start,input_time_end_filling)-1;
current_of_z=Bars(_Symbol,PERIOD_M1,real_start,input_end_time_indicator)-1;
if(start_of_z<current_of_z-1)
{
 for(int z=start_of_z; z<current_of_z-1; z++)
 {
output_c[input_end_bar_indicator]=input_rates[z].close;
if(output_h[input_end_bar_indicator]<input_rates[z].high)output_h[input_end_bar_indicator]=input_rates[z].high;
if(output_l[input_end_bar_indicator]>input_rates[z].low)output_l[input_end_bar_indicator]=input_rates[z].low;
if(output_o[input_end_bar_indicator]>output_c[input_end_bar_indicator])output_col[input_end_bar_indicator]=0;
else output_col[input_end_bar_indicator]=1;
 }
 input_end_time_indicator=input_rates[current_of_z].time;
}
// 配列のティックを取得する
static int x=0;                   // 配列カウンタと開始フラグ
static double tick_current[];
static int tick_current_size=0;
if(x==0)
{
 func_tick_generation(input_rates[current_of_z-1],tick_current);
 tick_current_size=ArraySize(tick_current);
 if(output_h[input_end_bar_indicator]==0)
 {output_h[input_end_bar_indicator]=tick_current[x];}
 if(output_l[input_end_bar_indicator]==0)
 {output_l[input_end_bar_indicator]=tick_current[x];}
 output_c[input_end_bar_indicator]=tick_current[x];
}
if(x<tick_current_size)
{
 output_c[input_end_bar_indicator]=tick_current[x];
 if(tick_current[x]>output_h[input_end_bar_indicator])
 {output_h[input_end_bar_indicator]=tick_current[x];}
 if(tick_current[x]<output_l[input_end_bar_indicator])
 {output_l[input_end_bar_indicator]=tick_current[x];}
 if(output_o[input_end_bar_indicator]>output_c[input_end_bar_indicator])output_col[input_end_bar_indicator]=0;
 else output_col[input_end_bar_indicator]=1;
 x++;
}
else
{
 input_end_time_indicator=input_rates[current_of_z+1].time;
 x=0;
 tick_current_size=0;
 ArrayFree(tick_current);
}
if(input_end_time_indicator>input_time_next_filling)
{work_status=1;}
 }
}

ローソク足を生成するための3つの関数はすべてMerger関数で結合されています。

複合シミュレーションのためのfunc_merger()関数

作業に使用される関数は、スイッチ演算子によって選択された速度に応じて決定されます。この関数には3種類あります。いずれの場合もfunc_filling()関数から始まり、制御はfunc_of_form_jeweler_candle()、func_of_form_candle()またはfunc_candle_per_seconds()の3つのローソク足生成関数のいずれかに渡されます。時刻は2回目から6回目までの各パスで再計算されます。func_calc_time()関数は、現在の時間枠の必要な部分を計算し、現在の時刻に追加します。ビッドは現在のローソク足の終値から取られ、アスクはサーバから受け取ったスプレッドデータに基づいて計算されます。

//+------------------------------------------------------------------+
//| Merger関数                                                        |
//+------------------------------------------------------------------+
void func_merger()
{
 switch(button_speed)
 {
case 1:
{
 func_filling(period_array,end_time_indicator,all_bars_indicator,time_open_end_rates,time_open_next_rates,end_bar_indicator,TST_C_O,TST_C_H,TST_C_L,TST_C_C,TST_C_Col,status);
 func_of_form_jeweler_candle(period_m1,bars_m1,time_open_end_rates,end_time_indicator,time_open_next_rates,end_bar_indicator,TST_C_O,TST_C_H,TST_C_L,TST_C_C,TST_C_Col,status);
 price_bid_now=TST_C_C[end_bar_indicator];
 price_ask_now=price_bid_now+(spread*_Point);
}
break;
case 2:
{
 func_filling(period_array,end_time_indicator,all_bars_indicator,time_open_end_rates,time_open_next_rates,end_bar_indicator,TST_C_O,TST_C_H,TST_C_L,TST_C_C,TST_C_Col,status);
 func_of_form_candle(period_m1,bars_m1,time_open_end_rates,end_time_indicator,time_open_next_rates,end_bar_indicator,TST_C_O,TST_C_H,TST_C_L,TST_C_C,TST_C_Col,status);
 price_bid_now=TST_C_C[end_bar_indicator];
 price_ask_now=price_bid_now+(spread*_Point);
 end_time_indicator+=func_calc_time(time_open_end_rates,time_open_next_rates,13);
}
break;
case 3:
{
 ...
 end_time_indicator+=func_calc_time(time_open_end_rates,time_open_next_rates,11);
}
break;
case 4:
{
 ...
 end_time_indicator+=func_calc_time(time_open_end_rates,time_open_next_rates,9);
}
break;
case 5:
{
 ...
 end_time_indicator+=func_calc_time(time_open_end_rates,time_open_next_rates,7);
}
break;
case 6:
{
 ...
 end_time_indicator+=func_calc_time(time_open_end_rates,time_open_next_rates,5);
}
break;
case 7:
{
 func_filling(period_array,end_time_indicator,all_bars_indicator,time_open_end_rates,time_open_next_rates,end_bar_indicator,TST_C_O,TST_C_H,TST_C_L,TST_C_C,TST_C_Col,status);
 func_candle_per_seconds(period_array,end_time_indicator,bars_now_rates,number_now_rates,end_bar_indicator,TST_C_O,TST_C_H,TST_C_L,TST_C_C,TST_C_Col,status);
 price_bid_now=TST_C_C[end_bar_indicator];
 price_ask_now=price_bid_now+(spread*_Point);
}
break;
 }
}

考えられる使用法

このアイデアを使って、新しいアイデアや取引戦略をテストし、特定の状況で初心者トレーダーの行動をモデリングし、市場参入とエグジットを練習することをお勧めします。これは、主に技術的ツールに関係します。例えば、Elliott波やチャネルをプロットするため、または支持/抵抗線の作業をテストするために使用できます。

指標操作の例：

終わりに

ここで秘密を明らかにします。生成の種類の一つが「ジュエリー」と呼ばれているのは何故でしょうか。

簡単なことです。このアプリケーションの開発中、私は、ほとんどの戦略をテストには、これほど滑らかで正確なモデリングは必要ではないという結論に達しました。よって、それは宝石のような贅沢品です。これらのティックは、スプレッドにほぼ匹敵して変動をシミュレートし、テストの速度を考慮すると特に、戦略の流れにほとんど影響を与えません。次の便利なポイントに逆戻りすることが可能なときに、エントリーポイントをキャッチするのに数日を浪費したい人もいそうにありません。

コードに関してですが、さまざまな失敗の可能性が排除されているわけではありません。しかし、これは戦略分析全体には影響しないはずです。結局のところ、すべての基本的なアクションはグローバル変数に格納され、（指標ウィンドウを閉じることなく）時間枠やターミナルを再び読み込むだけで、エミュレーションを続けることができます。

コードの説明では多くの補助関数が省略されています。それらは簡単なものであるか、すでに説明されているものです。いずれにしても、わからないことがあったら自由にご質問ください。いつものように、コメントをお待ちしています。