Neural Networks in Trading: Hybrid Graph Sequence Models (GSM++)

In recent years, graph transformers adapted from natural language processing and computer vision domains have attracted particular attention. Their ability to model long-range dependencies and efficiently handle irregular financial structures makes them a promising tool for tasks such as volatility forecasting, market anomaly detection, and the construction of optimal investment strategies. However, classical transformers face a number of fundamental challenges, including high computational costs and difficulties in adapting to unordered graph structures.

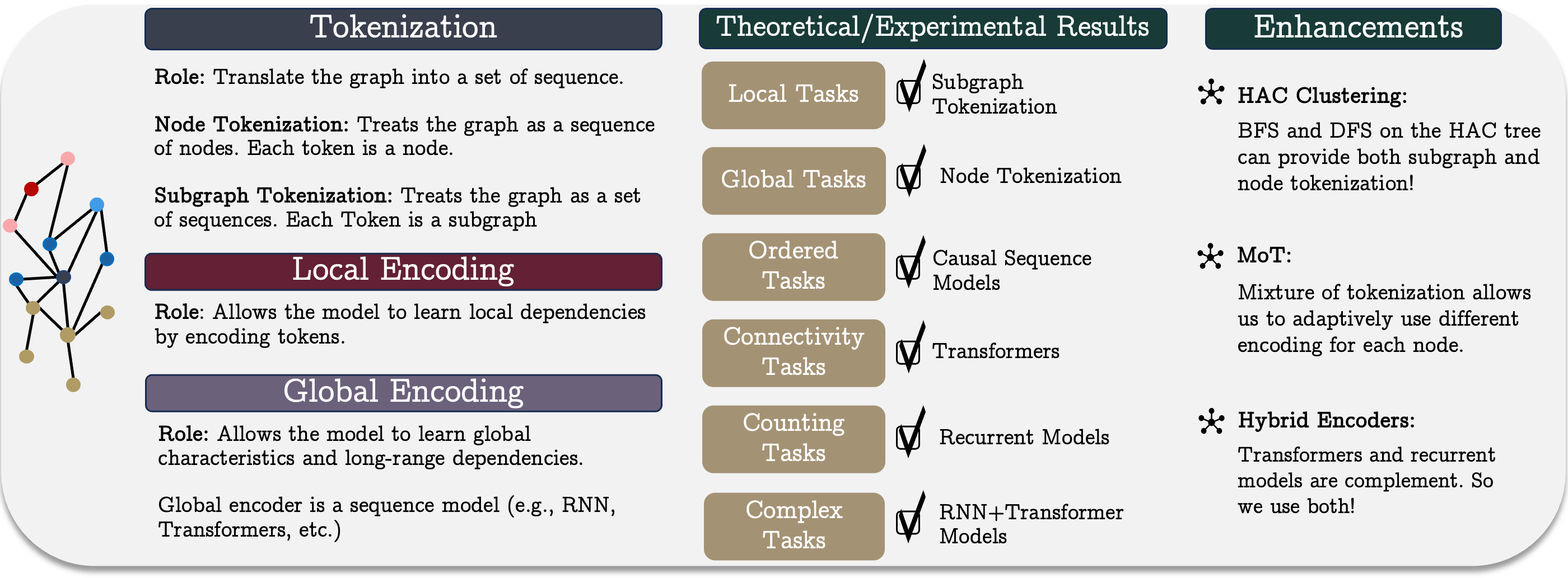
The authors of "Best of Both Worlds: Advantages of Hybrid Graph Sequence Models" propose a unified Graph Sequence Model, GSM++, which combines the strengths of various architectures to create an effective method for representing and processing graphs. The model is built around three key stages: graph tokenization, local node encoding, and global dependency encoding. This approach allows the model to capture both local and global relationships in financial systems, making it versatile and applicable to a wide range of tasks.

A core component of the proposed model is the hierarchical graph tokenization method, which transforms market data into a compact sequential representation while preserving its topological and temporal features. Unlike standard time series encoding methods, this approach improves feature extraction quality and simplifies the processing of large volumes of market data. Combining hierarchical tokenization with a hybrid architecture, that includes transformer and recurrent mechanisms, yields superior performance across multiple tasks. This makes the method a powerful tool for handling complex financial datasets.

Empirical studies and theoretical analysis conducted by the GSM++ framework authors demonstrate that the proposed model not only competes with traditional graph transformers but also surpasses them in several key metrics.

GSM++ Algorithm

The unified graph sequence model represents a conceptual framework comprising three key stages: tokenization, local encoding, and global encoding. This method enables efficient representation and analysis of complex graph structures, which is particularly critical in financial markets. Complex market systems, encompassing numerous participants and interactions, require powerful modeling tools capable of capturing nonlinear dependencies and hidden correlations.

Tokenization plays a fundamental role in transforming a graph structure into a sequential representation suitable for sequence-based models. The primary tokenization strategies include node or edge tokenization and subgraph tokenization. The choice of tokenization method significantly impacts model effectiveness, as it determines how fully the graph’s structural information is preserved and which organizational features are considered during analysis.

Node or edge tokenization treats the graph as a sequence of individual elements, disregarding their interconnections. Preserving structural information requires additional positional or structural encoding. The main drawback of this method is its high computational complexity, as the sequence length corresponds to the number of nodes or edges, complicating model training. However, it is useful when detailed information on each system element is needed—for instance, in constructing individualized asset strategies based on microscopic characteristics. In high-frequency trading, this approach allows more precise analysis of short-term market fluctuations and the detection of abnormal trading patterns.

Subgraph tokenization reduces computational costs by representing the graph as a sequence of subgraphs, enhancing the model's ability to capture local structure. This approach is particularly useful in financial applications, such as analyzing trading patterns where subgraphs correspond to clusters of correlated assets or groups of investors. Interactions between assets often have a hidden network nature, and subgraph-based analysis helps uncover persistent market patterns, critical for portfolio management, liquidity assessment, and arbitrage strategies.

Each tokenization method has advantages and limitations, so the choice depends on the task. In some cases, hybrid approaches combining both strategies achieve a better balance between data representation fidelity and computational efficiency.

Based on these ideas, the GSM++ framework authors proposed a hierarchical tokenization algorithm, based on clustering nodes by similarity (Hierarchical Affinity Clustering, HAC).

The algorithm starts by treating each graph vertex as a separate cluster. At each step, two clusters connected by the least "expensive" edge (determined by the similarity of their encodings) are merged. This process continues until the entire graph is merged into a single cluster. The result is a hierarchical tree, with the root representing the whole graph and the leaves corresponding to the original nodes.

This approach offers two key advantages. First, it organizes nodes so that similar elements are closer together, improving graph representation in models. Second, it enables multi-level graph encoding, allowing flexible structural analysis. Two tree traversal strategies are developed: depth-first search (DFS) and breadth-first search (BFS). DFS generates node sequences reflecting their hierarchical positions. BFS produces sequences where similar nodes are adjacent.

This tokenization method preserves the graph’s local structure and works efficiently with recurrent models, especially for tasks requiring global connectivity analysis.

Additionally, a hierarchical positional encoding method is used, considering the shortest paths between nodes and their positions in the cluster hierarchy. Experiments show that this encoding significantly improves graph representation quality.

Since different nodes may require different tokenization methods depending on the graph structure and task, the Mix of Tokenization (MoT) approach was proposed. It allows each node to use the most suitable encoding method by selecting optimal tokenizers and combining their representations.

After tokenization, data is converted into vector representations to study local graph features. At this stage, Graph Neural Networks (GNNs) are commonly used, as they efficiently capture local dependencies between nodes. In financial markets, this helps analyze asset correlations, detect local anomalies, and generate predictions based on microstructural data. Due to their adaptability and ability to extract complex patterns, GNNs are applied in algorithmic trading and market volatility forecasting.

Global encoding is crucial for modeling long-term dependencies within the graph. Sequential encoding is applied to identify complex relationships between structural elements. In financial applications, this enables modeling macroeconomic trends, analyzing the influence of global factors on markets, and developing strategies based on deep data interconnections. Long-term financial trends, such as the impact of monetary policy or global economic crises, require algorithms capable of capturing complex dependencies across multiple time horizons.

When selecting a sequence model for graph training, a key question arises: which model is most effective? The standard approach allows combining various sequence encoders with different tokenization methods, generating multiple possible architectures. However, there is no clear consensus on which are best suited for specific graph tasks.

Counting tasks require determining the number of nodes of a certain type. Attention-based models without causal dependencies cannot solve such tasks correctly. This raises the question: can recurrent models, which account for order, handle this problem?

It turns out that if the width of the recurrent model matches the number of distinct node classes, it can count them accurately. This demonstrates the effectiveness of recurrent models in tasks where sequential structure is more critical than graph topology.

Certain graph tasks, such as algorithmic reasoning, require strict adherence to node order. Modern sequence models mostly rely on causal dependencies, which must be considered when integrating them with graph models. Research shows that excessive information compression can reduce representational fidelity. In recurrent models, sensitivity to initial data decreases with the distance between elements, whereas transformers maintain constant sensitivity. However, both models are prone to representation collapse as depth increases.

Information at the beginning of a sequence has a higher chance of being retained. This leads to a U-shaped effect, where tokens at the sequence start and end retain their significance better than those in the middle. This behavior is observed in both transformers and recurrent models Therefore, when ordering nodes in a sequence, important elements should be placed closer together to enhance mutual influence.

Connectivity-related tasks require global graph structure analysis. Connectivity can be framed as a binary classification problem. Studies show that transformers of sufficient depth and embedding size can solve such tasks effectively. Recurrent models and limited-attention transformers, however, require significantly more parameters or depth to achieve similar results.

Recurrent models are most effective when data has a natural order and tokenization respects graph structure. Node locality defining the maximum distance between neighboring vertices is an important parameter. For graphs with limited locality, a compact recurrent model can determine connectivity efficiently. Fixed-parameter transformers, in contrast, struggle with such tasks.

Choosing a model requires understanding trade-offs in graph analysis tasks. Examination of different architectures highlights several key observations:

1. Transformers excel in connectivity tasks using minimal parameters. They are particularly useful for complex graphs requiring parallel computations. Their ability to form context-dependent representations makes them powerful for analyzing complex networks and graphs.
2. Recurrent Neural Networks (RNNs) perform well on graphs where vertex connections have a clearly localized structure. They require fewer parameters and computations, making them energy-efficient and suitable for streaming data.
3. Hybrid models, combining RNNs and transformers, leverage the advantages of both architectures. They balance computational complexity and prediction accuracy, especially when global context and local details are both critical.
4. State-space models are highly effective where strict element order is important. They possess long-term memory properties, making them useful for time series analysis and modeling sequential actions in agent-based systems.
5. Sparse attention reduces transformer computational costs, particularly for large graphs. Its effective use requires additional mechanisms to identify the most significant node connections, which can complicate implementation.

Thus, model selection depends on the structure of input data and available computational resources. Transformers are suited for complex graphs with pronounced global dependencies, RNNs are optimal for localized sequences, and state-space models excel in tasks requiring strict operation order. Hybrid approaches allow balancing computational efficiency with prediction accuracy, making them a versatile choice for many applied scenarios.

Based on this analysis, the authors present the GSM++ framework, incorporating hierarchical node tokenization based on similarity, convolutional GNNs as the local encoder, and a hybrid global encoder containing Mamba and Transformer modules.

Implementation in MQL5

After reviewing the theoretical aspects of the approaches proposed by the GSM++ framework authors, we now move to the practical part of our work. In this section, we focus on implementing our own interpretation of the discussed approaches using MQL5 tools.

It should be noted that while preserving the general concept embedded in the original approaches, our implementation differs significantly in detail.

First and foremost, in our implementation, we decided to forgo hierarchical similarity-based clustering (HAC). It is reasonable to consider that the candlesticks formed on a financial instrument chart are dynamic and evolving objects that cannot be easily standardized. Their analysis and clustering is a complex, multifaceted process requiring a much deeper and comprehensive approach.

Therefore, as before, we use trainable modules for tokenizing the representations of the bars under analysis. This approach allows us to retain the flexibility and adaptability of the model under real-world data conditions, which is particularly important when working with financial markets.

Nevertheless, in our implementation we employ the proposed Mix of Tokenization (MoT) algorithm, albeit in a somewhat modified and adapted form to accommodate the specifics of our task. The GSM++ framework authors suggest using a trainable clustering model to select the two most relevant tokenization algorithms, after which the outputs of these algorithms are summed to produce the final representation. In contrast, we prepare four different types of tokens for each bar and combine their outputs using an Attention Pooling algorithm borrowed from the R-MAT framework.

This approach significantly improves analytical quality, as it allows consideration of more aspects of the data and more precise extraction of relevant information. In our work, the following tokenization variants are employed:

• Node tokenization – each bar represents a separate analytical element that the model processes to extract data.
• Edge tokenization – focuses on interactions between two consecutive bars, highlighting important connections across different parts of the data.
• Subgraph tokenization – enables the formation of more complex structures by accounting for connections among multiple bars within a single group.
• Subgraph tokenization of individual unitary sequences – provides detailed analysis of structural sequences, allowing for deeper-level data processing.

The use of these tokenization methods allows consideration of both individual elements and their interrelations, substantially improving the quality of information representation for each bar and enhancing overall model performance. Combining all tokens via Attention Pooling enables the model to adapt flexibly and focus on the most significant features, improving decision-making.

To implement this solution, we create a new object, CNeuronMoT. Its structure is shown below.

class CNeuronMoT  :  public CNeuronMHAttentionPooling
  {
protected:
   CNeuronConvOCL             cNodesTokenizer;
   CNeuronConvOCL             cEdgesTokenizer;
   CNeuronConvOCL             cSubGraphsTokenizer;
   CLayer                     cUnitarSubGraphsTokenizer;
   CNeuronBaseOCL             cConcatenate;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronMoT(void){};
                    ~CNeuronMoT(void){};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint units_count,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronMoT; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

The parent object in this case is CNeuronMHAttentionPooling, which already implements the Attention Pooling algorithm intended for use at the output stage of the module to combine different tokenization variants. This approach offers several significant advantages.

First, using the parent class avoids code redundancy, eliminating the need to re-implement the Attention Pooling module in other objects or components. Instead, we integrate a ready and optimized implementation of the algorithm, maintaining a high level of abstraction and simplifying code maintenance.

Second, all operations related to token combination and processing are executed through the functionality of the parent class. This significantly simplifies system architecture and improves resource efficiency, as the parent class already contains all necessary methods and algorithms for attention processing. This minimizes functional duplication and enhances modularity and extensibility.

The new object's structure includes a familiar set of virtual overridable methods, essential for our model's implementation. These methods provide flexibility and allow customization of object behavior depending on task requirements.

Additionally, the class contains several internal objects, which play a key role in our algorithm.Кроме того, в классе присутствуют несколько внутренних объектов, которые играют ключевую роль в построении нашего алгоритма. Their specific purpose will be explained in detail during the implementation of the class methods, where their operation and interactions will be fully described.

All internal objects are declared as static, allowing us to keep the class constructor and destructor empty. The initialization of all declared and inherited objects, as usual, is handled within the Init method.

bool CNeuronMoT::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                      uint window, uint units_count,
                      ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronMHAttentionPooling::Init(numOutputs, myIndex, open_cl, window, units_count, 4, optimization_type, batch))
      return false;

The method parameters receive constants describing the dimensionality of the input data. Please note that this implementation expects output in the same dimensionality. Consequently, the parameters are immediately passed to the identically named parent class method, which already implements initialization for all inherited objects and interfaces.

After successful execution of the parent class method, we proceed to initialize the newly declared objects. First, we initialize the node tokenization object. It is implemented as a convolutional layer with convolution window size, step, and number of filters equal to the vector describing a single sequence element.

This approach enables efficient processing of sequential data, where each element (node) is represented as a vector corresponding to specific features. Convolution allows extraction of important local features, forming the foundation for subsequent data processing and tokenization. Matching the convolution parameters to the element description vector ensures seamless integration of the convolutional layer into the overall model structure, maintaining efficiency and consistency across all processing stages.

int index = 0;
if(!cNodesTokenizer.Init(0, index, OpenCL, iWindow, iWindow, iWindow, iUnits, 1, optimization, iBatch))
   return false;
cNodesTokenizer.SetActivationFunction(SoftPlus);

Next, we initialize the edge tokenization convolutional layer. Unlike the previous object, here we use the convolution window of two consecutive elements. This allows modeling of interactions and connections between neighboring elements, important for deeper structural analysis.

index++;
if(!cEdgesTokenizer.Init(0, index, OpenCL, 2 * iWindow, iWindow, iWindow, iUnits, 1, optimization, iBatch))
   return false;
cEdgesTokenizer.SetActivationFunction(SoftPlus);

It should be noted that using a double window with a single step generally reduces the sequence length by one element. However, subsequent token combination requires tensor dimensional compatibility across all stages. Therefore, we preserve the original sequence length by padding missing elements at the end with zeros.

Similarly, we initialize the subgraph tokenization convolutional layer, expanding the window to three sequence elements while maintaining all other parameters.

index++;
if(!cSubGraphsTokenizer.Init(0, index, OpenCL, 3 * iWindow, iWindow, iWindow, iUnits, 1, optimization, iBatch))
   return false;
cSubGraphsTokenizer.SetActivationFunction(SoftPlus);

At all tokenization levels, we apply the SoftPlus activation function. This choice offers several advantages. SoftPlus is smooth and monotonic, avoiding sharp jumps and improving training stability. Unlike ReLU, SoftPlus does not have an abrupt transition from zero to positive values, preventing "dead neuron" issues.

Also, SoftPlus derivative is always positive, facilitating good differentiability and smooth weight updates during backpropagation. This is especially important for complex neural networks requiring precise and stable parameter adjustments.

Applying SoftPlus across all tokenization levels creates a more flexible and stable model, ensuring smoothness and robustness, critical for processing and analyzing complex sequential data.

The generation of tokens for unitary sequences of a multidimensional time series requires several sequential operations. To perform this functionality, we will need to perform several sequential operations, which we will combine into an internal model, and store pointers to objects stored in the dynamic array cUnitarSubGraphsTokenizer.

We first initialize a dynamic array and declare local variables for temporary storage of object pointers.

cUnitarSubGraphsTokenizer.Clear();
cUnitarSubGraphsTokenizer.SetOpenCL(OpenCL);
CNeuronConvOCL *conv = NULL;
CNeuronTransposeOCL *transp = NULL;

For convenience in working with unitary sequences, we transpose the input data.

index++;
transp = new CNeuronTransposeOCL();
if(!transp ||
   !transp.Init(0, index, OpenCL, iUnits, iWindow, optimization, iBatch) ||
   !cUnitarSubGraphsTokenizer.Add(transp))
  {
   delete transp;
   return false;
  }

Then, we use a convolutional layer to generate subgraph tokens. Here we again analyze 3-element subgraphs. Each element is represented by a single value, and the number of analyzed variables equals the number of unitary sequences.

index++;
conv = new CNeuronConvOCL();
if(!conv ||
   !conv.Init(0, index, OpenCL, 3, 1, 1, iUnits, iWindow, optimization, iBatch) ||
   !cUnitarSubGraphsTokenizer.Add(conv))
  {
   delete conv;
   return false;
  }
conv.SetActivationFunction(SoftPlus);

This approach enables detailed analysis of transitions and patterns within individual unitary sequences.

Generated values are then transposed back to their original state.

index++;
transp = new CNeuronTransposeOCL();
if(!transp ||
   !transp.Init(0, index, OpenCL, iWindow, iUnits, optimization, iBatch) ||
   !cUnitarSubGraphsTokenizer.Add(transp))
  {
   delete transp;
   return false;
  }
transp.SetActivationFunction((ENUM_ACTIVATION)conv.Activation());

Finally, we initialize the object responsible for concatenating results from different tokenization approaches.

   index++;
   if(!cConcatenate.Init(0, index, OpenCL, 4 * iWindow * iUnits, optimization, iBatch))
      return false;
   cConcatenate.SetActivationFunction(None);
//---
   return true;
  }

Note that activation is intentionally disabled for the concatenation object. Of course, we use same activation functions for all token-generating objects. We could move it to the concatenation object, which could slightly simplify the gradient distribution algorithm in the backpropagation pass. However, in general, we allow the use of different activation functions for individual token generation objects. In this case, specifying an activation function for the concatenation object would only distort the data. 

At the end of the method, we return the logical result of the operations performed to the calling program.

Next, we need to implement the feed-forward pass algorithm in the feedForward method. Its algorithm is quite simple.

bool CNeuronMoT::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cNodesTokenizer.FeedForward(NeuronOCL))
      return false;
   if(!cEdgesTokenizer.FeedForward(NeuronOCL))
      return false;
   if(!cSubGraphsTokenizer.FeedForward(NeuronOCL))
      return false;

The method receives a pointer to the object containing input data, which is passed to the corresponding methods of internal objects at different tokenization levels.

For token generation in unitary sequences, a loop iterates through objects in the internal model.

   CNeuronBaseOCL *prev = NeuronOCL, *current = NULL;
   for(int i = 0; i < cUnitarSubGraphsTokenizer.Total(); i++)
     {
      current = cUnitarSubGraphsTokenizer[i];
      if(!current ||
         !current.FeedForward(prev))
         return false;
      prev = current;
     }

All generated tokens are collected into a single tensor representing the sequence elements.

   if(!Concat(cNodesTokenizer.getOutputIndex(), cEdgesTokenizer.getOutputIndex(),
              cSubGraphsTokenizer.getOutputIndex(), current.getOutputIndex(),
              cConcatenate.getOutputIndex(), iWindow, iWindow, iWindow, iWindow, iUnits))
      return false;

The resulting tensor is passed to the identically named parent class method to obtain the final graph representation.

   return CNeuronMHAttentionPooling::feedForward(cConcatenate.AsObject());
  }

We return the logical result of the performed operations to the calling program and complete the execution of the method.

Although conceptually simple, the feedForward method executes four parallel information streams, complicating gradient distribution. Its algorithm is implemented in the calcInputGradients method.

bool CNeuronMoT::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;

The method receives a pointer to the same source data object. This time we also have to pass into it the error gradient in the amount of input data influence on the model output. Data can only be passed to a valid object. Therefore, validity of the pointer is verified first.

The error gradient from subsequent objects is distributed down to the token concatenation object using the parent class.

if(!CNeuronMHAttentionPooling::calcInputGradients(cConcatenate.AsObject()))
   return false;

The gradient is then divided among all information streams.

CNeuronBaseOCL *current = cUnitarSubGraphsTokenizer[-1];
if(!current ||
   !DeConcat(cNodesTokenizer.getGradient(), cEdgesTokenizer.getGradient(),
             cSubGraphsTokenizer.getGradient(), current.getGradient(),
             cConcatenate.getGradient(), iWindow, iWindow, iWindow, iWindow, iUnits))
   return false;

Next, we need to distribute the error gradient across all information steams.

From the concatenation object, we get the error gradient that ha snot been adjusted for the derivative of the activation function. Therefore, before starting the operations of each information stream, we need to adjust the values to the derivatives of the corresponding activation functions.

First, we distribute the error gradient along univariate sequences. First, we check the presence of the activation function and, if necessary, adjust the obtained values.

if(current.Activation() != None &&
   !DeActivation(current.getOutput(), current.getGradient(),
                 current.getGradient(), current.Activation()))
   return false;

Next, we run a backpropagation loop over the objects of the internal model, sequentially calling the relevant methods.

for(int i = cUnitarSubGraphsTokenizer.Total() - 2; i >= 0; i--)
  {
   current = cUnitarSubGraphsTokenizer[i];
   if(!current ||
      !current.calcHiddenGradients(cUnitarSubGraphsTokenizer[i + 1]))
      return false;
  }

After that, we propagate the error gradient to the level of source data.

if(!NeuronOCL.calcHiddenGradients(current.AsObject()))
   return false;

At this stage, we have propagated the error gradient to the source data layer via only one branch. We need to do this for three more branches.

In order to preserve the previously obtained values, we perform a swap of pointers to the corresponding data buffers.

CBufferFloat *temp = NeuronOCL.getGradient();
if(!NeuronOCL.SetGradient(current.getPrevOutput(), false))
   return false;

Once we are sue the previously obtained data has been saved, we propagate gradients along the remaining branches. Here we sequentially check the presence of the activation function and, if necessary, adjust the values to the corresponding derivative of the activation function.

if(cNodesTokenizer.Activation() != None &&
   !DeActivation(cNodesTokenizer.getOutput(), cNodesTokenizer.getGradient(),
                 cNodesTokenizer.getGradient(), cNodesTokenizer.Activation()))
   return false;
if(!NeuronOCL.calcHiddenGradients(cNodesTokenizer.AsObject()) ||
   !SumAndNormilize(temp, NeuronOCL.getGradient(), temp, iWindow, false, 0, 0, 0, 1))
   return false;

Then, we propagate the error gradient to the level of the source data and sum it with the previously accumulated values. Repeat the operations for the next branch.

if(cEdgesTokenizer.Activation() != None &&
   !DeActivation(cEdgesTokenizer.getOutput(), cEdgesTokenizer.getGradient(),
                 cEdgesTokenizer.getGradient(), cEdgesTokenizer.Activation()))
   return false;
if(!NeuronOCL.calcHiddenGradients(cEdgesTokenizer.AsObject()) ||
   !SumAndNormilize(temp, NeuronOCL.getGradient(), temp, iWindow, false, 0, 0, 0, 1))
   return false;

if(cSubGraphsTokenizer.Activation() != None &&
   !DeActivation(cSubGraphsTokenizer.getOutput(), cSubGraphsTokenizer.getGradient(),
                 cSubGraphsTokenizer.getGradient(), cSubGraphsTokenizer.Activation()))
   return false;
if(!NeuronOCL.calcHiddenGradients(cSubGraphsTokenizer.AsObject()) ||
   !SumAndNormilize(temp, NeuronOCL.getGradient(), temp, iWindow, false, 0, 0, 0, 1))
   return false;

After successfully propagating error gradients across all information streams, we return the pointers to their original state, return the booolean result of the operation to the caller, and complete the method.

   if(!NeuronOCL.SetGradient(temp, false))
      return false;
//---
   return true;
  }

With this, we conclude the review of the algorithmic construction of the methods of the adaptive mixed tokenization object CNeuronMoT. The complete implementation of this object and all its methods can be found in the attachment.
 
We have reached the end of this article, but our work is not yet complete. Let's take a short break and continue this work in the next part.

Conclusion

In this article, we explored an innovative approach to using hybrid graph sequence models (GSM++), combining the power of graph structures with sequential data analysis. These models provide high accuracy for forecasting and analysis, efficiently processing complex financial data. In addition, they optimize computational resource usage, which makes them particularly valuable for working with large data volumes. A key advantage of GSM++ is its ability to adapt to rapidly changing market conditions.

In the practical section, we implemented our own vision of the proposed approaches and constructed a mixed tokenization module. In the next article, we will continue this work to completion, including testing the effectiveness of our implementation on real historical data.

References

• Best of Both Worlds: Advantages of Hybrid Graph Sequence Models
• Other articles from this series

Programs used in the article

#	Name	Type	Description
1	Research.mq5	Expert Advisor	Expert Advisor for collecting samples
2	ResearchRealORL.mq5	Expert Advisor	Expert Advisor for collecting samples using the Real-ORL method
3	Study.mq5	Expert Advisor	Model training Expert Advisor
4	Test.mq5	Expert Advisor	Model testing Expert Advisor
5	Trajectory.mqh	Class library	System state and model architecture description structure
6	NeuroNet.mqh	Class library	A library of classes for creating a neural network
7	NeuroNet.cl	Code Base	OpenCL program code