
Нейросети в трейдинге: Гибридные модели последовательностей графов (GSM++)
В последние годы особое внимание привлекают графовые трансформеры, адаптированные для применения из областей обработки естественного языка и компьютерного зрения. Их способность моделировать дальнодействующие зависимости и эффективно работать с нерегулярными финансовыми структурами делает их перспективным инструментом для задач, таких как прогнозирование волатильности, выявление рыночных аномалий и построение оптимальных инвестиционных стратегий. Однако, классические трансформеры сталкиваются с рядом фундаментальных проблем, включая высокие вычислительные затраты и трудности адаптации к неупорядоченным структурам графов.
Авторы работы "Best of Both Worlds: Advantages of Hybrid Graph Sequence Models" предлагают унифицированную модель графовых последовательностей GSM++, объединяющая сильные стороны различных архитектур для создания эффективного метода представления и обработки графов. Она основана на трёх ключевых этапах: токенизации графа, локальном кодировании узлов и глобальном кодировании зависимостей. Такой подход позволяет учесть как локальные, так и глобальные связи в финансовой системе, делая модель универсальной и применимой к широкому спектру задач.
Ключевым элементом предложенной модели является разработанный метод иерархической токенизации графов, который позволяет преобразовывать рыночные данные в компактное последовательное представление, сохраняя их топологические и временные особенности. В отличие от стандартных методов кодирования временных рядов, этот подход улучшает качество извлечения признаков и упрощает обработку больших объемов рыночных данных. Сочетание иерархической токенизации с гибридной архитектурой, включающей механизмы трансформеров и рекуррентных моделей, позволяет достичь превосходных результатов в различных задачах. Это делает предложенный метод эффективным инструментом для обработки сложных финансовых данных.
Эмпирические исследования и теоретический анализ, проведенные авторами фреймворка GSM++, показывают, что предложенная модель не только конкурирует с традиционными графовыми трансформерами, но и превосходит их по ряду ключевых характеристик.
Алгоритм GSM++
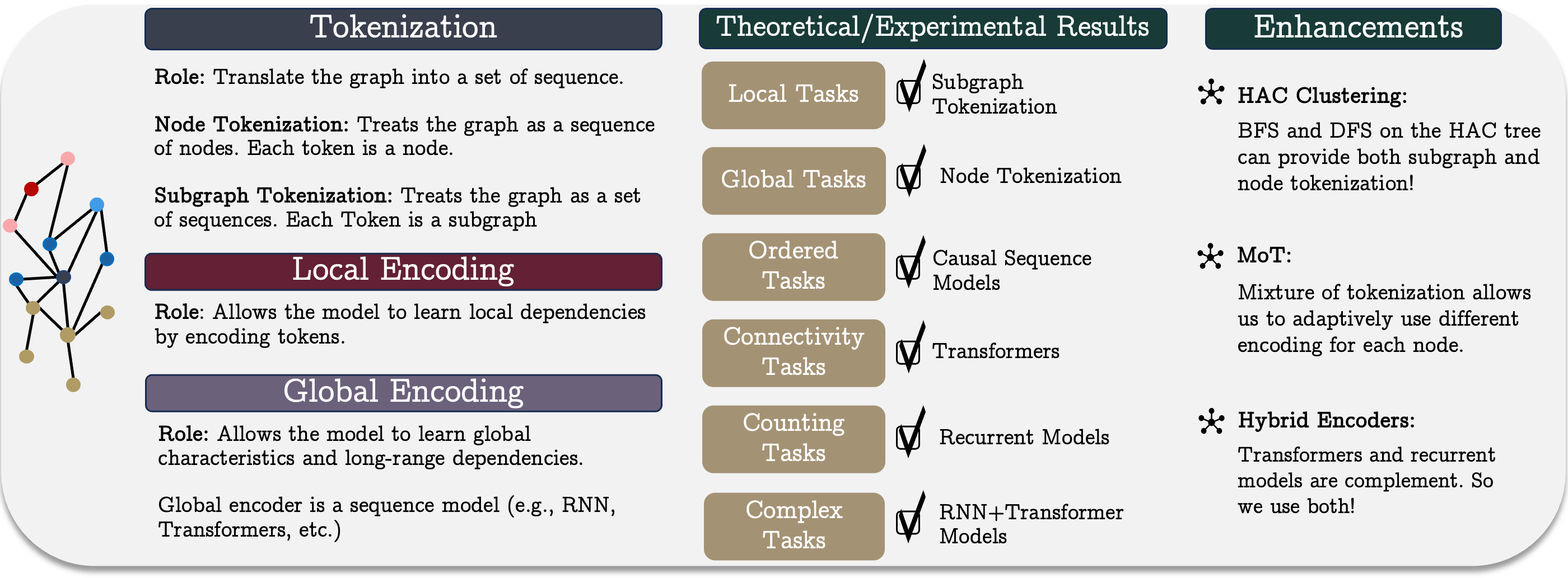
Унифицированная модель последовательностей графов представляет собой концептуальный подход, включающий три ключевых этапа: токенизацию, локальное кодирование и глобальное кодирование. Этот метод позволяет эффективно представлять и анализировать сложные графовые структуры, что особенно важно в контексте финансовых рынков. Сложные рыночные системы, включающие множество участников и взаимодействий, требуют использования мощных инструментов моделирования, способных выявлять нелинейные зависимости и скрытые корреляции.
Токенизация играет фундаментальную роль в преобразовании графовой структуры в представление последовательности, что необходимо для обработки данных с использованием моделей последовательностей. Различают следующие основные методы токенизации: токенизацию узлов или ребер, токенизацию подграфов. Выбор метода токенизации оказывает значительное влияние на эффективность модели, поскольку определяет, насколько полно сохраняется структурная информация графа, и какие особенности его организации будут учтены при последующем анализе.
Токенизация узлов или ребер предполагает, что граф рассматривается в виде последовательности соответствующих элементов без учета их взаимосвязей. Чтобы сохранить структурную информацию, требуется дополнительное позиционное или структурное кодирование. Основным недостатком такого метода является его высокая вычислительная сложность, так как длина последовательности соответствует количеству узлов или ребер, что усложняет обучение моделей. Однако, этот метод может быть полезен в ситуациях, когда необходимо учитывать детализированную информацию о каждом элементе системы, например, при построении индивидуальных стратегий для активов на основе их микроскопических характеристик. В условиях высокочастотного трейдинга такой подход позволяет более точно анализировать влияние краткосрочных рыночных колебаний и выявлять аномальные торговые паттерны.
Токенизация подграфов позволяет уменьшить вычислительные затраты за счет представления графа в виде последовательностей подграфов, что повышает способность модели учитывать локальную структуру. Такой подход особенно полезен для финансовых приложений, например, при анализе торговых моделей, где подграфы могут соответствовать кластерам связанных активов, или группам инвесторов. Взаимодействие между активами зачастую имеет скрытую сетевую природу, а использование подграфов позволяет выявлять устойчивые рыночные закономерности, что критически важно в задачах портфельного инвестирования, оценки ликвидности и арбитражных стратегий.
Каждый из методов токенизации имеет свои преимущества и ограничения, поэтому выбор конкретного метода зависит от специфики задачи. В некоторых случаях комбинированные подходы, объединяющие свойства обеих стратегий токенизации, позволяют достичь лучшего баланса между точностью представления данных и вычислительной эффективностью.
Основываясь на представленных идеях, авторы фреймворка GSM++ предложили алгоритм иерархической токенизации, основанный на кластеризации узлов по их схожести (Hierarchical Affinity Clustering — HAC).
Алгоритм начинается с того, что каждая вершина графа рассматривается как отдельный кластер. Затем на каждом шаге объединяются два кластера, соединенные наименее "дешевым" ребром, вычисленным на основе сходства их кодировок. Этот процесс продолжается до тех пор, пока весь граф не объединится в один кластер. В результате формируется иерархическое дерево, где корень представляет весь граф, а листья соответствуют исходным узлам.
Этот подход имеет два важных преимущества. Во-первых, он упорядочивает узлы так, что похожие элементы оказываются ближе друг к другу, что улучшает представление графа в моделях. Во-вторых, он позволяет кодировать графы на различных уровнях детализации, создавая возможность гибкого анализа структуры. Разработаны два варианта токенизации: обход дерева в глубину (DFS) и в ширину (BFS). DFS-подход создает последовательности узлов, отражающие их иерархическое положение. BFS-подход формирует последовательности, где узлы упорядочены так, что схожие элементы находятся рядом друг с другом.
Предложенная методика токенизации сохраняет локальную структуру графа и эффективно работает с рекуррентными моделями, особенно при решении задач, требующих анализа глобальной связности.
Дополнительно используется метод иерархического позиционного кодирования, который учитывает кратчайшие пути между узлами и их положение в иерархии кластеров. Эксперименты показали, что такой способ кодирования улучшает качество представления графов.
Так как в зависимости от структуры графа и решаемой задачи, различные узлы могут требовать различных методов токенизации, был предложен подход Mix of Tokenization (MoT). Он позволяет каждому узлу использовать наиболее подходящий метод кодирования, выбирая оптимальные токенизаторы и объединяя их представления.
После этапа токенизации, данные преобразуются в векторное представление с целью изучения локальных характеристик графа. На этом этапе наиболее часто используются сверточные нейронные сети на графах (GNN), так как они эффективно выявляют локальные зависимости между узлами. В контексте финансовых рынков этот шаг помогает анализировать корреляции между активами, выявлять локальные аномалии и строить прогнозы на основе микроструктурных данных. Благодаря своей адаптивности и способности извлекать сложные паттерны, графовые нейросети применяются для автоматизации торговли и прогнозирования рыночной волатильности.
Глобальное кодирование играет решающую роль в изучении долгосрочных зависимостей внутри графа. На этом этапе применяется последовательное кодирование для выявления сложных взаимосвязей между элементами структуры. В финансовых приложениях это позволяет моделировать макроэкономические тенденции, анализировать влияния глобальных факторов на рынки и строить стратегии на основе глубокой взаимосвязанности данных. Долгосрочные тренды в финансовых данных, такие как влияние монетарной политики или глобальных экономических кризисов, требуют использования мощных алгоритмов, способных выявлять сложные зависимости на разных временных горизонтах.
При выборе модели последовательности для обучения графов, возникает вопрос: какая модель будет наиболее эффективной? Согласно принятому подходу, можно комбинировать различные кодировщики последовательностей с разными методами токенизации, создавая множество возможных архитектур. Однако, нет четкого понимания, какие из них наиболее подходят для различных графовых задач.
Задачи подсчета предполагают определение количества узлов определенного типа в графе. Модели, использующие механизмы внимания без причинно-следственных зависимостей, не способны корректно решать такие задачи. Следовательно, возникает вопрос: могут ли рекуррентные модели, учитывающие порядок, решить эту проблему?
Оказывается, если ширина рекуррентной модели соответствует количеству различных классов узлов, то она способна точно подсчитывать их количество. Это подтверждает эффективность рекуррентных моделей в задачах, где последовательная структура важнее топологии графа.
Некоторые графовые задачи, например, алгоритмические рассуждения, требуют строгого соблюдения порядка узлов. Современные модели последовательностей, в основном, используют причинно-следственные связи, что нужно учитывать при их интеграции в графовые модели. Исследования показывают, что чрезмерное сжатие информации может привести к потере репрезентативности. В рекуррентных моделях чувствительность к исходным данным снижается с увеличением расстояния между элементами, тогда как у трансформеров она остается постоянной. Однако, обе модели подвержены коллапсу представлений при увеличении глубины.
Информация, расположенная в начале последовательности, имеет больше шансов быть сохраненной. Это приводит к U-образному эффекту, когда токены, находящиеся в начале и конце последовательности, сохраняют свое значение лучше, чем токены в середине. Такое поведение наблюдается как у трансформеров, так и у рекуррентных моделей. Поэтому при организации узлов в последовательности следует размещать важные элементы ближе друг к другу, чтобы усилить их взаимное влияние.
Задачи, связанные с определением связности графа, требуют глобального анализа его структуры. Связность можно рассматривать как задачу бинарной классификации. Исследования показывают, что трансформеры с определенной глубиной и размером вложений способны эффективно решать такие задачи. Однако, рекуррентные модели и трансформеры с ограниченным вниманием требуют значительно большего количества параметров или глубины модели для достижения аналогичных результатов.
Рекуррентные модели проявляют наибольшую эффективность, когда данные имеют естественный порядок, а токенизация учитывает структуру графа. Важным параметром является локальность узла, определяющая максимальное расстояние между соседними вершинами. Для графов с ограниченной локальностью можно построить компактную рекуррентную модель, способную определять связность. Однако трансформеры с фиксированным числом параметров не могут эффективно справляться с такими задачами.
При выборе модели, важно понимать компромиссы, которые возникают при их применении в задачах анализа графов. Рассмотрение различных архитектур позволяет выделить несколько ключевых особенностей:
- Трансформеры демонстрируют высокую эффективность в решении задач графовой связности, используя минимальное количество параметров. Они особенно полезны в случаях, когда граф имеет сложную структуру и требует параллельных вычислений. А способность формировать контекстно-зависимые представления делает их мощным инструментом для анализа сложных сетей и графов.
- Рекуррентные нейронные сети (RNN) хорошо работают с графами, где связи между вершинами обладают четкой локализованной структурой. В таких случаях они требуют меньше параметров и вычислений, что делает их более энергоэффективными и подходящими для работы с потоковыми данными.
- Гибридные модели, сочетающие RNN и трансформеры, позволяют комбинировать преимущества обеих архитектур. Они обеспечивают баланс между вычислительной сложностью и точностью предсказаний, что особенно полезно в задачах, где необходим как глобальный контекст, так и локальные детали.
- Модели пространства состояний проявляют высокую эффективность в ситуациях, где важен строгий порядок следования элементов. Они обладают свойствами долговременной памяти, что делает их полезными для анализа временных рядов и моделирования последовательностей действий в агентных системах.
- Разреженное внимание снижает вычислительные затраты трансформеров, особенно при работе с крупными графами. Однако для его эффективного использования, требуется разработка дополнительных механизмов, для выявления наиболее значимых связей между вершинами, что может усложнить реализацию модели.
Таким образом, выбор модели зависит от структуры исходных данных и доступных вычислительных ресурсов. Трансформеры подходят для сложных графов с выраженными глобальными зависимостями, RNN — оптимальны для локализованных последовательностей, а модели пространства состояний лучше всего работают в задачах, требующих строгого порядка выполнения операций. Гибридные подходы предоставляют возможность сбалансировать вычислительную эффективность и точность прогнозов, что делает их универсальным выбором для многих прикладных задач.
По результатам проведенного в авторской работе анализа, был представлен фреймворк GSM++, который включает иерархическую токенизацию узлов по подобию, сверточные графовые нейронные сети в качестве локального энкодера и гибридный глобальный энкодер, содержащий модули Mamba и Transformer.
Реализация средствами MQL5
После ознакомления с теоретическими аспектами подходов, предложенных авторами фреймворка GSM++, мы переходим к практической часте нашей работы. В этом разделе мы сосредотачиваемся на реализации собственного видения рассмотренных подходов, с использованием инструментов и возможностей языка программирования MQL5.
Стоит обратить внимание, что при сохранении общей концепции, заложенной в оригинальных подходах, наша реализация будет существенно отличаться в деталях.
Прежде всего, в рамках нашей реализации, мы решили отказаться от использования иерархической кластеризации на основе сходства (HAC). Думаю, вы согласитесь, что свечи, формируемые на графике финансового инструмента, являются динамическими и изменяющимися объектами, которые не поддаются простой стандартизации. Их анализ и кластеризация — это сложный и многогранный процесс, который требует гораздо более глубокого и всестороннего подхода.
Поэтому, мы, как и ранее, будем использовать обучаемые модули для токенизации представлений анализируемых баров. Такой подход позволяет нам сохранить гибкость и адаптивность модели в условиях реальных данных, что особенно важно при работе с финансовыми рынками.
Тем не менее, в нашей реализации мы используем предложенный алгоритм смешанной токенизации (MoT), однако, в несколько изменённой и адаптированной форме, с учётом специфики нашей задачи. Авторы фреймворка GSM++ предлагают использовать обучаемую модель кластеризации для выбора двух наиболее актуальных алгоритмов токенизации, после чего значения этих алгоритмов суммируются, для получения финального представления. Мы же, в отличие от предложенного подхода, подготовим четыре различных варианта токенов для каждого бара и объединим их значения с помощью алгоритма Attention Pooling, заимствованного из фреймворка R-MAT.
Такой подход позволяет значительно улучшить качество анализа, поскольку позволяет учитывать большее количество аспектов данных и более точно выделять важную информацию. В нашей работе для токенизации мы будем использовать следующие варианты:
- Токенизация узлов — в этом случае каждый бар будет представлять собой отдельный элемент анализа, с которым модель будет работать для извлечения данных.
- Токенизация рёбер — здесь внимание будет сосредоточено на взаимодействиях между двумя соседними барами, что позволяет выделить важные связи между различными частями данных.
- Токенизация подграфов — этот метод позволит нам формировать более сложные структуры, учитывая связи между множеством баров в рамках одной группы.
- Токенизация подграфов отдельных унитарных последовательностей — этот вариант предполагает более детальный анализ структурных последовательностей, что позволяет обрабатывать данные на более глубоком уровне.
Использование выбранных методов токенизации позволяет учесть как отдельные элементы, так и их взаимосвязи, что значительно повысит качество представления информации о каждом баре и улучшит общую эффективность модели. Объединение всех этих токенов через Attention Pooling позволит модели гибко адаптироваться и фокусировать внимание на наиболее значимых признаках, улучшая процесс принятия решений.
Для реализации подобного решения мы создадим новый объект CNeuronMoT, структура которого представлена ниже.
class CNeuronMoT : public CNeuronMHAttentionPooling { protected: CNeuronConvOCL cNodesTokenizer; CNeuronConvOCL cEdgesTokenizer; CNeuronConvOCL cSubGraphsTokenizer; CLayer cUnitarSubGraphsTokenizer; CNeuronBaseOCL cConcatenate; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronMoT(void){}; ~CNeuronMoT(void){}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint units_count, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) override const { return defNeuronMoT; } //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; virtual void SetOpenCL(COpenCLMy *obj) override; };
В качестве родительского объекта в данном случае используется объект CNeuronMHAttentionPooling, в котором уже реализован алгоритм Attention Pooling, предполагаемый к использованию на выходе модуля для объединения различных вариантов токенизации. Такой подход имеет несколько существенных преимуществ.
Во-первых, использование родительского класса позволяет нам избежать избыточности кода, исключая необходимость повторной реализации модуля Attention Pooling в рамках других объектов или компонентов. Вместо этого, мы интегрируем уже готовую и оптимизированную реализацию этого алгоритма, сохраняя высокий уровень абстракции и облегчая поддержку кода.
Во-вторых, необходимость выполнения всех операций по объединению токенов и их обработке сводится к вызову функционала, реализованного в родительском классе. Это значительно упрощает архитектуру системы и способствует более эффективному использованию ресурсов, поскольку родительский класс уже содержит все необходимые методы и алгоритмы для работы с вниманием. Таким образом, мы минимизируем дублирование функционала и повышаем модульность и расширяемость системы.
В структуре нового объекта мы видим уже знакомый набор виртуальных переопределяемых методов, которые являются неотъемлемой частью реализации нашей модели. Эти методы предоставляют нам гибкость и возможность кастомизации поведения объекта в зависимости от специфики задачи.
Кроме того, в классе присутствуют несколько внутренних объектов, которые играют ключевую роль в построении нашего алгоритма. Назначение каждого из них будет более подробно раскрыто в процессе реализации методов класса, где мы детально разберем их работу и взаимодействие.
Все внутренние объекты объявлены статично, что позволяет нам оставить пустыми конструктор и деструктор класса. А инициализации всех объявленных и унаследованных объектов осуществляется в методе Init.
bool CNeuronMoT::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint units_count, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronMHAttentionPooling::Init(numOutputs, myIndex, open_cl, window, units_count, 4, optimization_type, batch)) return false;
В параметрах метода мы получаем константы описания размерности исходных данных. И здесь следует обратить внимание, что в данной реализации предполагается получение результатов в той же размерности. Поэтому, полученные параметры мы сразу передаем в одноименный метод родительского класса, в котором уже реализованы инициализации всех унаследованных объектов и интерфейсов.
После успешного выполнения операций метода родительского класса, мы переходим к инициализации вновь объявленных объектов. Первым мы инициализируем объект токенизации узлов. Его роль выполняет сверточный слой, в котором окно свертки, его шаг и количество фильтров имеют одинаковые значения и равны вектору описания одного элемента последовательности.
Этот подход позволяет нам эффективно работать с последовательностями данных, где каждый элемент (или узел) будет представлен как вектор, соответствующий определённым характеристикам. С помощью свертки мы можем извлечь важные локальные признаки, что является основой для дальнейшей обработки и токенизации данных. Единство значений этих параметров с вектором описания элемента позволяет гармонично интегрировать сверточный слой в общую структуру модели, обеспечивая её эффективность и согласованность на всех этапах обработки.
int index = 0; if(!cNodesTokenizer.Init(0, index, OpenCL, iWindow, iWindow, iWindow, iUnits, 1, optimization, iBatch)) return false; cNodesTokenizer.SetActivationFunction(SoftPlus);
Далее, инициализируем сверточный слой токенизации ребер. В отличие от предыдущего объекта, здесь мы используем окно свертки в размере полных двух элементов анализируемой последовательности. Такой подход позволяет моделировать взаимодействия и связи между соседними элементами, что важно для более глубокого анализа структуры данных.
index++; if(!cEdgesTokenizer.Init(0, index, OpenCL, 2 * iWindow, iWindow, iWindow, iUnits, 1, optimization, iBatch)) return false; cEdgesTokenizer.SetActivationFunction(SoftPlus);
Здесь стоит обратить внимание, что использование двойного окна свертки с одинарным шагом в общем случаем ведет к сокращению последовательности на 1 элемент. Однако, последующее комбинирования токенов требует сопоставимости размерности тензоров на всех этапах. Поэтому мы не изменяем длину последовательности нашего сверточного слоя, что подразумевает заполнение недостающих элементов в конце последовательности нулевыми значениями.
Аналогичным образом инициализируем сверточный слой токенизации подграфов, увеличив окно свертки до 3 элементов последовательности с сохранением всех прочих параметров.
index++; if(!cSubGraphsTokenizer.Init(0, index, OpenCL, 3 * iWindow, iWindow, iWindow, iUnits, 1, optimization, iBatch)) return false; cSubGraphsTokenizer.SetActivationFunction(SoftPlus);
Для всех уровней токенизации мы применяем функцию активации SoftPlus. Этот выбор обусловлен рядом преимуществ, которые предоставляет данная функция. SoftPlus является гладкой и монотонной функцией, что позволяет избежать резких скачков и улучшить стабильность обучения. В отличие от ReLU, SoftPlus не имеет резкого перехода от нуля к положительным значениям, что помогает предотвратить возможные проблемы с "мёртвыми" нейронами.
Кроме того, SoftPlus обладает свойством, при котором её производная всегда положительна, что способствует хорошей дифференцируемости и более плавному обновлению весов во время обратного распространения ошибки. Это особенно важно для сложных нейронных сетей, где требуются высокоточные и стабильные обновления параметров на всех этапах обучения.
Использование SoftPlus на всех уровнях токенизации позволяет создать более гибкую и стабильную модель, обеспечивая плавность и устойчивость её работы, что критично при обработке и анализе сложных последовательностей данных.
Несколько иначе обстоят дела с генерацией токенов в разрезе унитарных последовательностей анализируемого многомерного временного ряда. Для выполнения данного функционала нам потребуется совершить несколько последовательных операций, которые объединим во внутреннюю модель, сохраним указатели на объекты в динамическом массиве cUnitarSubGraphsTokenizer.
Вначале подготовим динамический массив и объявим локальные переменные для временного хранения указателей на объекты.
cUnitarSubGraphsTokenizer.Clear(); cUnitarSubGraphsTokenizer.SetOpenCL(OpenCL); CNeuronConvOCL *conv = NULL; CNeuronTransposeOCL *transp = NULL;
Для удобства работы с отдельными унитарными последовательностями мы транспонируем исходные данные.
index++; transp = new CNeuronTransposeOCL(); if(!transp || !transp.Init(0, index, OpenCL, iUnits, iWindow, optimization, iBatch) || !cUnitarSubGraphsTokenizer.Add(transp)) { delete transp; return false; }
А затем воспользуемся сверточным слоем для генерации токенов подграфов. Здесь мы, как и ранее, анализируем подграфы из 3 элементов. Только в данном случае каждый элемент представлен одним значением, а число анализируемых переменных равно количеству анализируемых унитарных последовательностей.
index++; conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, index, OpenCL, 3, 1, 1, iUnits, iWindow, optimization, iBatch) || !cUnitarSubGraphsTokenizer.Add(conv)) { delete conv; return false; } conv.SetActivationFunction(SoftPlus);
Такой подход позволяет нам более детально проанализировать переходы и паттерны в рамках отдельных унитарных последовательностей.
Полученные значения транспонируем в исходное состояние.
index++; transp = new CNeuronTransposeOCL(); if(!transp || !transp.Init(0, index, OpenCL, iWindow, iUnits, optimization, iBatch) || !cUnitarSubGraphsTokenizer.Add(transp)) { delete transp; return false; } transp.SetActivationFunction((ENUM_ACTIVATION)conv.Activation());
И "последним штрихом" будет инициализация объекта для конкатенации результатов различных подходов токенизации.
index++; if(!cConcatenate.Init(0, index, OpenCL, 4 * iWindow * iUnits, optimization, iBatch)) return false; cConcatenate.SetActivationFunction(None); //--- return true; }
Обратите внимание, что мы намеренно отключаем функцию активации для объекта конкатенации данных. Конечно, в своей реализации мы используем одинаковые функции активации для всех объектов генерации токенов. И могли бы её перенести в объект конкатенации, что могло бы немного упростить алгоритм распределения градиента ошибки в рамках обратного прохода. Однако, в общем случае, мы допускаем использование различных функций активации для отдельных объектов генерации токенов. И в таком случае, указание функции активации для объекта конкатенации лишь исказит данные.
В завершении метода инициализации, мы возвращаем логический результат выполнения операций вызывающей программе и завершаем его работу.
Следующим этапом нашей работы является построение метода прямого прохода feedForward. Его алгоритм довольно прост.
bool CNeuronMoT::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!cNodesTokenizer.FeedForward(NeuronOCL)) return false; if(!cEdgesTokenizer.FeedForward(NeuronOCL)) return false; if(!cSubGraphsTokenizer.FeedForward(NeuronOCL)) return false;
В параметрах метода получаем указатель на объект, содержащий исходные данные, который сразу же передаем в одноименные методы внутренних объектов различного уровня токенизации.
Для генерации токенов в рамках унитарных последовательностей мы организуем цикл перебора объектов внутренней модели.
CNeuronBaseOCL *prev = NeuronOCL, *current = NULL; for(int i = 0; i < cUnitarSubGraphsTokenizer.Total(); i++) { current = cUnitarSubGraphsTokenizer[i]; if(!current || !current.FeedForward(prev)) return false; prev = current; }
Все сгенерированные токены собираем в единый тензор по размерности элементов анализируемой последовательности.
if(!Concat(cNodesTokenizer.getOutputIndex(), cEdgesTokenizer.getOutputIndex(), cSubGraphsTokenizer.getOutputIndex(), current.getOutputIndex(), cConcatenate.getOutputIndex(), iWindow, iWindow, iWindow, iWindow, iUnits)) return false;
Полученный объект передаем в одноимённый метод родительского класса для получения итогового представления графа.
return CNeuronMHAttentionPooling::feedForward(cConcatenate.AsObject());
}
Логический результат выполнения операций возвращаем вызывающей программе и завершаем работу метода.
За видимой простотой метода прямого прохода кроется параллельное использование 4 информационных потоков, что накладывает некоторые сложности в организации процесса распределения градиента ошибки. Его алгоритм мы реализуем в рамках метода calcInputGradients.
bool CNeuronMoT::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
В параметрах метода мы получаем указатель на тот же объект исходных данных. Только на этот раз нам предстоит передать в него градиент ошибки в размере влияния исходных данных на результат работы модели. Передать данные мы можем только в действительный объект. Поэтому, первой операцией нашего метода является проверка актуальности полученного указателя.
Далее распределяем градиент ошибки, полученный от последующих объектов модели, до уровня объекта конкатенации токенов средствами родительского класса.
if(!CNeuronMHAttentionPooling::calcInputGradients(cConcatenate.AsObject())) return false;
И распределим полученные значения по соответствующим информационным потокам.
CNeuronBaseOCL *current = cUnitarSubGraphsTokenizer[-1]; if(!current || !DeConcat(cNodesTokenizer.getGradient(), cEdgesTokenizer.getGradient(), cSubGraphsTokenizer.getGradient(), current.getGradient(), cConcatenate.getGradient(), iWindow, iWindow, iWindow, iWindow, iUnits)) return false;
И далее нам предстоит распределить градиент ошибки по всем информационным потокам.
Здесь следует напомнить, что от объекта конкатенации мы получаем градиент ошибки не скорректированный на производную функции активации. Следовательно, перед началом операций каждого информационного потока нам предстоит скорректировать значения на производные соответствующих функций активации.
Первым мы распределим градиент ошибки по магистрали унитарных последовательностей. Сначала проверяем наличие функции активации и, при необходимости, корректируем полученные значения.
if(current.Activation() != None && !DeActivation(current.getOutput(), current.getGradient(), current.getGradient(), current.Activation())) return false;
Далее организуем цикл обратного перебора объектов внутренней модели с последовательным вызовом одноименных методов.
for(int i = cUnitarSubGraphsTokenizer.Total() - 2; i >= 0; i--) { current = cUnitarSubGraphsTokenizer[i]; if(!current || !current.calcHiddenGradients(cUnitarSubGraphsTokenizer[i + 1])) return false; }
И опустим градиент ошибки до уровня исходных данных.
if(!NeuronOCL.calcHiddenGradients(current.AsObject())) return false;
На данном этапе мы передали градиент ошибки на уровень исходных данных только по одной магистрали. И нам предстоит еще провести погрешности по трем оставшимся.
С целью сохранения ранее полученных данных, мы осуществляем подмену указателя на буфер градиентов ошибки исходных данных.
CBufferFloat *temp = NeuronOCL.getGradient(); if(!NeuronOCL.SetGradient(current.getPrevOutput(), false)) return false;
И только при уверенности в сохранности ранее полученных данных, мы осуществляем передачу градиентов по остальным магистралям. Здесь последовательно проверяем наличие функции активации и, при необходимости, корректируем значения на соответствующую производную функции активации.
if(cNodesTokenizer.Activation() != None && !DeActivation(cNodesTokenizer.getOutput(), cNodesTokenizer.getGradient(), cNodesTokenizer.getGradient(), cNodesTokenizer.Activation())) return false; if(!NeuronOCL.calcHiddenGradients(cNodesTokenizer.AsObject()) || !SumAndNormilize(temp, NeuronOCL.getGradient(), temp, iWindow, false, 0, 0, 0, 1)) return false;
Затем, проводим градиент ошибки до уровня исходных данных и суммируем с ранее накопленными значениями. Повторяем операции для следующей магистрали.
if(cEdgesTokenizer.Activation() != None && !DeActivation(cEdgesTokenizer.getOutput(), cEdgesTokenizer.getGradient(), cEdgesTokenizer.getGradient(), cEdgesTokenizer.Activation())) return false; if(!NeuronOCL.calcHiddenGradients(cEdgesTokenizer.AsObject()) || !SumAndNormilize(temp, NeuronOCL.getGradient(), temp, iWindow, false, 0, 0, 0, 1)) return false;
if(cSubGraphsTokenizer.Activation() != None && !DeActivation(cSubGraphsTokenizer.getOutput(), cSubGraphsTokenizer.getGradient(), cSubGraphsTokenizer.getGradient(), cSubGraphsTokenizer.Activation())) return false; if(!NeuronOCL.calcHiddenGradients(cSubGraphsTokenizer.AsObject()) || !SumAndNormilize(temp, NeuronOCL.getGradient(), temp, iWindow, false, 0, 0, 0, 1)) return false;
После успешной передачи градиентов ошибки по всем информационным потокам возвращаем указатели в исходное состояние и завершаем работу метода, предварительно вернув логический результат выполнения операций вызывающей программе.
if(!NeuronOCL.SetGradient(temp, false)) return false; //--- return true; }
На этом мы завершаем рассмотрение алгоритмов построения методов объекта адаптивной смешанной токенизации CNeuronMoT. С полным кодом данного объекта и всех его методов вы можете ознакомиться во вложении.
К сожалению, мы исчерпали объем статьи, но наша работа ещё не завершена. Сделаем небольшой перерыв и продолжим её в следующей статье.
Заключение
В данной статье мы познакомились с инновационным подходом к использованию гибридных моделей последовательностей графов (GSM++), которые сочетают в себе мощь графовых структур и последовательного анализа данных. Эти модели обеспечивают высокую точность прогнозирования и анализа, позволяя эффективно обрабатывать сложные финансовые данные. Кроме того, они оптимизируют использование вычислительных ресурсов, что делает их особенно ценными при работе с большими объемами информации. Одним из ключевых преимуществ GSM++ является их способность адаптироваться к быстро меняющимся рыночным условиям.
В практической части нашей работы мы начали реализацию собственного видения предложенных подходов и построили модуль смешанной токенизации. В следующей статье продолжим начатую работу до логического завершения, с проверкой эффективности реализованных подходов на реальных исторических данных.
Ссылки
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | Research.mq5 | Советник | Советник сбора примеров |
| 2 | ResearchRealORL.mq5 | Советник | Советник сбора примеров методом Real-ORL |
| 3 | Study.mq5 | Советник | Советник обучения моделей |
| 4 | Test.mq5 | Советник | Советник для тестирования модели |
| 5 | Trajectory.mqh | Библиотека класса | Структура описания состояния системы и архитектуры моделей |
| 6 | NeuroNet.mqh | Библиотека класса | Библиотека классов для создания нейронной сети |
| 7 | NeuroNet.cl | Библиотека | Библиотека кода OpenCL-программы |
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Оптимизация наследованием крови — Blood inheritance optimization (BIO)
Оптимизация наследованием крови — Blood inheritance optimization (BIO)
 Интеграция MQL5: Python
Интеграция MQL5: Python
 Как функции столетней давности могут обновить ваши торговые стратегии
Как функции столетней давности могут обновить ваши торговые стратегии
 Разработка системы репликации (Часть 68): Настройка времени (I)
Разработка системы репликации (Часть 68): Настройка времени (I)
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования