
Redes neuronales en el trading: Modelos híbridos de secuencias de grafos (GSM++)
En los últimos años, los transformadores de grafos adaptados para aplicaciones de los campos del procesamiento del lenguaje natural y la visión por computadora han atraído especial atención. Su capacidad para modelizar dependencias a largo plazo y trabajar eficazmente con estructuras financieras irregulares los convierte en una herramienta prometedora para tareas como la previsión de la volatilidad, la detección de anomalías del mercado y la construcción de estrategias de inversión óptimas. No obstante, los transformadores clásicos se enfrentan a una serie de problemas fundamentales, como los elevados costes computacionales y las dificultades para adaptarse a estructuras de grafos desordenadas.
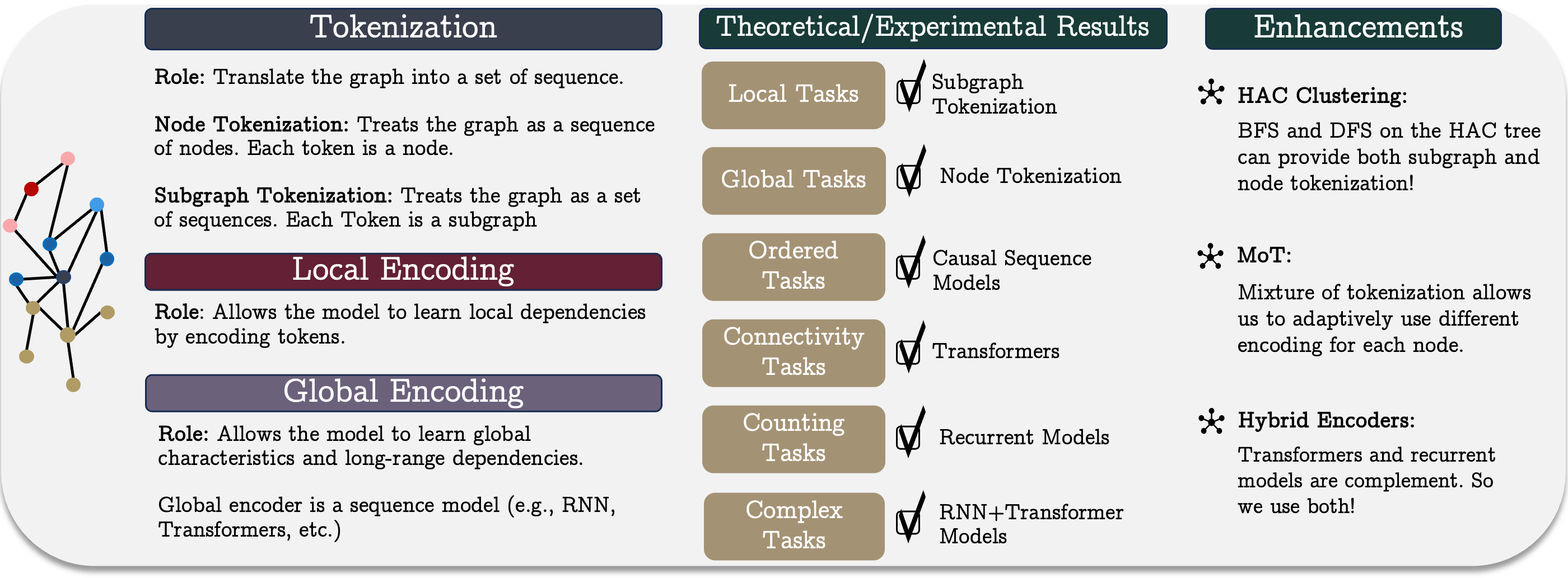
Los autores del artículo: "Best of Both Worlds: Advantages of Hybrid Graph Sequence Models" proponen el modelo unificado de secuencia de grafos GSM++, que combina los puntos fuertes de diferentes arquitecturas para crear un método eficiente de representación y procesamiento de grafos. Se basa en tres pasos clave: tokenización del grafo, la codificación local de nodos y la codificación global de dependencias. Este enfoque nos permite considerar los vínculos tanto locales como globales del sistema financiero, lo cual hace que el modelo sea universal y aplicable a una amplia gama de problemas.
El elemento clave del modelo propuesto es el método desarrollado de tokenización de grafos jerárquicos, que permite transformar los datos de mercado en una representación secuencial compacta conservando sus características topológicas y temporales. A diferencia de los métodos habituales de codificación de series temporales, este enfoque mejora la calidad de la extracción de características y simplifica el procesamiento de grandes volúmenes de datos de mercado. La combinación de la tokenización jerárquica con una arquitectura híbrida que incorpora mecanismos de transformadores y modelos de recurrencia permite obtener resultados superiores en diversas tareas. Esto convierte al método propuesto en una herramienta eficaz para procesar datos financieros complejos.
Los estudios empíricos y análisis teóricos realizados por los autores del framework GSM++ demuestran que el modelo propuesto no solo compite con los transformadores de grafos tradicionales, sino que los supera en una serie de características clave.
El algoritmo GSM
El modelo unificado de secuencias de grafos es un enfoque conceptual que incluye tres pasos clave: la tokenización, la codificación local y la codificación global. Este método permite representar y analizar eficazmente estructuras gráficas complejas, lo cual resulta especialmente importante en el contexto de los mercados financieros. Los sistemas de mercado complejos con múltiples participantes e interacciones requieren de potentes herramientas de modelización capaces de detectar dependencias no lineales y correlaciones ocultas.
La tokenización desempeña un papel fundamental en la conversión de la estructura de grafos en una representación secuencial, lo que resulta esencial para el procesamiento de datos mediante modelos secuenciales. Se distinguen los siguientes métodos principales de tokenización: la tokenización de nodos o aristas, y la tokenización de subgrafos. La elección del método de tokenización tiene un impacto significativo en la eficacia del modelo, pues determina hasta qué punto se conserva la información estructural del grafo y qué características de su organización se tendrán en cuenta en el análisis posterior.
La tokenización de nodos o aristas implica que el grafo se considera como una secuencia de elementos relevantes sin tener en cuenta sus interconexiones. Para conservar la información estructural, se requiere una codificación posicional o estructural adicional. El principal inconveniente de este método es su elevada complejidad computacional, dado que la longitud de la secuencia se corresponde con el número de nodos o aristas, lo que complica el entrenamiento de los modelos. Sin embargo, este método puede resultar útil en situaciones en las que es necesario considerar información detallada sobre cada elemento del sistema, como cuando se construyen estrategias individuales para activos basadas en sus características microscópicas. En condiciones de negociación de alta frecuencia, este enfoque permite analizar con mayor precisión el impacto de las fluctuaciones del mercado a corto plazo e identificar pautas comerciales anómalas.
La tokenización de subgrafos reduce el coste computacional representando el grafo como secuencias de subgrafos, lo que mejora la capacidad del modelo para tener en cuenta la estructura local. Este enfoque es especialmente útil para aplicaciones financieras, por ejemplo en el análisis de patrones comerciales donde los subgrafos pueden corresponder a clústeres de activos relacionados, o a grupos de inversores. Las interacciones entre activos tienen a menudo un carácter de red oculta, y el uso de subgrafos permite identificar patrones de mercado estables, lo cual resulta fundamental en la inversión de portafolios, la evaluación de la liquidez y las estrategias de arbitraje.
Cada uno de los métodos de tokenización tiene sus propias ventajas y limitaciones, por lo que la elección de un método concreto dependerá de las características específicas de la tarea. En algunos casos, los enfoques combinados que unen propiedades de ambas estrategias de tokenización logran un mejor equilibrio entre la precisión de la representación de los datos y la eficiencia computacional.
Basándose en las ideas presentadas, los autores del framework GSM++ proponen un algoritmo de tokenización jerárquica basado en la clusterización jerárquica por afinidad (Hierarchical Affinity Clustering — HAC).
El algoritmo comienza tratando cada vértice del grafo como un clúster independiente. A continuación, cada paso fusiona los dos clústeres conectados por la arista menos "barata" calculada según la similitud de sus codificaciones. Este proceso continúa hasta que todo el gráfico se fusione en un único clúster. Como resultado, se forma un árbol jerárquico, donde la raíz representa el grafo completo, mientras que las hojas se corresponden con los nodos fuente.
Este planteamiento tiene dos ventajas importantes. En primer lugar, clasifica los nodos de modo que los elementos similares aparezcan más cerca unos de otros, lo cual mejora la representación del grafo en modelos. En segundo lugar, permite codificar grafos con distintos niveles de detalle, lo que crea la posibilidad de realizar análisis de estructuras flexibles. Se han desarrollado dos variantes de tokenización: el recorrido del árbol en profundidad (DFS) y en anchura (BFS). El enfoque DFS crea secuencias de nodos que reflejan su posición jerárquica. El enfoque BFS genera secuencias en las que los nodos se clasifican de tal manera que los elementos similares estén uno al lado del otro.
La técnica de tokenización propuesta preserva la estructura local del grafo y funciona eficazmente con modelos recurrentes, sobre todo para problemas que requieren un análisis de conectividad global.
De forma adicional, se usa un método de codificación de posición jerárquica que considera los caminos más cortos entre nodos y su posición en la jerarquía de clústeres. Los experimentos han demostrado que esta forma de codificación mejora la calidad de la representación gráfica.
Dado que, dependiendo de la estructura del grafo y del problema a resolver, distintos nodos pueden requerir distintos métodos de tokenización, se ha propuesto el enfoque Mix of Tokenization (MoT). Este permite a cada nodo utilizar el método de codificación más adecuado seleccionando los tokenizadores óptimos y combinando sus representaciones.
Tras la etapa de tokenización, los datos se transforman en una representación vectorial para explorar las características locales del grafo. En esta fase, las redes neuronales convolucionales basadas en grafos (GNN) son las más utilizadas, ya que resultan eficaces a la hora de identificar dependencias locales entre nodos. En el contexto de los mercados financieros, este paso ayuda a analizar las correlaciones entre activos, identificar anomalías locales y realizar predicciones basadas en datos microestructurales. Por su adaptabilidad y capacidad para extraer patrones complejos, las redes neuronales gráficas se usan para automatizar las operaciones y prever la volatilidad de los mercados.
La codificación global desempeña un papel crucial en el estudio de las dependencias de largo alcance dentro de un grafo. En esta fase se aplica la codificación secuencial para identificar relaciones complejas entre los elementos del framework. En aplicaciones financieras, esto permite modelizar tendencias macroeconómicas, analizar el impacto de factores globales en los mercados y construir estrategias basadas en una profunda interconectividad de datos. Las tendencias a largo plazo de los datos financieros, como el impacto de la política monetaria o las crisis económicas mundiales, requieren de potentes algoritmos capaces de identificar dependencias complejas en distintos horizontes temporales.
A la hora de elegir un modelo de secuencia para el aprendizaje de grafos, nos surge la pregunta: ¿qué modelo será el más eficaz? Según el enfoque adoptado, pueden combinarse distintos codificadores de secuencias con métodos de tokenización distintos, creando así muchas arquitecturas posibles. Sin embargo, no sabemos a ciencia cierta cuáles son los más adecuados para los distintos problemas de grafos.
Las tareas de recuento consisten en determinar el número de nodos de un tipo determinado en un grafo. Los modelos que usan mecanismos de atención sin dependencias causales no son capaces de resolver correctamente este tipo de problemas. De ahí que surja la pregunta: ¿pueden resolver este problema los modelos de recurrencia sensibles al orden?
Resulta que si la anchura del modelo de recurrencia se corresponde con el número de diferentes clases de nodos, será capaz de contar con precisión su número. Esto confirma la eficacia de los modelos recurrentes en problemas en los que la estructura secuencial resulta más importante que la topología del grafo.
Algunos problemas de grafos, como el razonamiento algorítmico, requieren respetar estrictamente el orden de los nodos. Los modelos secuenciales modernos usan principalmente relaciones causales, lo que debe tenerse en cuenta a la hora de integrarlos en modelos gráficos. La investigación demuestra que la compresión excesiva de la información puede provocar una pérdida de representatividad. En los modelos recurrentes, la sensibilidad a los datos de origen disminuye al aumentar la distancia entre elementos, mientras que permanece constante en los transformadores. Sin embargo, ambos modelos resultan propensos al colapso de las representaciones a medida que aumenta la profundidad.
La información situada al principio de la secuencia tiene más posibilidades de ser almacenada. Esto provoca un efecto en forma de U, en el que los tokens situados al principio y al final de la secuencia conservan mejor su valor que los situados en el medio. Este comportamiento se observa tanto para los transformadores como para los modelos recurrentes. Por consiguiente, al organizar los nodos en una secuencia, los elementos importantes deben colocarse más cerca unos de otros para potenciar su influencia mutua.
Las tareas relacionadas con la determinación de la conectividad de un grafo requieren un análisis global de su estructura. La conectividad puede considerarse una tarea de clasificación binaria. La investigación demuestra que los transformadores con una cierta profundidad y tamaño de incorporaciones pueden hacer frente eficazmente a estas tareas. Sin embargo, los modelos recurrentes y los transformadores con atención limitada requieren muchos más parámetros o profundidad del modelo para lograr resultados similares.
Los modelos de recurrencia presentan el mejor rendimiento cuando los datos tienen un orden natural y la tokenización considera la estructura del grafo. Un parámetro importante es la localidad del nodo, que determina la distancia máxima entre vértices vecinos. Para grafos con localidad acotada, podemos construir un modelo de recurrencia compacto capaz de determinar la conectividad. No obstante, los transformadores con un número fijo de parámetros no pueden hacer frente eficazmente a estas tareas.
A la hora de elegir un modelo, debemos comprender los compromisos que surgen al aplicarlos a problemas de análisis de grafos. El análisis de las distintas arquitecturas nos permite identificar algunas características clave:
- Los transformadores muestran una gran eficacia en la resolución de problemas de conectividad de grafos utilizando el mínimo número de parámetros. Son especialmente útiles cuando el grafo posee una estructura compleja y requiere un cálculo paralelo. Y su capacidad para generar representaciones conscientes del contexto las convierte en una poderosa herramienta para analizar redes y grafos complejos.
- Las redes neuronales recurrentes (RNN) funcionan bien con grafos en los que las conexiones entre vértices tienen una clara estructura localizada. En estos casos, requieren menos parámetros y cálculos, lo cual las hace más eficientes energéticamente y adecuadas para el flujo de datos.
- Los modelos híbridos, que combinan RNNs y transformadores permiten combinar las ventajas de ambas arquitecturas, logrando un equilibrio entre la complejidad computacional y la precisión de la predicción, lo que resulta especialmente útil en tareas en las que se necesitan tanto el contexto global como los detalles locales.
- Los modelos de espacio de estados presentan una gran eficacia en situaciones en las que resulta importante un orden estricto de los elementos. Estos tienen propiedades de memoria a largo plazo, lo que los hace útiles para el análisis de series temporales y la modelización de secuencias de acciones en sistemas basados en agentes.
- La atención dispersa reduce el coste computacional de los transformadores, sobre todo cuando hablamos de grafos grandes. Sin embargo, para usarla eficazmente, se requiere el desarrollo de mecanismos adicionales para identificar los vínculos más significativos entre vértices, lo cual puede complicar la aplicación del modelo.
Así pues, la elección del modelo dependerá de la estructura de los datos de origen y de los recursos informáticos disponibles. Los transformadores resultan adecuados para grafos complejos con dependencias globales pronunciadas, las RNN son óptimas para secuencias localizadas y los modelos de espacio de estados funcionan mejor en problemas que requieren un orden estricto de ejecución de las operaciones. Los enfoques híbridos ofrecen la oportunidad de equilibrar la eficiencia computacional y la precisión de la predicción, lo cual los convierte en una opción versátil para muchas aplicaciones.
A partir de los resultados del análisis realizado en el trabajo del autor, se presenta el framework GSM++, que incluye tokenización jerárquica de nodos por similitud, redes neuronales convolucionales de grafos como codificador local y un codificador global híbrido que contiene los módulos Mamba y Transformer.
Implementación con MQL5
Tras familiarizarnos con los aspectos teóricos de los enfoques propuestos por los autores del framework GSM++, pasaremos a la parte práctica de nuestro trabajo. En esta sección, vamos a centrarnos en implementar nuestra propia visión de los enfoques considerados utilizando las herramientas y capacidades del lenguaje de programación MQL5.
Cabe señalar que, aunque se mantiene el concepto general de los enfoques originales, nuestra aplicación se distinguirá significativamente en los detalles.
En primer lugar, en nuestra aplicación hemos decidido abandonar el uso de la clusterización jerárquica basada en la similitud (HAC). Creo que el lector estará de acuerdo conmigo en que las velas que se forman en el gráfico de un instrumento financiero son objetos dinámicos y cambiantes que no se prestan a una simple normalización. Su análisis y clusterización supone un proceso complejo y polifacético que requiere un enfoque mucho más profundo y exhaustivo.
Por ello, como antes, utilizaremos los módulos entrenados para tokenizar las representaciones de las barras analizadas. Este planteamiento nos permite mantener la flexibilidad y adaptabilidad del modelo frente a los datos reales, lo cual resulta especialmente importante cuando se trata de mercados financieros.
No obstante, en nuestra implementación usamos el algoritmo de tokenización mixta (MoT) propuesto, aunque de forma ligeramente modificada y adaptada, considerando las especificidades de nuestro problema. Los autores del framework GSM++ proponen usar un modelo de clusterización entrenado para seleccionar los dos algoritmos de tokenización más relevantes, tras lo cual se suman los valores de estos algoritmos, para obtener la representación final. A diferencia del enfoque propuesto, vamos a preparar cuatro variantes de tokens diferentes para cada barra y a combinar sus valores utilizando el algoritmo Attention Pooling tomado del framework de trabajo R-MAT.
Este planteamiento mejora notablemente la calidad de los análisis al permitir considerar más aspectos de los datos y resaltar con mayor precisión la información importante. En nuestro trabajo, usaremos las siguientes variantes para la tokenización:
- Tokenización de nodos: en este caso, cada barra representará un elemento de análisis independiente con el que el modelo trabajará para extraer datos.
- Tokenización de aristas: en este caso, la atención se centra en las interacciones entre dos barras vecinas, lo cual pone de relieve las relaciones importantes entre las distintas partes de los datos.
- Tokenización de subgrafos: este método permite formar estructuras más complejas considerando los vínculos entre varias barras de un mismo grupo.
- Tokenización de subgrafos de secuencias unitarias individuales: esta opción implica un análisis más detallado de las secuencias estructurales, lo que permite procesar los datos a un nivel más profundo.
El uso de los métodos de tokenización seleccionados permite considerar tanto los elementos individuales como sus interrelaciones, lo que mejorará notablemente la calidad de la representación de la información sobre cada barra y mejorará el rendimiento global del modelo. La combinación de todos estos tokens mediante Attention Pooling permitirá al modelo adaptarse con flexibilidad y centrar la atención en las características más relevantes, mejorando la toma de decisiones.
Para implementar dicha solución, crearemos un nuevo objeto CNeuronMoT, cuya estructura se muestra a continuación.
class CNeuronMoT : public CNeuronMHAttentionPooling { protected: CNeuronConvOCL cNodesTokenizer; CNeuronConvOCL cEdgesTokenizer; CNeuronConvOCL cSubGraphsTokenizer; CLayer cUnitarSubGraphsTokenizer; CNeuronBaseOCL cConcatenate; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronMoT(void){}; ~CNeuronMoT(void){}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint units_count, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) override const { return defNeuronMoT; } //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; virtual void SetOpenCL(COpenCLMy *obj) override; };
En este caso se usa como objeto padre el objeto CNeuronMHAttentionPooling, en el que ya se implementa el algoritmo Attention Pooling, que se supone que se utilizará en la salida del módulo para combinar diferentes opciones de tokenización. Este planteamiento presenta varias ventajas significativas.
En primer lugar, el uso de una clase padre nos permite evitar la redundancia de código eliminando la necesidad de reimplementar el módulo Attention Pooling dentro de otros objetos o componentes. En su lugar, integramos una implementación optimizada y estándar de este algoritmo, manteniendo un alto nivel de abstracción y facilitando el mantenimiento del código.
En segundo lugar, la necesidad de realizar todas las operaciones de fusión y procesamiento de tokens se reduce a llamar a la funcionalidad implementada en la clase padre. Esto simplifica enormemente la arquitectura del sistema y posibilita un uso más eficiente de los recursos, pues la clase padre ya contiene todos los métodos y algoritmos necesarios para trabajar con la atención. De este modo, minimizamos la duplicación de funciones y aumentamos la modularidad y extensibilidad del sistema.
En la estructura del nuevo objeto, vemos el conjunto familiar de métodos virtuales redefinidos, que forman una parte integral de la implementación de nuestro modelo. Estos métodos ofrecen tanto flexibilidad como la capacidad de personalizar el comportamiento del objeto en función de las particularidades de la tarea.
Además, la clase contiene varios objetos internos que desempeñan un papel esencial en la construcción de nuestro algoritmo. El propósito de cada uno de ellos se revelará con más detalle durante la implementación de los métodos de clase, entonces describiremos su trabajo e interacción con detalle.
Todos los objetos internos se declararán estáticamente, lo que nos permitirá dejar vacíos el constructor y el destructor de la clase, mientras que la inicialización de todos los objetos declarados y heredados se realizará en el método Init.
bool CNeuronMoT::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint units_count, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronMHAttentionPooling::Init(numOutputs, myIndex, open_cl, window, units_count, 4, optimization_type, batch)) return false;
En los parámetros del método, obtenemos las constantes para describir la dimensionalidad de los datos de origen. Y aquí debemos señalar que en esta implementación se presupone la obtención de los resultados en la misma dimensionalidad. Por consiguiente, transmitimos directamente los parámetros recibidos al método homónimo de la clase padre, que ya implementa la inicialización de todos los objetos e interfaces heredados.
Tras ejecutar con éxito las operaciones del método de la clase padre, procederemos a inicializar los objetos recién declarados. Primero inicializamos el objeto para la tokenización de nodos. Su función la cumplirá la capa convolucional, en la que la ventana convolucional, su paso y el número de filtros tienen los mismos valores y son iguales al vector de descripción de un elemento de la secuencia.
Este enfoque nos permite trabajar eficazmente con secuencias de datos en las que cada elemento (o nodo) se representará como un vector correspondiente a determinadas características. Con ayuda de la convolución, podemos extraer características locales importantes que son la base para el procesamiento posterior y la tokenización de los datos. La unidad de los valores de estos parámetros con el vector de descripción del elemento nos permite integrar armoniosamente la capa convolucional en la estructura global del modelo, garantizando su eficacia y coherencia en todas las etapas del procesamiento.
int index = 0; if(!cNodesTokenizer.Init(0, index, OpenCL, iWindow, iWindow, iWindow, iUnits, 1, optimization, iBatch)) return false; cNodesTokenizer.SetActivationFunction(SoftPlus);
A continuación, inicializamos la capa convolucional de tokenización de los aristas. A diferencia del objeto anterior, aquí usamos una ventana convolucional con un tamaño igual a dos elementos completos de la secuencia analizada. Este enfoque nos permite modelizar las interacciones y relaciones entre elementos vecinos, lo que es importante para un análisis más profundo de la estructura de datos.
index++; if(!cEdgesTokenizer.Init(0, index, OpenCL, 2 * iWindow, iWindow, iWindow, iUnits, 1, optimization, iBatch)) return false; cEdgesTokenizer.SetActivationFunction(SoftPlus);
Aquí cabe señalar que el uso de una ventana de doble convolución con un solo paso en el caso general conduce a una reducción de la secuencia en 1 elemento. Sin embargo, la posterior combinación de tokens requiere la comparabilidad de la dimensionalidad de los tensores en todas las etapas. Por consiguiente, no cambiamos la longitud de la secuencia de nuestra capa convolucional, lo que implica rellenar con valores cero los elementos que faltan al final de la secuencia.
Del mismo modo, inicializamos la capa convolucional de tokenización de subgrafos aumentando la ventana convolucional a 3 elementos de secuencia con todos los demás parámetros intactos.
index++; if(!cSubGraphsTokenizer.Init(0, index, OpenCL, 3 * iWindow, iWindow, iWindow, iUnits, 1, optimization, iBatch)) return false; cSubGraphsTokenizer.SetActivationFunction(SoftPlus);
Para todos los niveles de tokenización, aplicamos la función de activación SoftPlus. Esta elección se debe a una serie de ventajas que ofrece la presente característica. SoftPlus es una función suave y monótona que evita los picos y mejora la estabilidad del aprendizaje. A diferencia de ReLU, SoftPlus no tiene una transición brusca de valores cero a positivos, lo cual ayuda a evitar posibles problemas con neuronas "muertas".
Además, SoftPlus tiene la propiedad de que su derivada es siempre positiva, lo cual contribuye a una buena diferenciabilidad y a una actualización más suave de los pesos durante la propagación inversa del error. Esto resulta especialmente importante para las redes neuronales complejas, en las que se requieren actualizaciones de parámetros muy precisas y estables en todas las fases del entrenamiento.
El uso de SoftPlus en todos los niveles de tokenización permite crear un modelo más flexible y estable, garantizando la fluidez y estabilidad de su funcionamiento, lo cual resulta crítico a la hora de procesar y analizar secuencias de datos complejas.
La situación con la generación de tokens en cuanto a las secuencias unitarias de las series temporales multivariantes analizadas es algo diferente. Para implementar esta funcionalidad, necesitaremos realizar varias operaciones secuenciales que combinaremos en un modelo interno, almacenando los punteros a los objetos en el array dinámico cUnitarSubGraphsTokenizer.
Primero, preparamos un array dinámico y declaramos las variables locales para almacenar temporalmente los punteros a los objetos.
cUnitarSubGraphsTokenizer.Clear(); cUnitarSubGraphsTokenizer.SetOpenCL(OpenCL); CNeuronConvOCL *conv = NULL; CNeuronTransposeOCL *transp = NULL;
Por comodidad al trabajar con secuencias unitarias individuales, transponemos los datos de origen.
index++; transp = new CNeuronTransposeOCL(); if(!transp || !transp.Init(0, index, OpenCL, iUnits, iWindow, optimization, iBatch) || !cUnitarSubGraphsTokenizer.Add(transp)) { delete transp; return false; }
Y luego usamos la capa convolucional para generar tokens de subgrafos. Aquí, como antes, analizamos subgrafos de 3 elementos. Solo en este caso, cada elemento está representado por un valor, mientras que el número de variables analizadas es igual al número de secuencias unitarias analizadas.
index++; conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, index, OpenCL, 3, 1, 1, iUnits, iWindow, optimization, iBatch) || !cUnitarSubGraphsTokenizer.Add(conv)) { delete conv; return false; } conv.SetActivationFunction(SoftPlus);
Este enfoque nos permite analizar con más detalle las transiciones y los patrones dentro de las secuencias unitarias individuales.
Los valores obtenidos los transponemos al estado inicial.
index++; transp = new CNeuronTransposeOCL(); if(!transp || !transp.Init(0, index, OpenCL, iWindow, iUnits, optimization, iBatch) || !cUnitarSubGraphsTokenizer.Add(transp)) { delete transp; return false; } transp.SetActivationFunction((ENUM_ACTIVATION)conv.Activation());
Y el "toque final" consistirá en inicializar el objeto para concatenar los resultados de los distintos enfoques de tokenización.
index++; if(!cConcatenate.Init(0, index, OpenCL, 4 * iWindow * iUnits, optimization, iBatch)) return false; cConcatenate.SetActivationFunction(None); //--- return true; }
Observe que, en este caso, desactivamos deliberadamente la función de activación para el objeto de concatenación de datos. Obviamente, en nuestra implementación, utilizamos las mismas funciones de activación para todos los objetos de generación de tokens. Y podríamos moverla al objeto de concatenación, lo que podría simplificar un poco el algoritmo de distribución del gradiente de error dentro de la pasada inversa. Sin embargo, en general, permitimos distintas funciones de activación para objetos individuales de generación de tokens. Y en tal caso, especificar una función de activación para el objeto de concatenación solo distorsionará los datos.
Al final del método de inicialización, retornamos el resultado lógico de las operaciones al programa que realiza la llamada y lo finalizamos.
El siguiente paso en nuestro trabajo consistirá en construir el método de pasada directa feedForward. Su algoritmo es bastante simple.
bool CNeuronMoT::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!cNodesTokenizer.FeedForward(NeuronOCL)) return false; if(!cEdgesTokenizer.FeedForward(NeuronOCL)) return false; if(!cSubGraphsTokenizer.FeedForward(NeuronOCL)) return false;
En los parámetros del método obtenemos el puntero al objeto que contiene los datos iniciales, que pasamos directamente a los métodos homónimos de objetos internos de distintos niveles de tokenización.
Para generar tokens dentro de secuencias unitarias, organizamos un ciclo de enumeración de objetos del modelo interno.
CNeuronBaseOCL *prev = NeuronOCL, *current = NULL; for(int i = 0; i < cUnitarSubGraphsTokenizer.Total(); i++) { current = cUnitarSubGraphsTokenizer[i]; if(!current || !current.FeedForward(prev)) return false; prev = current; }
Luego recopilamos todos los tokens generados en un único tensor según la dimensionalidad de los elementos de la secuencia analizada.
if(!Concat(cNodesTokenizer.getOutputIndex(), cEdgesTokenizer.getOutputIndex(), cSubGraphsTokenizer.getOutputIndex(), current.getOutputIndex(), cConcatenate.getOutputIndex(), iWindow, iWindow, iWindow, iWindow, iUnits)) return false;
El objeto obtenido se transmite al método homónimo de la clase padre para obtener la representación gráfica final.
return CNeuronMHAttentionPooling::feedForward(cConcatenate.AsObject());
}
Después retornaremos el resultado lógico de las operaciones al programa que realiza la llamada y finalizaremos el método.
Detrás de la aparente simplicidad del método de pasada directa se esconde la utilización paralela de 4 flujos de información, lo que impone algunas dificultades en la organización del proceso de distribución del gradiente de error. Implementaremos su algoritmo dentro del método calcInputGradients.
bool CNeuronMoT::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
En los parámetros del método, obtenemos el puntero al mismo objeto de datos de origen. Solo que esta vez deberemos pasarle un gradiente de error con un tamaño igual a la influencia de los datos de entrada en la salida del modelo. Solo podemos transferir los datos a un objeto válido. Por consiguiente, la primera operación de nuestro método consiste en comprobar la pertinencia del puntero obtenido.
A continuación, distribuimos el gradiente de error obtenido de los objetos modelo subsiguientes al nivel del objeto de concatenación de tokens mediante la clase padre.
if(!CNeuronMHAttentionPooling::calcInputGradients(cConcatenate.AsObject())) return false;
Y distribuimos los valores obtenidos a los flujos de información correspondientes.
CNeuronBaseOCL *current = cUnitarSubGraphsTokenizer[-1]; if(!current || !DeConcat(cNodesTokenizer.getGradient(), cEdgesTokenizer.getGradient(), cSubGraphsTokenizer.getGradient(), current.getGradient(), cConcatenate.getGradient(), iWindow, iWindow, iWindow, iWindow, iUnits)) return false;
Luego debemos distribuir el gradiente de error entre todos los flujos de información.
Aquí tenemos que recordar que del objeto de concatenación obtenemos el gradiente de error sin corregir por la derivada de la función de activación. Como consecuencia, debemos ajustar los valores a las derivadas de las funciones de activación correspondientes antes de iniciar las operaciones de cada flujo de información.
Primero distribuimos el gradiente de error a lo largo de la línea troncal de las secuencias unitarias. En primer lugar, comprobamos si la función de activación está presente y, si es necesario, corregimos los valores obtenidos.
if(current.Activation() != None && !DeActivation(current.getOutput(), current.getGradient(), current.getGradient(), current.Activation())) return false;
A continuación, organizamos un ciclo de iteración inversa de objetos del modelo interno con llamadas consecutivas de los métodos homónimos.
for(int i = cUnitarSubGraphsTokenizer.Total() - 2; i >= 0; i--) { current = cUnitarSubGraphsTokenizer[i]; if(!current || !current.calcHiddenGradients(cUnitarSubGraphsTokenizer[i + 1])) return false; }
Y bajamos el gradiente de error al nivel de los datos de origen.
if(!NeuronOCL.calcHiddenGradients(current.AsObject())) return false;
En esta etapa, hemos transmitido el gradiente de error a la capa de datos de origen en una sola línea troncal. Y aún tenemos que analizar el margen de error de las tres restantes.
Para conservar los datos adquiridos previamente, sustituimos los punteros al búfer de gradiente de error de los datos de origen.
CBufferFloat *temp = NeuronOCL.getGradient(); if(!NeuronOCL.SetGradient(current.getPrevOutput(), false)) return false;
Y solo tras asegurarnos de que los datos adquiridos previamente se han mantenido, transferimos los gradientes al resto de la línea troncal. Aquí debemos comprobar sistemáticamente la presencia de la función de activación y, si es necesario, corregiremos los valores mediante la derivada correspondiente de la función de activación.
if(cNodesTokenizer.Activation() != None && !DeActivation(cNodesTokenizer.getOutput(), cNodesTokenizer.getGradient(), cNodesTokenizer.getGradient(), cNodesTokenizer.Activation())) return false; if(!NeuronOCL.calcHiddenGradients(cNodesTokenizer.AsObject()) || !SumAndNormilize(temp, NeuronOCL.getGradient(), temp, iWindow, false, 0, 0, 0, 1)) return false;
A continuación, iteramos por el gradiente de error hasta el nivel de los datos de origen y realizamos la suma con los valores acumulados anteriormente. Repetiremos las operaciones para la siguiente línea troncal.
if(cEdgesTokenizer.Activation() != None && !DeActivation(cEdgesTokenizer.getOutput(), cEdgesTokenizer.getGradient(), cEdgesTokenizer.getGradient(), cEdgesTokenizer.Activation())) return false; if(!NeuronOCL.calcHiddenGradients(cEdgesTokenizer.AsObject()) || !SumAndNormilize(temp, NeuronOCL.getGradient(), temp, iWindow, false, 0, 0, 0, 1)) return false;
if(cSubGraphsTokenizer.Activation() != None && !DeActivation(cSubGraphsTokenizer.getOutput(), cSubGraphsTokenizer.getGradient(), cSubGraphsTokenizer.getGradient(), cSubGraphsTokenizer.Activation())) return false; if(!NeuronOCL.calcHiddenGradients(cSubGraphsTokenizer.AsObject()) || !SumAndNormilize(temp, NeuronOCL.getGradient(), temp, iWindow, false, 0, 0, 0, 1)) return false;
Una vez transferidos con éxito los gradientes de error a lo largo de todos los flujos de información, retornamos los punteros al estado inicial y finalizamos el método, devolviendo previamente el resultado lógico de las operaciones al programa que realiza la llamada.
if(!NeuronOCL.SetGradient(temp, false)) return false; //--- return true; }
Aquí concluimos nuestro análisis de los algoritmos para construir los métodos de tokenización mixta adaptativa de objetos CNeuronMoT. Podrá ver el código completo de este objeto y todos sus métodos en el archivo adjunto.
Por desgracia, hemos llegado al final del artículo, pero nuestro trabajo aún no ha terminado. Haremos una breve pausa y continuaremos en el próximo artículo.
Conclusión
En este artículo hemos presentado un enfoque innovador consistente en utilizar modelos híbridos de secuencias de grafos (GSM++) que combinan la potencia de las estructuras de grafos y el análisis secuencial de datos. Estos modelos ofrecen una gran precisión en la previsión y el análisis, y permiten procesar eficazmente datos financieros complejos. También optimizan el uso de los recursos informáticos, lo cual los hace especialmente valiosos al gestionar grandes cantidades de información. Una de las principales ventajas del GSM++ es su capacidad para adaptarse a las cambiantes condiciones del mercado.
En la parte práctica de nuestro trabajo, hemos comenzado a aplicar nuestra propia visión de los enfoques propuestos y a construir un módulo de tokenización mixta. En el próximo artículo continuaremos este trabajo hasta su conclusión lógica, probando la eficacia de los enfoques implementados con datos históricos reales.
Enlaces
Programas usados en el artículo
| # | Nombre | Tipo | Descripción |
|---|---|---|---|
| 1 | Research.mq5 | Asesor | Asesor de recopilación de datos |
| 2 | ResearchRealORL.mq5 | Asesor | Asesor experto para recopilar ejemplos con el método Real-ORL |
| 3 | Study.mq5 | Asesor | Asesor de entrenamiento de modelos |
| 4 | Test.mq5 | Asesor | Asesor para la prueba de modelos |
| 5 | Trajectory.mqh | Biblioteca de clases | Estructura de descripción del estado del sistema y la arquitectura del modelo |
| 6 | NeuroNet.mqh | Biblioteca de clases | Biblioteca de clases para crear una red neuronal |
| 7 | NeuroNet.cl | Biblioteca | Biblioteca de código del programa OpenCL |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/17279
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Simulación de mercado (Parte 14): Sockets (VIII)
Simulación de mercado (Parte 14): Sockets (VIII)
 Mecanismos de compuertas en el aprendizaje en conjuntos
Mecanismos de compuertas en el aprendizaje en conjuntos
 Simulación de mercado (Parte 15): Sockets (IX)
Simulación de mercado (Parte 15): Sockets (IX)
 Simulación de mercado (Parte 13): Sockets (VII)
Simulación de mercado (Parte 13): Sockets (VII)
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso