
古典的な戦略を再構築する(第5回):USDZARの多銘柄分析
はじめに
AIを取引戦略に組み込む方法は無数にありますが、残念ながら、どの戦略に資本を託すかを決める前に、それぞれの戦略を評価することはできません。本日は、人気の高い取引戦略である多銘柄分析について再考し、AIを使って戦略を改善できるかどうかを検証します。この戦略が読者の投資家プロファイルに適しているかどうかを、十分な情報に基づいた判断を下すために必要な情報を提供します。
取引戦略の概要
複数の銘柄を分析する取引戦略は、主にそれらの銘柄間に見られる相関関係に基づいています。相関関係とは、2つの変数間の線形依存関係の尺度です。相関関係はしばしば2つの変数の関係を示していると誤解されますが、必ずしもそうとは限りません。
世界中のトレーダーが、投資判断の指針やリスクレベルの測定、さらにはエグジットシグナルとして、相関資産の基本的理解を活用してきました。例えば、USDZARの通貨ペアを考えてみましょう。米政府は世界有数の石油輸入国であり、一方、南アフリカ政府は世界最大の金輸出国です。
これらの商品は両国の国内総生産に大きな割合を占めているため、当然、これらの商品の価格水準がUSDZAR通貨ペアの変動の一部を説明する可能性があると予想されます。つまり、現物市場で原油が金よりも良好なパフォーマンスを示している場合、ドルがランドより強くなることが予想され、逆の場合も同様です。
方法論の概要
この関係を評価するために、MQL5で書かれたスクリプトを使用して、MetaTrader 5端末からすべての市場データをエクスポートしました。モデルに対する2つの可能な入力グループを使って様々なモデルを訓練しました。
- USDZARの通常のOHLC相場
- 原油価格と金価格の組み合わせ
収集されたデータから、原油は金よりもUDZAR通貨ペアとの相関水準が強いようです。
データのスケールが異なっていたため、訓練前にデータを標準化および正規化しました。異なる入力セット間で精度を比較するために、ランダムシャッフルなしで10分割交差検証を実施しました。
結果は、最初のグループが最も誤差が少ないことを示唆しています。最も優れたモデルは、通常のOHLCデータを用いた線形回帰でした。しかし、後者のグループ2において、最も良いパフォーマンスを示したモデルはKNeigborsRegressorアルゴリズムでした。
モデルの5つのパラメータについて、ランダムサーチを500回繰り返し、ハイパーパラメータのチューニングに成功しました。過剰適合を検証するために、最適化中に保持した検証セットで、カスタマイズしたモデルの誤差レベルとデフォルトモデルの誤差レベルを比較しました。両モデルを同等の訓練セットで訓練した結果、検証セットにおいてデフォルトモデルを上回るパフォーマンスを発揮しました。
最後に、カスタマイズしたモデルをONNX形式にエクスポートし、MQL5のEAに統合しました。
データ抽出
MetaTrader 5端末から必要なデータを抽出するのに便利なスクリプトを作成しました。スクリプトを希望の銘柄にドラッグ&ドロップするだけで、データが抽出されパス「\MetaTrader 5\MQL5\Files\..”」に配置されます。
//+------------------------------------------------------------------+ //| ProjectName | //| Copyright 2020, CompanyName | //| http://www.companyname.net | //+------------------------------------------------------------------+ #property copyright "Gamuchirai Zororo Ndawana" #property link "https://www.mql5.com/ja/users/gamuchiraindawa" #property version "1.00" #property script_show_inputs //---Amount of data requested input int size = 100000; //How much data should we fetch? //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void OnStart() { //---File name string file_name = "Market Data " + Symbol() + ".csv"; //---Write to file int file_handle=FileOpen(file_name,FILE_WRITE|FILE_ANSI|FILE_CSV,","); for(int i= size;i>=0;i--) { if(i == size) { FileWrite(file_handle,"Time","Open","High","Low","Close"); } else { FileWrite(file_handle,iTime(Symbol(),PERIOD_CURRENT,i), iOpen(Symbol(),PERIOD_CURRENT,i), iHigh(Symbol(),PERIOD_CURRENT,i), iLow(Symbol(),PERIOD_CURRENT,i), iClose(Symbol(),PERIOD_CURRENT,i)); } } } //+------------------------------------------------------------------+
Pythonによる探索的データ分析
まずは標準ライブラリをインポートします。
#Libraries import pandas as pd import numpy as np import seaborn as sns
次に先ほど抽出したデータを読み込みます。
#Dollar VS Rand USDZAR = pd.read_csv("/home/volatily/market_data/Market Data USDZAR.csv") #US Oil USOIL = pd.read_csv("/home/volatily/market_data/Market Data US Oil.csv") #SA Gold SAGOLD = pd.read_csv("/home/volatily/market_data/Market Data XAUUSD.csv")
データを検査します。
USOIL
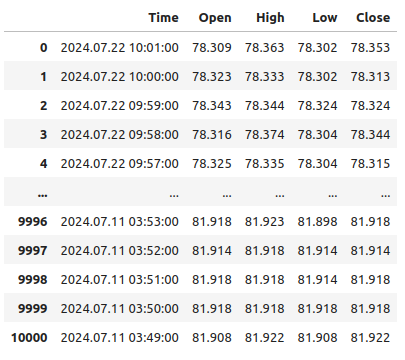
図1:時間的に逆方向に進んでいるデータ
タイムスタンプが現在に近いところから過去に向かって進んでいます。これは、機械学習のタスクには望ましくありません。過去ではなく未来を予測するために、データの順序を逆にします。
#Format the data USDZAR = USDZAR[::-1] USOIL = USOIL[::-1] SAGOLD = SAGOLD[::-1]
データセットを結合する前に、まずデータセットがすべて日付列をインデックスとして使っていることを確認しましょう。そうすることで、すべてのデータセットが共有する日だけを、正しい時系列で選択することができます。
#Set the indexes USOIL = USOIL.set_index("Time") SAGOLD = SAGOLD.set_index("Time") USDZAR = USDZAR.set_index("Time")
データセットを結合します。
#Merge the dataframes merged_df = pd.merge(USOIL,SAGOLD,how="inner",left_index=True,right_index=True,suffixes=(" US OIL"," SA GOLD")) merged_df = pd.merge(merged_df,USDZAR,how="inner",left_index=True,right_index=True)
予測期間を定義します。
#Define the forecast horizon look_ahead = 10
ターゲットはUSDZARペアの将来の終値とし、可視化のためにバイナリターゲットも含めます。
#Label the data merged_df["Target"] = merged_df["Close"].shift(-look_ahead) merged_df["Binary Target"] = 0 merged_df.loc[merged_df["Close"] < merged_df["Target"],"Binary Target"] = 1
空の行はすべて削除します。
#Drop empty rows
merged_df.dropna(inplace=True)
相関レベルを観察します。
#Let's observe the correlation levels merged_df.corr()
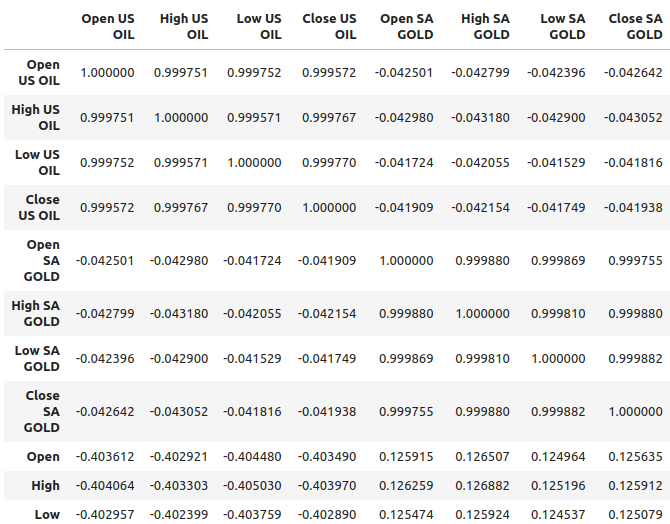
図2:データセットの相関レベル
原油はUSD/ZAR通貨ペアとおおよそ-0.4の相関レベルを示しており、比較的強い相関関係が見られます。一方、金はこの通貨ペアとの相関レベルが約0.1と比較的弱いことがわかります。相関関係が常に変数間の関係を示すわけではないことを忘れないことが重要です。時には、相関が両方の変数に影響を与える共通の原因から生じることもあります。
例えば、歴史的に金とドルの関係は逆転していました。ドルが下落するたびに、トレーダーはドルから資金を引き上げ、代わりに金に投資しました。このため、歴史的にドルのパフォーマンスが悪いときには金価格が上昇する傾向がありました。つまり、この単純な例では、両方の市場に参加しているトレーダーが共通の原因ということになります。
散布図は2つの変数の関係を可視化するのに役立つので、金価格に対する原油価格の散布図を作成し、USDZARの価格水準が上昇(赤)したか下落(緑)したかによってポイントを色分けしました。見てわかるように、データに明確な分離レベルはありません。実際、作成された散布図はどれも強い関係を示唆していません。
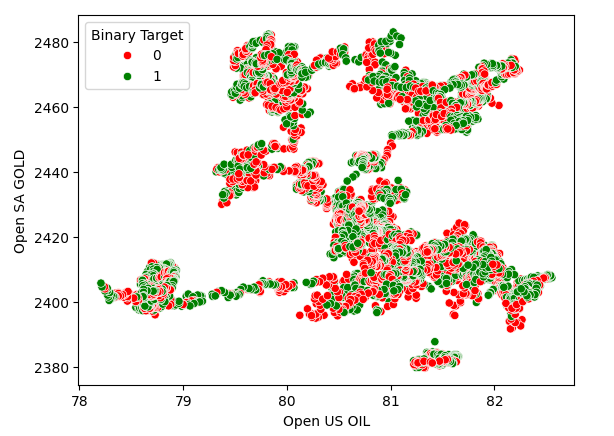
図3:原油価格と金価格の散布図
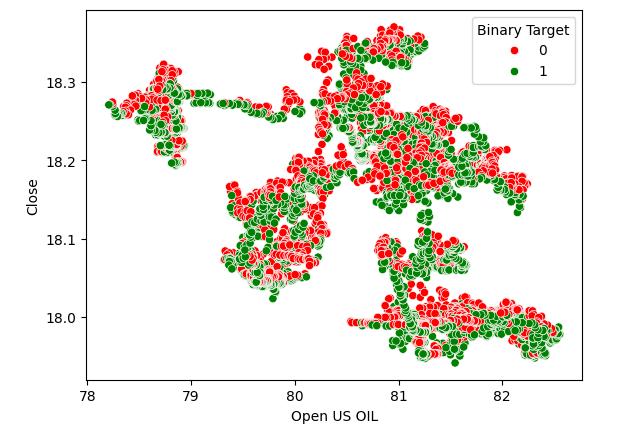
図4:原油価格とUSDZARの終値の散布図
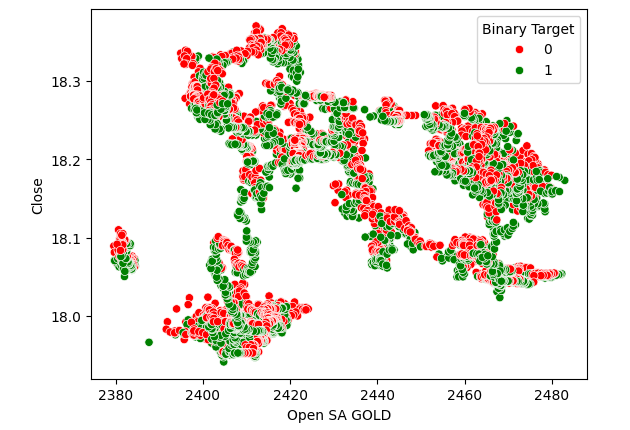
図5:USDZAR終値と金価格の散布図
関係のモデル化
交差検証をおこなうために、データセットのインデックスをリセットします。
#Reset the index
merged_df.reset_index(inplace=True)
次に、データの関係をモデル化するために必要なライブラリをインポートします。
#Import the libraries we need from sklearn.linear_model import LinearRegression from sklearn.linear_model import Lasso from sklearn.ensemble import GradientBoostingRegressor from sklearn.ensemble import RandomForestRegressor from sklearn.ensemble import AdaBoostRegressor from sklearn.ensemble import BaggingRegressor from sklearn.neighbors import KNeighborsRegressor from sklearn.svm import LinearSVR from sklearn.neural_network import MLPRegressor from sklearn.model_selection import TimeSeriesSplit from sklearn.metrics import root_mean_squared_error from sklearn.preprocessing import RobustScaler
予測因子とターゲットを定義します。
#Define the predictors normal_predictors = ["Open","High","Low","Close"] oil_gold_predictors = ["Open US OIL","High US OIL","Low US OIL","Close US OIL","Open SA GOLD","High SA GOLD","Low SA GOLD","Close SA GOLD"] target = "Target"
データをスケーリングします。
#Scale the data all_predictors = normal_predictors + oil_gold_predictors scaler = RobustScaler() scaled_data = pd.DataFrame(scaler.fit_transform(merged_df.loc[:,all_predictors]),columns=all_predictors,index=np.arange(0,merged_df.shape[0]))
モデルを初期化します。
#Now prepare the models models = [ LinearRegression(), Lasso(), GradientBoostingRegressor(), RandomForestRegressor(), AdaBoostRegressor(), BaggingRegressor(), KNeighborsRegressor(), LinearSVR(), MLPRegressor(hidden_layer_sizes=(10,5),early_stopping=True), MLPRegressor(hidden_layer_sizes=(50,15),early_stopping=True) ] columns = [ "Linear Regression", "Lasso", "Gradient Boosting Regressor", "Random Forest Regressor", "AdaBoost Regressor", "Bagging Regressor", "KNeighbors Regressor", "Linear SVR", "Small Neural Network", "Large Neural Network" ]
時系列交差検証オブジェクトをインスタンス化します。
#Prepare the time-series split object splits = 10 tscv = TimeSeriesSplit(n_splits=splits,gap=look_ahead)
誤差レベルを保存するデータフレームを作成します。
#Prepare the dataframes to store the error levels normal_error = pd.DataFrame(columns=columns,index=np.arange(0,splits)) new_error = pd.DataFrame(columns=columns,index=np.arange(0,splits))
ネストされたforループを使って交差検証を実行します。最初のループはモデルのリストを繰り返し、2番目のループは各モデルをクロス検証し、誤差レベルを保存します。
#First we iterate over all the models we have available for j in np.arange(0,len(models)): #Now we have to perform cross validation with each model for i,(train,test) in enumerate(tscv.split(scaled_data)): #Get the data X_train = scaled_data.loc[train[0]:train[-1],oil_gold_predictors] X_test = scaled_data.loc[test[0]:test[-1],oil_gold_predictors] y_train = merged_df.loc[train[0]:train[-1],target] y_test = merged_df.loc[test[0]:test[-1],target] #Fit the model models[j].fit(X_train,y_train) #Measure the error new_error.iloc[i,j] = root_mean_squared_error(y_test,models[j].predict(X_test))
通常のモデル入力を用いた誤差レベルです。
normal_error
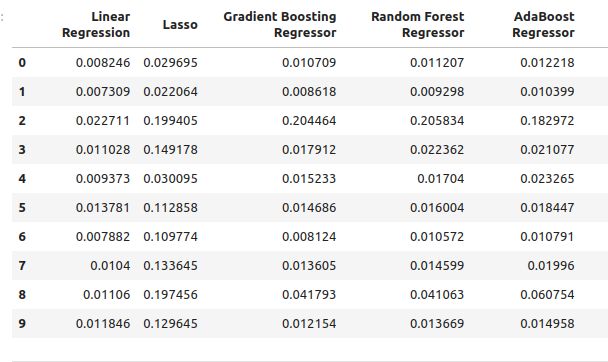
図6:OHLC予測因子を使って予測した場合の誤差レベル
titleOHLC予測因子を使って予測した場合の誤差レベル IItitlealtOHLC予測因子を使って予測した場合の誤差レベル II.alt
図7:OHLC予測因子を使って予測した場合の誤差レベル II
では、原油価格と金価格だけを使った場合の誤差レベルを見てみましょう。
new_error
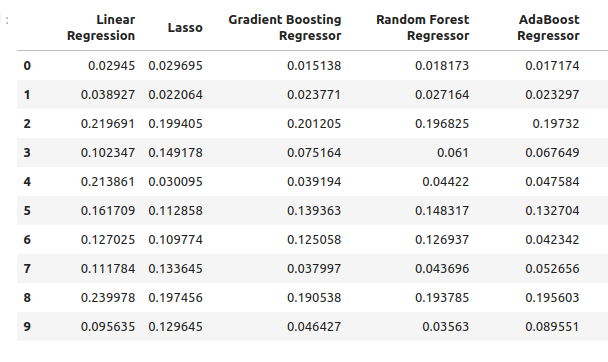
図8:原油価格と金価格を用いた予測の精度レベル
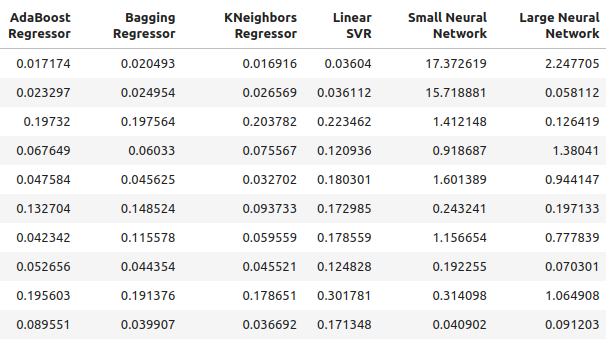
図9:原油価格と金価格を用いて予測した場合の精度レベル II
通常の予測因子を使った各モデルの平均パフォーマンスを見てみましょう。
#Let's see our average performance on the normal dataset
for i in (np.arange(0,normal_error.shape[0])):
print(f"{models[i]} normal error {((normal_error.iloc[:,i].mean()))}")
Lasso() normal error 0.11138143304314707
GradientBoostingRegressor() normal error 0.03472997520534606
RandomForestRegressor() normal error 0.03616484012058101
AdaBoostRegressor() normal error 0.037484107657877755
BaggingRegressor() normal error 0.03670486223028821
KNeighborsRegressor() normal error 0.035113189373409175
LinearSVR() normal error 0.01085610361276552
MLPRegressor(early_stopping=True, hidden_layer_sizes=(10, 5)) normal error 2.558754334716706
MLPRegressor(early_stopping=True, hidden_layer_sizes=(50, 15)) normal error 1.0544369296125597
次に、新しい予測因子を用いて平均的なパフォーマンスを評価します。
#Let's see our average performance on the new dataset
for i in (np.arange(0,normal_error.shape[0])):
print(f"{models[i]} normal error {((new_error.iloc[:,i].mean()))}")
Lasso() normal error 0.11138143304314707
GradientBoostingRegressor() normal error 0.0893855335909897
RandomForestRegressor() normal error 0.08957454602573789
AdaBoostRegressor() normal error 0.08658796789785872
BaggingRegressor() normal error 0.08887059320664067
KNeighborsRegressor() normal error 0.07696901077705855
LinearSVR() normal error 0.15463529064256165
MLPRegressor(early_stopping=True, hidden_layer_sizes=(10, 5)) normal error 3.8970873719426784
MLPRegressor(early_stopping=True, hidden_layer_sizes=(50, 15)) normal error 0.6958177634524169
精度の変化を観察してみましょう。
#Let's see our average performance on the normal dataset
for i in (np.arange(0,normal_error.shape[0])):
print(f"{models[i]} changed by {((normal_error.iloc[:,i].mean()-new_error.iloc[:,i].mean()))/normal_error.iloc[:,i].mean()}%") Lasso() changed by 0.0%
GradientBoostingRegressor() changed by -1.573728690057642%
RandomForestRegressor() changed by -1.4768406476311784%
AdaBoostRegressor() changed by -1.3099914419240863%
BaggingRegressor() changed by -1.421221271695885%
KNeighborsRegressor() changed by -1.1920256220116057%
LinearSVR() changed by -13.244087580439862%
MLPRegressor(early_stopping=True, hidden_layer_sizes=(10, 5)) changed by -0.5230408480672479%
MLPRegressor(early_stopping=True, hidden_layer_sizes=(50, 15)) changed by 0.34010489967561475%
特徴量の選択
原油と金の予測子から得られた最も優れたモデルはKNeighbors回帰です。どの特徴量が最も重要であるかを見てみましょう。
#Our best performing model was the KNeighbors Regressor #Let us perform feature selection to test how stable the relationship is from mlxtend.feature_selection import SequentialFeatureSelector as SFS
モデルの新しいインスタンスを作成します。
#Let us select our best model
model = KNeighborsRegressor()
前方選択を使用して、モデルにとって最も重要な特徴量を特定します。次に、モデルにすべての予測因子に一度にアクセスできるようにします。
#Create the sequential selector object sfs1 = SFS( model, k_features=(1,len(all_predictors)), forward=True, scoring="neg_mean_squared_error", cv=10, n_jobs=-1 )
逐次特徴量選択器の適合
#Fit the sequential selector sfs1 = sfs1.fit(scaled_data.loc[:,all_predictors],merged_df.loc[:,"Target"])アルゴリズムによって選択された最良の特徴量を観察すると、石油や金の価格はUSDZARの予測にはあまり役立たないと結論付けるかもしれません。なぜなら、アルゴリズムはUSDZARの始値、安値、終値の3つの特徴量だけを選択したからです。
#Now let us see which predictors were selected
sfs1.k_feature_names_
ハイパーパラメータの調整
scikit-learnのRandomizedSearchCVモジュールを使用して、ハイパーパラメータのチューニングをおこなってみましょう。このアルゴリズムは、完全にサンプリングするには大きすぎる応答曲面をサンプリングするのに役立ちます。多数のパラメータを持つモデルを使う場合、入力の組み合わせの総計はかなり速い速度で増えていきます。したがって、多くの可能な値を持つ多くのパラメータを扱う場合には、ランダムサーチアルゴリズムが好ましくなります。
このアルゴリズムでは、許容する反復回数を調整することで、結果の精度と計算時間のトレードオフをコントロールできます。アルゴリズムのランダムな性質のため、この記事で示された結果を正確に再現するのは難しいかもしれません。
Import the scikit-learn module.
#Now we will load the libraries we need
from sklearn.model_selection import RandomizedSearchCV
専用の訓練セットとテストセットを準備します。
#Let us see if we can tune the model #First we will create train test splits train_X = scaled_data.loc[:(scaled_data.shape[0]//2),:] train_y = merged_df.loc[:(merged_df.shape[0]//2),"Target"] test_X = scaled_data.loc[(scaled_data.shape[0]//2):,:] test_y = merged_df.loc[(merged_df.shape[0]//2):,"Target"]
パラメータチューニングをおこなうためには、scikit-learnインターフェイスを実装した推定器を渡し、その後に推定器のパラメータに対応するキーと、各パラメータの許可される入力範囲に対応する値を含む辞書を渡す必要があります。そこから、5分割交差検証を実施したいことを指定し、次にスコアリングメトリックとして負の平均二乗誤差を指定する必要があります。
#Create the tuning object rs = RandomizedSearchCV(KNeighborsRegressor(n_jobs=-1),{ "n_neighbors": [1,2,3,4,5,8,10,16,20,30,60,100], "weights":["uniform","distance"], "leaf_size":[1,2,3,4,5,10,15,20,40,60,90], "algorithm":["ball_tree","kd_tree"], "p":[1,2,3,4,5,6,7,8] },cv=5,n_iter=500,return_train_score=False,scoring="neg_mean_squared_error")
訓練セットでパラメータチューニングをおこないます。
#Let's perform the hyperparameter tuning rs.fit(train_X,train_y)
得られた結果を、良いものから悪いものまで見ていきます。
#Let's store the results from our hyperparameter tuning tuning_results = pd.DataFrame(rs.cv_results_) tuning_results.loc[:,["param_n_neighbors","param_weights","param_leaf_size","param_algorithm","param_p","mean_test_score"]].sort_values(by="mean_test_score",ascending=False)
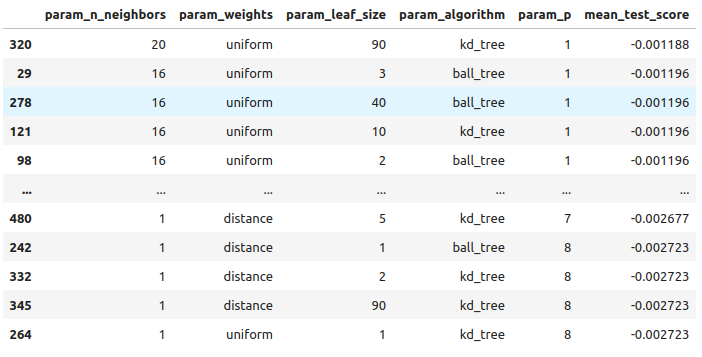
図10:最良のモデルをチューニングした結果
以下が、見つかった最良のパラメータです。
#The best parameters we came across
rs.best_params_
'p':1,
'n_neighbors':4,
'leaf_size':15,
'algorithm': 'ball_tree'}
過剰適合の確認
カスタマイズモデルとデフォルトモデルを比較する準備をしましょう。両モデルは同じ訓練セットで学習します。検証セットにおいてデフォルトモデルがカスタマイズモデルを上回った場合、訓練データが過剰適合している可能性があります。しかし、カスタマイズモデルがより良い結果を出す場合、これは過剰適合せずにモデルパラメータのチューニングに成功したことを示唆しているかもしれません。
#Create instances of the default model and the custmoized model default_model = KNeighborsRegressor() customized_model = KNeighborsRegressor(p=rs.best_params_["p"],weights=rs.best_params_["weights"],n_neighbors=rs.best_params_["n_neighbors"],leaf_size=rs.best_params_["leaf_size"],algorithm=rs.best_params_["algorithm"])
デフォルトモデルの精度を測ってみましょう。
#Measure the accuracy of the default model default_model.fit(train_X,train_y) root_mean_squared_error(test_y,default_model.predict(test_X))
次に、カスタマイズされたモデルの精度です。
#Measure the accuracy of the customized model
customized_model.fit(train_X,train_y)
root_mean_squared_error(test_y,customized_model.predict(test_X)) 過剰適合することなく、うまくモデルをチューニングできたようです。それでは、カスタマイズしたモデルをONNX形式にエクスポートする準備をしましょう。
ONNX形式へのエクスポート
Open Neural Network Exchange (ONNX)は、言語にとらわれずに機械学習モデルを構築展開するための相互運用可能なフレームワークです。ONNXを使用することで、ONNX APIをサポートしている言語であれば、どのようなプログラミング言語でも機械学習モデルを簡単に使用することができます。本稿執筆時点では、ONNX APIは世界最大の企業で構成されるコンソーシアムによって開発維持されています。
Import the libraries we need #Let's prepare to export the customized model to ONNX format import onnx from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType
MetaTrader 5端末で再現できるように、データがスケーリングされ、正規化されていることを確認する必要があります。したがって、後で端末でいつでも実行できる標準的な変換を実行します。各列の平均値を引いて、データの中心を決めます。そして、各値をその列の標準偏差で割ります。こうすることで、モデルが異なるスケールの変数間の変化をよりよく理解できるようになります。
#Train the model on all the data we have #But before doing that we need to first scale the data in a way we can repeat in MQL5 scale_factors = pd.DataFrame(columns=all_predictors,index=["mean","standard deviation"]) for i in np.arange(0,len(all_predictors)): scale_factors.iloc[0,i] = merged_df.loc[:,all_predictors[i]].mean() scale_factors.iloc[1,i] = merged_df.loc[:,all_predictors[i]].std() scale_factors

図12:データのスケーリングと標準化に使用する値の抜粋
正規化と標準化をおこないます。
for i in all_predictors:
merged_df.loc[:,i] = (merged_df.loc[:,i] - merged_df.loc[:,i].mean()) / merged_df.loc[:,i].std()
では、データを見てみましょう。
merged_df
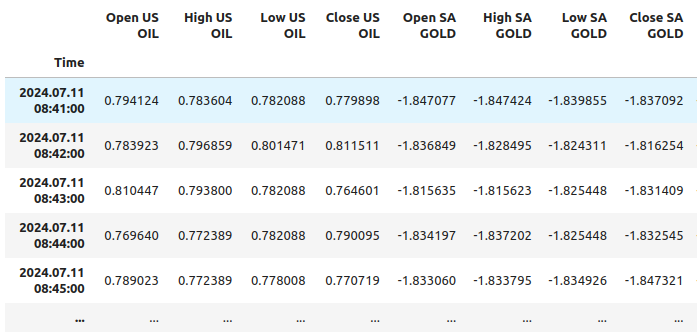
図11:スケーリング後のデータの抜粋
カスタマイズしたモデルを初期化します。
customized_model = KNeighborsRegressor(p=rs.best_params_["p"],weights=rs.best_params_["weights"],n_neighbors=rs.best_params_["n_neighbors"],leaf_size=rs.best_params_["leaf_size"],algorithm=rs.best_params_["algorithm"]) customized_model.fit(merged_df.loc[:,all_predictors],merged_df.loc[:,"Target"])
モデルの入力形状を定義します。
#Define the input shape and type initial_type = [("float_tensor_type",FloatTensorType([1,train_X.shape[1]]))]
ONNX表現を作成します。
#Create an ONNX representation
onnx_model = convert_sklearn(customized_model,initial_types=initial_type)
ONNXモデルを保存します。
#Store the ONNX model onnx_model_name = "USDZAR_FLOAT_M1.onnx" onnx.save_model(onnx_model,onnx_model_name)
ONNXモデルの可視化
Netronは、機械学習モデルのためのオープンソースのビジュアライザーです。NetronはONNX以外にもKerasのような様々なフレームワークへのサポートを拡張しています。netronを使って、ONNXモデルが期待通りの入出力形状を持つことを確認します。
netronモジュールをインポートします。
#Let's visualize the model in netron import netron
これでnetronを使ってモデルを可視化できます。
#Run netron
netron.start(onnx_model_name)
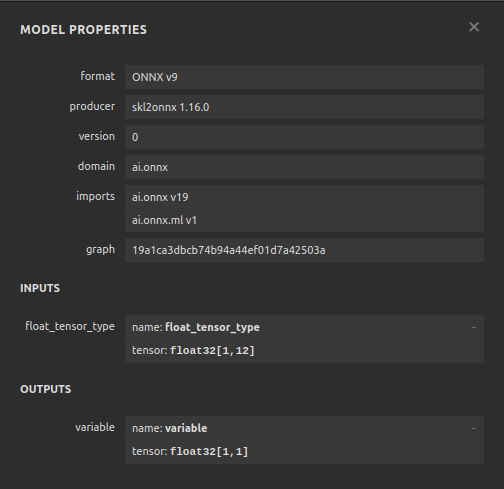
図12:ONNXモデルの仕様
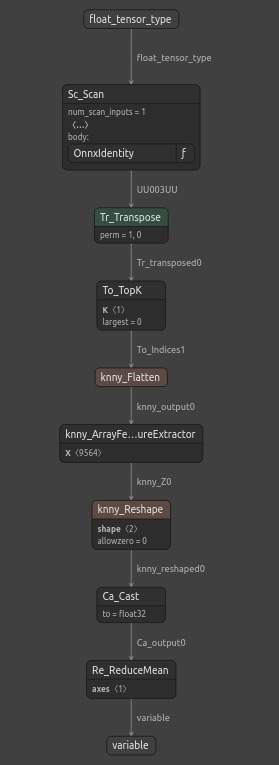
図13:ONNXモデルの構造
ONNXモデルは期待に応えており、入出力の形状は期待するところに正確に収まっています。次に、ONNXモデルの上にEAを構築します。
MQL5での実装
まずONNXモデルをアプリケーションに統合することから始めましょう。ONNXファイルをリソースとして指定することで、ONNXファイルは.ex5の拡張子でコンパイルされたプログラムに含まれます。
//+------------------------------------------------------------------+ //| USDZAR.mq5 | //| Gamuchirai Zororo Ndawana | //| https://www.mql5.com/ja/gamuchiraindawa | //+------------------------------------------------------------------+ #property copyright "Gamuchirai Zororo Ndawana" #property link "https://www.mql5.com/ja/gamuchiraindawa" #property version "1.00" //+-----------------------------------------------------------------+ //| Require the ONNX file | //+-----------------------------------------------------------------+ #resource "\\Files\\USDZAR_FLOAT_M1.onnx" as const uchar onnx_model_buffer[];
では、取引ライブラリをインポートしましょう。
//+-----------------------------------------------------------------+ //| Libraries we need | //+-----------------------------------------------------------------+ #include <Trade/Trade.mqh> CTrade Trade;
エンドユーザーがコントロールできる入力を定義しましょう。
//+------------------------------------------------------------------+ //| Inputs | //+------------------------------------------------------------------+ double input sl_width = 0.4; //How tight should our stop loss be? int input lot_multiple = 10; //How many times bigger than minimum lot should we enter? double input max_risk = 10; //After how much profit/loss should we close?
次に、いくつかのグローバル変数が必要です。
//+------------------------------------------------------------------+ //| Global Variables | //+------------------------------------------------------------------+ long onnx_model; //Our onnx model double mean_values[12],std_values[12]; //The scaling factors we used for our data vector model_inputs = vector::Zeros(12); //Our model's inputs vector model_forecast = vector::Zeros(1); //Our model's output double bid,ask; //Market prices double minimum_volume; //Smallest lot size double state = 0; //0 means we have no positions, 1 means we have buy position, 2 means we have sell position.
ここで、繰り返し実行する必要のあるタスクのためのヘルパー関数を定義してみましょう。まず、リスクレベルをコントロールしましょう。利益と損失の合計が、定義したリスクレベルを超えた場合、自動的にポジションを決済します。
//+------------------------------------------------------------------+ //| Check if we have reached our risk level | //+------------------------------------------------------------------+ void check_risk_level(void) { //--- Check if we have surpassed our maximum risk level if(MathAbs(PositionGetDouble(POSITION_PROFIT)) > max_risk) { //--- We should close our positions Trade.PositionClose("USDZAR"); } }
せっかく統合AIシステムがあるのだから、それを使って反転を検知してみましょう。システムが、価格が当社に対して不利に動くと予測した場合、ポジションを決済し、エンドユーザーに反転の可能性が検出されたことを警告します。
//+------------------------------------------------------------------+ //| Check if there is a reversal may be coming | //+------------------------------------------------------------------+ void check_reversal(void) { if(((state == 1) && (model_forecast[0] < iClose("USDZAR",PERIOD_M1,0))) ||((state == 2) && (model_forecast[0] > iClose("USDZAR",PERIOD_M1,0)))) { //--- There may be a reversal coming Trade.PositionClose("USDZAR"); //--- Give the user feedback Alert("Potential reversal detected"); } }
エントリ機会を見つける関数が必要です。モデルの予測が上位時間枠での価格水準の変化と一致した場合のみ、エントリが有効であると判断します。
//+------------------------------------------------------------------+ //| Find an entry opportunity | //+------------------------------------------------------------------+ void find_entry(void) { //---Check for the change in price on higher timeframes if(iClose("USDZAR",PERIOD_D1,0) > iClose("USDZAR",PERIOD_D1,21)) { //--- We're looking for buy oppurtunities if(model_forecast[0] > iClose("USDZAR",PERIOD_M1,0)) { //--- Open the position Trade.Buy(minimum_volume,"USDZAR",ask,(ask - sl_width),(ask + sl_width),"USDZAR AI"); //--- Update the system state state = 1; } } //---Check for the change in price on higher timeframes else if(iClose("USDZAR",PERIOD_D1,0) < iClose("USDZAR",PERIOD_D1,21)) { //--- We're looking for sell oppurtunities if(model_forecast[0] < iClose("USDZAR",PERIOD_M1,0)) { //--- Open sell position Trade.Sell(minimum_volume,"USDZAR",bid,(bid + sl_width),(bid - sl_width),"USDZAR AI"); //--- Update the system state state = 2; } } }
次に、モデルから予測を取得する関数が必要です。そのためには、まず現在の市場価格を取得し、平均を引いて標準偏差で割ることで変換する必要があります。
//+------------------------------------------------------------------+ //| Obtain a forecast from our model | //+------------------------------------------------------------------+ void model_predict(void) { //Let's fetch our model's inputs //--- USDZAR model_inputs[0] = ((iOpen("USDZAR",PERIOD_M1,0) - mean_values[0]) / std_values[0]); model_inputs[1] = ((iHigh("USDZAR",PERIOD_M1,0) - mean_values[1]) / std_values[1]); model_inputs[2] = ((iLow("USDZAR",PERIOD_M1,0) - mean_values[2]) / std_values[2]); model_inputs[3] = ((iClose("USDZAR",PERIOD_M1,0) - mean_values[3]) / std_values[3]); //--- XTI OIL US model_inputs[4] = ((iOpen("XTIUSD",PERIOD_M1,0) - mean_values[4]) / std_values[4]); model_inputs[5] = ((iHigh("XTIUSD",PERIOD_M1,0) - mean_values[5]) / std_values[5]); model_inputs[6] = ((iLow("XTIUSD",PERIOD_M1,0) - mean_values[6]) / std_values[6]); model_inputs[7] = ((iClose("XTIUSD",PERIOD_M1,0) - mean_values[7]) / std_values[7]); //--- GOLD SA model_inputs[8] = ((iOpen("XAUUSD",PERIOD_M1,0) - mean_values[8]) / std_values[8]); model_inputs[9] = ((iHigh("XAUUSD",PERIOD_M1,0) - mean_values[9]) / std_values[9]); model_inputs[10] = ((iLow("XAUUSD",PERIOD_M1,0) - mean_values[10]) / std_values[10]); model_inputs[11] = ((iClose("XAUUSD",PERIOD_M1,0) - mean_values[11]) / std_values[11]); //--- Get a prediction OnnxRun(onnx_model,ONNX_DEFAULT,model_inputs,model_forecast); }
複数の銘柄を分析するので、気配値表示に追加する必要があります。
//+------------------------------------------------------------------+ //| Load the symbols we need and add them to the market watch | //+------------------------------------------------------------------+ void load_symbols(void) { SymbolSelect("XAUUSD",true); SymbolSelect("XTIUSD",true); SymbolSelect("USDZAR",true); }
スケーリング係数、各列の平均と標準偏差をロードする関数が必要です。
//+------------------------------------------------------------------+ //| Load the scale values | //+------------------------------------------------------------------+ void load_scale_values(void) { //--- Mean //--- USDZAR mean_values[0] = 18.14360511919699; mean_values[1] = 18.145737421580925; mean_values[2] = 18.141568574864074; mean_values[3] = 18.14362306984525; //--- XTI US OIL mean_values[4] = 80.76956702216644; mean_values[5] = 80.7864452112087; mean_values[6] = 80.75236177331661; mean_values[7] = 80.76923546633206; //--- GOLD SA mean_values[8] = 2430.5180384776245; mean_values[9] = 2430.878959640318; mean_values[10] = 2430.1509598494354; mean_values[11] = 2430.5204140526976; //--- Standard Deviation //--- USDZAR std_values[0] = 0.11301636249300206; std_values[1] = 0.11318116432297631; std_values[2] = 0.11288670156099372; std_values[3] = 0.11301994613848391; //--- XTI US OIL std_values[4] = 0.9802409859148413; std_values[5] = 0.9807944310705999; std_values[6] = 0.9802449355481064; std_values[7] = 0.9805961626626833; //--- GOLD SA std_values[8] = 26.397404261230328; std_values[9] = 26.414599597905003; std_values[10] = 26.377605644853944; std_values[11] = 26.395208330942864; }
最後に、ONNXファイルをロードする関数が必要です。
//+------------------------------------------------------------------+ //| Load the onnx file from buffer | //+------------------------------------------------------------------+ bool load_onnx_file(void) { //--- Create the model from the buffer onnx_model = OnnxCreateFromBuffer(onnx_model_buffer,ONNX_DEFAULT); //--- The input size for our onnx model ulong input_shape [] = {1,12}; //--- Check if we have the right input size if(!OnnxSetInputShape(onnx_model,0,input_shape)) { Comment("Incorrect input shape, the model has input shape ",OnnxGetInputCount(onnx_model)); return(false); } //--- The output size for our onnx model ulong output_shape [] = {1,1}; //--- Check if we have the right output size if(!OnnxSetOutputShape(onnx_model,0,output_shape)) { Comment("Incorrect output shape, the model has output shape ",OnnxGetOutputCount(onnx_model)); return(false); } //--- Everything went fine return(true); } //+------------------------------------------------------------------+
これらのヘルパー関数を定義したので、EAで使い始めることができます。まず、アプリケーションが初めてロードされたときの動作を定義しましょう。ONNXモデルをロードし、スケーリング係数を準備し、その後市場データを取得します。
//+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- Load the onnx file if(!load_onnx_file()) { return(INIT_FAILED); } //--- Load our scaling values load_scale_values(); //--- Add the symbols we need to the market watch load_symbols(); //--- The smallest lotsize we can use minimum_volume = SymbolInfoDouble("USDZAR",SYMBOL_VOLUME_MIN) * lot_multiple; //--- Everything went fine return(INIT_SUCCEEDED); }
プログラムが停止されるたびに、使わなくなったリソースを解放する必要があります。
//+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- Release the resources we used for our onnx model OnnxRelease(onnx_model); //--- Remove the expert advisor ExpertRemove(); }
最後に、価格が変わるたびに、モデルから新しい予測を取得し、更新された市場価格を取得し、新しいポジションを建てるか、現在開いているポジションを管理する必要があります。
//+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- We always need a forecast from our model model_predict(); //--- Fetch market prices bid = SymbolInfoDouble("USDZAR",SYMBOL_BID); ask = SymbolInfoDouble("USDZAR",SYMBOL_ASK); //--- If we have no open positions, find an entry if(PositionsTotal() == 0) { //--- Find an entry find_entry(); //--- Reset the system state state = 0; } //--- If we have open postitions, manage them else { //--- Check for a reveral warning from our AI check_reversal(); //--- Check if we have not reached our max risk levels check_risk_level(); } }
これらすべてをまとめると、プログラムの動作を観察することができます。
図17:EA
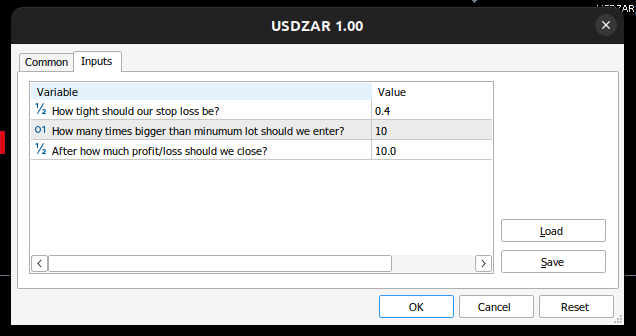
図14:EAの入力
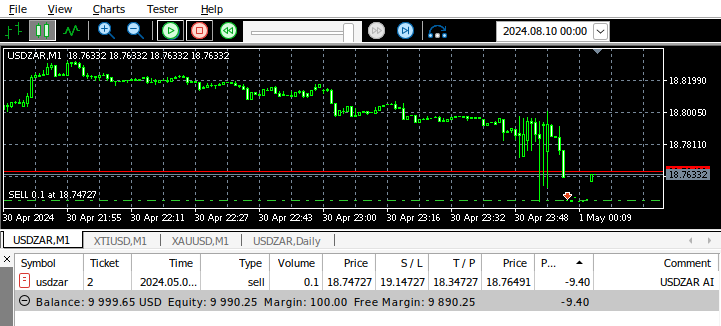
図15:プログラムの動作
結論
この記事では、AIを搭載した多銘柄EAを構築する方法を示しました。通常のOHLCデータを使用することで、より低い誤差レベルを得ることができましたが、必ずしもMetaTrader 5端末にあるすべての銘柄に同じことが当てはまるわけではありません。
MetaQuotes Ltdにより英語から翻訳されました。
元の記事: https://www.mql5.com/en/articles/15570
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。
この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。
 古典的な戦略を再構築する(第6回):多時間枠分析
古典的な戦略を再構築する(第6回):多時間枠分析
 どんな市場でも優位性を得る方法(第3回):VISA消費指数
どんな市場でも優位性を得る方法(第3回):VISA消費指数
 古典的な戦略を再構築する(第4回):SP500と米財務省中期証券
古典的な戦略を再構築する(第4回):SP500と米財務省中期証券
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索

素晴らしい。ワークブックをありがとう。ありがとう。