Redes neuronales en el trading: Modelos del espacio de estados

Introducción

Recientemente, se ha generalizado el paradigma de adaptar grandes modelos a nuevos problemas previamente entrenados con grandes conjuntos de datos de origen aleatorios de una amplia gama de áreas, como texto, imágenes, audio, series temporales, etc.

Aunque este concepto es independiente de la elección específica de la arquitectura, la mayoría de los modelos se basan en un tipo de arquitectura: el Transformer y su capa central de Self-Attention. La eficacia de la capa de Self-Attention se debe a su capacidad de dirigir la información de forma precisa a una ventana de contexto, lo que permite modelar datos complejos. Sin embargo, esta propiedad posee desventajas fundamentales: la imposibilidad de modelar algo fuera de una ventana finita y el escalamiento cuadrático con respecto a la longitud de la ventana.

En problemas de modelado de secuencias, una solución alternativa podría ser el uso de modelos de secuencia del espacio de estados estructurados (Space Sequence Models — SSM). Estos modelos pueden interpretarse como una combinación de redes neuronales recurrentes (RNN) y redes neuronales convolucionales (CNN). Esta clase de modelos se puede calcular de forma muy eficiente usando una escala lineal o casi lineal de la longitud de la secuencia. Además, posee mecanismos fundamentales para modelar dependencias de largo alcance en ciertas modalidades de datos.

Uno de los algoritmos que permite usar modelos del espacio de estados para el pronóstico de series temporales se propone en el artículo "Mamba: Linear-Time Sequence Modeling with Selective State Spaces". En este se introduce una nueva clase de modelos del espacio de estados de muestra.

Los autores del artículo identifican una limitación clave de los modelos existentes: la capacidad de seleccionar información de forma efectiva según los datos iniciales (es decir, centrarse en datos iniciales específicos o ignorarlos). Y desarrollan un mecanismo de selección simple, haciendo que los parámetros SSM dependan de los datos iniciales. Esto permite que el modelo filtre la información irrelevante y recuerde la información relevante indefinidamente.

Los autores del método simplifican las arquitecturas de los modelos de secuencia profunda anteriores combinando el diseño de las arquitecturas SSM y MLP en un bloque, lo cual da como resultado un diseño de arquitectura simple y homogéneo (Mamba) que incorpora espacios de estados muestreados.

Los SSM de muestreo y, por extensión, la arquitectura Mamba son modelos totalmente recurrentes con propiedades clave que los hacen adecuados como base para modelos básicos generales que trabajan en secuencias.

1. Alta calidad: la selectividad garantiza un alto rendimiento en modalidades densas.
2. Entrenamiento e inferencia rápidos: el cálculo y la memoria se escalan de forma lineal según la longitud de la secuencia durante el entrenamiento, mientras que el desarrollo del modelo autorregresivo durante la inferencia solo requiere un tiempo constante por paso, ya que no necesita una caché de elementos anteriores.
3. Contexto a largo plazo: la calidad y la eficiencia se combinan para ofrecer un mejor rendimiento al trabajar con secuencias de gran tamaño.

1. El algoritmo Mamba

Los autores del método Mamba afirman que el problema fundamental del modelado de secuencias es la compresión del contexto en un estado más pequeño. Desde esta perspectiva podemos analizar las ventajas y desventajas de los modelos de secuencia populares. Por ejemplo, la atención resulta a la vez eficiente e ineficiente porque claramente no comprime el contexto en absoluto. Esto resulta evidente por el hecho de que la inferencia autorregresiva requiere almacenar explícitamente todo el contexto (es decir, la caché Key-Value), lo cual provoca directamente una inferencia lenta en tiempo lineal y un entrenamiento del Transformer en tiempo cuadrático.

Por otro lado, los modelos recurrentes resultan eficientes porque tienen un estado finito, lo que implica inferencia en tiempo constante y aprendizaje en tiempo lineal. Sin embargo, su eficacia está limitada por lo bien que el estado haya comprimido el contexto.

Para comprender este principio, los autores del método prestan especial atención a la solución de dos problemas sintéticos:

• La tarea de la copia selectiva. Se requiere un razonamiento consciente del contenido para poder recordar los tokens relevantes y filtrar los irrelevantes.
• La tarea de las cabezas de inducción: este mecanismo explica la mayoría de las capacidades de aprendizaje contextual del LLM. Resolver una tarea requiere un razonamiento sensible al contexto para saber cuándo sacar la conclusión correcta en el contexto correspondiente.

Estas tareas identifican el modo de falla de los modelos LTI. Desde un punto de vista recurrente, su dinámica constante les impide seleccionar la información correcta de su contexto o influir en el estado oculto transmitido a través de la secuencia, dependiendo de los datos iniciales. Desde una perspectiva de convolución, sabemos que las convoluciones globales pueden resolver el problema de copiado simple porque solo requieren el conocimiento del tiempo, pero tienen dificultades con el problema del copiado selectivo debido a la falta de conocimiento del contenido. Más específicamente, la distancia entre las entradas y las salidas varía y no puede modelarse usando núcleos de convolución estáticos.

Por consiguiente, el equilibrio de eficiencia de los modelos de secuencia se caracteriza por lo bien que comprimen su estado. A su vez, los autores del método sugieren que el principio fundamental en la construcción de los modelos de secuencia es la selectividad, o la capacidad dependiente del contexto de centrarse en los datos de origen o filtrarlos en un estado secuencial. En particular, el mecanismo de selección controla cómo se distribuye la información o cómo interactúa esta a lo largo de la dimensionalidad de la secuencia.

Un método para incorporar la selección a los modelos consistiría en permitir que los parámetros que influyen en las interacciones a lo largo de la secuencia dependan de los datos de entrada. La principal diferencia sería simplemente hacer que unos pocos parámetros Δ B, C supongan funciones de los datos de origen, así como los cambios asociados con ellos en las formas de los tensores. En particular, estos parámetros ahora tienen la dimensionalidad de longitud L. Esto significa que el modelo ha cambiado de invariante en el tiempo a variable en el tiempo. 

Los autores del método seleccionan específicamente:

• SB(x) = LinearN(x)
• SC(x) = LinearN(x)
• SΔ(x) = BroadcastD(Linear1(x))
• τΔ = SoftPlus

La elección de S Δ y τ Δ surge de la conexión a los mecanismos de puerta RNN.

Los autores del método pretenden hacer que losSSM selectivos sean eficientes en el hardware moderno (GPU). A un nivel alto, los modelos recurrentes como SSM siempre buscan un equilibrio entre eficiencia y velocidad: los modelos con dimensionalidades de estados ocultos más altas deberían ser más eficientes pero más lentos. Así, los autores del método Mamba se enfrentaron a la tarea de maximizar la dimensionalidad del estado oculto sin perder la velocidad del modelo y aumentar el consumo de memoria.

El mecanismo de selección tiene como objetivo superar las limitaciones de los modelos LTI. No obstante, debemos volver al problema del cálculo del SSM. Los autores del método resuelven este problema usando tres métodos clásicos: fusión de núcleos, escaneo paralelo y recálculo. Hacen dos observaciones principales:

• El cálculo recurrente ingenuo usa O(BLDN) FLOP, mientras que el cálculo convolucional utiliza O(BLD log(L)) FLOP. Y el primero posee un coeficiente constante más pequeño. Por consiguiente, para secuencias largas y una dimensionalidad de estado N no demasiado grande, el modo recurrente puede en realidad utilizar menos FLOP.
• Dos problemas suponen la naturaleza secuencial de la repetición y el elevado uso de memoria. Para resolver esto último, como en el modo convolucional, podemos intentar no calcular realmente el estado completo h.

La idea principal consiste en utilizar las propiedades de los aceleradores modernos (GPU) para calcular el estado h solo en niveles más eficientes de la jerarquía de memoria. En particular, la mayoría de las operaciones están limitadas por el ancho de banda de la memoria. Esto también se aplica a la operación de escaneo. Los autores del método usan la fusión del núcleo para reducir el número de operaciones de E/S de memoria, lo que da como resultado una aceleración significativa en comparación con la implementación estándar.

Además, los autores del método aplican cuidadosamente la técnica de recálculo clásica para reducir los requisitos de memoria: los estados intermedios no se guardan, sino que se recalculan en la dirección opuesta al cargar los datos de origen.

Los SSM selectivos son transformaciones de secuencia autónomas que pueden integrarse de forma flexible en redes neuronales.

El mecanismo de selección supone un concepto más amplio que puede aplicarse de forma diferente a otros parámetros o utilizando diferentes transformaciones.

La selectividad nos permite filtrar tokens de ruido irrelevantes que puedan ocurrir entre los datos de entrada de interés. Un ejemplo de esto sería el problema del copiado selectivo, pero ocurre en todas las modalidades de datos comunes, especialmente en datos discretos. Esta propiedad surge porque el modelo puede filtrar mecánicamente cualquier dato de entrada particular X t.

Se ha observado empíricamente que muchos modelos de secuencia no mejoran con un contexto más largo, a pesar del principio que dice que un mayor contexto debería redundar en un rendimiento estrictamente mejor. La explicación es que muchos modelos de secuencia no logran ignorar con eficacia un contexto irrelevante cuando es necesario.

Por otro lado, los modelos de elección pueden simplemente restablecer su estado en cualquier momento para eliminar la historia extraña y, por consiguiente, su desempeño en principio mejora monótonamente con el aumento de la longitud del contexto.

A continuación le presentamos la visualización del método por parte del autor.

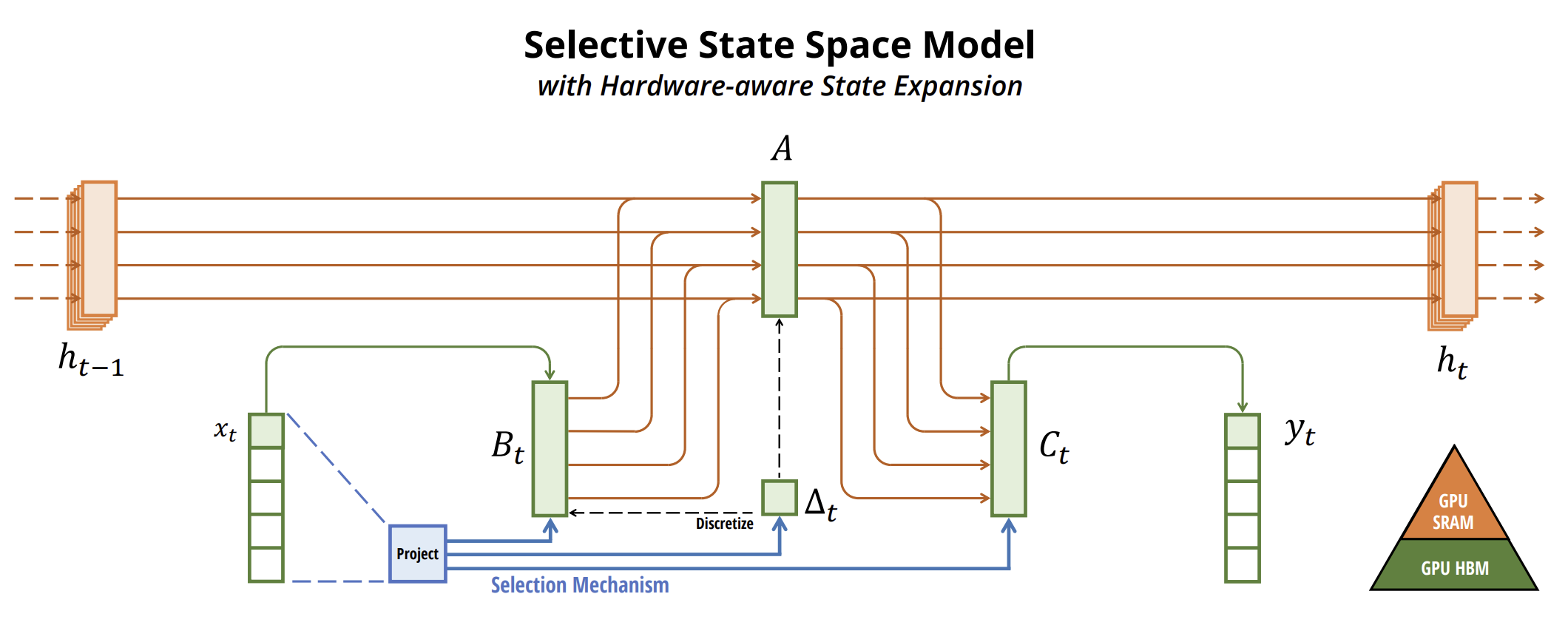
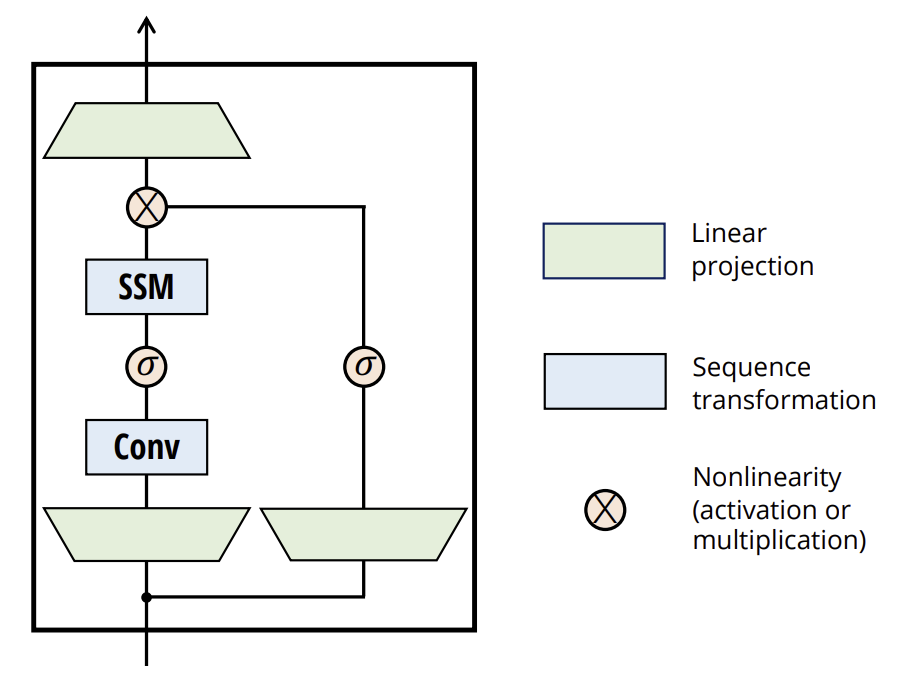
2. Implementación con MQL5

Tras familiarizarnos con los aspectos teóricos del método Mamba, vamos a pasar a la implementación práctica de los enfoques propuestos utilizando MQL5. Y aquí dividiremos el trabajo en dos etapas. Primero, construiremos una clase que implemente el algoritmo SSM, que será una de las capas anidadas del método complejo Mamba. Y luego construiremos los procesos del algoritmo de nivel superior.

2.1 Implementación del SSM

Debemos decir de inmediato que existen muchos algoritmos diferentes para construir SSM. Y en el marco de este experimento, nos hemos desviado un poco del algoritmo implementado por los autores del método Mamba, construyendo uno de los modelos más simples de selección del espacio de estados. Lo implementaremos en la clase CNeuronSSMOCL. Como objeto padre usaremos la clase básica de la capa neuronal completamente conectada CNeuronBaseOCL. A continuación, mostraremos la estructura de la nueva clase.

class CNeuronSSMOCL  :  public CNeuronBaseOCL
  {
protected:
   uint              iWindowHidden;
   CNeuronBaseOCL    cHiddenStates;
   CNeuronConvOCL    cA;
   CNeuronConvOCL    cB;
   CNeuronBaseOCL    cAB;
   CNeuronConvOCL    cC;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
   //---

public:
                     CNeuronSSMOCL(void)  {};
                    ~CNeuronSSMOCL(void)  {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key, uint units_count, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronSSMOCL; }
   //---
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
   virtual void      SetOpenCL(COpenCLMy *obj);
  };

En la estructura presentada vemos la declaración de una constante que determina la dimensionalidad del estado oculto de un elemento (iWindowHidden), y 5 capas neuronales internas con cuya funcionalidad nos familiarizaremos durante la implementación.

El conjunto de métodos redefinibles en nuestra clase resulta bastante familiar. Y creo que ya habrá adivinado su carga funcional.

Todos los objetos internos de la clase se declaran estáticamente, lo cual nos permite dejar el constructor y el destructor de la clase "vacíos". La inicialización de todos los objetos declarados y heredados se realiza, como siempre, en el método Init. En los parámetros de este método recibimos las constantes que nos permiten determinar claramente qué objeto quería crear el usuario.

bool CNeuronSSMOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                         uint window, uint window_key, uint units_count, 
                         ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch))
      return false;

Aquí solo hay 3 parámetros de este tipo:

• window — tamaño del vector de un elemento de la secuencia;
• window_key — tamaño del vector de representación interna de un elemento de la secuencia;
• units_count — tamaño de la secuencia que se está analizando.

Como hemos dicho, en este experimento utilizamos un algoritmo SSM simplificado. En particular, no implementamos la división de una secuencia multimodal en canales independientes.

En el cuerpo del método, llamaremos inmediatamente al método homónimo de la clase padre, que ya implementa la inicialización de objetos y variables heredados. También realizará el control mínimo necesario de los parámetros recibidos desde un programa externo.

Tras ejecutar con éxito el método de la clase padre, procederemos a inicializar los objetos declarados en esta clase. Aquí primero inicializaremos la capa de almacenamiento del estado oculto interno.

   if(!cHiddenStates.Init(0, 0, OpenCL, window_key * units_count, optimization, iBatch))
      return false;
   cHiddenStates.SetActivationFunction(None);
   iWindowHidden = window_key;

E inmediatamente guardaremos el tamaño del vector de estado interno de un elemento de la secuencia en una variable local.

Tenga en cuenta que estamos almacenando decididamente el valor del parámetro sin verificar su valor. El truco reside en que primero inicializaremos deliberadamente el objeto de la capa interna cuyo tamaño está determinado por este parámetro. Y si el usuario ha especificado un valor incorrecto, obtendríamos errores en la etapa de inicialización de la clase. De esta forma, la inicialización cuidadosa de la capa interna realizará indirectamente la función de control de los parámetros. Por consiguiente, no realizaremos operaciones innecesarias en esta etapa.

Cabe decir de inmediato que el objeto cHiddenStates se usa solo para el almacenamiento temporal de datos, así que deshabilitaremos a la fuerza la función de activación en él.

A continuación, inicializaremos dos capas de proyección de datos que controlarán la influencia de los datos en el resultado. Primero inicializaremos la capa de proyección del estado oculto.

   if(!cA.Init(0, 1, OpenCL, iWindowHidden, iWindowHidden, iWindowHidden, units_count, 1, optimization, iBatch))
      return false;
   cA.SetActivationFunction(SIGMOID);

Aquí utilizaremos una capa convolucional que nos permitirá realizar proyecciones independientes del estado oculto de cada elemento de la secuencia. Y para regular la influencia de un elemento en el resultado, utilizaremos una sigmoide como función de activación de esta capa. Como ya sabrá, el rango de esta función es [0, 1]. Si es "0" el elemento no tendrá efecto en el resultado general.

Y de forma similar inicializaremos la capa de proyección de los datos de origen.

   if(!cB.Init(0, 2, OpenCL, window, window, iWindowHidden, units_count, 1, optimization, iBatch))
      return false;
   cB.SetActivationFunction(SIGMOID);

Tenga en cuenta que, aunque reciban tensores de diferentes tamaños como entrada, ambas capas de proyección retornarán un tensor del tamaño del estado oculto. Esto se puede ver en el tamaño de la ventana de datos analizados y su paso al inicializar los objetos.

Para obtener la influencia conjunta de los datos de origen y el estado oculto en el resultado, planeamos usar la suma ponderada. Y para reducir el número de operaciones realizadas, hemos decidido combinar este proceso con la proyección de datos a la dimensionalidad requerida de resultados. Por consiguiente, primero concatenaremos los datos en un tensor común a lo largo de las dimensionalidades de los elementos de la secuencia.

   if(!cAB.Init(0, 3, OpenCL, 2 * iWindowHidden * units_count, optimization, iBatch))
      return false;
   cAB.SetActivationFunction(None);

Y luego usaremos otra capa convolucional interna.

   if(!cC.Init(0, 4, OpenCL, 2*iWindowHidden, 2*iWindowHidden, window, units_count, 1, optimization, iBatch))
      return false;
   cC.SetActivationFunction(None);

Al final del método de inicialización, reemplazaremos los punteros a los búferes de gradiente de resultados y errores de nuestra clase con búferes similares de la capa de proyección de resultados interna. Este simple paso nos permitirá eliminar operaciones de copiado de datos innecesarias al realizar las pasadas directa e inversa.

   SetActivationFunction(None);
   if(!SetOutput(cC.getOutput()) || !SetGradient(cC.getGradient()))
      return false;
//---
   return true;
  }

Y por supuesto, no nos olvidaremos de controlar el proceso de realización de las operaciones y, al final del método, retornaremos el valor lógico de las operaciones realizadas al programa que ha realizado la llamada.

Tras completar el proceso de inicialización de la clase, construiremos los algoritmos de pasada directa. Como sabe, implementaremos esta funcionalidad en el método feedForward redefinido. Y aquí todo resultará bastante prosaico y simple.

bool CNeuronSSMOCL::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cA.FeedForward(cHiddenStates.AsObject()))
      return false;
   if(!cB.FeedForward(NeuronOCL))
      return false;

En los parámetros del método obtendremos el puntero al objeto de la capa neuronal anterior, que nos proporcionará los datos de origen.

Y en el cuerpo del método realizaremos directamente dos proyecciones (de los datos iniciales y del estado oculto) a una forma comparable. Para ello, utilizaremos los métodos de pasada directa de las capas convolucionales internas correspondientes.

Luego concatenaremos las proyecciones resultantes en un solo tensor según la dimensionalidad de los elementos de la secuencia.

   if(!Concat(cA.getOutput(), cB.getOutput(), cAB.getOutput(), iWindowHidden, iWindowHidden, 
                                                               cA.Neurons() / iWindowHidden))
      return false;

Y finalmente, proyectaremos la capa concatenada a la dimensionalidad de resultados requerida.

   if(!cC.FeedForward(cAB.AsObject()))
      return false;

Hay dos puntos a tener en cuenta aquí. En primer lugar, no transmitiremos el resultado obtenido al búfer de resultados de la capa actual: hemos logrado eliminar esta operación reemplazando los punteros del búfer de datos.

Y el segundo punto: probablemente haya notado que no hemos actualizado el estado oculto. De esta forma, el método de pasada directa parece incompleto. Pero el problema es que todavía necesitaremos los datos del estado oculto actual para realizar la pasada inversa. Y en este caso, tendrá sentido actualizar el estado oculto durante la pasada inversa, ya que se usa solo en el algoritmo de la capa actual.

Pero la divisa también tiene una desventaja: durante el funcionamiento del modelo no utilizaremos métodos de pasada inversa. Y si trasladamos la actualización del estado oculto a los métodos de pasada inversa, no se actualizará en absoluto durante el funcionamiento del modelo, lo que derrumbará todo el algoritmo.

Por consiguiente, primero verificaremos el modo de funcionamiento actual del modelo y solo si el modelo está en marcha actualizaremos el estado oculto. Para ello, sumaremos y normalizaremos las proyecciones del estado oculto anterior y los datos de origen.

   if(!bTrain)
      if(!SumAndNormilize(cA.getOutput(), cB.getOutput(), cHiddenStates.getOutput(), iWindowHidden, true))
      return false;
//---
   return true;
  }

Ahora nuestro método de pasada directa está completo. Y podremos retornar al programa que realiza la llamada el valor lógico de las operaciones realizadas.

Después de ejecutar el algoritmo de pasada directa, pasaremos a trabajar con métodos de pasada inversa. Como de costumbre, aquí redefiniremos dos métodos:

• calcInputGradients — distribución de gradientes de error;
• updateInputWeights — actualización de los parámetros del modelo.

El algoritmo del método de distribución de gradiente de error repetirá el método de pasada directa en orden inverso. Así que le sugiero que lo lea usted mismo en el archivo adjunto. No obstante, debemos decir algunas palabras sobre el método de actualización de los parámetros del modelo. Aquí es donde hemos sacado la actualización del estado oculto durante el proceso de entrenamiento del modelo.

bool CNeuronSSMOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cA.UpdateInputWeights(cHiddenStates.AsObject()))
      return false;
   if(!SumAndNormilize(cA.getOutput(), cB.getOutput(), cHiddenStates.getOutput(), iWindowHidden, true))
      return false;

Primero ajustaremos los parámetros de la capa de proyección del estado oculto interno. Y sólo entonces actualizaremos los valores de estado ocultos.

Tenga en cuenta que aquí no verificaremos el modo de funcionamiento del modelo, ya que solo será posible llamar a este método durante el entrenamiento.

A continuación, llamaremos a los métodos homónimos de los objetos internos restantes con parámetros entrenables.

   if(!cB.UpdateInputWeights(NeuronOCL))
      return false;
   if(!cC.UpdateInputWeights(cAB.AsObject()))
      return false;
//---
   return true;
  }

Y después de que se completen todas las operaciones del método, devolveremos su resultado lógico al programa que ha realizado la llamada.

Con esto concluiremos nuestra discusión de los métodos de clase para implementar SSM. Podrá familiarizarse con el código completo de todos sus métodos en el archivo adjunto.

2.2 Clase del método Mamba

Arriba hemos implementado una clase para realizar la capa SSM. Y ahora podemos pasar a la implementación del algoritmo de nivel superior del método Mamba. Para implementarlo, crearemos una clase CNeuronMambaOCL, que, al igual que la anterior, heredará la funcionalidad básica de la capa CNeuronBaseOCL totalmente conectada. A continuación, mostraremos la estructura de la nueva clase.

class CNeuronMambaOCL   :  public CNeuronBaseOCL
  {
protected:
   CNeuronConvOCL    cXProject;
   CNeuronConvOCL    cZProject;
   CNeuronConvOCL    cInsideConv;
   CNeuronSSMOCL     cSSM;
   CNeuronBaseOCL    cZSSM;
   CNeuronConvOCL    cOutProject;
   CBufferFloat      Temp;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
   //---

public:
                     CNeuronMambaOCL(void) {};
                    ~CNeuronMambaOCL(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window, uint window_key, uint units_count, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronMambaOCL; }
   //---
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
   virtual void      SetOpenCL(COpenCLMy *obj);
  };

Aquí vemos el conjunto ya familiar de métodos reemplazables y la declaración de capas neuronales internas, con cuya funcionalidad nos familiarizaremos durante la implementación de los métodos de clase.

Sin embargo, aquí no se declarará ninguna variable interna para almacenar las constantes. También hablaremos de las soluciones que nos han permitido abandonar el almacenamiento de constantes durante el proceso de implementación.

Como viene siendo habitual, todos los objetos internos se declararán estáticamente y, por consiguiente, el constructor y el destructor de la clase permanecerán vacíos. Y la inicialización de objetos se realizará en el método Init.

bool CNeuronMambaOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                           uint window, uint window_key, uint units_count, 
                           ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch))
      return false;

Aquí vemos una lista de parámetros similar al método homónimo en la clase CNeuronSSMOCL analizada anteriormente. Es fácil adivinar que tendrán una funcionalidad similar.

En el cuerpo del método, llamaremos inmediatamente al método de inicialización de la clase padre, en el que se realizará el trabajo con los objetos y variables heredados.

Como recordará de la descripción teórica del método Mamba, los datos iniciales aquí pasarán a través de dos flujos paralelos. Y para ambos flujos realizaremos la proyección de datos, que se realizará mediante capas convolucionales.

   if(!cXProject.Init(0, 0, OpenCL, window, window, window_key + 2, units_count, 1, optimization, iBatch))
      return false;
   cXProject.SetActivationFunction(None);
   if(!cZProject.Init(0, 1, OpenCL, window, window, window_key, units_count, 1, optimization, iBatch))
      return false;
   cZProject.SetActivationFunction(SIGMOID);

En la primera secuencia usaremos una capa convolucional y SSM. Y en el segundo, se utilizará la función de activación y se usarán los datos para fusionar los flujos de información. En consecuencia, la salida de las dos flujos deberían ser tensores de un tamaño comparable. Para lograr este resultado, aumentaremos ligeramente el tamaño de la proyección del primer flujo, lo que se compensará con la compresión de datos durante la convolución.

Tenga en cuenta que solo usaremos la función de activación para la segunda proyección del flujo.

El siguiente paso consistirá en inicializar la capa convolucional.

   if(!cInsideConv.Init(0, 2, OpenCL, 3, 1, 1, window_key, units_count, optimization, iBatch))
      return false;
   cInsideConv.SetActivationFunction(SIGMOID);

Aquí realizaremos una convolución independiente dentro de los elementos individuales de la secuencia. Por consiguiente, especificaremos el tamaño del tensor de estado oculto como el número de elementos de convolución. Y luego sumaremos el número de elementos de la secuencia como el número de variables independientes.

El tamaño de la ventana de convolución y su paso se corresponderán con nuestro aumento en la proyección del primer flujo de datos.

Y aquí ya añadiremos la función de activación, que hace que los datos de ambos flujos de información sean comparables.

A continuación vendrá nuestro bloque SSM, que realizará la selección de estado.

   if(!cSSM.Init(0, 3, OpenCL, window_key, window_key, units_count, optimization, iBatch))
      return false;

Al final del algoritmo, para conferir no linealidad a la combinación de los dos flujos de información, como en el caso anterior, concatenaremos la información de los flujos en un solo tensor.

   if(!cZSSM.Init(0, 4, OpenCL, 2 * window_key * units_count, optimization, iBatch))
      return false;
   cZSSM.SetActivationFunction(None);

Y proyectaremos los datos al tamaño requerido dentro de elementos individuales de la secuencia usando una capa convolucional.

   if(!cOutProject.Init(0, 5, OpenCL, 2*window_key, 2*window_key, window, units_count, 1, optimization, iBatch))
      return false;
   cOutProject.SetActivationFunction(None);

Asimismo, añadiremos un búfer para almacenar los resultados intermedios.

   if(!Temp.BufferInit(window * units_count, 0))
      return false;
   if(!Temp.BufferCreate(OpenCL))
      return false;

Y realizaremos la operación de reemplazo de punteros por búferes de datos.

   if(!SetOutput(cOutProject.getOutput()))
      return false;
   if(!SetGradient(cOutProject.getGradient()))
      return false;
   SetActivationFunction(None);
//---
   return true;
  }

Bueno, al final del método retornaremos el resultado lógico de las operaciones realizadas al programa que ha realizado la llamada.

Después de finalizar el método de inicialización de clase, comenzaremos a construir los algoritmos de pasada directa en el método feedForward. El algoritmo del método se anunció parcialmente al crear el método de inicialización. Ahora veremos la implementación del algoritmo en el código.

bool CNeuronMambaOCL::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cXProject.FeedForward(NeuronOCL))
      return false;
   if(!cZProject.FeedForward(NeuronOCL))
      return false;

En los parámetros del método obtendremos el puntero al objeto de la capa anterior, cuyo búfer contendrá nuestros datos iniciales. Y en el cuerpo del método realizaremos directamente la proyección de los datos obtenidos llamando a los métodos de pasada directa de nuestras capas convolucionales de proyección de datos.

En este punto, podemos decir que se habrán completado las operaciones del segundo flujo de información. Pero todavía debemos ejecutar las principales operaciones de flujo de datos. Aquí primero realizaremos la convolución de datos.

   if(!cInsideConv.FeedForward(cXProject.AsObject()))
      return false;

Después de lo cual efectuaremos la selección del estado.

   if(!cSSM.FeedForward(cInsideConv.AsObject()))
      return false;

Ahora que se han realizado las operaciones en ambos flujos de datos, combinaremos los resultados en un solo tensor.

   if(!Concat(cSSM.getOutput(), cZProject.getOutput(), cZSSM.getOutput(), 1, 1, cSSM.Neurons()))
      return false;

Y luego deberemos recordar que no hemos guardado la dimensionalidad del estado interno de un elemento de la secuencia. Ningún problema. Sabemos que los tensores de ambos flujos de información tienen la misma dimensionalidad, y esto significa que si tomamos un elemento de cada tensor secuencialmente, no violaremos la estructura general.

Y ahora todo lo que nos quedará por hacer es proyectar los datos a la dimensionalidad de resultados requerida.

   if(!cOutProject.FeedForward(cZSSM.AsObject()))
      return false;
//---
   return true;
  }

Al final del método, retornaremos el resultado lógico de las operaciones realizadas al programa que ha realizado la llamada.

Como puede ver, el algoritmo del método de pasada directa no resulta particularmente complejo. Lo mismo puede decirse de los métodos de pasada inversa. Así que le propongo no detenernos ahora a analizar sus algoritmos: podrá estudiarlos por cuenta propia. Encontrará el código completo de esta clase y todos sus métodos en el archivo adjunto.

2.3 Arquitectura del modelo

Más arriba hemos implementado nuestra visión de los enfoques propuestos por los autores del método Mamba. Pero el trabajo realizado debe producir resultados. Para evaluar la efectividad de los algoritmos implementados, necesitaremos implementarlos en nuestro modelo. Probablemente se haya imaginado que añadiremos las capas recién creadas al modelo del Codificador del estado del entorno. Después de todo, es precisamente este el modelo que entrenaremos con el paradigma de pronóstico del movimiento de precios posterior.

La arquitectura del modelo indicado se presenta en el método CreateEncoderDescriptions.

bool CreateEncoderDescriptions(CArrayObj *&encoder)
  {
//---
   CLayerDescription *descr;
//---
   if(!encoder)
     {
      encoder = new CArrayObj();
      if(!encoder)
         return false;
     }

En los parámetros del método obtendremos el puntero a un array dinámico en el que deberemos escribir una descripción de la arquitectura del modelo que se está creando.

En el cuerpo del método, verificaremos la relevancia del puntero recibido y, si es necesario, crearemos una nueva instancia del objeto. Con esto finalizaremos nuestro trabajo preparatorio y pasaremos a crear una descripción de la arquitectura del modelo.

La primera capa está diseñada para transferir los datos iniciales al modelo. Aquí, como siempre, utilizaremos una capa completamente conectada de tamaño suficiente.

//--- Encoder
   encoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Normalmente transmitimos los datos iniciales "brutos" al modelo en la forma en que los recibimos del terminal. Es bastante natural que dichos datos se refieran a distribuciones diferentes. Y sabemos que la eficiencia de cualquier modelo aumenta sustancialmente al trabajar con valores comparables en los datos de origen. Para que los diversos datos de origen puedan compararse entre sí, utilizaremos una capa de normalización por lotes.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

A continuación crearemos un bloque de 3 capas del método Mamba con arquitectura idéntica. Para ello, crearemos una descripción de la arquitectura del bloque, tras lo cual la añadiremos al array el número de veces requerido.

   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronMambaOCL;
   descr.window = BarDescr;                                       //window
   descr.window_out = 4 * BarDescr;                               //Inside Dimension
   prev_count = descr.count = HistoryBars;                        //Units
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   for(int i = 2; i <= 4; i++)
      if(!encoder.Add(descr))
        {
         delete descr;
         return false;
        }

Tenga en cuenta que el tamaño de la ventana de datos analizados será igual al número de elementos en la descripción de un elemento de la secuencia, mientras que el tamaño de la representación interna lo haremos 4 veces más grande. Después de todo, en el método Mamba los autores recomiendan implementar una proyección expansiva.

El número de elementos de la secuencia será igual a la profundidad de la historia analizada.

Como hemos dicho durante la implementación de las clases, en esta implementación no asignaremos canales de información separados. Sin embargo, nuestro algoritmo funcionará con elementos independientes de la secuencia. Y si necesitamos analizar canales independientes, podremos pre-transponer los datos y cambiar los parámetros de la capa en consecuencia. Pero esto lo dejaremos para otro experimento.

No obstante, pronosticaremos las secuencias en el contexto de canales independientes. Para ello, añadiremos la transposición de datos después del bloque Mamba.

//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTransposeOCL;
   descr.count = prev_count;
   descr.window = BarDescr;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Y utilizaremos dos capas convolucionales para predecir los valores posteriores de los canales independientes.

//--- layer 6
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = BarDescr;
   descr.window = prev_count;
   descr.window_out = 4 * NForecast;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 7
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = BarDescr;
   descr.window = 4 * NForecast;
   descr.window_out = NForecast;
   descr.activation = TANH;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Después de lo cual retornaremos los valores predichos a la representación original.

//--- layer 8
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTransposeOCL;
   descr.count = BarDescr;
   descr.window = NForecast;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Y les añadiremos las características estadísticas de la distribución de los datos de origen eliminadas durante la normalización.

//--- layer 9
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronRevInDenormOCL;
   descr.count = BarDescr * NForecast;
   descr.activation = None;
   descr.optimization = ADAM;
   descr.layers = 1;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

El toque final de nuestro modelo será hacer coincidir los resultados en el dominio de la frecuencia.

//--- layer 10
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronFreDFOCL;
   descr.window = BarDescr;
   descr.count =  NForecast;
   descr.step = int(true);
   descr.probability = 0.7f;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

La arquitectura de los modelos del Actor y el Crítico permanecerá inalterada. No hay cambios en los programas de interacción con el entorno. Pero necesitábamos hacer algunos ajustes específicos en los programas de entrenamiento de modelos. Después de todo, el uso de un estado oculto en el bloque SSM requiere un cambio en la secuencia de datos de entrada, lo que resulta típico de los modelos recurrentes. Así que realizaremos cambios similares siempre que utilicemos modelos con estados ocultos donde la información se acumula con el tiempo a medida que se ejecuta el modelo. Le sugiero que los mire usted mismo en el archivo adjunto. Permítame recordarle que allí encontrará el código de todos los programas y clases utilizados en la preparación del artículo. Y con esto podemos dar por concluido nuestro análisis de la implementación de los enfoques propuestos y pasar a las pruebas prácticas con datos históricos reales.

3. Simulación

Nuestro trabajo está llegando a su fin, ahora pasaremos a la etapa final: el entrenamiento de los modelos y la prueba de los resultados obtenidos. Entrenaremos los modelos utilizando los datos históricos de 2023 para el instrumento EURUSD y el marco temporal H1. Los parámetros de todos los indicadores se usarán por defecto.

En el primer paso, entrenaremos el modelo del Codificador del estado del entorno en un intento de predecir el movimiento de precios posterior durante un horizonte de planificación determinado. Este modelo analizará únicamente los datos históricos del movimiento de los precios e ignorará por completo las acciones del Actor. Esto nos permitirá entrenar al completo el modelo utilizando los datos de entrenamiento recopilados previamente sin tener que actualizarlo. Sin embargo, dicha actualización podría ser necesaria si el periodo histórico de entrenamiento cambia o aumenta.

Lo primero que podemos destacar es que el modelo ha resultado bastante compacto y rápido. Y el proceso de aprendizaje ha sido relativamente estable y sostenible. No obstante, el modelo ha mostrado resultados interesantes.

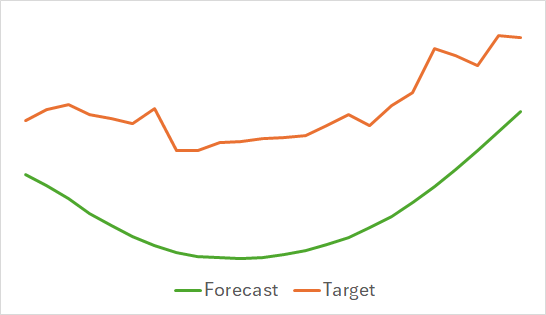
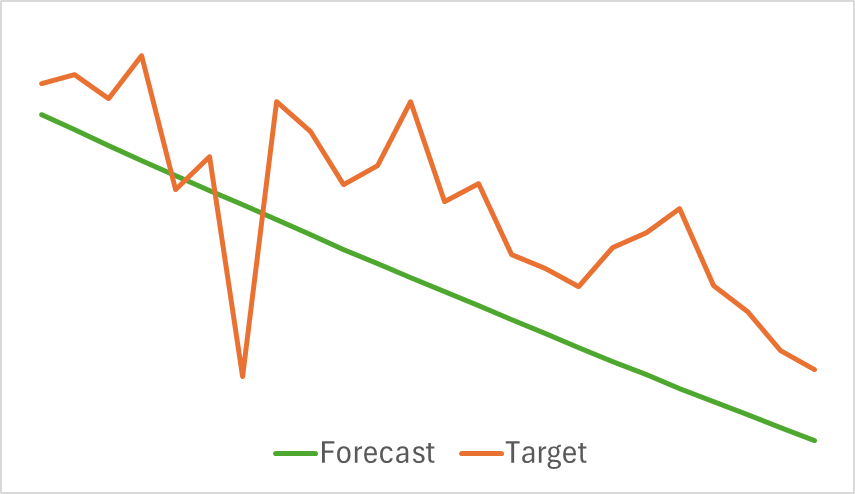
Arriba se muestran los resultados del pronóstico del próximo movimiento de precios para las próximas 24 horas. Podemos observar que la línea de pronóstico en el primer caso describe el punto de cambio de la tendencia con bastante suavidad. Mientras que en el segundo caso indica casi linealmente la tendencia actual.

En la segunda etapa, realizaremos el entrenamiento iterativo de la política del Actor. Y con ello entrenaremos la función de coste del Crítico. El papel del Crítico consiste en ofrecer orientación al Actor para mejorar la eficacia de su política.

Como hemos mencionado antes, la segunda etapa del entrenamiento será iterativa. Y esto significa que durante el entrenamiento de los modelos, actualizaremos periódicamente la muestra de entrenamiento para llenarla con los datos relevantes para la política del Actor actual. El estado actual de la muestra de entrenamiento será la clave para un correcto entrenamiento de los modelos.

Sin embargo, durante el entrenamiento no hemos obtenido una política con una tendencia claramente expresada hacia el crecimiento de los depósitos. Sí, nuestro modelo ha logrado obtener beneficios en el periodo histórico de prueba de enero de 2024, pero no existe una tendencia claramente definida.

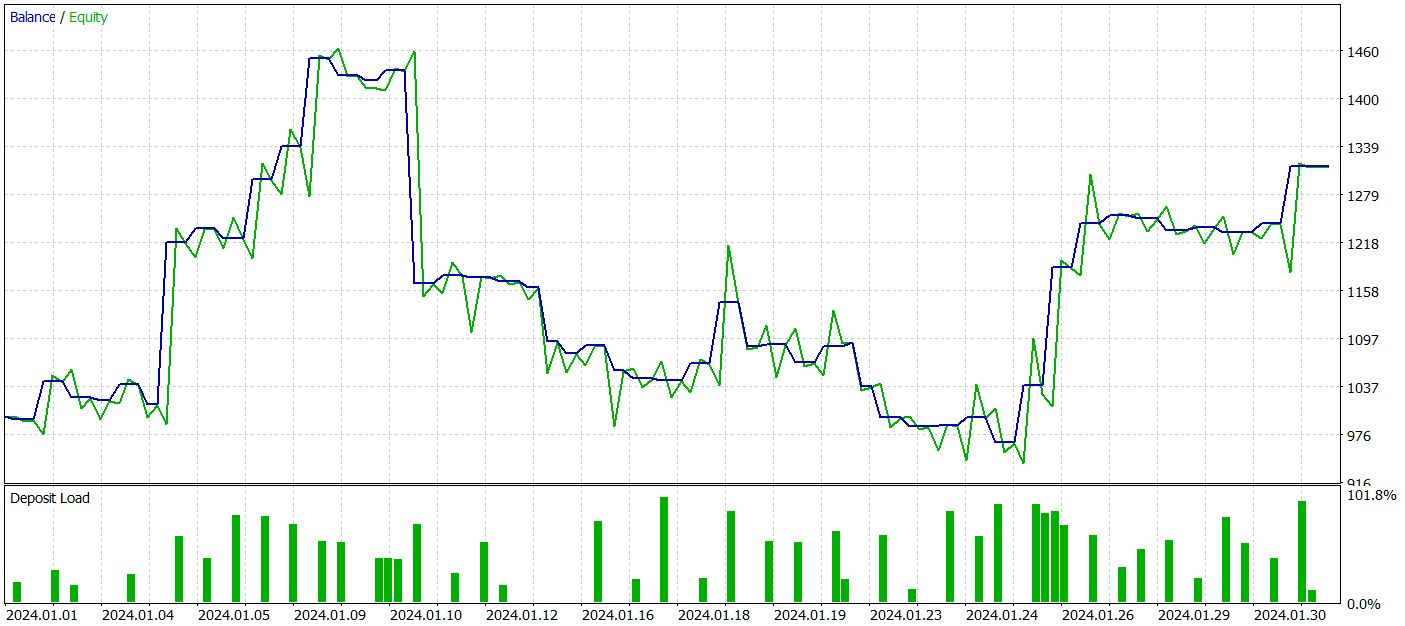
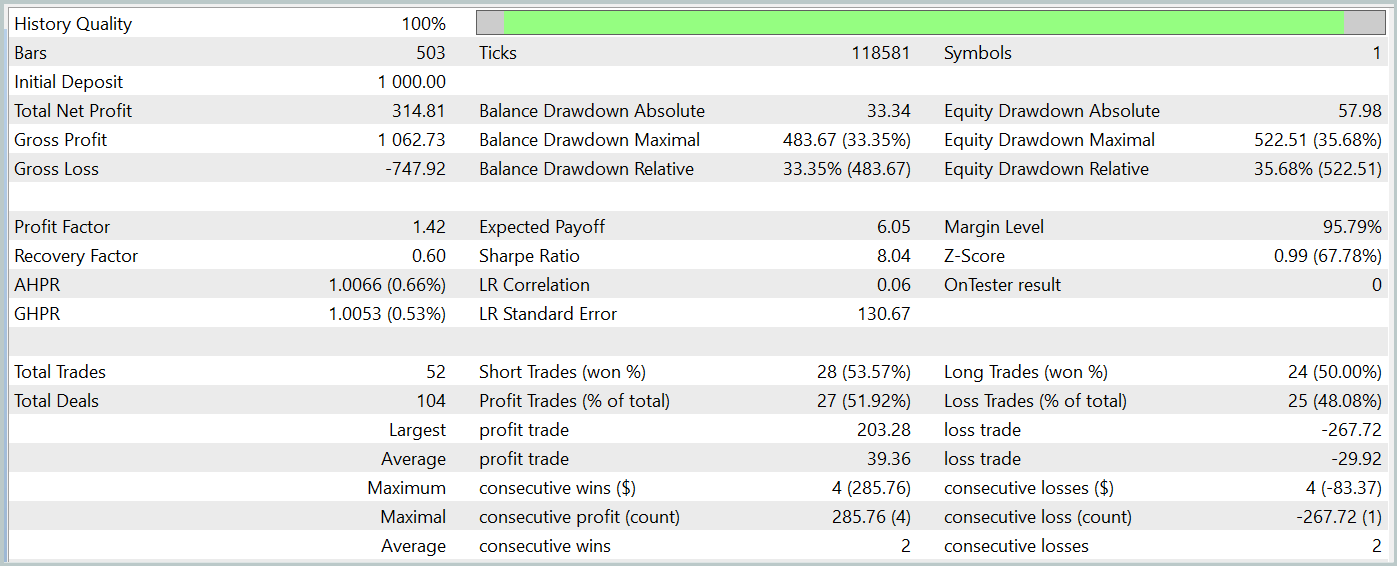
Durante el periodo de prueba, el modelo ha realizado 52 transacciones y 27 de ellas se han cerrado con beneficios, lo que representa casi el 52%. La transacción rentable promedio supera el mismo indicador para las transacciones perdedoras (39,36 frente a -29,82). Sin embargo, la pérdida máxima es un 30% mayor que la transacción rentable máxima. Además, vemos una caída de la equidad de más del 35%. Este modelo claramente requiere más trabajo.

También resultan de interés los gráficos de beneficio y pérdidas por horas y días.

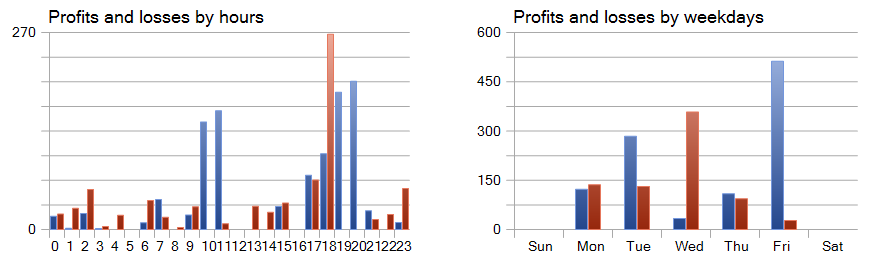
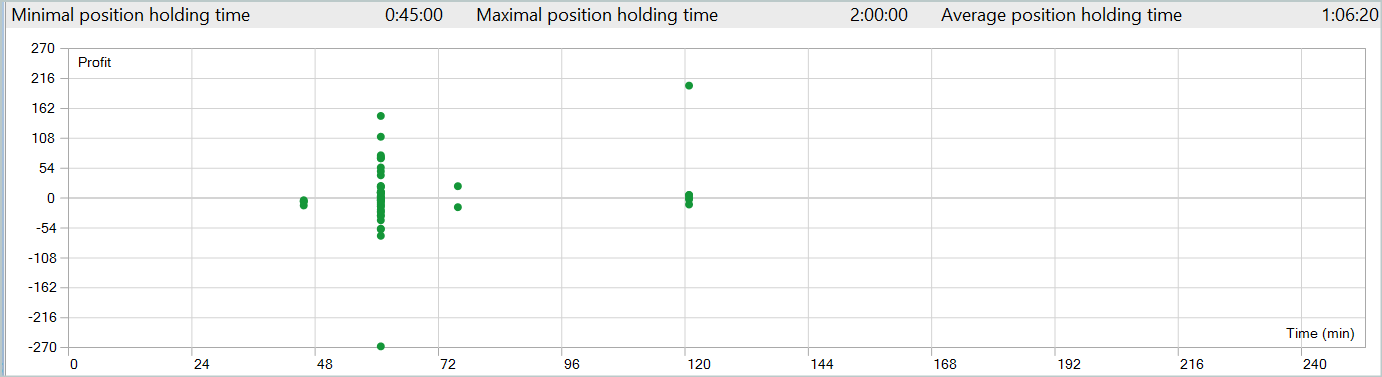
Aquí el viernes destaca como un día muy positivo, mientras que el miércoles, por el contrario, no resulta rentable. También podemos identificar periodos dentro del día con un gran número de transacciones rentables y no rentables. Hay mucho que pensar aquí. Además, la duración media de mantenimiento de la posición es de poco más de una hora, mientras que la máxima es de 2 horas.

Conclusión

En este artículo, hemos presentado un nuevo método de pronóstico de series temporales, Mamba, que ofrece una alternativa eficiente y de alto rendimiento a las arquitecturas tradicionales como la del Transformer. Gracias a la integración de los modelos del espacio de estados muestreados (SSM), Mamba logra un alto rendimiento y un escalamiento lineal en la longitud de la secuencia.

En la parte práctica de nuestro artículo, hemos implementado nuestra visión de los enfoques propuestos utilizando MQL5. Asimismo, hemos entrenado los modelos con datos reales y hemos obtenido resultados discutibles.

Enlaces

• Mamba: Linear-Time Sequence Modeling with Selective State Spaces
• Otros artículos de la serie

Programas usados en el artículo

#	Nombre	Tipo	Descripción
1	Research.mq5	Asesor	Asesor de recopilación de datos
2	ResearchRealORL.mq5	Asesor	Asesor de recopilación de ejemplos con el método Real-ORL
3	Study.mq5	Asesor	Asesor de entrenamiento de Modelos
4	StudyEncoder.mq5	Asesor	Asesor de entrenamiento del Codificador
5	Test.mq5	Asesor	Asesor para la prueba de modelos
6	Trajectory.mqh	Biblioteca de clases	Estructura de descripción del estado del sistema.
7	NeuroNet.mqh	Biblioteca de clases	Biblioteca de clases para crear una red neuronal
8	NeuroNet.cl	Biblioteca	Biblioteca de código de programa OpenCL