MetaTrader 5 / トレーディングシステム
English Русский Deutsch Português
preview
ニューラルネットワークが簡単に（第83回）：「Conformer」Spatio-Temporal Continuous Attention Transformerアルゴリズム

ニューラルネットワークが簡単に（第83回）：「Conformer」Spatio-Temporal Continuous Attention Transformerアルゴリズム

MetaTrader 5 — トレーディングシステム | 11 9月 2024, 10:13
59 0
Dmitriy Gizlyk
Dmitriy Gizlyk

はじめに

金融市場の予測の難しさは、天候の変動性に例えることができるかもしれません。人類は天気予報の分野で多くの成果を上げてきており、今日の気象予報は非常に信頼性が高くなっています。では、その技術を金融市場の「天気」を予測するために活用できるのでしょうか。本稿では、天気予報を目的として開発され、論文「Conformer: Embedding Continuous Attention in Vision Transformer for Weather Forecasting」で発表された、Spatio-Temporal Continuous Attention Transformerの複雑なアルゴリズムについて解説します。この手法では、Continuous Attentionアルゴリズムを提案し、前回のニューラルODE記事で説明したアルゴリズムと組み合わせています。


1. Conformerアルゴリズム

Conformerは、Multi-head Attentionメカニズムに連続性を持たせることで、時間の経過に伴う連続的な天候の変化を研究するように設計されています。AAttentionメカニズムは、Transformerアーキテクチャの微分可能な関数としてエンコードされ、複雑な気象ダイナミクスのモデル化を可能にしています。

当初、この手法の著者は、(XN*W*H, T)の形式で気象データを入力とするモデルの構築という課題に直面しました。ここでNは、気温、風速、気圧などの気象変数の数を表し、W*Hは変数の空間分解能を示します。Tはシステムが進展する時間軸です。このモデルは、時間tにおける気象変数を受け取り、時空間システムの進化を解析し、次の時間ステップt+1での気象を予測します。

天候は時間とともに常に変化するため、データにおける一定期間の連続的な変化を記録することが重要です。そこで、微分方程式ソルバーを用いて気象データの連続的な潜在表現を学習するアイデアが提案されています。これにより、このモデルは単に時刻Tにおける気象変数の値を予測するだけでなく、定積分を通じて、最初の時刻から時刻Tまでの気温などの気象変数の変化も分析します。システムは次のように表すことができます。

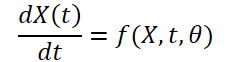
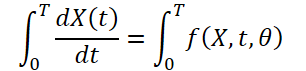
気象情報は変動が激しく、時間的にも空間的にも予測が困難です。各気象変数の時間微分を計算することで、気象ダイナミクスを保持し、離散データからより良い特徴を抽出することができます。この手法の著者は、気象現象の連続的な時間変化を捉えるために、画素レベルで選択的な微分をおこなっています。

微分の正規化は、ディープラーニングモデルの動作の安定性を確保するために最も重要なステップの1つです。この手法の著者は、正規化の考え方をモデルアーキテクチャの別個の要素として拡張し、微分に直接適用する場合の正規化の役割を探求しています。この論文では、最も一般的な2つの正規化方法と事前微分層がモデルの性能に与える影響を検討し、連続系におけるそれらの利点を実証しています。

Attentionは、Transformerアーキテクチャの重要な構成要素の1つであり、予測の最終段階でソースデータの最も重要なブロックを特定するという考えに基づいています。Transformerは様々な問題を解決することに成功していますが、天気予報のような非常に動的なシステムに対する情報埋め込みを学習する能力にはまだ限界があります。そこで、Conformer法の著者は、気象変数の連続的な変化をモデル化するためにContinuous Attentionメカニズムを開発しました。まず、初期状態の要素間の依存関係の分析を、異なる環境状態の対応するパラメータ間のAttentionに置き換えます。これにより、時変気象変数ごとの文脈埋め込み空間の計算が可能になります。このステップにより、モデルは同じ環境状態のブロックにアクセスするのではなく、異なる状態の同じ変数を一括して処理することができます。変数変換は、単一環境状態でおこなわれる方法と同様に、ソースデータサンプルごとに各変数に独自のQuery、Key、Valueを割り当てることで学習されます。Attentionメカニズムは、異なるサンプル（同じ変数位置）の変数間の依存性推定値を計算します。従来のAttentionメカニズムと同様に、異なるバッチに対して学習された依存性の重みは、それらの変数に関連する情報を集約または重み付けするために使用されます。

この修正により、異なる環境状態における同じ気象変数間の関係や依存関係を捉えることができます。これは、モデルが各気象変数の連続的に変化する特性を表現できる気象予報シナリオにおいて有用であることが証明されています。継続的な学習を保証するために、このメソッドの著者は、Continuous Attentionメカニズムに微分を導入しています。微分方程式は、時間経過に伴う物理システムのダイナミクスを表し、データの欠損値を考慮します。この手法の作者は、Attentionメカニズムと微分方程式学習パラダイムを組み合わせ、空間的時間的特性における大気の変化をモデル化しました。さらに、このアプローチは、複雑な物理方程式をモデル化することに関連する制限を取り除きます。Conformerは、あるタイムスタンプに対してのみ予測予測をおこなうのではなく、あるタイムステップから別のタイムステップへの過渡的な変化を学習します。

Continuous Attentionを計算するために、この方法の著者は、各データサンプルの同じ変数について類似度の微分を計算することを提案しています。ここで、サイズ(N*W*H)の2つの入力サンプルを考え、時刻t0のサンプルをX0、t1のサンプルをX1とします。各変数について、両サンプルにはそれぞれテンソルQ、K、V対応します。Continuous Attentionは以下のように計算されます。

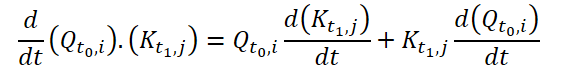
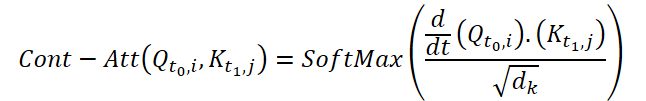
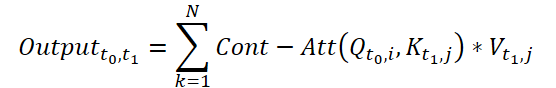
得られる結果は、ある時点t0とt1における入力データの類似した変数の値のAttention加重和です。このプロセスでは、すべての時間ステップにわたって入力データの類似変数間のAttentionを計算し、入力サンプルのシーケンス全体にわたって変数間の関係や相互作用を捉えることができます。


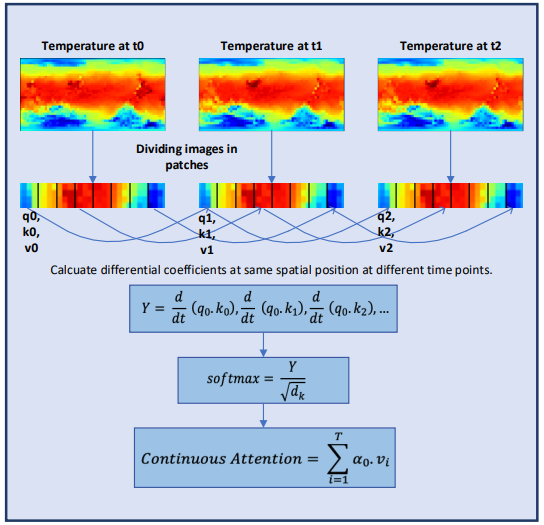
気象情報の連続的な特性をさらに調査するために、Conformerの著者はニューラルODEモデルに層を追加しました。アダプティブサイズソルバーは固定サイズソルバーよりも高い精度を提供するため、この手法の作者はドルマン＝プリンス法(Dopri5)を選択しました。これにより、時間の経過に伴う気象の微細な変化を詳細に研究することができます。ConformerとニューラルODE層の配置を含む完全なワークフローは、以下の図に示された筆者による手法の視覚化で確認できます。



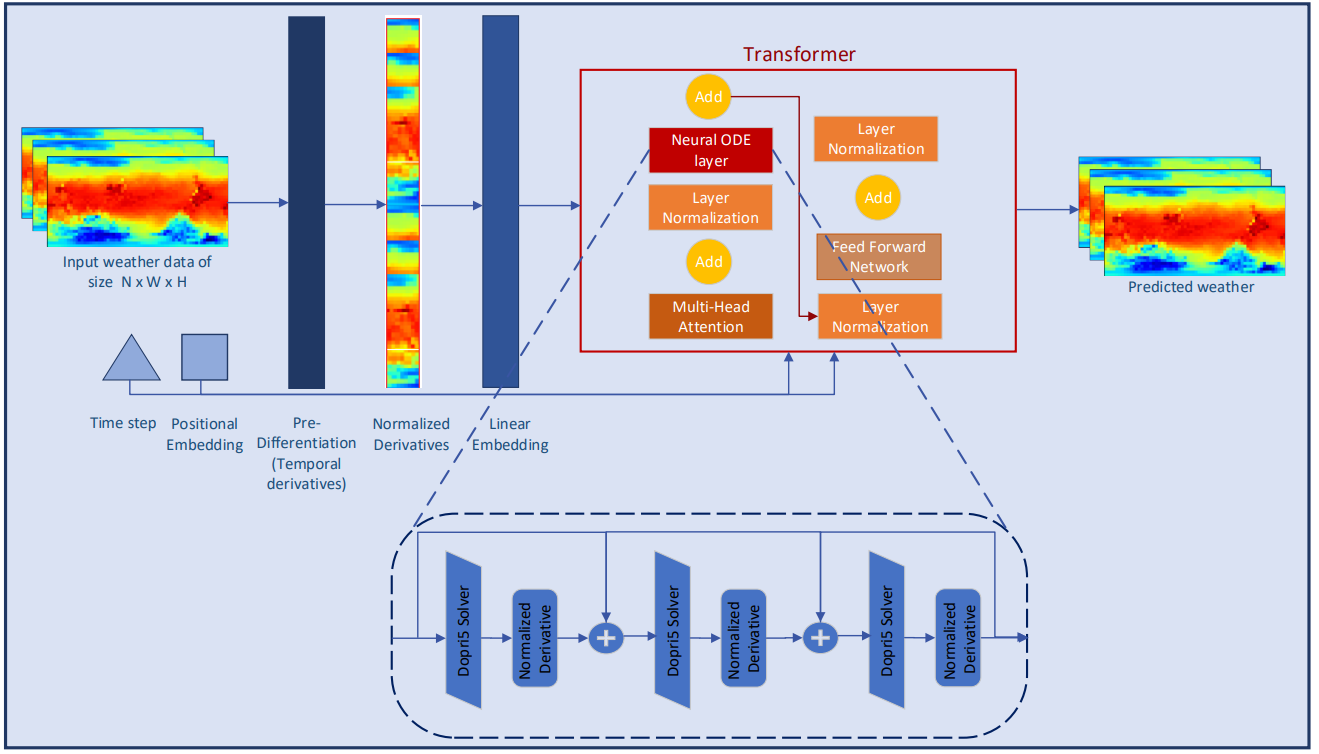
2. MQL5での実装

Conformer法の理論的側面を確認した後で、MQL5を用いた提案アプローチの実用的な実装に移ります。主な機能は新しいクラスCNeuronConformerに実装し、ニューラル層基本クラスCNeuronBaseOCLから派生させます。

2.1 CNeuronConformerクラスのアーキテクチャ

CNeuronConformerのクラス構造では、Attentionメソッドを実装するすべてのクラスで再定義されるおなじみのメソッドがすでに見られます。しかし、Continuous Attentionは、これまで考えられてきたAttention法とは大きく異なるため、アルゴリズムをゼロから実装することにしました。とはいえ、この実装では、過去の作品からの発展が使用されます。

層アーキテクチャの主要なパラメータを書くために、5つの変数を導入します。

  • iWindow：初期データテンソルの1つのパラメータを記述するベクトルのサイズ
  • iDimension：1つのQuery、Key、Valueエンティティのベクトルの次元
  • iHeads：Attention Headの数
  • iVariables：環境の1つの状態を記述するパラメータの数
  • iCount：環境の分析された状態の数（初期データのシーケンスの長さ）

Query、Key、Valueエンティティの生成には、これまでと同様、畳み込み層cQKVを使用します。このアプローチにより、3つのエンティティをすべて並行して実装することができます。ここでは、基本ニューラル層cdQKVにおけるエンティティの経時微分を記述します。

依存係数は、ネイティブのTransformerアルゴリズムと同様に、Score行列に保存されます。しかし今回の実装では、メインプログラム側に行列のコピーを作成しません。OpenCLコンテキストのバッファのみを作成します。CNeuronConformerクラスのローカル変数iScoreにバッファへのポインタを保存します。

Multi-head Attentionの結果は、基本ニューラル層のAttentionOutバッファに保存されます。畳み込み層cW0を使って、得られたデータの次元を減らします。

Conformerアルゴリズムによれば、Attentionブロックの後に、常微分方程式のニューラル層のブロックが続きます。そのためにcNODE配列を作成します。同様に、フィードフォワードブロックでは、cFF配列を作成します。

    class CNeuronConformer  :  public CNeuronBaseOCL
  {
protected:
   //---
   int               iWindow;
   int               iDimension;
   int               iHeads;
   int               iVariables;
   int               iCount;
   //---
   CNeuronConvOCL    cQKV;
   CNeuronBaseOCL    cdQKV;
   int               iScore;
   CNeuronBaseOCL    cAttentionOut;
   CNeuronConvOCL    cW0;
   CNeuronNODEOCL    cNODE[3];
   CNeuronConvOCL    cFF[2];
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   virtual bool      attentionOut(void);
   //---
   virtual bool      AttentionInsideGradients(void);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL);

public:
                     CNeuronConformer(void) {};
                    ~CNeuronConformer(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key, uint heads,
                          uint variables, uint units_count,
                          ENUM_OPTIMIZATION optimization_type,
                          uint batch);
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *prevLayer);
   //---
   virtual int       Type(void)   const   {  return defNeuronConformerOCL;   }
   //--- methods for working with files
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   //---
   virtual void      SetOpenCL(COpenCLMy *obj);
   virtual CLayerDescription* GetLayerInfo(void);
  };

    クラスの内部オブジェクトはすべてstaticとして宣言されています。これにより、クラスのコンストラクタとデストラクタを空のままにすることができます。ユーザー要件に従ったクラスオブジェクトの初期化は、Initメソッドで実装されます。メソッドのパラメータには、オブジェクトアーキテクチャの主要なパラメータを渡します。

    bool CNeuronConformer::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                            uint window, uint window_key, uint heads,
                            uint variables, uint units_count,
                            ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * variables * units_count, 
                                                                  optimization_type, batch))
      return false;

    メソッド本体では、親クラスの関連するメソッドを呼び出します。このメソッドは、受け取ったパラメータの最低限必要な制御と、継承されたオブジェクトの初期化を実装しています。メソッドが返す論理的な結果から、コントロールや初期化の結果を確認することができます。

    次に、内部層cQKVを初期化します。この層はQuery、Key、Valueエンティティを生成します。Conformerメソッドでは、エンティティは個々の変数ごとに作成されます。したがって、ウィンドウサイズと畳み込みステップは、1変数の埋め込みベクトルの長さに等しくなります。畳み込み要素の数は、環境の1つの状態を記述する変数の数と、分析されるそのような状態の数との積に等しくなります。畳み込みフィルタの数は、1つのエンティティの長さとAttention Headの数の3倍に等しくなります。

       if(!cQKV.Init(0, 0, OpenCL, window, window, 3 * window_key * heads, variables * units_count,
                                                                         optimization, iBatch))
      return false;

    上記の2つのメソッドが成功したら、受け取ったパラメータを内部変数に保存します。

       iWindow = int(fmax(window, 1));
   iDimension = int(fmax(window_key, 1));
   iHeads = int(fmax(heads, 1));
   iVariables = int(fmax(variables, 1));
   iCount = int(fmax(units_count, 1));

    内部層を初期化し、時間とともに偏微分を書くようにします。

       if(!cdQKV.Init(0, 1, OpenCL, 3 * iDimension * iHeads * iVariables * iCount, optimization, 
                                                                                     iBatch))
      return false;

    Attention係数のバッファを作ります。

       iScore = OpenCL.AddBuffer(sizeof(float) * iCount * iHeads * iVariables * iCount,
                                                                          CL_MEM_READ_WRITE);
   if(iScore < 0)
      return false;

    内部層AttentionOutとcW0を初期化することで、Attentionブロックのオブジェクトの準備が完了します。

       if(!cAttentionOut.Init(0, 2, OpenCL, iDimension * iHeads * iVariables * iCount,
                                                                        optimization, iBatch))
      return false;
   if(!cW0.Init(0, 3, OpenCL, iDimension * iHeads, iDimension * iHeads, iWindow, 
                                                   iVariables * iCount, optimization, iBatch))
      return false;

    Attentionブロックの出力は、受信したソースデータの次元と一致するデータ次元を持たなければならないことに注意してください。さらに、Conformerアルゴリズムには、1つの変数内の依存関係の分析も含まれますが、環境の状態が異なるため、個々の変数の枠組みでの次元削減も実施します。

    常微分方程式のニューラル層はすべて同じアーキテクチャです。これにより、ループの中で初期化することができます。

       for(int i = 0; i < 3; i++)
      if(!cNODE[i].Init(0, 4 + i, OpenCL, iWindow, iVariables, iCount, optimization, iBatch))
         return false;

    つまり、あとはFeedForwardブロックオブジェクトを初期化するだけです。

       if(!cFF[0].Init(0, 7, OpenCL, iWindow, iWindow, 4 * iWindow, iVariables * iCount, 
                                                                   optimization, iBatch))
      return false;
   if(!cFF[1].Init(0, 8, OpenCL, 4 * iWindow, 4 * iWindow, iWindow, iVariables * iCount,
                                                                   optimization, iBatch))
      return false;

    メソッドが完了する前に、クラスの勾配バッファポインタをFeedForwardブロックの最後の層の勾配バッファに置き換えます。このテクニックを使えば、不必要なデータのコピーを避けることができます。これは、他の多くのメソッドの実装でも何度も使ってきました。

       if(getGradientIndex() != cFF[1].getGradientIndex())
      SetGradientIndex(cFF[1].getGradientIndex());
//---
   return true;
  }

    2.2 フィードフォワードパスの実装

    クラスインスタンスを初期化した後、フィードフォワードアルゴリズムの実装に進みます。Conformer法の著者が提案したContinuous Attentionアルゴリズムに注目してみましょう。これは、QueryとKeyのエンティティの時間的な偏微分を使用します。

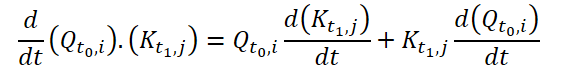
    明らかに、モデル訓練の段階では、これらのエンティティの時間依存性の関数の最も近い近似以上のものは持っていません。そこで、微分の定義という問題に、別の角度からアプローチすることにします。まず、関数の微分の幾何学的な意味を思い出してみましょう。これは、ある関数の、ある点における引数に関する微分は、その点における関数のグラフの接線の傾斜角である、というものです。これは、引数が1だけ変化したときの関数の値のおおよその（または一次関数の場合は正確な）変化を示しています。

    入力データでは、分析時間枠に等しい一定の時間ステップで環境の状態を得ます。実装を簡単にするため、特定の時間枠を無視し、後続の2つの状態間の時間ステップを1に設定します。したがって、前の状態から現在の状態への遷移と、現在の状態から次の状態への遷移の2回にわたる関数の値の変化の平均をとることによって、関数の微分の近似値を解析的に求めることができます。

    提案するメカニズムをOpenCLのコンテキストサイドのTimeDerivativeカーネルに実装します。カーネルのパラメータには、入力データと結果の2つのバッファへのポインタを渡します。また、1つのエンティティの次元も渡します。

    __kernel void TimeDerivative(__global float *qkv, __global float *dqkv,
                             int dimension)
  {
   const size_t pos = get_global_id(0);
   const size_t variable = get_global_id(1);
   const size_t head = get_global_id(2);
   const size_t total = get_global_size(0);
   const size_t variables = get_global_size(1);
   const size_t heads = get_global_size(2);

    カーネルは3次元で立ち上げる予定です。

    • 分析した環境状態の数
    • 環境の1つの状態を表す変数の数
    • Attention Headの数

    カーネル本体では、3次元すべてにおいて現在のスレッドを即座に特定します。その後、処理中のエンティティに対するバッファのシフトを決定します。便宜上、元データと結果には同じサイズのバッファを使用します。したがって、シフトは同じになります。

       const int shift = 3 * heads * variables * dimension;
   const int shift_query = pos * shift + (3 * variable * heads + head) * dimension;
   const int shift_key = shift_query + heads * dimension;

    次に、1つのエンティティの全要素を通るループの中で、偏差の計算を整理します。まず、Queryの微分を解析的に決定します。

       for(int i = 0; i < dimension; i++)
     {
      //--- dQ/dt
        {
         int count = 0;
         float delta = 0;
         float value = qkv[shift_query + i];
         if(pos > 0)
           {
            delta = value - qkv[shift_query + i - shift];
            count++;
           }
         if(pos < (total - 1))
           {
            delta += qkv[shift_query + i + shift] - value;
            count++;
           }
         if(count > 0)
            dqkv[shift_query + i] = delta / count;
        }

    ここでは、シーケンスの最初と最後の要素の特殊なケースに注意する必要があります。これらの状態では、トランジションは1つしかありません。アルゴリズムを複雑にせず、利用可能なデータのみを使用します。

    同様に、Keyについても微分を計算します。

          //--- dK/dt
        {
         int count = 0;
         float delta = 0;
         float value = qkv[shift_key + i];
         if(pos > 0)
           {
            delta = value - qkv[shift_key + i - shift];
            count++;
           }
         if(pos < (total - 1))
           {
            delta += qkv[shift_key + i + shift] - value;
            count++;
           }
         if(count > 0)
            dqkv[shift_key + i] = delta / count;
        }
     }
  }

    時間に関する偏微分を決定した後、Continuous Attentionを実行するために必要なすべてのデータを手に入れました。OpenCLコンテキスト側では、提案アルゴリズムをFeedForwardContAttカーネルに実装します。カーネルパラメータには、4つのデータバッファへのポインタを渡します。初期データ（エンティティとその微分）のバッファ2個、依存係数の行列のバッファ1個、Multi-head Attentionの結果のバッファ1個です。さらに、カーネルパラメータに2つの定数（1つのエンティティのベクトルの次元とAttention Headの数）を渡します。

    __kernel void FeedForwardContAtt(__global float *qkv, __global float *dqkv,
                                 __global float *score, __global float *out,
                                 int dimension,
                                 int heads)
  {
   const size_t query = get_global_id(0);
   const size_t key = get_global_id(1);
   const size_t variable = get_global_id(2);
   const size_t queris = get_global_size(0);
   const size_t keis = get_global_size(1);
   const size_t variables = get_global_size(2);

    カーネル本体では、いつものように、まずタスク空間のすべての次元で現在のスレッドを特定します。この場合、3次元のタスク空間を使用します。ローカルグループは、1つの変数に対する1つのリクエスト内で作成されます。

    ここでは、中間データ用のローカル配列も宣言しています。

       const uint ls_score = min((uint)keis, (uint)LOCAL_ARRAY_SIZE);
   __local float local_score[LOCAL_ARRAY_SIZE];

    次に、Attention Headの数に応じて反復するループを実行します。ループ本体では、すべてのAttention Headのデータ解析を順次おこないます。

       for(int head = 0; head < heads; head++)
     {
      const int shift = 3 * heads * variables * dimension;
      const int shift_query = query * shift + (3 * variable * heads + head) * dimension;
      const int shift_key = key * shift + (3 * variable * heads + heads + head) * dimension;
      const int shift_out = dimension * (heads * (query * variables + variable) + head);
      int shift_score = keis * (heads * (query * variables + variable) + head) + key;

    ここではまず、必要な要素へのデータバッファのシフトを決定します。その後、依存係数を計算します。これらの係数は3段階で決定されます。まず、指数値d/dt(QK)を計算し、依存係数バッファの対応する要素に保存します。計算は1つのワーキンググループの並列スレッドでおこなわれます。

          //--- Score
      float scr = 0;
      for(int d = 0; d < dimension; d++)
         scr += qkv[shift_query + d] * dqkv[shift_key + d] +
                qkv[shift_key + d] * dqkv[shift_query + d];
      scr = exp(min(scr / sqrt((float)dimension), 30.0f));
      score[shift_score] = scr;
      barrier(CLK_LOCAL_MEM_FENCE);

    2番目のステップでは、得られたすべての値の合計を収集します。

          if(key < ls_score)
        {
         local_score[key] = scr;
         for(int k = ls_score + key; k < keis; k += ls_score)
            local_score[key] += score[shift_score + k];
        }
      barrier(CLK_LOCAL_MEM_FENCE);
      //---
      int count = ls_score;
      do
        {
         count = (count + 1) / 2;
         if(key < count)
           {
            if((key + count) < keis)
              {
               local_score[key] += local_score[key + count];
               local_score[key + count] = 0;
              }
           }
         barrier(CLK_LOCAL_MEM_FENCE);
        }
      while(count > 1);

    3番目のステップでは、依存係数を正規化します。

          score[shift_score] /= local_score[0];
      barrier(CLK_LOCAL_MEM_FENCE);

    ループの反復が終わったら、上で定義した依存係数に従って、Attentionブロックの結果の値を計算します。

          shift_score -= key;
      for(int d = key; d < dimension; d += keis)
        {
         float sum = 0;
         int shift_value = (3 * variable * heads + 2 * heads + head) * dimension + d;
         for(int v = 0; v < keis; v++)
            sum += qkv[shift_value + v * shift] * score[shift_score + v];
         out[shift_out + d] = sum;
        }
      barrier(CLK_LOCAL_MEM_FENCE);
     }
//---
  }

    OpenCLコンテキスト側でContinuous Attentionアルゴリズムを実装するためのカーネルを作成したら、メインプログラムから上記で作成したカーネルの呼び出しを実装する必要があります。そのために、CNeuronConformerクラスにattentionOutメソッドを追加します。

    カーネル呼び出しは並行して呼び出されるため、別々のメソッドに分割しません。ただし、タスク空間の違いから、OpenCLプログラム側でアルゴリズムを分割しました。 

    このメソッドはクラス内で呼び出すためだけに作られるため、そのアルゴリズムは内部オブジェクトと変数の使用に完全に基づいています。これにより、メソッドのパラメータを完全に排除することが可能になりました。

    bool CNeuronConformer::attentionOut(void)
  {
   if(!OpenCL)
      return false;

    メソッド本体では、OpenCLコンテキストへのポインタの妥当性を確認します。その後、派生エンティティを定義するための最初のカーネルを呼び出す準備をします。

    まず、タスク空間を定義します。

    bool CNeuronConformer::attentionOut(void)
  {
   if(!OpenCL)
      return false;
//--- Time Derivative
     {
      uint global_work_offset[3] = {0, 0, 0};
      uint global_work_size[3] = {iCount, iVariables, iHeads};

    そして、パラメータをカーネルに渡します。

          ResetLastError();
      if(!OpenCL.SetArgumentBuffer(def_k_TimeDerivative, def_k_tdqkv, cQKV.getOutputIndex()))
        {
         printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, 
                                                                   GetLastError(), __LINE__);
         return false;
        }
      if(!OpenCL.SetArgumentBuffer(def_k_TimeDerivative, def_k_tddqkv, cdQKV.getOutputIndex()))
        {
         printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__,
                                                                    GetLastError(), __LINE__);
         return false;
        }
      if(!OpenCL.SetArgument(def_k_TimeDerivative, def_k_tddimension, int(iDimension)))
        {
         printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, 
                                                                    GetLastError(), __LINE__);
         return false;
        }

    カーネルを実行キューに入れます。

          if(!OpenCL.Execute(def_k_TimeDerivative, 3, global_work_offset, global_work_size))
        {
         printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError());
         return false;
        }
     }

    2番目のカーネルを実行キューに入れる一般的なアルゴリズムも同様です。しかし今回は、ワークグループのタスクスペースを追加します。

    //--- MH Attention Out
     {
      uint global_work_offset[3] = {0, 0, 0};
      uint global_work_size[3] = {iCount, iCount, iVariables};
      uint local_work_size[3] = {1, iCount, 1};

    さらに、転送されるパラメータの数も増えます。

          ResetLastError();
      if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardContAtt, def_k_caqkv,
                                                                       cQKV.getOutputIndex()))
        {
         printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__,
                                                                     GetLastError(), __LINE__);
         return false;
        }
      if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardContAtt, def_k_cadqkv, 
                                                                       cdQKV.getOutputIndex()))
        {
         printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__,
                                                                     GetLastError(), __LINE__);
         return false;
        }
      if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardContAtt, def_k_cascore, iScore))
        {
         printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__,
                                                                     GetLastError(), __LINE__);
         return false;
        }
      if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardContAtt, def_k_caout, 
                                                               cAttentionOut.getOutputIndex()))
        {
         printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, 
                                                                     GetLastError(), __LINE__);
         return false;
        }
      if(!OpenCL.SetArgument(def_k_FeedForwardContAtt, def_k_cadimension, int(iDimension)))
        {
         printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, 
                                                                     GetLastError(), __LINE__);
         return false;
        }
      if(!OpenCL.SetArgument(def_k_FeedForwardContAtt, def_k_caheads, int(iHeads)))
        {
         printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, 
                                                                     GetLastError(), __LINE__);
         return false;
        }

    準備作業が終わったら、カーネルを実行キューに入れます。

          if(!OpenCL.Execute(def_k_FeedForwardContAtt, 3, global_work_offset, global_work_size, 
                                                                          local_work_size))
        {
         printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError());
         return false;
        }
     }
//---
   return true;
  }

    しかし、2つのカーネルを呼び出すことは、提案されているConformer法の一部しか実装していません。これがメインとなるContinuous Attention部分です。CNeuronConformer::feedForwardメソッドで、このクラスのフィードフォワードパスの完全なアルゴリズムを説明します。先に作成したクラスの関連メソッドと同様に、feedForwardメソッドは、このクラスの入力データを含む前の層オブジェクトへのポインタをパラメータとして受け取ります。

    bool CNeuronConformer::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
//--- Generate Query, Key, Value
   if(!cQKV.FeedForward(NeuronOCL))
      return false;

    メソッド本体では、まず内部層cQKVのフィードフォワードメソッドを呼び出して、Query、Key、Valueエンティティテンソルを形成します。その後、上記で作成したメソッドを呼び出し、Continuous Attentionメカニズムのカーネルを呼び出します。

    //--- MH Continuas Attention
   if(!attentionOut())
      return false;

    次に、得られたMulti-Head Attentionの結果の次元を小さくします。得られたテンソルを入力データに加え、個々の変数内で正規化します。

       if(!cW0.FeedForward(GetPointer(cAttentionOut)))
      return false;
   if(!SumAndNormilize(NeuronOCL.getOutput(), cW0.getOutput(), cW0.getOutput(), iDimension,
                                                                            true, 0, 0, 0, 1))
      return false;

    Conformerアルゴリズムに従ったContinuous Attentionブロックに続いて、常微分方程式ソルバーのブロックが続きます。それらの呼び出しをループで実装します。その後、ブロックの入力と出力のテンソルを合計し、結果を正規化します。

    //--- Neural ODE
   CNeuronBaseOCL *prev = GetPointer(cW0);
   for(int i = 0; i < 3; i++)
     {
      if(!cNODE[i].FeedForward(prev))
         return false;
      prev = GetPointer(cNODE[i]);
     }
   if(!SumAndNormilize(prev.getOutput(), cW0.getOutput(), prev.getOutput(), iDimension,
                                                                             true, 0, 0, 0, 1))
      return false;

    フィードフォワードメソッドの最後に、FeedForwardブロックのフィードフォワードパスを実行し、その結果を合計して正規化します。

    //--- Feed Forward
   for(int i = 0; i < 2; i++)
     {
      if(!cFF[i].FeedForward(prev))
         return false;
      prev = GetPointer(cFF[i]);
     }
   if(!SumAndNormilize(prev.getOutput(), cNODE[2].getOutput(), getOutput(), iDimension,
                                                                             true, 0, 0, 0, 1))
      return false;
//---
   return true;
  }

    フィードフォワードアルゴリズムの実装に関する研究はこれで完了しました。しかし、モデルを訓練するためには、バックプロパゲーションパスを実装し、最終結果に対する影響力に応じてすべての要素に誤差勾配を伝播させ、モデルの全体的な誤差を減らすためにモデルのパラメータを調整する必要もあります。

    2.3 バックプロパゲーションパスの整理

    バックプロパゲーションアルゴリズムを実装するには、新しいカーネルを作る必要もあります。まず最初に、Continuous AttentionのHiddenGradientContAttブロックを通して誤差勾配を伝播させるカーネルを作成する必要があります。カーネルパラメータには、6つのデータバッファと1つの定数へのポインタを渡しています。

    __kernel void HiddenGradientContAtt(__global float *qkv, __global float *qkv_g,
                                    __global float *dqkv,
                                    __global float *dqkv_g,
                                    __global float *score,
                                    __global float *out_g, int dimension)
  {
   const size_t pos = get_global_id(0);
   const size_t variable = get_global_id(1);
   const size_t head = get_global_id(2);
   const size_t total = get_global_size(0);
   const size_t variables = get_global_size(1);
   const size_t heads = get_global_size(2);

    フィードフォワードカーネルと同様に、3次元のタスク空間でバックプロパゲーションパスを実装するが、ワークグループにグループ化しません。カーネル本体では、タスク空間のすべての次元でスレッドを識別します。

    さらなるカーネルアルゴリズムは、誤差勾配の対象によって3つの部分に分けられます。最初のブロックでは、誤差勾配をValueエンティティに分配します。

    //--- Value gradient
     {
      const int shift_value = dimension * (heads * (3 * variables * pos + 3 * variable + 2)
                                                                                    + head);
      const int shift_out = dimension * (head + variable * heads);
      const int shift_score = total * (variable * heads + head);
      const int step_out = variables * heads * dimension;
      const int step_score = variables * heads * total;
      //---
      for(int d = 0; d < dimension; d++)
        {
         float sum = 0;
         for(int g = 0; g < total; g++)
            sum += out_g[shift_out + g * step_out + d] *
                   score[shift_score + g * step_score];
         qkv_g[shift_value + d] = sum;
        }
     }

    ここではまず、必要な要素へのデータバッファのシフトを決定します。次に、ループシステムで、すべての従属要素と実体ベクトルのすべての要素における誤差勾配を収集します。

    2番目のブロックでは、誤差の勾配をQueryまで伝播させます。しかし、ここでのアルゴリズムはもう少し複雑です。

    //--- Query gradient
     {
      const int shift_out = dimension * (heads * (pos * variables + variable) + head);
      const int step = 3 * variables * heads * dimension;
      const int shift_query = dimension * (3 * heads * variable + head) + pos * step;
      const int shift_key = dimension * (heads * (3 * variable + 1) + head);
      const int shift_value = dimension * (heads * (3 * variable + 2) + head);
      const int shift_score = total * (heads * (pos * variables + variable) + head);

    最初のブロックと同様に、まずデータバッファ内の解析対象要素へのシフトを決定します。その後、まず依存係数の行列に勾配を分配し、SoftMax関数の微分のためにそれを調整しなければなりません。

          //--- Score gradient
      for(int k = 0; k < total; k++)
        {
         float score_grad = 0;
         float scr = score[shift_score + k];
         for(int v = 0; v < total; v++)
           {
            float grad = 0;
            for(int d = 0; d < dimension; d++)
               grad += qkv[shift_value + v * step + d] * out_g[shift_out + d];
            score_grad += score[shift_score + v] * grad * ((float)(pos == v) - scr);
           }
         score_grad /= sqrt((float)dimension);

    そうして初めて、誤差勾配をQueryエンティティに伝播することができます。しかし、ネイティブのTransformerアルゴリズムとは異なり、この場合、誤差勾配を時間ごとにQueryエンティティの対応する微分にも伝播させます。

             //--- Query gradient
         for(int d = 0; d < dimension; d++)
           {
            if(k == 0)
              {
               dqkv_g[shift_query + d] = score_grad * qkv[shift_key + k * step + d];
               qkv_g[shift_query + d] = score_grad * dqkv[shift_key + k * step + d];
              }
            else
              {
               dqkv_g[shift_query + d] += score_grad * qkv[shift_key + k * step + d];
               qkv_g[shift_query + d] += score_grad * dqkv[shift_key + k * step + d];
              }
           }
        }
     }

    誤差勾配のKeyエンティティへの伝搬とその偏微分も同様におこなわれます。しかし、依存係数の行列では、別の次元を通過します。

    //--- Key gradient
     {
      const int shift_key =
         dimension * (heads * (3 * variables * pos + 3 * variable + 1) + head);
      const int shift_out = dimension * (heads * variable + head);
      const int step_out = variables * heads * dimension;
      const int step = 3 * variables * heads * dimension;
      const int shift_query = dimension * (3 * heads * variable + head);
      const int shift_value =
         dimension * (heads * (3 * variable + 2) + head) + pos * step;
      const int shift_score = total * (heads * variable + head);
      const int step_score = variables * heads * total;
      //--- Score gradient
      for(int q = 0; q < total; q++)
        {
         float score_grad = 0;
         float scr = score[shift_score + q * step_score];
         for(int g = 0; g < total; g++)
           {
            float grad = 0;
            for(int d = 0; d < dimension; d++)
               grad += qkv[shift_value + d] * out_g[shift_out + d + g * step_out];
            score_grad += score[shift_score + q * step_score + g] * grad * ((float)(q == pos)
                                                                                      - scr);
           }
         score_grad /= sqrt((float)dimension);
         //--- Key gradient
         for(int d = 0; d < dimension; d++)
           {
            if(q == 0)
              {
               dqkv_g[shift_key + d] = score_grad * qkv[shift_query + q * step + d];
               qkv_g[shift_key + d] = score_grad * dqkv[shift_query + q * step + d];
              }
            else
              {
               qkv_g[shift_key + d] += score_grad * dqkv[shift_query + q * step + d];
               dqkv_g[shift_key + d] += score_grad * qkv[shift_query + q * step + d];
              }
           }
        }
     }
  }

    おわかりのように、前のカーネルでは、誤差勾配をエンティティ自身とその微分の両方に伝播させました。環境のさまざまな状態について、実体の値に基づいて時間に関する偏微分を解析的に計算したことを思い出してください。論理的には、同様の方法で誤差勾配を伝播させることができます。このようなアルゴリズムをHiddenGradientTimeDerivativeカーネルに実装します。

    __kernel void HiddenGradientTimeDerivative(__global float *qkv_g,
                                           __global float *dqkv_g,
                                           int dimension)
  {
   const size_t pos = get_global_id(0);
   const size_t variable = get_global_id(1);
   const size_t head = get_global_id(2);
   const size_t total = get_global_size(0);
   const size_t variables = get_global_size(1);
   const size_t heads = get_global_size(2);

    カーネルパラメータとタスクスペースはフィードフォワードパスと同様です。ただ、結果バッファの代わりに誤差勾配バッファを使用します。

    メソッドの本体では、使用されるタスク空間のすべての次元でスレッドを特定します。その後、データバッファのシフトを決定します。

       const int shift = 3 * heads * variables * dimension;
   const int shift_query = pos * shift + (3 * variable * heads + head) * dimension;
   const int shift_key = shift_query + heads * dimension;

    微分の計算と同様に、誤差勾配の分布を実装します。

       for(int i = 0; i < dimension; i++)
     {
      //--- dQ/dt
        {
         int count = 0;
         float grad = 0;
         float current = dqkv_g[shift_query + i];
         if(pos > 0)
           {
            grad += current - dqkv_g[shift_query + i - shift];
            count++;
           }
         if(pos < (total - 1))
           {
            grad += dqkv_g[shift_query + i + shift] - current;
            count++;
           }
         if(count > 0)
            grad /= count;
         qkv_g[shift_query + i] += grad;
        }

          //--- dK/dt
        {
         int count = 0;
         float grad = 0;
         float current = dqkv_g[shift_key + i];
         if(pos > 0)
           {
            grad += current - dqkv_g[shift_key + i - shift];
            count++;
           }
         if(pos < (total - 1))
           {
            grad += dqkv_g[shift_key + i + shift] - current;
            count++;
           }
         if(count > 0)
            grad /= count;
         qkv_g[shift_key + i] += dqkv_g[shift_key + i] + grad;
        }
     }
  }

    メインプログラム側でのこれらのカーネルの呼び出しは、CNeuronConformer::AttentionInsideGradientsメソッドの中でおこなわれます。この方法を構築するアルゴリズムは、対応するフィードフォワードパス法と同様です。カーネルだけが逆の順序で呼び出されます。まず、Continuous Attentionブロックを通して勾配伝搬カーネルの実行をエンキューします。

    bool CNeuronConformer::AttentionInsideGradients(void)
  {
   if(!OpenCL)
      return false;
//--- MH Attention Out Gradient
     {
      uint global_work_offset[3] = {0, 0, 0};
      uint global_work_size[3] = {iCount, iVariables, iHeads};

          ResetLastError();
      if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientContAtt, def_k_hgcaqkv,
                                                                       cQKV.getOutputIndex()))
        {
         printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__,
                                                                    GetLastError(), __LINE__);
         return false;
        }
      if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientContAtt, def_k_hgcaqkv_g,
                                                                      cQKV.getGradientIndex()))
        {
         printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__,
                                                                     GetLastError(), __LINE__);
         return false;
        }
      if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientContAtt, def_k_hgcadqkv,
                                                                       cdQKV.getOutputIndex()))
        {
         printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__,
                                                                     GetLastError(), __LINE__);
         return false;
        }
      if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientContAtt, def_k_hgcadqkv_g,
                                                                    cdQKV.getGradientIndex()))
        {
         printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__,
                                                                     GetLastError(), __LINE__);
         return false;
        }
      if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientContAtt, def_k_hgcascore, iScore))
        {
         printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, 
                                                                     GetLastError(), __LINE__);
         return false;
        }
      if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientContAtt, def_k_hgcaout_g,
                                                             cAttentionOut.getGradientIndex()))
        {
         printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__,
                                                                     GetLastError(), __LINE__);
         return false;
        }
      if(!OpenCL.SetArgument(def_k_HiddenGradientContAtt, def_k_hgcadimension, 
                                                                              int(iDimension)))
        {
         printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__,
                                                                     GetLastError(), __LINE__);
         return false;
        }

          if(!OpenCL.Execute(def_k_HiddenGradientContAtt, 3, global_work_offset, global_work_size))
        {
         printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError());
         return false;
        }
     }

    次に、偏微分から誤差勾配を加えます。

    //--- Time Derivative Gradient
     {
      uint global_work_offset[3] = {0, 0, 0};
      uint global_work_size[3] = {iCount, iVariables, iHeads};

          ResetLastError();
      if(!OpenCL.SetArgumentBuffer(def_k_HGTimeDerivative, def_k_tdqkv, 
                                                                     cQKV.getGradientIndex()))
        {
         printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__,
                                                                     GetLastError(), __LINE__);
         return false;
        }
      if(!OpenCL.SetArgumentBuffer(def_k_HGTimeDerivative, def_k_tddqkv, 
                                                                    cdQKV.getGradientIndex()))
        {
         printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, 
                                                                     GetLastError(), __LINE__);
         return false;
        }
      if(!OpenCL.SetArgument(def_k_HGTimeDerivative, def_k_tddimension, int(iDimension)))
        {
         printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, 
                                                                     GetLastError(), __LINE__);
         return false;
        }

          if(!OpenCL.Execute(def_k_HGTimeDerivative, 3, global_work_offset, global_work_size))
        {
         printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError());
         return false;
        }
     }
//---
   return true;
  }

    準備作業を終えたら、誤差勾配分布アルゴリズム全体をCNeuronConformer::calcInputGradientsメソッドに組み立てます。パラメータには、前の層のオブジェクトへのポインタを受け取ります。この層に誤差勾配を渡す必要があります。

    bool CNeuronConformer::calcInputGradients(CNeuronBaseOCL *prevLayer)
  {
//--- Feed Forward Gradient
   if(!cFF[1].calcInputGradients(GetPointer(cFF[0])))
      return false;
   if(!cFF[0].calcInputGradients(GetPointer(cNODE[2])))
      return false;
   if(!SumAndNormilize(Gradient, cNODE[2].getGradient(), cNODE[2].getGradient(), iDimension,
                                                                                      false))
      return false;

    準備した勾配バッファの入れ替えのおかげで、次の層は、FeedForwardブロックの最後の内部層のバッファに直接誤差勾配を渡してくれました。そこで、不要なコピー操作をせずに、FeedForwardブロックオブジェクトのバックプロパゲーションパスのメソッドを順次呼び出していきます。

    フィードフォワードパスの間に、フィードフォワードブロックの入力と出力のバッファの値を合計しました。同様に、誤差勾配を合計します。そして、得られた結果を常微分方程式の層を持つブロックの出力に渡します。その後、ニューラルODEブロックの内部層を逆ループさせ、誤差勾配を伝搬させます。

    //--- Neural ODE Gradient
   CNeuronBaseOCL *prev = GetPointer(cNODE[1]);
   for(int i = 2; i > 0; i--)
     {
      if(!cNODE[i].calcInputGradients(prev))
         return false;
      prev = GetPointer(cNODE[i - 1]);
     }
   if(!cNODE[0].calcInputGradients(GetPointer(cW0)))
      return false;
   if(!SumAndNormilize(cW0.getGradient(), cNODE[2].getGradient(), cW0.getGradient(), 
                                                                  iDimension, false))
      return false;

    ここでは、ブロックの入力と出力の誤差勾配も合計します。

    フィードフォワードパスの最初のものと、バックプロパゲーションパスの最後のものがContinuous Attentionです。まず、Attention Head間の誤差勾配を分配します。

    //--- MH Attention Gradient
   if(!cW0.calcInputGradients(GetPointer(cAttentionOut)))
      return false;

    次に、Attentionブロックを通して誤差勾配を分配します。

       if(!AttentionInsideGradients())
      return false;

    次に、誤差勾配を前の層のレベルに伝搬します。

    //--- Query, Key, Value Graddients
   if(!cQKV.calcInputGradients(prevLayer))
      return false;

    メソッドの最後に、Attentionブロックの入力と出力における誤差勾配を合計します。

       if(!SumAndNormilize(cW0.getGradient(), prevLayer.getGradient(), prevLayer.getGradient(),
                                                                            iDimension, false))
      return false;
//---
   return true;
  }

    最終的な結果に対する影響度に従って、すべてのオブジェクト間で誤差勾配を分配した後、モデルの全体的な誤差を減らすためにパラメータの最適化を進めます。

    ここで、CNeuronConformerクラスのすべての学習パラメータは、内側のニューラル層に含まれていることを述べておきます。したがって、モデルパラメータを更新するには、内部オブジェクトの同名メソッドを1つずつ呼び出すだけで済みます。

    bool CNeuronConformer::updateInputWeights(CNeuronBaseOCL *NeuronOCL)
  {
//--- MH Attention
   if(!cQKV.UpdateInputWeights(NeuronOCL))
      return false;
   if(!cW0.UpdateInputWeights(GetPointer(cAttentionOut)))
      return false;

    //--- Neural ODE
   CNeuronBaseOCL *prev = GetPointer(cW0);
   for(int i = 0; i < 3; i++)
     {
      if(!cNODE[i].UpdateInputWeights(prev))
         return false;
      prev = GetPointer(cNODE[i]);
     }

    //--- Feed Forward
   for(int i = 0; i < 2; i++)
     {
      if(!cFF[i].UpdateInputWeights(prev))
         return false;
      prev = GetPointer(cFF[i]);
     }
//---
   return true;
  }

    これをもって、新しいCNeuronConformerクラスのメソッドについての説明を終わります。ここでは、Conformer法の著者によって提案された主なアプローチを実装しました。残念ながら、記事の形式上、このクラスの補助メソッドについて詳しく説明することはできません。添付ファイルにあるファイルを使って、これらの方法をご自分で研究してください。添付ファイルには、記事で使用されているすべてのプログラムの完全なコードも含まれています。次へ移りましょう。

    2.4 訓練用モデルアーキテクチャ

    訓練済みモデルのアーキテクチャに移る前に、Conformer法に従って、環境記述の個々のパラメータについて分析を行う必要があります。したがって、入力データの初期処理では、分析対象の各パラメータに対して適切な埋め込みを作成することが求められます。

    まず、分析対象データの構造を見てみましょう。

    .........
.........
      sState.state[shift] = (float)(Rates[b].close - open);
      sState.state[shift + 1] = (float)(Rates[b].high - open);
      sState.state[shift + 2] = (float)(Rates[b].low - open);
      sState.state[shift + 3] = (float)(Rates[b].tick_volume / 1000.0f);
      sState.state[shift + 4] = rsi;
      sState.state[shift + 5] = cci;
      sState.state[shift + 6] = atr;
      sState.state[shift + 7] = macd;
      sState.state[shift + 8] = sign;
........
........

    実装では、ソースデータを次のように分割しました。

    1. 最後のローソク足の説明（4要素）
    2. RSI（1要素）
    3. CCI（1要素）
    4. ATF（1要素）
    5. MACD（2要素）

    この分け方はあくまで私のビジョンです。別の分け方を使うこともできますが、訓練済みモデルのアーキテクチャに反映されなければなりません。

    訓練済みモデルのアーキテクチャは、CreateDescriptionsメソッドに記述されています。パラメータで、このメソッドは3つのモデルのアーキテクチャを転送する動的配列への3つのポインタを受け取ります。

    メソッド本体では、まず受け取ったポインタを確認し、必要であれば新しい動的配列オブジェクトを作成します。

    bool CreateDescriptions(CArrayObj *encoder, CArrayObj *actor, CArrayObj *critic)
  {
//---
   CLayerDescription *descr;
//---
   if(!encoder)
     {
      encoder = new CArrayObj();
      if(!encoder)
         return false;
     }
   if(!actor)
     {
      actor = new CArrayObj();
      if(!actor)
         return false;
     }
   if(!critic)
     {
      critic = new CArrayObj();
      if(!critic)
         return false;
     }

    エンコーダーモデルには、現在の環境状態を表す未処理のデータを入力します。

    //--- Encoder
   encoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

    受信したデータはバッチ正規化層で前処理されます。

    //--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = MathMax(1000, GPTBars);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

    その後、上に示した構造に従って、現在の状態パラメータの埋め込みを作成します。

    //--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronEmbeddingOCL;
     {
      int temp[] = {4, 1, 1, 1, 2};
      ArrayCopy(descr.windows, temp);
     }

    先に述べた埋め込みアーキテクチャでは、入力データサイズに等しいウィンドウサイズを指定しています。これにより、個別の状態を埋め込むことが可能になります。ただし、この場合は、最後のバーの記述の分析から進め、パラメータを上記のブロックに分割します。もし複数のバーやその他のデータ構成を分析する場合は、分析データウィンドウのサイズをそれに合わせて調整する必要があります。

       prev_count = descr.count = GPTBars;
   int prev_wout = descr.window_out = EmbeddingSize / 2;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

    続く畳み込み層は、元データの埋め込みを生成するプロセスを完了します。

    //--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = prev_count * 5;
   descr.step = descr.window = prev_wout;
   prev_wout = descr.window_out = EmbeddingSize;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

    埋め込みに位置符号化ハーモニクスを加えてみましょう。

    //--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronPEOCL;
   descr.count = prev_count;
   descr.window = prev_wout * 5;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

    エンコーダーモデルの最後に、5つの連続したConformer層のブロックを作ります。層のパラメータは、他のAttention層と同じように指定します。分析する変数の数は、desc.layersに示されています。 

       for(int i = 0; i < 5; i++)
     {
      if(!(descr = new CLayerDescription()))
         return false;
      descr.type = defNeuronConformerOCL;
      descr.count = prev_count;
      descr.window = prev_wout;
      descr.step = 4;
      descr.window_out = EmbeddingSize;
      descr.layers = 5;
      if(!encoder.Add(descr))
        {
         delete descr;
         return false;
        }
     }

    Actorモデルの中核にあるのは、前回と同様、現在の口座状態と、エンコーダーから受け取った現在の環境状態の圧縮表現との間の依存関係を推定するCross-Attention層です。

    まず、口座ステータスの説明をモデルに与えます。

    //--- Actor
   actor.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = AccountDescr;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

    埋め込みに変換します。

    //--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = EmbeddingSize;
   descr.activation = SIGMOID;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

    Cross-Attention層を3ブロック追加します。

    //--- layer 2-4
   for(int i = 0; i < 3; i++)
     {
      if(!(descr = new CLayerDescription()))
         return false;
      descr.type = defNeuronCrossAttenOCL;
        {
         int temp[] = {1, GPTBars * 5};
         ArrayCopy(descr.units, temp);
        }
        {
         int temp[] = {EmbeddingSize, EmbeddingSize};
         ArrayCopy(descr.windows, temp);
        }
      descr.window_out = 16;
      descr.step = 4;
      descr.activation = None;
      descr.optimization = ADAM;
      if(!actor.Add(descr))
        {
         delete descr;
         return false;
        }
     }

    Cross-Attentionブロックから得られたデータに基づいて、Actorの確率的方策を形成します。

    //--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = SIGMOID;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 6
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = 2 * NActions;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 7
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronVAEOCL;
   descr.count = NActions;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

    Criticのモデルも同様の構造で成り立っています。しかし、口座の状態ではなく、Actorの行動と環境の状態を比較します。

    生成されたActorの行動をモデルに送り込みます。

    //--- Critic
   critic.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = NActions;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!critic.Add(descr))
     {
      delete descr;
      return false;
     }

    それらは埋め込みに変換されます。

    //--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = EmbeddingSize;
   descr.activation = SIGMOID;
   descr.optimization = ADAM;
   if(!critic.Add(descr))
     {
      delete descr;
      return false;
     }

    次は3層のCross-Attentionブロックです。

    //--- layer 2-4
   for(int i = 0; i < 3; i++)
     {
      if(!(descr = new CLayerDescription()))
         return false;
      descr.type = defNeuronCrossAttenOCL;
        {
         int temp[] = {1, GPTBars * 5};
         ArrayCopy(descr.units, temp);
        }
        {
         int temp[] = {EmbeddingSize, EmbeddingSize};
         ArrayCopy(descr.windows, temp);
        }
      descr.window_out = 16;
      descr.step = 4;
      descr.activation = None;
      descr.optimization = ADAM;
      if(!critic.Add(descr))
        {
         delete descr;
         return false;
        }
     }

    行動はパーセプトロンブロックで評価されます。

    //--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = SIGMOID;
   descr.optimization = ADAM;
   if(!critic.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 6
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = SIGMOID;
   descr.optimization = ADAM;
   if(!critic.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 7
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = NRewards;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!critic.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

    2.5 モデルの訓練

    ここでおこなった変更は、環境との相互作用のプロセスには影響していないため、「...\ConformerResearch.mq5」EAをそのまま使って初期訓練データを収集し、訓練データセットを更新することができます。また、入力データを分析するアプローチは変わってもデータ構造体は変わっていないので、以前に収集した訓練データセットを使ってモデルを訓練することができます。

    ただし、「...\Conformer\Study.mq5」EAのアルゴリズム内のモデル訓練プロセスには若干の変更を加えています。この記事では、モデル訓練方法Trainのみを検討します。

    前回と同様、メソッドの最初に、収益性に応じて軌道を選択する確率のベクトルを生成します。最も収益性の高いパスは、モデルの訓練過程で選択される確率が高くなります。

    void Train(void)
  {
//---
   vector<float> probability = GetProbTrajectories(Buffer, 0.9);

    次に、ローカル変数を初期化します。

       vector<float> result, target;
   bool Stop = false;
//---
   uint ticks = GetTickCount();

    ネストされたモデル訓練ループのシステムを作成します。外側ループの本体では、経験再生バッファから軌跡をサンプリングし、その上に初期訓練状態を置きます。

          int tr = SampleTrajectory(probability);
      int batch = GPTBars + 48;
      int state = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * 
                         (Buffer[tr].Total - 2 - PrecoderBars - batch));
      if(state <= 0)
        {
         iter--;
         continue;
        }

    その後、エンコーダーのリカレントバッファをクリアし、訓練データセットの最終状態を決定します。

          Encoder.Clear();
      int end = MathMin(state + batch, Buffer[tr].Total - PrecoderBars);

    準備作業を終えたら、訓練の状態をネストしたループで整理します。

          for(int i = state; i < end; i++)
        {
         bState.AssignArray(Buffer[tr].States[i].state);
         //--- State Encoder
         if(!Encoder.feedForward((CBufferFloat*)GetPointer(bState), 1, false, 
                                                          (CBufferFloat*)NULL))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

    ループの本体では、まず経験再生バッファから環境の状態を読み込み、フィードフォワードメソッドを呼び出してエンコーダーでそれを分析します。

    次に、Actorの行動を経験再生バッファからロードし、Criticで評価します。

             //--- Critic
         bActions.AssignArray(Buffer[tr].States[i].action);
         if(bActions.GetIndex() >= 0)
            bActions.BufferWrite();
         if(!Critic.feedForward((CBufferFloat*)GetPointer(bActions), 1, false,
                                                                    GetPointer(Encoder)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

    そして、Criticの評価を、経験再生バッファからの実際の報酬に向けて調整します。

             result.Assign(Buffer[tr].States[i + 1].rewards);
         target.Assign(Buffer[tr].States[i + 2].rewards);
         result = result - target * DiscFactor;
         Result.AssignArray(result);
         Critic.TrainMode(true);
         if(!Critic.backProp(Result, (CNet *)GetPointer(Encoder)) ||
            !Encoder.backPropGradient((CBufferFloat*)NULL))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

    また、環境の状態を分析するために、Critic誤差勾配をエンコーダーに渡します。

    次に、経験値再生バッファから、分析された環境の状態に対応する口座ステータスの記述を読み込みます。

             //--- Policy
         float PrevBalance = Buffer[tr].States[MathMax(i - 1, 0)].account[0];
         float PrevEquity = Buffer[tr].States[MathMax(i - 1, 0)].account[1];
         bAccount.Clear();
         bAccount.Add((Buffer[tr].States[i].account[0] - PrevBalance) / PrevBalance);
         bAccount.Add(Buffer[tr].States[i].account[1] / PrevBalance);
         bAccount.Add((Buffer[tr].States[i].account[1] - PrevEquity) / PrevEquity);
         bAccount.Add(Buffer[tr].States[i].account[2]);
         bAccount.Add(Buffer[tr].States[i].account[3]);
         bAccount.Add(Buffer[tr].States[i].account[4] / PrevBalance);
         bAccount.Add(Buffer[tr].States[i].account[5] / PrevBalance);
         bAccount.Add(Buffer[tr].States[i].account[6] / PrevBalance);
         double time = (double)Buffer[tr].States[i].account[7];
         double x = time / (double)(D'2024.01.01' - D'2023.01.01');
         bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         x = time / (double)PeriodSeconds(PERIOD_MN1);
         bAccount.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0));
         x = time / (double)PeriodSeconds(PERIOD_W1);
         bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         x = time / (double)PeriodSeconds(PERIOD_D1);
         bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         if(bAccount.GetIndex() >= 0)
            bAccount.BufferWrite();

    このデータをもとに、現在の方策に従ってActorの行動を生成します。

             //--- Actor
         if(!Actor.feedForward((CBufferFloat*)GetPointer(bAccount), 1, false, 
                                                                     GetPointer(Encoder)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

    そして、その行動をCriticで評価します。

             if(!Critic.feedForward((CNet *)GetPointer(Actor), -1, (CNet*)GetPointer(Encoder)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

    Actorの方策は2段階で調整されます。まず、エージェントの実際の行動との乖離が最小になるように方策を調整します。これにより、Actorの方策を訓練セットに近い分布に保つことができます。

             if(!Actor.backProp(GetPointer(bActions), GetPointer(Encoder)) ||
            !Encoder.backPropGradient((CBufferFloat*)NULL))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

    2番目のステップでは、Criticの評価に従ってActorの方策を調整します。このため、Criticの訓練モードを無効にし、Criticを介してActorに誤差勾配を伝播させます。その後、得られた誤差勾配に向かって方策を調整します。

             Critic.TrainMode(false);
         if(!Critic.backProp(Result, (CNet *)GetPointer(Encoder)) ||
            !Actor.backPropGradient((CNet *)GetPointer(Encoder), -1, -1, false) ||
            !Encoder.backPropGradient((CBufferFloat*)NULL))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

    Actorの方策を調整するどちらの場合も、誤差勾配をエンコーダーに伝搬し、環境の「見方」を調整することに注意してください。このようにして、環境分析の情報量を最大化するように努めています。

    すべてのモデルのパラメータを更新した後は、訓練プロセスの進捗状況をユーザーに知らせ、ループシステムの次の反復に移るだけで済みます。

             if(GetTickCount() - ticks > 500)
           {
            double percent = (double(i - state) / 
                             ((end - state)) + iter) * 100.0 / (Iterations);
            string str = StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Actor", 
                                      percent, Actor.getRecentAverageError());
            str += StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Critic", 
                                      percent, Critic.getRecentAverageError());
            Comment(str);
            ticks = GetTickCount();
           }
        }
     }

    ループシステムのすべての反復が完全に終了するまで、訓練プロセスが繰り返されます。訓練が無事終了したら、チャートのコメント欄を消去します。

       Comment("");
//---
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Actor", 
                                          Actor.getRecentAverageError());
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Critic",
                                          Critic.getRecentAverageError());
   ExpertRemove();
//---
  }

    モデル訓練処理の結果をログに出力し、訓練EAの終了を初期化します。

    これで、プログラム記事で使用されたアルゴリズムの分析は終わりです。全コードは添付ファイルにあります。


    3. テスト

    この記事では、Conformer法について説明し、MQL5を用いて提案されたアプローチを実装しました。ここで、提案した方法でモデルを訓練し、実際のデータでテストします。

    いつものように、MetaTrader 5のストラテジーテスターを使用して、実際のEURUSD、H1履歴データでモデルを訓練およびテストします。モデルを訓練するために、2023年の最初の7ヶ月間の履歴データを使用します。次に、訓練済みモデルを2023年8月からの履歴データでテストします。

    この記事を準備する間、この連載の前の記事でモデルを訓練するために収集したサンプルでモデルを訓練しました。

    モデルのアーキテクチャと訓練プロセスのアルゴリズムを変更したことで、反復あたりのコストがわずかに上昇したと言わざるを得ません。しかし、提案されたアプローチは訓練プロセスの安定性を示しており、モデルの訓練に必要な反復回数を減らすことができると私は感じています。

    、訓練データセットとテストデータセットの両方で高い性能を発揮するモデルを得ることができました。

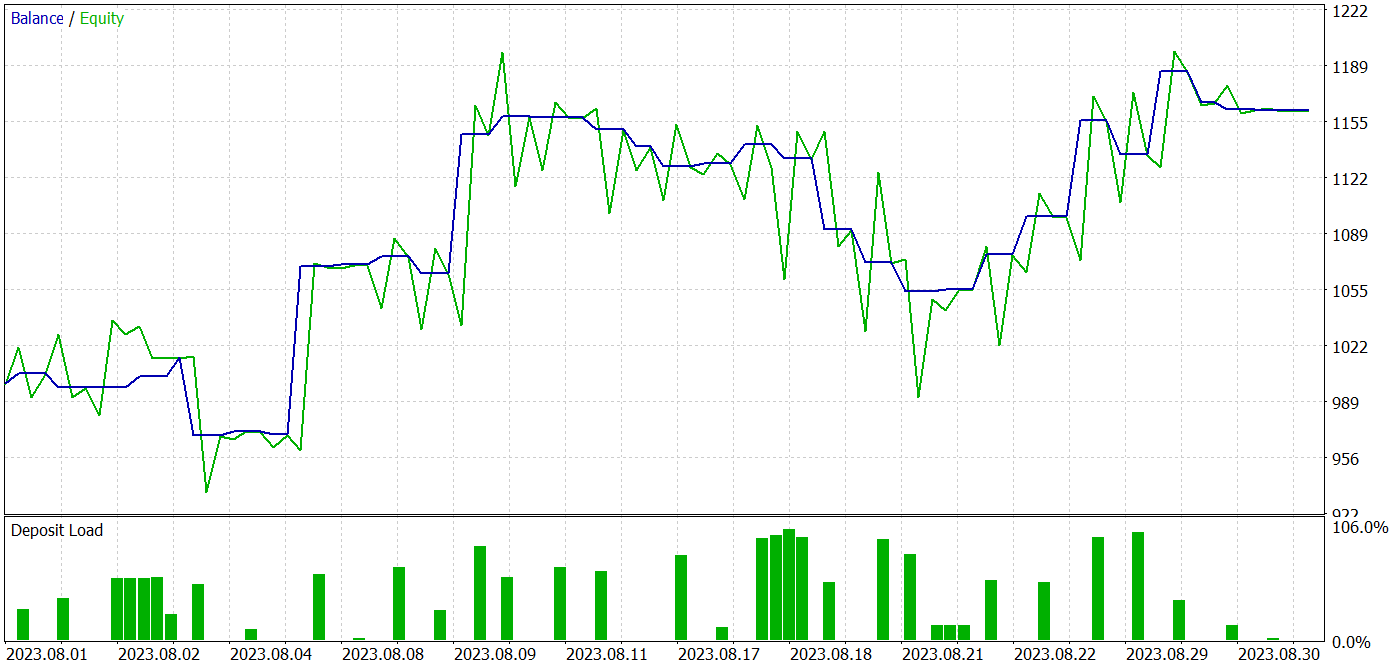
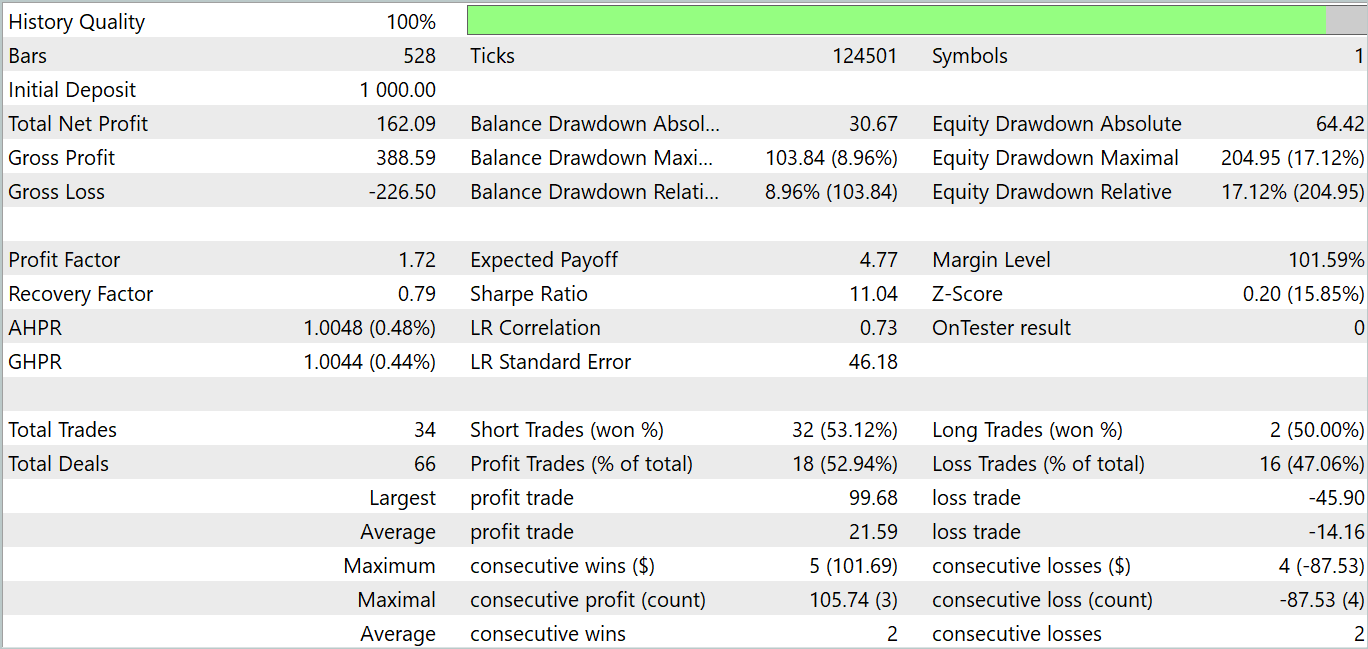
    モデル訓練結果

    モデル訓練結果

    テスト期間中、このモデルは34回の取引をおこない、うち18回は利益で決済しました。つまり、52.94%が利益を上げています。さらに、平均利益率は平均損失率を52.47%上回っています。最大利益は同じ損失変数の2倍以上です。全体として、このモデルは1.72のプロフィットファクターを示し、バランスグラフは上昇傾向を示しています。エクイティの最大ドローダウンは17.12%、残高のドローダウンは8.96%でした。


    結論

    本稿では、天気予報に特化して開発された論文「Conformer:Embedding Continuous Attention in Vision Transformer for Weather Forecasting」で発表された、Spatio-Temporal Continuous Attention Transformer「Conformer」の複雑なアルゴリズムについて解説しました。この手法の著者は、Continuous Attentionアルゴリズムを提案し、それをニューラルODEと組み合わせています。

    本稿の実践的な部分では、提案された手法をMQL5で実装し、モデルを訓練およびテストしました。テスト結果は非常に有望であり、訓練データセットとテストデータセットの両方で利益を生み出すことが確認されました。

    なお、本記事で紹介されているプログラムおよび手法は、あくまで情報提供を目的としており、提案されたアプローチの実証を目的としています。その点をご理解いただければ幸いです。


    参照文献

  • Embedding Continuous Attention in Vision Transformer for Weather Forecasting
  • この連載の他の記事記事


    • 記事で使用されているプログラム

    # 名前 種類 詳細
    1 Research.mq5 EA コレクションEAの例
    2 ResearchRealORL.mq5
    		 EA
    		 Real-ORL法による事例収集のためのEA
    3 Study.mq5  EA モデル訓練EA
    4 Test.mq5 EA モデルをテストするEA
    5 Trajectory.mqh クラスライブラリ システム状態記述の構造体
    6 NeuroNet.mqh クラスライブラリ ニューラルネットワークを作成するためのクラスのライブラリ
    7 NeuroNet.cl コードベース OpenCLプログラムコードライブラリ

    MetaQuotes Ltdによってロシア語から翻訳されました。
    元の記事: https://www.mql5.com/ru/articles/14615

    添付されたファイル |
    ZIPをダウンロード
    MQL5.zip (1093.34 KB)
    警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

    この著者による他の記事

    ディスカッションに移動
    ブレインストーム最適化アルゴリズム(第1部）：クラスタリング ブレインストーム最適化アルゴリズム(第1部）：クラスタリング
    この記事では、「ブレインストーミング」と呼ばれる現象にヒントを得た、BSO (Brain Storm Optimization)と呼ばれる革新的な最適化手法を見ていきます。また、BSO法が適用するマルチモーダル最適化問題を解くための新しいアプローチについても説明します。これにより、部分集団の数を事前に決定することなく、複数の最適解を見つけることができるのです。K-MeansとK-Means++のクラスタリング法も検討します。
    リプレイシステムの開発（第45回）：Chart Tradeプロジェクト(IV) リプレイシステムの開発（第45回）：Chart Tradeプロジェクト(IV)
    この記事の主な目的は、C_ChartFloatingRADクラスの紹介と説明です。Chart Trade指標は、非常に興味深い方法で機能しています。チャート上のオブジェクトの数はまだ少ないものの、期待通りの機能を実現しています。指標の値は編集可能ですが、その実現方法については疑問が残るかもしれません。この記事を読めば、これらの疑問が解消されるでしょう。
    多通貨エキスパートアドバイザーの開発（第8回）：新しいバーの負荷テストと処理 多通貨エキスパートアドバイザーの開発（第8回）：新しいバーの負荷テストと処理
    進歩に伴い、1つのEAでより多くの取引戦略インスタンスを同時に実行するようになりました。リソースの限界に達する前に、どのくらいのインスタンスが利用可能かを検討することが重要です。
    因果推論における時系列クラスタリング 因果推論における時系列クラスタリング
    機械学習におけるクラスタリングアルゴリズムは、元データを類似した観察結果を持つグループに分けることができる重要な教師なし学習法です。これらのクラスタを用いることで、特定の市場クラスタを分析したり、新しいデータを基に最も安定したクラスタを探索したり、因果関係を推定したりすることが可能です。本稿では、Pythonによる時系列クラスタリングのための独自の手法を提案します。