MetaTrader 5 / 测试者
English Русский Español Deutsch 日本語 Português
preview
随机数生成器质量对优化算法效率的影响

随机数生成器质量对优化算法效率的影响

MetaTrader 5 — 测试者 | 15 十月 2024, 10:57
240 0
Andrey Dik
Andrey Dik

简介

当提及使用优化算法时，许多读者会好奇使用高质量的随机数生成器究竟有多重要。这个问题的答案并不像初看时那么简单。然而，可以直观地理解，随机数的质量会对算法的搜索能力产生重大影响，因为基于种群的算法绝大多数都是基于随机搜索的。

让我们一起来深入探讨这个问题。在开始之前，我们需要考虑不同类型的随机数生成器、它们对结果的影响以及在哪里可以找到可靠的选项。

随机数生成器（RNGs）是创建数字或值序列的算法或设备，这些数字看起来是随机的。重要的是要注意，在计算机科学和数学中，这样的序列通常被称为“伪随机数”，因为它们是由确定性算法生成的，而不是通过真正的随机过程生成的。

随机数生成器主要有两种类型：

1. 伪随机数生成器 (PRGs)。这些生成器使用数学方程或算法来创建看似随机的数字序列。它们通过一个称为“种子”的初始值进行初始化，并且每次调用生成器时，它都会产生序列中的下一个数字。通过选择合适的算法和种子，伪随机数生成器（PRG）在许多需要伪随机序列的应用中都非常有用。
2. 真随机数生成器（TRNGs）这些生成器利用真正的随机过程（如放射性衰变噪声或量子噪声）来生成随机数。这类生成器通常用于密码学、彩票抽奖以及其他需要高度随机性的领域。

伪随机数生成器在编程中经常使用，例如那些内置于标准编程语言库中的生成器。

编程语言中内置的随机数生成器的准确性取决于用于生成随机数的具体实现和算法。大多数现代编程语言，如MQL5、Python、C++、C#、Java等，都提供了内置的伪随机数生成器，这些生成器对于大多数常见应用而言，能提供质量相当不错的随机数。

一般来说，编程语言中内置的随机数生成器通常适用于大多数常见任务，但对于需要高度随机性或安全性的任务，需要考虑使用特别的解决方案。

对于需要高度随机性和安全性的任务，可以使用以下专用随机数生成解决方案。这些解决方案包括：

1. 密码学随机数生成器。 这些生成器用于需要高度安全性的密码学应用中。它们提供随机性、抗预测性和抗密码分析能力。
2. 硬件随机数生成器。 这些生成器利用物理过程（如热噪声或量子现象）来创建随机数。它们提供真正的随机数，并广泛用于需要高度随机性的领域。
3. 随机数生成库。有一些专用库提供了比编程语言中标准内置生成器更复杂的随机数生成算法。例如，OpenSSL库提供了密码学函数，包括随机数生成器。

编程语言中内置随机数生成器常用的一些算法包括：

1. 线性同余生成器（LCG）。 这是生成伪随机数最简单且最广泛使用的算法之一。但它有缺点，如周期短和随机性程度低。
2. 梅森旋转算法（Mersenne Twister）。该算法具有长周期和良好的随机性程度，并且经常在多种编程语言中使用。
3. Xorshift. 这是一组伪随机数生成算法，具有良好的随机性程度和高速度。
4. PCG （置换同余生成器）。 这类相对较新的生成器在随机性质量和性能之间有很好的平衡。

选择随机数生成器取决于您任务的具体要求。以下是一些可能帮助您做出决定的考虑因素：

1. 随机性质量。如果您的应用需要高度随机性，特别是用于密码学目的，那么最好使用专用的密码学随机数生成器，如密码学安全伪随机数生成器（CSPRNGs）。
2. 性能。 如果您重视随机数生成的速度，那么Xorshift或PCG等高性能算法可能更合适。
3. 周期和质量。 一些算法，诸如梅森旋转算法, 具有长周期和良好的随机性质量。
4. 易用性。对于一些开发人员来说，重要的是随机数生成器易于访问和使用。在这种情况下，标准编程语言库提供的内置生成器可能很方便。

如果您需要密码学级别的安全性，建议使用专用的密码学随机数生成器，如Python中的CryptoRandom或Java中的SecureRandom。I如果您希望在随机性质量和性能之间取得平衡，那么梅森旋转算法或PCG等算法可能是不错的选择。

此外，重要的是要记住，安全性和随机性在系统可靠性和安全性中发挥着关键作用，因此选择随机数生成器时应深思熟虑，并符合特定应用的要求。但本文关注的是RNG质量对优化算法结果的影响。我将仅在此背景下进行研究。


梅森旋转算法（Mersenne Twister）。

在众多可用的随机数生成器中，要找到一个既能提供高质量生成又能保持可接受速度的生成器并不容易。毕竟，生成速度对优化过程的整体执行时间有着重要影响。

因此，选择一个可靠的生成器是一个重要问题，需要在随机数质量和生成速度之间找到平衡。必须找到一个最优解，以确保在不耗费过多时间的基础上有足够高的生成质量。

对于大多数用户来说，硬件生成器难以获取，因此我们在这里立即将其排除在考虑之外。在软件生成器中，高质量的梅森旋转算法（Mersenne Twister）广为人知。

梅森旋转算法是一种由松本真（Makoto Matsumoto）和西村拓司（Takuji Nishimura）于1997年开发的伪随机数生成算法。由于其周期长、随机性好和性能相对较高，它成为使用最广泛的随机数生成算法之一。

梅森旋转算法的主要特点：

  • 周期长。梅森旋转算法具有非常长的周期，这意味着它可以生成大量唯一的伪随机数，直到序列开始重复。
  • 随机性好。该算法确保良好的随机性质量，即生成的数字应符合随机数的统计特性。
  • 性能优越。梅森旋转算法性能良好，使其成为许多应用的理想选择。

梅森旋转算法的工作原理基于线性递归方法生成伪随机数。算法使用一个大数（通常为32位或64位）作为生成器的状态，然后通过复杂运算将其转换以生成下一个伪随机数。在本文中，我们将使用64位生成器。

让我们考虑MersenneTwister64这个类，它基于梅森旋转算法实现了64位数的伪随机数生成器。以下是其方法和功能的简要描述：

  • Init - 随机数生成器初始化方法。它接受一个种子（初始值）作为参数，并设置类的内部变量。基于种子填充梅森数组（Mersenne array）
  • RND_ulong - 返回随机64位无符号整数的方法。如果当前索引大于312，则调用twist()方法来更新梅森数组中的值。然后执行几个位移和位异或运算以生成随机数。在返回结果之前，索引值增加1。
  • RND_ulong_In_Range - 返回给定范围内（包括边界）的随机64位无符号整数的方法。如果min和max相等，则返回min。如果min大于max，则交换min和max的值。然后调用RND_ulong()方法生成一个随机数，并通过移位和缩放使其落在指定范围内。
  • twist - 执行梅森数组“混合”操作的内部方法。对于数组中的每个元素，使用位移和位异或运算组合相邻元素。在混合操作完成后，索引值设置为0。
//——————————————————————————————————————————————————————————————————————————————
class MersenneTwister64
{
public: //--------------------------------------------------------------------

  void Init (ulong seed)
  {
    index = 312;

    MT [0] = seed;
    for (int i = 1; i < 312; i++)
    {
      MT [i] = (6364136223846793005 * (MT [i - 1] ^ (MT [i - 1] >> 62)) + i) & 0xFFFFFFFFFFFFFFFF;
    }
  }

  //from 0 to 18 446 744 073 709 551 615
  ulong RND_ulong ()
  {
    if (index >= 312)
    {
      twist ();
    }

    ulong y = MT [index];
    y = y ^ (y >> 29) & 0x5555555555555555;
    y = y ^ (y << 17) & 0x71D67FFFEDA60000;
    y = y ^ (y << 37) & 0xFFF7EEE000000000;
    y = y ^ (y >> 43);

    index++;
    return y;
  }

  ulong RND_ulong_In_Range (ulong min, ulong max)
  {
    if (min == max) return min;
    if (min > max)
    {
      ulong temp = min;
      min = max;
      max = temp;
    }
    return min + RND_ulong () % (max - min + 1);
  }

private: //-------------------------------------------------------------------
  ulong MT [312];
  int index;

  void twist ()
  {
    for (int i = 0; i < 312; i++)
    {
      ulong y = (MT [i] & 0x8000000000000000) + (MT [(i + 1) % 312] & 0x7FFFFFFFFFFFFFFF);
      MT [i] = MT [(i + 156) % 312] ^ (y >> 1);
      if (y % 2 != 0)
      {
        MT [i] = MT [i] ^ 0xB5026F5AA96619E9;
      }
    }
    index = 0;
  }
};
//——————————————————————————————————————————————————————————————————————————————


比较随机数生成器及其测试结果

让我们通过视觉对比两种随机数生成器的工作：一种是MQL5内置的（以下简称“标准”），另一种是梅森旋转算法（Mersenne Twister）。为此，我们生成了两张图像并对它们的外观进行了分析。乍一看，两张图像都没有明显的模式和周期性，他们的设计都是均匀的。我们没有观察到这两种生成器之间有任何明显的视觉差异。

StandRND

由标准生成器生成的图像

MersRND

由梅森旋转算法生成器生成的图像

然而，为了更客观地比较随机数生成器，建议使用能够评估所生成数字的随机程度及其统计特性的统计学测试。重要的是要注意，视觉评估可能具有局限性，并不总是能够从真正的随机性中检测到隐藏的系统性偏差。

因此，为了更准确地比较生成器，我们将使用统计测试进行额外分析，以获得更可靠的结果。我们关注的是均匀性，因此将使用卡方（χ²）测试，这是一种评估随机生成数字均匀程度的统计测试。在这种情况下，有10,000个观测值，每个观测值包含10,000个生成的值。

卡方测试（χ² test）用于测试数据分布的均匀性。它允许我们确定观察到的频率与均匀分布中预期频率的接近程度。

在卡方测试中，自由度为9999（10,000个观测值减去1）且显著性水平为0.05的临界值为10232.73727。这个值是一个常数，用于在卡方测试中比较预期频率和观察频率。它来自卡方分布表，有助于确定观察值和预期值之间的差异是否显著。

当我们执行卡方测试时，会将计算出的统计量与临界值进行比较。如果计算出的统计量大于临界值，我们可以拒绝原假设，即分布与预期一致。否则，我们接受原假设。

让我们看一下测试脚本代码的一部分（通常，该脚本用于构建图像、测量生成器的执行时间并计算卡方检测值）。

创建并初始化两个数组：“observed”（观察值）和“expected”（预期值）。“observed”数组将用于存储每个BoxesNumber区间内观察到的随机数的数量。“expected”数组将存储生成器以完美的均匀分布产生的，每个区间内预期的随机数的数量。

代码然后检查StandardRND变量的值，该变量指定使用哪个随机数生成器。如果StandardRND为'true'，则使用MQL5中的标准随机数生成器。否则，使用梅森旋转算法生成器。循环生成随机数，并递增区间内对应的“observed”数组元素。

生成随机数后，计算卡方统计值。对于每个区间，计算“(observed - expected)^2 / expected”的值，并将其累加到“chiSquareStatistic”变量中。然后，将“chiSquareCriticalValue”的临界值设置为0.05*。

比较结果在代码的最后显示出来。如果“chiSquareStatistic”的值大于“chiSquareCriticalValue”，则显示一条消息，表示我们拒绝原假设：分布与预期不同。否则，显示另一条消息，表示我们不拒绝原假设：分布与预期一致。

* - 显著性水平0.05（或5%）是最常见的显著性水平之一，在科学研究的许多领域中被广泛使用。这意味着在进行显著性水平为0.05的统计测试时，我们允许5%的第一类错误（即错误地拒绝了真实的原假设）的可能性。在统计学中，显著性水平是用于判断统计结果的可接受程度的阈值。它通常用α（alpha）表示，并代表第一类错误的概率。

int observed [];
ArrayResize     (observed, BoxesNumber);
ArrayInitialize (observed, 0);

int expected [];
ArrayResize     (expected, BoxesNumber);
ArrayInitialize (expected, ThrowsNumber / BoxesNumber);

if (StandardRND)
{
  Print ("Standard, ", ThrowsNumber, " throws, ", BoxesNumber, " boxes");
  for (int i = 0; i < ThrowsNumber; i++)
  {
    observed [rndS.RNDintInRange (0, BoxesNumber - 1)]++;
  }
}
else
{
  Print ("Mersenne, ", ThrowsNumber, " throws, ", BoxesNumber, " boxes");
  for (int i = 0; i < ThrowsNumber; i++)
  {
    observed [(int)rndM.RND_ulong_In_Range (0, BoxesNumber  - 1)]++;
  }
}

// Calculate the chi-square statistic
double chiSquareStatistic = 0;
for (int i = 0; i < ArraySize(observed); i++)
{
  chiSquareStatistic += MathPow(observed[i] - expected[i], 2) / expected[i];
}

// Critical value for the significance level of 0.05
double chiSquareCriticalValue = 10232.73727; //10000

// Output results
if (chiSquareStatistic > chiSquareCriticalValue)
{
  Print("We reject the null hypothesis: The distribution differs from the expected one.");
}
else
{
  Print("We do not reject the null hypothesis: The distribution is consistent with the expected one.");
}


让我们运行该脚本5次，以计算统计数据值和标准生成器的执行时间。同时测量Mersenne Twister生成器的执行时间。计算执行时间的差异，即梅森旋转算法生成器的执行时间与标准生成器执行时间的 比值。

2024.03.18 20:54:33.456    stand: 120353 mcs
2024.03.18 20:54:33.456    mers : 397920 mcs
2024.03.18 20:54:33.456    diff : 3.3062740438543283
2024.03.18 20:54:33.459    Standard, 100000000 throws, 10000 boxes
2024.03.18 20:54:33.854    We reject the null hypothesis: The distribution differs from the expected one.
2024.03.18 20:54:38.802    stand: 121670 mcs
2024.03.18 20:54:38.802    mers : 403180 mcs
2024.03.18 20:54:38.802    diff : 3.3137174323991125
2024.03.18 20:54:38.805    Standard, 100000000 throws, 10000 boxes
2024.03.18 20:54:33.854    We reject the null hypothesis: The distribution differs from the expected one.
2024.03.18 20:54:38.802    stand: 121670 mcs
2024.03.18 20:54:38.802    mers : 403180 mcs
2024.03.18 20:54:38.802    diff : 3.3137174323991125
2024.03.18 20:54:38.805    Standard, 100000000 throws, 10000 boxes
2024.03.18 20:54:44.156    We reject the null hypothesis: The distribution differs from the expected one.
2024.03.18 20:54:48.476    stand: 119246 mcs
2024.03.18 20:54:48.476    mers : 400319 mcs
2024.03.18 20:54:48.476    diff : 3.3570853529678146
2024.03.18 20:54:48.479    Standard, 100000000 throws, 10000 boxes
2024.03.18 20:54:48.873    We reject the null hypothesis: The distribution differs from the expected one.
2024.03.18 20:54:53.144    stand: 119309 mcs
2024.03.18 20:54:53.144    mers : 404502 mcs
2024.03.18 20:54:53.144    diff : 3.390372897266761
2024.03.18 20:54:53.148    Standard, 100000000 throws, 10000 boxes
2024.03.18 20:54:53.553    We reject the null hypothesis: The distribution differs from the expected one.

不幸的是，当使用卡方检验进行测试时，标准随机数生成器在五次测试中均未能通过，这表明其存在系统性偏差，未能达到预期的均匀随机分布。

现在，我们将测试梅森旋转算法（Mersenne Twister）生成器，同时继续测量两个生成器的执行时间。

2024.03.18 20:55:48.133    stand: 115447 mcs
2024.03.18 20:55:48.133    mers : 413258 mcs
2024.03.18 20:55:48.133    diff : 3.57963394458063
2024.03.18 20:55:48.138    Mersenne, 100000000 throws, 10000 boxes
2024.03.18 20:55:49.504    We do not reject the null hypothesis: The distribution is consistent with the expected one.
2024.03.18 20:55:56.340    stand: 117433 mcs
2024.03.18 20:55:56.340    mers : 402337 mcs
2024.03.18 20:55:56.340    diff : 3.4260982858310696
2024.03.18 20:55:56.346    Mersenne, 100000000 throws, 10000 boxes
2024.03.18 20:55:57.717    We do not reject the null hypothesis: The distribution is consistent with the expected one.
2024.03.18 20:56:05.837    stand: 120129 mcs
2024.03.18 20:56:05.837    mers : 400705 mcs
2024.03.18 20:56:05.837    diff : 3.3356225391037966
2024.03.18 20:56:05.843    Mersenne, 100000000 throws, 10000 boxes
2024.03.18 20:56:07.219    We do not reject the null hypothesis: The distribution is consistent with the expected one.
2024.03.18 20:56:12.206    stand: 119980 mcs
2024.03.18 20:56:12.206    mers : 397436 mcs
2024.03.18 20:56:12.206    diff : 3.312518753125521
2024.03.18 20:56:12.211    Mersenne, 100000000 throws, 10000 boxes
2024.03.18 20:56:13.582    We do not reject the null hypothesis: The distribution is consistent with the expected one.
2024.03.18 20:56:18.837    stand: 118140 mcs
2024.03.18 20:56:18.837    mers : 397565 mcs
2024.03.18 20:56:12.206    diff : 3.312518753125521
2024.03.18 20:56:18.842    Mersenne, 100000000 throws, 10000 boxes
2024.03.18 20:56:20.220    We do not reject the null hypothesis: The distribution is consistent with the expected one.

梅森旋转算法（Mersenne Twister）在所有五次卡方测试中都成功完成了任务。同时，我们发现该生成器存在一个显著缺点——梅森旋转算法的速度大约比标准生成器慢3.4倍，这可能会对优化算法的速度产生显著影响。

现在到了最有趣的部分，也是本研究的亮点：我们将进行测试，以了解随机数生成器的质量对优化结果的影响有多大。您可能还记得，标准生成器生成的数字范围在[0;32,767]内，而64位梅森旋转算法生成的数字范围则在[0;18,446,744,073,709,551,615]内。

为了进行实验，我们选择了50个Hilly函数，并对每个函数进行了10,000次迭代。为什么我选择50个Hilly特征以及为什么选择Hilly？首先，这个数量是精心挑选的，以确保算法在有限的适配函数运行次数内无法达到100%的收敛。这使得我们能够观察到使用不同类型随机数生成器时的差异。其次，选择Hilly函数是因为其平滑性，如果我们使用离散测试函数，这可以让我们避免与随机数生成无关的结果自然离散。我重复了实验20次，并对结果进行了平均处理，以获得更可靠且具有统计意义的数据。. 作为优化算法，我们选择了在我们的评分表中排名第一的BGA，同时它在平滑函数上展示的结果离散度非常小。

从打印输出的结果中可以看出，在使用标准随机数生成器和梅森生成器时，BGA算法的优化结果几乎相同。差异仅在第三位小数上，这对于我们的目标来说并不关键并且差异非常小。

标准C_AO_BGA:50:50:1.0:3:0.001:0.7:16
=============================
50 Hilly's; Func runs: 10000; result: 0.9257245560389498
=============================
All score: 0.92572

//Mersenne
C_AO_BGA:50:50:1.0:3:0.001:0.7:16
=============================
50 Hilly's; Func runs: 10000; result: 0.9221148477644971
=============================
All score: 0.92572<br5/>

将算法运行可视化后，我们发现，在算法逻辑中使用两种不同类型的随机数生成器时，并未出现显著的偏差。结果分布的差异完全处于算法本身的变异性范围内。

BGA standard rnd

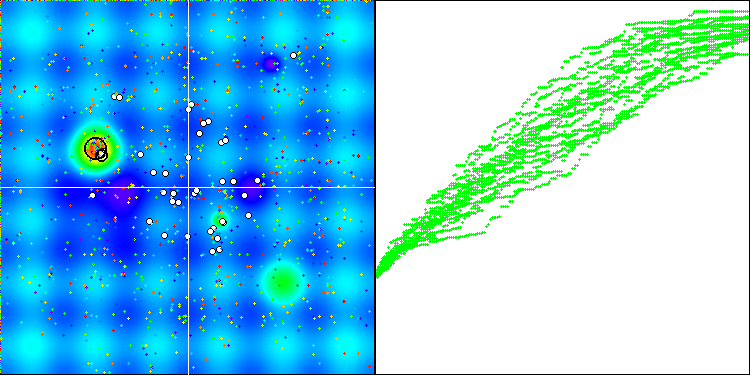
标准生成器下的BGA 

BGA mersenne rnd

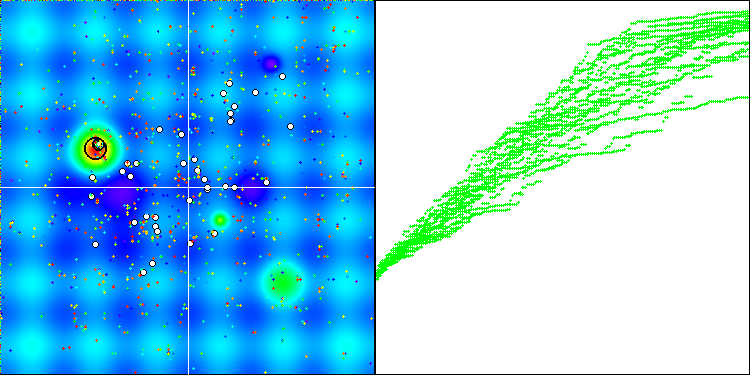
Mersenne Twister生成器下的BGA

初步结论是：随机数生成器的质量不影响优化算法的性能。

我们假设，在BGA（二进制遗传算法）优化算法中使用上述生成器时结果存在的细微差异，可能是由于在BGA中，参与进化的位（bit）都是独立于其他位生成的。事实上，随机数生成器的作用简化为了布尔型的“是/否”操作，而“是”与“否”出现的次数差异仅为千分之几。

因此，对于二进制遗传算法来说，使用随机数生成器并无差异，尽管这一结论乍一看并不明显。但是，这一结论对于其他优化算法，特别是那些在整个由[min, max]坐标界定的空间中使用连续概率的优化算法来说，也成立吗？

让我们尝试进行更多的实验来验证或反驳这一结论。这次，我们将采用在我们的评分表中名列前茅的(P_O)ES算法，该算法在其逻辑中使用了大量的随机数操作，并在整个搜索空间中应用了连续概率。

(P_O)ES算法使用标准随机数生成器进行五次测试运行的结果为：

C_AO_(P_O)ES:100:150:0.02:8.0:10
=============================
50 Hilly's; Func runs: 10000; result: 0.9221148477644971
=============================
All score: 0.96113

C_AO_(P_O)ES:100:150:0.02:8.0:10
=============================
50 Hilly's; Func runs: 10000; result: 0.9515388684155862
=============================
All score: 0.95154

C_AO_(P_O)ES:100:150:0.02:8.0:10
=============================
50 Hilly's; Func runs: 10000; result: 0.9374143219597522
=============================
All score: 0.93741

C_AO_(P_O)ES:100:150:0.02:8.0:10
=============================
50 Hilly's; Func runs: 10000; result: 0.9408961932771648
=============================
All score: 0.94090

C_AO_(P_O)ES:100:150:0.02:8.0:10
=============================
50 Hilly's; Func runs: 10000; result: 0.9533447716768805
=============================
All score: 0.96113

(P_O)ES on five test runs with Mersenne Twister generator:

C_AO_(P_O)ES:100:150:0.02:8.0:10

=============================
50 Hilly's; Func runs: 10000; result: 0.9726583883537465
=============================
All score: 0.97266

C_AO_(P_O)ES:100:150:0.02:8.0:10
=============================
50 Hilly's; Func runs: 10000; result: 0.9699307111435692
=============================
All score: 0.96993

C_AO_(P_O)ES:100:150:0.02:8.0:10
=============================
50 Hilly's; Func runs: 10000; result: 0.9864631937799934
=============================
All score: 0.98646

C_AO_(P_O)ES:100:150:0.02:8.0:10
=============================
50 Hilly's; Func runs: 10000; result: 0.9608040257741147
=============================
All score: 0.96080

C_AO_(P_O)ES:100:150:0.02:8.0:10
=============================
50 Hilly's; Func runs: 10000; result: 0.9540192199550924
=============================
All score: 0.95402

从实验结果可以看出，第一组实验涉及在算法中使用标准随机数生成器。我们发现，使用标准随机数生成器时的平均结果值约为0.95，而使用梅森旋转算法时的平均结果值为0.96，虽然差异不显著，但显示出如果采用梅森旋转算法，实验结果会略高一些。然而，请注意，使用该算法所花费的时间比标准算法的运行时间多3.5倍。


总结

因此，我们进行了一项有趣的实验，以解决许多交易者所担忧的问题：当与优化算法结合使用时，随机数生成器的质量是否重要？我在公开领域从未见过这样的研究。

对于一些使用布尔运算的算法，如BGA（二进制遗传算法），以及在一些小离散范围内使用随机数的算法，如DE（差分进化算法，其中随机数用于在种群中选择父代），随机数生成器的质量几乎无关紧要。

对于其他使用随机数在整个优化参数范围内生成新解决方案的算法，如(P_O)ES（大多数种群算法都类似），随机数生成器的作用微乎其微，几乎可以归入测量误差。重要的是，高质量的梅森旋转算法生成器比标准生成器慢3.5倍。

在优化问题中，质量与计算时间之间的平衡无疑起着重要作用。最终，我们选择优先考虑计算速度。使用高质量生成器带来的算法结果的提升在测量误差允许的范围内，而速度却显著降低。


下面附上本文中已进行测试的代码。文章中表述的结论和论断是基于实验的结果。

本文由MetaQuotes Ltd译自俄文
原文地址： https://www.mql5.com/ru/articles/14413

附加的文件 |
下载ZIP
The_world_of_AO_RND_quality.zip (24.24 KB)
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

该作者的其他文章

前往讨论
因果推断中的时间序列聚类 因果推断中的时间序列聚类
在机器学习中，聚类算法是重要的无监督学习算法，它们可以将原始数据划分为具有相似观测值的组。利用这些组，可以分析特定聚类的市场情况，使用新数据寻找最稳定的聚类，并进行因果推断。本文提出了一种在Python中进行时间序列聚类的原创方法。
手动交易的风险管理 手动交易的风险管理
在本文中，我们将详细探讨如何从头编写手动交易的风险管理类。这个类也可以被用作自动化程序的算法交易者继承的基类。
神经网络变得简单（第 73 部分）：价格走势预测 AutoBot 神经网络变得简单（第 73 部分）：价格走势预测 AutoBot
我们将继续讨论训练轨迹预测模型的算法。在本文中，我们将领略一种称为 “AutoBots” 的方法。
种群优化算法：二进制遗传算法（BGA）。第 I 部分 种群优化算法：二进制遗传算法（BGA）。第 I 部分
在本文中，我们将探讨二进制遗传和其它种群算法中所用的各种方法。我们将见识到算法的主要组成部分，例如选择、交叠和突变，以及它们对优化的影响。此外，我们还将研究数据表示方法，及其对优化结果的影响。