Role of random number generator quality in the efficiency of optimization algorithms

Introduction

When it comes to using optimization algorithms, many readers wonder how important it is to use a high-quality random number generator. The answer to this question is not as simple as it might seem at first glance. However, it is intuitive that the quality of random numbers can have a significant impact on the search capabilities of algorithms, since population algorithms are overwhelmingly based on stochastic search.

Let's look into this matter together. Before we get started, we need to consider different types of random number generators, their impact on the results and where you can find reliable options.

Random number generators (RNGs) are algorithms or devices that create a sequence of numbers or values and the numbers appear random. It is important to note that in computer science and mathematics such sequences are usually called "pseudo-random" because they are generated by deterministic algorithms rather than truly random processes.

There are two main types of random number generators:

1. Pseudorandom generators (PRGs). These generators use mathematical equations or algorithms to create a sequence of numbers that appear random. They are initialized with an initial value known as the "seed", and each time the generator is called, it produces the next number in the sequence. With the right choice of an algorithm and a seed, PSG can be useful for many applications where a pseudo-random sequence is required.
2. True random number generators (TRNGs). These generators use truly random processes, such as radioactive decay noise or quantum noise, to generate random numbers. Such generators are commonly used in cryptography, lotteries and other areas where a high degree of randomness is required.

Pseudo-random number generators are often used in programming, such as those built into standard programming language libraries.

The accuracy of random number generators built into programming languages depends on the specific implementation and algorithm that is used to generate the random numbers. Most modern programming languages, such as MQL5, Python, C++, C#, Java and others, provide built-in pseudo-random number generators that provide fairly good quality random numbers for most common applications.

In general, built-in random number generators in programming languages are usually suitable for most common tasks, but for tasks where a high level of randomness or security is required, it is worth looking at specialized solutions.

For tasks that require a high level of randomness and security, specialized solutions for generating random numbers can be used. Some of these solutions include:

1. Cryptographic random number generators. These generators are intended for use in cryptographic applications where a high level of security is required. They provide randomness, resistance to prediction and resistance to cryptanalysis.
2. Hardware random number generators. These generators use physical processes, such as thermal noise or quantum phenomena to create random numbers. They provide truly random numbers and are widely used in areas where a high degree of randomness is required.
3. Libraries for generating random numbers. There are specialized libraries that provide more complex algorithms for generating random numbers than standard built-in generators in programming languages. For example, the OpenSSL library provides cryptographic functions, including random number generation.

Some of the most common algorithms that can be used in built-in random number generators in programming languages include:

1. Linear Congruential Generator (LCG). This is one of the simplest and most widely used algorithms for generating pseudorandom numbers. It has disadvantages, such as short period and low degree of randomness.
2. Mersenne Twister. This algorithm has a long period and a good degree of randomness, and it is often used in many programming languages.
3. Xorshift. This is a family of pseudorandom number generation algorithms that have a good degree of randomness and high speed.
4. PCG (Permuted Congruential Generator). This relatively new class of generators has a good balance between randomness quality and performance.

The choice of a random number generator depends on the specific requirements of your tasks. Below are a few considerations that may help you make your decision:

1. Randomness quality. If your application requires a high level of randomness, especially for cryptographic purposes, then it is best to use specialized cryptographic random number generators such as Cryptographically Secure Pseudo-Random Number Generators (CSPRNGs).
2. Performance. If speed of random number generation is important to you, then higher performance algorithms such as Xorshift or PCG may be preferable.
3. Period and quality. Some algorithms, such as Mersenne Twister, have a long period and good quality of randomness.
4. Ease of use. For some developers, it is important that the random number generator is easily accessible and easy to use. Built-in generators, such as those provided by standard programming language libraries, can be convenient in such cases.

If you need a cryptographic level of security, it is recommended to use specialized cryptographic random number generators, such as CryptoRandom in Python or SecureRandom in Java. If you want a balance between performance and quality of randomness, then such algorithms as Mersenne Twister or PCG may be good options.

It is also important to remember that safety and randomness play a key role in system reliability and safety, so the choice of generator should be thoughtful and suited to the requirements of the specific application. But in this article we are interested in the influence of the RNG quality on the results of optimization algorithms. I will conduct my research exclusively in this context.

Mersenne Twister

Among the many random number generators available, it is not easy to find one that provides high quality generation while maintaining an acceptable speed. After all, the generation speed has a significant impact on the overall execution time of the optimization process.

Therefore, choosing a reliable generator is an important issue that requires a balance between the quality of random numbers and their generation speed. It is necessary to find an optimal solution that will ensure sufficient quality of generation without spending unnecessary time on this process.

Hardware generators are difficult to access for most users, so we immediately discard them from consideration here. Among the software generators, the high-quality Mersenne generator is widely known.

Mersenne Twister is a pseudorandom number generation algorithm that was developed by Makoto Matsumoto and Takuji Nishimura in 1997. It is one of the most widely used random number generation algorithms due to its good combination of long period, good randomness quality and relatively high performance.

Main characteristics of the Mersenne Twister:

• Long period. Mersenne Twister has a very long period, which means it can generate a huge number of unique pseudo-random numbers before the sequence begins to repeat itself.
• Good quality of randomness. The algorithm ensures good quality of randomness, which means that the numbers generated should match the statistical properties of random numbers.
• Performance. The Mersenne Twister has good performance making it an attractive choice for many applications.

The operating principle of the Mersenne Twister is based on a linear recurrent method of generating pseudo-random numbers. The algorithm uses a large number (usually 32-bit or 64-bit) as the state of the generator, which is then transformed using complex operations to produce the next pseudo-random number. In our case, we will use a 64-bit generator.

Let's consider the MersenneTwister64 class, which implements a pseudo-random number generator based on the Mersenne Twister algorithm for 64-bit numbers. Below is a brief description of its methods and functionality:

• Init - random number generator initialization method. It takes a seed (initial value) as an argument and sets the internal variables of the class. The MT array (Mersenne array) is filled with values based on the seed.
• RND_ulong - method that returns a random 64-bit unsigned integer. If the current index is greater than 312, the twist() method is called to update the values in the MT array. Then several bitwise shift and bitwise XOR operations are performed to produce a random number. The index value is incremented by 1 before returning the result.
• RND_ulong_In_Range - method that returns a random 64-bit unsigned integer within a given range (including the bounds). If min and max are equal, min is returned. If min is greater than max, the values of min and max are swapped. The RND_ulong() method is then called to generate a random number that is shifted and scaled to fall within the specified range.
• twist - internal method that performs the "mixing" operation of the MT array. For each array element, a combination of neighboring elements occurs using bitwise shift and bitwise XOR operations. The index value is set to 0 after the shuffle operation is performed.

//——————————————————————————————————————————————————————————————————————————————
class MersenneTwister64
{
public: //--------------------------------------------------------------------

  void Init (ulong seed)
  {
    index = 312;

    MT [0] = seed;
    for (int i = 1; i < 312; i++)
    {
      MT [i] = (6364136223846793005 * (MT [i - 1] ^ (MT [i - 1] >> 62)) + i) & 0xFFFFFFFFFFFFFFFF;
    }
  }

  //from 0 to 18 446 744 073 709 551 615
  ulong RND_ulong ()
  {
    if (index >= 312)
    {
      twist ();
    }

    ulong y = MT [index];
    y = y ^ (y >> 29) & 0x5555555555555555;
    y = y ^ (y << 17) & 0x71D67FFFEDA60000;
    y = y ^ (y << 37) & 0xFFF7EEE000000000;
    y = y ^ (y >> 43);

    index++;
    return y;
  }

  ulong RND_ulong_In_Range (ulong min, ulong max)
  {
    if (min == max) return min;
    if (min > max)
    {
      ulong temp = min;
      min = max;
      max = temp;
    }
    return min + RND_ulong () % (max - min + 1);
  }

private: //-------------------------------------------------------------------
  ulong MT [312];
  int index;

  void twist ()
  {
    for (int i = 0; i < 312; i++)
    {
      ulong y = (MT [i] & 0x8000000000000000) + (MT [(i + 1) % 312] & 0x7FFFFFFFFFFFFFFF);
      MT [i] = MT [(i + 156) % 312] ^ (y >> 1);
      if (y % 2 != 0)
      {
        MT [i] = MT [i] ^ 0xB5026F5AA96619E9;
      }
    }
    index = 0;
  }
};
//——————————————————————————————————————————————————————————————————————————————

Comparing random number generators and test results

Let's try to visually compare the work of two random number generators: the one built into MQL5 (hereinafter called "standard") and the Mersenne Twister. To do this, we generated two images and analyzed their appearance. At first glance, both images are devoid of patterns and periodicity, and their design is homogeneous. We do not observe any obvious visual differences between the generators.

The image generated by the standard generator

The image generated by Mersenne Twister generator

However, for a more objective comparison of random number generators, it is recommended to use statistical tests that allow us to evaluate the degree of randomness and the statistical properties of the generated numbers. It is important to note that visual assessment may be limited and may not always be able to detect hidden systematic deviations from true randomness.

Thus, for a more accurate comparison of generators, we will conduct additional analysis using a statistical test to obtain more reliable results. We are interested in uniformity, so we will use the chi-square test, which is a statistical test that evaluates how uniform the randomly generated numbers are. In this case, there were 10,000 observations, each containing 10,000 generated values.

The chi-square test (χ² test) is used to test the data distribution evenness. It allows us to determine how closely the observed frequencies correspond to those expected in a uniform distribution.

The critical value for the significance level of 0.05 in the chi-square test (χ² test) with 9999 degrees of freedom (10,000 observations minus 1) is 10232.73727. This value is a constant used to compare expected frequencies with observed frequencies in the chi-square test. It is taken from the chi-square table of the distribution and helps determine how significant the differences between observed and expected values are.

When we perform the chi-square test, we compare the calculated statistic with the critical value. If the calculated statistic is greater than the critical value, we can reject the null hypothesis that the distribution is consistent with the expected one. Otherwise, the null hypothesis is accepted.

Let's look at a section of the test script code (in general, the script builds images, measures the execution time of generators and calculates the chi-square test).

Two arrays are created and initialized: "observed" and "expected". The "observed" array will be used to store the observed number of random numbers in each of the BoxesNumber intervals. The "expected" array will contain the expected number of random numbers in each bin if the generators were running with a perfect uniform distribution.

The code then checks the value of the StandardRND variable, which specifies which random number generator to use. If StandardRND is 'true', then the standard random number generator in MQL5 is used. Otherwise, Mersenne Twister generator is used. The loop generates random numbers and increments the corresponding element of the "observed" array for the interval.

After random numbers are generated, the chi-square statistic is calculated. For each interval, the "(observed - expected)^2 / expected" value is calculated and summed into the "chiSquareStatistic" variable. The "chiSquareCriticalValue" critical value is then set for the significance level of 0.05*.

The comparison results are displayed at the end of the code. If the value of "chiSquareStatistic" is greater than "chiSquareCriticalValue", then a message is displayed that we reject the null hypothesis: the distribution differs from expected. Otherwise, a message is displayed that we do not reject the null hypothesis: the distribution is consistent with the expected one.

* - Significance level of 0.05 (or 5%) is one of the most common significance levels and is widely used in many areas of scientific research. This means that when conducting a statistical test with a significance level of 0.05, we allow a 5% chance of a type I error. Significance level in statistics is a threshold value used to make decisions about the statistical significance of results. It is usually denoted as α (alpha) and represents the probability of a type I error, that is, the probability of rejecting a true null hypothesis.

int observed [];
ArrayResize     (observed, BoxesNumber);
ArrayInitialize (observed, 0);

int expected [];
ArrayResize     (expected, BoxesNumber);
ArrayInitialize (expected, ThrowsNumber / BoxesNumber);

if (StandardRND)
{
  Print ("Standard, ", ThrowsNumber, " throws, ", BoxesNumber, " boxes");
  for (int i = 0; i < ThrowsNumber; i++)
  {
    observed [rndS.RNDintInRange (0, BoxesNumber - 1)]++;
  }
}
else
{
  Print ("Mersenne, ", ThrowsNumber, " throws, ", BoxesNumber, " boxes");
  for (int i = 0; i < ThrowsNumber; i++)
  {
    observed [(int)rndM.RND_ulong_In_Range (0, BoxesNumber  - 1)]++;
  }
}

// Calculate the chi-square statistic
double chiSquareStatistic = 0;
for (int i = 0; i < ArraySize(observed); i++)
{
  chiSquareStatistic += MathPow(observed[i] - expected[i], 2) / expected[i];
}

// Critical value for the significance level of 0.05
double chiSquareCriticalValue = 10232.73727; //10000

// Output results
if (chiSquareStatistic > chiSquareCriticalValue)
{
  Print("We reject the null hypothesis: The distribution differs from the expected one.");
}
else
{
  Print("We do not reject the null hypothesis: The distribution is consistent with the expected one.");
}

Let's run the script 5 times to calculate statistics and standard generator execution time execution of a standard generator. Mersenne Twister generator execution time is measured at the same time. Calculate the difference in the execution time as a quotient of the Twister and standard generator execution time.

2024.03.18 20:54:33.456    stand: 120353 mcs
2024.03.18 20:54:33.456    mers : 397920 mcs
2024.03.18 20:54:33.456    diff : 3.3062740438543283
2024.03.18 20:54:33.459    Standard, 100000000 throws, 10000 boxes
2024.03.18 20:54:33.854    We reject the null hypothesis: The distribution differs from the expected one.
2024.03.18 20:54:38.802    stand: 121670 mcs
2024.03.18 20:54:38.802    mers : 403180 mcs
2024.03.18 20:54:38.802    diff : 3.3137174323991125
2024.03.18 20:54:38.805    Standard, 100000000 throws, 10000 boxes
2024.03.18 20:54:39.194    We reject the null hypothesis: The distribution differs from the expected one.
2024.03.18 20:54:43.767    stand: 121222 mcs
2024.03.18 20:54:43.767    mers : 400986 mcs
2024.03.18 20:54:43.767    diff : 3.3078649090099157
2024.03.18 20:54:43.770    Standard, 100000000 throws, 10000 boxes
2024.03.18 20:54:44.156    We reject the null hypothesis: The distribution differs from the expected one.
2024.03.18 20:54:48.476    stand: 119246 mcs
2024.03.18 20:54:48.476    mers : 400319 mcs
2024.03.18 20:54:48.476    diff : 3.3570853529678146
2024.03.18 20:54:48.479    Standard, 100000000 throws, 10000 boxes
2024.03.18 20:54:48.873    We reject the null hypothesis: The distribution differs from the expected one.
2024.03.18 20:54:53.144    stand: 119309 mcs
2024.03.18 20:54:53.144    mers : 404502 mcs
2024.03.18 20:54:53.144    diff : 3.390372897266761
2024.03.18 20:54:53.148    Standard, 100000000 throws, 10000 boxes
2024.03.18 20:54:53.553    We reject the null hypothesis: The distribution differs from the expected one.

Unfortunately, the standard random number generator failed all of the five tests when tested using the chi-square test indicating that there were systematic deviations from the expected uniform random distribution.

Now we will test the Mersenne Twister, while continuing to measure the execution time of both generators.

2024.03.18 20:55:48.133    stand: 115447 mcs
2024.03.18 20:55:48.133    mers : 413258 mcs
2024.03.18 20:55:48.133    diff : 3.57963394458063
2024.03.18 20:55:48.138    Mersenne, 100000000 throws, 10000 boxes
2024.03.18 20:55:49.504    We do not reject the null hypothesis: The distribution is consistent with the expected one.
2024.03.18 20:55:56.340    stand: 117433 mcs
2024.03.18 20:55:56.340    mers : 402337 mcs
2024.03.18 20:55:56.340    diff : 3.4260982858310696
2024.03.18 20:55:56.346    Mersenne, 100000000 throws, 10000 boxes
2024.03.18 20:55:57.717    We do not reject the null hypothesis: The distribution is consistent with the expected one.
2024.03.18 20:56:05.837    stand: 120129 mcs
2024.03.18 20:56:05.837    mers : 400705 mcs
2024.03.18 20:56:05.837    diff : 3.3356225391037966
2024.03.18 20:56:05.843    Mersenne, 100000000 throws, 10000 boxes
2024.03.18 20:56:07.219    We do not reject the null hypothesis: The distribution is consistent with the expected one.
2024.03.18 20:56:12.206    stand: 119980 mcs
2024.03.18 20:56:12.206    mers : 397436 mcs
2024.03.18 20:56:12.206    diff : 3.312518753125521
2024.03.18 20:56:12.211    Mersenne, 100000000 throws, 10000 boxes
2024.03.18 20:56:13.582    We do not reject the null hypothesis: The distribution is consistent with the expected one.
2024.03.18 20:56:18.837    stand: 118140 mcs
2024.03.18 20:56:18.837    mers : 397565 mcs
2024.03.18 20:56:18.837    diff : 3.3652023023531403
2024.03.18 20:56:18.842    Mersenne, 100000000 throws, 10000 boxes
2024.03.18 20:56:20.220    We do not reject the null hypothesis: The distribution is consistent with the expected one.

The Mersenne vortex coped with the task in all five tests (runs of the chi-square test). At the same time, we see that the generator has a significant drawback - Twister is approximately 3.4 times slower than the standard one, which can significantly affect the speed of optimization algorithms.

Now it is time for the most interesting part - the highlight of this study: we will conduct tests to find out how much the quality of random number generators affects the optimization results. As you might remember, the standard generator creates numbers in the range [0;32,767], while the 64-bit Mersenne Twister - in the range [0;18,446,744,073,709,551,615].

To conduct the experiment, we selected 50 Hilly functions and performed 10,000 iterations for each function. Why did I choose Hilly's 50 features and why Hilly? Firstly, this number was chosen in such a way that the algorithm could not achieve 100% convergence in a limited number of runs of the fitness function. This made it possible to observe the difference in the use of different types of random number generators. Secondly, the choice of Hilly functions is due to its smoothness, which allows us to avoid the natural scatter of results not associated with the generation of random numbers if we used a discrete test function. I repeated the experiment 20 times and averaged the results to obtain more reliable and statistically significant data. As an optimization algorithm, we chose BGA, which ranks first in our rating table and at the same time demonstrates a very small scatter of results on smooth functions.

From the printout of the results, it can be seen that the optimization results are almost the same for the BGA algorithm when using both a standard random number generator and Mersenne generator. The differences are observed only in the third decimal place, which are not critical for our purposes and are considered quite small.

//Standard
C_AO_BGA:50:50:1.0:3:0.001:0.7:16
=============================
50 Hilly's; Func runs: 10000; result: 0.9257245560389498
=============================
All score: 0.92572

//Mersenne
C_AO_BGA:50:50:1.0:3:0.001:0.7:16
=============================
50 Hilly's; Func runs: 10000; result: 0.9221148477644971
=============================
All score: 0.92211

While visualizing the algorithm operation, we did not find significant deviations when using two different types of random number generators within the algorithm logic. The difference in the spread of results is well within the variability of the algorithm operation itself.

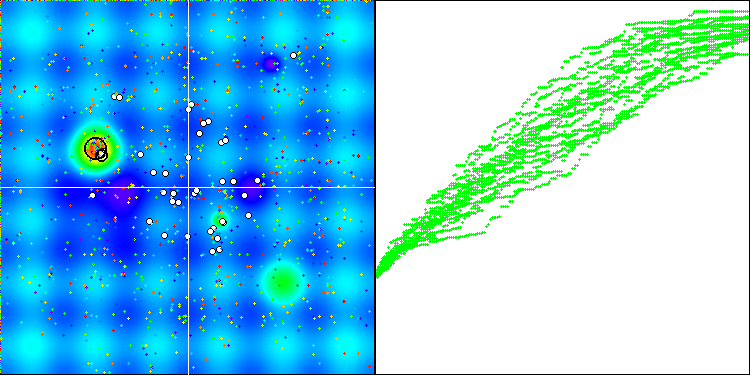
BGA with the standard generator 

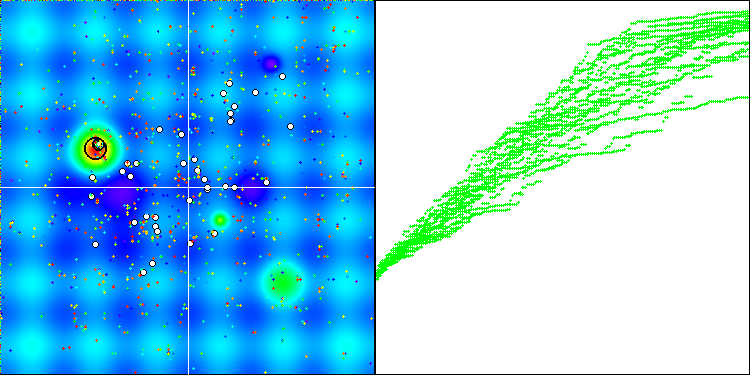
BGA with Mersenne Twister

The preliminary conclusion is this: the quality of random number generators does not affect the performance of optimization algorithms.

Let us make the assumption that the slight difference in results when using the above-mentioned generators in the BGA optimization algorithm may be due to the fact that in BGA each bit in the chromosome is generated independently of the other bits. In fact, the role of random generators comes down to the Boolean "yes/no" operation and the difference between the number of "yes" and "no" occurrences is only thousandths of a percent.

So, for a binary genetic algorithm there is no difference in using random number generators, although this conclusion was not at all obvious at first glance, but is this true for other optimization algorithms, especially those that use continuous probabilities throughout the space bounded by [min, max] by coordinates?

Let's try to conduct a few more experiments to confirm the obtained statement or refute it. This time we will take the (P_O)ES algorithm, which is among the leaders in our rating table and uses a large number of operations with random numbers in its logic, as well as applies continuous probabilities on the entire search space.

(P_O)ES on five test runs with the standard random generator:

C_AO_(P_O)ES:100:150:0.02:8.0:10
=============================
50 Hilly's; Func runs: 10000; result: 0.9611258962207798
=============================
All score: 0.96113

C_AO_(P_O)ES:100:150:0.02:8.0:10
=============================
50 Hilly's; Func runs: 10000; result: 0.9515388684155862
=============================
All score: 0.95154

C_AO_(P_O)ES:100:150:0.02:8.0:10
=============================
50 Hilly's; Func runs: 10000; result: 0.9374143219597522
=============================
All score: 0.93741

C_AO_(P_O)ES:100:150:0.02:8.0:10
=============================
50 Hilly's; Func runs: 10000; result: 0.9408961932771648
=============================
All score: 0.94090

C_AO_(P_O)ES:100:150:0.02:8.0:10
=============================
50 Hilly's; Func runs: 10000; result: 0.9533447716768805
=============================
All score: 0.95334

(P_O)ES on five test runs with Mersenne Twister generator:

C_AO_(P_O)ES:100:150:0.02:8.0:10

=============================
50 Hilly's; Func runs: 10000; result: 0.9726583883537465
=============================
All score: 0.97266

C_AO_(P_O)ES:100:150:0.02:8.0:10
=============================
50 Hilly's; Func runs: 10000; result: 0.9699307111435692
=============================
All score: 0.96993

C_AO_(P_O)ES:100:150:0.02:8.0:10
=============================
50 Hilly's; Func runs: 10000; result: 0.9864631937799934
=============================
All score: 0.98646

C_AO_(P_O)ES:100:150:0.02:8.0:10
=============================
50 Hilly's; Func runs: 10000; result: 0.9608040257741147
=============================
All score: 0.96080

C_AO_(P_O)ES:100:150:0.02:8.0:10
=============================
50 Hilly's; Func runs: 10000; result: 0.9540192199550924
=============================
All score: 0.95402

As can be seen from the results of the experiments performed, the first series of experiments related to the use of the standard random number generator in the algorithm. We see that the average result value is approximately 0.95, and the average result value when using the Mersenne Twister is 0.96, which does not make a significant difference, but shows us that the results of the experiments are still higher if Mersenne Twister is present. However, keep in mind that the time spent using this algorithm exceeds the running time of the standard algorithm by 3.5 times.

Summary

So, we conducted an interesting experiment to put an end to the question that worries many traders: Is the quality of random number generators important when used in conjunction with optimization algorithms? I have never seen such a study in the public domain.

For some algorithms that use Boolean operations, such as BGA, and algorithms that use random numbers in a small discrete range, such as DE (differential evolution, where random numbers are used to select parents in a population), the RNG quality plays almost no role.

For other algorithms that use random numbers to generate new solutions over the entire range of optimized parameters, such as (P_O)ES (most population algorithms are similar), the RNG plays minor role fitting into the measurement error. It is important that the higher quality Mersenne Twister generator is 3.5 times slower than the standard one.

In optimization problems, the balance between quality and computation time certainly plays an important role. Eventually, we choose speed in this case. The increase in algorithm results from the use of high-quality generators is within the measurement error, while the speed drops significantly.

The archive with the codes of the tests performed is attached below. The conclusions and judgments presented in the article are based on the results of the experiments.