ニューラルネットワークが簡単に（第72回）：ノイズ環境における軌道予測

MetaTrader 5 — トレーディングシステム | 8 8月 2024, 09:47

240

Dmitriy Gizlyk

はじめに

過去の軌跡を分析することで将来の資産の動きを予測することは、過去のトレンドの分析が戦略を成功させる重要な要因となる金融市場取引において重要です。将来の資産の軌道は、基礎的要因の変化とそれに対する市場の反応による不確実性を含んでいることが多く、それが将来の資産の潜在的な動きの多くを決定します。したがって、市場の動きを予測する効果的な方法は、潜在的な将来の軌道の分布、あるいは少なくともいくつかのもっともらしいシナリオを生成できなければなりません。

最も可能性の高い予測のための既存のアーキテクチャはかなり多様であるにもかかわらず、金融資産の将来の軌道を予測する場合、モデルは過度に単純化された予測という問題に直面する可能性があります。この問題が解決しないのは、モデルが訓練セットのデータを狭く解釈しているからです。資産の軌跡の明確なパターンがない場合、予測モデルは、金融商品の動きの変化の多様性を捉えることができない、単純または同種の動きのシナリオを生成してしまいます。これは予測精度の低下につながります。

論文「Enhancing Trajectory Prediction through Self-Supervised Waypoint Noise Prediction」の著者は、これらの問題を解決するための新しいアプローチとして、2つのモジュールからなる、自己教師ありウェイポイントノイズ予測(Self-Supervised Waypoint Noise Prediction: SSWNP)を提案しました。

空間整合性モジュール
ノイズ予測モジュール

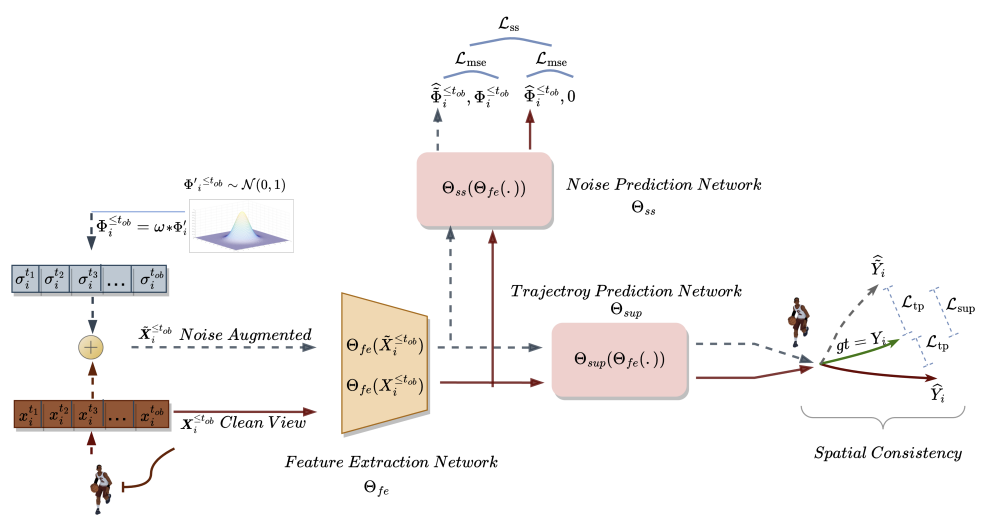
1つ目は、歴史的に観測された軌跡の2つの異なるビューを作成することで、キーポイントの空間領域のクリーンなビューとノイズ拡張したビューを作成します。その名の通り、クリーンバージョンは元の軌跡を表し、ノイズ拡張バージョンはノイズを加えて元の特徴量空間を移動した過去の軌跡を表します。このアプローチは、過去の軌跡のノイズの多いバージョンは、訓練セットからのデータの狭い解釈に対応しないという事実を利用します。モデルはこの追加情報を使って、単純すぎる予測の問題を克服し、より多様なシナリオを探求します。2つの異なる過去の軌跡を生成した後、未来の軌跡予測モデルを訓練することで、2つからの予測間の空間的整合性を維持し、運動予測タスクを超える時空間的特徴を学習します。

ノイズ予測モジュールは、解析された軌道のノイズを特定するという補助的な問題を解決します。これは、移動予測モデルが潜在的な空間的多様性をより適切にモデル化し、移動予測における基礎となる表現についての理解を深め、将来の予測を改善するのに役立ちます。

この手法の著者は、SSWNPの空間的一貫性とノイズ予測モジュールの重要性を実証的に示すために、追加実験をおこないました。移動予測問題を解くために空間的一貫性モジュールだけを使用する場合、訓練されたモデルの性能は最適でないことが観察されます。そのため、両モジュールを統合しています。

1.SSWNPアルゴリズム

軌跡予測の目的は、ダイナミックな環境におけるエージェントの最も可能性の高い将来の軌跡を、過去に観測された軌跡に基づいて決定することです。軌跡はウェイポイントと呼ばれる空間点の時系列で表されます。観測された軌跡はt1からtobまでの期間をカバーし、次のように表すことができます。

ここでXi*は時間ステップ t*におけるiの座標に対応します。同様に、期間 [tob+1,tfu]におけるエージェントiの予測される将来の軌道はŶtob+1≤t≤tfuと記述できます。エージェントiの将来の移動に対応する真の軌跡は、Ytob+1≤t≤tfuと記述できます。

SSWNP法では、まず軌跡の2つの異なるビューが作成されます。1つはクリーンなビュー(X≤tob)、もう1つはノイズ拡張ビュー(Ẍ≤tob)として特徴付けられます。クリーンなビューは、訓練データセットからの元の軌道に対応し、ノイズ拡張ビューは、ノイズを加えることによって特徴空間内で移動した軌道に対応します。

標準正規分布N(0, 1)からのノイズは、クリーンな軌道を歪めるために使用されます。この方法の著者は、ウェイポイントの空間的な動きを制御するノイズファクター(ω)というパラメータを導入しています。

クリーンビューとノイズ拡張ビューを作成した後、それらを特徴量抽出モデル(Θfe)に送り、クリーンビューとノイズ拡張ビューの両方に対応する特徴を生成します。得られた特徴量を軌跡予測モデル(Θsup)に入力し、下式のように、軌跡Ŷtob+1≤t≤tfuとŸtob+1≤t≤tfuを予測します。

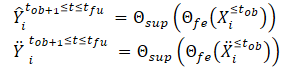
予測された軌跡と訓練データセットからの真の軌跡との間のギャップを最小化するようにモデルを訓練します。このことからわかるように、ノイズのない初期データ(ŶおよびŸ)から、訓練データセット(Y)からの真の軌道を予測する際の誤差を最小化することで、間接的に2つの予測軌道間のギャップを小さくしています。これにより、観測されたクリーン軌跡に基づく将来の軌跡予測と、ノイズ拡張軌跡との間の空間的整合性が保たれます。

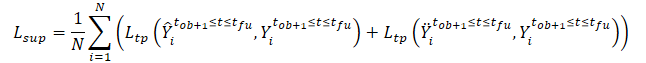
さらに、SSWNP法は、自己教師ありノイズ予測の問題を解決します。この問題には、観測された過去の軌跡X≤tobと同様に、ノイズ拡張形式Ẍ≤tobで存在するノイズを予測することが含まれます。ここでの目的は、観測されたウェイポイントに関連するノイズ値を推定することです。

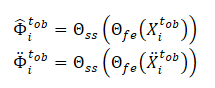
モデルΘfeによって抽出された特徴は、ノイズ予測モデル(Θss)の入力データとして使用され、観測された軌跡（クリーンビューとオーグメントビュー）のノイズレベルを決定します。ノイズ予測モデルの自己教師付き学習のための損失関数として、この手法の著者は二乗平均平方根誤差(MSE)の使用を提案しています。

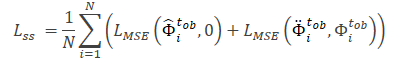
ここでの値0は、クリーンフォームの軌跡にノイズがないことを示します。

SSWNP法の一般的な損失関数は次のように表されます。

ここでλは、提案アプローチを用いてモデルを学習する際の、全誤差に対するノイズ予測誤差の寄与を示します。

自己教師ありウェイポイントノイズ予測法のオリジナルは下にあります。

2.MQL5を使用した実装

ここまで、自己教師ありウェイポイントノイズ予測法の理論的側面を見てきました。おわかりのように、提案されたアプローチは、使用するモデルのアーキテクチャやソースデータの構造に対していかなる制限も課していません。これにより、提案されたアプローチを、これまで検討してきた多くのアルゴリズムと統合することができます。特にこの記事では、目標条件付き予測符号化(GCPC)に関する最近の記事で取り上げた方法であるオートエンコーダ訓練アルゴリズムTrajNetに、提案されたアプローチを追加します。

前述したように、GCPCアルゴリズムは2段階のモデル訓練を提供します。

本稿で取り上げるSSWNP法は、将来の軌道を予測する効率を向上させることを目的としています。そのため、「軌道関数の訓練」段階のみを対象としています。この段階で必要な調整をおこないます。第2段階である「行動方針訓練」は、従来の形を踏襲します。

2.1 方法統合の問題

新しいアプローチを既製の構造に統合する場合、すでに構築されたプロセスを混乱させないような変更を加えなければなりません。したがって、作業を開始する前に、新しいアプローチが以前に作成した学習プロセスやモデルのその後の操作に与える影響を分析しなければなりません。

訓練データセットの軌道にノイズを加えると、元のデータの分布は明らかに変化します。その結果、これはソースデータを前処理するバッチ正規化層のパラメータに影響します。一方では、これが私たちが達成しようとしていることでもあります。私たちは、確率の高い環境において、実際の条件に近い状態で動作するモデルを訓練したいと考えています。一方、ランダムなノイズが加わると、元のデータが分析パラメータの実際の値を超えてしまう可能性があります。この要因の悪影響を最小限に抑えるため、アルゴリズムの作者は、データシフト量を調整するノイズ係数(ω)を追加しました。正規化されていない「生」データがある場合、ソースデータの各指標に対して個別のノイズ係数が必要になります。したがって、ノイズ要因のベクトルを使用することになります。そして、ハイパーパラメータのベクトルを選択することは、かなり複雑なタスクとなり、その複雑さは、分析されるパラメータの数が増えるにつれて増大します。

結局のところ、この問題の解決策は非常に簡単です。正規分布のノイズにある係数を掛けることは、実は変分オートエンコーダー層で使った再パラメータ化トリック(reparameterization trick)によく似ています。

したがって、訓練データセットの分布のパラメータを使用することで、モデルを元の分布内に保つことができます。同時に、分析された環境に内在する確率性も加えます。

しかし、ここでもう一点考慮しなければならないことがあります。訓練データセットの実際の軌跡をランダムな値に置き換えるのではなく、その軌跡にノイズを加えます。この問題を直接解くと、初期データの分布パラメータが得られます。

ノイズを使用するというアイデアをもう一度見てみましょう。特定の時点で、分析した各パラメータの実際のデータを持っています。次の時間ステップでは、パラメータが一定量変化します。各パラメータの変化の大きさは、多数の異なる要因に依存するため、確率変数に近くなります。同時に、このような変化には限界があります。したがって、元のデータの自然な分布を維持するために、各分析パラメータの後続の2つの値の間のこのような偏差の分布パラメータを決定することができます。これらは、ノイズを再パラメトリック化するためのパラメータとなります。

ここで、パラメータ値の大幅な変化は、しばしば市場状況の変化を示すという事実を考慮しなければなりません。SSWNP法によれば、モデルはクリーンなデータとノイズの多いデータからの軌道予測間のギャップを最小化するように訓練されます。そのため、本手法の著者が提案したノイズ係数を用いて、訓練セットから得られる実際の軌跡からのバイアスを制限します。

2つ目のポイントは、GCPC法におけるDropOut層の使用です。これは一種の正則化としても機能し、いくつかの「外れ値」を無視して欠損パラメータを復元するようにモデルを訓練するように設計されています。メソッドを組み合わせる場合、DropOut層によってマスクされたパラメータにノイズが加わります。一方、パラメータのマスキングは、ノイズを加えるのに比べ、モデルによって解決される問題をより難しくします。

前述したように、以前に構築したプロセスを破ってはなりません。したがって、DropOut層をエンコーダーアーキテクチャから除外することはしません。モデルの訓練結果を観察するのは興味深いことです。

それでは、自己教師ありウェイポイントノイズ予測法の構成を見てみましょう。アルゴリズムに従って、3つのモデルを訓練します。

特徴量抽出モデル
軌道予測モデル
ノイズ予測モデル

ここでは、SSWNPアルゴリズムを以前に構築したGCPCプロセスに統合する予定です。両者のモデルを比較してみましょう。SSWNP特徴量抽出モデルはGCPCエンコーダーに対応します。GCPCデコーダはSSWNP軌道予測モデルとして表現できます。そこで、ノイズ予測モデルを追加する必要があります。

2.2 モデルアーキテクチャ

モデルアーキテクチャはCreateTrajNetDescriptionsメソッドで記述され、そこに3番目のモデルの記述を追加します。パラメータで、このメソッドは、これら3つのモデルのアーキテクチャを記述する3つの動的配列へのポインタを受け取ります。メソッド本体では、受け取ったポインタの妥当性を確認し、必要であればオブジェクトの新しいインスタンスを生成します。

bool CreateTrajNetDescriptions(CArrayObj *encoder, CArrayObj *decoder, CArrayObj *noise)
  {
//---
   CLayerDescription *descr;
//---
   if(!encoder)
     {
      encoder = new CArrayObj();
      if(!encoder)
         return false;
     }
   if(!decoder)
     {
      decoder = new CArrayObj();
      if(!decoder)
         return false;
     }
   if(!noise)
     {
      noise = new CArrayObj();
      if(!noise)
         return false;
     }

エンコーダーとデコーダーのアーキテクチャーの説明をそのままコピーします。これまでの記事で見てきたように、エンコーダーに生の初期データを入力し、その中で過去の価格変動と分析された指標のみを示します。

//--- Encoder
   encoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

これらはバッチ正規化層で一次処理を受けます。

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1000;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

正規化されたデータは、DropOut層でランダムにマスクされます。

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronDropoutOCL;
   descr.count = prev_count;
   descr.probability = 0.8f;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

その後、畳み込み層のブロックを使って安定したパターンを探索します。

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   prev_count = descr.count = prev_count - 2;
   descr.window = 3;
   descr.step = 1;
   int prev_wout = descr.window_out = 3;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronSoftMaxOCL;
   descr.count = prev_count;
   descr.step = prev_wout;
   descr.optimization = ADAM;
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   prev_count = descr.count = prev_count;
   descr.window = prev_wout;
   descr.step = prev_wout;
   prev_wout = descr.window_out = 8;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 6
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronSoftMaxOCL;
   descr.count = prev_count;
   descr.step = prev_wout;
   descr.optimization = ADAM;
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

次に、全結合層ブロックでデータを処理します。

//--- layer 7
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.optimization = ADAM;
   descr.activation = LReLU;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 8
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = EmbeddingSize;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

エンコーダーの以前のパスの結果を再帰的に追加します。

//--- layer 9
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConcatenate;
   descr.count = 2 * EmbeddingSize;
   descr.window = prev_count;
   descr.step = EmbeddingSize;
   descr.optimization = ADAM;
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

そして、分析対象の履歴の内部スタックにデータを転送します。

//--- layer 10
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronEmbeddingOCL;
   prev_count = descr.count = GPTBars;
     {
      int temp[] = {EmbeddingSize, EmbeddingSize};
      ArrayCopy(descr.windows, temp);
     }
   prev_wout = descr.window_out = EmbeddingSize;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

その結果得られた履歴データのセットは、アテンションブロックで分析されます。

//--- layer 11
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronMLMHAttentionOCL;
   descr.count = prev_count * 2;
   descr.window = prev_wout;
   descr.step = 4;
   descr.window_out = 16;
   descr.layers = 4;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

解析結果は全結合層で圧縮されます。

//--- layer 12
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = EmbeddingSize;
   descr.optimization = ADAM;
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 13
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronSoftMaxOCL;
   descr.count = prev_count;
   descr.step = 1;
   descr.optimization = ADAM;
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

エンコーダー出力では、SoftMax関数を使ってデータを正規化します。

エンコーダーのフィードフォワードパスの結果はデコーダーに送られます。

//--- Decoder
   decoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = EmbeddingSize;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!decoder.Add(descr))
     {
      delete descr;
      return false;
     }

この場合、すでに正規化された前のモデルから得られたデータを扱っています。したがって、データの前処理は必要ありません。早速、全結合層を使って拡張してみます。

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = (HistoryBars + PrecoderBars) * EmbeddingSize;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!decoder.Add(descr))
     {
      delete descr;
      return false;
     }

受信したデータはアテンションブロックで分析されます。

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronMLMHAttentionOCL;
   prev_count = descr.count = prev_count / EmbeddingSize;
   prev_wout = descr.window = EmbeddingSize;
   descr.step = 4;
   descr.window_out = 16;
   descr.layers = 2;
   descr.optimization = ADAM;
   if(!decoder.Add(descr))
     {
      delete descr;
      return false;
     }

アテンションブロックの出力には、予測された各ローソク足の埋め込みがあります。得られた埋め込みをデコードするために、多モデル全結合層を使用します。

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronMultiModels;
   descr.count = 3;
   descr.window = prev_wout;
   descr.step = prev_count;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!decoder.Add(descr))
     {
      delete descr;
      return false;
     }

エンコーダーとデコーダーのアーキテクチャーの説明の後に、ノイズ予測モデルのアーキテクチャーの説明を加える必要があります。このモデルはデコーダーと同様、エンコーダーの結果を入力データとして使用します。したがって、元のデコーダーのデータ層をコピーするだけです。

//--- Noise Prediction
   noise.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.Copy(decoder.At(0));
   if(!noise.Add(descr))
     {
      delete descr;
      return false;
     }

次に、全結合層を使って、受信したデータをエンコーダー入力の元データのサイズに拡張します。

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = HistoryBars * EmbeddingSize;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!noise.Add(descr))
     {
      delete descr;
      return false;
     }

ご注意ください。次のステップでは、おそらくこの連載で初めて、選択したハイパーパラメータに応じてモデルアーキテクチャの分岐を作成します。ここで重要なのは、エンコーダー入力で分析されたローソク足の数です。複数のローソク足を分析する場合、モデルアーキテクチャはデコーダーに似ています。アテンションブロックとマルチモデル層を使って埋め込みをデコードします。ただ、ここでお話ししているのは予想ローソク足ではなく、分析ローソク足です。

//---
   if(HistoryBars > 1)
     {
      //--- layer 2
      if(!(descr = new CLayerDescription()))
         return false;
      descr.type = defNeuronMLMHAttentionOCL;
      prev_count = descr.count = prev_count / EmbeddingSize;
      prev_wout = descr.window = EmbeddingSize;
      descr.step = 4;
      descr.window_out = 16;
      descr.layers = 2;
      descr.optimization = ADAM;
      if(!noise.Add(descr))
        {
         delete descr;
         return false;
        }
      //--- layer 3
      if(!(descr = new CLayerDescription()))
         return false;
      descr.type = defNeuronMultiModels;
      descr.count = BarDescr;
      descr.window = prev_wout;
      descr.step = prev_count;
      descr.activation = None;
      descr.optimization = ADAM;
      if(!noise.Add(descr))
        {
         delete descr;
         return false;
        }
     }

エンコーダー入力で1本のローソク足だけを分析する場合、異なるローソク足間の関係を分析するアテンション層を使用する意味はありません。したがって、ここでは単純なパーセプトロンを使用します。

   else
     {
      //--- layer 2
      if(!(descr = new CLayerDescription()))
         return false;
      descr.type = defNeuronBaseOCL;
      descr.count = LatentCount;
      descr.optimization = ADAM;
      descr.activation = LReLU;
      if(!noise.Add(descr))
        {
         delete descr;
         return false;
        }
      //--- layer 3
      if(!(descr = new CLayerDescription()))
         return false;
      descr.type = defNeuronBaseOCL;
      prev_count = descr.count = BarDescr;
      descr.activation = None;
      descr.optimization = ADAM;
      if(!noise.Add(descr))
        {
         delete descr;
         return false;
        }
     }
//---
   return true;
  }

上記の説明は、軌跡関数モデルの訓練に参加するモデルのアーキテクチャについてのみ提供されています。エージェント行動方策の訓練モデルのアーキテクチャをそのまま使用します。添付ファイルをご覧ください。詳しい説明は前回の記事でおこないました。

2.3 モデル訓練プログラム

使用されているモデルのアーキテクチャを説明した後、プログラムのアルゴリズムを検討します。SSWNP法の著者は、ソースデータの選択と訓練のための観測された軌道の収集に関する要件を提示していないことにご注意ください。そのため、環境と相互作用するプログラムは、調整することなくそのまま使用されます。この記事で使用されているすべてのプログラムの完全なコードは添付ファイルから入手可能です。説明が必要な場合は、前回の記事を参照するか、ディスカッションで質問してください。

次に軌跡関数学習EA (..\Experts\SSWNP\StudyEncoder.mq5)で3つのモデルを同時に訓練します。

特徴量抽出モデル(Encoder)
軌道予測モデル(Decoder)
ノイズ予測モデル(Noise)

CNet                 Encoder;
CNet                 Decoder;
CNet                 Noise;

理論の部分で述べたように、SSWNPアルゴリズムを実装するためには、2つのハイパーパラメータを定義する必要があります。プログラムでは定数として実装します。

#define        STE_Noise_Multiplier    1.0f/10        // λ determined the impact of noise prediction error
#define        STD_Delta_Multiplier    1.0f/10        // noise factor ω

EAの初期化メソッドでは、まず訓練セットをアップロードします。

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//---
   ResetLastError();
   if(!LoadTotalBase())
     {
      PrintFormat("Error of load study data: %d", GetLastError());
      return INIT_FAILED;
     }

次に、以前に訓練したモデルを開いてみます。モデルの読み込みにエラーがあれば、新しいモデルを作成し、ランダムなパラメータで初期化します。

//--- load models
   float temp;
   if(!Encoder.Load(FileName + "Enc.nnw", temp, temp, temp, dtStudied, true) ||
      !Decoder.Load(FileName + "Dec.nnw", temp, temp, temp, dtStudied, true) ||
      !Noise.Load(FileName + "NP.nnw", temp, temp, temp, dtStudied, true))
     {
      Print("Init new models");
      CArrayObj *encoder = new CArrayObj();
      CArrayObj *decoder = new CArrayObj();
      CArrayObj *noise = new CArrayObj();
      if(!CreateTrajNetDescriptions(encoder, decoder, noise))
        {
         delete encoder;
         delete decoder;
         delete noise;
         return INIT_FAILED;
        }
      if(!Encoder.Create(encoder) || !Decoder.Create(decoder) ||
         !Noise.Create(noise))
        {
         delete encoder;
         delete decoder;
         delete noise;
         return INIT_FAILED;
        }
      delete encoder;
      delete decoder;
      delete noise;
      //---
     }

すべてのモデルを1つのOpenCLコンテキストに転送します。

//---
   OpenCL = Encoder.GetOpenCL();
   Decoder.SetOpenCL(OpenCL);
   Noise.SetOpenCL(OpenCL);

そして、使用するモデルのアーキテクチャーの主要なパラメータのコントロールを追加します。

//---
   Encoder.getResults(Result);
   if(Result.Total() != EmbeddingSize)
     {
      PrintFormat("The scope of the Encoder does not match the embedding size count (%d <> %d)", EmbeddingSize, 
                                                                                                     Result.Total());
      return INIT_FAILED;
     }
//---
   Encoder.GetLayerOutput(0, Result);
   if(Result.Total() != (HistoryBars * BarDescr))
     {
      PrintFormat("Input size of Encoder doesn't match state description (%d <> %d)", Result.Total(), 
                                                                                           (HistoryBars * BarDescr));
      return INIT_FAILED;
     }
//---
   Decoder.GetLayerOutput(0, Result);
   if(Result.Total() != EmbeddingSize)
     {
      PrintFormat("Input size of Decoder doesn't match Encoder output (%d <> %d)", Result.Total(), EmbeddingSize);
      return INIT_FAILED;
     }
//---
   Noise.GetLayerOutput(0, Result);
   if(Result.Total() != EmbeddingSize)
     {
      PrintFormat("Input size of Noise Prediction model doesn't match Encoder output (%d <> %d)", Result.Total(), 
                                                                                                      EmbeddingSize);
      return INIT_FAILED;
     }
//---
   Noise.getResults(Result);
   if(Result.Total() != (HistoryBars * BarDescr))
     {
      PrintFormat("Output size of Noise Prediction model doesn't match state description (%d <> %d)", Result.Total(), 
                                                                                           (HistoryBars * BarDescr));
      return INIT_FAILED;
     }

すべてのコントロールの受け渡しに成功したら、補助データバッファを作成します。

//---
   if(!LastEncoder.BufferInit(EmbeddingSize, 0) ||
      !Gradient.BufferInit(EmbeddingSize, 0) ||
      !LastEncoder.BufferCreate(OpenCL) ||
      !Gradient.BufferCreate(OpenCL))
     {
      PrintFormat("Error of create buffers: %d", GetLastError());
      return INIT_FAILED;
     }

学習過程開始のカスタムイベントを生成します。

//---
   if(!EventChartCustom(ChartID(), 1, 0, 0, "Init"))
     {
      PrintFormat("Error of create study event: %d", GetLastError());
      return INIT_FAILED;
     }
//---
   return(INIT_SUCCEEDED);
  }

EAの非初期化メソッドでは、学習済みモデルを保存し、以前に作成した動的オブジェクトのメモリをクリアします。

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//---
   if(!(reason == REASON_INITFAILED || reason == REASON_RECOMPILE))
     {
      Encoder.Save(FileName + "Enc.nnw", 0, 0, 0, TimeCurrent(), true);
      Decoder.Save(FileName + "Dec.nnw", Decoder.getRecentAverageError(), 0, 0, TimeCurrent(), true);
      Noise.Save(FileName + "NP.nnw", Noise.getRecentAverageError(), 0, 0, TimeCurrent(), true);
     }
   delete Result;
   delete OpenCL;
  }

モデルを訓練する実際のプロセスは、Trainメソッドに実装されています。前回と同様、メソッドの本体では、まず経験再生バッファから軌道を選択する確率を計算しました。

//+------------------------------------------------------------------+
//| Train function                                                   |
//+------------------------------------------------------------------+
void Train(void)
  {
//---
   vector<float> probability = GetProbTrajectories(Buffer, 0.9);

次に、必要なローカル変数を作成して初期化します。

//---
   vector<float> result, target, inp;
   matrix<float> targets;
   matrix<float> delta;
   STE = vector<float>::Zeros((HistoryBars + PrecoderBars) * 3);
   STE_Noise = vector<float>::Zeros(HistoryBars * BarDescr);
   int std_count = 0;
   int batch = GPTBars + 50;
   bool Stop = false;
   uint ticks = GetTickCount();

これで準備作業は終了です。次に、モデルの訓練サイクルのシステムを作ります。ご記憶の通り、エンコーダーで使用されているGPTアーキテクチャは、入力データのシーケンスに厳格な要件を設定しています。そのため、入れ子になったループのシステムを作ります。外側ループの本体では、軌道とその軌道上の状態をサンプリングし、訓練バッチを開始します。入れ子になったループでは、1つの軌跡から連続した状態のバッチでモデルを訓練します。

ここでまた新たな挑戦が始まります。同じシーケンス内で、クリーンなデータとノイズ拡張データを使用することはできません。SSWNP法によれば、ノイズは個々の状態ではなく軌跡に加えられます。

同時に、1回の反復で、きれいな状態とノイズを加えた状態を交互にモデルに投入することはできません。内部スタックでは、状態モデルは混合され、モデルはそれらを1つの軌道として認識します。これは、分析されたシーケンスを大きく歪めます。

許容できる解決策は、軌道を交互に変えることです。このモデルは、まずクリーンな軌跡で訓練され、次にノイズ拡張軌跡で訓練されます。このアプローチによって、ノイズの再パラメータ化係数のベクトルに関する別の問題を同時に解決することができます。クリーンデータでモデルを訓練する場合、パラメータの変化の分布に関する情報を収集します。収集した分布の値を用いて、ノイズ拡張データでモデルを訓練する際に加えられるノイズを再パラメトリック化します。

上述したように、軌跡と初期状態をサンプリングする外側ループを作ります。

   for(int iter = 0; (iter < Iterations && !IsStopped() && !Stop); iter ++)
     {
      int tr = SampleTrajectory(probability);
      int state = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 3 - PrecoderBars - batch));
      if(state < 0)
        {
         iter--;
         continue;
        }

次に、モデルのスタックと補助バッファをクリアします。

      Encoder.Clear();
      Decoder.Clear();
      Noise.Clear();
      LastEncoder.BufferInit(EmbeddingSize, 0);

軌道上の訓練パッケージの最終状態を決定し、分析されたパラメータの変化に関する情報を収集するための行列をクリアします。

      int end = MathMin(state + batch, Buffer[tr].Total - PrecoderBars);
      delta = matrix<float>::Zeros(end - state - 1, Buffer[tr].States[state].state.Size());

分散行列のサイズは訓練バッチより1行小さいことに注意してください。この行列では、後続する2つの状態間の変化のデルタを保存するからです。

この段階で、クリーンな軌道でモデルの訓練を開始する準備はすべて整いました。そこで、最初の入れ子された訓練ループを作成します。

      for(int i = state; i < end; i++)
        {
         inp.Assign(Buffer[tr].States[i].state);
         State.AssignArray(inp);
         int row = i - state;
         if(i < (end - 1))
            delta.Row(inp, row);

ループの本体では、訓練サンプルから分析された状態を抽出し、ソースデータバッファに転送します。

同じ状態を使って偏差を計算します。まず、現在の状態が訓練データバッチの最後の状態であるかどうかを確認し、分析した状態を偏差行列の対応する行に追加します（最後の状態は追加されない）。

これは偏差行列なのに、なぜ状態をそのまま加えるのでしょうか。答えは次のステップにあります。その後のループの各反復では、前のステップで保存された前の状態を含む偏差行列の前の行から、分析中のアクションを引く。もちろん、前ステップがない最初の状態では、このステップはスキップします。

         if(row > 0)
            delta.Row(delta.Row(row - 1) - inp, row - 1);

次に、訓練済みモデルのフィードフォワードパスメソッドを順次呼び出します。まずはエンコーダーです。

         if(!LastEncoder.BufferWrite() || 
            !Encoder.feedForward((CBufferFloat*)GetPointer(State), 1, false, (CBufferFloat*)GetPointer(LastEncoder)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

その後にデコーダーが続きます。

         if(!Decoder.feedForward(GetPointer(Encoder), -1, (CBufferFloat*)NULL))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

フォワードフォワードブロックは、ノイズ予測モデルで終わります。

         if(!Noise.feedForward(GetPointer(Encoder), -1, (CBufferFloat*)NULL))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

通常通り、フィードフォワードブロックの後、訓練済みモデルのバックプロパゲーションパスを実行し、誤差を最小化するためにモデルのパラメータを調整します。まず、デコーダーのバックプロパゲーションパスを実行し、誤差勾配をエンコーダーに渡します。モデルのバックプロパゲーションパスを呼び出す前に、目標値を準備する必要があります。

デコーダーの出力には、エンコーダーに入力される初期状態のパラメータと、ある計画期間の予測値が入力されます。各ローソク足の予測パラメータの構成については前回説明しました。ここでも同じ意見に固執します。したがって、デコーダーのアーキテクチャも目標値を作成するアルゴリズムも変わっていません。まず、エンコーダー入力に供給されたデータで目標値行列を埋めます。

         target.Assign(Buffer[tr].States[i].state);
         ulong size = target.Size();
         targets = matrix<float>::Zeros(1, size);
         targets.Row(target, 0);
         if(size > BarDescr)
            targets.Reshape(size / BarDescr, BarDescr);
         ulong shift = targets.Rows();

そして、与えられた計画期間に対する経験再生バッファのデータを補足します。

         targets.Resize(shift + PrecoderBars, 3);
         for(int t = 0; t < PrecoderBars; t++)
           {
            target.Assign(Buffer[tr].States[i + t].state);
            if(size > BarDescr)
              {
               matrix<float> temp(1, size);
               temp.Row(target, 0);
               temp.Reshape(size / BarDescr, BarDescr);
               temp.Resize(size / BarDescr, 3);
               target = temp.Row(temp.Rows() - 1);
              }
            targets.Row(target, shift + t);
           }
         targets.Reshape(1, targets.Rows()*targets.Cols());
         target = targets.Row(0);

受信した情報をベクトルに変換し、デコーダーのフィードフォワード結果と比較します。

         Decoder.getResults(result);
         vector<float> error = target - result;

前回と同様、訓練の過程では、最も大きな偏差に注目します。そこで、まず移動平均二乗誤差を計算します。

         std_count = MathMin(std_count, 999);
         STE = MathSqrt((MathPow(STE, 2) * std_count + MathPow(error, 2)) / (std_count + 1));

次に、現在の誤差を標準偏差に基づく閾値と比較します。バックプロパゲーションパスは、現在の誤差が少なくとも1つのパラメータで閾値を超えた場合にのみ実行されます。

         vector<float> check = MathAbs(error) - STE * STE_Multiplier;
         if(check.Max() > 0)
           {
            //---
            Result.AssignArray(CAGrad(error) + result);
            if(!Decoder.backProp(Result, (CNet *)NULL) ||
               !Encoder.backPropGradient(GetPointer(LastEncoder), GetPointer(Gradient)))
              {
               PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
               Stop = true;
               break;
              }
           }

最大偏差を強調するというアイデアは、CFPI法から拝借したものです。

ノイズ予測モデルにも同様のバックプロパゲーションアルゴリズムを使用します。ただし、ここでは、目標値のベクトルを整理するアプローチはもっと単純で、クリーン軌道を扱うときは、単純にゼロ値のベクトルを使用します。

         target = vector<float>::Zeros(delta.Cols());
         Noise.getResults(result);
         error = (target - result) * STE_Noise_Multiplier;

誤差を計算する際、結果として生じる偏差に定数STE_Noise_Multiplierを掛けることに注意してください。これは、モデル全体の誤差に対するノイズ予測誤差の影響を決定します。

また、最大偏差に注目し、少なくとも1つのパラメータで閾値以上の誤差がある場合にのみバックプロパゲーションパスを実行します。

         STE_Noise = MathSqrt((MathPow(STE_Noise, 2) * std_count + MathPow(error, 2)) / (std_count + 1));
         std_count++;
         check = MathAbs(error) - STE_Noise;
         if(check.Max() > 0)
           {
            //---
            Result.AssignArray(CAGrad(error) + result);
            if(!Noise.backProp(Result, (CNet *)NULL) ||
               !Encoder.backPropGradient(GetPointer(LastEncoder), GetPointer(Gradient)))
              {
               PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
               Stop = true;
               break;
              }
           }

ノイズ予測モデルの誤差勾配をエンコーダーに渡し、必要に応じてバックプロパゲーションメソッドを呼び出します。

すべての訓練済みモデルのパラメータを更新した後、エンコーダーのフィードフォワードパスの最新の結果を補助バッファに保存します。

         Encoder.getResults(result);
         LastEncoder.AssignArray(result);

学習プロセスの進捗状況をユーザーに知らせ、入れ子になったループの次の反復に移ります。

         if(GetTickCount() - ticks > 500)
           {
            double percent = (double(i - state) / (2 * (end - state)) + iter) * 100.0 / (Iterations);
            string str = StringFormat("%-20s %6.2f%% -> Error %15.8f\n", "Decoder", percent, 
                                                                    Decoder.getRecentAverageError());
            str += StringFormat("%-20s %6.2f%% -> Error %15.8f\n", "Noise Prediction", percent, 
                                                                      Noise.getRecentAverageError());
            Comment(str);
            ticks = GetTickCount();
           }
        }

ここでは通常、モデル学習ループのシステムにおける反復の説明を完了します。しかし、今回のケースは違います。クリーンな軌道上で訓練モデルのバッチを処理したので、次に、ノイズ拡張軌道に対して操作を繰り返す必要があります。そこで、まずノイズ分布の統計パラメータを定義します。

      //--- With noise
      vector<float> std_delta = delta.Std(0) * STD_Delta_Multiplier;
      vector<float> mean_delta = delta.Mean(0);

なお、標準偏差は、分析された特徴量の値の可能な限り大きな偏りを減らすために、ノイズ係数を乗じています。

ノイズを生成するためにベクトルと配列を作成します。

      ulong inp_total = std_delta.Size();
      vector<float> noise = vector<float>::Zeros(inp_total);
      double ar_noise[];

その後、新しい軌道と初期状態をサンプリングします。

      tr = SampleTrajectory(probability);
      state = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 3 - PrecoderBars - batch));
      if(state < 0)
        {
         iter--;
         continue;
        }

モデルスタックと補助バッファをクリアします。

      Encoder.Clear();
      Decoder.Clear();
      Noise.Clear();
      LastEncoder.BufferInit(EmbeddingSize, 0);

次に、ノイズ拡張軌跡を扱うために、別の入れ子になったループを作ります。

      end = MathMin(state + batch, Buffer[tr].Total - PrecoderBars);
      for(int i = state; i < end; i++)
        {
         if(!Math::MathRandomNormal(0, 1, (int)inp_total, ar_noise))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }
         noise.Assign(ar_noise);

ループの本体では、まず正規分布からノイズを生成し、それをベクトルに移します。その後、再パラメトリック化します。

         noise = mean_delta + std_delta * noise;

この段階で、現在の訓練反復のためのノイズを準備しました。経験再生バッファからクリーンな状態をロードし、そこに生成されたノイズを加えます。

         inp.Assign(Buffer[tr].States[i].state);
         inp = inp + noise;

その結果、ノイズ拡張状態がソースデータバッファにロードされます。

         State.AssignArray(inp);

次に、クリーンな軌道を扱うのと同じように、フィードフォワードブロックを実行します。

         if(!LastEncoder.BufferWrite() || 
            !Encoder.feedForward((CBufferFloat*)GetPointer(State), 1, false, (CBufferFloat*)GetPointer(LastEncoder)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

         if(!Decoder.feedForward(GetPointer(Encoder), -1, (CBufferFloat*)NULL))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

         if(!Noise.feedForward(GetPointer(Encoder), -1, (CBufferFloat*)NULL))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

SSWNP法によれば、クリーンな軌道とノイズ拡張軌跡の予測軌跡の間に空間的な整合性を持たせる必要があります。理論的な部分で見てきたように、どちらの軌道も同じゴールに収束します。従って、デコーダーのバックプロパゲーションブロックは、クリーンな軌跡の場合と同じように構成します。

         target.Assign(Buffer[tr].States[i].state);
         ulong size = target.Size();
         targets = matrix<float>::Zeros(1, size);
         targets.Row(target, 0);
         if(size > BarDescr)
            targets.Reshape(size / BarDescr, BarDescr);
         ulong shift = targets.Rows();
         targets.Resize(shift + PrecoderBars, 3);
         for(int t = 0; t < PrecoderBars; t++)
           {
            target.Assign(Buffer[tr].States[i + t].state);
            if(size > BarDescr)
              {
               matrix<float> temp(1, size);
               temp.Row(target, 0);
               temp.Reshape(size / BarDescr, BarDescr);
               temp.Resize(size / BarDescr, 3);
               target = temp.Row(temp.Rows() - 1);
              }
            targets.Row(target, shift + t);
           }
         targets.Reshape(1, targets.Rows()*targets.Cols());
         target = targets.Row(0);

         Decoder.getResults(result);
         vector<float> error = target - result;
         std_count = MathMin(std_count, 999);
         STE = MathSqrt((MathPow(STE, 2) * std_count + MathPow(error, 2)) / (std_count + 1));
         vector<float> check = MathAbs(error) - STE * STE_Multiplier;
         if(check.Max() > 0)
           {
            //---
            Result.AssignArray(CAGrad(error) + result);
            if(!Decoder.backProp(Result, (CNet *)NULL) ||
               !Encoder.backPropGradient(GetPointer(LastEncoder), GetPointer(Gradient)))
              {
               PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
               Stop = true;
               break;
              }
           }

ノイズ予測モデルの場合、違いは目標値にあります。クリーンな軌跡にはゼロ値で満たされたベクトルを使用したが、今度はエンコーダーの入力に与える前にクリーンな状態に加えられたノイズを目標値として使用します。

         target = noise;
         Noise.getResults(result);
         error = (target - result) * STE_Noise_Multiplier;

         STE_Noise = MathSqrt((MathPow(STE_Noise, 2) * std_count + MathPow(error, 2)) / (std_count + 1));
         std_count++;
         check = MathAbs(error) - STE_Noise;
         if(check.Max() > 0)
           {
            //---
            Result.AssignArray(CAGrad(error) + result);
            if(!Noise.backProp(Result, (CNet *)NULL) ||
               !Encoder.backPropGradient(GetPointer(LastEncoder), GetPointer(Gradient)))
              {
               PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
               Stop = true;
               break;
              }
           }

モデルパラメータを更新した後、最後のエンコーダーパスの結果を補助バッファに保存します。

         Encoder.getResults(result);
         LastEncoder.AssignArray(result);

学習過程の進捗状況をユーザーに知らせ、サイクルの次の反復に移ります。

         if(GetTickCount() - ticks > 500)
           {
            double percent = (double(i - state) / (2 * (end - state)) + iter + 0.5) * 100.0 / (Iterations);
            string str = StringFormat("%-20s %6.2f%% -> Error %15.8f\n", "Decoder", percent, 
                                                                          Decoder.getRecentAverageError());
            str += StringFormat("%-20s %6.2f%% -> Error %15.8f\n", "Noise Prediction", percent, 
                                                                            Noise.getRecentAverageError());
            Comment(str);
            ticks = GetTickCount();
           }
        }
     }

これで、モデルの訓練サイクルにおける反復の説明は終わりです。すべての反復が成功したら、金融商品チャートのコメント欄を消去します。

   Comment("");
//---
   PrintFormat("%s -> %d -> %-20s %10.7f", __FUNCTION__, __LINE__, "Decoder", Decoder.getRecentAverageError());
   PrintFormat("%s -> %d -> %-20s %10.7f", __FUNCTION__, __LINE__, "Noise Prediction", Noise.getRecentAverageError());
   ExpertRemove();
//---
  }

訓練の結果をログに出力し、EAを終了します。

記事で使用したすべてのプログラムの完全なコードは、添付ファイルでご覧いただけます。

上記は、軌道関数訓練EAのアルゴリズムを更新したものです。方策訓練アルゴリズムに変更はありません。その詳しい説明は前回の記事でおこないました。EA「...\Experts\SSWNP\Study.mq5」のフルコードを以下に添付します。

3.検証

本稿の実践編では、先に構築した目標条件付き予測符号化(GCPC)法による軌道関数学習EAに、自己教師ありウェイポイントノイズ予測法のアプローチを統合しました。値動き予測の質の向上が期待されます。それではいよいよ、MetaTrader 5のストラテジーテスターで実際のデータを使って結果をテストしてみましょう。

前回と同様、モデルはEURUSD H1の履歴データを使用して訓練およびテストされます。モデルは2023年の最初の7ヶ月間のデータを使用して訓練されています。訓練済みモデルをテストするために、2023年8月からの履歴データを使用します。ご覧の通り、テスト期間は訓練期間の直後にあります。

モデルを訓練する前に、一次訓練データセットを収集する必要があります。モデルのアーキテクチャやデータ構造を変更することなく、以前に構築されたEAに新しいアプローチを実装したので、このステップを省略し、GCPC法を使用してモデルを訓練する際に作成された既存の例データベースを使用することができます。SSWNP.bdという名前の経験再生バッファファイルのコピーを作成します。そして、そのままモデルの訓練プロセスに移ります。

GCPC法のアルゴリズムに従い、モデルは2段階で学習されます。第一段階では、軌道関数を訓練します。この段階には、新しいSSWNPメソッドのアプローチが含まれています。エンコーダー入力には、過去の値動きと指標データのみが入力されます。この段階では、軌跡の違いを生む口座ステータスやポジションの値は分析されないため、経験再生バッファ内のすべての軌跡が同一になります。したがって、既存の例データベースを使用し、追加の例を収集することなく、許容できる結果が得られるまで軌跡関数を訓練することができます。

モデル訓練の第二段階である行動方策の訓練では、市場状況やエージェントの行動によって口座状況やポジションが変化する過去の市場状況下で、エージェントの最適な行動を探索します。この段階では、モデルの訓練と、エージェントの更新された行動方針をより正確に評価するための追加的な例の収集を交互に繰り返しながら、モデルの訓練をおこないます。

私たちの訓練は一定の成果を上げました。訓練データセットの過去のデータとテスト期間の両方で利益を生み出すことができるモデルを訓練することができました。

訓練済みモデルのテスト結果

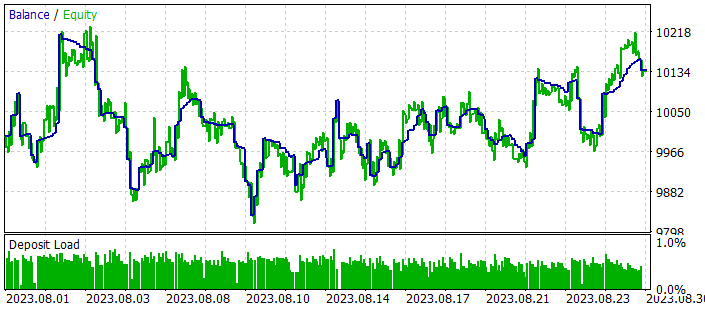
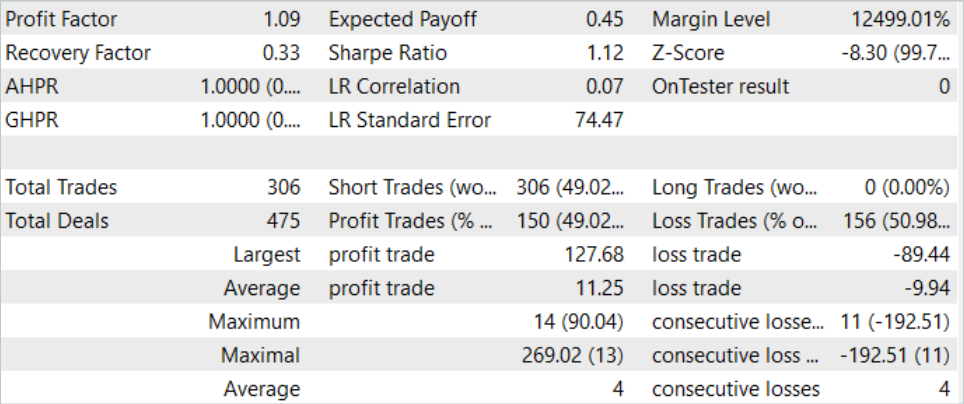
結論

本稿では、自己教師ありウェイポイントノイズ予測法を紹介しました。このアプローチにより、変化する条件や物理的制約のためにエージェントの将来の軌道が不確実性を伴う複雑な確率的環境において、モデルの効率を向上させることができます。この目標は、過去の軌跡にノイズを補強することで達成され、将来の軌跡をより正確かつ多様に予測することに貢献します。ここで提示された革新的な方法論は、空間的整合性モジュールとノイズ予測モジュールの2つのモジュールから構成され、これらのモジュールは、確率的シナリオにおける正確で信頼性の高い予測をサポートします。

この手法の著者が提案した構成は非常に普遍的であり、さまざまなモデル学習アルゴリズムに組み込むことができます。強化学習法に限ったことではありません。その論文の中で、この手法の著者たちは、提案されたアプローチの実装が、基本的な手法の効率をどのように向上させるかの例を示しています。

本稿の実践編では、SSWNP法が提案するアプローチをGCPCアルゴリズムの構造に統合しました。テストの結果、提案手法の有効性が確認されました。

ただし、繰り返しになりますが、この記事で紹介するプログラムはすべて、技術のデモンストレーションを目的としたものであり、実際の金融取引に使用できるものではないことをお断りしておきます。

参照文献

記事で使用されているプログラム

#	ファイル名	種類	詳細
1	Research.mq5	EA	コレクションEAの例
2	ResearchRealORL.mq5	EA	Real-ORL法による事例収集のためのEA
3	Study.mq5	EA	方策訓練EA
4	StudyEncoder.mq5	EA	SSWNPアプローチによるオートエンコーダ学習EA
5	Test.mq5	EA	モデルをテストするEA
6	Trajectory.mqh	クラスライブラリ	システム状態記述の構造体
7	NeuroNet.mqh	クラスライブラリ	ニューラルネットワークを作成するためのクラスのライブラリ
8	NeuroNet.cl	コードベース	OpenCLプログラムコードライブラリ

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/14044

添付されたファイル |

ZIPをダウンロード

MQL5.zip (789.06 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動

ニューラルネットワークが簡単に（第73回）：値動きを予測するAutoBot

引き続き、軌道予測モデルを訓練するアルゴリズムについて説明します。この記事では、「AutoBot」と呼ばれるメソッドを紹介します。

Rest APIを統合したMQL5強化学習エージェントの開発（第4回）：MQL5でクラス内の関数を整理する

この記事では、MQL5における手続き型コーディングからオブジェクト指向プログラミング(OOP)への移行について、REST APIとの統合を中心に説明します。今日は、HTTPリクエスト関数（GETとPOST）をクラスにまとめる方法について説明します。コードのリファクタリングについて詳しく見ていき、孤立した関数をクラスメソッドに置き換える方法を紹介します。記事には実践的な例とテストが含まれています。

ニューラルネットワークが簡単に（第74回）：適応による軌道予測

本稿では、様々な環境条件に適応可能なマルチエージェントの軌道予測について、かなり効果的な手法を紹介します。

リプレイシステムの開発（第41回）：第2段階(II)の開始

もし、この時点まですべてが正しく思えたとしたら、それはアプリケーションの開発を始めるときに、長期的なことをあまり考えていないということです。時間が経つにつれて、新しいアプリケーションをプログラムする必要はなくなり、それらを連携させるだけで済むようになります。それでは、マウス指標を組み立てる方法を説明しましょう。