Нейросети — это просто (Часть 72): Прогнозирование траекторий в условиях наличия шума

MetaTrader 5 — Торговые системы | 12 января 2024, 14:28

978

Dmitriy Gizlyk

Введение

Прогнозирование будущего движения актива путем анализа его исторических траекторий имеет важное значение в контексте торговли на финансовых рынках, где анализ прошлых тенденций может быть ключевым фактором для успешной стратегии. Будущие траектории активов часто обладают неопределенностью из-за изменения фундаментальных факторов и реакции рынка на них, что определяет множество потенциальных будущих движений для активов. Следовательно, эффективный метод прогнозирования движения на рынках должен быть способен генерировать распределение потенциальных будущих траекторий или, по крайней мере, несколько вероятных сценариев.

Несмотря на значительное разнообразие существующих архитектурных решений для наиболее вероятных прогнозов, в процессе прогнозирования будущих траекторий финансовых активов модели могут столкнуться с проблемой чрезмерно упрощенных прогнозов. Которая сохраняется из-за узкой интерпретации моделью данных из обучающей выборки. В условиях отсутствия четких шаблонов траекторий активов модель прогнозирования приходит к генерации простых или однородных сценариев движения, неспособных улавливать разнообразие изменений в движении финансовых инструментов. Что может привести к снижению точности прогнозов.

Для решения указанных проблем в статье «Enhancing Trajectory Prediction through Self-Supervised Waypoint Noise Prediction» был предложен новый подход Self-Supervised Waypoint Noise Prediction (SSWNP), который состоит из двух модулей:

модуль пространственной согласованности
модуль прогнозирования шума.

В первом создаются два различных вида наблюдаемых в прошлом траекторий: в чистом и шумовом видах пространственной области ключевых точек. Как следует из названия, чистый вариант представляет собой оригинальную пройденную траекторию, в то время как шумовой вариант представляет собой прошлые траектории, которые перемещены в исходном пространстве анализируемых признаков с добавлением шума. Данный подход использует тот факт, что шумовой вариант прошлых траекторий не соответствует узкой интерпретации данных из обучающей выборки. Модель использует эту дополнительную информацию для преодоления проблемы чрезмерно упрощенных прогнозов и изучения более разнообразных сценариев движения. После создания двух различных вариантов пройденных траекторий мы обучаем модель прогнозирования будущих траекторий поддерживать пространственную согласованность между прогнозами из этих двух вариантов и изучать пространственно-временные характеристики, помимо задачи прогнозирования движения.

В модуле прогнозирования шума решается вспомогательная задача выделения шума в анализируемых траекториях. Это помогает модели прогнозирования движения лучше моделировать потенциальное пространственное разнообразие и улучшает понимание базового представления в прогнозировании движения, тем самым улучшая будущие прогнозы.

Авторы метода проводят дополнительные эксперименты, чтобы эмпирически продемонстрировать критическую важность модулей пространственной согласованности и прогнозирования шума для SSWNP. При использовании только модуля пространственной согласованности для решения задачи прогнозирования движения наблюдается субоптимальная производительность обучаемой модели. Поэтому в своей работе они интегрируют оба модуля.

1. Алгоритм SSWNP

Цель прогнозирования траектории заключается в определении наиболее вероятной будущей траектории агента в динамической среде на основе его ранее пройденных траекторий. Траектория представлена временным рядом пространственных точек, называемых точками маршрута. Наблюдаемая траектория охватывает период с t1 по tob и может быть обозначена как

где Xi* соответствует координатам агента i на временном шаге t*. Аналогично, прогнозируемая будущая траектория для агента i в течение периода [tob+1,tfu] может быть описана как Ŷtob+1≤t≤tfu. Соответствующая истинная траектория для будущего движения агента i может быть описана как Ytob+1≤t≤tfu.

В методе SSWNP сначала создается два различных вида пройденных траекторий: один характеризуется как чистый вид (X≤tob), а другой — как вид с добавлением шума (Ẍ≤tob). Чистый вид соответствует оригинальной траектории из обучающей выборки, в то время как вид с добавлением шума соответствует траектории, которая была перемещена в пространстве анализируемых признаков путем добавления шума.

Для искажения чистой траектории используется шум из стандартного нормального распределения N(0, 1). Авторы метода вводят параметр, называемый коэффициентом шума (ω), который контролирует пространственное перемещение точек маршрута.

После создания чистого и аугментированного видов траектории мы передаем их в модель извлечения признаков (Θfe), которая генерирует признаки, соответствующие как чистому виду, так и виду с добавлением шума. Полученные признаки затем передаются в модель прогнозирования траектории (Θsup) для прогнозирования траекторий Ŷtob+1≤t≤tfu и Ÿtob+1≤t≤tfu, как показано в уравнениях ниже:

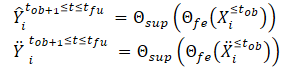
Мы обучаем модель минимизировать разрыв между прогнозными траекториями и истинной траекторией из обучающей выборки. Как можно заметить, минимизируя ошибку прогнозирования траекторий от чистых и зашумленных исходных данных (Ŷ и Ÿ) к истинной траектории из обучающей выборки (Y), мы косвенно уменьшая разрыв между 2 прогнозными траекториями. Таким образом, поддерживается пространственная согласованность между прогнозами будущей траектории на основе чистых наблюдаемых траекторий и траекторий с добавлением шума.

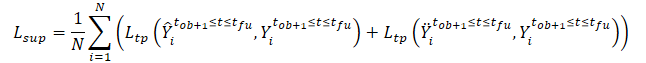
Дополнительно в методе SSWNP решается задача самостоятельного прогнозирования шума, которая включает в себя прогнозирование шума, присутствующего как в чистом виде, наблюдаемой прошлой траектории X≤tob, так и в виде с добавлением шума Ẍ≤tob. Здесь цель заключается в оценке значения шума, связанного с заданной наблюдаемой точкой маршрута.

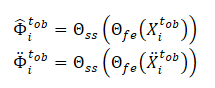
Обратите внимание, что признаки, извлеченные моделью Θfe, используются в качестве исходных данных для модели прогнозирования шума (Θss). Которая определяет уровень шума в наблюдаемых траекториях (чистом и аугментированном видах). В качестве функции потерь для самостоятельного обучения модели прогнозирования шума авторы метода предлагают использовать среднеквадратичную ошибку (MSE).

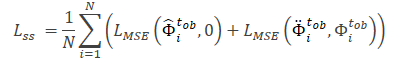
Здесь значение «0» обозначает отсутствие шума в траектории чистого вида.

Общая функция потерь метода SSWNP представляется в виде:

Где λ обозначает вклад ошибки прогнозирования шума в общую ошибку при обучении модели с использованием предложенного подхода.

Авторская визуализация метода Self-Supervised Waypoint Noise Prediction представлена ниже.

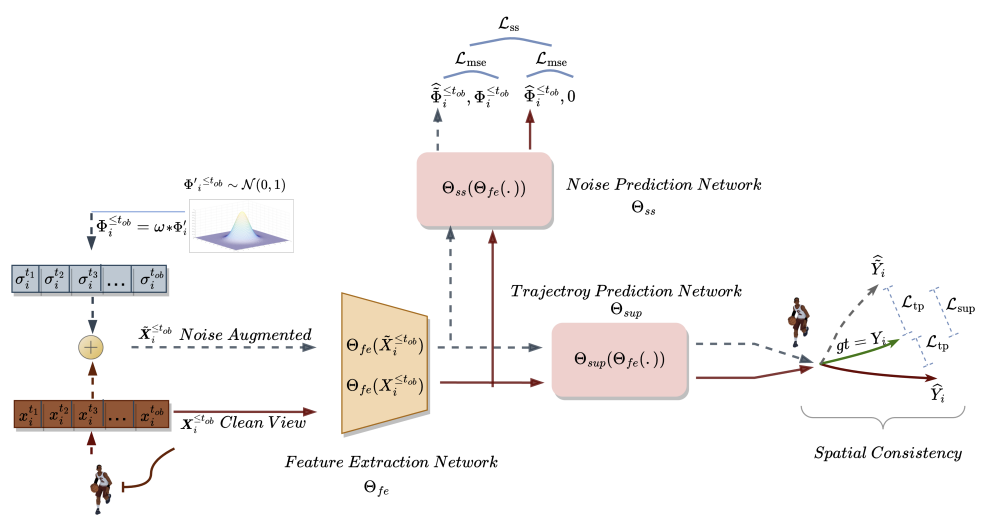
2. Реализация средствами MQL5

Выше мы познакомились с теоретическими аспектами метода Self-Supervised Waypoint Noise Prediction. Как можно заметить, предложенные подходы не налагают каких-либо ограничений ни на архитектуру используемых моделей, ни на структуру исходных данных. Это позволяет интегрировать предложенные подходы с большим количеством рассмотренных нами ранее алгоритмов. В частности, в рамках данной статьи мы добавим предложенные подходы в алгоритм обучения автоэнкодера TrajNet, рассмотренного нами в прошлой статье метода Goal-Conditioned Predictive Coding.

Напомню, что алгоритмом GCPC предусмотрено 2 этапа обучения модели:

Рассматриваемый в данной статье метод SSWNP направлен на повышение эффективности прогнозирования будущих траекторий. Следовательно, затрагивает только первый этап «обучение функции траектории». В него мы и внесем необходимые корректировки. Второй же этап «обучение политики поведения» будет перенесен без изменений.

2.1 Вопросы интеграции методов

Нужно обратить внимание, интегрируя новые подходы в уже готовую структуру, мы должны предусмотреть, чтобы вносимые нами изменения не нарушили уже построенный процесс. Поэтому, перед началом работ мы должны проанализировать влияние новых подходов на созданный ранее процесс обучения и последующую работу модели в процессе эксплуатации.

Первое, нужно понимать, что добавление шума к траекториям из обучающей выборки очевидно внесет изменения в распределение исходных данных. Следовательно, это скажется на параметрах слоя пакетной нормализации, в котором мы осуществляем первичную обработку исходных данных. С одной стороны, мы этого и добиваемся. Ведь мы хотим обучить модель работы в условиях, близких к реальным в окружающей среде с высокой стохастичностью. С другой стороны, добавление случайного шума может вывести исходные данные за пределы реальных значений анализируемых параметров. Для минимизации отрицательного влияния указанного фактора авторами алгоритма добавлен коэффициент шума (ω), который регулирует величину смещения данных. В наших условиях «сырых» не нормализованных данных нам потребуется отдельный коэффициент шума по каждому показателю исходных данных. Т.е. мы приходим к использованию вектора коэффициентов шума. И подбор вектора гиперпараметров становится довольно сложной задачей, сложность которой растет с увеличением количества анализируемых параметров.

Решение данного вопроса, как оказалось, лежит на поверхности. Если задуматься, то умножение шума из нормального распределения на некий коэффициент очень напоминает уже знакомый нам reparameterization trick, который мы использовали в слое вариационного автоэнкодера..

Следовательно, использованием параметров распределения обучающей выборки мы можем удержать модель в рамках исходного распределения. При этом добавим стохастичность, присущую анализируемой окружающей среде.

Однако, здесь надо учесть ещё один момент. Мы добавляем шум к реальным траекториям из обучающей выборки, а не заменяем их данные случайными значениями. В то время как при решении задачи «в лоб» мы получаем параметры распределения исходных данных.

Давайте ещё раз посмотрим на идею использования шума. В конкретный момент времени мы имеем фактические данные каждого из анализируемых параметров. На следующем временном шаге параметры изменяются на некоторую величину. Размер изменения по каждому параметру зависит от большого количества различных факторов, что приближает его практически к случайной величине. В то же время такое изменение отнюдь не безгранично и имеет свои пределы. Следовательно, чтобы сохранить естественное распределение исходных данных мы можем определить параметры распределения таких отклонений между 2 последующими значениями каждого анализируемого параметра. Это и будут параметры для репараметризации нашего шума.

Тут надо учесть момент, что значительное изменение показателей параметров часто свидетельствует об изменении рыночной ситуации. А методом SSWNP предусмотрено обучение модели минимизации разрыва между прогнозами траекторий из чистых и зашумленных данных. Поэтому мы воспользуемся предложенным авторами метода коэффициентом шума, чтобы ограничить смещение от реальных траекторий из обучающей выборки.

Второй момент, на который хочу обратить внимание — использование слоя DropOut в методе GCPC, который так же выполняет роль своеобразной регуляризации и призван обучить модель игнорировать некоторые «выбивающиеся» значения и восстанавливать пропущенные параметры. В случае объединения методов мы получаем игнорирование шума, добавленного к параметрам, маскированным слоем DropOut. С другой стороны, маскирование параметра делает задачу, решаемую моделью, значительно сложнее по сравнению с добавлением шума.

Как уже было сказано ранее, мы не нарушаем построенный ранее процесс. Поэтому мы не будем исключать слой DropOut из архитектуры Энкодера. И будет интересно понаблюдать за результатами обучения модели.

Теперь давайте посмотри на построение метода Self-Supervised Waypoint Noise Prediction. Его алгоритм включает обучение 3 моделей:

модель извлечения признаков
модель прогнозирования траектории
модель прогнозирования шума.

Мы планируем интегрировать алгоритм SSWNP в построенный ранее процесс GCPC. Давайте попробуем сопоставить модели обоих методов. Модели извлечения признаков SSWNP соответствует Энкодер GCPC. В свою очередь, Декодер GCPC можно представить в виде модели прогнозирования траектории SSWNP. А вот модель прогнозирования шума нам предстоит добавить.

2.2 Архитектура моделей

Архитектуры моделей будут описаны в методе CreateTrajNetDescriptions, в который мы добавим описание третьей модели. В параметрах метод получает указатели на 3 динамических массива для описания архитектуры 3 моделей. В теле метода мы проверяем актуальность полученных указателей и, при необходимости, создаем новые экземпляры объектов.

bool CreateTrajNetDescriptions(CArrayObj *encoder, CArrayObj *decoder, CArrayObj *noise)
  {
//---
   CLayerDescription *descr;
//---
   if(!encoder)
     {
      encoder = new CArrayObj();
      if(!encoder)
         return false;
     }
   if(!decoder)
     {
      decoder = new CArrayObj();
      if(!decoder)
         return false;
     }
   if(!noise)
     {
      noise = new CArrayObj();
      if(!noise)
         return false;
     }

Как уже было сказано выше, описание архитектуры Энкодера и Декодера мы переносим без изменений. Напомню, на вход Энкодера мы подаем сырые исходные данные, среди которых мы указываем только исторические данные изменения цены и анализируемых индикаторов.

//--- Encoder
   encoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Которые проходят первичную обработку в слое пакетной нормализации.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1000;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Нормализованные данные подвергаются случайному маскированию в слое DropOut.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronDropoutOCL;
   descr.count = prev_count;
   descr.probability = 0.8f;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

После чего мы осуществляем поиск устойчивых паттернов с помощью блока сверточных слоев.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   prev_count = descr.count = prev_count - 2;
   descr.window = 3;
   descr.step = 1;
   int prev_wout = descr.window_out = 3;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronSoftMaxOCL;
   descr.count = prev_count;
   descr.step = prev_wout;
   descr.optimization = ADAM;
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   prev_count = descr.count = prev_count;
   descr.window = prev_wout;
   descr.step = prev_wout;
   prev_wout = descr.window_out = 8;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 6
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronSoftMaxOCL;
   descr.count = prev_count;
   descr.step = prev_wout;
   descr.optimization = ADAM;
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Затем мы обрабатываем данные в блоке полносвязных слоем.

//--- layer 7
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.optimization = ADAM;
   descr.activation = LReLU;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 8
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = EmbeddingSize;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Рекуррентно добавляем результаты предыдущих проходов Энкодера.

//--- layer 9
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConcatenate;
   descr.count = 2 * EmbeddingSize;
   descr.window = prev_count;
   descr.step = EmbeddingSize;
   descr.optimization = ADAM;
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

И перенесем данные во внутренний стек анализируемой истории.

//--- layer 10
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronEmbeddingOCL;
   prev_count = descr.count = GPTBars;
     {
      int temp[] = {EmbeddingSize, EmbeddingSize};
      ArrayCopy(descr.windows, temp);
     }
   prev_wout = descr.window_out = EmbeddingSize;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Полученный набор исторических данных анализируется в блоке внимания.

//--- layer 11
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronMLMHAttentionOCL;
   descr.count = prev_count * 2;
   descr.window = prev_wout;
   descr.step = 4;
   descr.window_out = 16;
   descr.layers = 4;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Результаты анализа сжимаются полносвязным слоем.

//--- layer 12
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = EmbeddingSize;
   descr.optimization = ADAM;
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 13
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronSoftMaxOCL;
   descr.count = prev_count;
   descr.step = 1;
   descr.optimization = ADAM;
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

И на выходе Энкодера нормализуем данные функцией SoftMax.

Результаты прямого прохода Энкодера подаются на вход Декодера.

//--- Decoder
   decoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = EmbeddingSize;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!decoder.Add(descr))
     {
      delete descr;
      return false;
     }

В данном случае мы имеем дело с данными, полученными от предыдущей модели, которые уже нормализованы. Следовательно, нам нет необходимости осуществлять первичную обработку данных. И мы сразу их разворачиваем с помощью полносвязного слоя.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = (HistoryBars + PrecoderBars) * EmbeddingSize;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!decoder.Add(descr))
     {
      delete descr;
      return false;
     }

Полученные данные анализируются в блоке внимания.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronMLMHAttentionOCL;
   prev_count = descr.count = prev_count / EmbeddingSize;
   prev_wout = descr.window = EmbeddingSize;
   descr.step = 4;
   descr.window_out = 16;
   descr.layers = 2;
   descr.optimization = ADAM;
   if(!decoder.Add(descr))
     {
      delete descr;
      return false;
     }

На выходе блока внимания мы имеем эмбединг каждой прогнозируемой свечи. И для дешифровки полученных эмбедингов мы воспользуемся мультимодельным полносвязным слоем.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronMultiModels;
   descr.count = 3;
   descr.window = prev_wout;
   descr.step = prev_count;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!decoder.Add(descr))
     {
      delete descr;
      return false;
     }

После описания архитектуры Энкодера и Декодера нам предстоит добавить описание архитектуры модели прогнозирования шума. Данная модель, как и Декодер, в качестве исходных данных использует результаты работы Энкодера. И мы просто скопируем слой исходных данных Декодера.

//--- Noise Prediction
   noise.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.Copy(decoder.At(0));
   if(!noise.Add(descr))
     {
      delete descr;
      return false;
     }

Далее мы с помощью полносвязного слоя разворачиваем полученные данные до размера исходных данных на входе Энкодера.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = HistoryBars * EmbeddingSize;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!noise.Add(descr))
     {
      delete descr;
      return false;
     }

А вот на следующем шаге я, наверное, впервые за всю серию статей сделал разветвление для архитектуры модели в зависимости от выбранных гиперпараметров. И здесь ключевым является количество анализируемых свечей на входе Энкодера. При анализе более одной свечи архитектура модели напомнит Декодер. Мы используем блок внимания и мультимодельный слой для дешифровки эмбедингов. Только здесь мы говорим не о прогнозных свечах, а об анализируемых.

//---
   if(HistoryBars > 1)
     {
      //--- layer 2
      if(!(descr = new CLayerDescription()))
         return false;
      descr.type = defNeuronMLMHAttentionOCL;
      prev_count = descr.count = prev_count / EmbeddingSize;
      prev_wout = descr.window = EmbeddingSize;
      descr.step = 4;
      descr.window_out = 16;
      descr.layers = 2;
      descr.optimization = ADAM;
      if(!noise.Add(descr))
        {
         delete descr;
         return false;
        }
      //--- layer 3
      if(!(descr = new CLayerDescription()))
         return false;
      descr.type = defNeuronMultiModels;
      descr.count = BarDescr;
      descr.window = prev_wout;
      descr.step = prev_count;
      descr.activation = None;
      descr.optimization = ADAM;
      if(!noise.Add(descr))
        {
         delete descr;
         return false;
        }
     }

А вот при анализе только одной свечи на входе Энкодера теряется весь смысл использования слоя внимания, который анализирует взаимосвязи между различными свечами. Поэтому мы воспользуемся простым перцептроном.

   else
     {
      //--- layer 2
      if(!(descr = new CLayerDescription()))
         return false;
      descr.type = defNeuronBaseOCL;
      descr.count = LatentCount;
      descr.optimization = ADAM;
      descr.activation = LReLU;
      if(!noise.Add(descr))
        {
         delete descr;
         return false;
        }
      //--- layer 3
      if(!(descr = new CLayerDescription()))
         return false;
      descr.type = defNeuronBaseOCL;
      prev_count = descr.count = BarDescr;
      descr.activation = None;
      descr.optimization = ADAM;
      if(!noise.Add(descr))
        {
         delete descr;
         return false;
        }
     }
//---
   return true;
  }

Хочу напомнить, что выше описаны архитектуры моделей, участвующих только в этапе обучения модели функции траекторий. Архитектура моделей обучения политики поведения Агента перенесены без изменений. И вы можете самостоятельно ознакомиться с ними во вложении. А детальное описание дано в предыдущей статье.

2.3 Программы обучения моделей

После описания архитектуры используемых моделей мы переходим к рассмотрению алгоритмов используемых программ. Сразу скажу, что авторами метод SSWNP не представлено требований к выбору исходных данных и сбору пройденных траекторий для обучения. Поэтому программы взаимодействия с окружающей средой перенесены без каких-либо корректировок их алгоритмов. С полным кодом указанных программ Вы можете самостоятельно ознакомиться во вложении. При необходимости пояснений прошу обратиться к предыдущей статье или задать вопрос на форуме.

А мы переходим к советнику обучения функции траектории «...\Experts\SSWNP\StudyEncoder.mq5», в котором мы одновременно будем обучать 3 модели:

модель извлечения признаков (Encoder)
модель прогнозирования траектории (Decoder)
модель прогнозирования шума (Noise).

CNet                 Encoder;
CNet                 Decoder;
CNet                 Noise;

Как было указано в теоретической части, для реализации алгоритма SSWNP нам необходимо определить 2 гиперпараметра. Мы выведем их в константы нашей программы.

#define        STE_Noise_Multiplier    1.0f/10        // λ определяет влияние ошибки прогнозирования шума
#define        STD_Delta_Multiplier    1.0f/10        // коэффициент шума ω

В методе инициализации советника мы, как и ранее, сначала загружаем обучающую выборку.

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//---
   ResetLastError();
   if(!LoadTotalBase())
     {
      PrintFormat("Error of load study data: %d", GetLastError());
      return INIT_FAILED;
     }

А затем пробуем открыть ранее обученные модели. В случае возникновения ошибки загрузки моделей мы создаем новые и инициализируем их случайными параметрами.

//--- load models
   float temp;
   if(!Encoder.Load(FileName + "Enc.nnw", temp, temp, temp, dtStudied, true) ||
      !Decoder.Load(FileName + "Dec.nnw", temp, temp, temp, dtStudied, true) ||
      !Noise.Load(FileName + "NP.nnw", temp, temp, temp, dtStudied, true))
     {
      Print("Init new models");
      CArrayObj *encoder = new CArrayObj();
      CArrayObj *decoder = new CArrayObj();
      CArrayObj *noise = new CArrayObj();
      if(!CreateTrajNetDescriptions(encoder, decoder, noise))
        {
         delete encoder;
         delete decoder;
         delete noise;
         return INIT_FAILED;
        }
      if(!Encoder.Create(encoder) || !Decoder.Create(decoder) ||
         !Noise.Create(noise))
        {
         delete encoder;
         delete decoder;
         delete noise;
         return INIT_FAILED;
        }
      delete encoder;
      delete decoder;
      delete noise;
      //---
     }

Все модели переносим в один контекст OpenCL.

//---
   OpenCL = Encoder.GetOpenCL();
   Decoder.SetOpenCL(OpenCL);
   Noise.SetOpenCL(OpenCL);

Затем осуществляем контроль ключевых параметров архитектуры используемых моделей.

//---
   Encoder.getResults(Result);
   if(Result.Total() != EmbeddingSize)
     {
      PrintFormat("The scope of the Encoder does not match the embedding size count (%d <> %d)", EmbeddingSize, 
                                                                                                     Result.Total());
      return INIT_FAILED;
     }
//---
   Encoder.GetLayerOutput(0, Result);
   if(Result.Total() != (HistoryBars * BarDescr))
     {
      PrintFormat("Input size of Encoder doesn't match state description (%d <> %d)", Result.Total(), 
                                                                                           (HistoryBars * BarDescr));
      return INIT_FAILED;
     }
//---
   Decoder.GetLayerOutput(0, Result);
   if(Result.Total() != EmbeddingSize)
     {
      PrintFormat("Input size of Decoder doesn't match Encoder output (%d <> %d)", Result.Total(), EmbeddingSize);
      return INIT_FAILED;
     }
//---
   Noise.GetLayerOutput(0, Result);
   if(Result.Total() != EmbeddingSize)
     {
      PrintFormat("Input size of Noise Prediction model doesn't match Encoder output (%d <> %d)", Result.Total(), 
                                                                                                      EmbeddingSize);
      return INIT_FAILED;
     }
//---
   Noise.getResults(Result);
   if(Result.Total() != (HistoryBars * BarDescr))
     {
      PrintFormat("Output size of Noise Prediction model doesn't match state description (%d <> %d)", Result.Total(), 
                                                                                           (HistoryBars * BarDescr));
      return INIT_FAILED;
     }

После успешного прохождения всех контролей мы создаем вспомогательные буферы.

//---
   if(!LastEncoder.BufferInit(EmbeddingSize, 0) ||
      !Gradient.BufferInit(EmbeddingSize, 0) ||
      !LastEncoder.BufferCreate(OpenCL) ||
      !Gradient.BufferCreate(OpenCL))
     {
      PrintFormat("Error of create buffers: %d", GetLastError());
      return INIT_FAILED;
     }

И генерируем пользовательское событие начала процесса обучения.

//---
   if(!EventChartCustom(ChartID(), 1, 0, 0, "Init"))
     {
      PrintFormat("Error of create study event: %d", GetLastError());
      return INIT_FAILED;
     }
//---
   return(INIT_SUCCEEDED);
  }

В методе деинициализации советника мы сохраняем обученные модели и очищаем память от ранее созданных динамических объектов.

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//---
   if(!(reason == REASON_INITFAILED || reason == REASON_RECOMPILE))
     {
      Encoder.Save(FileName + "Enc.nnw", 0, 0, 0, TimeCurrent(), true);
      Decoder.Save(FileName + "Dec.nnw", Decoder.getRecentAverageError(), 0, 0, TimeCurrent(), true);
      Noise.Save(FileName + "NP.nnw", Noise.getRecentAverageError(), 0, 0, TimeCurrent(), true);
     }
   delete Result;
   delete OpenCL;
  }

Непосредственно процесс обучения моделей осуществляется в методе Train. Как и ранее, в теле метода мы сначала определяем вероятности выбора траекторий из буфера воспроизведения опыта.

//+------------------------------------------------------------------+
//| Train function                                                   |
//+------------------------------------------------------------------+
void Train(void)
  {
//---
   vector<float> probability = GetProbTrajectories(Buffer, 0.9);

После чего создаем и инициализируем необходимые локальные переменные.

//---
   vector<float> result, target, inp;
   matrix<float> targets;
   matrix<float> delta;
   STE = vector<float>::Zeros((HistoryBars + PrecoderBars) * 3);
   STE_Noise = vector<float>::Zeros(HistoryBars * BarDescr);
   int std_count = 0;
   int batch = GPTBars + 50;
   bool Stop = false;
   uint ticks = GetTickCount();

На этом завершается подготовительная работа и мы создаем систему циклов обучения моделей. Как вы помните, используемая в Энкодере архитектура GPT требовательна к последовательности подаваемых исходных данных. Поэтому мы создаем систему вложенных циклов. В теле внешнего цикла мы сэмплируем траекторию и состояние на ней для начала пакета обучения. А во вложенном цикле мы обучаем модель на пакете последовательных состояний из одной траектории.

И здесь нас ждет очередной вызов. В рамках одной последовательности мы не можем использовать чистые и зашумленные данные. Методом SSWNP предусматривается добавление шума в траектории, а не отдельные состояния.

В то же время мы не можем на одной итерации по очереди подавать в модель чистое состояние и с добавлением шума. Во внутреннем стеке модели состояния смешаются и модель воспримет их как единую траекторию. Что сильно искажает анализируемую последовательность.

Выход был найден в чередовании траекторий. Сначала модель обучается на чистой траектории, а затем на траектории с добавлением шума. Такой подход позволяет нам параллельно решить и другой вопрос — с вектором коэффициентов репараметризации шума. При обучении модели на чистых данных мы собираем информацию о распределении изменения параметров. И показатели собранного распределения мы используем для репараметризации шума, добавляемого при обучении модели на зашумленных данных.

Как уже сказано выше, мы создаем внешний цикл в котором сэмплируем траекторию и начальное состояние.

   for(int iter = 0; (iter < Iterations && !IsStopped() && !Stop); iter ++)
     {
      int tr = SampleTrajectory(probability);
      int state = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 3 - PrecoderBars - batch));
      if(state < 0)
        {
         iter--;
         continue;
        }

Затем мы очищаем стеки моделей и вспомогательный буфер.

      Encoder.Clear();
      Decoder.Clear();
      Noise.Clear();
      LastEncoder.BufferInit(EmbeddingSize, 0);

Определяем конечное состояние пакета обучения на траектории и очищаем матрицу сбора информации об изменении анализируемых параметров.

      int end = MathMin(state + batch, Buffer[tr].Total - PrecoderBars);
      delta = matrix<float>::Zeros(end - state - 1, Buffer[tr].States[state].state.Size());

Обратите внимание, что размер матрицы отклонений на 1 строку меньше пакета обучения. Это связано с тем, что в ней мы будем сохранять дельту изменения между 2 последующими состояниями.

На данном этапе все готово к началу обучения модели на чистой траектории и мы создаем первый вложенный цикл обучения.

      for(int i = state; i < end; i++)
        {
         inp.Assign(Buffer[tr].States[i].state);
         State.AssignArray(inp);
         int row = i - state;
         if(i < (end - 1))
            delta.Row(inp, row);

В теле цикла мы извлекаем из обучающей выборки анализируемое состояние и передаем его в буфер исходных данных.

Это же состояние мы используем для расчета отклонений. Сначала мы проверяем не является ли текущее состояние последним в пакете обучающих данных и добавляем анализируемое состояние в соответствующую строку матрицы отклонений (последнее состояние не добавляется).

Логичен вопрос: почему мы добавляем состояния как есть, ведь это матрица отклонений? Ответ кроется в следующем действии. На каждом последующей итерации цикла мы вычитаем анализируемое действие из предыдущей строки матрицы отклонений, в которой содержится предшествующее состояние, сохраненное на предыдущем шаге. Разумеется, этот шаг мы пропускаем для первого состояния, когда отсутствует предыдущее.

         if(row > 0)
            delta.Row(delta.Row(row - 1) - inp, row - 1);

Далее мы последовательно вызываем методы прямого прохода обучаемых моделей. Первым идет Энкодер.

         if(!LastEncoder.BufferWrite() || 
            !Encoder.feedForward((CBufferFloat*)GetPointer(State), 1, false, (CBufferFloat*)GetPointer(LastEncoder)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

За ним Декодер.

         if(!Decoder.feedForward(GetPointer(Encoder), -1, (CBufferFloat*)NULL))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

И завершает блок прямого прохода модель прогнозирования шума.

         if(!Noise.feedForward(GetPointer(Encoder), -1, (CBufferFloat*)NULL))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

Как обычно, за блоком прямого прохода мы организовываем обратный проход обучаемых моделей, в котором мы корректируем их параметры с целью минимизации ошибки. Вначале мы организуем обратный проход Декодера с передачей градиента ошибки Энкодеру. И прежде, чем вызвать обратный проход моделей нам необходимо подготовить целевые значения.

На выходе Декодера мы ожидаем получить параметры исходного состояния, подаваемого на вход Энкодера плюс прогноз на неготорый горизонт планирования. В предыдущей статье мы обсуждали состав прогнозируемых параметров по каждой свече. Я остаюсь при том же мнении. Поэтому ни архитектура Декодера, ни алгоритм подготовки целевых значений не изменились. Вначале мы заполняем матрицу целевых значений данными, поданными на вход Энкодера.

         target.Assign(Buffer[tr].States[i].state);
         ulong size = target.Size();
         targets = matrix<float>::Zeros(1, size);
         targets.Row(target, 0);
         if(size > BarDescr)
            targets.Reshape(size / BarDescr, BarDescr);
         ulong shift = targets.Rows();

Затем дополняем её данными из буфера воспроизведения опыта на заданный горизонт планирования.

         targets.Resize(shift + PrecoderBars, 3);
         for(int t = 0; t < PrecoderBars; t++)
           {
            target.Assign(Buffer[tr].States[i + t].state);
            if(size > BarDescr)
              {
               matrix<float> temp(1, size);
               temp.Row(target, 0);
               temp.Reshape(size / BarDescr, BarDescr);
               temp.Resize(size / BarDescr, 3);
               target = temp.Row(temp.Rows() - 1);
              }
            targets.Row(target, shift + t);
           }
         targets.Reshape(1, targets.Rows()*targets.Cols());
         target = targets.Row(0);

Полученную информацию переносим в вектор и сравниваем с результатами прямого прохода Декодера.

         Decoder.getResults(result);
         vector<float> error = target - result;

Как и ранее, в процессе обучения мы акцентируем внимание на максимальных отклонениях. Для этого мы сначала считаем скользящую среднеквадратическую ошибку.

         std_count = MathMin(std_count, 999);
         STE = MathSqrt((MathPow(STE, 2) * std_count + MathPow(error, 2)) / (std_count + 1));

А затем сравниваем текущую ошибку с пороговым значением на базе среднеквадратического отклонения. Обратный проход осуществляется только при превышении текущей ошибкой порогового значения хотя бы по одному показателю.

         vector<float> check = MathAbs(error) - STE * STE_Multiplier;
         if(check.Max() > 0)
           {
            //---
            Result.AssignArray(CAGrad(error) + result);
            if(!Decoder.backProp(Result, (CNet *)NULL) ||
               !Encoder.backPropGradient(GetPointer(LastEncoder), GetPointer(Gradient)))
              {
               PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
               Stop = true;
               break;
              }
           }

Напомню, что идею акцента на максимальных отклонениях мы позаимствовали из метода CFPI.

Аналогичный алгоритм организации обратного прохода мы используем для модели прогнозирования шума. Но здесь гораздо проще подход к организации вектора целевых значений — при работе с чистыми траекториями мы просто используем вектор нулевых значений.

         target = vector<float>::Zeros(delta.Cols());
         Noise.getResults(result);
         error = (target - result) * STE_Noise_Multiplier;

Обратите внимание, что при расчете ошибки мы умножаем полученное отклонение на константу STE_Noise_Multiplier, которая определяет влияние ошибки прогнозирования шума на общую ошибку модели.

Мы так же акцентируем внимание на максимальных отклонениях и осуществляем обратный проход только при наличии ошибки выше порогового значения хотя бы по одному параметру.

         STE_Noise = MathSqrt((MathPow(STE_Noise, 2) * std_count + MathPow(error, 2)) / (std_count + 1));
         std_count++;
         check = MathAbs(error) - STE_Noise;
         if(check.Max() > 0)
           {
            //---
            Result.AssignArray(CAGrad(error) + result);
            if(!Noise.backProp(Result, (CNet *)NULL) ||
               !Encoder.backPropGradient(GetPointer(LastEncoder), GetPointer(Gradient)))
              {
               PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
               Stop = true;
               break;
              }
           }

Градиент ошибки модели прогнозирования шума мы передаем на Энкодер и, при необходимости, вызываем его метод обратного прохода.

После обновления параметров всех обучаемых моделей мы сохраняем во вспомогательный буфер последние результаты прямого прохода Энкодера.

         Encoder.getResults(result);
         LastEncoder.AssignArray(result);

Информируем пользователя о прогрессе процесса обучения и переходим к следующей итерации вложенного цикла.

         if(GetTickCount() - ticks > 500)
           {
            double percent = (double(i - state) / (2 * (end - state)) + iter) * 100.0 / (Iterations);
            string str = StringFormat("%-20s %6.2f%% -> Error %15.8f\n", "Decoder", percent, 
                                                                    Decoder.getRecentAverageError());
            str += StringFormat("%-20s %6.2f%% -> Error %15.8f\n", "Noise Prediction", percent, 
                                                                      Noise.getRecentAverageError());
            Comment(str);
            ticks = GetTickCount();
           }
        }

На этом мы обычно завершаем описание итераций в системе циклов обучения модели, но не сегодня. Выше мы осуществили обработку пакета обучения моделей на чистой траектории. И далее нам предстоит повторить операции для траектории с добавлением шума. И здесь мы сначала определим статистические параметры распределения шума.

      //--- With noise
      vector<float> std_delta = delta.Std(0) * STD_Delta_Multiplier;
      vector<float> mean_delta = delta.Mean(0);

Обратите внимание, что среднеквадратическое отклонение умножается на коэффициент шума, чтобы уменьшить максимально возможное смещение значений анализируемых признаков.

Создадим вектор и массив для генерации шума.

      ulong inp_total = std_delta.Size();
      vector<float> noise = vector<float>::Zeros(inp_total);
      double ar_noise[];

После чего мы сэмплируем новую траекторию и начальное состояние на ней.

      tr = SampleTrajectory(probability);
      state = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 3 - PrecoderBars - batch));
      if(state < 0)
        {
         iter--;
         continue;
        }

Очистим стеки моделей и вспомогательный буфер.

      Encoder.Clear();
      Decoder.Clear();
      Noise.Clear();
      LastEncoder.BufferInit(EmbeddingSize, 0);

И организуем еще один вложенный цикл для работы с зашумленной траекторией.

      end = MathMin(state + batch, Buffer[tr].Total - PrecoderBars);
      for(int i = state; i < end; i++)
        {
         if(!Math::MathRandomNormal(0, 1, (int)inp_total, ar_noise))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }
         noise.Assign(ar_noise);

В теле цикла мы сначала генерируем шум из нормального распределения и переносим его в вектор. После чего осуществляем его репараметризацию.

         noise = mean_delta + std_delta * noise;

На данном этапе мы подготовили шум для текущей итерации обучения. Мы загружаем чистое состояние из буфера воспроизведения опыта и добавляем к нему сгенерированный шум.

         inp.Assign(Buffer[tr].States[i].state);
         inp = inp + noise;

Полученное состояние с добавлением шума загружаем в буфер исходных данных.

         State.AssignArray(inp);

Далее мы осуществляем блок прямого прохода, аналогично работе с чистыми траекториями.

         if(!LastEncoder.BufferWrite() || 
            !Encoder.feedForward((CBufferFloat*)GetPointer(State), 1, false, (CBufferFloat*)GetPointer(LastEncoder)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

         if(!Decoder.feedForward(GetPointer(Encoder), -1, (CBufferFloat*)NULL))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

         if(!Noise.feedForward(GetPointer(Encoder), -1, (CBufferFloat*)NULL))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

Методом SSWNP предусматривается создание пространственной согласованности между прогнозируемыми траекториями для чистых траекторий и с добавлением шума. Как было показано в теоретической части, обе траектории сближаются к одной цели. Следовательно, и блок обратного прохода Декодера мы построим так же, как сделали это выше для чистых траекторий.

         target.Assign(Buffer[tr].States[i].state);
         ulong size = target.Size();
         targets = matrix<float>::Zeros(1, size);
         targets.Row(target, 0);
         if(size > BarDescr)
            targets.Reshape(size / BarDescr, BarDescr);
         ulong shift = targets.Rows();
         targets.Resize(shift + PrecoderBars, 3);
         for(int t = 0; t < PrecoderBars; t++)
           {
            target.Assign(Buffer[tr].States[i + t].state);
            if(size > BarDescr)
              {
               matrix<float> temp(1, size);
               temp.Row(target, 0);
               temp.Reshape(size / BarDescr, BarDescr);
               temp.Resize(size / BarDescr, 3);
               target = temp.Row(temp.Rows() - 1);
              }
            targets.Row(target, shift + t);
           }
         targets.Reshape(1, targets.Rows()*targets.Cols());
         target = targets.Row(0);

         Decoder.getResults(result);
         vector<float> error = target - result;
         std_count = MathMin(std_count, 999);
         STE = MathSqrt((MathPow(STE, 2) * std_count + MathPow(error, 2)) / (std_count + 1));
         vector<float> check = MathAbs(error) - STE * STE_Multiplier;
         if(check.Max() > 0)
           {
            //---
            Result.AssignArray(CAGrad(error) + result);
            if(!Decoder.backProp(Result, (CNet *)NULL) ||
               !Encoder.backPropGradient(GetPointer(LastEncoder), GetPointer(Gradient)))
              {
               PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
               Stop = true;
               break;
              }
           }

Для модели прогнозирования шума отличие в целевых значениях. Если для чистых траекторий мы использовали вектор, заполненный нулевыми значениями, то сейчас в качестве целевых значений мы используем шум, добавленный к чистому состоянию перед подачей на вход Энкодера.

         target = noise;
         Noise.getResults(result);
         error = (target - result) * STE_Noise_Multiplier;

         STE_Noise = MathSqrt((MathPow(STE_Noise, 2) * std_count + MathPow(error, 2)) / (std_count + 1));
         std_count++;
         check = MathAbs(error) - STE_Noise;
         if(check.Max() > 0)
           {
            //---
            Result.AssignArray(CAGrad(error) + result);
            if(!Noise.backProp(Result, (CNet *)NULL) ||
               !Encoder.backPropGradient(GetPointer(LastEncoder), GetPointer(Gradient)))
              {
               PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
               Stop = true;
               break;
              }
           }

После обновления параметров моделей мы сохраняем во вспомогательный буфер результаты последнего прохода Энкодера.

         Encoder.getResults(result);
         LastEncoder.AssignArray(result);

Информируем пользователя о ходе процесса обучения и переходим на следующую итерацию цикла.

         if(GetTickCount() - ticks > 500)
           {
            double percent = (double(i - state) / (2 * (end - state)) + iter + 0.5) * 100.0 / (Iterations);
            string str = StringFormat("%-20s %6.2f%% -> Error %15.8f\n", "Decoder", percent, 
                                                                          Decoder.getRecentAverageError());
            str += StringFormat("%-20s %6.2f%% -> Error %15.8f\n", "Noise Prediction", percent, 
                                                                            Noise.getRecentAverageError());
            Comment(str);
            ticks = GetTickCount();
           }
        }
     }

На этом мы завершаем описание итераций в системе циклов обучения моделей. И после успешного завершения всех итераций мы очищаем поле комментариев на графике инструмента.

   Comment("");
//---
   PrintFormat("%s -> %d -> %-20s %10.7f", __FUNCTION__, __LINE__, "Decoder", Decoder.getRecentAverageError());
   PrintFormat("%s -> %d -> %-20s %10.7f", __FUNCTION__, __LINE__, "Noise Prediction", Noise.getRecentAverageError());
   ExpertRemove();
//---
  }

Выводим в журнал результаты процесса обучения и инициализируем завершение работы программы.

С полным кодом советника и всех, используемых в статье программ, Вы можете самостоятельно ознакомиться во вложении.

Выше представлен обновленный алгоритм советника обучения функции траектории. Алгоритм же обучения политики остался без изменений. И его подробное описание дано в предыдущей статье. А полный код советника «...\Experts\SSWNP\Study.mq5» Вы можете найти во вложении.

3. Тестирование

В практической части данной статьи мы интегрировали подходы метода Self-Supervised Waypoint Noise Prediction в ранее построенный советник обучения функции траектории метода Goal-Conditioned Predictive Coding и ожидаем повышения качества прогнозирования ценового движения. Теперь пришло время проверить результаты нашего труда на реальных данных в тестере стратегий MetaTrader 5.

Как и ранее, обучение и тестирование моделей осуществляется на исторических данных инструмента EURUSD тайм-фрейм H1. Для обучения моделей мы используем исторический интервал в первые 7 месяцев 2023 года. А тестирование обученных моделей осуществляется на исторических данных Августа 2023 года. Как можно заметить, тестовый период идет непосредственно за периодом обучения.

Перед обучением моделей нам предстоит собрать первичную обучающую выборку. Так как мы внедряли новые подходы в ранее построенный советник без изменения архитектуры моделей и структуры данных, то мы можем пропустить данный шаг и воспользоваться готовой базой примеров, которая была создана при обучении моделей методом GCPC. Мы создадим копию файла буфера воспроизведения опыта с именем «SSWNP.bd». После чего переходим непосредственно к процессу обучения моделей.

Как и предусмотрено методом GCPC, обучение моделей осуществляется в 2 этапа. На первом этапе мы обучаем функцию траектории. Именно на этом этапе мы внедрили подходы метода SSWNP. На вход Энкодера мы подаем только исторические данные ценового движения и показателей анализируемых индикаторов. Это делает все траектории в буфере воспроизведения опыта идентичными, т.к. показатели состояния счета и открытых позиций, вносящие различия в траектории, на данном этапе не анализируются. Следовательно, мы можем воспользоваться существующей базой примеров и обучить функцию траектории до получения приемлемого результата без сбора дополнительных примеров.

Второй этап обучения модели, обучение политики поведения, предполагает поиск оптимальных действий Агента в условиях исторических рыночных состояний с изменением состояния счета и открытых позиций, которые зависят от конъюнктуры рынка и совершенных Агентом действий. На этом этапе мы используем итерационное обучение моделей, чередуя процессы обучения моделей и сбора дополнительных примеров, которые позволяют более точно оценить обновленную политику поведения Агента.

Проведенный нами процесс обучения дал свои результаты. И нам удалось обучить модель, способную генерировать прибыль как на исторических данных обучающей выборки, так и на тестовом временном отрезке.

Результаты тестирования обученной модели

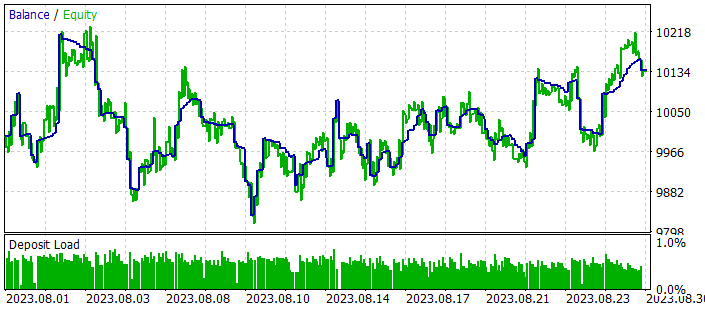
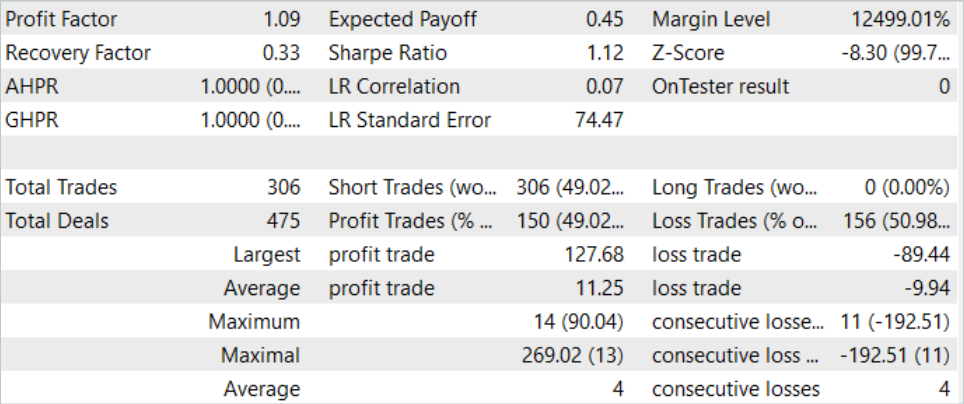
Заключение

В данной статье мы познакомились с методом Self-Supervised Waypoint Noise Prediction. Этот подход позволяет повысить эффективность моделей в условиях сложных стохастических окружений, где будущие траектории Агентов подвержены неопределенности из-за изменяющихся условий и физических ограничений. Поставленная цель достигается путем внесения шума в прошлые траектории, что способствует более точному и разнообразному прогнозированию будущих путей. Представленная новаторская методика состоит из двух модулей: модуля пространственной согласованности и модуля предсказания шума, которые в совокупности обеспечивают поддержку точного и надежного прогнозирования в стохастических сценариях.

Предложенная авторами метода конструкция довольно универсальна, что позволяет её интегрировать в большой спектр различных алгоритмов обучения моделей. И это касается не только методов обучения с подкреплением. В своей работе авторы метода демонстрируют примеры, как внедрение предложенных подходов повышает эффективность базовых методов.

В практической части данной статьи мы интегрировали подходы, предложенные методом SSWNP, в структуру алгоритма GCPC. И результаты проведенных нами тестов подтверждают эффективность предложенного метода.

Однако, все программы, представленные в статье предназначены только для демонстрации возможностей алгоритмов и не готовы для использования на реальных финансовых рынках.

Ссылки

Программы, используемые в статье

#	Имя	Тип	Описание
1	Research.mq5	Советник	Советник сбора примеров
2	ResearchRealORL.mq5	Советник	Советник сбора примеров методом Real-ORL
3	Study.mq5	Советник	Советник обучения Политики
4	StudyEncoder.mq5	Советник	Советник обучения Автокодировщика с использованием подходов SSWNP
5	Test.mq5	Советник	Советник для тестирования модели
6	Trajectory.mqh	Библиотека класса	Структура описания состояния системы
7	NeuroNet.mqh	Библиотека класса	Библиотека классов для создания нейронной сети
8	NeuroNet.cl	Библиотека	Библиотека кода программы OpenCL

Прикрепленные файлы |

Загрузить ZIP

MQL5.zip (787.87 KB)

Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Другие статьи автора

Перейти к обсуждению на форуме трейдеров

Выставление ордеров в MQL5

При создании любой торговой системы есть задача, которую необходимо эффективно решить. Эта задача заключается в выставлении ордеров либо в их автоматической обработке торговой системой. В статье рассмотрено создание торговой системы с точки зрения эффективного выставления ордеров.

Создаем алгоритм маркет-мейкинга на MQL5

Как работают маркет-мейкеры на рынке? Рассмотрим этот вопрос и создадим примитивный алгоритм маркет-мейкинга.

Популяционные алгоритмы оптимизации: Алгоритмы искусственной микро-иммунной системы (Micro Artificial immune system, Micro-AIS)

Статья рассказывает о методе оптимизации, основанном на принципах функционирования иммунной системы организма — Micro Artificial Immune System (Micro-AIS) — модификацию AIS. Micro-AIS использует более простую модель иммунной системы и простые операции обработки иммунной информации. Статья также обсуждает преимущества и недостатки Micro-AIS по сравнению с обычным AIS.

Разметка данных в анализе временных рядов (Часть 1)：Создаем набор данных с маркерами тренда с помощью графика советника

В этой серии статей представлены несколько методов маркировки временных рядов, которые могут создавать данные, соответствующие большинству моделей искусственного интеллекта (ИИ). Целевая маркировка данных может сделать обученную модель ИИ более соответствующей пользовательским целям и задачам, повысить точность модели и даже помочь модели совершить качественный скачок!