
ニューラルネットワークが簡単に(第70回):閉形式方策改善演算子(CFPI)
はじめに
エージェント方策の行動に制約を与えて最適化する方法は、オフライン強化学習問題の解決に有望であることが判明しました。過去の遷移を利用することで、エージェント方策は学習された価値関数を最大化するように訓練されます。
行動に制約のある方策は、エージェントの行動に関する大幅な分布の変化を回避するのに役立ち、行動コストの評価に十分な信頼性を与えます。前回の記事では、この方法を利用したSPOT法を紹介しました。このトピックの続きとして、論文『Offline Reinforcement Learning with Closed-Form Policy Improvement Operators』で紹介された閉形式方策改善(Closed-Form Policy Improvement :CFPI)アルゴリズムに触れることを提案します。
1.閉形式方策改善(CFPI)アルゴリズム
閉形式とは、有限回数の標準演算を用いて表現される数学関数のことです。定数、変数、標準演算子、関数を含むことができますが、通常、極限、微分、積分式は含まれません。このように、ここで検討しているCFPI法は、エージェントの方策学習アルゴリズムにいくつかの分析的な要素を導入しています。
既存のオフライン強化学習モデルのほとんどは、確率的勾配降下法(SGD)を用いて戦略を最適化しますが、学習過程で不安定になる可能性があるため、学習率を慎重に調整する必要があります。さらに、オフラインで訓練された戦略の性能は、特定の評価ポイントに依存する可能性があります。そのため、学習の最終段階で大きなばらつきが生じることが多くなります。オフライン強化学習では、環境との相互作用へのアクセスが制限されているため、ハイパーパラメータの調整が難しく、この不安定性が大きな課題となります。異なる評価ポイント間でのばらつきに加え、SGDを使用して戦略を改善すると、異なるランダムな初期条件下でパフォーマンスに大きなばらつきが生じる可能性があります。
CFPI法の著者は、オフラインRL学習の不安定性の軽減を試みています。彼らは安定した戦略改善演算子を開発します。特に、分布のシフトを制限する必要性から、一次テイラー近似の使用が動機付けられ、行動戦略の十分に小さな近傍範囲内で正確なエージェントの方策目的関数の線形近似が導かれることを指摘しています。この重要な観察に基づき、本手法の著者は、閉形式の解を返す戦略改善演算子を構築しています。
行動戦略を単一のガウス分布としてモデル化することで、CFPIの著者が提案する戦略改善演算子は、決定論的に値を改善する方向に行動方策をシフトさせます。その結果、提案されている閉形式方策改善法は、与えられたデータセットの基本的な行動戦略を学習するだけなので、戦略改善による学習の不安定さを回避することができます。
CFPI法の著者はまた、実用的なデータセットはしばしば異種戦略を用いて収集されることにも言及しています。これは、エージェントの行動のマルチモーダルな分布につながる可能性があります。単一ガウス分布では、基礎となる分布のモードの多くを捉えることができず、戦略の改善の可能性が制限されます。行動方策をガウス分布の混合としてモデル化することで、表現力は向上しますが、最適化にはさらなる困難が伴います。この手法の著者は、LogSumExpの下界とイェンセンの不等式を用いてこの問題を解決し、マルチモーダルな行動戦略に適用可能な閉形式戦略改善演算子を導きました。
著者は、閉形式方策改善法の貢献を次のように強調しています。
- CFPI演算子は、シングルモードおよびマルチモードの動作戦略と互換性があり、他のアルゴリズムによって学習された戦略を改善することができる
- 行動戦略をガウス分布の混合としてモデル化することの利点に関する実証的証拠
- 提案アルゴリズムのシングルステップおよび反復変種は、標準ベンチマークにおいて既存のアルゴリズムを上回る
CFPIの著者は、オフラインシナリオでの不安定さを避けるために、訓練なしで分析戦略改善演算子を作成します。彼らは、目的関数に関する最適化が、オフラインサンプルにおける行動戦略からの制約された逸脱を許容する戦略を生成することに注目しています。そのため、訓練中は動作の近辺のQ値のみを照会します。これは当然、一次線形近似を使用する動機となります。
同時に、更新された方策における行動の評価は、訓練サンプルの分布の十分に小さい近傍においてのみ、学習された価値関数の正確な線形近似を提供します。したがって、訓練データセットから「状態-行動」ペアを選択することは、最終的な学習結果にとって非常に重要です。
この問題を解決するために、著者は任意の状態Sに対して次のような近似問題を解くことを提案しています。
![]()
ここで、D(•,•)は数学的に定義された発散関数である必要はありません。エージェントの行動方策の訓練データセットの分布からの偏差を制約することができる任意の一般的なD(•,•)を考慮できます。
一般に、上記の問題は閉形式の解を持つとは限りません。CFPI法の著者は次の特殊なケースを分析しています。
- 訓練データセットの収集にガウス戦略を用いる
- そして、エージェントの決定論的な行動方策を訓練する
- D(•,•)は負の尤度関数
このようなシナリオでは、方策の訓練が訓練データセットの分布に集中するのが合理的な選択です。そうすると、提案された最適化問題は閉形式で表すことができます。
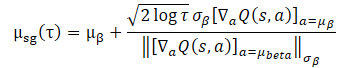
この閉形式を使用してエージェント方策を改善することで、計算効率が向上し、SGDに起因する潜在的な不安定性が回避されます。しかし、その適用可能性は、訓練データセットの収集戦略における単一ガウス(Single Gaussian)の仮定に依存します。実際のところ、履歴データセットは通常、さまざまなレベルの専門性を持つ異質な戦略によって収集されます。一次元のガウシアンでは分布の全体像を捉えられない可能性があるため、ガウシアンの混合を用いてデータ収集方策を表現するのが妥当と思われます。
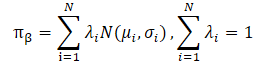
ただし、ガウシアンの混合を訓練データ収集方策に直接代入すると、目的関数が非凸になるため、上に示した問題の適用性に違反します。ここで、最適化問題を解く上で2つの大きな課題に直面します。
まず、訓練データセットから適切な行動を選択する方法が不明確です。ここで、目標方策の解が、選択された行動の小さい近傍に位置するようにすることも必要です。
第2に、ガウシアンの混合を使用すると凸形ができないため、最適化が難しくなります。
LogSumExpを使用すると、最適化問題を変換することができます。
![]()
これは閉形式で表すことができます。
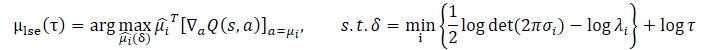
イェンセンの不等式を用いることで、以下の最適化問題が得られます。
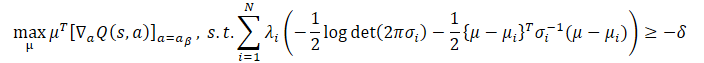
この問題の閉形式解は次のようになります。
![]()
元の最適化問題と比較して、提案された拡張はどちらもより厳しい信頼区間制約を課しています。これは、ある閾値以上の混合ガウスの対数尤度の下界を提供することによって達成されます。同時に、パラメータτは信頼区間の大きさを制御します。
どちらの最適化問題にも長所と短所があります。訓練データセット分布が明らかな多峰性を示す場合、イェンセンの不等式によって構成されるデータ収集方策の対数の下界は、その凹性によって異なるモードを捕捉することができず、データ収集方策をガウス混合としてモデル化する利点が失われます。この場合、LogSumExpの下界は、データ収集方策の対数の多峰性を保持するため、LogSumExp最適化問題は、元の最適化問題の合理的な代替として機能することができます。
訓練データセットの分布が単一ガウス分布になると、イェンセンの不等式による近似は等式になります。このように、μjensenは与えられた最適化問題を正確に解きます。しかしこの場合、LogSumExpの下界の精度は重みλi=1...Nに大きく依存します。
幸いなことに、両方法の長所を組み合わせることで、上記のすべてのシナリオを考慮したCFPI演算子を得ることができ、この演算子はµlseとµjensenから上位の行動を選択する行動方策を返します。
![]()
原著論文には、詳細な計算と、提示されたすべての式の適用可能性の証拠が掲載されています。
CFPI法の著者は、提案された手法が訓練データセットの非ガウス分布にも適用可能であることを指摘しています。同時に、提示されたCFPI演算子により、単一段階法、多段階法、反復法を得ることができるオフライン学習の一般的なテンプレートを作成することができます。
行動の評価には、事前に訓練されたCriticモデルが使用されます。訓練データセットに対して、既知の方法で訓練することができます。これはモデル訓練アルゴリズムの最初の段階です。
次に、訓練データセットから、ある状態のパケットをサンプリングします。行動は、現在のエージェント方策を考慮して、このパッケージのために生成されます。次に、上記のCFPI演算子を考慮して、結果の行動を評価します。
この評価結果に基づいて最適な状態が選択され、エージェント方策が更新されます。
多段階法や反復法を構築する場合は、この過程を繰り返します。
CFPI演算子の設計は、行動エージェント方策制約パラダイムに触発されていますが、提案された方法は、一般的な基本的な強化学習手法と互換性があります。論文では、CFPI演算子が他のアルゴリズムで学習した戦略の効率を高めた例が示されています。
2.MQL5を使用した実装
以上は、閉形式方策改善法の理論的説明です。提示された数式がかなり複雑に見えることには同意します。提案された方法を実施する過程で、それらをより詳細に理解することに努めましょう。
この論文の著者が提案したモデル訓練アルゴリズムは、CriticとActorの逐次的な訓練をおこなうものです。Criticモデルが最初に訓練されます。それができて初めて、Actor方策の訓練に着手できます。
この方法では、Criticがソースデータの予備処理にActorモデルを使用する場合の技法は無意味になります。なぜなら、Criticを訓練する段階では、Actorモデルはまだ形成されていないからです。もちろん、Actorモデルを生成して、以前と同じように使用することもできます。しかしこの場合、次のような問題が発生します。方策訓練の段階で、CFPIアルゴリズムはCriticモデルの更新を提供しません。Actorのパラメータを変更することは、必然的にソースデータの予備処理のパラメータを変更することにつながります。この場合、Critic入力での分布が変化します。これは一般的に、Actorの行動の評価に歪みをもたらします。
このような状況を改善するには、初期状態エンコーダを使用しないようにするか、別のモデルに移せばいいのです。
エンコーダをCriticモデルに動かすすることはできません。CriticのフィードフォワードパスにはActorが生成した行動が必要だからです。また、Actorのフィードフォワードパスにはエンコーダの結果が必要です。サークルが絞られました。
2.1 モデルのアーキテクチャ
実装では、環境的状態エンコーダを別のモデルとして作ることにしました。これは、モデルのアーキテクチャにも影響しました。モデルアーキテクチャの記述は、CreateDescriptionsメソッドでおこないます。ActorモデルとCriticモデルは一貫して訓練されているにもかかわらず、モデルアーキテクチャの説明は2つのメソッドに分けませんでした。そのため、このメソッドは、モデルアーキテクチャを記録するためのオブジェクトの3つの動的配列へのポインタをパラメータで受け取ります。
メソッド本体では、受け取ったポインタの妥当性を確認し、必要であれば新しい配列オブジェクトのインスタンスを生成します。
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ bool CreateDescriptions(CArrayObj *actor, CArrayObj *critic, CArrayObj *encoder) { //--- CLayerDescription *descr; //--- if(!actor) { actor = new CArrayObj(); if(!actor) return false; } if(!critic) { critic = new CArrayObj(); if(!critic) return false; } if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; }
1つ目は、現在状態エンコーダのアーキテクチャの説明です。モデルのアーキテクチャは、ソースデータの層から始まります。ソースデータの層は、分析された履歴の深さ全体の値動きと指標値に関する情報を記録するのに十分なサイズでなければなりません。
//--- State Encoder encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1000; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
得られた生データはバッチ正規化層で前処理されます。
次に畳み込みブロックが登場し、データの次元を減らすと同時に、データ内の安定したパターンを識別することができます。
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; prev_count = descr.count = HistoryBars; descr.window = BarDescr; descr.step = BarDescr; int prev_wout = descr.window_out = BarDescr / 2; descr.activation = LReLU; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronSoftMaxOCL; descr.count = prev_count; descr.step = prev_wout; descr.optimization = ADAM; descr.activation = None; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; prev_count = descr.count = prev_count; descr.window = prev_wout; descr.step = prev_wout; prev_wout = descr.window_out = 8; descr.activation = LReLU; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronSoftMaxOCL; descr.count = prev_count; descr.step = prev_wout; descr.optimization = ADAM; descr.activation = None; if(!encoder.Add(descr)) { delete descr; return false; }
畳み込みブロックの結果は、2つの全結合層によって処理されます。
//--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.optimization = ADAM; descr.activation = LReLU; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 7 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
このようにして処理されたデータは、タイムスタンプのハーモニクスを含む口座の状態に関する情報で補完されます。
//--- layer 8 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConcatenate; descr.count = 2 * LatentCount; descr.window = prev_count; descr.step = AccountDescr; descr.optimization = ADAM; descr.activation = SIGMOID; if(!encoder.Add(descr)) { delete descr; return false; }
エンコーダの出力に偶然性を作り出します。これにより、モデル過剰適合の可能性を減らすと同時に、確率的な外部環境におけるモデルの安定性を高めることができます。
//--- layer 9 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronVAEOCL; descr.count = LatentCount; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
続いて、Actorのアーキテクチャについて説明します。前述の環境エンコーダの結果を入力として受け取ります。
//--- Actor actor.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
ご覧のように、初期データを準備する作業はすべてエンコーダ内でおこなわれます。これにより、Actorのモデルを可能な限りシンプルにすることができます。ここでは3つの全結合層を作成します。
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = 2 * NActions; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
モデル出力では、連続行動空間における確率的方策を形成します。
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronVAEOCL; descr.count = NActions; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Criticモデルはエンコーダの結果も入力として使用します。しかし、Actorモデルとは異なり、評価された行動のベクトルで結果を補足します。したがって、ソースデータ層の後に、2つのソースデータテンソルを結合する連結層を使用します。
//--- Critic critic.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = LatentCount; descr.activation = None; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } //--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConcatenate; descr.count = LatentCount; descr.window = prev_count; descr.step = NActions; descr.optimization = ADAM; descr.activation = LReLU; if(!critic.Add(descr)) { delete descr; return false; }
次に、全結合層による意思決定ブロックが登場します。
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } //--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } //--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = NRewards; descr.optimization = ADAM; descr.activation = None; if(!critic.Add(descr)) { delete descr; return false; } //--- return true; }
モデルアーキテクチャの説明はここで終わり、モデル学習アルゴリズムの構築に移ります。
もちろん、モデルの訓練を開始する前に、訓練データセットを収集する必要があります。さて、次のことに注意してください。今回は、これまでの研究での環境との相互作用EAをそのままの形で使用することはできないため、モデルのアーキテクチャを変更し、環境的状態エンコーダを外部モデルに分離しました。これはEAのアルゴリズムにも影響を与えましたが、これらの変更は特定の箇所(「...\Experts\CFPI\Research.mq5」と「...\Experts\CFPI\Test.mq5」)のみにあります。これらは記事への添付ファイルとして提供されています。次に、Criticの学習アルゴリズムの構築に移ります。
2.2 Criticの訓練
Criticモデルの訓練アルゴリズムは、EA「...\Experts\CFPI\StudyCritic.mq5」に実装されています。このEAでは、2つのCriticモデルを並行して訓練しています。ご存知のように、2つのCriticを使用することで、その後のActor行動方策の訓練の安定性と効率を高めることができます。Criticsモデルとともに、環境状態の一般的なエンコーダを訓練します。
//+------------------------------------------------------------------+ //| Input parameters | //+------------------------------------------------------------------+ input int Iterations = 1e6; //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ STrajectory Buffer[]; CNet StateEncoder; CNet Critic1; CNet Critic2;
EA初期化メソッドでは、まず訓練データセットの読み込みを試みます。
//+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- ResetLastError(); if(!LoadTotalBase()) { PrintFormat("Error of load study data: %d", GetLastError()); return INIT_FAILED; }
それから必要なモデルを読み込みます。事前に訓練されたモデルを読み込むことができない場合は、ランダムなパラメータを含む新しいモデルを生成します。
//--- load models float temp; if(!StateEncoder.Load(FileName + "Enc.nnw", temp, temp, temp, dtStudied, true) || !Critic1.Load(FileName + "Crt1.nnw", temp, temp, temp, dtStudied, true) || !Critic2.Load(FileName + "Crt2.nnw", temp, temp, temp, dtStudied, true)) { Print("Init new models"); CArrayObj *actor = new CArrayObj(); CArrayObj *critic = new CArrayObj(); CArrayObj *encoder = new CArrayObj(); if(!CreateDescriptions(actor, critic, encoder)) { delete actor; delete critic; delete encoder; return INIT_FAILED; } if(!Critic1.Create(critic) || !Critic2.Create(critic) || !StateEncoder.Create(encoder)) { delete actor; delete critic; delete encoder; return INIT_FAILED; } delete actor; delete critic; delete encoder; //--- }
すべてのモデルを1つのOpenCLコンテキストに転送することで、不必要な情報をメインプログラムメモリに転送したり戻したりすることなく、モデル間のデータ交換を可能にしています。
//---
OpenCL = Critic1.GetOpenCL();
Critic2.SetOpenCL(OpenCL);
StateEncoder.SetOpenCL(OpenCL);
モデル間のデータ転送で起こりうるエラーを排除するため、使用するデータの統一レイアウトへの準拠を確認します。
//--- StateEncoder.getResults(Result); if(Result.Total() != LatentCount) { PrintFormat("The scope of the State Encoder does not match the latent size count (%d <> %d)", LatentCount, Result.Total()); return INIT_FAILED; } //--- StateEncoder.GetLayerOutput(0, Result); if(Result.Total() != (HistoryBars * BarDescr)) { PrintFormat("Input size of State Encoder doesn't match state description (%d <> %d)", Result.Total(), (HistoryBars * BarDescr)); return INIT_FAILED; } //--- Critic1.GetLayerOutput(0, Result); if(Result.Total() != LatentCount) { PrintFormat("Input size of Critic1 doesn't match State Encoder output (%d <> %d)", Result.Total(), LatentCount); return INIT_FAILED; } //--- Critic2.GetLayerOutput(0, Result); if(Result.Total() != LatentCount) { PrintFormat("Input size of Critic2 doesn't match State Encoder output (%d <> %d)", Result.Total(), LatentCount); return INIT_FAILED; }
すべての制御の受け渡しに成功したら、補助データバッファを初期化します。
//--- Gradient.BufferInit(AccountDescr, 0);
また、モデルの訓練過程を開始するために、カスタムイベントを初期化します。
//--- if(!EventChartCustom(ChartID(), 1, 0, 0, "Init")) { PrintFormat("Error of create study event: %d", GetLastError()); return INIT_FAILED; } //--- return(INIT_SUCCEEDED); }
その後、EA初期化メソッドの動作を完了します。
EAの初期化解除メソッドでは、訓練済みモデルを保存し、メモリをクリアします。
//+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- if(!(reason == REASON_INITFAILED || reason == REASON_RECOMPILE)) { StateEncoder.Save(FileName + "Enc.nnw", 0, 0, 0, TimeCurrent(), true); Critic1.Save(FileName + "Crt1.nnw", Critic1.getRecentAverageError(), 0, 0, TimeCurrent(), true); Critic2.Save(FileName + "Crt2.nnw", Critic2.getRecentAverageError(), 0, 0, TimeCurrent(), true); } delete Result; delete OpenCL; }
モデルを訓練する実際のプロセスは、Trainメソッドに実装されています。メソッドの本体では、まず経験再生バッファから軌跡を選択する加重確率を計算します。
//+------------------------------------------------------------------+ //| Train function | //+------------------------------------------------------------------+ void Train(void) { //--- vector<float> probability = GetProbTrajectories(Buffer, 0.9);
次に、ローカル変数を宣言し、EAの外部パラメータでユーザーが指定した値に等しい反復回数の訓練ループを作成します。
vector<float> rewards, rewards1, rewards2, target_reward; uint ticks = GetTickCount(); //--- for(int iter = 0; (iter < Iterations && !IsStopped()); iter ++) {
訓練ループ本体では、軌道とその軌道上の状態をサンプリングします。
int tr = SampleTrajectory(probability); int i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 3)); if(i < 0) { iter--; continue; }
その後、ソースデータバッファに書き入れます。まず、環境の状態を記述するためのバッファに、経験再生バッファから価格の動きと分析された指標の値に関するデータを書き入れます。
//--- Q-function study
State.AssignArray(Buffer[tr].States[i].state);
次に、口座のステータスと未決済のポジションを記述したバッファに書き入れます。
float PrevBalance = Buffer[tr].States[MathMax(i - 1, 0)].account[0]; float PrevEquity = Buffer[tr].States[MathMax(i - 1, 0)].account[1]; Account.Clear(); Account.Add((Buffer[tr].States[i].account[0] - PrevBalance) / PrevBalance); Account.Add(Buffer[tr].States[i].account[1] / PrevBalance); Account.Add((Buffer[tr].States[i].account[1] - PrevEquity) / PrevEquity); Account.Add(Buffer[tr].States[i].account[2]); Account.Add(Buffer[tr].States[i].account[3]); Account.Add(Buffer[tr].States[i].account[4] / PrevBalance); Account.Add(Buffer[tr].States[i].account[5] / PrevBalance); Account.Add(Buffer[tr].States[i].account[6] / PrevBalance);
タイムスタンプのハーモニクスでバッファを補います。
double time = (double)Buffer[tr].States[i].account[7]; double x = time / (double)(D'2024.01.01' - D'2023.01.01'); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_MN1); Account.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_W1); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_D1); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); if(Account.GetIndex() >= 0) Account.BufferWrite();
収集されたデータは、環境的状態エンコーダのフィードフォワードパスに十分です。
//--- if(!StateEncoder.feedForward(GetPointer(State), 1, false, GetPointer(Account))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
前述の通り、現段階ではActorモデルは使用していません。Criticは、訓練データセットにあらかじめ保存されている実際の行動と環境から受け取った報酬の評価を用いて、教師あり学習法によって訓練されます。したがって、両Criticのフィードフォワードパスには、環境的状態エンコーダの結果と訓練データセットからの行動ベクトルを使用します。
//--- Actions.AssignArray(Buffer[tr].States[i].action); if(Actions.GetIndex() >= 0) Actions.BufferWrite(); //--- if(!Critic1.feedForward(GetPointer(StateEncoder), -1, GetPointer(Actions)) || !Critic2.feedForward(GetPointer(StateEncoder), -1, GetPointer(Actions))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
操作の正しさを確認し、両Criticのフィードフォワードパスの結果を読み込みます。
//---
Critic1.getResults(rewards1);
Critic2.getResults(rewards2);
次のステップは、モデルを訓練するための目標値を生成することです。上述したように、訓練データセットから実際の値を訓練します。この段階では、新しい状態への1回の遷移に対して報酬を使用します。収束を改善するために、CAGradメソッドを用いて誤差勾配ベクトルの方向を調整します。
モデルのパラメータは1つずつ調整されます。まず、最初のCriticのパラメータを調整し、環境的状態エンコーダのバックプロパゲーションパスメソッドを呼び出します。
rewards.Assign(Buffer[tr].States[i + 1].rewards); target_reward.Assign(Buffer[tr].States[i + 2].rewards); rewards = rewards - target_reward * DiscFactor; Result.AssignArray(CAGrad(rewards - rewards1) + rewards1); if(!Critic1.backProp(Result, GetPointer(Actions), GetPointer(Gradient)) || !StateEncoder.backPropGradient(GetPointer(Account), GetPointer(Gradient))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
次に、2つ目のCriticに対してこの操作を繰り返します。
Result.AssignArray(CAGrad(rewards - rewards2) + rewards2); if(!Critic2.backProp(Result, GetPointer(Actions), GetPointer(Gradient)) || !StateEncoder.backPropGradient(GetPointer(Account), GetPointer(Gradient))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
各Criticを更新した後、エンコーダのパラメータが調整されます。このように、環境埋め込みを可能な限り有益で正確なものにしようとしています。
モデルパラメータの更新に成功したら、訓練の進捗状況をユーザーに知らせ、ループの次の反復に進むだけです。
//--- if(GetTickCount() - ticks > 500) { string str = StringFormat("%-15s %5.2f%% -> Error %15.8f\n", "Critic1", iter * 100.0 / (double)(Iterations), Critic1.getRecentAverageError()); str += StringFormat("%-15s %5.2f%% -> Error %15.8f\n", "Critic2", iter * 100.0 / (double)(Iterations), Critic2.getRecentAverageError()); Comment(str); ticks = GetTickCount(); } }
学習ループのすべての反復が完了したら、チャートのコメント欄を消去します。また、訓練結果の情報をログに出力し、EAの終了を開始します。
Comment(""); //--- PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Critic1", Critic1.getRecentAverageError()); PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Critic2", Critic2.getRecentAverageError()); ExpertRemove(); //--- }
EAの完全なコードは、添付ファイルに記載されています。
2.3 行動方策の訓練
Criticを訓練した後、次の段階、つまりActorの行動方策を訓練します。この機能は、EA「....\Experts\CFPI\Study.mq5」に実装しています。まず、外部パラメータに、訓練に最適なポイントを選択するパケットのサイズを追加します。
//+------------------------------------------------------------------+ //| Input parameters | //+------------------------------------------------------------------+ input int Iterations = 10000; input int BatchSize = 256;
このEAでは4つのモデルを使いますが、訓練するのはActorだけです。
CNet Actor; CNet Critic1; CNet Critic2; CNet StateEncoder;
EAの初期化メソッドでは、まず訓練セットをアップロードします。
//+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- ResetLastError(); if(!LoadTotalBase()) { PrintFormat("Error of load study data: %d", GetLastError()); return INIT_FAILED; }
その後、モデルを読み込みます。まず、事前に訓練された環境的状態エンコーダとCriticモデルを読み込みます。これらのモデルが利用できなければ、それ以上学習過程を進めることはできません。そのため、モデルの読み込み中にエラーが発生した場合は、EAの操作を終了します。
//--- load models float temp; if(!StateEncoder.Load(FileName + "Enc.nnw", temp, temp, temp, dtStudied, true) || !Critic1.Load(FileName + "Crt1.nnw", temp, temp, temp, dtStudied, true) || !Critic2.Load(FileName + "Crt2.nnw", temp, temp, temp, dtStudied, true)) { Print("Can't load Critic models"); return INIT_FAILED; }
事前に訓練されたActorがない場合は、ランダムなパラメータで満たされた新しいモデルを初期化します。
if(!Actor.Load(FileName + "Act.nnw", temp, temp, temp, dtStudied, true)) { Print("Init new models"); CArrayObj *actor = new CArrayObj(); CArrayObj *critic = new CArrayObj(); if(!CreateDescriptions(actor, critic, critic)) { delete actor; delete critic; return INIT_FAILED; } if(!Actor.Create(actor)) { delete actor; delete critic; return INIT_FAILED; } delete actor; delete critic; }
すべてのモデルを1つのOpenCLコンテキストに転送し、エンコーダとCriticsの訓練モードを無効にします。
OpenCL = Actor.GetOpenCL(); Critic1.SetOpenCL(OpenCL); Critic2.SetOpenCL(OpenCL); StateEncoder.SetOpenCL(OpenCL); //--- StateEncoder.TrainMode(false); Critic1.TrainMode(false); Critic2.TrainMode(false);
その後、モデルアーキテクチャの互換性を確認します。
//--- Actor.getResults(Result); if(Result.Total() != NActions) { PrintFormat("The scope of the actor does not match the actions count (%d <> %d)", NActions, Result.Total()); return INIT_FAILED; }
StateEncoder.GetLayerOutput(0, Result); if(Result.Total() != (HistoryBars * BarDescr)) { PrintFormat("Input size of State Encoder doesn't match state description (%d <> %d)", Result.Total(), (HistoryBars * BarDescr)); return INIT_FAILED; }
StateEncoder.getResults(Result); int latent_state = Result.Total(); Critic1.GetLayerOutput(0, Result); if(Result.Total() != latent_state) { PrintFormat("Input size of Critic1 doesn't match output State Encoder (%d <> %d)", Result.Total(), latent_state); return INIT_FAILED; }
Critic2.GetLayerOutput(0, Result); if(Result.Total() != latent_state) { PrintFormat("Input size of Critic2 doesn't match output State Encoder (%d <> %d)", Result.Total(), latent_state); return INIT_FAILED; }
Actor.GetLayerOutput(0, Result); if(Result.Total() != latent_state) { PrintFormat("Input size of Actor doesn't match output State Encoder (%d <> %d)", Result.Total(), latent_state); return INIT_FAILED; }
確認ブロックが正常に終了すれば、次のステップに進むことができます。補助バッファを初期化し、カスタムイベントを生成して学習過程を開始します。
Gradient.BufferInit(AccountDescr, 0); //--- if(!EventChartCustom(ChartID(), 1, 0, 0, "Init")) { PrintFormat("Error of create study event: %d", GetLastError()); return INIT_FAILED; } //--- return(INIT_SUCCEEDED); }
これでEA初期化メソッドの操作は完了しました。EAの初期化解除メソッドでは、訓練済みモデルを保存し、メモリをクリアします。
//+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- if(!(reason == REASON_INITFAILED || reason == REASON_RECOMPILE)) Actor.Save(FileName + "Act.nnw", 0, 0, 0, TimeCurrent(), true); delete Result; delete OpenCL; }
Actorモデルの訓練過程は、Trainメソッドで実装されています。メソッドの本体では、まず訓練データセットから軌道を選択する確率を決定します。
//+------------------------------------------------------------------+ //| Train function | //+------------------------------------------------------------------+ void Train(void) { //--- vector<float> probability = GetProbTrajectories(Buffer, 0.9);
その後、必要なローカル変数を作成します。
//--- vector<float> rewards, rewards1, rewards2, target_reward; vector<float> action, action_beta; float Improve = 0; int bar = (HistoryBars - 1) * BarDescr; uint ticks = GetTickCount();
次に、EAの外部パラメータで指定された反復回数のモデル訓練ループを作成します。
//--- for(int iter = 0; (iter < Iterations && !IsStopped()); iter ++) {
Actorの行動方策を学習するループの本体では、CFPI法の方法を使用します。まず、訓練データセットからデータのバッチをサンプリングする必要があります。特定の状態における現在のActor方策の行動を生成し、評価する必要があります。これらの処理を実行するために、分析対象のパッケージのサイズに等しい反復回数の入れ子ループを作成しましょう。演算結果をローカルのmBatch行列に保存します。
matrix<float> mBatch = matrix<float>::Zeros(BatchSize, 4); for(int b = 0; b < BatchSize; b++) { int tr = SampleTrajectory(probability); int i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2)); if(i < 0) { b--; continue; }
サンプリング操作は、先におこなったものと同様です。
環境状態を記述するバッファに、選択された各状態からのデータを書き入れます。
//--- State
State.AssignArray(Buffer[tr].States[i].state);
口座ステータスバッファを追加します。
float PrevBalance = Buffer[tr].States[MathMax(i - 1, 0)].account[0]; float PrevEquity = Buffer[tr].States[MathMax(i - 1, 0)].account[1]; Account.Clear(); Account.Add((Buffer[tr].States[i].account[0] - PrevBalance) / PrevBalance); Account.Add(Buffer[tr].States[i].account[1] / PrevBalance); Account.Add((Buffer[tr].States[i].account[1] - PrevEquity) / PrevEquity); Account.Add(Buffer[tr].States[i].account[2]); Account.Add(Buffer[tr].States[i].account[3]); Account.Add(Buffer[tr].States[i].account[4] / PrevBalance); Account.Add(Buffer[tr].States[i].account[5] / PrevBalance); Account.Add(Buffer[tr].States[i].account[6] / PrevBalance);
タイムスタンプのハーモニクスを追加します。
double time = (double)Buffer[tr].States[i].account[7]; double x = time / (double)(D'2024.01.01' - D'2023.01.01'); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_MN1); Account.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_W1); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_D1); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); if(Account.GetIndex() >= 0) Account.BufferWrite();
状態エンコーダのフィードフォワードメソッドを実行します。
//--- State embedding if(!StateEncoder.feedForward(GetPointer(State), 1, false, GetPointer(Account))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
環境状態の埋め込みを生成した後、現在の方策を考慮してエージェントの行動を生成します。
//--- Action if(!Actor.feedForward(GetPointer(StateEncoder), -1, NULL, 1)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
生成された行動は両Criticによって評価されます。
//--- Cost if(!Critic1.feedForward(GetPointer(StateEncoder), -1, GetPointer(Actor)) || !Critic2.feedForward(GetPointer(StateEncoder), -1, GetPointer(Actor))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
すべての操作が成功したら、結果をローカルベクトルにアップロードします。次に、訓練データセットから類似データベクトルを形成します。
Critic1.getResults(rewards1); Critic2.getResults(rewards2); Actor.getResults(action); action_beta.Assign(Buffer[tr].States[i].action); rewards.Assign(Buffer[tr].States[i + 1].rewards); target_reward.Assign(Buffer[tr].States[i + 2].rewards);
分析された状態の座標は、軌跡とその中の状態のインデックスの形で結果行列に保存されます。また、行動ベクトルの偏差とその結果への影響も保存します。
//--- Collect mBatch[b, 0] = float(tr); mBatch[b, 1] = float(i); mBatch[b, 2] = MathMin(rewards1.Sum(), rewards2.Sum()) - (rewards - target_reward * DiscFactor).Sum(); mBatch[b, 3] = MathSqrt(MathPow(action - action_beta, 2).Sum()); }
その後、次の状態のサンプリングと評価に移ります。
パッケージ全体のデータを処理して収集した後、Actorの行動方策を最適化するために最適な状態を選択する必要があります。この段階では、信頼できるCritic評価と、モデル結果に対する最大限の影響力を持つ状態を選択する必要があります。
行動評価の信頼性については、Criticからの行動評価は、訓練データセットの分布からの乖離が小さいほど正確であることは既に述べました。偏差が大きくなるにつれて、Criticの評価の精度は低下します。このロジックに従えば、行動評価の正確さの基準は、分析行列のインデックス3の列に格納された行動間の距離となります。
ここで信頼区間を選択する必要があります。元の論文では、CFPI法の著者は分布の分散を使用しました。しかし、行動偏差のベクトルの分散を取ることはできません。実は、分散は分布の真ん中からの標準偏差と考えられています。私たちの場合は、偏差の絶対値を保持しました。したがって、Criticの推定が最も正確である偏差値ゼロは、極端にしかなりえません。分布の平均値はこの点から離れています。その結果、このケースで分散を使用することは、望ましい行動推定の精度を保証するものではありません。
ただし、ここでは「3 シグマ」ルールを使用できます。正規分布では、データの68%が数学的期待値から1標準偏差以上外れることはないということです。つまり、信頼区間を決定するために分位関数を使用することができます。非常に簡単な数学的操作を使用して、信頼区間よりも大きな偏差を持つ行動の値がゼロで、それ以外の行動の値が1の重みベクトルを作成します。
action = mBatch.Col(3); float quant = action.Quantile(0.68); vector<float> weights = action - quant - FLT_EPSILON; weights.Clip(weights.Min(), 0); weights = weights / weights; weights.ReplaceNan(0);
信頼区間が決まりました。これで、行動を適切に評価した状態の配列を選択できるようになります。Actorの行動方策を最適化するためには、最適な状態を選択する必要があります。アルゴリズム全体を単純化し、モデル訓練過程を高速化するため、CFPIアルゴリズムの作者が提案した解析法は使用せず、代わりにもっと単純なものを使用することにしました。
明らかに、私たちのケースでは、最適化の最適な方向は、エージェント行動方策の収益性が行動部分空間の最小シフトで変化するものです。私たちは方策の収益性を最大化したいのであり、最小限の偏差はCriticによる行動のより正確な評価を示唆するからです。もちろん、私たちの分析マトリックスでは、行動の評価にはプラスとマイナスの両方の偏差があります。全体的な収益性の向上は、利益の増加と損失の減少の両方から等しく影響を受けます。そこで、最適な選択基準を計算するために、遷移報酬偏差の絶対値を用います。
rewards = mBatch.Col(2); weights = MathAbs(rewards) * weights / action;
出来上がったベクトルの中で、最も高い値を持つ要素を選択します。そのインデックスは、モデル最適化アルゴリズムで使用する最適な状態を指します。
ulong pos = weights.ArgMax(); int sign = (rewards[pos] >= 0 ? 1 : -1);
ここでは、報酬偏差の符号をローカル変数に保存します。
少し先の話になりますが、Criticモデルを通して渡される誤差勾配を利用して、Actorの行動方策を更新します。この学習モードでは、Actor予測の誤差を計算することはできません。学習過程を制御するために、使用する状態の平均改善係数を導入しました。
Improve = (Improve * iter + weights[pos]) / (iter + 1);
次に方策モデルを最適化するおなじみのアルゴリズムが登場します。ただし、今回はランダムな状態ではなく、モデルのパフォーマンスを最大化できる状態を使用します。
int tr = int(mBatch[pos, 0]); int i = int(mBatch[pos, 1]);
前回同様、環境の状態と口座の状態を記述するためのバッファに書き入れます。
//--- Policy study State.AssignArray(Buffer[tr].States[i].state); float PrevBalance = Buffer[tr].States[MathMax(i - 1, 0)].account[0]; float PrevEquity = Buffer[tr].States[MathMax(i - 1, 0)].account[1]; Account.Clear(); Account.Add((Buffer[tr].States[i].account[0] - PrevBalance) / PrevBalance); Account.Add(Buffer[tr].States[i].account[1] / PrevBalance); Account.Add((Buffer[tr].States[i].account[1] - PrevEquity) / PrevEquity); Account.Add(Buffer[tr].States[i].account[2]); Account.Add(Buffer[tr].States[i].account[3]); Account.Add(Buffer[tr].States[i].account[4] / PrevBalance); Account.Add(Buffer[tr].States[i].account[5] / PrevBalance); Account.Add(Buffer[tr].States[i].account[6] / PrevBalance);
タイムスタンプの状態を追加します。
double time = (double)Buffer[tr].States[i].account[7]; double x = time / (double)(D'2024.01.01' - D'2023.01.01'); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_MN1); Account.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_W1); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_D1); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
環境状態の埋め込みを生成します。
//--- State if(Account.GetIndex() >= 0) Account.BufferWrite(); if(!StateEncoder.feedForward(GetPointer(State), 1, false, GetPointer(Account))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
現在の方策を考慮したエージェントの行動
//--- Action if(!Actor.feedForward(GetPointer(StateEncoder), -1, NULL, 1)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
エージェント行動のコストを見積もります。
//--- Cost if(!Critic1.feedForward(GetPointer(StateEncoder), -1, GetPointer(Actor)) || !Critic2.feedForward(GetPointer(StateEncoder), -1, GetPointer(Actor))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
エージェントの行動方策を最適化するために、最小スコアを持つCriticを使用します。収束性を高めるために、CAGradメソッドを用いて勾配方向ベクトルを調整します。
Critic1.getResults(rewards1); Critic2.getResults(rewards2); //--- rewards.Assign(Buffer[tr].States[i + 1].rewards); target_reward.Assign(Buffer[tr].States[i + 2].rewards); rewards = rewards - target_reward * DiscFactor; CNet *critic = NULL; if(rewards1.Sum() <= rewards2.Sum()) { Result.AssignArray(CAGrad((rewards1 - rewards)*sign) + rewards1); critic = GetPointer(Critic1); } else { Result.AssignArray(CAGrad((rewards2 - rewards)*sign) + rewards2); critic = GetPointer(Critic2); }
CriticとActorのバックプロパゲーションパスを順次実行します。
if(!critic.backProp(Result, GetPointer(Actor), -1) || !Actor.backPropGradient((CBufferFloat *)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
なお、現段階ではCriticモデルの最適化はおこなっていません。したがって、環境的状態エンコーダをバックプロパゲーションで通過する必要はありません。
これで、エージェントの行動方策を更新する1回の反復の操作は完了です。学習過程の進捗状況をユーザーに知らせ、サイクルの次の反復に移ります。
if(GetTickCount() - ticks > 500) { string str = StringFormat("%-15s %5.2f%% -> %15.8f\n", "Mean Improvement", iter * 100.0 / (double)(Iterations), Improve); Comment(str); ticks = GetTickCount(); } }
訓練サイクルのすべての反復が完了したら、チャートのコメントフィールドを消去し、訓練結果に関する情報をログに表示し、EAのシャットダウンを開始します。
Comment(""); //--- PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Mean Improvement", Improve); ExpertRemove(); //--- }
ここで、この記事で使用されているアルゴリズムについての考察を終えます。全プログラムの全コードを以下に添付します。結果の確認に移ります。
3.検証
以上、閉形式方策改善法について見てきましたが、MQL5を使用してその方法を実装するために、かなり多くの作業をおこないました。この手法の著者が提案したアイデアを使用しましたが、最適な状態を選択するために使用された分析手法は、論文で提案されたものとは異なっています。加えて、私たちの研究には、これまでの経験からの発展が生かされています。したがって、得られた結果は、著者が論文で示したものとは大きく異なる可能性があります。当然ながら、テスト環境も元の論文に書かれた実験とは異なります。
いつものように、モデルはEURUSD H1の履歴データを使用して訓練およびテストされています。モデルは2023年の最初の7ヶ月間のデータを使用して訓練されています。訓練済みモデルをテストするために、2023年8月からの履歴データを使用します。すべての指標はデフォルトのパラメータで使用されています。
CFPI法の実装にはモデルアーキテクチャに若干の変更が必要でしたが、ソースデータの構造には影響しませんでした。したがって、訓練の最初の段階では、先に説明した学習アルゴリズムのいずれかをテストする際に、先に作成した訓練データセットを使用することができます。以前の記事で使用した訓練データセットを使用しました。今回の記事では、CFPI.bdというファイルのコピーを作成しました。しかし、先に説明した手法のいずれかを使用して、まったく新しい訓練データセットを作成することもできます。この部分では、CFPI方式は制限を課していません。
ただし、アーキテクチャの変更により、以前に訓練したモデルを使用することはできなかったため、学習過程全体がゼロから実施されました。
まず、状態エンコーダモデルとCriticモデルをEA「...\Experts\CFPI\StudyCritic.mq5」を用いて訓練しました。
訓練データセットには、それぞれ3591の環境状態を持つ500の軌跡が含まれています。これは合計で約180万セットの「状態-行動-報酬」に相当します。Criticsモデルの一次訓練は100万回の反復でおこなわれ、理論的にはほぼ毎秒の状態を分析できます。連続的な軌跡の場合、環境が変化するたびに市場の状況が根本的に変わるわけではありませんが、これはかなり良い結果です。収益性が最大となる軌道を重視することを考えれば、Criticはそのような軌道をほぼ完全に研究し、収益性の低い峠まで「視野」を広げることができます。
次に、EA「...\Experts\CFPI\Study.mq5」でActorの動作方策を学習します。ここでは、256状態のパッケージで訓練を1万回反復します。合計で250万以上の状態を分析することができ、これは訓練データセットよりも大きくなります。
最初の訓練の反復がテストに合格した後、収益性の高いストラテジーを作成するためのいくつかの前提条件に気づくことができたと言わなければなりません。残高チャートには利益の出る間隔があります。訓練軌道の追加収集の過程で、200パス中、3パスが利益を伴って完了しました。もちろん、これは私の主観的な意見かもしれないし、手法とは無関係にある要因が重なった結果かもしれません。例えば、運がよく、モデルのランダムな初期化がかなり良い結果を生み出したのかもしれません。いずれにせよ、モデルの訓練と追加パスの収集を繰り返した結果、パスの平均収益率とプロフィットファクターが上昇したことは確かです。
何度かモデル訓練を繰り返した結果、訓練データセットの履歴データ上でも、訓練データセットに含まれないテストデータ上でも利益を生み出すことができるActorの行動方策が得られました。モデルテストの結果を以下に示します。
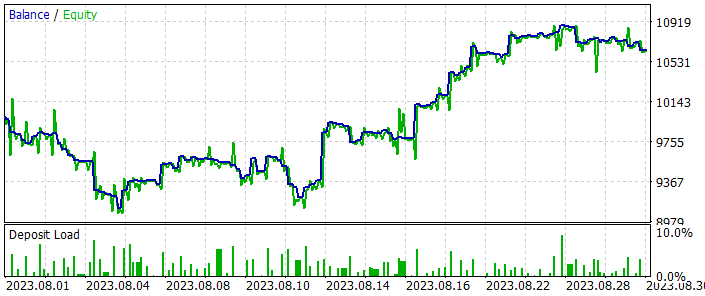
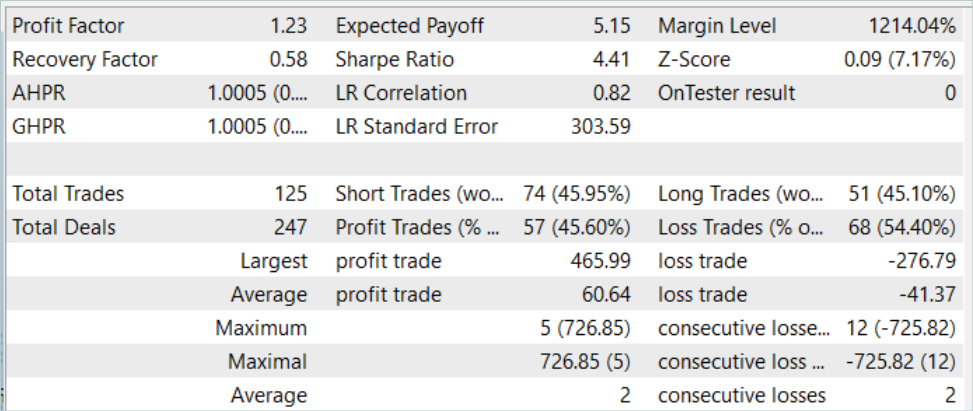
残高チャートでは、テスト期間開始時に若干のドローダウンが見られます。しかしその後、このモデルはかなり均等な残高成長傾向を示しています。これにより、失ったものを取り戻し、利益を増やすことができます。テスト期間中、このモデルは合計で125件の取引をおこない、そのうち45.6%が利益で決済されました。最高利益率と平均利益率の取引は、対応する損失指標よりも50%高くなります。その結果、プロフィットファクターは1.23となりました。
結論
この記事では、閉形式方策改善という、あと1つのモデル訓練アルゴリズムを紹介しました。この手法の主な貢献は、訓練済みモデルの最適化方向を選択するための分析的方法が加わったことでしょう。さて、この過程にはさらなる計算コストがかかります。しかし、奇妙なことに、この方法は全体としてモデルの訓練コストを削減します。というのも、私たちは提示された軌道のベストを完全に繰り返そうとしているわけではないからです。その代わり、最大効率の領域に集中しており、最適なノイズ現象を探すために時間を浪費することはありません。
記事の実用的な部分では、CFPI法の著者が提案したアイデアを実装しました。そのオリジナルの数学的計算と比較して若干の変更はあるものの、肯定的なな経験と良いテスト結果を得ることができました。
私の個人的な意見としては、閉形式の方策改善法は検討に値すると思います。その方法を使用して独自の取引戦略を構築することができます。
参照文献
記事で使用されているプログラム
| # | ファイル名 | 種類 | 詳細 |
|---|---|---|---|
| 1 | Research.mq5 | EA | コレクションEAの例 |
| 2 | ResearchRealORL.mq5 | EA | Real-ORL法による事例収集のためのEA |
| 3 | Study.mq5 | EA | Actor訓練EA |
| 4 | StudyCritic.mq5 | EA | Critic訓練EA |
| 5 | Test.mq5 | EA | モデルをテストするEA |
| 6 | Trajectory.mqh | クラスライブラリ | システム状態記述の構造体 |
| 7 | NeuroNet.mqh | クラスライブラリ | ニューラルネットワークを作成するためのクラスのライブラリ |
| 8 | NeuroNet.cl | コードベース | OpenCLプログラムコードライブラリ |
MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/13982
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。
この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。
 ニューラルネットワークが簡単に(第71回):目標条件付き予測符号化(GCPC)
ニューラルネットワークが簡単に(第71回):目標条件付き予測符号化(GCPC)
 初心者からプロまでMQL5をマスターする(第2回):基本的なデータ型と変数の使用
初心者からプロまでMQL5をマスターする(第2回):基本的なデータ型と変数の使用
 母集団最適化アルゴリズム:2進数遺伝的アルゴリズム(BGA)(第1回)
母集団最適化アルゴリズム:2進数遺伝的アルゴリズム(BGA)(第1回)
 ニューラルネットワークが簡単に(第69回):密度に基づく行動方策の支持制約(SPOT)
ニューラルネットワークが簡単に(第69回):密度に基づく行動方策の支持制約(SPOT)
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索