MetaTrader 5 / トレーディングシステム
English Русский 中文 Español Deutsch Português
preview
ニューラルネットワークが簡単に（第54回）：ランダムエンコーダを使った効率的な研究(RE3)

ニューラルネットワークが簡単に（第54回）：ランダムエンコーダを使った効率的な研究(RE3)

MetaTrader 5 — トレーディングシステム | 22 1月 2024, 16:51
179 0
Dmitriy Gizlyk
Dmitriy Gizlyk

はじめに

環境の効率的な探索の問題は、強化学習法の主な問題の1つです。この問題については何度も議論しました。そのたびに、提案された解決策によってアルゴリズムがさらに複雑化しました。ほとんどの場合、モデルが新しい行動を探索し、未踏のパスを探索することを促すために、追加の内部報酬メカニズムを使用することにしました。

ただし、行動と訪問した状態の新規性を評価するには、追加のモデルを訓練する必要がありました。「行動の新規性」という概念は、環境研究の完全性や均一性と必ずしも一致しないことに注意することが重要です。この側面では、行動と状態のエントロピーの推定に基づく方法が最も魅力的に見えます。ただし、訓練されたモデルに独自の制限を課します。エントロピーを使用するには、行動の実行と新しい状態への遷移の確率をある程度理解する必要がありますが、行動と状態の連続空間の場合、直接計算するのは非常に困難です。よりシンプルで効果的な方法を求めて、記事「State Entropy Maximization with Random Encoders for Efficient Exploration」で紹介されているランダムエンコーダによる効率的な探索（Random Encoders for Efficient Exploration、RE3）アルゴリズムを理解することをお勧めします。


1.RE3の主なアイデア

行動と状態の連続空間を含む実際のケースを分析すると、各状態と行動のペアが訓練セット内で1回だけ発生する状況に直面します。将来同じ状態が観察される可能性は「0」に近いです。近い（類似した）状態と行動をグループ化する方法を検索する必要が生じ、追加のモデルを訓練する必要があります。例えば、BACメソッドでは、状態と行動の新規性を評価するために自動エンコーダを訓練しました。

ただし、追加のモデルを訓練すると、アルゴリズムがある程度複雑になります。結局のところ、追加のハイパーパラメータの選択とモデルの訓練の両方に追加の時間とリソースが必要になります。追加モデルの訓練の品質は、メインのActor方策の訓練の結果に大きな影響を与える可能性があります。

ランダムエンコーダによる効率的な探索(RE3)メソッドの主な目的は、訓練されたモデルの数を最小限に抑えることです。RE3メソッドの著者らは、研究の中で、画像処理の分野では畳み込みネットワークのみが個々のオブジェクトの特徴や特性を識別できるという事実に注目しています。畳み込みネットワークは、多次元空間の次元を削減し、特徴的な特徴を強調し、元のオブジェクトのスケーリングに対処するのに役立ちます。

ここでの極めて当然の疑問は、畳み込みネットワークにさらに目を向けた場合、訓練済みモデルのどのような最小化について話しているのかということです。

この面でのキーワードは「訓練」です。この方法の著者らは、ランダムなパラメータで初期化された畳み込みエンコーダでも2つの状態の近接性に関する情報を効果的に取得できるという事実に注目しました。以下は、ランダムに初期化されたエンコーダ（ランダムエンコーダ）の表現空間と、記事の真の状態の空間での距離を測定することによって見つかったk近傍状態の視覚化です。

k近傍状態の可視化

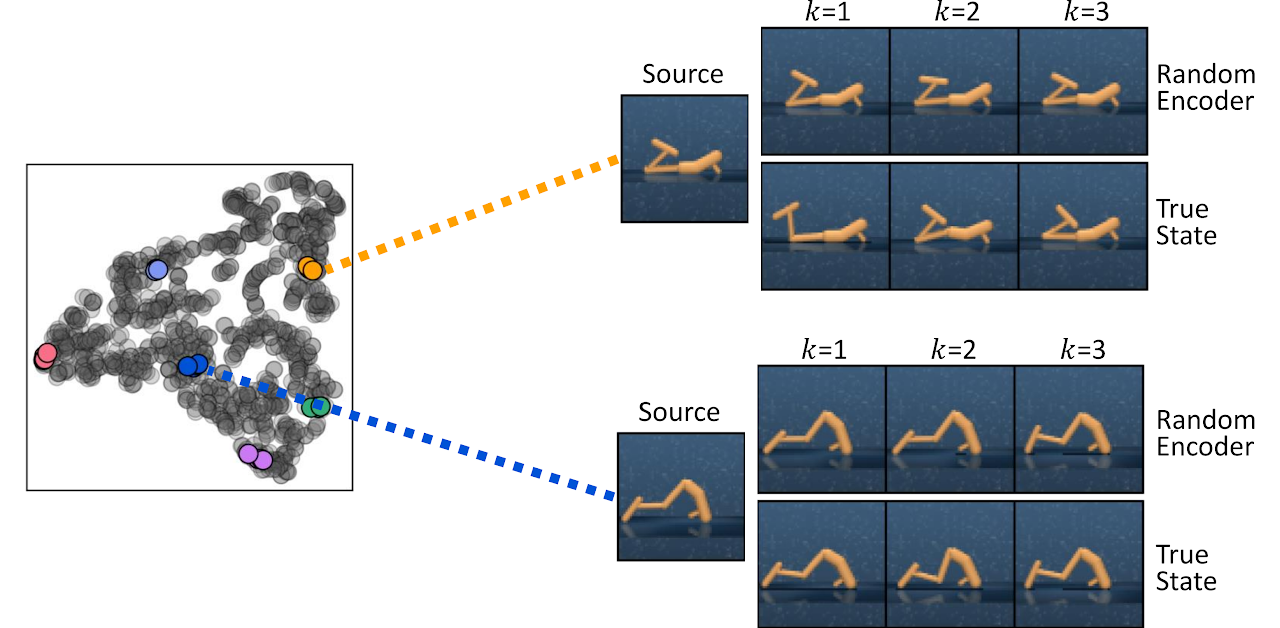
この観察に基づいて、RE3法の著者らは、モデルの訓練中にランダムに初期化されたエンコーダの固定表現空間で状態エントロピー推定を最大化することを提案します。

ランダムエンコーダによる効率的な探索(RE3)メソッドは、状態エントロピーを最大化することで高次元の観測空間での探索を促進します。RE3の主なアイデアは、ランダムに初期化されたエンコーダを使用して取得された低次元空間内の推定器k近傍を使用してエントロピーを推定することです。

この方法の著者らは、ランダムエンコーダのf(θ)表現空間における状態間の距離を計算することを提案しています。ランダムエンコーダのθパラメータはランダムに初期化され、訓練全体を通じて固定されます。

エージェントの動機は、ランダムなエンコーダ表現空間内の距離が、表現の訓練を必要とせずに類似の状態を見つけるのにすでに役立つという観察から生じます。

この場合、内部報酬は状態エントロピーの評価に比例し、次の方程式で決定されます。

ここで、yiはランダムエンコーダ空間内の状態表現です。

提示された内部報酬方程式では、常に非負であるL2距離ノルムを使用します。ノルムを「1」増やすと、常に負でない対数値を取得できます。したがって、常に負ではない内部報酬を受け取ります。さらに、十分な数の決済状態があると、内部報酬が「0」に近いことが容易にわかります。

実際に示したように、固定表現空間で状態間の距離を測定すると、状態のペア間の距離が訓練中に変化しないため、より安定した内部報酬が得られます。

潜在空間内の距離を計算するには、環境と対話しながら低次元の状態表現を経験再生バッファに保存することが計算効率的です。これにより、モデル更新の反復ごとに表現を取得するためにエンコーダを通じて高次元の状態を処理する必要がなくなります。さらに、これにより、ミニバッチからの単一サンプルの前ではなく、すべての状態レコードの前に距離を計算することができます。このスキームは、計算効率を備えた安定した正確なエントロピー推定を提供します。

一般に、RE3メソッドはエージェントをリアルタイムで訓練するために使用でき、エージェントは環境からの外部報酬の最大化に基づいて方策を学習します。内部報酬はエージェントに環境を探索するよう刺激します。

ここで、βは研究と開発の間のバランスを決定する温度比です(β≥0)。

この手法の著者らは、訓練の進行に応じてエージェントが環境からの外部報酬にさらに集中するよう、訓練全体を通してβの指数関数的減少を使用することを提案しています。

ここで、pは減少率です。

訓練中により多くの類似した状態が収集されると、内部報酬は「0」に収束しますが、手法の著者は、経験的にβの減少によりパフォーマンスが安定することを発見しました。

さらに、RE3メソッドを使用して、外部報酬がない場合でも高次元の環境空間を探索するエージェントを事前訓練することができます。その後、エージェントの方策をさらに訓練して、特定の問題を解決できます。

以下は、著者によるRE3メソッドの視覚化です。

著者によるメソッドの視覚化

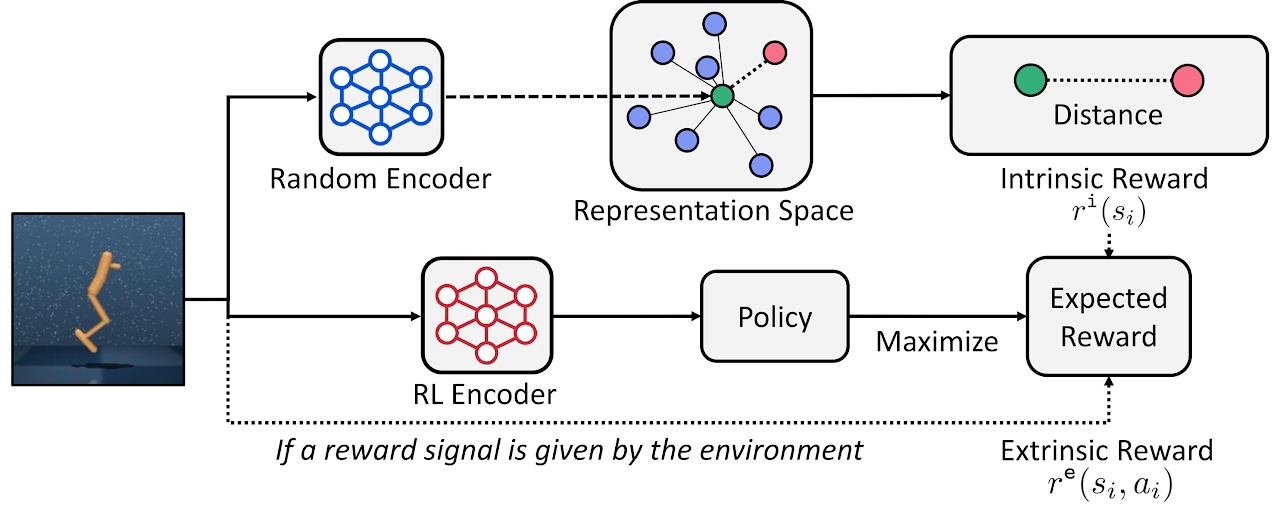
「State Entropy Maximization with Random Encodersfor Efficient Exploration」の記事では、方法の効率性を実証するさまざまなテストの結果が示されています。提案されたアルゴリズムのバージョンを実装し、タスクを解決するためのその効率を評価します。


2.MQL5を使用した実装

この手法の実装を開始する際に、著者のアルゴリズムを完全に繰り返すわけではないことにすぐに注意してください。いつものように、この方法の主要なアイデアを使用し、それらを以前に検討したアプローチと組み合わせます。ここでは、現在および以前に研究されたアルゴリズムの特定の複合体を作成します。

Actor-Criticファミリのアルゴリズムに基づいて実装を構築します。畳み込みエンコーダを構築するには、モデルアーキテクチャを記述するメソッドにその記述を追加します。

bool CreateDescriptions(CArrayObj *actor, CArrayObj *critic, CArrayObj *convolution)
  {
//---
   CLayerDescription *descr;
//---
   if(!actor)
     {
      actor = new CArrayObj();
      if(!actor)
         return false;
     }
   if(!critic)
     {
      critic = new CArrayObj();
      if(!critic)
         return false;
     }
   if(!convolution)
     {
      convolution = new CArrayObj();
      if(!convolution)
         return false;
     }

継続的な行動空間で確率的エージェント方策を訓練します。以前の記事と同様に、Actor-Criticファミリのアルゴリズムを使用してActorを訓練します。RE3メソッドのアプローチを使用して報酬のエントロピーコンポーネントを推定するため、Actorモデルを簡素化できます。この場合、記事「Behavior-GuidedActor-Critic」からActorアーキテクチャを再作成します。

//--- Actor
   actor.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1000;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   prev_count = descr.count = prev_count - 1;
   descr.window = 2;
   descr.step = 1;
   descr.window_out = 8;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   prev_count = descr.count = prev_count;
   descr.window = 8;
   descr.step = 8;
   descr.window_out = 8;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = 256;
   descr.optimization = ADAM;
   descr.activation = LReLU;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = 128;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 6
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConcatenate;
   descr.count = LatentCount;
   descr.window = prev_count;
   descr.step = AccountDescr;
   descr.optimization = ADAM;
   descr.activation = SIGMOID;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 7
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = 256;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 8
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = 256;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 9
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = 2 * NActions;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 10
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronVAEOCL;
   descr.count = NActions;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

以前と同様に、Criticにはソースデータの事前処理のブロックがありません。Actorの潜在的な状態をCriticの入力として使用します。報酬ポイントの数を少し減らしながら、報酬分解も使用します。各行動のエントロピーコンポーネントの6つの個別の要素の代わりに、内部報酬の要素は1つだけになります。

//+------------------------------------------------------------------+
//| Rewards structure                                                |
//|   0     -  Delta Balance                                         |
//|   1     -  Delta Equity ( "-" Drawdown / "+" Profit)             |
//|   2     -  Penalty for no open positions                         |
//|   3     -  Mean distance                                         |
//+------------------------------------------------------------------+

その結果、次のようなCriticアーキテクチャが得られます。

//--- Critic
   critic.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = LatentCount;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!critic.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConcatenate;
   descr.count = LatentCount;
   descr.window = prev_count;
   descr.step = NActions;
   descr.optimization = ADAM;
   descr.activation = LReLU;
   if(!critic.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!critic.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!critic.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = NRewards;
   descr.optimization = ADAM;
   descr.activation = None;
   if(!critic.Add(descr))
     {
      delete descr;
      return false;
     }

次に、畳み込みエンコーダのアーキテクチャについて説明する必要があります。ここで、説明した方法との最初の違いがあります。RE3メソッドは、潜在状態表現間の距離の推定に基づいて内部報酬を提供します。対照的に、エンコーダのソースデータ層のサイズに反映される「状態と行動」のペアの潜在表現を使用します。

//--- Convolution
   convolution.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = (HistoryBars * BarDescr) + AccountDescr + NActions;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!convolution.Add(descr))
     {
      delete descr;
      return false;
     }

私たちのエンコーダモデルは訓練されていないため、バッチデータ正規化層を使用する意味がありません。ただし、全結合層を使用し、その出力で畳み込み層で処理できる同等のデータを取得します。

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = 512;
   descr.window = prev_count;
   descr.step = NActions;
   descr.optimization = ADAM;
   descr.activation = SIGMOID;
   if(!convolution.Add(descr))
     {по
      delete descr;
      return false;
     }

次に、3つの連続した畳み込み層を使用してデータの次元を削減します。それらの仕事は、同様の状態や動作を識別するための特徴を決定することです。

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   prev_count = descr.count = 512 / 8;
   descr.window = 8;
   descr.step = 8;
   int prev_wout = descr.window_out = 2;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!convolution.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   prev_count = descr.count = (prev_count * prev_wout) / 4;
   descr.window = 4;
   descr.step = 4;
   prev_wout = descr.window_out = 2;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!convolution.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   prev_count = descr.count = (prev_count * prev_wout) / 4;
   descr.window = 4;
   descr.step = 4;
   prev_wout = descr.window_out = 2;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!convolution.Add(descr))
     {
      delete descr;
      return false;
     }

エンコーダを完成させるには、全結合層を使用し、データの隠れた表現を特定の次元に縮小します。

//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = EmbeddingSize;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!convolution.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

ニューロンを活性化するために、すべてのニューラル層（最初の層を除く）でLReLUを使用したことに注意してください。活性化関数の結果の範囲に制限がないため、オブジェクトをできるだけ正確にグループに分割できます。

モデルのアーキテクチャの説明を作成した後、経験再生バッファについて少し説明しましょう。この手法の著者は、状態の潜在表現を標準データセットとともに経験再生バッファに同時に保存することを提案しています。私もそれに同意します。状態の潜在表現を一度計算し、それを反復ごとに再計算せずに訓練プロセスで使用することは非常に論理的です。

一連の行動で、最初に訓練データ収集EA「...\RE3\Research.mq5」を起動したとき、事前訓練されたモデルはまだ保存されていません。ActorモデルはEAによって作成され、ランダムなパラメータが入力されます。ランダムなエンコーダモデルを生成することもできます。ただし、ストラテジーテスターの最適化モードで複数のEAインスタンスを並行して起動すると、EAパスごとにエンコーダが作成されます。問題は、各パスでランダムなエンコーダが得られ、その潜在表現が他のパスの同様の表現と比較できないことです。これは、RE3メソッドの考え方と原則に完全に違反しています。

考えられる解決策は2つあります。

  • 「...\RE3\Research.mq5」EAの最初の起動前のモデルの予備作成と保存
  • 「...\RE3\Study.mq5」モデル訓練EAの本体でのエンコーダとエンコード表現の生成

私の実装では2番目のオプションを選択しました。したがって、データストレージ構造と「...\RE3\Research.mq5」訓練サンプルコレクションEAには変更を加えません。すべてのコードは添付ファイルにあります。

次に、「...\RE3\Study.mq5」モデル訓練EAの作業に進みます。ここでは6つのモデルのオブジェクトを作成しますが、そのうちの3つだけを訓練します。ターゲットモデルについては、ꚍ比率を使用してパラメータのソフト更新を適用します。

CNet                 Actor;
CNet                 Critic1;
CNet                 Critic2;
CNet                 TargetCritic1;
CNet                 TargetCritic2;
CNet                 Convolution;

EA初期化メソッドでは、訓練セットと事前訓練されたモデルを読み込みます。モデルを読み込めない場合は、ランダムなパラメータを含む新しいモデルを生成します。

int OnInit()
  {
//---
   ResetLastError();
   if(!LoadTotalBase())
     {
      PrintFormat("Error of load study data: %d", GetLastError());
      return INIT_FAILED;
     }
//--- load models
   float temp;
   if(!Actor.Load(FileName + "Act.nnw", temp, temp, temp, dtStudied, true) ||
      !Critic1.Load(FileName + "Crt1.nnw", temp, temp, temp, dtStudied, true) ||
      !Critic2.Load(FileName + "Crt2.nnw", temp, temp, temp, dtStudied, true) ||
      !Convolution.Load(FileName + "CNN.nnw", temp, temp, temp, dtStudied, true) ||
      !TargetCritic1.Load(FileName + "Crt1.nnw", temp, temp, temp, dtStudied, true) ||
      !TargetCritic2.Load(FileName + "Crt2.nnw", temp, temp, temp, dtStudied, true))
     {
      CArrayObj *actor = new CArrayObj();
      CArrayObj *critic = new CArrayObj();
      CArrayObj *convolution = new CArrayObj();
      if(!CreateDescriptions(actor, critic, convolution))
        {
         delete actor;
         delete critic;
         delete convolution;
         return INIT_FAILED;
        }
      if(!Actor.Create(actor) || !Critic1.Create(critic) || !Critic2.Create(critic) ||
         !Convolution.Create(convolution))
        {
         delete actor;
         delete critic;
         delete convolution;
         return INIT_FAILED;
        }
      if(!TargetCritic1.Create(critic) || !TargetCritic2.Create(critic))
        {
         delete actor;
         delete critic;
         delete convolution;
         return INIT_FAILED;
        }
      delete actor;
      delete critic;
      delete convolution;
      //---
      TargetCritic1.WeightsUpdate(GetPointer(Critic1), 1.0f);
      TargetCritic2.WeightsUpdate(GetPointer(Critic2), 1.0f);
      StartTargetIter = StartTargetIteration;
     }
   else
      StartTargetIter = 0;

前回の記事と同様に、新しいモデルを生成する際に、対象モデルの使用時間を延長します。これにより、その後のエージェントの状態や行動を推定するためにターゲットモデルを使用する前に、ターゲットモデルを事前訓練することができます。

ここでは、すべてのモデルを単一のOpenCLコンテキストに転送します。

//---
   OpenCL = Actor.GetOpenCL();
   Critic1.SetOpenCL(OpenCL);
   Critic2.SetOpenCL(OpenCL);
   TargetCritic1.SetOpenCL(OpenCL);
   TargetCritic2.SetOpenCL(OpenCL);
   Convolution.SetOpenCL(OpenCL);

訓練の前に、使用されるモデルのアーキテクチャへの準拠を確認します。

   Actor.getResults(Result);
   if(Result.Total() != NActions)
     {
      PrintFormat("The scope of the actor does not match the actions count (%d <> %d)", NActions, Result.Total());
      return INIT_FAILED;
     }
//---
   Actor.GetLayerOutput(0, Result);
   if(Result.Total() != (HistoryBars * BarDescr))
     {
      PrintFormat("Input size of Actor doesn't match state description (%d <> %d)", Result.Total(), 
                                                                                        (HistoryBars * BarDescr));
      return INIT_FAILED;
     }
//---
   Actor.GetLayerOutput(LatentLayer, Result);
   int latent_state = Result.Total();
   Critic1.GetLayerOutput(0, Result);
   if(Result.Total() != latent_state)
     {
      PrintFormat("Input size of Critic doesn't match latent state Actor (%d <> %d)", Result.Total(), latent_state);
      return INIT_FAILED;
     }

メソッドの最後に、補助バッファを作成し、モデル訓練イベントを生成します。

   Gradient.BufferInit(AccountDescr, 0);
//---
   if(!EventChartCustom(ChartID(), 1, 0, 0, "Init"))
     {
      PrintFormat("Error of create study event: %d", GetLastError());
      return INIT_FAILED;
     }
//---
   return(INIT_SUCCEEDED);
  }

EA初期化解除方法では、ターゲットモデルのパラメータを更新し、訓練結果を保存します。

void OnDeinit(const int reason)
  {
//---
   TargetCritic1.WeightsUpdate(GetPointer(Critic1), Tau);
   TargetCritic2.WeightsUpdate(GetPointer(Critic2), Tau);
   Actor.Save(FileName + "Act.nnw", 0, 0, 0, TimeCurrent(), true);
   TargetCritic1.Save(FileName + "Crt1.nnw", Critic1.getRecentAverageError(), 0, 0, TimeCurrent(), true);
   TargetCritic2.Save(FileName + "Crt2.nnw", Critic2.getRecentAverageError(), 0, 0, TimeCurrent(), true);
   Convolution.Save(FileName + "CNN.nnw", 0, 0, 0, TimeCurrent(), true);
   delete Result;
  }

モデルを訓練する実際のプロセスは、訓練手順にまとめられています。ただし、ここでのアルゴリズムは、以前に検討されたEAの同様の手順とは若干異なります。

まず、訓練セット内の状態の総数を数えます。ご存知のとおり、個々のパスの状態の数はTotal変数に格納されます。ループを配置し、各パスから指定された変数の値の合計を収集します。

void Train(void)
  {
   int total_tr = ArraySize(Buffer);
   uint ticks = GetTickCount();
//---
   int total_states = Buffer[0].Total;
   for(int i = 1; i < total_tr; i++)
      total_states += Buffer[i].Total;

状態と行動のペアの圧縮表現の行列と環境から収集された実際の報酬を宣言するには、結果の値が必要です。

   vector<float> temp;
   Convolution.getResults(temp);
   matrix<float> state_embedding = matrix<float>::Zeros(total_states,temp.Size());
   matrix<float> rewards = matrix<float>::Zeros(total_states,NRewards);

次に、ループシステムを配置して、訓練セットからすべての状態と行動のペアの潜在表現を作成します。ここでは、まず元のデータを単一のデータバッファに収集します。

   for(int tr = 0; tr < total_tr; tr++)
     {
      for(int st = 0; st < Buffer[tr].Total; st++)
        {
         State.AssignArray(Buffer[tr].States[st].state);
         float PrevBalance = Buffer[tr].States[MathMax(st,0)].account[0];
         float PrevEquity = Buffer[tr].States[MathMax(st,0)].account[1];
         State.Add((Buffer[tr].States[st].account[0] - PrevBalance) / PrevBalance);
         State.Add(Buffer[tr].States[st].account[1] / PrevBalance);
         State.Add((Buffer[tr].States[st].account[1] - PrevEquity) / PrevEquity);
         State.Add(Buffer[tr].States[st].account[2]);
         State.Add(Buffer[tr].States[st].account[3]);
         State.Add(Buffer[tr].States[st].account[4] / PrevBalance);
         State.Add(Buffer[tr].States[st].account[5] / PrevBalance);
         State.Add(Buffer[tr].States[st].account[6] / PrevBalance);
         double x = (double)Buffer[tr].States[st].account[7] / (double)(D'2024.01.01' - D'2023.01.01');
         State.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         x = (double)Buffer[tr].States[st].account[7] / (double)PeriodSeconds(PERIOD_MN1);
         State.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0));
         x = (double)Buffer[tr].States[st].account[7] / (double)PeriodSeconds(PERIOD_W1);
         State.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         x = (double)Buffer[tr].States[st].account[7] / (double)PeriodSeconds(PERIOD_D1);
         State.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         State.AddArray(Buffer[tr].States[st].action);

次に、畳み込みエンコーダのフォワードパスを呼び出します。

         if(!Convolution.feedForward(GetPointer(State),1,false,NULL))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            ExpertRemove();
            return;
           }

得られた結果は、状態と行動の埋め込み行列の対応する行に保存されます。対応する外部報酬を同じ文字列番号で報酬行列に保存します。その後、記録された行のカウンタを増やします。

         Convolution.getResults(temp);
         state_embedding.Row(temp,state);
         temp.Assign(Buffer[tr].States[st].rewards);
         rewards.Row(temp,state);
         state++;

このプロセスに費やされる時間は訓練サンプルのサイズによって異なり、かなり長くなる可能性があります。したがって、ループ本体に、プロセスを視覚的に制御するための情報メッセージを追加します。

         if(GetTickCount() - ticks > 500)
           {
            string str = StringFormat("%-15s %6.2f%%", "Embedding ", state * 100.0 / (double)(total_states));
            Comment(str);
            ticks = GetTickCount();
           }
        }
     }

ループシステムの反復が完了したら、保存されている行数に合わせて行列のサイズを調整します。

   if(state != total_states)
     {
      rewards.Resize(state,NRewards);
      state_embedding.Reshape(state,state_embedding.Cols());
      total_states = state;
     }

これで準備段階は終了です。モデルの訓練に直接移りましょう。ここでは、以前と同様に、ユーザーがEA外部パラメータで指定した反復数で訓練サイクルを調整します。

   vector<float> rewards1, rewards2;
   for(int iter = 0; (iter < Iterations && !IsStopped()); iter ++)
     {
      int tr = (int)((MathRand() / 32767.0) * (total_tr - 1));
      int i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2));
      if(i < 0)
        {
         iter--;
         continue;
        }

ループ本体では、モデル訓練の現在の反復のパスと状態をランダムに選択します。次に、対象モデルを使用する必要性を確認します。

訓練プロセスがターゲットモデルを使用するしきい値に達した場合、それらのモデルを通過するフォワードパスのためのポスト状態入力を生成します。

      vector<float> reward, target_reward = vector<float>::Zeros(NRewards);
      reward.Assign(Buffer[tr].States[i].rewards);
      //--- Target
      if(iter >= StartTargetIter)
        {
         State.AssignArray(Buffer[tr].States[i + 1].state);
         float PrevBalance = Buffer[tr].States[i].account[0];
         float PrevEquity = Buffer[tr].States[i].account[1];
         Account.Clear();
         Account.Add((Buffer[tr].States[i + 1].account[0] - PrevBalance) / PrevBalance);
         Account.Add(Buffer[tr].States[i + 1].account[1] / PrevBalance);
         Account.Add((Buffer[tr].States[i + 1].account[1] - PrevEquity) / PrevEquity);
         Account.Add(Buffer[tr].States[i + 1].account[2]);
         Account.Add(Buffer[tr].States[i + 1].account[3]);
         Account.Add(Buffer[tr].States[i + 1].account[4] / PrevBalance);
         Account.Add(Buffer[tr].States[i + 1].account[5] / PrevBalance);
         Account.Add(Buffer[tr].States[i + 1].account[6] / PrevBalance);
         double x = (double)Buffer[tr].States[i + 1].account[7] / (double)(D'2024.01.01' - D'2023.01.01');
         Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         x = (double)Buffer[tr].States[i + 1].account[7] / (double)PeriodSeconds(PERIOD_MN1);
         Account.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0));
         x = (double)Buffer[tr].States[i + 1].account[7] / (double)PeriodSeconds(PERIOD_W1);
         Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         x = (double)Buffer[tr].States[i + 1].account[7] / (double)PeriodSeconds(PERIOD_D1);
         Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         //---
         if(Account.GetIndex() >= 0)
            Account.BufferWrite();

Criticsのターゲットモデルのダイレクトパスには、環境の初期状態とエージェントの行動の記述が必要であることは覚えています。ここでは、Actorのダイレクトパスが必要な点が2つあります。

  • Criticにはソースデータの前処理ユニットがありません（Actorの潜在表現を使用しません）。
  • Criticのターゲットモデルは、現在のActor方策の使用を考慮してその後の状態を評価します（行動の新しいベクトルの生成が必要です）。

したがって、最初に前方Actorパスを実行します。

         if(!Actor.feedForward(GetPointer(State), 1, false, GetPointer(Account)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            break;
           }

次に、ターゲットCriticの2つのモデルのダイレクトパスのメソッドを呼び出します。

         if(!TargetCritic1.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actor)) ||
            !TargetCritic2.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actor)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            break;
           }

次に、SoftActor-Criticアルゴリズムに従って、その後の状態の推定値が最小になるターゲットモデルを選択する必要があります。私の実装では、報酬要素の単純な合計を使用しました。ただし、モデルが報酬関数の個々の要素に異なる重み付け比率を提供する場合は、モデルの結果と重み付け比率のベクトルのベクトル積を使用できます。

         TargetCritic1.getResults(rewards1);
         TargetCritic2.getResults(rewards2);
         if(rewards1.Sum() <= rewards2.Sum())
            target_reward = rewards1;
         else
            target_reward = rewards2;

次に、選択したモデルの予測結果から、環境との対話から受け取った実際の報酬を差し引き、割引係数を調整します。

         for(ulong r = 0; r < target_reward.Size(); r++)
            target_reward -= Buffer[tr].States[i + 1].rewards[r];
         target_reward *= DiscFactor;
        }

したがって、target_rewardベクトルでは、Criticの予測スコアと環境からの実際の報酬の間の各報酬アイテムの分散を取得しました。これがどのように役立つでしょうか。

覚えていらっしゃるかもしれませんが、各「状態と行動」のペアの経験再生バッファには、割引係数を考慮して、通過の終了までの累積報酬額が保存されます。この合計報酬は、環境との相互作用中にエージェントによって使用される方策に基づいて蓄積されます。

エージェントの現在の方策を考慮して上記の「状態と行動」のペアのコストを予測し、経験再生バッファから行動を考慮しながら同じ状態の推定値を差し引きました。したがって、target_rewardベクトルは、状態値に対するActorの方策変更の影響を特徴とするようになりました。

ここでは話しているのは状態値の変化についてです。結局のところ、実際にはエージェントに依存しません。ただし、同じ状態であっても、使用される方策によって動作が異なる場合があります。

Actorの行動方策の変更が全体的な結果に及ぼす影響を評価した後、Criticの訓練ブロックに進みます。Actorの行動に誤差勾配を渡す正確さに影響を与えるのは、訓練の品質です。

ここでは、価格変動や指標の過去のデータを含む環境記述データも準備します。口座ステータスデータも別のバッファとして用意します。

      //--- Q-function study
      State.AssignArray(Buffer[tr].States[i].state);
      float PrevBalance = Buffer[tr].States[MathMax(i - 1, 0)].account[0];
      float PrevEquity = Buffer[tr].States[MathMax(i - 1, 0)].account[1];
      Account.Clear();
      Account.Add((Buffer[tr].States[i].account[0] - PrevBalance) / PrevBalance);
      Account.Add(Buffer[tr].States[i].account[1] / PrevBalance);
      Account.Add((Buffer[tr].States[i].account[1] - PrevEquity) / PrevEquity);
      Account.Add(Buffer[tr].States[i].account[2]);
      Account.Add(Buffer[tr].States[i].account[3]);
      Account.Add(Buffer[tr].States[i].account[4] / PrevBalance);
      Account.Add(Buffer[tr].States[i].account[5] / PrevBalance);
      Account.Add(Buffer[tr].States[i].account[6] / PrevBalance);
      double x = (double)Buffer[tr].States[i].account[7] / (double)(D'2024.01.01' - D'2023.01.01');
      Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
      x = (double)Buffer[tr].States[i].account[7] / (double)PeriodSeconds(PERIOD_MN1);
      Account.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0));
      x = (double)Buffer[tr].States[i].account[7] / (double)PeriodSeconds(PERIOD_W1);
      Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
      x = (double)Buffer[tr].States[i].account[7] / (double)PeriodSeconds(PERIOD_D1);
      Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
      if(Account.GetIndex() >= 0)
         Account.BufferWrite();

データの準備作業が完了したら、前方Actorパスを実行します。

      if(!Actor.feedForward(GetPointer(State), 1, false, GetPointer(Account)))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         break;
        }

ただし、今回はActorから環境状態の潜在的な表現のみを取得します。経験再生バッファからのエージェントの行動を使用します。結局のところ、この行動に対してこそ、環境から実際の報酬を得ているのです。

このデータを使って、両方のCriticのダイレクトパスを実行します。

      Actions.AssignArray(Buffer[tr].States[i].action);
      if(Actions.GetIndex() >= 0)
         Actions.BufferWrite();
      //---
      if(!Critic1.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actions)) ||
         !Critic2.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actions)))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         break;
        }

次に、目標値を生成し、Criticsのリバースパスを実行する必要があります。同様の操作をすでに数回行っています。通常、この段階では、変更された方策の効果に合わせて経験再生バッファからの実際の報酬を調整し、結果の値をターゲット値として両方のCriticモデルに渡します。ただし、この実装では分解された報酬を使用します。前回の記事では、Conflict-Averse Gradient Descent (CAGrad)アルゴリズムを使用して誤差勾配を修正しました。CNet_SAC_D_DICE::CAGradメソッドの値の偏差を修正し、得られた値をニューラル結果層の誤差勾配バッファに直接保存しました。現在、モデルの最後のニューラル層の勾配バッファに直接アクセスする機能がないため、ターゲット値が必要です。

少しデータ操作を実行して、競合回避型勾配降下法を使用して補正されたターゲット値を取得してみましょう。まず、利用可能なデータから目標値を生成します。次に、それらからCriticの予測値を減算し、偏差（誤差）を求めます。すでにおなじみのCAGradメソッドを使用して、結果の偏差を修正してみましょう。先ほど減算したCriticの予測値を結果に加算します。

これにより、競合回避型勾配降下法を使用して調整された目標値が得られます。ただし、そのような目標値は1つのCriticモデルにのみ関連します。Criticの2番目のモデルでは、その予測値を考慮して操作を繰り返す必要があります。

Criticsバックパスを実行した後、部分的なActorバックパスを実行して、データ前処理ブロック全体に誤差勾配を分散します。

      Critic1.getResults(rewards1);
      Result.AssignArray(CAGrad(reward + target_reward - rewards1) + rewards1);
      if(!Critic1.backProp(Result, GetPointer(Actions), GetPointer(Gradient)) ||
         !Actor.backPropGradient(GetPointer(Account), GetPointer(Gradient), LatentLayer))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         break;
        }
      Critic2.getResults(rewards2);
      Result.AssignArray(CAGrad(reward + target_reward - rewards2) + rewards2);
      if(!Critic2.backProp(Result, GetPointer(Actions), GetPointer(Gradient)) ||
         !Actor.backPropGradient(GetPointer(Account), GetPointer(Gradient), LatentLayer))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         break;
        }

Criticsのパラメータの更新の後に、Actor方策の更新ブロックが続きます。Soft Actor-Criticアルゴリズムに従って、最小状態推定値を持つCriticを使用してActorパラメータが更新されます。平均誤差が最小のCriticを使用します。これにより、誤差勾配がより正確に送信される可能性があります。

      //--- Policy study
      CNet *critic = NULL;
      if(Critic1.getRecentAverageError() <= Critic2.getRecentAverageError())
         critic = GetPointer(Critic1);
      else
         critic = GetPointer(Critic2);

ここでは、RE3メソッドを訓練プロセスに導入します。更新された方策を考慮して、分析された環境の状態、口座の状態、エージェントの選択された行動の説明を1つのデータバッファに収集します。Criticsのパラメータを更新する段階で、Actorのダイレクトパスを実行したことを思い出してください。

その後、選択したCriticにダイレクトパスを実行します。今回は、更新された方策を考慮して、分析された状態のActorの行動を評価します。エンコーダのダイレクトパスを呼び出して、分析された状態とActorの行動のペアと更新された方策の埋め込みを取得します。

      Actor.getResults(rewards1);
      State.AddArray(GetPointer(Account));
      State.AddArray(rewards1);
      if(!critic.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actor)) ||
         !Convolution.feedForward(GetPointer(State)))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         break;
        }

フォワードパスの後に、モデルのリバースパスが続きます。したがって、再びCriticの目標値を形成する必要があります。ただし、今回はCAGradアルゴリズムとRE3アルゴリズムを組み合わせる必要があります。さらに、更新された方策では、分析された状態とActor行動の正しい目標値がありません。

RE3アプローチを使用した目標値の定義を別のKNNReward関数に移動しました。そのアルゴリズムについては後ほど見ていきます。分解された報酬の調整は、Criticsのパラメータ更新ブロックで説明されているアルゴリズムに従って実行されます。

      Convolution.getResults(rewards1);
      critic.getResults(reward);
      reward += CAGrad(KNNReward(7,rewards1,state_embedding,rewards) - reward);
      //---
      Result.AssignArray(reward + target_reward);

次に、Criticの訓練モードを無効にして、CriticとActorのバックパスメソッドを順番に呼び出すだけです。また、運用結果の確認も忘れてはなりません。

      critic.TrainMode(false);
      if(!critic.backProp(Result, GetPointer(Actor)) ||
         !Actor.backPropGradient(GetPointer(Account), GetPointer(Gradient)))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         critic.TrainMode(true);
         break;
        }
      critic.TrainMode(true);

Actor方策を更新した後、Criticをモデル訓練モードに戻します。

モデルの訓練サイクルの最後に、ターゲットモデルのパラメータを更新し、訓練の進行状況をユーザーに通知します。

      //--- Update Target Nets
      TargetCritic1.WeightsUpdate(GetPointer(Critic1), Tau);
      TargetCritic2.WeightsUpdate(GetPointer(Critic2), Tau);
      //---
      if(GetTickCount() - ticks > 500)
        {
         string str = StringFormat("%-15s %5.2f%% -> Error %15.8f\n", "Critic1", 
                                     iter * 100.0 / (double)(Iterations), Critic1.getRecentAverageError());
         str += StringFormat("%-15s %5.2f%% -> Error %15.8f\n", "Critic2", 
                                     iter * 100.0 / (double)(Iterations), Critic2.getRecentAverageError());
         Comment(str);
         ticks = GetTickCount();
        }
     }

モデル訓練プロセスのすべての反復が完了したら、コメントフィールドをクリアし、訓練結果をログに表示して、EAの終了を開始します。

   Comment("");
//---
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Critic1", Critic1.getRecentAverageError());
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Critic2", Critic2.getRecentAverageError());
   ExpertRemove();
//---
  }

モデルの訓練方法のアルゴリズムについてはすでに検討しました。プロセスを完全に理解するには、CAGrad関数とKNNReward関数のアルゴリズムを分析する必要があります。最初のアルゴリズムは、前の記事で説明した同じ名前のメソッドから完全に移植されています。添付ファイルをご覧ください。2番目の関数アルゴリズムに注目するようお勧めします。上記の本来のアルゴリズムとは異なります。

KNNReward関数は、パラメータで、分析する近傍の数、目的の状態の埋め込みベクトル、訓練セットからの状態埋め込み行列、および報酬行列を受け取ります。経験と報酬の再生バッファからの状態埋め込み行列は行ごとに同期されることを思い出してください。この重要な点は後で活用します。

関数演算の結果は、対応する報酬の値のベクトルとして返されます。

vector<float> KNNReward(ulong k, vector<float> &embedding, matrix<float> &state_embedding, matrix<float> &rewards)
  {
   if(embedding.Size() != state_embedding.Cols())
     {
      PrintFormat("%s -> %d Inconsistent embedding size", __FUNCTION__, __LINE__);
      return vector<float>::Zeros(0);
     }

関数本体では、まず、分析された状態の埋め込みのサイズと、経験再生バッファの作成された埋め込みのサイズを確認します。

次に、埋め込みベクトル間の距離を決定します。これをおこなうには、経験再生バッファの状態の各埋め込み列から、分析された状態の記述の対応する要素の値を減算します。結果の値を二乗します。

   ulong size = embedding.Size();
   ulong states = state_embedding.Rows();
   ulong rew_size = rewards.Cols();
   matrix<float> temp = matrix<float>::Zeros(states,size);
//---
   for(ulong i = 0; i < size; i++)
      temp.Col(MathPow(state_embedding.Col(i) - embedding[i],2.0f),i);

行ごとの合計の平方根を抽出し、結果のベクトルを行列の最初の列に配置します。

   temp.Col(MathSqrt(temp.Sum(1)),0);

したがって、行列の最初の列の経験再現バッファから、望ましい状態と例の間の距離を取得しました。

行列の次元を変更し、対応する報酬要素を経験再生バッファから隣接する列に追加してみましょう。

   temp.Resize(states,1 + rew_size);
   for(ulong i = 0; i < rew_size; i++)
      temp.Col(rewards.Col(i),i + 1);

これらの操作の結果、最初の列に圧縮された埋め込み空間内の目的の状態までの距離が含まれる報酬行列を受け取りました。

覚えていらっしゃるかもしれませんが、この場合、望ましい状態は、更新された方策に従ってActorの行動が実行された分析された状態です。

ここで、特定のActor行動の内部報酬を決定するには、k個の最近傍を決定する必要があります。結果の行列を距離の降順に並べ替えた後、それらを簡単に見つけることができるのは非常に論理的です。ただし、値を完全に並べ替えるには、距離ベクトル全体にわたって複数の連続パスが必要になります。同時に、行列を完全に並べ替える必要はありません。私たちのタスクは、k個の最小値を見つけることです。結果の小さな行列におけるそれらの順序は、それほど重要ではありません。したがって、距離ベクトルに沿ったパスは1回だけ必要です。

最初のk行だけを結果行列にコピーします。小さな行列内の最大距離と最大距離要素の位置を決定します。次に、元の行列の残りの行を検索するサイクルを設定します。ループの本体では、分析された状態までの距離と結果行列の最大値を順番に確認します。より近い状態が見つかった場合は、それを結果行列の最大距離行に保存します。次に、最大距離の値と、最小距離の行列内のその位置を更新します。

   matrix<float> min_dist = temp;
   min_dist.Resize(k,rew_size + 1);
   float max = min_dist.Col(0).Max();
   ulong max_row = min_dist.Col(0).ArgMax();
   for(ulong i = k; i < states; i++)
     {
      if(temp[i,0] >= max)
         continue;
      min_dist.Row(temp.Row(i),max_row);
      max = min_dist.Col(0).Max();
      max_row = min_dist.Col(0).ArgMax();
     }

距離と報酬の行列のすべての行が完全に列挙されるまで反復を繰り返します。min_dist最小距離行列での1回の完全な検索の後、k個の最小距離（k個の最近傍）と、対応する報酬が経験再生バッファから取得されます。並び替えされていない可能性がありますが、内部報酬を計算するためにこれは必要ありません。 

   vector<float> t = vector<float>::Ones(k);
   vector<float> ri = MathLog(min_dist.Col(0) + 1.0f);

この段階では、分析対象の行動の内部報酬（エントロピー）を決定するためのデータがすべて揃っています。しかし、分析された状態と行動に対する報酬の目標値については、まだ疑問が残っています。ここで、取得されたk個の最近傍にもう一度注目する価値があります。結局のところ、それらには適切な報酬を付けています。モデルを訓練するプロセス全体は、状態、行動、および受け取った報酬の統計に基づいています。したがって、k個の最近傍が代表的なサンプルであり、目的の行動に対するそれらの報酬の関連性は、埋め込み距離に正比例します。

したがって、目標報酬をk個の最近傍からの報酬の距離加重平均として定義します。

   t = (t - ri) / k;
//---
   vector<float> result = vector<float>::Zeros(rew_size);
   for(ulong i = 0; i < rew_size - 1; i++)
      result[i] = (t * min_dist.Col(i + 1)).Sum();

報酬関数のエントロピー成分のフィールドでは、RE3法を使用して平均値を距離の対数として書き込みます。

   result[rew_size - 1] = ri.Mean();
//---
   return (result);
  }

分解された報酬目標値のベクトルを完全に定義し、結果のベクトルを呼び出し側プログラムに返します。

これで、「...\RE3\Study.mq5」モデル訓練EAのメソッドと関数の確認が終わりました。このEAの完全なコードと記事で使用されているすべてのプログラムは添付ファイルにあります。


3.検証

上記の実装は、おそらく純粋な形ではランダムエンコーダによる効率的な探索(RE3)メソッドとはほとんど言えません。ただし、私たちはこのアルゴリズムの基本的なアプローチを使用し、以前に研究したアルゴリズムのビジョンでそれらを補完しました。次に、実際の過去のデータを使用して結果を評価します。

以前と同様に、モデルの訓練とテストはEURUSDH1の2023年の最初の5か月に実行されます。すべての指標パラメータがデフォルトで使用されます。初期残高は10,000米ドルです。

モデルの訓練は反復的なプロセスであることをもう一度繰り返します。まず、ストラテジーテスターでEAを起動し、「...\RE3\Research.mq5」環境と相互作用し、訓練サンプルを収集します。


ここでは、パラメータを徹底的に検索する低速最適化モードを使用します。これにより、経験再生バッファを最も多様なデータで埋めることができます。これにより、モデル環境の性質を可能な限り幅広く理解できるようになります。

収集された訓練サンプルは、CriticsとActorの訓練中に「...\RE3\Study.mq5」モデル訓練EAによって使用されます。

目的の結果が得られるまで、訓練例の収集とモデルの訓練を何度か繰り返します。

記事の準備中に、訓練セットで利益を生み出すことができるActor方策を訓練することができました。訓練セットでは、EAは83%の収益性の高い取引を示しました。ただし、実行された取引数が非常に少ないことは認めます。5か月の訓練期間中、私のActorはわずか6回の取引をおこないました。そのうちの1つだけが18.62米ドルという比較的小さな損失で取引を終了しました。収益性の高い取引の平均は114.96米ドルです。その結果、プロフィットファクターは30を超え、リカバリーファクターは4.62となりました。

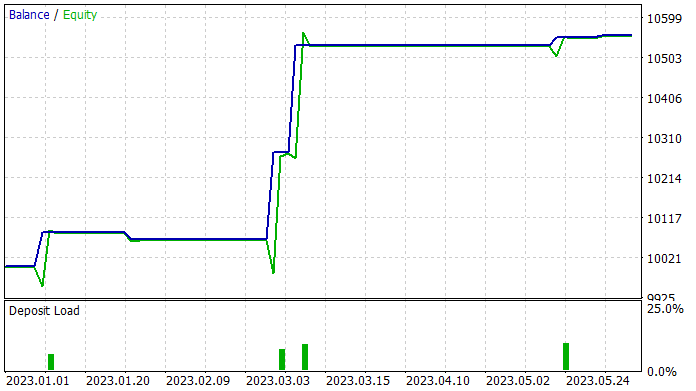
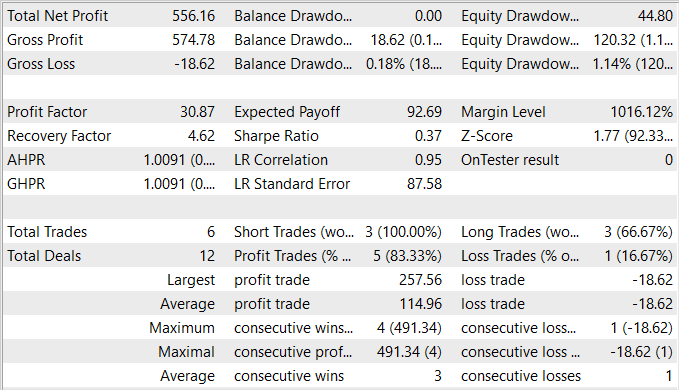
モデルの訓練結果モデルの訓練結果

テスト結果に基づいて、提案されたアルゴリズムにより効果的な組み合わせを見つけることが可能であると結論付けることができます。ただし、5.5%の収益性と5か月で6回の取引操作はかなり低い結果です。より良い結果を達成するには、実行される取引の数を増やすことに重点を置く必要があります。ただし、操作数の増加が戦略全体の効率の低下につながるわけではないことに留意してください。


結論

この記事では、強化学習のコンテキストで環境を探索するための効率的なアプローチであるランダムエンコーダによる効率的な探索(RE3)メソッドを紹介しました。この手法は、深層強化学習の分野における主要な課題の1つである、複雑な環境を効率的に探索するという問題を解決することを目的としています。

RE3の主なアイデアは、ランダムに初期化されたエンコーダを使用して取得された低次元表現の空間における状態のエントロピーを推定することです。エンコーダのパラメータは訓練全体を通じて固定されます。これにより、追加のモデルや訓練表現の導入が回避され、方法がより単純になり、計算効率が高まります。

記事の実践的な部分では、私のビジョンと提案された方法の実装について説明しました。実装では、提案されたアルゴリズムの基本的なアイデアが使用されていますが、以前に検討されたアルゴリズムからのいくつかのアプローチによって補足されています。これにより、かなり興味深いモデルを作成して訓練することが可能になりました。利益を上げている取引の割合は非常に驚くべきものですが、残念ながら総取引数は非常に少ないです。

一般に、結果として得られるモデルには可能性がありますが、取引数を増やす方法を見つけるには追加の作業が必要です。


リンク


記事で使用されているプログラム

# 名前 種類 詳細
1 Research.mq5 EA コレクションEAの例
2 Study.mq5  EA エージェント訓練EA
3 Test.mq5 EA モデルテストEA
4 Trajectory.mqh クラスライブラリ システム状態記述の構造
5 NeuroNet.mqh クラスライブラリ ニューラルネットワークを作成するためのクラスのライブラリ
6 NeuroNet.cl コードベース OpenCLプログラムコードライブラリ


MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/13158

添付されたファイル |
ZIPをダウンロード
MQL5.zip (442.11 KB)
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動
ニューラルネットワークが簡単に（第55回）：対照的内発制御（Contrastive intrinsic control、CIC） ニューラルネットワークが簡単に（第55回）：対照的内発制御（Contrastive intrinsic control、CIC）
対照訓練は、教師なしで表現を訓練する方法です。その目標は、データセットの類似点と相違点を強調するためにモデルを訓練することです。この記事では、対照訓練アプローチを使用してさまざまなActorスキルを探究する方法について説明します。
MQL5を使ったシンプルな多通貨エキスパートアドバイザーの作り方（第2回）：指標シグナル：多時間枠放物線SAR指標 MQL5を使ったシンプルな多通貨エキスパートアドバイザーの作り方（第2回）：指標シグナル：多時間枠放物線SAR指標
この記事の多通貨エキスパートアドバイザー(EA)は、1つの銘柄チャートからのみ複数の銘柄ペアの取引（注文を出す、注文を決済する、トレーリングストップロスとトレーリングプロフィットなどで注文を管理するなど）ができるEAまたは自動売買ロボットです。今回は、PERIOD_M15からPERIOD_D1までの多時間枠でパラボリックSARまたはiSARという1つの指標のみを使用します。
ニューラルネットワークが簡単に（第56回）：核型ノルムを研究の推進力に ニューラルネットワークが簡単に（第56回）：核型ノルムを研究の推進力に
強化学習における環境の研究は喫緊の課題です。いくつかのアプローチについてすでに見てきました。この記事では、核型ノルムの最大化に基づくもう一つの方法について見てみましょう。これにより、エージェントは新規性と多様性の高い環境状態を特定することができます。
GUI：MQLで独自のグラフィックライブラリを作成するためのヒントとコツ GUI：MQLで独自のグラフィックライブラリを作成するためのヒントとコツ
GUIライブラリの基本的な使い方を説明し、GUIライブラリがどのように機能するのかを理解し、さらには自分自身のライブラリを作り始めることができるようにします。