MetaTrader 5 / 交易系统
English Русский Español Deutsch 日本語 Português
preview
神经网络变得轻松（第五十四部分）：利用随机编码器（RE3）进行高效研究

神经网络变得轻松（第五十四部分）：利用随机编码器（RE3）进行高效研究

MetaTrader 5 — 交易系统 | 19 四月 2024, 14:49
836 0
Dmitriy Gizlyk
Dmitriy Gizlyk

概述

对环境的有效探索问题是强化学习方法的主要问题之一。我们不止一次探讨过这个问题。每次，拟议的方案都会导致算法的额外复杂性。在大多数情况下，我们求助于使用额外的内部奖励机制来鼓励模型探索新的动作，并探索未涉足的路径。

然而，为了评估动作和访问状态的新颖性，我们必须训练额外的模型。重点要注意的是，“动作新颖性”的概念并不总是与环境研究的完整性和统一性相吻合。在这个层面，基于估算动作熵值和状态的方法看起来最有吸引力。但是它们对已训练模型施加了自己的限定。熵的使用需要对执行动作和过渡到新状态的概率有一定的了解，而在动作和状态的连续空间情况下，直接计算可能非常困难。为了寻找更简单、更有效的方法，我建议您熟悉《使用随机编码器进行高效探索的状态熵最大化》一文中讲述的用于高效探索的随机编码器（RE3）算法。


1. RE3 的主要思路

分析具有连续动作和状态空间的真实案例，我们面临着每个状态-动作对在训练集中只出现一次的情况。未来观察到相同状态的几率近乎为 “0”。需要搜索对接近（相似）状态和动作进行分组的方法，而这会导致训练额外模型。例如，在 BAC 方法中，我们训练了一个自动编码器来评估状态和动作的新颖性。

不过，训练额外模型会给算法引入一定的复杂性。毕竟，选择其它超参数和训练模型都需要额外的时间和资源。训练附加模型的品质可能会对训练主要扮演者政策的结果产生重大影响。

高效探索的随机编码器（RE3）方法的主要目标是最大限度地降低训练模型的数量。在它们的工作中，RE3 方法的作者提请注意这样一个事实，即在图像处理领域，只有卷积网络能够识别单个对象的外在特点和内在特征。卷积网络将有助于降低多维空间的维度，突出特征并应对原始对象的缩放。

此处相当合理的问题是，如果我们另外转向卷积网络，我们正在谈论的已训练模型的最小化是什么样的？

在这个层面，关键词是 “已训练”。该方法的作者提请注意这样一个事实，即使卷积编码器采用随机参数初始化，也能有效地捕获有关两个状态相近度的信息。下面是可视化查找 k-最近态，通过测量随机初始化编码器（随机编码器）的表述空间，以及来自文章的真实状态空间中的距离。

k-最近态的可视化

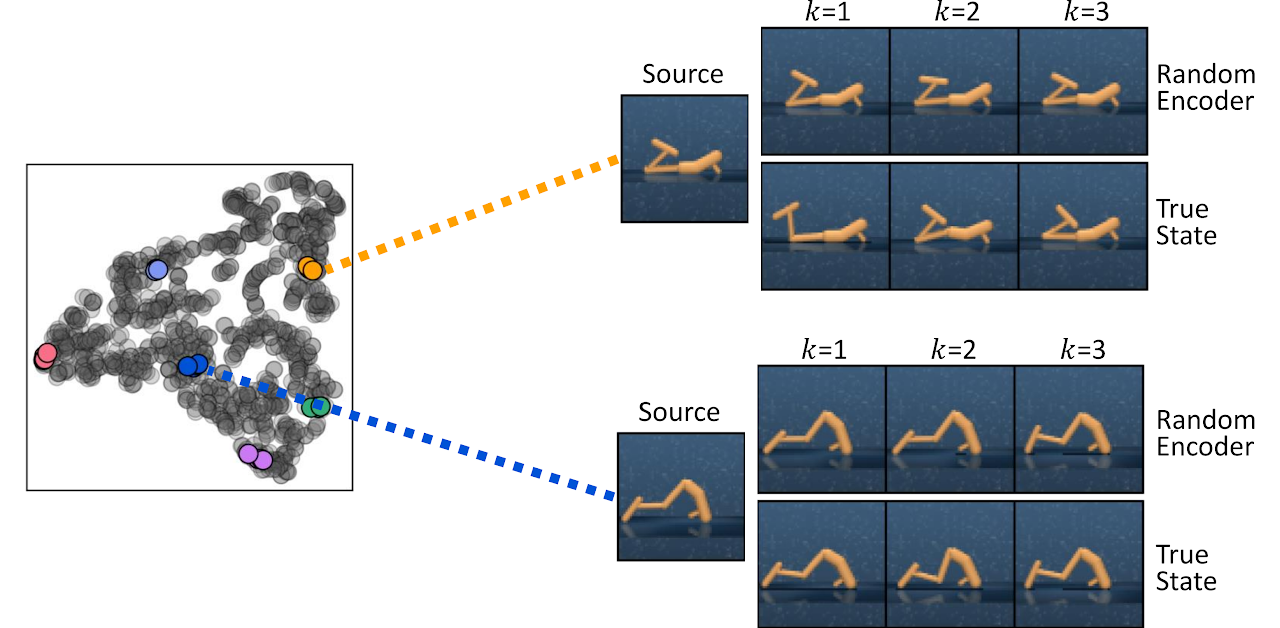
基于这一观察结果，RE3 方法的作者提出在模型训练期间在随机初始化编码器的固定表述空间中最大化状态熵估值。

高效探索的随机编码器（RE3）方法通过最大化状态熵来鼓励在高维观察空间中进行探索。RE3 的主要思路是使用随机初始化编码器获得的低维空间中的估算器 k-最近邻来估算熵值。

该方法的作者建议计算随机编码器的 f(θ) 表述空间中状态之间的距离，其 θ 参数贯穿训练过程中随机初始化且固定。

代理者的动机源于这样的观察，即随机编码器表述空间中的距离对于查找相似状态已经够用了，无需进行表述训练。

在这种情况下，内部奖励与状态熵的估值成正比，并由以下公式确定：

其中 yi 是随机编码器空间中的状态表示。

在给出的内部奖励方程中，我们使用 L2 距离范数，该范数始终为非负数。将范数增加 “1” 可令我们始终获得非负对数值。因此，我们总是得到非负面的内部奖励。此外，很容易注意到，在足够数量的接近状态下，内部奖励接近 “0”。

实践表明，在固定表述空间中测量状态之间的距离，可以提供更稳定的内部奖励，因为状态对之间的距离在训练期间不会改变。

为了计算隐含空间中的距离，在与环境交互时将低维状态表示存储在经验回放缓冲区中是计算效率最高的。这样就无需通过编码器处理高维状态，从而在每次模型更新迭代时获取表示。甚至，这允许在所有状态记录之前计算距离，而非在小批量的单个样品之前计算距离。该制程提供了稳定准确的熵估值，并计算高效。

通常，RE3 方法可用于实时训练代理者，其中代理者基于来自环境得最大外部奖励来学习策略。内部奖励会刺激代理者探索环境。

其中 β 是温度比率，决定研究和开发之间得平衡（β≥0）。

该方法的作者建议在贯穿训练过程中针对 β 采用指数递减，从而鼓励代理者随着训练进度，更多地关注来自环境的外部奖励。

其中 p 是衰减率。

虽然在训练期间会收集到更多相似状态，内部奖励将收敛到 “0”，但方法作者凭经验发现，β 的衰减稳定了性能。

此外，RE3 方法可在没有外部奖励的情况下预训练代理者探索高维环境空间。随后，可以进一步训练代理者政策来解决特定问题。

以下是作者对 RE3 方法的可视化。

作者的方法可视化

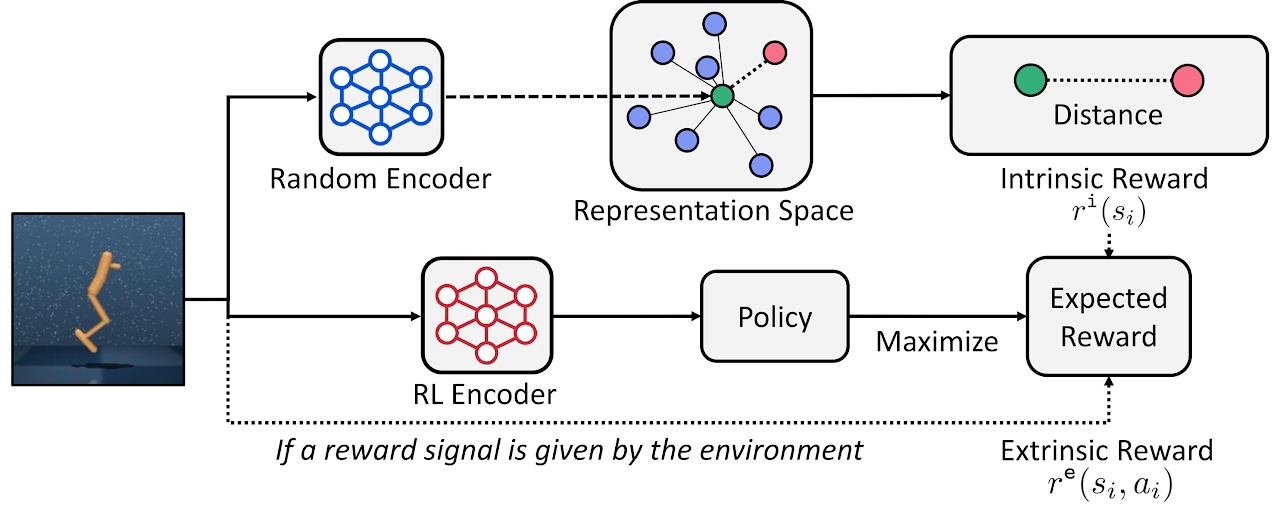
《凭借随机编码器实现状态熵最大化》进行高效探索一文讲述了各种测试的结果，证明了该方法的效率。我们将实现我们提出的算法版本，并评估其在解决我们任务时的效率。


2. 以 MQL5 实现

当我们开始实现这种方法时，值得注意的是，我们不会完整重复作者的算法。始终如一，我们将运用该方法的主要思路，并将它们与先前研究的方式相结合。在此，我们将创建某个糅合了当前和以前所研究算法的集合体。

我们将基于扮演者-评论者家族算法构建我们的实现。为了构建卷积编码器，我们将其描述添加到定义模型架构的方法之中。

bool CreateDescriptions(CArrayObj *actor, CArrayObj *critic, CArrayObj *convolution)
  {
//---
   CLayerDescription *descr;
//---
   if(!actor)
     {
      actor = new CArrayObj();
      if(!actor)
         return false;
     }
   if(!critic)
     {
      critic = new CArrayObj();
      if(!critic)
         return false;
     }
   if(!convolution)
     {
      convolution = new CArrayObj();
      if(!convolution)
         return false;
     }

我们将在连续动作空间中训练随机代理者政策。与之前的文章一样，我们将运用扮演者-评论者家族算法来训练扮演者。鉴于我们将运用 RE3 方法来估算奖励的熵分量，因此我们可以简化扮演者模型。在这种情况下，我们将重新创建来自《行为指引扮演者-评论者》一文中的扮演者架构。

//--- Actor
   actor.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1000;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   prev_count = descr.count = prev_count - 1;
   descr.window = 2;
   descr.step = 1;
   descr.window_out = 8;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   prev_count = descr.count = prev_count;
   descr.window = 8;
   descr.step = 8;
   descr.window_out = 8;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = 256;
   descr.optimization = ADAM;
   descr.activation = LReLU;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = 128;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 6
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConcatenate;
   descr.count = LatentCount;
   descr.window = prev_count;
   descr.step = AccountDescr;
   descr.optimization = ADAM;
   descr.activation = SIGMOID;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 7
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = 256;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 8
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = 256;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 9
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = 2 * NActions;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 10
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronVAEOCL;
   descr.count = NActions;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

如前，我们的评论者不会阻止对源数据进行初步处理。我们将使用扮演者的隐含状态作为评论者的输入。我们还将采用奖励分解，同时略微降低奖励点的数量。我们只用一个内部奖励元素，替代每个动作的 6 个单独熵分量元素。

//+------------------------------------------------------------------+
//| Rewards structure                                                |
//|   0     -  Delta Balance                                         |
//|   1     -  Delta Equity ( "-" Drawdown / "+" Profit)             |
//|   2     -  Penalty for no open positions                         |
//|   3     -  Mean distance                                         |
//+------------------------------------------------------------------+

因此，我们得到了以下评论者架构。

//--- Critic
   critic.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = LatentCount;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!critic.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConcatenate;
   descr.count = LatentCount;
   descr.window = prev_count;
   descr.step = NActions;
   descr.optimization = ADAM;
   descr.activation = LReLU;
   if(!critic.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!critic.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!critic.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = NRewards;
   descr.optimization = ADAM;
   descr.activation = None;
   if(!critic.Add(descr))
     {
      delete descr;
      return false;
     }

接下来，我们必须定义卷积编码器的架构。此处是与所述方法的第一个区别。RE3 方法基于对隐含状态表述之间距离的估算提供内部奖励。对比之下，我们将使用反映在编码器源数据层大小中的“状态-动作”对的隐含表述。

//--- Convolution
   convolution.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = (HistoryBars * BarDescr) + AccountDescr + NActions;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!convolution.Add(descr))
     {
      delete descr;
      return false;
     }

我们的编码器模型未经训练，因此使用批量数据常规化层没有意义。但我们将用到一个完全连接层，在其输出时，我们将得到可由卷积层处理过的可比较数据。

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = 512;
   descr.window = prev_count;
   descr.step = NActions;
   descr.optimization = ADAM;
   descr.activation = SIGMOID;
   if(!convolution.Add(descr))
     {по
      delete descr;
      return false;
     }

然后，我们使用 3 个连续卷积层来降低数据的维数。它们的任务是判定识别相似状态和动作的特征。

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   prev_count = descr.count = 512 / 8;
   descr.window = 8;
   descr.step = 8;
   int prev_wout = descr.window_out = 2;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!convolution.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   prev_count = descr.count = (prev_count * prev_wout) / 4;
   descr.window = 4;
   descr.step = 4;
   prev_wout = descr.window_out = 2;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!convolution.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   prev_count = descr.count = (prev_count * prev_wout) / 4;
   descr.window = 4;
   descr.step = 4;
   prev_wout = descr.window_out = 2;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!convolution.Add(descr))
     {
      delete descr;
      return false;
     }

为了完成编码器，我们将用到一个全连接层，并将数据的隐藏表述降低到给定的维度。

//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = EmbeddingSize;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!convolution.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

请注意，我们在所有神经层（第一层除外）都使用了 LReLU 来激活神经元。激活函数的结果范围没有限制，尽可能允许准确地将对象分组。

在创建模型架构的定义之后，我们来谈谈经验回放缓冲区。该方法的作者建议将状态的隐含表述与标准数据集同时保存到经验回放缓冲区当中。我同意这一点。一次性计算状态的隐含表述，然后将其用于训练过程，而无需在每次迭代时重新计算，这是非常合乎逻辑的。

在我们的动作序列中，当我们第一次启动训练数据收集 EA “...\RE3\Research.mq5” 时，还没有保存的预训练模型。扮演者模型由 EA 创建，并填充随机参数。我们还可以生成一个随机编码器模型。但是，在策略测试器的优化模式下并行启动多个 EA 实例，且每次 EA 验算都会创建一个编码器。问题在于，在每次验算中，我们都会得到一个随机编码器，其隐含表述将无法与其它验算中的类似表述进行比较。这完全违反了 RE3 方法的思想和原则。

我看到了两种可能的解决方案：

  • 在 “...\RE3\Research.mq5” EA 首次启动之前初步创建和保存模型
  • 在 “...\RE3\Study.mq5” 模型训练 EA 的主体中生成编码器和编码表述。

我在实现中选择了第二个选项。因此，我们不会对数据存储结构和 “...\RE3\Research.mq5” 训练样本集合 EA 进行修改。您可以在附件中找到其完整代码。

接下来，我们转入 “...\RE3\Study.mq5” 模型训练 EA。在此，我们为 6 个模型创建对象，而我们只会训练其中的 3 个。对于目标模型，我们使用 ꚍ 比率应用参数的软更新。

CNet                 Actor;
CNet                 Critic1;
CNet                 Critic2;
CNet                 TargetCritic1;
CNet                 TargetCritic2;
CNet                 Convolution;

在 EA 初始化方法中，我们加载训练集和预训练模型。如果无法加载模型，则生成填充了随机参数的新模型。

int OnInit()
  {
//---
   ResetLastError();
   if(!LoadTotalBase())
     {
      PrintFormat("Error of load study data: %d", GetLastError());
      return INIT_FAILED;
     }
//--- load models
   float temp;
   if(!Actor.Load(FileName + "Act.nnw", temp, temp, temp, dtStudied, true) ||
      !Critic1.Load(FileName + "Crt1.nnw", temp, temp, temp, dtStudied, true) ||
      !Critic2.Load(FileName + "Crt2.nnw", temp, temp, temp, dtStudied, true) ||
      !Convolution.Load(FileName + "CNN.nnw", temp, temp, temp, dtStudied, true) ||
      !TargetCritic1.Load(FileName + "Crt1.nnw", temp, temp, temp, dtStudied, true) ||
      !TargetCritic2.Load(FileName + "Crt2.nnw", temp, temp, temp, dtStudied, true))
     {
      CArrayObj *actor = new CArrayObj();
      CArrayObj *critic = new CArrayObj();
      CArrayObj *convolution = new CArrayObj();
      if(!CreateDescriptions(actor, critic, convolution))
        {
         delete actor;
         delete critic;
         delete convolution;
         return INIT_FAILED;
        }
      if(!Actor.Create(actor) || !Critic1.Create(critic) || !Critic2.Create(critic) ||
         !Convolution.Create(convolution))
        {
         delete actor;
         delete critic;
         delete convolution;
         return INIT_FAILED;
        }
      if(!TargetCritic1.Create(critic) || !TargetCritic2.Create(critic))
        {
         delete actor;
         delete critic;
         delete convolution;
         return INIT_FAILED;
        }
      delete actor;
      delete critic;
      delete convolution;
      //---
      TargetCritic1.WeightsUpdate(GetPointer(Critic1), 1.0f);
      TargetCritic2.WeightsUpdate(GetPointer(Critic2), 1.0f);
      StartTargetIter = StartTargetIteration;
     }
   else
      StartTargetIter = 0;

与上一篇文章一样，在生成新模型时，我们延长了使用目标模型的时间。这令我们能够在使用目标模型来估算后续代理者状态和动作之前对其进行预训练。

此处，我们将所有模型转移到单个 OpenCL 关联环境中。

//---
   OpenCL = Actor.GetOpenCL();
   Critic1.SetOpenCL(OpenCL);
   Critic2.SetOpenCL(OpenCL);
   TargetCritic1.SetOpenCL(OpenCL);
   TargetCritic2.SetOpenCL(OpenCL);
   Convolution.SetOpenCL(OpenCL);

在训练之前，我们会检查所用模型的架构是否符合要求。

   Actor.getResults(Result);
   if(Result.Total() != NActions)
     {
      PrintFormat("The scope of the actor does not match the actions count (%d <> %d)", NActions, Result.Total());
      return INIT_FAILED;
     }
//---
   Actor.GetLayerOutput(0, Result);
   if(Result.Total() != (HistoryBars * BarDescr))
     {
      PrintFormat("Input size of Actor doesn't match state description (%d <> %d)", Result.Total(), 
                                                                                        (HistoryBars * BarDescr));
      return INIT_FAILED;
     }
//---
   Actor.GetLayerOutput(LatentLayer, Result);
   int latent_state = Result.Total();
   Critic1.GetLayerOutput(0, Result);
   if(Result.Total() != latent_state)
     {
      PrintFormat("Input size of Critic doesn't match latent state Actor (%d <> %d)", Result.Total(), latent_state);
      return INIT_FAILED;
     }

在方法的最后，我们创建一个辅助缓冲区，并生成一个模型正在训练事件。

   Gradient.BufferInit(AccountDescr, 0);
//---
   if(!EventChartCustom(ChartID(), 1, 0, 0, "Init"))
     {
      PrintFormat("Error of create study event: %d", GetLastError());
      return INIT_FAILED;
     }
//---
   return(INIT_SUCCEEDED);
  }

在 EA 逆初始化方法中，我们更新目标模型的参数，并保存训练结果。

void OnDeinit(const int reason)
  {
//---
   TargetCritic1.WeightsUpdate(GetPointer(Critic1), Tau);
   TargetCritic2.WeightsUpdate(GetPointer(Critic2), Tau);
   Actor.Save(FileName + "Act.nnw", 0, 0, 0, TimeCurrent(), true);
   TargetCritic1.Save(FileName + "Crt1.nnw", Critic1.getRecentAverageError(), 0, 0, TimeCurrent(), true);
   TargetCritic2.Save(FileName + "Crt2.nnw", Critic2.getRecentAverageError(), 0, 0, TimeCurrent(), true);
   Convolution.Save(FileName + "CNN.nnw", 0, 0, 0, TimeCurrent(), true);
   delete Result;
  }

训练模型的实际过程均组织在 Train 过程当中。但在此，它的算法将与之前研究的 EA 的类似程序略有不同。

首先，我们将计数训练集中的状态总量。如您所知，每次验算中的状态数量都保存在 Total 变量当中。我们将安排一个循环，并从每次验算中收集指定变量值的总和。

void Train(void)
  {
   int total_tr = ArraySize(Buffer);
   uint ticks = GetTickCount();
//---
   int total_states = Buffer[0].Total;
   for(int i = 1; i < total_tr; i++)
      total_states += Buffer[i].Total;

我们需要结果值来声明状态-动作对的压缩表示矩阵，以及从环境中收集的实际奖励。

   vector<float> temp;
   Convolution.getResults(temp);
   matrix<float> state_embedding = matrix<float>::Zeros(total_states,temp.Size());
   matrix<float> rewards = matrix<float>::Zeros(total_states,NRewards);

接下来，我们将安排一个循环系统，在其内，我们将为训练集中的所有状态-动作对创建隐含表述。在此，我们首先将原始数据收集到单个数据缓冲区之中。

   for(int tr = 0; tr < total_tr; tr++)
     {
      for(int st = 0; st < Buffer[tr].Total; st++)
        {
         State.AssignArray(Buffer[tr].States[st].state);
         float PrevBalance = Buffer[tr].States[MathMax(st,0)].account[0];
         float PrevEquity = Buffer[tr].States[MathMax(st,0)].account[1];
         State.Add((Buffer[tr].States[st].account[0] - PrevBalance) / PrevBalance);
         State.Add(Buffer[tr].States[st].account[1] / PrevBalance);
         State.Add((Buffer[tr].States[st].account[1] - PrevEquity) / PrevEquity);
         State.Add(Buffer[tr].States[st].account[2]);
         State.Add(Buffer[tr].States[st].account[3]);
         State.Add(Buffer[tr].States[st].account[4] / PrevBalance);
         State.Add(Buffer[tr].States[st].account[5] / PrevBalance);
         State.Add(Buffer[tr].States[st].account[6] / PrevBalance);
         double x = (double)Buffer[tr].States[st].account[7] / (double)(D'2024.01.01' - D'2023.01.01');
         State.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         x = (double)Buffer[tr].States[st].account[7] / (double)PeriodSeconds(PERIOD_MN1);
         State.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0));
         x = (double)Buffer[tr].States[st].account[7] / (double)PeriodSeconds(PERIOD_W1);
         State.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         x = (double)Buffer[tr].States[st].account[7] / (double)PeriodSeconds(PERIOD_D1);
         State.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         State.AddArray(Buffer[tr].States[st].action);

然后我们调用卷积编码器的前向验算。

         if(!Convolution.feedForward(GetPointer(State),1,false,NULL))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            ExpertRemove();
            return;
           }

得到的结果保存在状态和动作嵌入矩阵的相应行中。我们将相应的外部奖励保存到含有相同字符串编号的奖励矩阵之中。之后，递增已记录行数的计数器。

         Convolution.getResults(temp);
         state_embedding.Row(temp,state);
         temp.Assign(Buffer[tr].States[st].rewards);
         rewards.Row(temp,state);
         state++;

在此过程中花费的时间取决于训练样本的规模，并且可能很长。因此，在循环体中，我们将添加信息消息来得到可视化过程控制。

         if(GetTickCount() - ticks > 500)
           {
            string str = StringFormat("%-15s %6.2f%%", "Embedding ", state * 100.0 / (double)(total_states));
            Comment(str);
            ticks = GetTickCount();
           }
        }
     }

循环系统迭代完成后，我们将矩阵大小调整为存储的行数。

   if(state != total_states)
     {
      rewards.Resize(state,NRewards);
      state_embedding.Reshape(state,state_embedding.Cols());
      total_states = state;
     }

准备阶段到此结束。现在是时候直接转入训练模型了。在此，如前，我们安排一个训练循环，迭代次数由用户在 EA 外部参数中指定。

   vector<float> rewards1, rewards2;
   for(int iter = 0; (iter < Iterations && !IsStopped()); iter ++)
     {
      int tr = (int)((MathRand() / 32767.0) * (total_tr - 1));
      int i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2));
      if(i < 0)
        {
         iter--;
         continue;
        }

在循环主体中，我们随机从当前迭代的模型训练中选择验算和状态。然后，我们检查是否需要使用目标模型。

如果我们的训练过程已经达到使用目标模型的阈值，那么我们就会为贯穿这些模型的前向验算生成后期状态输入。

      vector<float> reward, target_reward = vector<float>::Zeros(NRewards);
      reward.Assign(Buffer[tr].States[i].rewards);
      //--- Target
      if(iter >= StartTargetIter)
        {
         State.AssignArray(Buffer[tr].States[i + 1].state);
         float PrevBalance = Buffer[tr].States[i].account[0];
         float PrevEquity = Buffer[tr].States[i].account[1];
         Account.Clear();
         Account.Add((Buffer[tr].States[i + 1].account[0] - PrevBalance) / PrevBalance);
         Account.Add(Buffer[tr].States[i + 1].account[1] / PrevBalance);
         Account.Add((Buffer[tr].States[i + 1].account[1] - PrevEquity) / PrevEquity);
         Account.Add(Buffer[tr].States[i + 1].account[2]);
         Account.Add(Buffer[tr].States[i + 1].account[3]);
         Account.Add(Buffer[tr].States[i + 1].account[4] / PrevBalance);
         Account.Add(Buffer[tr].States[i + 1].account[5] / PrevBalance);
         Account.Add(Buffer[tr].States[i + 1].account[6] / PrevBalance);
         double x = (double)Buffer[tr].States[i + 1].account[7] / (double)(D'2024.01.01' - D'2023.01.01');
         Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         x = (double)Buffer[tr].States[i + 1].account[7] / (double)PeriodSeconds(PERIOD_MN1);
         Account.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0));
         x = (double)Buffer[tr].States[i + 1].account[7] / (double)PeriodSeconds(PERIOD_W1);
         Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         x = (double)Buffer[tr].States[i + 1].account[7] / (double)PeriodSeconds(PERIOD_D1);
         Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         //---
         if(Account.GetIndex() >= 0)
            Account.BufferWrite();

我们记得，我们需要定义环境的初始状态和代理者的动作，以便直接验算评论者的目标模型。这里有两点我们需要扮演者的直接验算：

  • 评论者没有源数据的预处理单元（它们不使用扮演者的隐含表述）;
  • 评论者的目标模型根据当前所用扮演者政策（需要生成新的动作向量）来估算后续状态。

因此，我们首先执行扮演者前向验算。

         if(!Actor.feedForward(GetPointer(State), 1, false, GetPointer(Account)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            break;
           }

然后，我们调用目标评论者的两种模型的直接验算方法。

         if(!TargetCritic1.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actor)) ||
            !TargetCritic2.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actor)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            break;
           }

接下来，根据软性扮演者-评论者算法，我们需要选择一个目标模型，对估算后续状态的最小值。在我的实现中，我使用了奖励元素的简单求和。但是，如果模型为奖励函数的各个元素提供了不同的权重比率，则可以使用模型结果的向量乘积和权重比率向量。

         TargetCritic1.getResults(rewards1);
         TargetCritic2.getResults(rewards2);
         if(rewards1.Sum() <= rewards2.Sum())
            target_reward = rewards1;
         else
            target_reward = rewards2;

然后，我们从所选模型的预测结果中减去与环境交互获得的实际奖励，并调整折扣因子。

         for(ulong r = 0; r < target_reward.Size(); r++)
            target_reward -= Buffer[tr].States[i + 1].rewards[r];
         target_reward *= DiscFactor;
        }

因此，在 target_reward 向量中，我们获得了每个奖励项在评论者的预测分数与环境的实际奖励之间的方差。这有什么帮助？

您也许还记得，考虑到折扣因子，每个“状态-行动”对的经验回放缓冲区会存储累积奖励金额，直到段落结束。此总奖励是根据代理者在与环境交互时使用的政策累积的。

我们预测了上述“状态-动作”对的成本，同时考虑了代理者的当前政策，并在考虑经验回放缓冲区中的动作时减去相同状态的估值。因此，target_reward 向量现在具有依据状态值改变扮演者政策的效力。

注意，我们正谈论的是状态值的变化。毕竟，它实际上不依赖于代理者。不过，根据所使用的策略，其在同一状态下的动作可能会有所不同。

在评估了改变扮演者的行动政策对整体结果的影响之后，我们转入评论者训练模块。正是它们的训练品质影响了将误差梯度传递给扮演者动作的正确性。

在此，我们还准备了环境描述数据，其中包括价格变动和指标的历史数据。我们还准备帐户状态数据作为单独的缓冲区。

      //--- Q-function study
      State.AssignArray(Buffer[tr].States[i].state);
      float PrevBalance = Buffer[tr].States[MathMax(i - 1, 0)].account[0];
      float PrevEquity = Buffer[tr].States[MathMax(i - 1, 0)].account[1];
      Account.Clear();
      Account.Add((Buffer[tr].States[i].account[0] - PrevBalance) / PrevBalance);
      Account.Add(Buffer[tr].States[i].account[1] / PrevBalance);
      Account.Add((Buffer[tr].States[i].account[1] - PrevEquity) / PrevEquity);
      Account.Add(Buffer[tr].States[i].account[2]);
      Account.Add(Buffer[tr].States[i].account[3]);
      Account.Add(Buffer[tr].States[i].account[4] / PrevBalance);
      Account.Add(Buffer[tr].States[i].account[5] / PrevBalance);
      Account.Add(Buffer[tr].States[i].account[6] / PrevBalance);
      double x = (double)Buffer[tr].States[i].account[7] / (double)(D'2024.01.01' - D'2023.01.01');
      Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
      x = (double)Buffer[tr].States[i].account[7] / (double)PeriodSeconds(PERIOD_MN1);
      Account.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0));
      x = (double)Buffer[tr].States[i].account[7] / (double)PeriodSeconds(PERIOD_W1);
      Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
      x = (double)Buffer[tr].States[i].account[7] / (double)PeriodSeconds(PERIOD_D1);
      Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
      if(Account.GetIndex() >= 0)
         Account.BufferWrite();

数据准备工作完成后，我们将执行前向扮演者验算。

      if(!Actor.feedForward(GetPointer(State), 1, false, GetPointer(Account)))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         break;
        }

不过，这一次我们只从扮演者中获取环境状态的隐含表述。我们使用来自经验回放缓冲区中的代理者动作。毕竟，正是因为这一动作，我们才从环境中获得了实际的回报。

利用这些数据，我们对两个评论者进行了直接验算。

      Actions.AssignArray(Buffer[tr].States[i].action);
      if(Actions.GetIndex() >= 0)
         Actions.BufferWrite();
      //---
      if(!Critic1.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actions)) ||
         !Critic2.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actions)))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         break;
        }

接下来，我们需要生成目标值，并执行评论者的逆向验算。我们已经多次执行了类似的操作。典型地，在此阶段，我们会根据政策变更的效果调整经验回放缓冲区中的实际奖励，并将结果值作为目标值传递给两个评论者模型。但是我们在这个实现中用到了分解奖励。在上一篇文章中，我们使用了冲突防范梯度下降（CAGrad）算法来校正误差梯度。我们调整了 CNet_SAC_D_DICE::CAGrad 方法中的值偏差，并将获得的值直接保存到神经结果层的误差梯度缓冲区当中。目前，我们无法直接访问模型最后一个神经层的梯度缓冲区，我们需要目标值。

我们执行一些数据操纵，以便获得调用冲突规避梯度下降方法校正的目标值。首先，我们从可用数据中生成目标值。然后我们从中减去评论者的预测值，从而得到偏差（误差）。我们调用已经熟悉的 CAGrad 方法校正由此产生的偏差。将我们之前减去的评论者预测值添加到结果中。

调用冲突规避梯度下降方法，为我们提供了一个调整过的目标值。不过，这样的目标值仅与一个评论者模型相关。对于评论者的第二个模型，我们将不得不重复考虑其预测值的操作。

在执行评论者后向验算后，我们执行部分扮演者后向验算，以便在数据预处理模块中分配误差梯度。

      Critic1.getResults(rewards1);
      Result.AssignArray(CAGrad(reward + target_reward - rewards1) + rewards1);
      if(!Critic1.backProp(Result, GetPointer(Actions), GetPointer(Gradient)) ||
         !Actor.backPropGradient(GetPointer(Account), GetPointer(Gradient), LatentLayer))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         break;
        }
      Critic2.getResults(rewards2);
      Result.AssignArray(CAGrad(reward + target_reward - rewards2) + rewards2);
      if(!Critic2.backProp(Result, GetPointer(Actions), GetPointer(Gradient)) ||
         !Actor.backPropGradient(GetPointer(Account), GetPointer(Gradient), LatentLayer))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         break;
        }

更新评论者的参数，后随扮演者政策更新模块。根据软性扮演者-评论者算法，使用具有最小状态估值的评论者来更新扮演者参数。我们将使用平均误差最小的评论者，这可能会产生更正确的误差梯度传输。

      //--- Policy study
      CNet *critic = NULL;
      if(Critic1.getRecentAverageError() <= Critic2.getRecentAverageError())
         critic = GetPointer(Critic1);
      else
         critic = GetPointer(Critic2);

此处，我们将 RE3 方法引入我们的训练过程。我们将环境的分析状态、帐户状态和代理者的选定动作的定义收集到单个数据缓冲区之中，同时考虑到更新的政策。我要提醒您，我们在更新评论者参数的阶段运作一次扮演者直接验算。

之后，对选定的评论者运作一次直接验算。这一次，我们评估扮演者在所分析状态下的动作，同时考虑到更新的政策。调用编码器的直接验算，从而获取所分析状态和扮演者动作对与更新政策的嵌入。

      Actor.getResults(rewards1);
      State.AddArray(GetPointer(Account));
      State.AddArray(rewards1);
      if(!critic.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actor)) ||
         !Convolution.feedForward(GetPointer(State)))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         break;
        }

正向验算之后是模型的逆向验算。因此，我们必须再次形成品滚着的目标值。但这一次我们必须结合 CAGrad 和 RE3 算法。此外，我们没有针对已分析状态和具有更新策略的扮演者动作的正确目标值。

我们已将使用 RE3 方法的目标值定义移至单独的 KNNReward 函数之中。稍后我们将看到它的算法。分解奖励的调整是根据评论者参数更新模块中描述的算法进行的。

      Convolution.getResults(rewards1);
      critic.getResults(reward);
      reward += CAGrad(KNNReward(7,rewards1,state_embedding,rewards) - reward);
      //---
      Result.AssignArray(reward + target_reward);

接下来，我们只需要禁用评论者的训练模式，并依次调用评论者和扮演者的后向验算方法。另外，我们不应该忘记检查操作的结果。

      critic.TrainMode(false);
      if(!critic.backProp(Result, GetPointer(Actor)) ||
         !Actor.backPropGradient(GetPointer(Account), GetPointer(Gradient)))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         critic.TrainMode(true);
         break;
        }
      critic.TrainMode(true);

更新扮演者策略后，我们返回到评论者模型训练模式。

在模型训练循环结束时，我们更新目标模型的参数，并通知用户训练进度。

      //--- Update Target Nets
      TargetCritic1.WeightsUpdate(GetPointer(Critic1), Tau);
      TargetCritic2.WeightsUpdate(GetPointer(Critic2), Tau);
      //---
      if(GetTickCount() - ticks > 500)
        {
         string str = StringFormat("%-15s %5.2f%% -> Error %15.8f\n", "Critic1", 
                                     iter * 100.0 / (double)(Iterations), Critic1.getRecentAverageError());
         str += StringFormat("%-15s %5.2f%% -> Error %15.8f\n", "Critic2", 
                                     iter * 100.0 / (double)(Iterations), Critic2.getRecentAverageError());
         Comment(str);
         ticks = GetTickCount();
        }
     }

在完成模型训练过程的所有迭代后，我们清除注释字段，日志中显示训练结果，并终止 EA。

   Comment("");
//---
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Critic1", Critic1.getRecentAverageError());
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Critic2", Critic2.getRecentAverageError());
   ExpertRemove();
//---
  }

我们已经研究了模型训练方法 Train 的算法。为了充分理解该过程，有必要分析 CAGrad 和 KNNReward 函数的算法。第一个算法完全是从上一篇文章中讨论的同名方法转移而来的。您可以在附件中找到它。我建议把重点放在第二个函数算法上。甚至，它与上述原始算法不同。

在其参数中，KNNReward 函数接收要分析的邻居数量、所需状态的嵌入向量、来自训练集的状态嵌入矩阵、和奖励矩阵。我要提醒您，经验和奖励回放缓冲区中的状态嵌入矩阵是按行同步的。我们稍后将利用这一重要观点。

函数操作的结果作为相应奖励值的向量返回。

vector<float> KNNReward(ulong k, vector<float> &embedding, matrix<float> &state_embedding, matrix<float> &rewards)
  {
   if(embedding.Size() != state_embedding.Cols())
     {
      PrintFormat("%s -> %d Inconsistent embedding size", __FUNCTION__, __LINE__);
      return vector<float>::Zeros(0);
     }

在函数主体中，我们首先检查所分析状态的嵌入大小和创建的经验回放缓冲区的嵌入。

接下来，我们判定嵌入向量之间的距离。为此，我们从经验回放缓冲区状态的每个嵌入列中减去所分析状态描述的相应元素的值。对结果值取平方。

   ulong size = embedding.Size();
   ulong states = state_embedding.Rows();
   ulong rew_size = rewards.Cols();
   matrix<float> temp = matrix<float>::Zeros(states,size);
//---
   for(ulong i = 0; i < size; i++)
      temp.Col(MathPow(state_embedding.Col(i) - embedding[i],2.0f),i);

提取逐行求和的平方根，并将结果向量放在矩阵的第一列中。

   temp.Col(MathSqrt(temp.Sum(1)),0);

因此，我们从矩阵第一列的经验回放缓冲区获得了所需状态和样本之间的距离。

我们更改矩阵的维度，并将经验回放缓冲区中的相应奖励元素添加到相邻的列中。

   temp.Resize(states,1 + rew_size);
   for(ulong i = 0; i < rew_size; i++)
      temp.Col(rewards.Col(i),i + 1);

作为这些操作的结果，我们得到了一个奖励矩阵，其第一列包含压缩嵌入空间中到所需状态的距离。

您也许还记得，在本例中，所需的状态是根据更新的政策执行扮演者动作的分析状态。

现在，为了判定给定扮演者动作的内部奖励，我们需要判定 k-最近邻。在按距离降序对结果矩阵进行排序后，我们可以很容易地找到它们，这是非常合乎逻辑的。不过，若要对数值进行完全排序，我们需要在整个距离向量上连续验算若干次。同时，我们不需要对矩阵进行完全排序。我们的任务是只找到 k 个最小值。它们在小结果矩阵中的顺序对我们来说并不太重要。因此，我们只需要沿距离向量验算一次。

我们只将 k 的第一行复制到我们的结果矩阵中。判定最大距离以及小矩阵中最大距离元素的位置。接下来，安排一个循环搜索原始矩阵其余行。在循环的主体中，我们依次检查所分析状态的距离和结果矩阵中的最大状态。如果我们找到一个更接近的状态，我们将其存储在结果矩阵的最大距离行中。然后，我们更新最大距离的值，及其在最小距离矩阵中的位置。

   matrix<float> min_dist = temp;
   min_dist.Resize(k,rew_size + 1);
   float max = min_dist.Col(0).Max();
   ulong max_row = min_dist.Col(0).ArgMax();
   for(ulong i = k; i < states; i++)
     {
      if(temp[i,0] >= max)
         continue;
      min_dist.Row(temp.Row(i),max_row);
      max = min_dist.Col(0).Max();
      max_row = min_dist.Col(0).ArgMax();
     }

重复迭代，直到距离和奖励矩阵的所有行都彻底列举完毕。在 min_dist 最小距离矩阵中完成一次搜索后，我们会得到 k 的最小距离（k-最近邻），并从经验回放缓冲区获得相应的奖励。它们可能不会被排序，但我们不需要这个来计算内部奖励。 

   vector<float> t = vector<float>::Ones(k);
   vector<float> ri = MathLog(min_dist.Col(0) + 1.0f);

在该阶段，我们拥有所有数据来判定所分析动作的内部奖励（熵）。但是，对于所分析状态和动作的奖励目标值，我们仍然有一个悬而未决的问题。此处，值得再一次关注获得的 k-最近邻。毕竟，我们已经为它们附上了相应的奖励。我们的整个训练模型过程都是基于状态行动和获得奖励的统计数据。因此，k-最近邻是我们的代表性样本，它们奖励与所需动作的相关性与嵌入距离成正比。

因此，我们将目标奖励定义为与 k-最近邻的奖励的距离加权平均值。

   t = (t - ri) / k;
//---
   vector<float> result = vector<float>::Zeros(rew_size);
   for(ulong i = 0; i < rew_size - 1; i++)
      result[i] = (t * min_dist.Col(i + 1)).Sum();

在奖励函数的熵分量字段中，我们调用 RE3 方法得到的距离对数写入平均值。

   result[rew_size - 1] = ri.Mean();
//---
   return (result);
  }

我们已经完全定义了分解奖励目标值的向量，并将结果的向量返回给调用程序。

我们对 “...\RE3\Study.mq5” 模型训练 EA 的方法和函数的回顾到此完毕。该 EA 的完整代码，和本文中用到的所有程序都可以在附件中找到。


3. 测试

上面讲述的实现可能很难称为纯粹形式的高效探索的随机编码器（RE3）方法。然而，我们用到了该算法的基本方式，并按我们之前研究该算法的看法进行了补充。现在是依据真实历史数据评估结果的时候了。

如前，模型的训练和测试是依据 2023 年前 5 个月 EURUSD H1 上进行的。所有指标参数采用默认值。初始本金为 10,000 美元。

我要再次重申，训练模型是一个迭代过程。首先，我们在策略测试器中启动 EA，以便与 “...\RE3\Research.mq5” 环境进行交互，并收集训练样本。


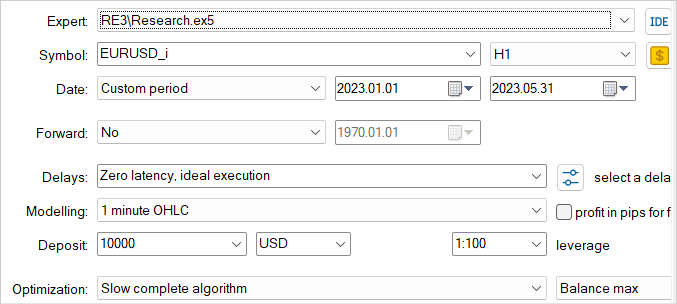
在此，我们使用慢速优化模式和详尽的参数搜索，这令我们能够用最多样化的数据填充经验回放缓冲区。这提供了对模型环境性质的最广泛的理解。

收集到的训练样本会在 “...\RE3\Study.mq5” 模型训练 EA 训练评论者和扮演者时所用。

我们重复多次收集训练样本和训练模型的迭代，直到获得所需的结果。

在准备本文时，我能够训练一个在训练集上产生盈利的扮演者政策。在训练集上，EA 显示了令人印象深刻的 83% 的盈利交易。虽然我要承认执行的交易数量非常少。在训练期间的 5 个月里，我的扮演者只做了 6 笔交易。其中只有一笔以相对较小的损失收盘，损失为 18.62 美元。平均盈利交易为 114.96 美元。结果就是，盈利系数超过 30，而恢复系数为 4.62。

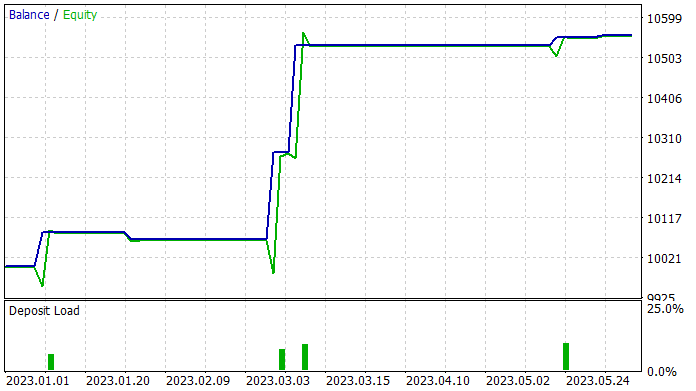
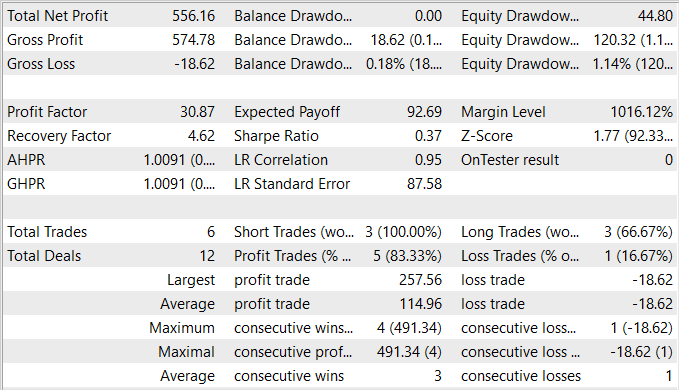
模型训练结果 模型训练结果

根据测试结果，我们可以得出结论，所提出的算法可以找到有效的组合。然而，5.5% 的盈利能力和 5 个月内的 6 次交易操作是一个相当低的结果。为了取得更好的结果，我们应该专注于增加执行的交易数量。不过，请记住，操作数量的增加不应导致整体策略效率的下降。


结束语

在本文中，我们讲述了高效探索的随机编码器（RE3）方法，这是一种在强化学习背景下探索环境的有效方法。该方法旨在解决高效探索复杂环境的问题，这是深度强化学习领域的主要挑战之一。

RE3 的主要思路是估算使用随机初始化编码器获得的低维表示空间中的状态熵。编码器参数在整个训练过程中是固定的。这避免了引入额外的模型和训练表述，这令该方法更简单，且计算效率更高。

在文章的实践部分，我讲述了我对所拟议方法的愿景和实现。我的实现使用了所提议算法的基本思路，但补充了以前研究过的算法中的许多方法。这令创建和训练一个相当有趣的模型成为可能。可盈利交易份额非常惊人，但不幸的是，交易总数非常少。

一般来说，由此产生的模型具有潜力，但需要额外的工作来找到增加交易数量的方法。


链接


本文中用到的程序

# 名称 类型 说明
1 Research.mq5 智能交易系统 样本收集 EA
2 Study.mq5  智能交易系统 代理者训练 EA
3 Test.mq5 智能交易系统 模型测试 EA
4 Trajectory.mqh 类库 系统状态定义结构
5 NeuroNet.mqh 类库 用于创建神经网络的类库
6 NeuroNet.cl 代码库 OpenCL 程序代码库


本文由MetaQuotes Ltd译自俄文
原文地址： https://www.mql5.com/ru/articles/13158

附加的文件 |
下载ZIP
MQL5.zip (442.11 KB)
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

该作者的其他文章

前往讨论
MQL5 中的范畴论 (第 17 部分)：函子与幺半群 MQL5 中的范畴论 (第 17 部分)：函子与幺半群
本文是我们系列文章的最后一篇，将函子作为一个主题来讨论，且把幺半群作为一个范畴来重新审视。幺半群已在我们的系列中多次讲述，于此配合多层感知器帮助确定持仓规模。
MQL5中的范畴论（第19部分）：自然性四边形归纳法 MQL5中的范畴论（第19部分）：自然性四边形归纳法
我们继续通过探讨自然性四边形归纳法来研究自然变换。对于使用MQL5向导构建的EA交易来说，对多货币实现的轻微限制意味着我们正在通过脚本展示我们的数据分类能力。所考虑的主要应用是价格变化分类及其预测。
为 MetaTrader 5 开发一款 MQTT 客户端：TDD 方式 - 第2部分 为 MetaTrader 5 开发一款 MQTT 客户端：TDD 方式 - 第2部分
本文是描述 MQTT 协议的本机MQL5客户端开发步骤系列文章的一部分。在这一部分中，我们将描述我们的代码组织、第一个头文件和类，以及我们如何编写测试。本文还包括关于测试驱动开发实践以及我们如何将其应用于该项目的简要说明。
MQL5中的范畴论（第18部分）：自然性四边形 MQL5中的范畴论（第18部分）：自然性四边形
本文通过介绍自然变换这一主题中的一个关键支柱，继续我们的范畴理论系列。我们研究看似复杂的定义，然后深入研究本系列“面包和黄油”的示例和应用程序；波动性预测。