記事「母集団最適化アルゴリズム：Spiral Dynamics Optimization (SDO)アルゴリズム」についてのディスカッション
また別のアルゴリズムをありがとう！
強調するのは良いことだ。
コミュニティと相談したい。
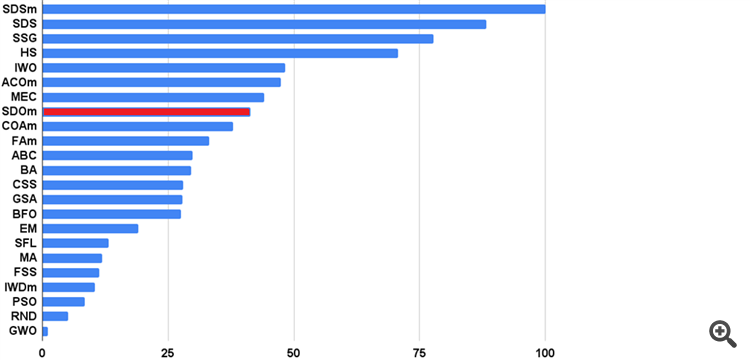
他の素晴らしいアルゴリズムも出番を待っている。比較表は見やすく分析するには大きくなりすぎる。
また、他の視覚化もできるかもしれない。
全般的に、ご意見やご提案をいただければ幸いです。
私の記事がトレーダーにとってアイデアやインスピレーションの源となり、新しい新鮮な目で平凡なものを見る助けとなり、また複雑な相互関係の探求における適切なツールの選択に役立ち、目標達成や新たな印象的な成功に役立つことを願っている。
そう、棒グラフ（ヒストグラム）は比較対象を表示する良い方法だ。
私が言いたかったのは、一般的なヒストグラムに加えて、各試験（しかも9つもある）ごとに分けて表示する価値があるのではないかということだ。色つきの表はいいし、各アルゴの特徴を明確に示すことができるが、分野によってどの程度違うのかがわからない。
また、私は正直なアルゴリズムしか挙げていないが（そうでないものもあったとしても、それらは作り直されている）、テスト関数の再現性を「武器」として使えるものもまだあるかもしれない。
最近そのようなアルゴリズムに出くわした。著者はラストリギン関数の最小値の探索を使ったが、最小値のglobが[0,0]（関数の定義領域のちょうど中央）にあることは絶対確実であり、結果としてそのようなアルゴリズムの想像上の「かっこよさ」がある。
そこで私は、多次元空間における2次元関数の重複をなくし、同時にテストプロセスを可視化する可能性を維持するために、テスト方法を見直すというアイデアに取り組んでいるのだが、これは一見すると非常に難しい問題である。
アンドレイ、これをどこで手に入れた？
それはあなたの頭の中にある疑問だ。
取引の機会を逃しています。
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索
新しい記事「母集団最適化アルゴリズム：Spiral Dynamics Optimization (SDO)アルゴリズム」はパブリッシュされました:
本稿では、軟体動物の殻など自然界における螺旋軌道の構築パターンに基づく最適化アルゴリズム、Spiral Dynamics Optimization（SDO、螺旋ダイナミクス最適化）アルゴリズムを紹介します。著者らが提案したアルゴリズムを徹底的に修正し、改変しました。この記事では、こうした変更の必要性について考えてみたいと思います。
Spiral Dynamics Optimization (SDO)は、2011年に田村健一と安田恵一郎によって提案された、自然界の対数螺旋現象を利用して開発された最も単純な物理アルゴリズムの1つです。アルゴリズムはシンプルで、制御パラメータもほとんどありません。さらに、このアルゴリズムは計算速度が高く、局所的な探索が可能で、初期段階では多様化し、後期段階では強化することができます。
銀河、オーロラ、動物の角、竜巻、貝殻、カタツムリ、アンモナイト、カメレオンの尻尾、タツノオトシゴなど、自然界にはたくさんの螺旋があります。螺旋は、人類がその黎明期に創り出した古代美術にも見られます。長年にわたり、何人かの研究者が螺旋のシーケンスと複雑さを理解し、螺旋の方程式とアルゴリズムを開発するために努力してきました。自然界で頻繁に起こる螺旋現象は、銀河や熱帯低気圧で観察される対数螺旋です。離散対数螺旋生成過程は、メタヒューリスティックスの効率的な探索動作として実装され、これが螺旋力学最適化アルゴリズムの開発のきっかけとなりました。
自然界に見られる可視螺旋列と呼ばれるパターンは、植物、樹木、波、その他多くの形を表しています。自然界の視覚的パターンは、カオス理論、フラクタル、螺旋、その他の数学的概念を用いてモデル化することができます。自然のパターンには、螺旋とフラクタルが密接に関係しているものがあります。例えば、フィボナッチ螺旋は黄金比とフィボナッチ数に基づく対数螺旋の変形です。対数であるため、曲線はどのスケールでも同じように見え、フラクタルとみなすこともできます。
作者: Andrey Dik