Обсуждение статьи "Популяционные алгоритмы оптимизации: Алгоритм оптимизации спиральной динамики (Spiral Dynamics Optimization, SDO)"
Хотелось бы посоветоваться с сообществом.
Своей очереди ждут ещё другие потрясающие алгоритмы, сравнительная таблица становится слишком большой для удобного просмотра и анализа, я думаю исключать из таблицы самые слабые, но с другой стороны не хотелось бы терять их из виду.
Ещё, может быть какие иные наглядные способы визуализации мне можно было бы делать.
В общем, буду рад услышать замечания и предложения.
Надеюсь, мои статьи послужат источником идей и вдохновения для трейдеров, помогут взглянуть на обычные вещи новым, свежим взглядом, а так же помогут в выборе подходящего инструментария в поиске сложнейших взаимосвязей, помогут в достижении целей и новых впечатляющих успехов.
Посмотрите на сайтах, где годами отработаны наиболее удачные варианты визуализации сравнительных данных.
Да, столбчатая диаграмма (гистограмма) - удачный способ отображать сравниваемое, с этим проблем нет.
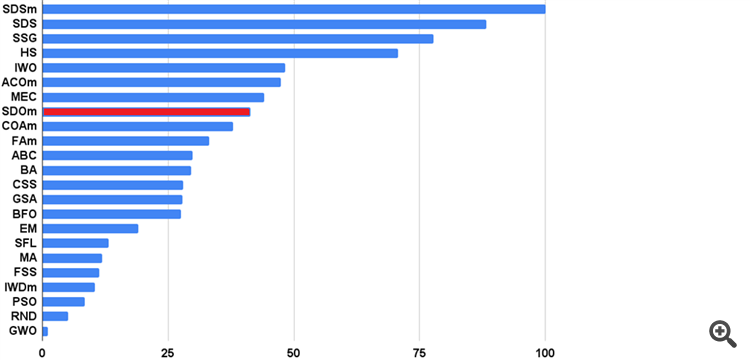
Я имел в виду, может быть стоит приводить в дополнение к общей гистограмме ещё и отдельно для каждого теста (а их 9). Цветная таблица это хорошо и позволяет наглядно выявить специфику каждого алго, но не даёт представления о степени их различия в разных дисциплинах.
И, хотя я привожу только честные алгоритмы (даже если некоторые из них не были таковыми, то они переделаны), но могут попасться всё же такие, которые могут использовать повторяемость в тестовых функциях как "оружие".
Недавно попался такой алгоритм, авторы использовали поиск минимума на функции Rastrigin, но ведь совершенно точно известно, что мин глоб находится в [0,0] (прямо в центре области определения функции), с вытекающей из этого мнимой "крутизной" такого алго.
Поэтому прорабатываю мысль пересмотреть методику тестирования, что бы избавиться от дублирования двумерных функций в многомерном пространстве и при этом сохранить возможность наглядной визуализации процесса тестирования - а этой очень непростой вопрос как может показаться на первый взгляд.
Андрей, где ты это берешь
это на свой ум вопрос
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Опубликована статья Популяционные алгоритмы оптимизации: Алгоритм оптимизации спиральной динамики (Spiral Dynamics Optimization, SDO):
В статье представлен алгоритм оптимизации, основанный на закономерностях построения спиральных траекторий в природе, таких как раковины моллюсков - алгоритм оптимизации спиральной динамики, SDO. Алгоритм, предложенный авторами, был мной основательно переосмыслен и модифицирован, в статье будет рассмотрено, почему эти изменения были необходимы.
Оптимизация спиральной динамики (SDO) — один из наиболее простых физических алгоритмов, предложенный Тамурой и Ясудой в 2011 году и разработанный с использованием явления логарифмической спирали в природе. Алгоритм прост и имеет мало управляющих параметров. Более того, алгоритм обладает высокой скоростью вычислений, возможностью локального поиска, диверсификацией на ранней стадии и интенсификацией на более позднем этапе.
В природе доступно множество спиралей, таких как галактики, полярные сияния, рога животных, торнадо, морские ракушки, улитки, аммониты, хвост хамелеона, морской конёк. Спирали также можно увидеть в древнем искусстве, созданном человечеством на заре своего существования. На протяжении многих лет несколько исследователей прилагали усилия, чтобы понять спиральные последовательности и сложности, а также разработать уравнения и алгоритмы спиралей. Более того, стоит подчеркнуть, что часто встречающимся спиральным явлением в природе является логарифмическая спираль, которую можно наблюдать в галактиках и тропических циклонах. Дискретные процессы генерации логарифмической спирали были реализованы как эффективное поведение поиска в метаэвристике, что вдохновило на разработку алгоритма оптимизации спиральной динамики.
Узоры, называемые видимыми спиральными последовательностями, встречающимися в природе, представляют собой растения, деревья, волны и многие другие формы. Визуальные узоры в природе могут быть моделированы с использованием теории хаоса, фракталов, спиралей и других математических концепций. В некоторых природных узорах спирали и фракталы тесно связаны между собой. Например, спираль Фибоначчи является вариантом логарифмической спирали, основанной на золотом сечении и числах Фибоначчи. Поскольку она является логарифмической, кривая в каждом масштабе выглядит одинаковой, и ее также можно считать фракталом.
Автор: Andrey Dik