Popülasyon optimizasyon algoritmaları: Yerçekimsel arama algoritması (Gravitational Search Algorithm, GSA)

İçindekiler

1. Giriş
2. Algoritma
3. Test sonuçları

1. Giriş

Yerçekimsel arama algoritması (Gravitational Search Algorithm, GSA), E. Rashedi tarafından optimizasyon problemlerini, özellikle doğrusal olmayan problemleri, Newton'un yerçekimi yasası ilkelerini izleyerek çözmek için önerilmiştir. Önerilen algoritmada, parçacıklar nesne olarak kabul edilir ve performansları kütleleri dikkate alınarak hesaplanır. Yerçekimi, kütlelerin birbirlerine doğru ivmelenme eğilimidir. Doğadaki dört temel kuvvetten biridir (diğerleri elektromanyetik kuvvet, zayıf nükleer kuvvet ve güçlü nükleer kuvvettir).

Evrendeki her parçacık diğer tüm parçacıkları çeker. Yerçekimi her yerde vardır. En zayıf kuvvet olmasına rağmen en görünür olanıdır. Yerçekimi kuvveti sayesinde insanlar Dünya üzerinde yürüyebilmekte ve gezegenler Güneş'in etrafında dönebilmektedir. Herhangi bir nesnenin yerçekimi kuvveti kütlesiyle orantılıdır. Dolayısıyla, daha fazla kütleye sahip nesneler daha fazla yerçekimine sahiptir. Yerçekiminin kaçınılmazlığı onu diğer tüm doğa güçlerinden ayırır. Newton'un yerçekimi kuvvetinin davranış şekline uzaktan etki denir. Isaac Newton'un tümevarımsal akıl yürütme dediği yöntemle deneysel gözlemlerden çıkarılan genel bir fizik yasasıdır. Newton'un ilk olarak 5 Temmuz 1687'de yayınlanan Philosophiae Naturalis Principia Mathematica (Principia) adlı eserinde formüle edilen klasik mekaniğin bir parçasıdır.

Nisan 1686'da Newton yayınlanmamış ilk kitabını Royal Society'ye sunduğunda, Robert Hooke Newton'un ters kare yasasını kendisinden aldığını iddia etmiştir. Günümüz dilinde bu yasa, her noktasal kütlenin diğer tüm noktasal kütleleri, iki noktayı kesen bir doğru boyunca etki eden bir kuvvetle çektiğini söyler.

2. Algoritma

Makale, Newton'un yerçekimi yasasına dayanan bir optimizasyon algoritması sunmaktadır: "Evrendeki her parçacık diğer tüm parçacıkları, kütlelerinin çarpımıyla doğru orantılı ve aralarındaki mesafenin karesiyle ters orantılı bir kuvvetle çeker". Önerilen algoritmada, arama temsilcileri Newton yerçekimi ve hareket yasalarına dayalı olarak birbirleriyle etkileşime giren bir dizi kütledir. Aynı zamanda, tüm temsilciler, arama uzayının neresinde olurlarsa olsunlar, kütleye (amaç fonksiyonunun değerlerinden hesaplanan) ve aralarındaki mesafeye bağlı bir çekim kuvveti aracılığıyla birbirleriyle bilgi alışverişinde bulunabilirler.

Temsilciler nesneler olarak ele alınır ve uygunlukları kütleleri ile ölçülür. Genel anlamda (gerçek fiziksel yasalara yakın algoritma ayarları ile), tüm bu nesneler yerçekimi kuvveti ile birbirlerine çekilir ve bu kuvvet tüm nesnelerin daha büyük kütleli nesnelere doğru global bir hareketine neden olur. Bu nedenle, kütleler yerçekimi kuvveti aracılığıyla doğrudan bir bağlantı biçimi kullanarak etkileşime girerler.

Klasik GSA'da her bir parçacığın üç çeşit kütlesi vardır:

a) aktif kütle
b) pasif kütle
c) eylemsizlik kütlesi

Çoğu durumda, kodları ve hesaplamaları basitleştirmek ve algoritma arama yeteneklerinin verimliliğini artırmak için bu kavramların eşitliğini kullanmak uygun ve yerindedir. Bu nedenle, algoritmada üç değil bir kütle olacaktır. GSA'da kullanılan fiziksel kanun denklemleri Şekil 1'de gösterilmektedir.

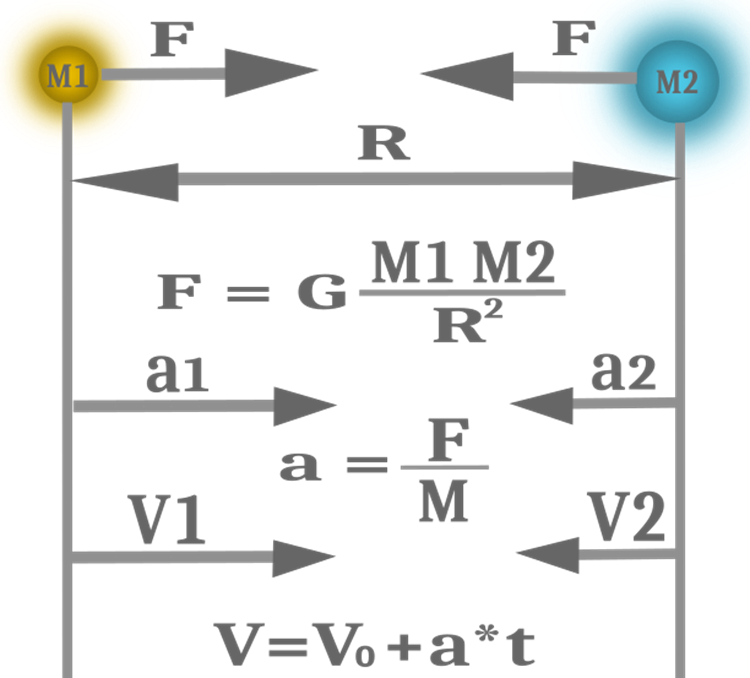
Şekil 1. Yerçekimi kuvveti, ivme ve hız

Parçacıkların konumu probleme çözüm sağlarken, uygunluk fonksiyonu kütleleri hesaplamak için kullanılır. Algoritmanın iki aşaması vardır: keşif ve sömürü. Bu algoritma, yerel optimumda takılıp kalmamak için başlangıçta zeka yeteneklerini kullanır ve bundan sonra ekstremum bölgelerinden yararlanır.

Yerçekimsel arama algoritması, uzayda hareket eden bir parçacığı belirli bir kütleye sahip bir nesneye dönüştürmelidir. Bu nesneler birbirleriyle olan yerçekimi etkileşimi nedeniyle çekilirler ve uzaydaki her parçacık, parçacıkların ivme yaratan karşılıklı çekimi nedeniyle çekilecektir. Her parçacık diğer parçacıklar tarafından çekilir ve kuvvet yönünde hareket eder. Küçük kütleli parçacıklar daha büyük kütleli parçacıklara doğru hareket eder, ancak büyük kütleli nesneler de hareket eder, ancak kütle ile ters orantılı olarak daha düşük bir hızda. Optimum çözüm, daha hızlı hareket eden "küçük" nesnelere kıyasla düşük hızda hareket ederek çözümü iyileştiren "büyük" nesneler tarafından bulunur. GSA, nesneler arasındaki etkileşim yoluyla bilgi aktarımını gerçekleştirir.

GSA adımları:

1. Temsilci başlatma
2. Uygunluk evrimi
3. Yerçekimi sabitinin hesaplanması
4. Temsilci kütlelerinin hesaplanması

1. Temsilci başlatma.
Tüm temsilciler rastgele başlatılır. Her bir temsilci bir aday çözüm olarak değerlendirilir. Kararlılık analizinin anlamlı ve güvenilir olabilmesi için denge başlangıç koşullarının belirlenmesi son derece önemlidir. Sonuçta, nesnelerin orijinal "diski" dengede değilse, simülasyonun ilk zaman adımlarındaki gevşemesi, "disk galaksilerin" kararlılığını anlamamız açısından çok az önem taşıyan kararsızlıklara neden olabilir. Ne yazık ki, karanlık madde halesinin ve/veya yıldız diskinin dış potansiyelinde hidrostatik dengede bulunan üç boyutlu bir gaz diskinin yoğunluğu, hız alanı ve sıcaklığı için analitik bir çözüm bilinmemektedir.

2. Uygunluk evrimi.
GSA'nın güvenilirliği ve etkinliği, keşif ve sömürü kabiliyetleri arasındaki dengeye bağlıdır. Çözüm arama sürecinin ilk yinelemelerinde, arama uzayının keşfedilmesi tercih edilir. Bu, temsilcilerin erken yinelemelerde büyük adım büyüklükleri kullanmasına izin vererek başarılabilir. Daha sonraki yinelemelerde, global optimumu kaçırma durumundan kaçınmak için arama uzayının iyileştirilmesi gerekir. Bu nedenle, aday çözümler sonraki yinelemelerde kullanılmak üzere küçük adım büyüklüklerine sahip olmalıdır.

3. Yerçekimi sabitinin hesaplanması.
G harfi ile gösterilen yerçekimi sabiti (evrensel yerçekimi sabiti, Newton yerçekimi sabiti veya Cavendish yerçekimi sabiti olarak da bilinir), Isaac Newton'un evrensel yerçekimi yasasında ve Albert Einstein'ın genel görelilik teorisinde yerçekimi etkilerinin hesaplanmasında yer alan deneysel bir fiziksel sabittir. Newton yasasında, iki cisim arasındaki çekim kuvvetini kütlelerinin çarpımı ve uzaklıklarının ters karesi ile ilişkilendiren orantı sabitidir. Einstein alan denklemlerinde, uzay zamanın geometrisi ile enerji-momentum tensörü arasındaki ilişkiyi ölçer.

4. Temsilci kütlelerinin hesaplanması.
Kütle, uzayda bulunan madde miktarıdır.

Algoritma yalancı kodu:

1. rastgele bir nesne sistemi oluştur.
2. her bir nesnenin uygunluğunu belirle.
3. yerçekimi sabitinin değerlerini güncelle, kütleleri ve en iyi ve en kötü nesneyi hesapla.
4. her bir koordinat üzerine etki eden kuvvetleri hesapla.
5. nesnelerin ivme ve hızlarını hesapla.
6. nesnelerin konumlarını güncelle.
7. her bir nesnenin uygunluğunu belirle.
8. durma kriteri karşılanana kadar 3. adımdan itibaren tekrarla.

GSA kodunu inceleyelim. Yerçekimsel etkileşim sistemindeki bir nesneyi tanımlamak için, yerçekimsel bir arama yapmak üzere yeterli olan nesnenin gerekli tüm fiziksel özelliklerini tanımlayacak olan S_Object yapısına ihtiyacımız vardır: c [] - arama uzayındaki koordinatlar, v [] - koordinatların her biri için hız vektörü (dizi boyutu koordinat sayısıdır), M - nesne kütlesi (GSA'da kütle, tüm nesne sistemi üzerindeki maksimum ve minimum uygunluğun değerine bağlı olarak hesaplanan göreceli bir değerdir), f - uygunluk değeri, R [] - diğer nesnelere olan Öklid mesafesi (dizinin boyutu nesne sayısıdır), F [] - her bir koordinat için kuvvet vektörü (dizinin boyutu koordinat sayısıdır).

//——————————————————————————————————————————————————————————————————————————————
struct S_Object
{
  double c  [];   //coordinates
  double v  [];   //velocity
  double M;       //mass
  double f;       //fitness
  double R  [];   //euclidean distance to other objects
  double F  [];   //force vector
};
//——————————————————————————————————————————————————————————————————————————————

Yerçekimsel arama algoritmasının sınıfını C_AO_GSA olarak tanımlayalım. Algoritmaya temsilci olarak katılan nesnelerin fiziksel özelliklerinden sadece bir şeye ihtiyaç vardır: en iyi çözümü temsil eden koordinatlar - fB değeri. Sınıf, arama uzayı koordinatlarının geçerli aralıklarını ve bir adımı bildirir. Yerçekimsel olarak bağlı nesneler sistemi, S_Object yapılarının bir dizisi olarak temsil edilir. Klasik algoritmada yalnızca üç harici parametre vardır: Nesnelerin yerçekimi etkileşiminin özelliklerini belirleyen G_constant, a_constant, e_constant ve sabitlerin geri kalanı hesaplama denklemlerine dahil edilmiştir, ancak bu sabitleri algoritmanın harici parametrelerine taşımanın uygun olduğunu düşündüm, bu da algoritmanın özelliklerinin bir bütün olarak daha esnek bir şekilde ayarlanmasına olanak tanır. Algoritmanın davranışını büyük ölçüde etkiledikleri için tüm parametreleri biraz sonra daha ayrıntılı olarak ele alacağım.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_GSA
{
  //----------------------------------------------------------------------------
  public: S_Object o       []; //object
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search
  public: double cB        []; //best coordinates
  public: double fB;           //FF of the best coordinates

  public: void Init (const int    coordinatesNumberP, //coordinates number
                     const int    objectsNumberP,     //objects number
                     const double PowerOfdistanceP,   //power of distance
                     const double GraviPert_MinP,     //gravitational perturbation Min
                     const double GraviPert_MaxP,     //gravitational perturbation Min
                     const double VelocityPert_MinP,  //Velocity perturbation Min
                     const double VelocityPert_MaxP,  //Velocity perturbation Max
                     const double G_constantP,        //G constant
                     const double a_constantP,        //a constant
                     const double e_constantP,        //e constant
                     const int    maxIterationsP);    //max Iterations

  public: void Moving   (int iter);
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coordinatesNumber; //coordinates number
  private: int    objectsNumber;     //objects number
  private: double PowerOfdistance;   //power of distance
  private: double GraviPert_Min;     //gravitational perturbation Min
  private: double GraviPert_Max;     //gravitational perturbation Min
  private: double VelocPert_Min;     //velocity perturbation Min
  private: double VelocPert_Max;     //velocity perturbation Max
  private: double G_constant;        //G constant
  private: double a_constant;        //a constant
  private: double e_constant;        //e constant
  private: int    maxIterations;
  private: bool   revision;

  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
  private: double Scale     (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers);
};
//——————————————————————————————————————————————————————————————————————————————

Algoritmanın Init () public metodu, hizmet değişkenlerini başlatmak ve dizilere boyutları atamak için algoritmanın harici parametrelerini dahili sabitlere iletmek için tasarlanmıştır.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_GSA::Init (const int    coordinatesNumberP, //coordinates number
                     const int    objectsNumberP,     //objects number
                     const double PowerOfdistanceP,   //power of distance
                     const double GraviPert_MinP,     //gravitational perturbation Min
                     const double GraviPert_MaxP,     //gravitational perturbation Min
                     const double VelocityPert_MinP,  //Velocity perturbation Min
                     const double VelocityPert_MaxP,  //Velocity perturbation Max
                     const double G_constantP,        //G constant
                     const double a_constantP,        //a constant
                     const double e_constantP,        //e constant
                     const int    maxIterationsP)     //max Iterations
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coordinatesNumber = coordinatesNumberP;
  objectsNumber     = objectsNumberP;
  PowerOfdistance   = PowerOfdistanceP;
  GraviPert_Min     = GraviPert_MinP;
  GraviPert_Max     = GraviPert_MaxP;
  VelocPert_Min     = VelocityPert_MinP;
  VelocPert_Max     = VelocityPert_MaxP;
  G_constant        = G_constantP;
  a_constant        = a_constantP;
  e_constant        = e_constantP;
  maxIterations     = maxIterationsP;

  ArrayResize (rangeMax,  coordinatesNumber);
  ArrayResize (rangeMin,  coordinatesNumber);
  ArrayResize (rangeStep, coordinatesNumber);

  ArrayResize (o,  objectsNumber);

  for (int i = 0; i < objectsNumber; i++)
  {
    ArrayResize (o [i].c,  coordinatesNumber);
    ArrayResize (o [i].v,  coordinatesNumber);
    ArrayResize (o [i].R,  objectsNumber);
    ArrayResize (o [i].F,  coordinatesNumber);
    o [i].f  = -DBL_MAX;
  }

  ArrayResize (cB, coordinatesNumber);
}
//——————————————————————————————————————————————————————————————————————————————

Her yinelemede çağrılan ilk public metot Moving ()'dir. Bu metot GSA algoritmasının tüm fizik ve mantığını içerir. Oldukça büyüktür, bu yüzden parçalara ayırarak gözden geçirelim. Metodun mevcut yinelemeyi bir parametre olarak aldığını, parametrenin yerçekimi sabitinin hesaplanmasına dahil olduğunu ve keşif ile sömürü arasındaki dengeyi ayarladığını unutmayın.

İlk yinelemede, nesne başlatma aşaması gerçekleşir. Nesnelerin tüm koordinatları için, tekdüze bir dağılımla izin verilen aralıkta rastgele değerler atarız ve aralık dışı olup olmadığını kontrol ederiz. Optimizasyon sürecinin başında, tüm nesnelerin hızı sıfırdır, yani nesneler koordinatlara göre arama uzayında hareketsizdir. Nesnelerin kütlesinin olmadığını, dolayısıyla ışık hızında hareket etmeleri gerektiğini unutmayın, ancak ilk yineleme için fizik yasalarını çiğneyeceğiz, çünkü bu an bir dereceye kadar Büyük Patlamaya eşdeğerdir. Şu anda nesnelerin uygunluğu, mümkün olan en küçük 'double' türündeki değerdir. Algoritmada hata ayıklama yaparken sıfır kütle ile ilgili hataları bulmak zordu, çözümü aşağıda görebilirsiniz.

//----------------------------------------------------------------------------
if (!revision)
{
  fB = -DBL_MAX;

  for (int obj = 0; obj < objectsNumber; obj++)
  {
    for (int c = 0; c < coordinatesNumber; c++)
    {
      o [obj].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      o [obj].c [c] = SeInDiSp (o [obj].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      o [obj].v [c] = 0.0;
      o [obj].M     = 0.0;
      o [obj].f     = -DBL_MAX;
    }
  }

  revision = true;
}

Moving () metoduna ilişkin kodun geri kalanı, nesnelerin kütle, hız ve ivme kazanacağı ikinci ve sonraki yinelemeleri ifade eder.

Öncelikle kütleyi hesaplamamız gerekiyor. Yukarıda belirtildiği gibi, nesnelerin kütlesi (tanım gereği pozitif skaler bir değer) uygunluk fonksiyonunun değerlerinden hesaplanır, bu nedenle elde edilen değerlere dayalı olarak kütleyi hesaplamadan önce minimum ve maksimum uygunluk değerlerini belirlemek gerekir. Bu ana kadar, uygunluk fonksiyonunun değeri bir önceki yinelemede zaten elde edilmiştir.

//find the minimum and maximum fitness==========================================
for (int obj = 0; obj < objectsNumber; obj++)
{
  if (o [obj].f < Fmin) Fmin = o [obj].f;
  if (o [obj].f > Fmax) Fmax = o [obj].f;
}

Kodun bu noktasında, kütle Mo = (Fo-Fmin)/(Fmax-Fmin) denklemi kullanılarak hesaplanır, burada:

• Mo - nesne kütlesi
• Fo - nesne uygunluğu
• Fmax - tüm nesneler arasında maksimum uygunluk değeri (en iyi değer)
• Fmin - tüm nesneler arasında minimum uygunluk değeri (en kötü değer)
  

Denklemden de görebileceğimiz gibi, kütle yalnızca 0 ila 1 aralığında pozitif değerler alabilir. Daha önce kütlenin sıfıra eşit olmaması gerektiğini, aksi takdirde hızın ışık hızına eşit olacağını tartıştığımızdan, kütlenin alt sınırını 0.1 ile sınırlayacağız. Üst değer 1'e eşit olabilir. Ayrıca, uygunluk fonksiyonunun minimum ve maksimum değerleri eşitse, tüm nesnelerin kütlesinin herkes için aynı ve 1'e eşit olacağına dikkat edin. Bu, arama uzayının nesnelerin bulunduğu alanda homojen olduğu ve tüm nesnelerin uygunluk fonksiyonunun kalitesi açısından eşit olduğu ve herhangi bir yöndeki hareketin eşit önceliğe sahip olduğu duruma karşılık gelir. Bu durumda tüm nesnelerin kademeli olarak ortak bir kütle merkezine doğru hareket etmesi ve yoğunlaşması gerekir, ancak yerçekimi kuvvetinin doğrusal olmayan etkisi nedeniyle bu gerçekleşmez.

//calculating the mass of objects===========================================
for (int obj = 0; obj < objectsNumber; obj++)
{
  Fo = o [obj].f;
  if (Fmax == Fmin) Mo = 1.0;
  else Mo = (Fo - Fmin) / (Fmax - Fmin);
  o [obj].M = Scale (Mo, 0.0, 1.0, 0.1, 1.0, false);
}

Nesneler için kütleyi hesapladık, şimdi R denkleminin bir bileşenini daha hesaplamak gerekiyor - her nesneden diğer her nesneye olan Öklid uzaklığı. Hesaplama, nesnelerin numaralandırıldığı iki döngüden ve koordinatların her biri için bir hesaplama döngüsünden oluşur. Hatırladığımız gibi, Öklid uzaklığı koordinat farklarının karelerinin toplamının köküdür.

//calculation of Euclidean distances between all objects====================
for (int obj = 0; obj < objectsNumber; obj++) ArrayInitialize (o [obj].R, 0.0);

for (int obj = 0; obj < objectsNumber; obj++)
{
  for (int obj2 = 0; obj2 < objectsNumber; obj2++)
  {
    if (obj != obj2)
    {
      if (o [obj].R [obj2] == 0.0)
      {
        for (int c = 0; c < coordinatesNumber; c++)
        {
          diffDist = o [obj].c [c] - o [obj2].c [c];
          o [obj].R [obj2] += diffDist * diffDist;
        }

        o [obj].R [obj2] = sqrt (o [obj].R [obj2]);
        o [obj2].R [obj] = o [obj].R [obj2];
      }
    }
  }
}

Şimdi nesneler için kuvvet vektörlerini hesaplayabiliriz. Bunu yapmak için, hız her koordinat için ayrı ayrı hesaplandığından, tüm nesneleri iki döngüde ve koordinatlar için bir döngüde geçmemiz gerekir. Nesne indekslerinin çakışmasını hariç tutan bir koşul eklemeliyiz, böylece nesne kuvvet hesaplamasında kendisinin hesaplanmasını hariç tutar. Burada Newton'un iyi bilinen denklemini kullanarak iki cismin çekim kuvvetini (Şekil 1) hesaplıyor ve mesafeyi e_constant oranına göre düzeltiyoruz. Öncelikle, algoritmanın optimizasyonun sonuna kadar yoğunlaştığını varsayarak her yinelemede aşağı doğru değişmesi gereken yerçekimi sabiti G'yi hesaplayalım.

//calculate the force vector for each object================================
for (int obj = 0; obj < objectsNumber; obj++) ArrayInitialize (o [obj].F, 0.0);

double G = G_constant * exp (-a_constant * (iter / maxIterations));

for (int obj = 0; obj < objectsNumber; obj++)
{
  for (int obj2 = 0; obj2 < objectsNumber; obj2++)
  {
    if (obj != obj2)
    {
      for (int c = 0; c < coordinatesNumber; c++)
      {
        diffDist = o [obj2].c [c] - o [obj].c [c];

        if (o [obj].R [obj2] != 0.0)
        {
          o [obj] .F [c] += G * o [obj].M * o [obj2].M * diffDist / (pow (o [obj].R [obj2], PowerOfdistance) + e_constant);
        }
      }
    }
  }
}

Şimdi nesnelerin hareket etmeye başlaması için sadece hızı hesaplamamız gerekiyor. Şekil 1'deki denklemden, hız hesaplamasının ivmeyi içerdiğini, ivmenin ise cisme etki eden kuvvetin kütleye bölünmesine eşit olduğunu görebiliriz. V = V0+a*t denkleminde ayrıca zaman da vardır. Algoritmamızda, yineleme zamanın rolünü oynar, bu nedenle hızdaki değişiklik, bir yinelemedeki hız artışından başka bir şey değildir. Hız vektörü yukarıda zaten hesaplanmıştır. Geriye kütleye bölmek kalıyor. Buna ek olarak, yazarlar kuvvet pertürbasyonunu ve hız pertürbasyonunu tanıtmaktadır. Pertürbasyon, 0 ile 1 arasında tekdüze olarak dağıtılmış rastgele bir sayıdır. Bu, cisimlerin hareketine rastgele bir bileşen ekler; bu bileşen olmadan hareket kesinlikle deterministik olur ve yalnızca cisimlerin ilk konumuna bağlı kalır. Pertürbasyon göstergelerini algoritmanın harici parametrelerine dahil etmenin makul olduğunu düşündüm, bu da nesnelerin hareketini tamamen deterministikten tamamen rastlantısal olana kadar düzenlemeye izin verecektir.

//calculation of acceleration and velocity for all objects==================
double a = 0.0; //acceleration

for (int obj = 0; obj < objectsNumber; obj++)
{
  for (int c = 0; c < coordinatesNumber; c++)
  {
    r = RNDfromCI (GraviPert_Min, GraviPert_Max);
    a = o [obj].F [c] * r / o [obj].M;
    r = RNDfromCI (GraviPert_Min, GraviPert_Max);
    o [obj].v [c] = o [obj].v [c] * r + a;
    o [obj].c [c] = o [obj].c [c] + o [obj].v [c];

    if (o [obj].c [c] > rangeMax [c]) o [obj].c [c] = rangeMin [c];
    if (o [obj].c [c] < rangeMin [c]) o [obj].c [c] = rangeMax [c];

    o [obj].c [c] = SeInDiSp (o [obj].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}

İkinci Revision () metodu, her yinelemede yürütülmesi zorunludur. Metot, mevcut yineleme için en iyi uygunluk değerini belirlemek üzere tasarlanmıştır. Döngüde, tüm nesneleri gözden geçiririz ve global en iyi çözümü değiştiririz.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_GSA::Revision ()
{
  for (int s = 0; s < objectsNumber; s++)
  {
    if (o [s].f > fB)
    {
      fB = o [s].f;
      ArrayCopy (cB, o [s].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

3. Test sonuçları

Test sonuçlarına geçelim. Aşağıda bulabildiğim en iyi GSA parametreleri ile test ortamı sonuçları yer almaktadır:

2023.02.03 14:12:43.440    Test_AO_GSA (EURUSD,M1)    C_AO_GSA:10;2.0;0.2;0.6;0.0;1.0;2.0;20.0;0.01
2023.02.03 14:12:43.440    Test_AO_GSA (EURUSD,M1)    =============================
2023.02.03 14:12:52.198    Test_AO_GSA (EURUSD,M1)    5 Rastrigin's; Func runs 10000 result: 73.64619475145881
2023.02.03 14:12:52.198    Test_AO_GSA (EURUSD,M1)    Score: 0.91252
2023.02.03 14:13:06.105    Test_AO_GSA (EURUSD,M1)    25 Rastrigin's; Func runs 10000 result: 59.4327218024363
2023.02.03 14:13:06.105    Test_AO_GSA (EURUSD,M1)    Score: 0.73640
2023.02.03 14:14:16.529    Test_AO_GSA (EURUSD,M1)    500 Rastrigin's; Func runs 10000 result: 37.550565227034724
2023.02.03 14:14:16.529    Test_AO_GSA (EURUSD,M1)    Score: 0.46527
2023.02.03 14:14:16.529    Test_AO_GSA (EURUSD,M1)    =============================
2023.02.03 14:14:30.577    Test_AO_GSA (EURUSD,M1)    5 Forest's; Func runs 10000 result: 0.741456333008312
2023.02.03 14:14:30.577    Test_AO_GSA (EURUSD,M1)    Score: 0.41941
2023.02.03 14:14:50.281    Test_AO_GSA (EURUSD,M1)    25 Forest's; Func runs 10000 result: 0.46894018717768426
2023.02.03 14:14:50.282    Test_AO_GSA (EURUSD,M1)    Score: 0.26526
2023.02.03 14:16:01.856    Test_AO_GSA (EURUSD,M1)    500 Forest's; Func runs 10000 result: 0.11382493516764165
2023.02.03 14:16:01.856    Test_AO_GSA (EURUSD,M1)    Score: 0.06439
2023.02.03 14:16:01.856    Test_AO_GSA (EURUSD,M1)    =============================
2023.02.03 14:16:18.195    Test_AO_GSA (EURUSD,M1)    5 Megacity's; Func runs 10000 result: 5.279999999999999
2023.02.03 14:16:18.195    Test_AO_GSA (EURUSD,M1)    Score: 0.44000
2023.02.03 14:16:34.536    Test_AO_GSA (EURUSD,M1)    25 Megacity's; Func runs 10000 result: 2.296
2023.02.03 14:16:34.536    Test_AO_GSA (EURUSD,M1)    Score: 0.19133
2023.02.03 14:17:46.887    Test_AO_GSA (EURUSD,M1)    500 Megacity's; Func runs 10000 result: 0.23399999999999999
2023.02.03 14:17:46.887    Test_AO_GSA (EURUSD,M1)    Score: 0.01950

Algorithm parameters:

input double PowerOfdistance_P  = 2.0;   //Power of distance
input double GraviPert_Min_P    = 0.2;   //Gravitational perturbation Min
input double GraviPert_Max_P    = 0.6;   //Gravitational perturbation Max
input double VelocityPert_Min_P = 0.0;   //Velocity perturbation Min
input double VelocityPert_Max_P = 1.0;   //Velocity perturbation Max
input double G_constant_P       = 2.0;   //G constant
input double a_constant_P       = 20.0;  //a constant
input double e_constant_P       = 0.01;  //e constant

PowerOfdistance_P - nesneler arasındaki mesafeyi artırdığımız derece, yerçekimsel olarak bağlı nesnelerin oluşumunu etkiler. Denklemdeki derece ne kadar yüksekse, nesnelerin diğer nesneler üzerindeki etkisi o kadar az olur.

• GraviPert_Min_P - yerçekimsel pertürbasyon aralığının alt sınırı.
• GraviPert_Max_P - yerçekimsel pertürbasyon aralığının üst sınırı.
• GraviPert_Min_P = 1.0 ve GraviPert_Max_P = 1.0 olması durumunda, yerçekim pertürbasyonu yoktur.
• VelocityPert_Min_P - hız pertürbasyon aralığının alt sınırı.
• VelocityPert_Max_P - hız pertürbasyon aralığının üst sınırı.

VelocityPert_Min_P = 1.0 ve VelocityPert_Max_P = 1.0 durumunda, hız pertürbasyonu yoktur.

• G_constant_P - yerçekimi sabiti bir ölçek faktörü olarak işlev görür: değer ne kadar yüksek olursa, yerçekimi kuvvetleri o kadar güçlü etki eder ve nesnelerin hızı o kadar hızlı değişir.
• a_constant_P - bulunan ekstremumları iyileştirmek amacıyla tüm optimizasyon sırasında arama alanını azaltmak için tasarlanmış yerçekimi sabiti için düzeltme faktörü.
• e_constant_P - nesneler arasındaki mesafe için düzeltme faktörü.

Görselleştirme testi sonuçlarına bir göz atalım. Algoritmanın test fonksiyonları üzerindeki davranışı çok özel ve ilginçtir. Aslında deney, yerçekimi kuvvetlerinin çalışmasını göstermektedir. Nesnelerin hareketi ve elde edilen optimizasyon sonuçları, algoritmanın harici parametrelerinden büyük ölçüde etkilenir. Başlangıçta, sıfır hıza sahip nesneler arama uzayına rastgele dağıtılır ve bir sonraki yinelemede hareket etmeye başlar. Testlerde kullanılan ayarlar (bulduklarımın en iyisi), nesnelerin ortak bir kütle merkezine doğru hareket etmesini sağlamaktadır.

Her nesnenin yerçekiminin, hareket yasaları algoritmada yeterince yüksek doğrulukla tanımlanan diğer nesneleri etkilediğini unutmayın. Ortak kütle merkezine yaklaşan nesneler yüksek hızda hareket etmeye devam eder. Parçacık kütlesinin ortak kütle merkezine doğru ve merkezden geriye doğru titreşimli bir hareketi gibi görünmektedir. Belirli sayıda yinelemeden sonra, nesnelerin hareketi, nesnelerin kütlesini etkileyen yerçekimsel bir homojensizlik gibi davranan uygunluk fonksiyonunun uzay rahatlamasının etkisi altında yörüngesini değiştirir. Daha önce tartıştığımız gibi, nesnelerin kütlesi uygunluk fonksiyonunun değerinden hesaplanır. Bununla birlikte, eksenler boyunca simetrik olan Rastrigin fonksiyonu, nesnelerin hareketi üzerinde oldukça düzgün bir etkiye sahiptir ve gruplara ayrılma özellikle fark edilmez.

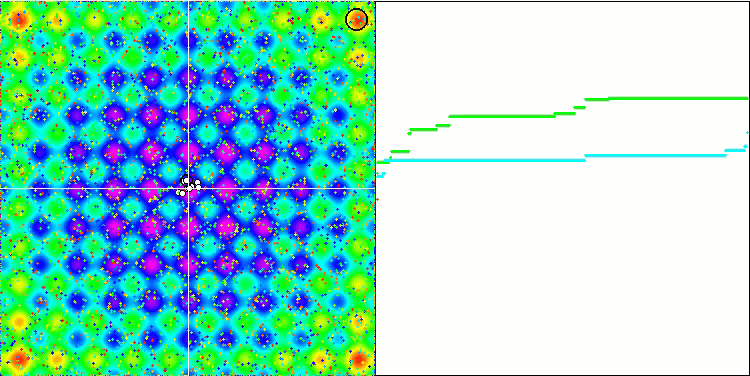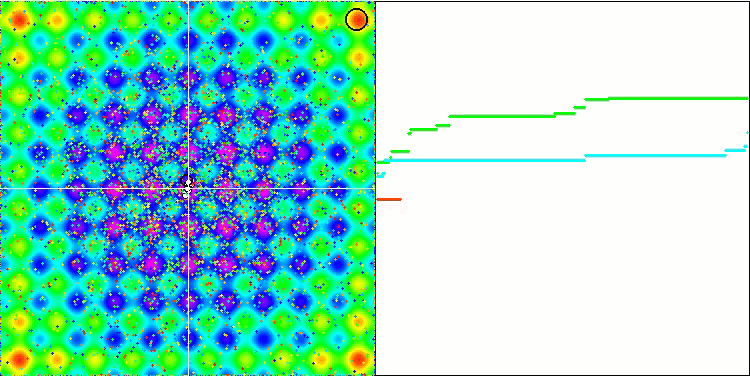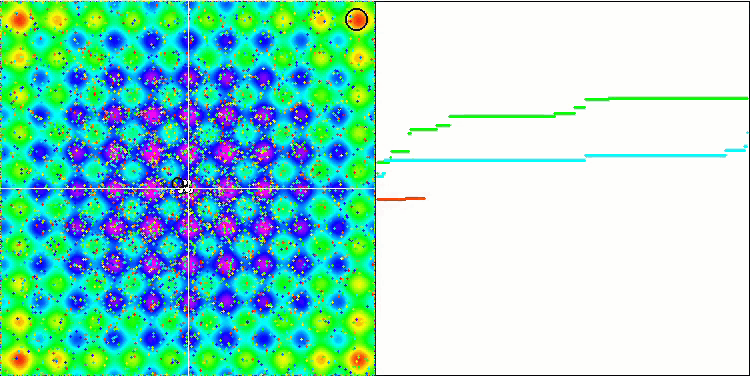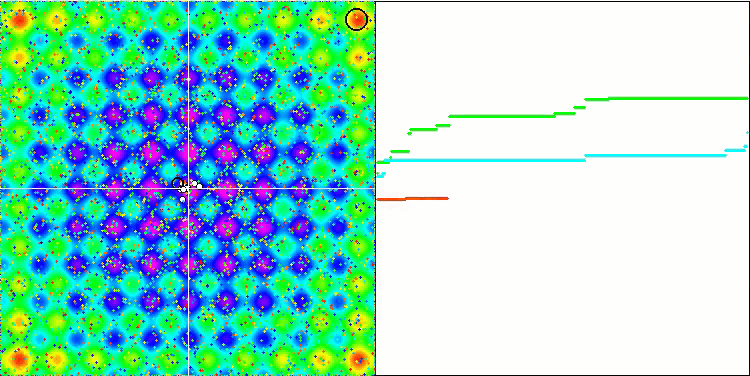
  Rastrigin test fonksiyonu üzerinde GSA

Forest ve Megacity fonksiyonlarındaki nesneler daha da ilginç davranışlar sergilemektedir. Bu fonksiyonlar simetrik değildir ve bu nedenle tüm nesne grubu üzerinde düzgün olmayan bir etkiye sahiptir.

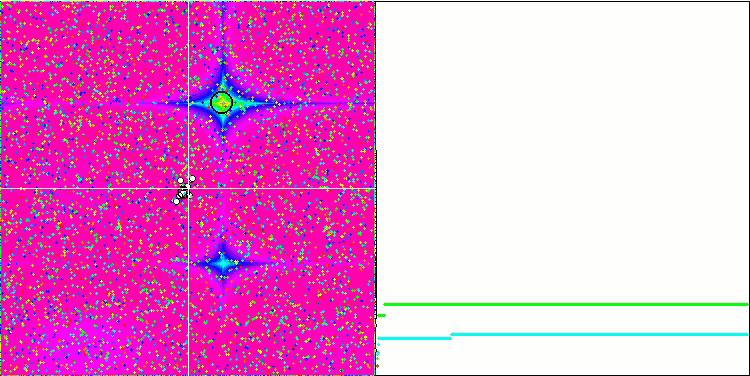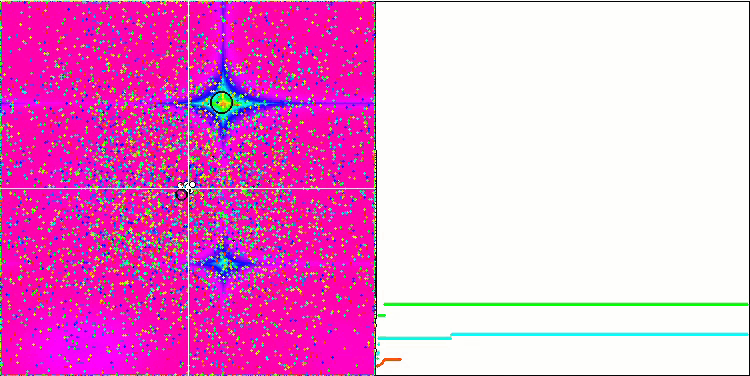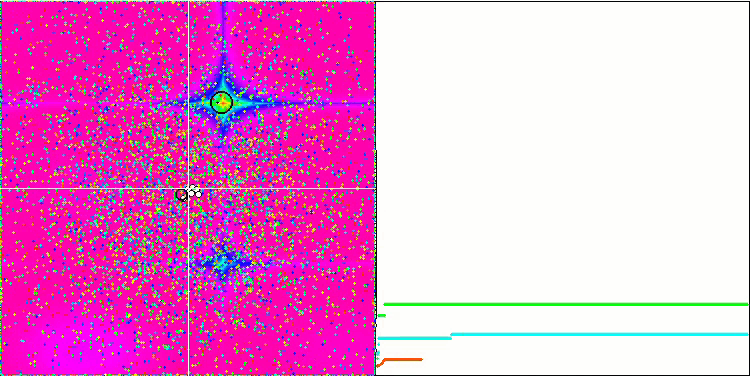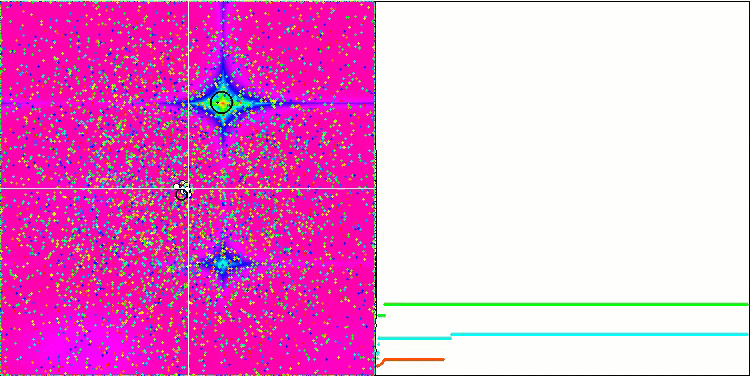
  Forest test fonksiyonu üzerinde GSA

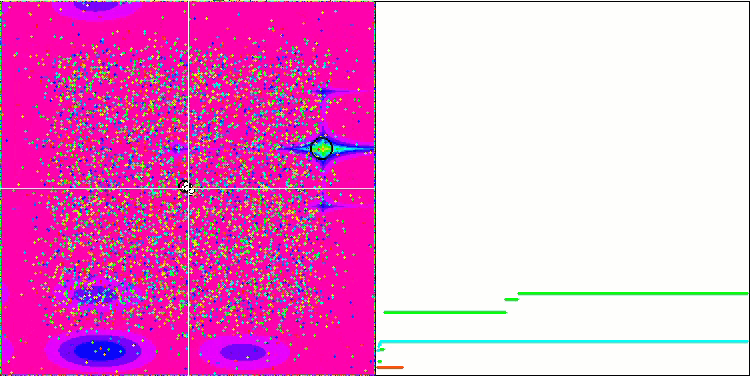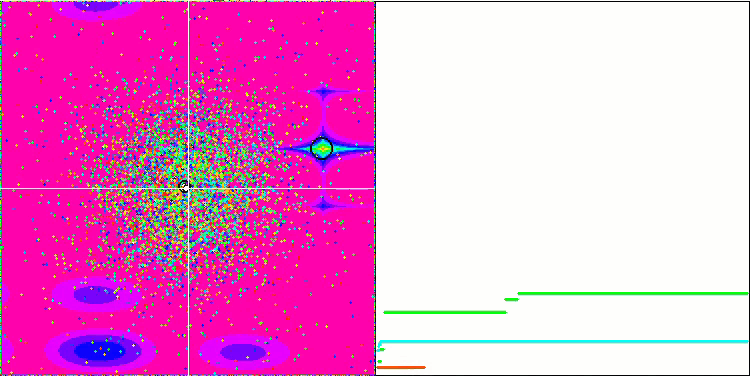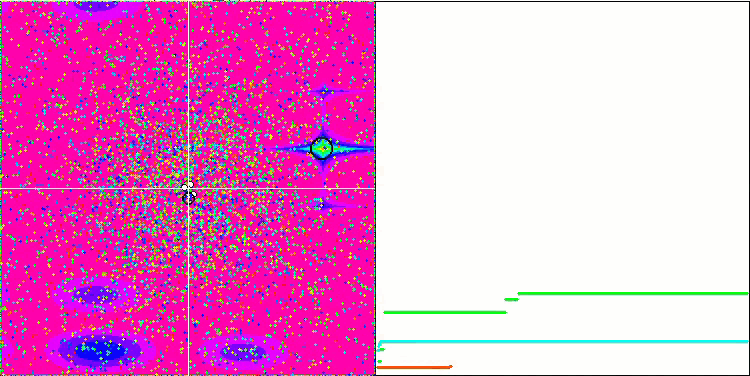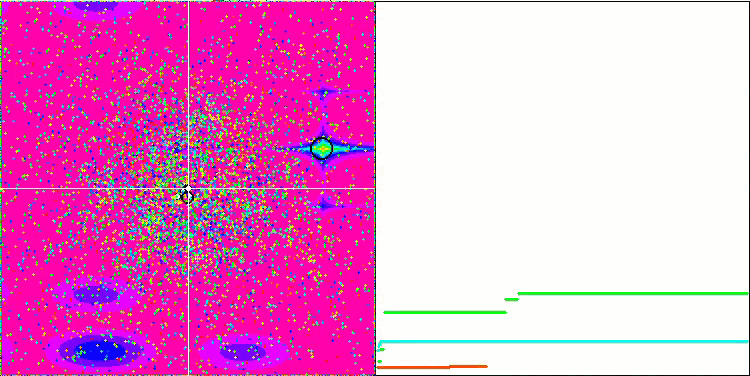
Megacity test fonksiyonu üzerinde GSA

GSA ile yaptığım birçok deneyden sonra, uzay nesnelerinin hareketini simüle eden bir simülatör yapma fikri aklıma geldi. Pratik bir değeri yoktur, ancak gezegen ve yıldız sistemleri üzerinde etkili olan fiziksel yasalar hakkında bir fikir veriyor. Simülatör, GSA'nın rastgelelik özelliği devre dışı bırakılmış bir versiyonudur. Ayrıca, üç yıldızı taklit eden üç nesne (bir mavi dev, bir sarı yıldız ve bir beyaz cüce) tanıtılmıştır. Kütle parametreleri, bunlar için ayarlarda ayrı olarak görüntülenmektedir.

Simülatör için özel olarak tekdüze bir uzaya sahip yeni bir Universe uygunluk fonksiyonu oluşturulmuştur. Simülatör, nesneler arasındaki mesafenin derecesinin (parametre) karşılıklı hareketlerini nasıl etkilediğini açıkça göstermektedir. Aşağıdaki görselleştirmede, Newton yasasının standart değeri olan 2 yerine 3'ün kuvveti uygulanmıştır. Derecenin, çift ve üçlü yıldız sistemleri gibi kütleçekimsel olarak bağlı sistemlerin oluşumunu nasıl etkilediği netleşmektedir.

Eğer evrenimizde uzaklık derecesi daha yüksek olsaydı, o zaman galaksiler gerçekte olduğundan çok daha önce oluşurdu. Animasyon, ortak bir kütle merkezi etrafında dolaşan eşleştirilmiş nesnelerin ilk yinelemelerde ortaya çıktığını açıkça göstermektedir. Beklendiği gibi, mavi dev etrafındaki en çok nesneyi topladı.

GSA algoritmasına dayalı uzay nesneleri hareket simülatörünün görselleştirmesi

GSA test sonuçlarının analizine geçelim. Algoritmada kullanılan orijinal özellikler, testlerimizde güçlü sonuçlar elde etmesine izin vermedi. Denediğim parametrelerin çok sayıda varyasyonu algoritmanın yakınsamasını iyileştirmedi. Algoritma, 10 değişkenli Rastrigin ve Megacity fonksiyonu üzerinde diğer test katılımcılarına göre bazı olumlu sonuçlar göstermiştir. Diğer testlerde GSA, 12 algoritmanın arasında 8. sırada yer alarak tabloda ortalamanın altında bir performans sergilemiştir.

AO	Açıklama	Rastrigin			Rastrigin için nihai sonuç	Forest			Forest için nihai sonuç	Megacity (ayrık)			Megacity için nihai sonuç	Nihai sonuç
		10 parametre (5 F)	50 parametre (25 F)	1000 parametre (500 F)		10 parametre (5 F)	50 parametre (25 F)	1000 parametre (500 F)		10 parametre (5 F)	50 parametre (25 F)	1000 parametre (500 F)
IWO	İstilacı yabancı ot optimizasyonu	1.00000	1.00000	0.35295	2.35295	0.79937	0.46349	0.41071	1.67357	0.75912	0.44903	0.94416	2.15231	100.000
ACOm	Karınca kolonisi optimizasyonu (m)	0.36118	0.26810	0.20182	0.83110	1.00000	1.00000	1.00000	3.00000	1.00000	1.00000	0.15901	2.15901	96.805
COAm	Guguk kuşu optimizasyon algoritması (m)	0.96423	0.69756	0.30792	1.96971	0.64504	0.34034	0.21362	1.19900	0.67153	0.34273	0.48451	1.49877	74.417
FAm	Ateş böceği algoritması (m)	0.62430	0.50653	0.20290	1.33373	0.55408	0.42299	0.64360	1.62067	0.21167	0.28416	1.00000	1.49583	70.740
BA	Yarasa algoritması	0.42290	0.95047	1.00000	2.37337	0.17768	0.17477	0.33595	0.68840	0.15329	0.07158	0.49268	0.71755	59.383
ABC	Yapay arı kolonisi	0.81573	0.48767	0.24656	1.54996	0.58850	0.21455	0.17249	0.97554	0.47444	0.26681	0.39496	1.13621	57.393
BFO	Bakteri yiyecek arama optimizasyonu	0.70129	0.46155	0.13988	1.30272	0.41251	0.26623	0.26695	0.94569	0.42336	0.34491	0.53694	1.30521	55.563
GSA	Yerçekimsel arama algoritması	0.73222	0.67404	0.00000	1.40626	0.31238	0.36416	0.42921	1.10575	0.51095	0.36658	0.00000	0.87753	52.786
FSS	Balık sürüsü arama	0.48850	0.37769	0.13383	1.00002	0.78060	0.05013	0.08423	0.91496	0.00000	0.01084	0.23493	0.24577	20.094
PSO	Parçacık sürüsü optimizasyonu	0.21339	0.12224	0.08478	0.42041	0.15345	0.10486	0.28099	0.53930	0.08028	0.02385	0.05550	0.15963	14.358
RND	Rastgele	0.17559	0.14524	0.09495	0.41578	0.08623	0.04810	0.06094	0.19527	0.00000	0.00000	0.13960	0.13960	8.117
GWO	Gri kurt optimizasyonu	0.00000	0.00000	0.02672	0.02672	0.00000	0.00000	0.00000	0.00000	0.18977	0.04119	0.07252	0.30348	1.000

Genel olarak, GSA algoritması optimize edilen fonksiyonda bir gradyanın varlığına karşı belirgin bir şekilde hassastır. Düşük ölçeklenebilirlik, çok sayıda değişken içeren ciddi görevler için kullanılmasına izin vermez, bu nedenle algoritmayı sinir ağları ile kullanım ve alım-satım sistemlerini optimize etmek için tavsiye etmem. Yerçekimsel arama algoritmasının olanaklarını tam olarak incelemedim. Ek araştırmalar, bu çok ilginç ve alışılmadık algoritmanın bilinmeyen yeni olumlu özelliklerini ortaya çıkarabilir. Algoritmanın temel avantajları, mevcut en iyi bulunan global çözümden bağımsız olması ve tüm temsilcilerin birbirleriyle etkileşime girebilmesidir. 

Şekil 2 algoritmanın test sonuçlarını göstermektedir

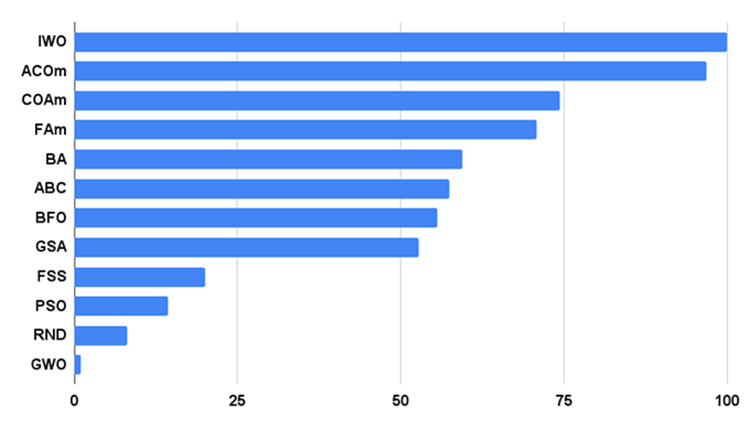
Şekil 2. Algoritmaların test sonuçlarının histogramı

Yerçekimsel arama algoritmasının (GSA) özelliklerine ilişkin sonuçlar:

Avantajları:
1. Kolay uygulama.
2. Az değişkenli düzgün fonksiyonlarda iyi performans.

Dezavantajları:
1. Yüksek hesaplama karmaşıklığı.
2. Ayrık fonksiyonlar üzerinde zayıf sonuçlar.
3. Kötü ölçeklenebilirlik.