MetaTrader 5 / 예
English Русский 中文 Español Deutsch 日本語 Português Français Italiano Türkçe
preview
모집단 최적화 알고리즘: 중력 검색 알고리즘(Gravitational Search Algorithm;GSA)

모집단 최적화 알고리즘: 중력 검색 알고리즘(Gravitational Search Algorithm;GSA)

MetaTrader 5 — 예 |
244 0
Andrey Dik
Andrey Dik

콘텐츠

1. 소개
2. 알고리즘
3. 테스트 결과


1. 소개

중력 검색 알고리즘(GSA)은 뉴턴의 중력 법칙의 원리에 따라 최적화 문제, 특히 비선형 문제를 해결하기 위해 E. 라쉬디가 제안한 알고리즘입니다. 이 알고리즘에서는 파티클을 오브젝트로 간주하고 질량을 고려하여 파티클들의 성능을 추정합니다. 중력은 질량이 서로를 향해 가속하는 경향을 말합니다. 중력은 자연의 네 가지 기본 힘 중 하나입니다(다른 힘은 전자기력, 약한 핵력, 강한 핵력입니다).

우주의 모든 입자는 다른 모든 입자를 끌어당깁니다. 중력은 어디에나 존재합니다. 중력은 가장 약한 힘이지만 가장 눈에 잘 띄는 힘입니다. 중력 덕분에 사람은 지구의 위에서 걸을 수 있고 행성은 태양의 궤도를 돌 수 있습니다. 모든 객체의 중력은 질량에 비례합니다. 따라서 질량이 큰 객체는 중력이 더 큽니다. 중력의 필연성은 중력을 다른 모든 자연의 힘과 구별합니다. 뉴턴의 중력이 작용하는 방식을 원거리에서의 작용이라고 합니다. 이는 아이작 뉴턴이 귀납적 추론이라고 부르는 방법으로 경험적 관찰을 통해 추론한 일반적인 물리 법칙입니다. 1687년 7월 5일에 처음 출판된 뉴턴의 『Philosophiae Naturalis Principia Mathematica』(Principia)에서 공식화된 고전 역학의 일부입니다.

1686년 4월 뉴턴이 왕립학회에 최초의 미공개 저서를 발표했을 때 로버트 후크는 뉴턴이 그에게서 역제곱 법칙을 받았다고 주장했습니다. 오늘날의 언어로 말하면 모든 점 질량은 두 점을 교차하는 선을 따라 작용하는 힘에 의해 다른 모든 점 질량을 끌어당긴다는 법칙입니다.


2. 알고리즘

이 기사에서는 뉴턴의 만유인력의 법칙에 기반한 최적화 알고리즘을 소개합니다: "우주의 모든 입자는 질량의 곱에 정비례하고 입자 사이의 거리의 제곱에 반비례하는 힘으로 다른 모든 입자를 끌어당깁니다." 이 알고리즘에서 검색 에이전트는 뉴턴의 중력과 운동 법칙에 따라 서로 상호 작용하는 질량 집합입니다. 동시에 모든 에이전트는 질량(목적 함수의 값으로 계산된 값)과 에이전트 간의 거리에 따라 달라지는 인력을 통해 검색 공간의 어느 위치에 있든 서로 정보를 교환할 수 있습니다.

에이전트는 객체로 취급되며 에이전트의 체력은 이들 에이전트의 질량으로 측정됩니다. 일반적으로 (실제 물리 법칙에 가까운 알고리즘 설정으로) 이러한 모든 객체는 중력에 의해 서로 끌어당겨지며 이러한 힘은 모든 객체가 질량이 더 큰 객체를 향해 전체적으로 움직이게 합니다. 따라서 질량은 중력을 통한 직접적인 형태의 연결을 통해 상호 작용합니다.

기존 GSA에서 각 파티클은 세 가지 종류의 질량을 가집니다:

a) 활성 질량
b) 비활성 질량
c) 관성 질량

대부분의 경우 이러한 개념의 동등성을 사용하여 코드와 계산을 단순화하고 알고리즘 검색 기능의 효율성을 높이는 것이 편리하고 빠릅니다. 따라서 알고리즘에는 3개가 아닌 하나의 질량이 있습니다. GSA에서 사용되는 물리 법칙 방정식은 그림 1에 나와 있습니다.


공식

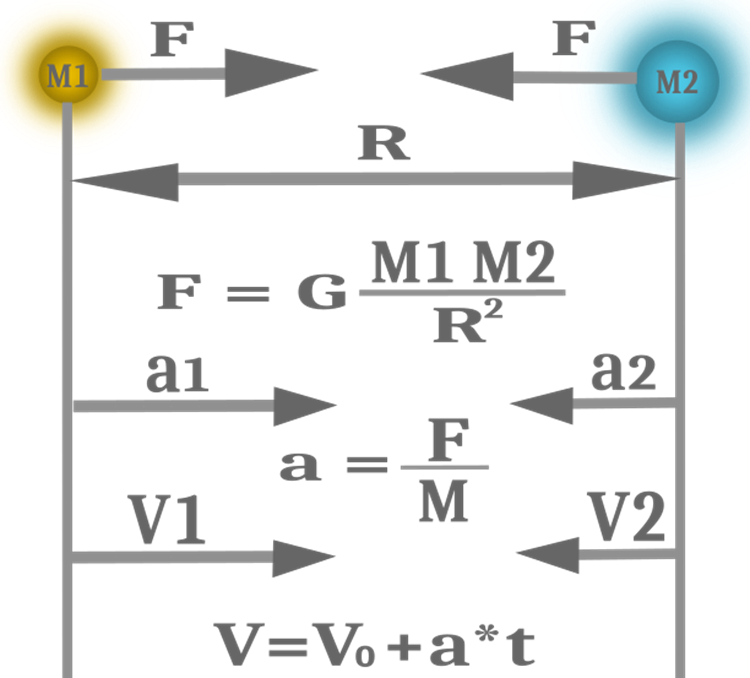
그림 1. 중력, 가속도 및 속도



입자의 위치는 문제에 대한 해결책을 제공하며 적합도 함수는 질량을 계산하는 데 사용됩니다. 알고리즘은 탐색과 개척의 두 단계로 구성됩니다. 이 알고리즘은 처음에는 인텔리전스 기능을 사용하여 로컬 최적값에 갇히지 않도록 하고 그 이후에는 극한 영역을 개척합니다.

중력 검색 알고리즘은 우주에서 움직이는 입자를 특정 질량을 가진 객체로 바꿔야 합니다. 이러한 객체는 서로 중력 상호작용으로 인해 끌어당겨지며 우주의 모든 입자는 입자의 상호 인력으로 인해 가속도를 생성하며 서로 끌어당기게 됩니다. 각각의 입자는 다른 입자에 이끌려 힘의 방향으로 이동합니다. 질량이 작은 입자는 질량이 큰 입자를 향해 이동하지만 질량이 큰 객체도 질량에 반비례하는 낮은 속도로 이동합니다. 최적의 솔루션은 더 빠르게 움직이는 '작은' 객체에 비해 저속으로 이동하여 솔루션을 구체화하는 '큰' 객체에 의해 찾아집니다. GSA는 객체 간의 상호 작용을 통해 정보의 전송을 구현합니다.

GSA 단계:

1. 에이전트 초기화
2. 피트니스의 진화
3. 중력 상수 계산
4. 에이전트 질량 계산


1. 에이전트 초기화.
모든 에이전트는 무작위로 초기화됩니다. 각 에이전트는 후보 솔루션으로 간주됩니다. 안정성 분석이 의미 있고 신뢰할 수 있으려면 평형 초기 조건을 지정하는 것이 매우 중요합니다. 결국 객체의 원래 '원반'이 평형을 이루지 못하면 시뮬레이션의 첫 번째 단계에서 이완으로 인해 우리의 '원반 은하'의 안정성에 대한 이해에 그리 중요하지 않은 불안정성이 발생할 수 있습니다. 안타깝게도 암흑 물질 후광 및/또는 항성 원반의 외부 전위에서 정수 평형 상태의 3차원 기체 원반의 밀도, 속도장 및 온도에 대한 분석 솔루션은 알려져 있지 않습니다.

2. 피트니스의 진화.
GSA의 신뢰성과 효과는 연구와 개척 능력 간의 균형에 달려 있습니다. 솔루션 검색 프로세스의 초기 반복에서는 검색 공간을 탐색하는 것이 우선시됩니다. 이는 에이전트가 초기 반복에서 큰 스텝 크기를 사용할 수 있도록 허용함으로써 달성할 수 있습니다. 이후 반복에서는 글로벌 최적값이 누락되는 상황을 피하기 위해 검색 공간을 세분화해야 합니다. 따라서 후보 솔루션은 후속적인 반복에 사용될 수 있는 작은 단계 크기를 가져야 합니다.

3. 중력 상수 계산.
문자 G로 표시되는 중력 상수(만유인력의 상수, 뉴턴 중력 상수 또는 캐번디시 중력 상수라고도 함)는 아이작 뉴턴의 만유인력의 법칙과 알버트 아인슈타인의 일반 상대성 이론에서 중력 효과의 계산에 관련된 경험적 물리 상수입니다. 뉴턴의 법칙에서 비례 상수는 두 객체 사이의 중력을 질량의 곱과 거리의 역제곱으로 연결한 값입니다. 아인슈타인 필드 방정식에서는 시공간 기하학과 에너지-모멘텀 텐서 사이의 관계를 정량화 합니다.

4. 에이전트 질량의 계산.
질량은 우주에 존재하는 물질의 양입니다.

알고리즘 의사 코드:

1. 무작위로 객체 시스템을 생성합니다.
2. 각 객체의 적합성을 결정합니다.
3. 중력 상수 값을 업데이트하고 질량, 최고 및 최악의 객체를 계산합니다.
4. 각 좌표에 작용하는 힘의 계산.
5. 객체의 가속도 및 속도 계산.
6. 객체의 위치 업데이트.
7. 각 객체의 적합성을 결정합니다.
8. 종료 기준이 충족될 때까지 3페이지부터 반복합니다.

GSA 코드를 살펴보겠습니다. 중력 상호작용 시스템에서 객체를 설명하려면 중력 검색을 수행하기에 충분한 객체의 모든 필요한 물리적 속성을 설명하는 S_Object 구조가 필요합니다: c [] - 검색 공간의 좌표, v [] - 각 좌표의 속도 벡터(배열 차원은 좌표의 수), M은 객체 질량(GSA에서 질량은 상대값으로, 전체 객체 시스템에 대한 최대 및 최소 적합성 값에 따라 계산된 값입니다), f는 적합도 값, R[]은 다른 객체와의 유클리드 거리(배열의 차원은 객체의 수), F[]는 각 좌표에 대한 힘의 벡터(배열의 차원은 좌표의 수), F []는 각 좌표에 대한 힘의 벡터(배열의 차원은 좌표의 수)입니다. 

//——————————————————————————————————————————————————————————————————————————————
struct S_Object
{
  double c  [];   //coordinates
  double v  [];   //velocity
  double M;       //mass
  double f;       //fitness
  double R  [];   //euclidean distance to other objects
  double F  [];   //force vector
};
//——————————————————————————————————————————————————————————————————————————————

중력 검색 알고리즘 C_AO_GSA의 클래스를 선언해 보겠습니다. 알고리즘에 에이전트로 참여하는 객체의 물리적 속성 중 가장 좋은 솔루션을 나타내는 좌표, 즉 fB 값 한 가지만 필요합니다. 이 클래스는 검색 공간의 좌표와 단계의 유효한 범위를 선언합니다. 중력적으로 결합된 객체 시스템은 S_Object 구조의 배열로 표현됩니다. 기존 알고리즘에는 외부 파라미터가 세 개뿐입니다: 객체의 중력 상호작용의 특성을 결정하는 G_상수, a_상수, e_상수와 나머지 상수는 계산 방정식에 포함되어 있지만 저는 이 상수를 알고리즘의 외부 파라미터로 이동하여 알고리즘 전체의 특성을 보다 유연하게 조정할 수 있도록 하는 것이 적절하다고 판단했습니다. 모든 매개 변수는 알고리즘의 동작에 큰 영향을 미치기 때문에 나중에 좀 더 자세히 살펴보겠습니다. 

//——————————————————————————————————————————————————————————————————————————————
class C_AO_GSA
{
  //----------------------------------------------------------------------------
  public: S_Object o       []; //object
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search
  public: double cB        []; //best coordinates
  public: double fB;           //FF of the best coordinates

  public: void Init (const int    coordinatesNumberP, //coordinates number
                     const int    objectsNumberP,     //objects number
                     const double PowerOfdistanceP,   //power of distance
                     const double GraviPert_MinP,     //gravitational perturbation Min
                     const double GraviPert_MaxP,     //gravitational perturbation Min
                     const double VelocityPert_MinP,  //Velocity perturbation Min
                     const double VelocityPert_MaxP,  //Velocity perturbation Max
                     const double G_constantP,        //G constant
                     const double a_constantP,        //a constant
                     const double e_constantP,        //e constant
                     const int    maxIterationsP);    //max Iterations

  public: void Moving   (int iter);
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coordinatesNumber; //coordinates number
  private: int    objectsNumber;     //objects number
  private: double PowerOfdistance;   //power of distance
  private: double GraviPert_Min;     //gravitational perturbation Min
  private: double GraviPert_Max;     //gravitational perturbation Min
  private: double VelocPert_Min;     //velocity perturbation Min
  private: double VelocPert_Max;     //velocity perturbation Max
  private: double G_constant;        //G constant
  private: double a_constant;        //a constant
  private: double e_constant;        //e constant
  private: int    maxIterations;
  private: bool   revision;

  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
  private: double Scale     (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers);
};
//——————————————————————————————————————————————————————————————————————————————

Init () 알고리즘의 공용 메서드는 서비스 변수를 초기화하고 배열에 크기를 할당하기 위해 알고리즘의 외부 파라미터를 내부 상수로 전달하기 위한 것으로

//——————————————————————————————————————————————————————————————————————————————
void C_AO_GSA::Init (const int    coordinatesNumberP, //coordinates number
                     const int    objectsNumberP,     //objects number
                     const double PowerOfdistanceP,   //power of distance
                     const double GraviPert_MinP,     //gravitational perturbation Min
                     const double GraviPert_MaxP,     //gravitational perturbation Min
                     const double VelocityPert_MinP,  //Velocity perturbation Min
                     const double VelocityPert_MaxP,  //Velocity perturbation Max
                     const double G_constantP,        //G constant
                     const double a_constantP,        //a constant
                     const double e_constantP,        //e constant
                     const int    maxIterationsP)     //max Iterations
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coordinatesNumber = coordinatesNumberP;
  objectsNumber     = objectsNumberP;
  PowerOfdistance   = PowerOfdistanceP;
  GraviPert_Min     = GraviPert_MinP;
  GraviPert_Max     = GraviPert_MaxP;
  VelocPert_Min     = VelocityPert_MinP;
  VelocPert_Max     = VelocityPert_MaxP;
  G_constant        = G_constantP;
  a_constant        = a_constantP;
  e_constant        = e_constantP;
  maxIterations     = maxIterationsP;

  ArrayResize (rangeMax,  coordinatesNumber);
  ArrayResize (rangeMin,  coordinatesNumber);
  ArrayResize (rangeStep, coordinatesNumber);

  ArrayResize (o,  objectsNumber);

  for (int i = 0; i < objectsNumber; i++)
  {
    ArrayResize (o [i].c,  coordinatesNumber);
    ArrayResize (o [i].v,  coordinatesNumber);
    ArrayResize (o [i].R,  objectsNumber);
    ArrayResize (o [i].F,  coordinatesNumber);
    o [i].f  = -DBL_MAX;
  }

  ArrayResize (cB, coordinatesNumber);
}
//——————————————————————————————————————————————————————————————————————————————

Moving () 반복의 각 반복에서 호출되는 첫 번째 공개 메서드입니다. 이 메서드에는 GSA 알고리즘의 모든 물리학과 로직이 포함되어 있습니다. 상당히 크므로 여러 부분으로 나누어 살펴 보겠습니다. 이 메서드는 현재 반복을 매개변수로 사용하며 이 매개변수는 중력 상수 계산에 관여하여 연구와 개척 간의 균형을 조정합니다.

첫 번째 반복에서는 객체 초기화 단계가 일어납니다. 객체의 모든 좌표에 대해 허용 범위 내의 임의 값을 균일한 분포로 할당하고 범위를 벗어나는지 확인합니다. 최적화 프로세스가 시작될 때 모든 객체의 속도는 0의 값입니다. 즉 좌표에 대해 검색 공간에서 객체가 움직이지 않는 상태입니다. 객체는 질량이 없으므로 빛의 속도로 움직여야 하지만 이 순간은 어느 정도는 빅뱅과 동일하기 때문에 첫 번째 반복에서는 물리 법칙을 깨뜨릴 것입니다. 이 순간 객체의 적합도는 '더블' 수의 가능한 값 중 가장 작은 값입니다. 알고리즘을 디버깅할 때 저는 제로 질량과 관련된 버그를 찾기가 어려웠는데 여러분은 아래에서 그 해결책을 확인할 수 있습니다.

//----------------------------------------------------------------------------
if (!revision)
{
  fB = -DBL_MAX;

  for (int obj = 0; obj < objectsNumber; obj++)
  {
    for (int c = 0; c < coordinatesNumber; c++)
    {
      o [obj].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      o [obj].c [c] = SeInDiSp (o [obj].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      o [obj].v [c] = 0.0;
      o [obj].M     = 0.0;
      o [obj].f     = -DBL_MAX;
    }
  }

  revision = true;
}

Moving () 메서드의 나머지 코드는 객체가 질량, 속도 및 가속도를 얻는 두 번째 및 후속 반복을 참조합니다.

우선 질량을 계산해야 합니다. 위에서 언급했듯이 객체의 질량(정의상 양의 스칼라 값)은 적합도 함수 값으로부터 계산되므로 얻은 값을 바탕으로 질량을 계산하기 전에 최소 및 최대 적합도 값을 결정해야 합니다. 이 시점에서는 이전 반복에서 이미 적합도 함수의 값을 구한 상태입니다.

//find the minimum and maximum fitness==========================================
for (int obj = 0; obj < objectsNumber; obj++)
{
  if (o [obj].f < Fmin) Fmin = o [obj].f;
  if (o [obj].f > Fmax) Fmax = o [obj].f;
}

코드의 이 시점에서 질량은 Mo=(Fo-Fmin)/(Fmax-Fmin) 방정식을 사용하여 계산되며 여기서 질량은 다음과 같습니다:

  • Mo - 객체 질량
  • Fo - 객체 피트니스
  • Fmax - 모든 객체 중 최대 적합도 값(최고 값)
  • Fmin - 모든 객체 중 최소 적합도 값(최악의 값)

방정식에서 볼 수 있듯이 질량은 0에서 1까지의 범위에서 양수 값만 취할 수 있습니다. 질량이 0이 아니어야 속도가 빛의 속도와 같은 것이라고 앞서 살펴 보았습니다. 그러므로 질량의 하한을 0.1로 제한합니다. 상한값은 1과 같을 수 있습니다. 또한 적합도 함수의 최소값과 최대값이 같으면 모든 객체의 질량은 모두 동일하며 1과 같다는 점에 유의하세요. 이는 검색 공간이 객체가 위치한 영역에서 균질하고 모든 객체가 적합도 함수의 품질 측면에서 동일하며 어떤 방향으로의 이동에서도 동일한 우선순위를 갖는 경우에 해당합니다. 이 경우 모든 객체는 점차적으로 이동하여 공통 질량 중심으로 집중해야 하지만 중력의 비선형 작용으로 인해 이런 일이 발생하지 않습니다.

//calculating the mass of objects===========================================
for (int obj = 0; obj < objectsNumber; obj++)
{
  Fo = o [obj].f;
  if (Fmax == Fmin) Mo = 1.0;
  else Mo = (Fo - Fmin) / (Fmax - Fmin);
  o [obj].M = Scale (Mo, 0.0, 1.0, 0.1, 1.0, false);
}

우리는 객체의 질량을 계산했습니다. 이제 R 방정식의 구성 요소인 각 객체에서 다른 모든 객체까지의 유클리드 거리를 더 계산해야 합니다. 계산은 객체를 열거하는 두 번의 사이클과 각 좌표에 대한 계산 주기로 구성됩니다. 기억하시겠지만 유클리드 거리는 좌표 차이의 제곱의 합의 근입니다.

//calculation of Euclidean distances between all objects====================
for (int obj = 0; obj < objectsNumber; obj++) ArrayInitialize (o [obj].R, 0.0);

for (int obj = 0; obj < objectsNumber; obj++)
{
  for (int obj2 = 0; obj2 < objectsNumber; obj2++)
  {
    if (obj != obj2)
    {
      if (o [obj].R [obj2] == 0.0)
      {
        for (int c = 0; c < coordinatesNumber; c++)
        {
          diffDist = o [obj].c [c] - o [obj2].c [c];
          o [obj].R [obj2] += diffDist * diffDist;
        }

        o [obj].R [obj2] = sqrt (o [obj].R [obj2]);
        o [obj2].R [obj] = o [obj].R [obj2];
      }
    }
  }
}

이제 객체에 대한 힘 벡터를 계산할 수 있습니다. 이렇게 하려면 각 좌표에 대해 속도가 개별적으로 계산되므로 우리는 모든 객체를 두 주기로, 좌표는 한 주기로 하도록 하는 과정을 거쳐야 합니다. 객체 인덱스의 우연성을 배제하는 조건을 추가하여야 합니다. 이를 통해 객체가 힘 계산에서 객체 자체의 계산을 제외하도록 해야 합니다. 여기서는 잘 알려진 뉴턴의 방정식을 사용하여 두 객체에 대한 중력을 계산하고(그림 1) e_constant 비율로 거리를 보정합니다. 먼저 최적화가 끝날 때까지 알고리즘이 강화된다고 가정하고 각 반복마다 아래 방향으로 변경되어야 하는 중력 상수 G를 계산해 보겠습니다.

//calculate the force vector for each object================================
for (int obj = 0; obj < objectsNumber; obj++) ArrayInitialize (o [obj].F, 0.0);

double G = G_constant * exp (-a_constant * (iter / maxIterations));

for (int obj = 0; obj < objectsNumber; obj++)
{
  for (int obj2 = 0; obj2 < objectsNumber; obj2++)
  {
    if (obj != obj2)
    {
      for (int c = 0; c < coordinatesNumber; c++)
      {
        diffDist = o [obj2].c [c] - o [obj].c [c];

        if (o [obj].R [obj2] != 0.0)
        {
          o [obj] .F [c] += G * o [obj].M * o [obj2].M * diffDist / (pow (o [obj].R [obj2], PowerOfdistance) + e_constant);
        }
      }
    }
  }
}

이제 객체가 움직이기 시작하기 위한 속도만 계산하면 됩니다. 그림 1의 방정식에서 속도 계산에는 가속도가 포함되며 가속도는 객체에 작용하는 힘을 질량으로 나눈 값입니다. 이 방정식에는 시간 V=V0+a*t도 포함되어 있습니다. 우리의 알고리즘에서 반복은 시간의 역할을 하므로 속도 변화는 한 번의 반복에서 속도가 증가하는 것에 지나지 않습니다. 속도 벡터는 이미 위에서 계산했습니다. 이를 질량으로 나누기만 하면 됩니다. 또한 저자는 힘 섭동과 속도 섭동에 대해서도 소개합니다. 섭동은 0과 1 사이에 균일하게 분포된 난수입니다. 이렇게 하면 객체의 움직임에 무작위 요소가 추가되어 움직임이 엄격하게 결정되고 몸체의 초기 위치에만 의존하게 됩니다. 저는 섭동 지표를 알고리즘의 외부 파라미터로 가져와 객체의 움직임을 완전히 결정론적인 것에서 완전히 무작위로 조절할 수 있도록 하는 것이 합리적이라고 생각했습니다.

//calculation of acceleration and velocity for all objects==================
double a = 0.0; //acceleration

for (int obj = 0; obj < objectsNumber; obj++)
{
  for (int c = 0; c < coordinatesNumber; c++)
  {
    r = RNDfromCI (GraviPert_Min, GraviPert_Max);
    a = o [obj].F [c] * r / o [obj].M;
    r = RNDfromCI (GraviPert_Min, GraviPert_Max);
    o [obj].v [c] = o [obj].v [c] * r + a;
    o [obj].c [c] = o [obj].c [c] + o [obj].v [c];

    if (o [obj].c [c] > rangeMax [c]) o [obj].c [c] = rangeMin [c];
    if (o [obj].c [c] < rangeMin [c]) o [obj].c [c] = rangeMax [c];

    o [obj].c [c] = SeInDiSp (o [obj].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}

두 번째 Revision () 메서드는 각 반복마다 실행해야 하는 필수 메서드입니다. 이 메서드는 현재 반복에 가장 맞는 적합도 값을 결정하도록 설계되었습니다. 루프에서 모든 객체를 살펴보고 글로벌 최적 솔루션을 교체합니다. 

//——————————————————————————————————————————————————————————————————————————————
void C_AO_GSA::Revision ()
{
  for (int s = 0; s < objectsNumber; s++)
  {
    if (o [s].f > fB)
    {
      fB = o [s].f;
      ArrayCopy (cB, o [s].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————


3. 테스트 결과

테스트 결과로 넘어가 보겠습니다. 아래는 제가 찾을 수 있는 최고의 GSA 매개변수를 사용한 테스트 스탠드 결과입니다:

2023.02.03 14:12:43.440 Test_AO_GSA (EURUSD,M1) C_AO_GSA:10;2.0;0.2;0.6;0.0;1.0;2.0;20.0;0.01
2023.02.03 14:12:43.440 Test_AO_GSA (EURUSD,M1) =============================
2023.02.03 14:12:52.198    Test_AO_GSA (EURUSD,M1)    5 Rastrigin's; Func runs 10000 result: 73.64619475145881
2023.02.03 14:12:52.198    Test_AO_GSA (EURUSD,M1)    Score: 0.91252
2023.02.03 14:13:06.105    Test_AO_GSA (EURUSD,M1)    25 Rastrigin's; Func runs 10000 result: 59.4327218024363
2023.02.03 14:13:06.105    Test_AO_GSA (EURUSD,M1)    Score: 0.73640
2023.02.03 14:14:16.529    Test_AO_GSA (EURUSD,M1)    500 Rastrigin's; Func runs 10000 result: 37.550565227034724
2023.02.03 14:14:16.529    Test_AO_GSA (EURUSD,M1)    Score: 0.46527
2023.02.03 14:14:16.529 Test_AO_GSA (EURUSD,M1) =============================
2023.02.03 14:14:30.577    Test_AO_GSA (EURUSD,M1)    5 Forest's; Func runs 10000 result: 0.741456333008312
2023.02.03 14:14:30.577    Test_AO_GSA (EURUSD,M1)    Score: 0.41941
2023.02.03 14:14:50.281    Test_AO_GSA (EURUSD,M1)    25 Forest's; Func runs 10000 result: 0.46894018717768426
2023.02.03 14:14:50.282    Test_AO_GSA (EURUSD,M1)    Score: 0.26526
2023.02.03 14:16:01.856    Test_AO_GSA (EURUSD,M1)    500 Forest's; Func runs 10000 result: 0.11382493516764165
2023.02.03 14:16:01.856    Test_AO_GSA (EURUSD,M1)    Score: 0.06439
2023.02.03 14:16:01.856 Test_AO_GSA (EURUSD,M1) =============================
2023.02.03 14:16:18.195    Test_AO_GSA (EURUSD,M1)    5 Megacity's; Func runs 10000 result: 5.279999999999999
2023.02.03 14:16:18.195    Test_AO_GSA (EURUSD,M1)    Score: 0.44000
2023.02.03 14:16:34.536    Test_AO_GSA (EURUSD,M1)    25 Megacity's; Func runs 10000 result: 2.296
2023.02.03 14:16:34.536    Test_AO_GSA (EURUSD,M1)    Score: 0.19133
2023.02.03 14:17:46.887    Test_AO_GSA (EURUSD,M1)    500 Megacity's; Func runs 10000 result: 0.23399999999999999
2023.02.03 14:17:46.887    Test_AO_GSA (EURUSD,M1)    Score: 0.01950

알고리즘 매개변수:

input double PowerOfdistance_P  = 2.0;   //거리의 거듭제곱
input double GraviPert_Min_P    = 0.2;   //중력 섭동 최소값
input double GraviPert_Max_P = 0.6; //중력 섭동 최대값
input double VelocityPert_Min_P = 0.0; //속도 섭동 최소값
input double VelocityPert_Max_P = 1.0; //속도 섭동 최대값
input double G_constant_P       = 2.0;   //G 상수
input double a_constant_P       = 20.0;  //a 상수
input double e_constant_P       = 0.01;  //e 상수

PowerOfdistance_P - 객체 사이의 거리를 높이는 정도는 중력적으로 결합된 객체의 형성에 영향을 줍니다. 방정식의 정도가 높을수록 객체들이 서로 다른 객체에 미치는 영향이 줄어듭니다.

  • GraviPert_Min_P - 중력 섭동 범위의 하한입니다.
  • GraviPert_Max_P - 중력 섭동 범위의 상한입니다.
  • GraviPert_Min_P이 1.0, GraviPert_Max_P이 1.0인 경우 중력 교란이 없습니다.
  • VelocityPert_Min_P - 속도 섭동 범위의 하한입니다.
  • VelocityPert_Max_P - 속도 섭동 범위의 상한입니다.

VelocityPert_Min_P = 1.0 및 VelocityPert_Max_P = 1.0의 경우 속도 섭동이 없습니다.

  • G_constant_P - 중력 상수는 척도로 작용하며 값이 높을수록 중력이 더 강하게 작용하고 객체의 속도가 더 빠르게 변화합니다.
  • a_constant_P - 발견된 극한값을 구체화하기 위해 전체 최적화 중에 검색 필드를 줄이기 위해 설계된 중력 상수 보정 계수입니다.
  • e_constant_P - 객체 간 거리에 대한 보정 계수입니다.

시각화 테스트 결과를 살펴보겠습니다. 테스트 함수에서 알고리즘의 동작은 매우 독특하고 흥미롭습니다. 이 실험은 실제로 중력의 작용을 보여줍니다. 객체의 움직임과 얻어진 최적화 결과는 알고리즘의 외부 매개변수에 의해 크게 영향을 받습니다. 처음에는 속도가 0인 객체들이 검색 공간에 무작위로 분포되어 있고 다음 반복에서 부터 움직이기 시작합니다. 테스트에 사용된 설정(제가 찾은 가장 좋은 설정)은 객체들이 공통 질량 중심을 향해 움직이게 합니다.

각 객체의 중력은 다른 객체에 영향을 미치며 그 운동 법칙은 알고리즘에서 충분히 높은 정확도로 설명된다는 것을 잊지 마세요. 공통 질량 중심에 가까워지면 객체들은 계속해서 빠른 속도로 움직입니다. 이는 입자 덩어리가 공통 질량 중심을 향해 맥동하는 움직임처럼 보입니다. 일정 횟수의 반복이 끝나면 객체의 질량에 영향을 미치는 중력 불균일성으로 작용하는 피트니스 함수의 공간 릴리프의 영향을 받아 객체들의 움직임이 궤적을 변경합니다. 앞서 설명한 것처럼 객체들의 질량은 피트니스 함수의 값으로 계산됩니다. 그러나 축을 따라 대칭인 라스트리긴 함수는 객체들의 움직임에 상당히 균일한 영향을 미치며 그룹으로의 분류는 특별히 눈에 띄지 않습니다.

Rastr

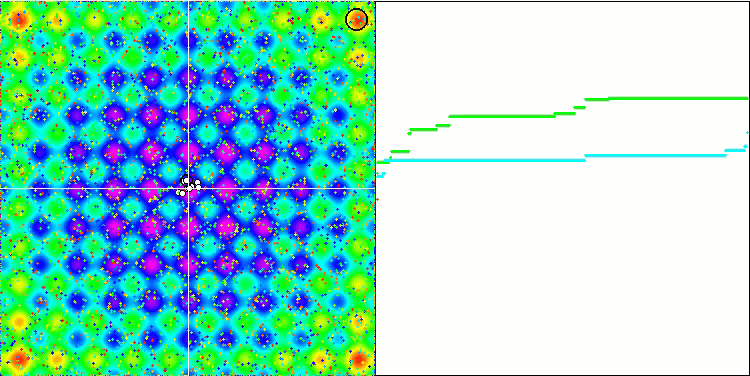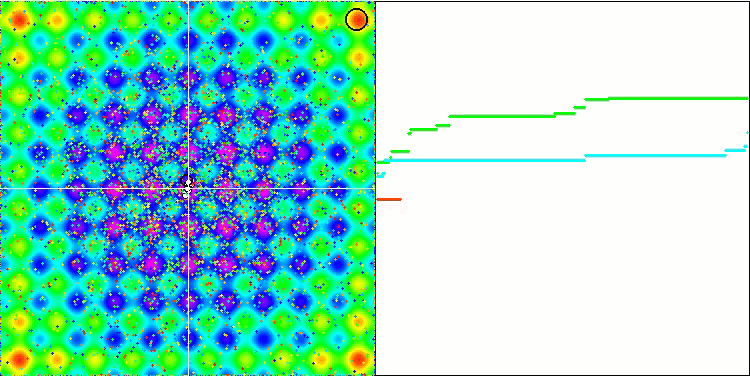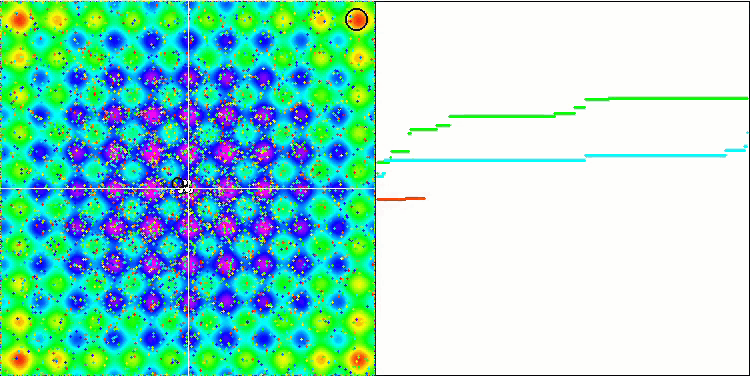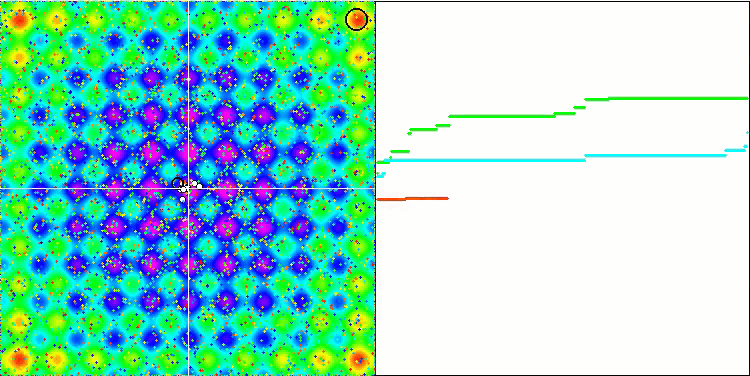
  Rastrigin 테스트 함수에 대한 GSA.

숲과 메가시티 함수의 객체들은 더욱 흥미로운 동작을 보여줍니다. 이러한 함수는 대칭이 아니므로 전체 객체 그룹에 균일하지 않은 영향을 미칩니다.

숲

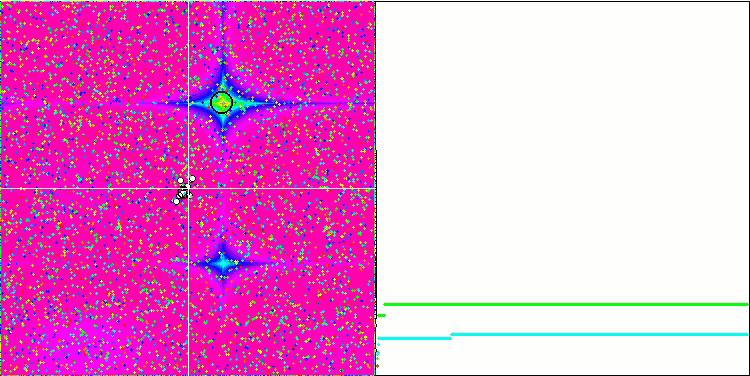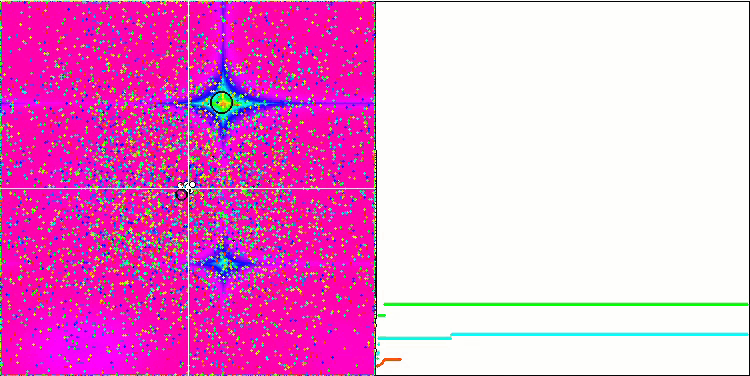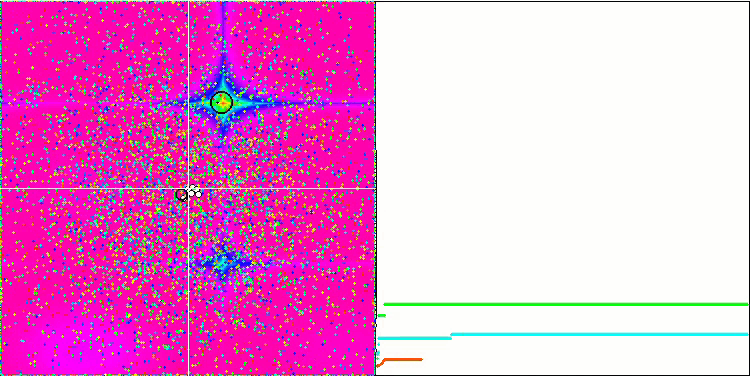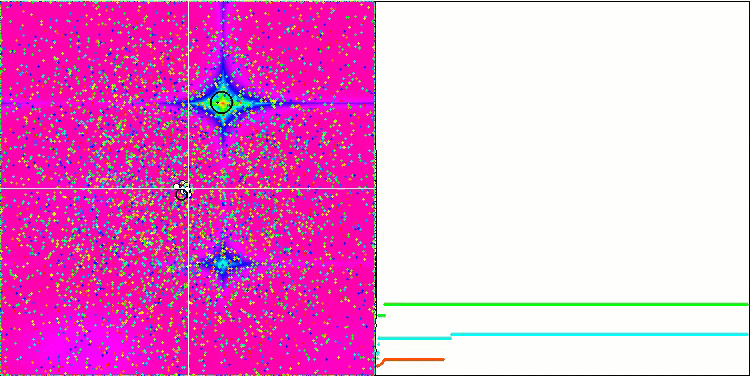
  숲 테스트 함수의 GSA.

메가시티

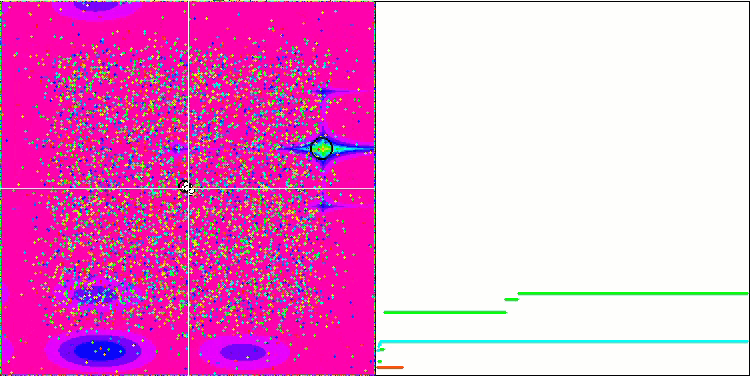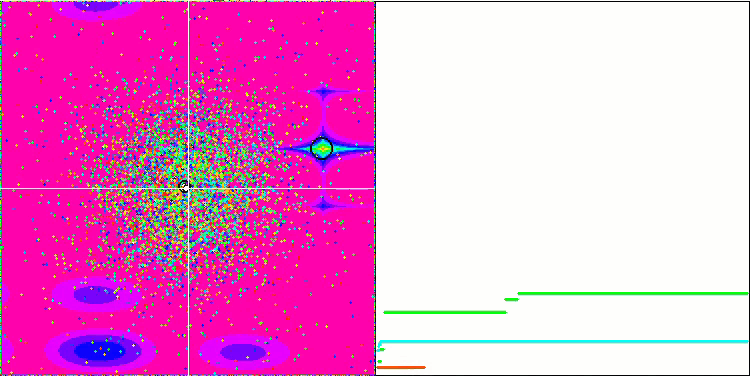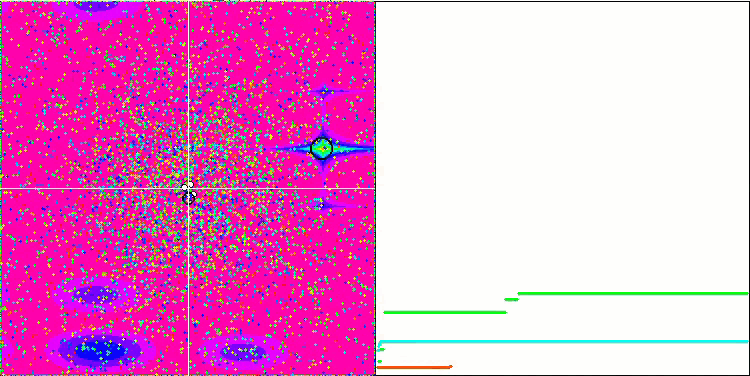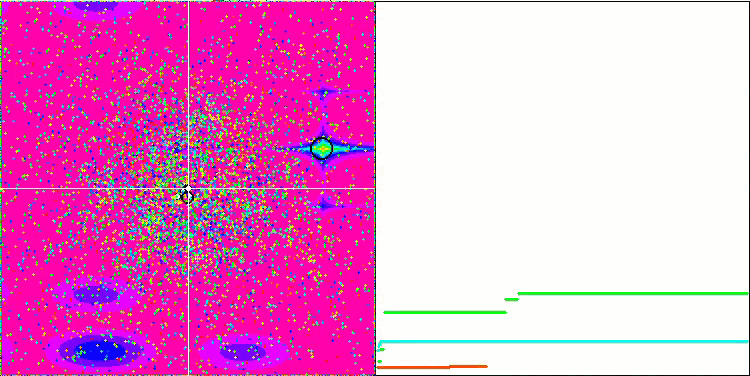
메가시티 테스트 함수에서 GSA

GSA로 많은 실험을 한 끝에 저는 우주 객체 이동 시뮬레이터를 만들자는 아이디어를 떠올렸습니다. 실용적인 가치는 없지만 행성과 항성계에 작용하는 물리 법칙에 대한 아이디어를 얻을 수 있습니다. 시뮬레이터는 무작위성이 비활성화된 GSA 버전입니다. 또한 세 개의 별(푸른 거인, 노란 별, 흰 난쟁이)을 모방한 세 개의 객체가 소개됩니다. 질량 매개변수는 해당 매개변수에 대한 설정에서 별도로 표시됩니다.

시뮬레이터를 위해 특별히 균일한 공간으로 새로운 유니버스 피트니스 함수가 만들어졌습니다. 시뮬레이터는 객체 간 거리의 정도(매개변수)가 서로의 이동에 어떤 영향을 미치는지 명확하게 보여줍니다. 아래 시각화에서는 뉴턴의 법칙 2의 표준값 대신 3의 거듭제곱이 적용되었습니다. 이와 같은 정도가 쌍성계 및 삼중성계와 같은 중력적으로 결합된 항성계의 형성에 어떤 영향을 미치는지 명확해집니다.

우리 우주에서 거리의 정도가 더 높았다면 은하계는 실제보다 훨씬 일찍 형성되었을 것입니다. 애니메이션은 공통 질량 중심을 중심으로 순환하는 쌍을 이루는 객체가 첫 번째 반복에 나타나는 것을 명확하게 보여줍니다. 예상대로 파란색 거인은 주변에 가장 많은 객체를 모았습니다.

Uni1

GSA 알고리즘을 기반으로 한 우주 객체 이동 시뮬레이터의 시각화


이제 GSA 테스트 결과 분석으로 넘어가겠습니다. 알고리즘에 사용된 원래 기능으로는 테스트에서 강력한 결과를 얻을 수 없었습니다. 제가 시도한 수많은 매개변수의 변형은 알고리즘의 수렴을 개선하지 못했습니다. 이 알고리즘은 10개의 변수와 메가시티를 사용한 부드러운 라스트리진 함수에서 다른 테스트 참가자들에 비해 긍정적인 결과를 보여주었습니다. 다른 테스트에서 GSA는 12개 중 8번째를 차지하여 표의 평균보다 낮은 성능을 보였습니다.

AO

설명

라스트리진

라스트리진 최종

숲

숲 최종

메가시티(이산)

메가시티 최종

최종 결과

10 params (5 F)

50 params (25 F)

1000 params(500 F)

10 params (5 F)

50 params (25 F)

1000 params(500 F)

10 params (5 F)

50 params (25 F)

1000 params(500 F)

IWO

침입성 잡초 최적화

1.00000

1.00000

0.35295

2.35295

0.79937

0.46349

0.41071

1.67357

0.75912

0.44903

0.94416

2.15231

100.000

ACOm

개미 식민지 최적화 M

0.36118

0.26810

0.20182

0.83110

1.00000

1.00000

1.00000

3.00000

1.00000

1.00000

0.15901

2.15901

96.805

COAm

뻐꾸기 최적화 알고리즘 M

0.96423

0.69756

0.30792

1.96971

0.64504

0.34034

0.21362

1.19900

0.67153

0.34273

0.48451

1.49877

74.417

FAm

반딧불이 알고리즘 M

0.62430

0.50653

0.20290

1.33373

0.55408

0.42299

0.64360

1.62067

0.21167

0.28416

1.00000

1.49583

70.740

BA

박쥐 알고리즘

0.42290

0.95047

1.00000

2.37337

0.17768

0.17477

0.33595

0.68840

0.15329

0.07158

0.49268

0.71755

59.383

ABC

인공 꿀벌 군집

0.81573

0.48767

0.24656

1.54996

0.58850

0.21455

0.17249

0.97554

0.47444

0.26681

0.39496

1.13621

57.393

BFO

박테리아 포식 최적화

0.70129

0.46155

0.13988

1.30272

0.41251

0.26623

0.26695

0.94569

0.42336

0.34491

0.53694

1.30521

55.563

GSA

중력 검색 알고리즘

0.73222

0.67404

0.00000

1.40626

0.31238

0.36416

0.42921

1.10575

0.51095

0.36658

0.00000

0.87753

52.786

FSS

물고기 떼 검색

0.48850

0.37769

0.13383

1.00002

0.78060

0.05013

0.08423

0.91496

0.00000

0.01084

0.23493

0.24577

20.094

PSO

파티클 스웜 최적화

0.21339

0.12224

0.08478

0.42041

0.15345

0.10486

0.28099

0.53930

0.08028

0.02385

0.05550

0.15963

14.358

RND

랜덤

0.17559

0.14524

0.09495

0.41578

0.08623

0.04810

0.06094

0.19527

0.00000

0.00000

0.13960

0.13960

8.117

GWO

회색 늑대 최적화

0.00000

0.00000

0.02672

0.02672

0.00000

0.00000

0.00000

0.00000

0.18977

0.04119

0.07252

0.30348

1.000


일반적으로 GSA 알고리즘은 최적화되는 함수에 경사가 있는 경우 눈에 띄게 민감합니다. 확장성이 낮기 때문에 많은 변수가 포함된 복잡한 작업에는 사용할 수 없습니다. 그러므로 신경망과 함께 사용하거나 거래 시스템을 최적화하는 데는 이 알고리즘을 권장하지 않습니다. 저는 중력 검색 알고리즘의 가능성에 대해 아직 완전히 연구하지 않았습니다. 추가 연구를 통해 이 매우 흥미롭고 특이한 알고리즘의 알려지지 않은 새로운 긍정적 기능을 발견할 수 있을 것입니다. 알고리즘의 주요 장점은 현재 가장 잘 알려진 글로벌 솔루션으로부터의 독립성과 모든 에이전트가 서로 상호 작용할 수 있다는 점입니다. 

그림 2는 알고리즘의 테스트 결과를 보여줍니다.

차트

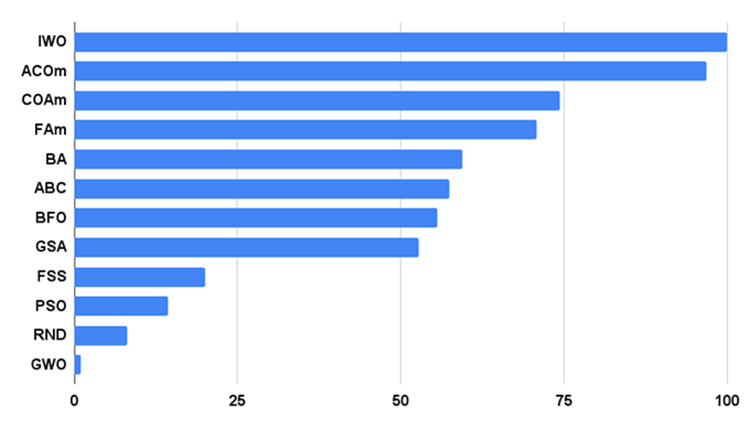
그림 2. 알고리즘 테스트 결과 히스토그램


중력 검색 알고리즘(GSA)의 속성에 대한 결론:

장점:
1. 간편한 구현.
2. 변수가 적은 부드러운 함수에서 좋은 성능을 발휘.

단점:
1. 높은 계산 복잡성.
2. 불연속 함수에 대한 결과가 좋지 않음.
3. 확장성이 좋지 않음.


MetaQuotes 소프트웨어 사를 통해 러시아어가 번역됨.
원본 기고글: https://www.mql5.com/ru/articles/12072

경고: 이 자료들에 대한 모든 권한은 MetaQuotes(MetaQuotes Ltd.)에 있습니다. 이 자료들의 전부 또는 일부에 대한 복제 및 재출력은 금지됩니다.

이 작가의 다른 글

토론으로 가기
MacOS용 MetaTrader 5 MacOS용 MetaTrader 5
당사는 macOS용 MetaTrader 5 트레이딩 플랫폼 전용 설치 프로그램을 제공합니다. 이 프로그램은 애플리케이션을 기본적으로 설치할 수 있는 본격적인 마법사 기능을 합니다. 설치 프로그램은 필요한 모든 단계를 수행합니다: 시스템을 식별하고 최신 Wine 버전을 다운로드 및 설치하고 구성한 다음 그 안에 MetaTrader를 설치합니다. 모든 단계는 자동화 모드로 완료되며 설치 후 즉시 플랫폼을 사용할 수 있습니다.
Expert Advisor를 선택하는 방법 트레이딩 봇을 선택하지 않을 20가지 강력한 기준 Expert Advisor를 선택하는 방법 트레이딩 봇을 선택하지 않을 20가지 강력한 기준
이 글에서는 올바른 Expert Advisor를 어떻게 선택할 수 있을지에 대한 질문에 답하고자 합니다. 우리 포트폴리오에 가장 적합한 트레이딩 봇은 무엇이며 시중에 나와 있는 기나긴 트레이딩 봇의 목록을 어떻게 필터링할 수 있을까요? 이 글에서는 거부해야 할 Expert Advisor에 대해 20가지의 명확하고 강력한 기준을 제시합니다. 각 기준이 제시되고 잘 설명되어 있어 여러분이 결정을 내리고 수익성 높은 Expert Advisor 컬렉션을 만드는 데 도움이 될 것입니다.
재구매 알고리즘: 효율성 향상을 위한 수학 모델 재구매 알고리즘: 효율성 향상을 위한 수학 모델
이 기사에서 우리는 거래 시스템의 효율성에 대한 더욱 깊은 이해를 위해 재구매 알고리즘과 수학과 논리를 사용하여 거래 효율성을 개선하는 일반적인 원칙관 관련한 작업을 수행하고 절대적인 측면에서 모든 거래 시스템의 사용 효율성을 높이는 가장 비표준 방법을 적용할 것입니다.
트레이딩에서 도덕적 기대 트레이딩에서 도덕적 기대
이 기사는 도덕적 기대치에 관한 내용입니다. 우리는 트레이딩에서 사용하는 몇 가지 예와 이를 통해 얻을 수 있는 결과를 살펴볼 것입니다.