统计分布在交易者工作中的作用
2 272
0
规律性使我们的生活更加容易，但是从随机性中获益也很重要。
(Georgiy Aleksandrov)
简介
本文是我的《用 MQL5 表示统计概率分布》一文的续篇，该文介绍了处理某些理论统计分布的类。我发现，必须首先以分布类的形式打下基础才能让用户更方便地在以后的实践中运用它们。
现在，我们已经有了理论基础，我建议我们应直接进入实际数据集，并尝试据此基础获得某些信息。同时，我们将阐明与数学统计有关的一些问题。
1. 指定分布下随机数的生成
但是在考虑实际数据集之前，能够获得与需要的理论分布紧密相关的几组值似乎非常重要。
换言之，用户应该只设置所需分布的参数和样本大小。一个程序（在我们的例子中为类的层次结构）应生成并输出此类值样本以供进一步处理。
另一个重要的细节是应将按指定规律生成的样本用于检查各种统计测试。数学统计的领域 - 在不同分布规律下随机变量的生成 - 是相当有趣且充满挑战的。
对我而言，我使用《Numerical Recipes:The Art of Scientific Computing（数值算法：科学计算的艺术）》一书 [2] 介绍的高质量生成器。其期段约等于 3.138*1057。以很简单的方式将 C 代码传递到 MQL5 中。
因此，我创建了 Random 类，如下所示：
//+------------------------------------------------------------------+ //| Random class definition | //+------------------------------------------------------------------+ class Random { private: ulong u, //unsigned 64-bit integers v, w; public: //+------------------------------------------------------------------+ //| The Random class constructor | //+------------------------------------------------------------------+ void Random() { randomSet(184467440737095516); } //+------------------------------------------------------------------+ //| The Random class set-method | //+------------------------------------------------------------------+ void randomSet(ulong j) { v=4101842887655102017; w=1; u=14757395258967641292; u=j^v; int64(); v = u; int64(); w = v; int64(); } //+------------------------------------------------------------------+ //| Return 64-bit random integer | //+------------------------------------------------------------------+ ulong int64() { uint k=4294957665; u=u*2862933555777941757+7046029254386353087; v^= v>> 17; v ^= v<< 31; v ^= v>> 8; w = k*(w & 0xffffffff) +(w>> 32); ulong x=u^(u<<21); x^=x>>35; x^=x<<4; return(x+v)^w; }; //+------------------------------------------------------------------+ //| Return random double-precision value in the range 0. to 1. | //+------------------------------------------------------------------+ double doub() { return 5.42101086242752217e-20*int64(); } //+------------------------------------------------------------------+ //| Return 32-bit random integer | //+------------------------------------------------------------------+ uint int32() { return(uint)int64(); } };
现在，我们可以为从一个分布取值的样本创建类。
作为一个例子，让我们看一看正态分布下的随机变量。CNormaldev 类如下所示：
//+------------------------------------------------------------------+ //| CNormaldev class definition | //+------------------------------------------------------------------+ class CNormaldev : public Random { public: CNormaldist N; //Normal Distribution instance //+------------------------------------------------------------------+ //| The CNormaldev class constructor | //+------------------------------------------------------------------+ void CNormaldev() { CNormaldist Nn; setNormaldev(Nn,18446744073709); } //+------------------------------------------------------------------+ //| The CNormaldev class set-method | //+------------------------------------------------------------------+ void setNormaldev(CNormaldist &Nn,ulong j) { N.mu=Nn.mu; N.sig=Nn.sig; randomSet(j); } //+------------------------------------------------------------------+ //| Return Normal deviate | //+------------------------------------------------------------------+ double dev() { double u,v,x,y,q; do { u = doub(); v = 1.7156*(doub()-0.5); x = u - 0.449871; y = fabs(v) + 0.386595; q = pow(x,2) + y*(0.19600*y-0.25472*x); } while(q>0.27597 && (q>0.27846 || pow(v,2)>-4.*log(u)*pow(u,2))); return N.mu+N.sig*v/u; } }; //+------------------------------------------------------------------+
如您所见，类有一个数据成员 N，其类型为 CNormaldist。原来的 C 代码缺少与分布的此类连接。对于此类（这里为 CNormaldev 类）生成的随机变量而言，我认为与其分布之间存在一个有逻辑的编程式连接是必不可少的。
在最初的版本中，Normaldev 类型的定义如下：
typedef double Doub; typedef unsigned __int64 Ullong; struct Normaldev : Ran { Doub mu,sig; Normaldev(Doub mmu, Doub ssig, Ullong i) ... }
此处使用 Leva 的均匀比例法从正态分布生成随机数。
帮助从各种分布计算随机变量的所有其他类，都在包含 Random_class.mqh 文件中列出。
现在，我们将结束随机数的生成，并在本文的实践部分讨论如何创建一个值数组以及测试一个样本。
2. 分布参数的估计、统计假设
显然我们将讨论离散变量。然而在实践中，如果离散变量的数量很多，则将此类离散变量的集合视为一组连续变量来考虑更加方便。这是数学统计中的一个标准方法。因此，要对它们进行分析，我们可以使用与连续变量有关的分析公式定义的分布。
那么，让我们开始经验分布的分析。
假定一个一般群体分布样本，其成员满足所研究的代表性条件。此外，还满足第 8.3 节指定的估值要求[9]。可通过点估值和区间方法找出数值分布参数。
2.1 使用 CExpStatistics 类处理样本
应该首先从样本中删除所谓的异常值；异常值指显著偏离样本主要部分的观察样本（包括向上和向下偏离）。删除异常值没有万能方法。
我建议使用在第 6.3 节中介绍的由 S.V. Bulashev 提出的方法 [5]。在 MQL4 论坛中已经创建了一个由统计函数组成的库，可以依据该库轻松地解决该问题。这就是说，我们将肯定应用 OOP 并对其稍微进行一些更新。
我将创建的统计特征的估值的类称为 CExpStatistics（预期统计类）。
它大体如下所述：
//+------------------------------------------------------------------+ //| Expected Statistics class definition | //+------------------------------------------------------------------+ class CExpStatistics { private: double arr[]; //initial array int N; //initial array size double Parr[]; //processed array int pN; //processed array size void stdz(double &outArr_st[],bool A); //standardization public: void setArrays(bool A,double &Arr[],int &n); //set array for processing bool isProcessed; //array processed? void CExpStatistics(){}; //constructor void setCExpStatistics(double &Arr[]); //set the initial array for the class void ZeroCheckArray(bool A); //check the input array for zero elements int get_arr_N(); //get the initial array length double median(bool A); //median double median50(bool A); //median of 50% interquantile range (midquartile range) double mean(bool A); //mean of the entire initial sample double mean50(bool A); //mean of 50% interquantile range double interqtlRange(bool A); //interquartile range double RangeCenter(bool A); //range center double meanCenter(bool A); //mean of the top five estimates double expVariance(bool A); //estimated variance double expSampleVariance(bool A); //shifted estimate of sample variance double expStddev(bool A); //estimated standard deviation double Moment(int index,bool A,int sw,double xm); //moment of distribution double expKurtosis(bool A,double &Skewness); ////estimated kurtosis and skewness double censorR(bool A); //censoring coefficient int outlierDelete(); //deletion of outliers from the sample int pArrOutput(double &outArr[],bool St); //processed array output void ~CExpStatistics(){};//destructor }; //+------------------------------------------------------------------+
在包含 ExpStatistics_class.mqh 文件中可详细讨论各个方法的实施，因此在这里我不做详细说明。
这个类做的重要事情是，它返回不含异常值的数组 (Parr[])（如果有的话）。此外，它有助于获取采样的某些描述性统计及其估值。
2.2 创建经过处理的样本直方图
现在，数组已经不含异常值，可以依据其数据绘制一个直方图（频率分布）。它帮助我们以可视方式估计随机变量分布规律。有一个创建直方图的分步过程。
应该首先计算需要的类的数量。在此上下文中，术语“类”指分组、区间。按 Sturges 的公式计算类的数量：
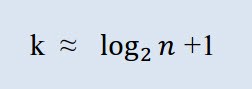
其中，k 是类的数量，n 是观察样本的数量。
在 MQL5 中，该公式可表示为：
int Sturges(int n) /* Function for determining the number of class intervals using Sturges' rule. Variables: y is the number of sampling observations. Returned value: number of class intervals. */ { double s; // Returned value s=1.+log2(y); if(s>15) // Empirical rule s=15; return(int) floor(s); }
在使用 Sturges 的公式得到需要的类（区间）的数量时，是将数组数据分成类的时候了。此数据被称为观察样本（英文为 observation）。我们将使用 Allocate 函数进行，如下所示：
void Allocate(double &data[],int n,double &f[],double &b[],int k) /* Function for allocating observations to classes. Variables: 1) data — initial sample (array) 2) n — sample size 3) f — calculated array of observations allocated to classes 4) b — array of class midpoints 5) k — number of classes */ { int i,j; // Loop counter double t,c; // Auxiliary variable t=data[ArrayMinimum(data)]; // Sample minimum t=t>0 ? t*0.99 : t*1.01; c=data[ArrayMaximum(data)]; // Sample maximum c=c>0 ? c*1.01 : c*0.99; c=(c-t)/k/2; // Half of the class interval b[0]=t+c; // Array of class interval midpoints f[0]= 0; for(i=1; i<k; i++) { b[i] = b[i - 1] + c + c; f[i] = 0; } // Grouping for(i=0; i<n; i++) for(j=0; j<k; j++) if(data[i]>b[j]-c && data[i]<=b[j]+c) { f[j]++; break; } }
如您所见，函数采用初始观察样本数组 (data)、其长度 (n)、类的数量 (k)，并将观察样本分配到数组 f 的某个 f[i] 类，其中 b[i] 是 f[i] 类的中点。现在，直方图的数据准备就绪。
我们将使用在以前提过的一文中介绍的工具显示直方图。为此，我编写了 histogramSave 函数，该函数将在 HTML 中显示所研究的序列的直方图。函数采用 2 个参数：类数组 (f) 和类的中点数组 (b)。
作为一个例子，我使用 volatilityTest.mq5 脚本建立了EURUSD 货币对在四小时时间框架上 500 根柱的最大点和最小点之间的绝对差值直方图。
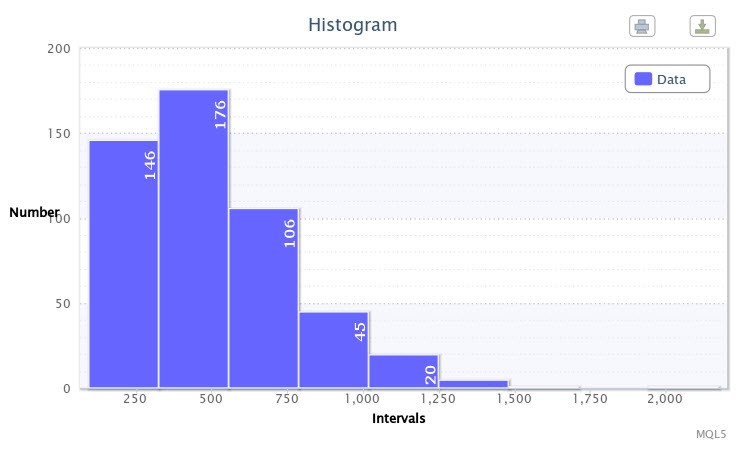
图 1. 数据直方图（EURUSD H4 的绝对波动）
如直方图（图 1）所示，第一类有 146 个观察样本，第二类有 176 个观察样本，等等。直方图函数对所研究的样本的经验分布提供了一个看得见的概念。
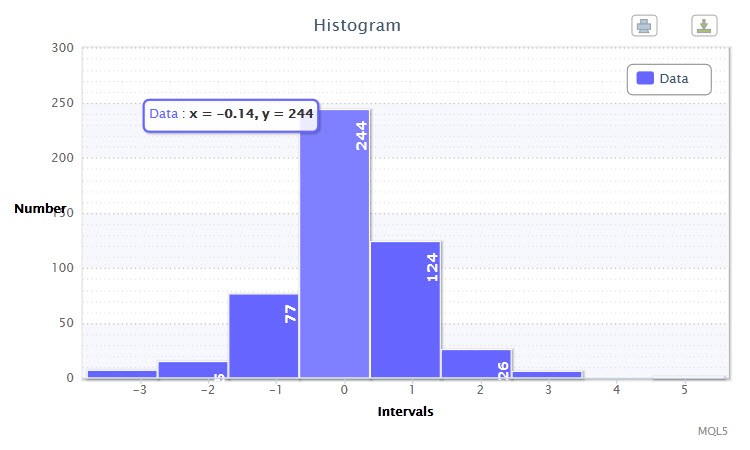
图 2. 数据直方图（EURUSD H4 标准化返回）
另一直方图（图 2）显示 EURUSD 货币对在 H4 时间框架上的 500 根柱的标准化对数返回。您会注意到，第四类和第五类给人的印象最深刻，因为它们分别有 244 个和 124 个观察样本。此直方图是使用 returnsTest.mq5 脚本建立的。
因此，直方图让我们能够选择将进一步估计其参数的分布规律。在不能明显看出供分布的情形中，您可以估算几种理论分布的参数。
我们考虑的两种分布在外观上都不像正态分布，尤其是第一种分布。然而，让我们不要相信图形，继续处理数字。
2.3 正态性假设
首先解决并测试所讨论的分布是正态分布这一假定（假设）是一个惯例。此类假设被称为主假设。Jarque-Bera 测试是测试样本的正态性的最流行方法之一。
其算法，尽管不是最复杂，但由于近似值，也相当麻烦。有几个以 C++ 和其他语言编写的算法。交叉平台数值分析库 ALGLIB 列出了其中一个最成功且经过证明的版本。其作者 [S.A. Bochkanov] 进行了大量的工作，特别是在测试分位数表的汇编方法方面。我仅仅是依据 MQL5 的需要对其稍微进行了一些更新。
主函数 jarqueberatest 如下所示：
//+------------------------------------------------------------------+ // the Jarque-Bera Test | //+------------------------------------------------------------------+ void jarqueberatest(double &x[],double &p) /* The Jarque-Bera test is used to check hypothesis about the fact that a given sample xS is a sample of normal random variable with unknown mean and variance. Variables: x - sample Xs; p - p-value; */ { int n=ArraySize(x); double s; p=0.; if(n<5)//N is too small { p=1.0; return; } //N is large enough jarquebera_jarqueberastatistic(x,n,s); p=jarquebera_jarqueberaapprox(n,s); } //+------------------------------------------------------------------+
它处理初始数据样本 (x) 并返回 р 值，即当零假设事实上成立时拒绝零假设的概率的特征值。
在函数主体中有 2 个辅助函数。第一个函数 - jarquebera_jarqueberastatistic - 计算 Jarque-Bera 统计，第二个函数 - jarquebera_jarqueberaapprox - 计算 p 值。应指出，第二个函数又调用与近似值有关的辅助函数，在算法中接近有 30 个。
那么，让我们尝试测试我们的样本是否有正态性。我们将使用 returnsTest.mq5 脚本，该脚本处理 EURUSD H4 的标准化返回的样本。
如我们所预期，测试显示拒绝一个成立的零假设的概率为 0.0000。换言之，此样本的分布不属于正态分布。为了处理 EURUSD 货币对的绝对波动样本，运行 volatilityTest.mq5 脚本。结果将是类似的 - 分布不是正态分布。
3. 分布拟合
有几种数学统计方法用于将经验分布与正态分布进行比较。最大的问题在于我们不知道正态分布参数，并且假设所研究的数据没有反映出分布的正态性。
因此，我们不得不使用非参数性测试，并且用从经验分布获得的估值填充未知参数。
3.1. 估算与测试
在这种情形中，χ2 测试是最流行、最重要的充分测试之一。它以 Pearson 的拟合优度度量为基础。
我们将使用 chsone 函数进行测试：
void chsone(double &f[],double &ebins[],double &df, double &chsq,double &prob,const int knstrn=1) /* 1) f — array of observations allocated to classes 2) ebins - array of expected frequencies 3) df - number of degrees of freedom 3) chsq — chi-square statistics 4) prob - probability of accepting a true null hypothesis 5) knstrn — constraint */ { CGamma gam; int j,nbins=ArraySize(bins),q,g; double temp; df=nbins-knstrn; chsq=0.0; q=nbins/2; g=nbins-1; for(j=0;j<nbins/2;j++) //passing through the left side of the distribution { if(ebins[j]<0.0 || (ebins[j]==0. && bins[j]>0.)) Alert("Bad expected number in chsone!"); if(ebins[j]<=5.0) { --df; ebins[j+1]+=ebins[j]; bins[j+1]+=bins[j]; } else { temp=bins[j]-ebins[j]; chsq+=pow(temp,2)/ebins[j]; } } for(j=nbins-1;j>nbins/2-1;j--) //passing through the right side of the distribution { if(ebins[j]<0.0 || (ebins[j]==0. && bins[j]>0.)) Alert("Bad expected number in chsone!"); if(ebins[j]<=5.0) { --df; ebins[j-1]+=ebins[j]; //starting with the last class bins[j-1]+=bins[j]; } else { temp=bins[j]-ebins[j]; chsq+=pow(temp,2)/ebins[j]; } } if(df<1)df=1; //compensate prob=gam.gammq(0.5*df,0.5*chsq); //Chi-square probability function }
如清单所示，使用 CGamma 类的一个实例来表示不完整的 gamma 函数，该函数以及所有提及的分布都包含在 Distribution_class.mqh 文件中。也应指出，将使用 estimateDistribution 和 expFrequency 函数获得预期频率数组 (ebins)。
现在，我们需要选择包含在理论分布的分析公式中的数值参数。参数数量取决于具体分布。例如，在正态分布中有两个参数，在经验分布中有一个参数，等等。
在确定分布参数时，我们通常使用瞬态法、分位数法和最大似然法等点估计法。第一种方法比较简单，因为它暗示采样估计（预期、差异、偏斜等）应与一般估计一致。
让我们使用一个例子为我们的样本选择一种理论分布。我们将采用已经为其绘制了直方图的 EURUSD H4 的一系列标准化返回。
第一印象是正态分布不适合该系列，因为观察到过大的峰度系数。作为比较，让我们尝试应用其他分布。
因此，在启动已知的 returnsTest.mq5 脚本时，我们将尝试选择 Hypersec （双曲线正割）等分布。此外，脚本将使用 estimateDistribution 函数估计并输出选择的分布参数，并立即运行 χ2 测试。选择的分布参数如下所示：
双曲线正割分布：X~HS(-0.00, 1.00)；
测试结果如下所示：
"Chi-square statistic:1.89; probability of rejecting a true null hypothesis: 0.8648"
应该指出，选择的分布有良好的拟合，因为 χ2 统计的值非常小。
此外，使用 histogramSaveE 函数绘制标准化返回的观察和预期频率比（频率比是以分数或百分数表示的频率）的双直方图（图 3）。您可以看到柱几乎是相互重复的。这是成功拟合的证明。
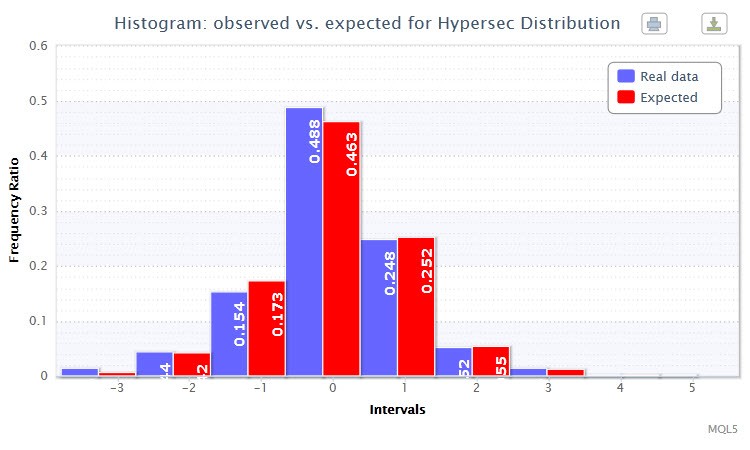
图 3. 观察和预期频率比的直方图（EURUSD H4 的标准化返回）
让我们使用已知的 volatilityTest.mq5 对波动数据执行类似的过程。
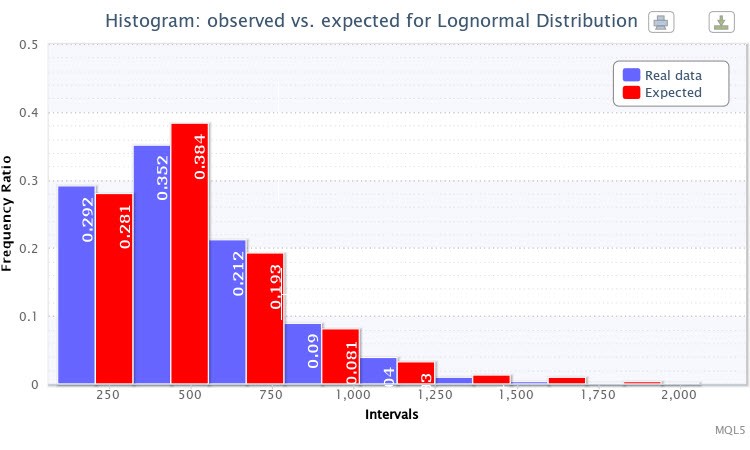
图 4. 观察和预期频率比的直方图（EURUSD H4 的绝对波动）
我选择对数正态分布 Lognormal 进行测试。结果得到以下参数估计：
对数正态分布：X~Logn(6.09, 0.53)；
测试结果如下所示：
"Chi-square statistic:6.17; probability of rejecting a true null hypothesis: 0.4040"
此经验分布的理论分布也选择得非常成功。因此，可以考虑不能拒绝零假设（在标准置信水平 p=0.05 时）。可以在图 4 中看到，期望和观察频率比的柱也非常类似。
现在，让我提醒您，我们有另一种可能性，从含有设定参数的分布生成随机变量样本。为了使用与此类操作有关的类的层次结构，我编写了 randomTest.mq5 脚本。
在开始，我们需要输入参数，如图 5 所示。
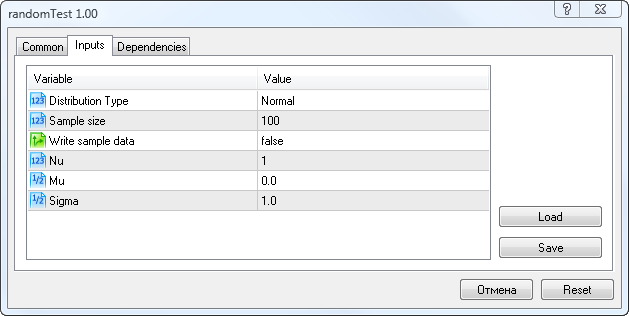
图 5. randomTest.mq5 脚本的输入参数
在这里，您可以选择分布类型 (Distribution Type)、样本中的随机变量的数量 (Sample Size)、样本保存选项 (Write sample data)、Nu 参数（学生 t 分布）、Mu 和 Sigma 参数。
如果您将 Write sample data 的值设为 true，则脚本会将含有自定义参数的随机变量的样本保存到 Randoms.csv 文件。否则它将从此文件读取样本数据，然后执行统计测试。
对于缺少 Mu 和 Sigma 参数的某些分布，我提供了与脚本启动窗口中的字段有关的参数表。
| 分布 | 第一个分布参数 | 第二个分布参数 |
|---|---|---|
| 逻辑分布 | alph --> Mu | bet --> Sigma |
| 指数分布 | lambda --> Mu | -- |
| 伽玛分布 | alph --> Mu | bet --> Sigma |
| 贝塔分布 | alph --> Mu | bet --> Sigma |
| 拉普拉斯分布 | alph --> Mu | bet --> Sigma |
| 二项 | n --> Mu | pe --> Sigma |
| 泊松分布 | lambda --> Mu | -- |
例如，如果选择了泊松分布，则将通过 Mu 字段输入 lambda 参数，等等。
脚本不估计学生 t 分布参数，因为在绝大多数的情形下，它仅在少数几个统计过程中使用：涉及来自正态分布的统计样本的未知平均值的点估计、置信区间的建立和假设测试。
作为一个例子，我针对参数为 X~Nor(3.50, 2.77) 的正态分布运行脚本，其中 Write sample data=true。脚本首先生成一个样本。在第二个上，我使用 Write sample data=false 运行脚本，绘制了如图 6 所示的直方图。
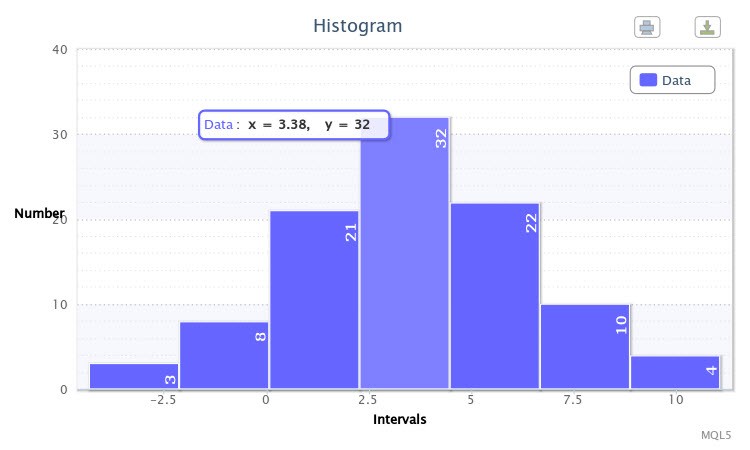
图 6. 随机变量 X~Nor(3.50,2.77) 的样本
客户端窗口中显示的剩余信息如下所示：
Jarque-Bera 测试："The Jarque-Bera test:probability of rejecting a true null hypothesis is 0.9381";
Parameter estimation:Normal distribution:X~Nor(3.58, 2.94);
Chi-square test results:"Chi-square statistic:0.38; probability of rejecting a true null hypothesis: 0.9843".
最后，显示了样本的观察和预期频率比的另一双直方图（图 7）。
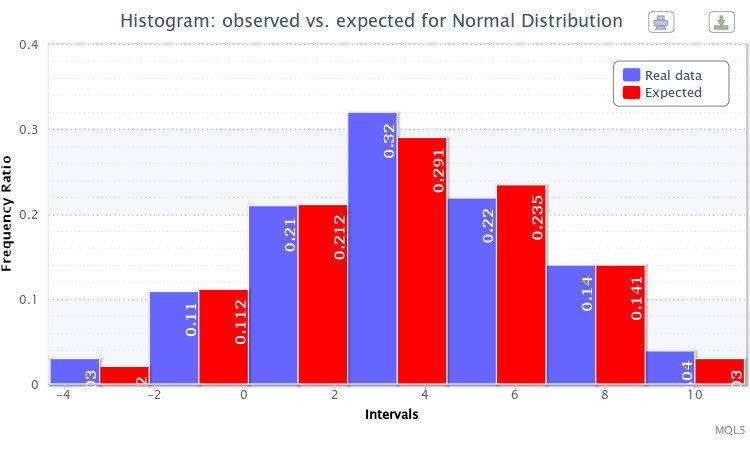
图 7. X~Nor(3.50,2.77) 的观察和预期频率比的直方图
整体而言，成功生成了指定分布。
我还编写了 fitAll.mq5 脚本，该脚本的工作方式与 randomTest.mq5 脚本类似。唯一区别是第一个脚本有 fitDistributions 函数。我设定了以下任务：对随机变量样本进行所有可用分布拟合，然后进行统计测试。
由于参数不匹配，并不是始终都能对样本进行分布拟合，导致在客户端中出现告知不能进行估计的行，即 "Beta distribution cannot be estimated!"（不能估计贝塔分布）。
此外，我决定此脚本应以小型 HTML 报告的形式显示统计结果，可以在HTML 中的图表》一文中找到一个例子（图 8）。
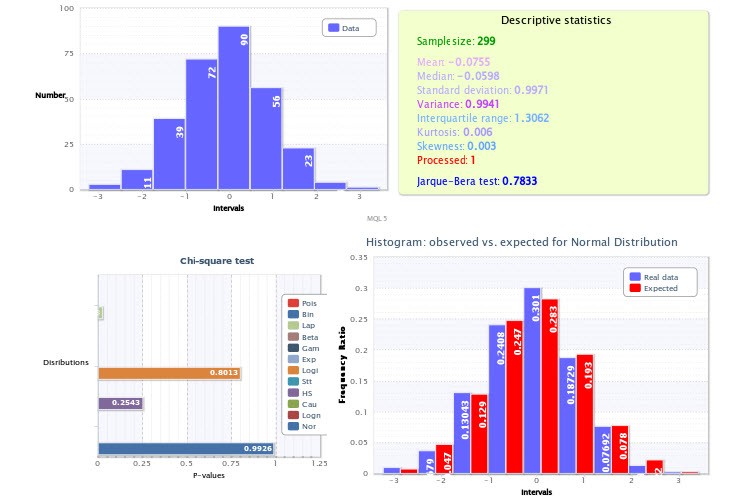
图 8. 有关样本估计的统计报告
在左上部分显示了样本的标准直方图；右上部分表示描述性统计和 Jarque-Bera 测试结果，其中 Processed 变量值等于 1 表示删除了异常值，等于 0 表示没有异常值。
在左下部分显示了每个选定分布的 χ2 测试的 P 值。在这里，正态分布是最好的拟合 (p=0.9926)。因此，在右下部分绘制了观察和预期频率比的直方图。
在我的库中还没有这么多的分布。但是如果存在大量的分布，则此脚本将为您节省很多时间。
现在，我们确切知道所研究样本的分布参数，我们可以继续进行概率推理。
3.2 随机变量值的概率
在关于理论分布的一文中，我给出 continuousDistribution.mq5 脚本作为一个例子。我们将使用该脚本来尝试显示可能让我们感兴趣的任何具有已知参数的分布规律。
那么，对于波动数据，我们将输入先前得到的对数正态分布参数（Mu=6.09，Sigma=0.53），选择 Lognormal 分布类型和 cdf 模式（图 9）。
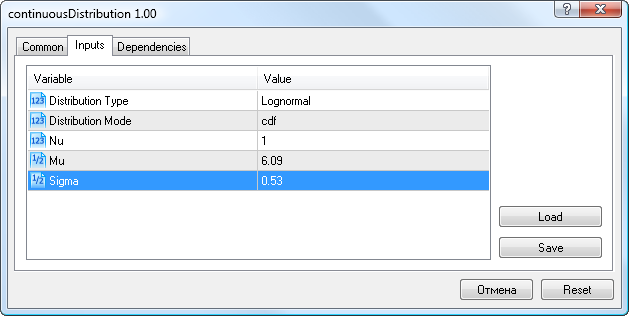
图 9. 对数正态分布参数 X~Logn(6.09,0.53)
之后，脚本将为我们的样本显示分布函数。它将如图 10 所示。
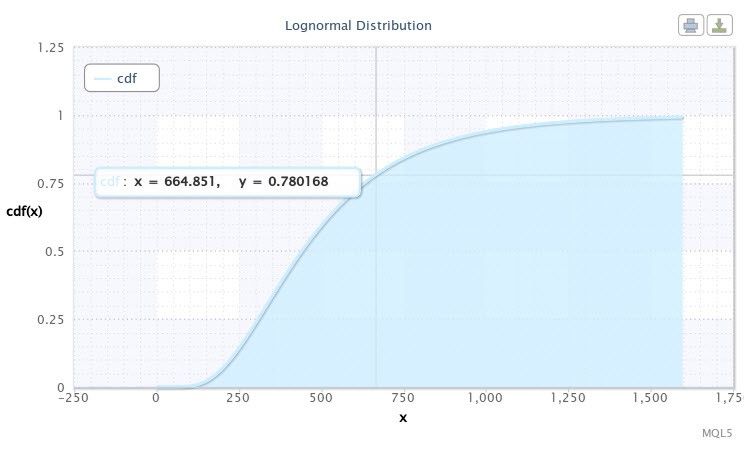
图 10. X~Logn(6.09,0.53) 的分布函数
我们可以在图表中看到，光标指向一个坐标大约为 [665;0.78] 的点。它表示有 78% 的概率 EURUSD H4 的波动不会超过 665 点。此信息可证明对 EA 交易的开发人员非常有用。可以通过移动光标在曲线上获取另外的值。
让我们假定我们对波动值在 500 和 750 点这一区间的事件的概率感兴趣。为此，需要进行以下操作：
cdf(750) - cdf(500) = 0.84 - 0.59 = 0.25.
因此，在四分之一的事件中，货币对的波动在 500 和 750 点的区间内变化。
让我们仅选择 sf 作为分布规律模式，使用相同的分布参数再次运行脚本。可靠性（生存）函数将如下图所示（图 11）。
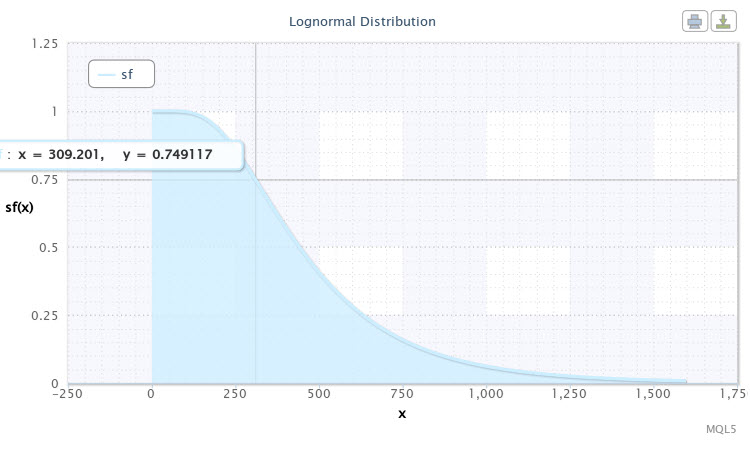
图 11. X~Logn(6.09,0.53) 的生存函数
可以如下解释在曲线图中标记的点：我们可以预期接近 75% 的概率货币对的波动将为 310 点。我们沿曲线下降越多，波动增大的概率就越小。因此，超过 1000 点的波动已经可以被视为罕见事件，因为其发生的概率小于 5%。
可以为标准化返回样本以及其他样本建立类似的分布曲线。我假定此方法通常很清晰。
总结
应该指出，所提议的分析推导并非完全成功，因为序列趋向于变化。例如，虽然它不涉及对数返回序列。然而，在本文中我并没有为我自己设定一个评估方法的任务。我建议感兴趣的读者对此问题做出评论。
需要从概率观点考虑市场、市场工具和交易专家，指出这点非常重要。这是我尝试证明的方法。我希望这一主题会引起读者的兴趣并引出一场建设性的讨论。
文件位置：
| # | 文件 | 路径 | 说明 |
|---|---|---|---|
| 1 | Distribution_class.mqh | %MetaTrader%\MQL5\Include | 分布类的库 |
| 2 | DistributionFigure_class.mqh | %MetaTrader%\MQL5\Include | 分布的图表显示类 |
| 3 | Random_class.mqh | %MetaTrader%\MQL5\Include | 随机数样本生成类 |
| 4 | ExpStatistics_class.mqh | %MetaTrader%\MQL5\Include | 统计特征估计的类和函数 |
| 5 | volatilityTest.mq5 | %MetaTrader%\MQL5\Scripts | EURUSD H4 波动样本估计的脚本 |
| 6 | returnsTest.mq5 | %MetaTrader%\MQL5\Scripts | EURUSD H4 返回样本估计的脚本 |
| 7 | randomTest.mq5 | %MetaTrader%\MQL5\Scripts | 随机变量样本估计的脚本 |
| 8 | fitAll.mq5 | %MetaTrader%\MQL5\Scripts | 所有分布的拟合及估计的脚本 |
| 9 | Volat.csv | %MetaTrader%\MQL5\Files | EURUSD H4 波动样本数据文件 |
| 10 | Returns_std.csv | %MetaTrader%\MQL5\Files | EURUSD H4 返回样本数据文件 |
| 11 | Randoms.csv | %MetaTrader%\MQL5\Files | 随机变量样本数据文件 |
| 12 | Histogram.htm | %MetaTrader%\MQL5\Files | HTML 格式的样本直方图 |
| 13 | Histogram2.htm | %MetaTrader%\MQL5\Files | HTML 格式的样本双直方图 |
| 14 | chi_test.htm | %MetaTrader%\MQL5\Files | 样本估计的统计 HTML 报告 |
| 15 | dataHist.txt | %MetaTrader%\MQL5\Files | 用于显示样本直方图的数据 |
| 16 | dataHist2.txt | %MetaTrader%\MQL5\Files | 用于显示样本双直方图的数据 |
| 17 | dataFitAll.txt | %MetaTrader%\MQL5\Files | 用于显示 HTML 报告的数据 |
| 18 | highcharts.js | %MetaTrader%\MQL5\Files | 互动式图表的 JavaScript 库 |
| 19 | jquery.min.js | %MetaTrader%\MQL5\Files | JavaScript 库 |
| 20 | ReturnsIndicator.mq5 | %MetaTrader%\MQL5\Indicators | 对数返回指标 |
参考资料：
本文由MetaQuotes Ltd译自俄文
原文地址： https://www.mql5.com/ru/articles/257
以线性回归为例说明指标加速的 3 种方法
用 MQL5 表示统计概率分布
移动极小化极大：技术分析的新指标及其在 MQL5 中的实施
