트레이딩 내 통계적 분산의 역할
196
0
규칙적인 것들을 통해 우리의 삶을 더 편하게 할 수 있지만, 무작위성에서도 무언가 건지는 것 또한 중요합니다.
(게오르기 알렉산드로프)
들어가며
본 문서는 MQL5의 통계 확률 분포에 대해 논하고 이론적 통계 분산을 다루는 클래스들을 다룬 제 다른 문서의 논리적 후속작입니다. 나중에 이용자들이 보다 편리하게 이용할 수 있도록 우선 배포 클래스 형태로 기반을 마련하는 것이 필요하다는 것을 알게 되었습니다.
이제 이론적 기반이 확보되었으므로 실제 데이터 셋으로 직접 이동하여 이 기반을 정보적으로 활용할 것을 제안합니다. 동시에 수학적 통계에 관한 몇가지 이슈에 대해 주목해볼 것입니다.
1. 주어진 분산으로 랜덤 숫자 생성하기
실제 데이터 세트를 고려하기 전에 원하는 이론적 분포와 밀접한 관련이 있는 값의 집합을 얻을 수 있는 것이 매우 중요해 보입니다.
즉, 사용자는 원하는 분포와 샘플 크기의 패러미터만 설정해야 한다는 것입니다. 프로그램(우리의 경우엔 클래스 계층)은 향후 작업을 위해 그러한 값의 샘플을 생성하고 출력해야 합니다.
또 다른 중요한 세부 사항은 특정 법률에 의해 생성된 샘플이 다양한 통계 테스트를 확인하는 데 사용된다는 것 입니다. 수리 통계 영역 - 각기 다른 분산 법칙에 따른 랜덤 변수의 생성 - 은 매우 흥미롭고 도전적입니다.
이 목적을 위해 Numerical Recipes: The Art of Scientific Computing [2] 에서 설명된 높은 퀄리티의 제너레이터를 활용합니다. 주기는 약 3.138*1057과 같습니다. C 코드가 쉽게 MQL5로 넘겨졌습니다.
그래서 Random 클래스를 다음과 같이 만들었습니다:
//+------------------------------------------------------------------+ //| Random class definition | //+------------------------------------------------------------------+ class Random { private: ulong u, //unsigned 64-bit integers v, w; public: //+------------------------------------------------------------------+ //| The Random class constructor | //+------------------------------------------------------------------+ void Random() { randomSet(184467440737095516); } //+------------------------------------------------------------------+ //| The Random class set-method | //+------------------------------------------------------------------+ void randomSet(ulong j) { v=4101842887655102017; w=1; u=14757395258967641292; u=j^v; int64(); v = u; int64(); w = v; int64(); } //+------------------------------------------------------------------+ //| Return 64-bit random integer | //+------------------------------------------------------------------+ ulong int64() { uint k=4294957665; u=u*2862933555777941757+7046029254386353087; v^= v>> 17; v ^= v<< 31; v ^= v>> 8; w = k*(w & 0xffffffff) +(w>> 32); ulong x=u^(u<<21); x^=x>>35; x^=x<<4; return(x+v)^w; }; //+------------------------------------------------------------------+ //| Return random double-precision value in the range 0. to 1. | //+------------------------------------------------------------------+ double doub() { return 5.42101086242752217e-20*int64(); } //+------------------------------------------------------------------+ //| Return 32-bit random integer | //+------------------------------------------------------------------+ uint int32() { return(uint)int64(); } };
이제 분산에서 샘플링된 값에 대한 클래스를 만들 수 있습니다.
예를 들어 정규 분포의 랜덤 변수를 살펴보겠습니다. CNormaldev 클래스는 다음과 같습니다:
//+------------------------------------------------------------------+ //| CNormaldev class definition | //+------------------------------------------------------------------+ class CNormaldev : public Random { public: CNormaldist N; //Normal Distribution instance //+------------------------------------------------------------------+ //| The CNormaldev class constructor | //+------------------------------------------------------------------+ void CNormaldev() { CNormaldist Nn; setNormaldev(Nn,18446744073709); } //+------------------------------------------------------------------+ //| The CNormaldev class set-method | //+------------------------------------------------------------------+ void setNormaldev(CNormaldist &Nn,ulong j) { N.mu=Nn.mu; N.sig=Nn.sig; randomSet(j); } //+------------------------------------------------------------------+ //| Return Normal deviate | //+------------------------------------------------------------------+ double dev() { double u,v,x,y,q; do { u = doub(); v = 1.7156*(doub()-0.5); x = u - 0.449871; y = fabs(v) + 0.386595; q = pow(x,2) + y*(0.19600*y-0.25472*x); } while(q>0.27597 && (q>0.27846 || pow(v,2)>-4.*log(u)*pow(u,2))); return N.mu+N.sig*v/u; } }; //+------------------------------------------------------------------+
이 클래스는 CNormaldist 타입의 데이터 N을 멤버로 가집니다. 원래의 C 코드는 정규 분포과 관련된 연관성이 조금 부족했습니다 저는 그 클래스(이 CNormaldev 클래스로 생성된) 로 생성된 랜덤 변수는 분산과 프로그래밍적으로, 그리고 논리적으로 연관되어야 한다고 생각하기에 필수라고 보았습니다.
원래 버전에서 Normaldev 타입이 다음과 같이 정의되었습니다:
typedef double Doub; typedef unsigned __int64 Ullong; struct Normaldev : Ran { Doub mu,sig; Normaldev(Doub mmu, Doub ssig, Ullong i) ... }
레바의 균일 메소드 비율을 사용하여 정규 분포로부터 임의의 숫자가 생성됩니다.
다양한 분포의 랜덤 변수 계산에 도움이 되는 다른 모든 클래스는 Random_class.mqh 파일에 들어있습니다.
이제 생성 과정을 마치고, 이 글의 실질적인 부분에서는 일련의 값을 생성하고 샘플을 테스트하는 방법에 대해 알아보겠습니다.
2. 분포 모수 추정, 통계적 가설
이제 이산 변수들을 들여다 봅시다. 그러나 실제로는 이산 변수의 수가 유의미할 정도로 있다면 연속형 변수 그룹으로 그러한 이산 변수 집합을 고려하는 것이 더 편리합니다 이는 수리 통계학에서는 교과서적인 접근방법입니다. 따라서 연속 변수와 관련된 분석 공식에 의해 정의된 분포를 사용할 수 있습니다.
경험적 누적 분포 분석으로 넘어가봅시다.
대표성 조건을 만족하는 일반 인구의 샘플을 사용하는 것이 기본 전제입니다. 또한 섹션 8.3[9]에 명시된 추정치의 요건이 충족됩니다. 숫자 분포 모수는 점 추정 및 구간 방법을 통해 확인할 수 있습니다.
2.1 CExpStatistics 클래스를 이용한 샘플 관리
먼저 표본에서 소위 아웃라이어를 제거해야 합니다. 이러한 관측치는 표본의 주요 부분(위쪽과 아래쪽 모두)의 관측치에서 크게 벗어난 것입니다. 아웃라이어를 배제하는 방법에 법칙이라할 만한 것은 딱히 없습니다.
S.V.에 의해 언급된 것을 활용하는 것을 추천드립니다 섹션 6.3 [5] 불라셰프. MQL4 포럼에서는 주어진 문제를 쉽게 해결할 수 있는 기초로 통계 기능의 라이브러리가 작성되었습니다. 그리 된 이상 OOP를 적용하고 약간 더 업데이트 할 것입니다.
저는 생성된 통계 특성 추정치 클래스를 CExpStatistics(예상 통계 클래스)라고 불렀습니다.
대충 이런 느낌입니다:
//+------------------------------------------------------------------+ //| Expected Statistics class definition | //+------------------------------------------------------------------+ class CExpStatistics { private: double arr[]; //initial array int N; //initial array size double Parr[]; //processed array int pN; //processed array size void stdz(double &outArr_st[],bool A); //standardization public: void setArrays(bool A,double &Arr[],int &n); //set array for processing bool isProcessed; //array processed? void CExpStatistics(){}; //constructor void setCExpStatistics(double &Arr[]); //set the initial array for the class void ZeroCheckArray(bool A); //check the input array for zero elements int get_arr_N(); //get the initial array length double median(bool A); //median double median50(bool A); //median of 50% interquantile range (midquartile range) double mean(bool A); //mean of the entire initial sample double mean50(bool A); //mean of 50% interquantile range double interqtlRange(bool A); //interquartile range double RangeCenter(bool A); //range center double meanCenter(bool A); //mean of the top five estimates double expVariance(bool A); //estimated variance double expSampleVariance(bool A); //shifted estimate of sample variance double expStddev(bool A); //estimated standard deviation double Moment(int index,bool A,int sw,double xm); //moment of distribution double expKurtosis(bool A,double &Skewness); ////estimated kurtosis and skewness double censorR(bool A); //censoring coefficient int outlierDelete(); //deletion of outliers from the sample int pArrOutput(double &outArr[],bool St); //processed array output void ~CExpStatistics(){};//destructor }; //+------------------------------------------------------------------+
각 메소드의 구현은 ExpStatistics_class.mqh 파일에서 자세하게 공부하실 수 있으니 여기서는 생략하겠습니다.
이 클래스의 중요성은 아웃라이어가 없는 어레이(Parr[])를 리턴한다는 것입니다. 그 외로 표본 추출 및 추정치에 대한 기술 통계량을 얻는 데에도 도움이 됩니다.
2.2 가공된 샘플 히스토그램 생성하기
이제 아웃라이어가 없는 어레이를 얻었으므로 데이터를 기반으로 히스토그램 (빈도 분포)을 그릴 수 있습니다. 랜덤 변수 분포 법칙을 시각적으로 추정하는 데 도움이 될 것입니다. 히스토그램을 생성하기 위한 단계별 절차가 있습니다.
우선 필요한 클래스 수를 계산해야 합니다. 이 경우에서 "클래스"라는 단어는 그룹, 인터벌을 말합니다. 클래스 수는 스터지스의 공식을 통해 계산됩니다:
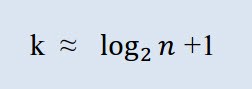
k는 클래스의 수 n은 관측값의 수 입니다.
MQL5에서 공식은 다음과 같이 나타낼 수 있습니다:
int Sturges(int n) /* Function for determining the number of class intervals using Sturges' rule. Variables: y is the number of sampling observations. Returned value: number of class intervals. */ { double s; // Returned value s=1.+log2(y); if(s>15) // Empirical rule s=15; return(int) floor(s); }
스터지스 공식을 사용하여 필요한 클래스 수(간격)를 수신한 경우 어레이 데이터를 클래스로 분해할 때입니다. 그런 데이터는 관측값들 (단수로는 관측). 우린 아래에서처럼 Allocate 함수를 통해 처리합니다:
void Allocate(double &data[],int n,double &f[],double &b[],int k) /* Function for allocating observations to classes. Variables: 1) data — initial sample (array) 2) n — sample size 3) f — calculated array of observations allocated to classes 4) b — array of class midpoints 5) k — number of classes */ { int i,j; // Loop counter double t,c; // Auxiliary variable t=data[ArrayMinimum(data)]; // Sample minimum t=t>0 ? t*0.99 : t*1.01; c=data[ArrayMaximum(data)]; // Sample maximum c=c>0 ? c*1.01 : c*0.99; c=(c-t)/k/2; // Half of the class interval b[0]=t+c; // Array of class interval midpoints f[0]= 0; for(i=1; i<k; i++) { b[i] = b[i - 1] + c + c; f[i] = 0; } // Grouping for(i=0; i<n; i++) for(j=0; j<k; j++) if(data[i]>b[j]-c && data[i]<=b[j]+c) { f[j]++; break; } }
보이는 것처럼 해당 함수는 초기 관측값 어레이(data), 그 길이(n), 클래스 수 (k) 를 받아 관측값을 f 어레이의 f[i] 클래스에 할당하며 b[i]는 f[i] 클래스의 중간값입니다. 히스토그램 자료가 준비되었습니다.
앞서 언급한 문서에서 설명한 도구를 사용하여 히스토그램을 표시하겠습니다. 이를 위해 저는 HTML에서 다뤄지는 시리즈의 히스토그램을 표시하는histogramSave 함수를 작성했습니다. 이 함수는 2개의 패러미터를 받습니다: 클래스 어레이(f) 및 클래스 중간값 어레이(b).
예를 들어, volatilityTest.mq5 스크립트를 사용하여 4시간 단위의 포인트에서 EURUSD 쌍 500바에 대한 최대값 최소값 간의 절대값 차이에 대한 히스토그램을 작성했습니다.
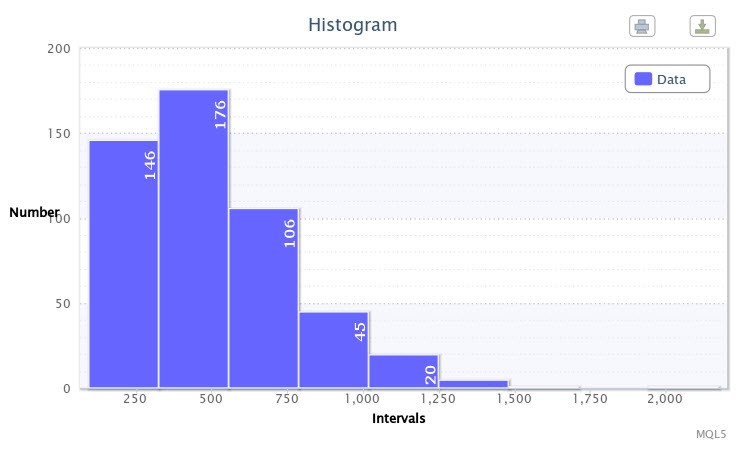
1번 그림. 데이터 히스토그램 (EURUSD H4의 절대 변동성)
히스토그램 (1번 그림)에 보여진 것 처럼, 첫 클래스는 146 개의 관측이 있고 두번째 클래스는 176 개의 관측이 있는 식입니다. 히스토그램의 기능은 연구 중인 샘플의 경험적 분포를 시각적으로 파악하는 것입니다.
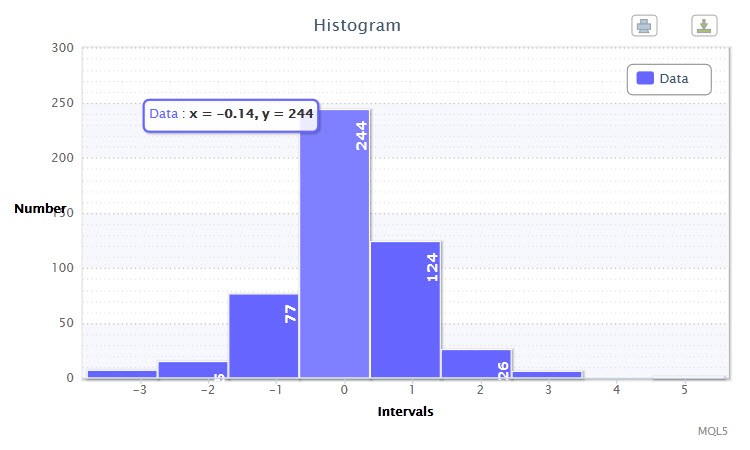
2번 그림. 데이터 히스토그램 (EURUSD H4의 표준화된 값)
다른 히스토그램 (2번 그림)은 H4 타임프레임에서의 EURUSD 쌍 바 500개에 대한 표준화된 로그 반환값을보여주고 있습니다. 눈치채셨겠다시피 4번째와 5번째 클래스들은 각각 인상깊은 244 개와 124 개의 관측값을 가지고 있습니다. 이 히스토그램은 returnsTest.mq5 스크립트를 이용하여 만들어졌습니다.
따라서 히스토그램에서는 모수를 추가로 추정할 분포 법칙을 선택할 수 있습니다. 어떤 분포를 선호할지 시각적으로 분명하지 않은 경우 여러 이론적인 분포의 모수를 추정할 수 있습니다.
우리가 고려한 두 분포 모두 외형상 일반 분포와 유사하지 않은데 이 점은 첫번째 분포가 좀 더 심합니다. 허나 그림을 믿지 말고 진행해야합니다.
2.3 정규성 가설
해당 분포가 정규 분포인지 여부에 대한 가정(가설)을 먼저 풀고 검정하는 것이 관례입니다. 그러한 가설은 주요 가설이라고 불립니다. 샘플의 정규성을 판단하는 방법 들 중의 하나는 자크-베라 테스트(Jarque-Bera test)입니다.
가장 복잡하지는 않지만 근사치 때문에 이 알고리즘은 상당히 양이 되는 편입니다. 자동 트레이딩 알고리즘은 C++나 다른 언어로 준비되어 있습니다. 가장 성공적이고 검증된 버전 중 하나는 교차 플랫폼 수치 분석 라이브러리 ALGLIB에 있는 버전입니다. 제작자 [S.A. 보흐카노프]는 테스트 분위수 표를 컴파일 하는 등, 대단한 일을 해냈습니다. 저는 이를 MQL5의 필요성에 맞춰 업데이트 했습니다.
메인 함수인 jarqueberatest는 다음과 같습니다:
//+------------------------------------------------------------------+ // the Jarque-Bera Test | //+------------------------------------------------------------------+ void jarqueberatest(double &x[],double &p) /* The Jarque-Bera test is used to check hypothesis about the fact that a given sample xS is a sample of normal random variable with unknown mean and variance. Variables: x - sample Xs; p - p-value; */ { int n=ArraySize(x); double s; p=0.; if(n<5)//N is too small { p=1.0; return; } //N is large enough jarquebera_jarqueberastatistic(x,n,s); p=jarquebera_jarqueberaapprox(n,s); } //+------------------------------------------------------------------+
이 함수는 초기 데이터 샘플 (x를 받아р-값을 반환합니다. 이는 귀무가설을 부정할 수 있는 가능성을 나타내는 값입니다.
함수 본문에는 2개의 보조 함수가 있습니다. 첫 함수 - jarquebera_jarqueberastatistic는 자크-베라 통계를 산출하며, 두번째 함수 - jarquebera_jarqueberaapprox는 p-값을 계산합니다. 후자는 알고리즘에서 거의 30인 근사치와 관련된 보조 기능을 실행한다는 점에 유의해야 합니다.
자 이제 정규성 샘플을 테스트해봅시다 우리는 EURUSD H4 샘플의 정규화된 리턴을 하는 returnsTest.mq5 스크립트를 써볼 것입니다.
예상대로 테스트에서는 진정한 귀무가설을 부정할 확률이 0.0000임을 보여줍니다. 즉, 이 표본의 분포는 정규 분포 계열에 속하지 않습니다. EURUSD 쌍의 절대변동성 표본을 처리하기 위해서 volatilityTest.mq5 스크립트를 기동시키세요. 결과는 비슷합니다. 분포가 정규적이지 않습니다.
3. 분포 맞춤
경험적 분포를 정규 분포와 비교할 수 있는 수학 통계학에는 몇 가지 방법이 있습니다. 가장 큰 문제는 정규 분포 모수가 알려져 있지 않으며 연구 대상 데이터가 분포의 정규성을 반영하지 않는다는 가정이 있다는 것입니다.
따라서 비모수 검정을 사용하고 미지 모수를 경험적 분포에서 얻은 추정치로 채워야 합니다.
3.1 추정 및 테스트
이 상황을 해결하기에 제일 걸맞고 제일 인기도 좋은 테스트는 χ2 테스트입니다. 이것은 피어슨의 적합도 검증법에 기반을 두고 있습니다.
이제 이 테스트를 chsone 함수를 이용하여 진행할 것입니다.
void chsone(double &f[],double &ebins[],double &df, double &chsq,double &prob,const int knstrn=1) /* 1) f — array of observations allocated to classes 2) ebins - array of expected frequencies 3) df - number of degrees of freedom 3) chsq — chi-square statistics 4) prob - probability of accepting a true null hypothesis 5) knstrn — constraint */ { CGamma gam; int j,nbins=ArraySize(bins),q,g; double temp; df=nbins-knstrn; chsq=0.0; q=nbins/2; g=nbins-1; for(j=0;j<nbins/2;j++) //passing through the left side of the distribution { if(ebins[j]<0.0 || (ebins[j]==0. && bins[j]>0.)) Alert("Bad expected number in chsone!"); if(ebins[j]<=5.0) { --df; ebins[j+1]+=ebins[j]; bins[j+1]+=bins[j]; } else { temp=bins[j]-ebins[j]; chsq+=pow(temp,2)/ebins[j]; } } for(j=nbins-1;j>nbins/2-1;j--) //passing through the right side of the distribution { if(ebins[j]<0.0 || (ebins[j]==0. && bins[j]>0.)) Alert("Bad expected number in chsone!"); if(ebins[j]<=5.0) { --df; ebins[j-1]+=ebins[j]; //starting with the last class bins[j-1]+=bins[j]; } else { temp=bins[j]-ebins[j]; chsq+=pow(temp,2)/ebins[j]; } } if(df<1)df=1; //compensate prob=gam.gammq(0.5*df,0.5*chsq); //Chi-square probability function }
리스트에서 볼 수 있듯이, CGamma 클래스의 인스턴스가 Distribution_class.mqh 파일에 들어있는 불완전 감마 함수 및 위에 언급한 분포를 나타내도록 사용됩니다. 예상 빈도 어레이 (ebins)는 estimateDistribution 및 expFrequency 함수를 통해 얻어질 것이란 것도 알아둬야 합니다.
이제 이론적 분포에 대한 분석 공식에 포함된 모수를 선택해야 합니다. 모수의 수는 분포에 따라 달라집니다. 예를 들어 정규 분포에는 두 개의 모수가 있고 지수 분포에는 한 개의 모수가 있습니다.
분포 모수를 결정할 때는 모멘트 방법, 분위수 방법 및 최대우도 방법과 같은 점 추정 방법을 주로 사용합니다. 첫 번째는 표본 추출 추정치(기대값, 분산, 왜도 등)가 일반 추정치와 일치해야 한다는 것을 의미하기 때문에 더 간단합니다.
예를 들어 샘플에 대한 이론적 분포를 선택하도록 합시다. 지금부터 우리는 이미 히스토그램으로 표시한 EURUSD H4의 정규화 반환 값을 시리즈로 만들 것입니다.
첫 눈에 보기엔 과도한 첨도 계수가 관찰되기 때문에 정규 분포가 시리즈에 적합하지 않아보입니다. 비교하기위해 다른 분포를 시도해봅시다.
그래서 이미 우리가 다뤄본 returnsTest.mq5 스크립트에서, Hypersec 같은 분포를 써봅니다.. 또한 해당 스크립트는 estimateDistribution 함수에 선택한 분포 모수를 이용하여 χ2 테스트를 시행한 후 계측과 결과를 생산할 것입니다. 선택한 분포 모수는 다음과 같습니다.
쌍곡선 구간 분포: X~HS(-0.00, 1.00);
테스트 결과는 아래와 같습니다:
카이-제곱 통계량: 1.89; 참 귀무 가설을 기각할 확률: 0.8648"
χ2 통계량의 값이 매우 작으므로 선택한 분포가 적합하다는 점에 유의해야 합니다.
추가적으로, histogramSaveE 함수를 통해 표준화된 리턴의 관측 및 예상 빈도비 (빈도비는 분수나 백분율로 표현된 빈도) 값이 그려집니다 (3번 그림). 바 들이 거의 겹치는 것을 볼 수 있습니다. 성공적인 근사의 증거입니다.
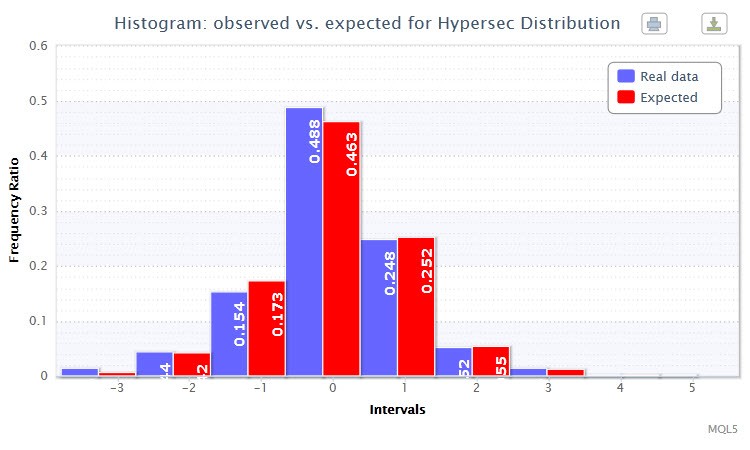
3번 그림. 관측 및 예상 빈도비 히스토그램(EURUSD H4의 표준화된 반환)
이미 사용한 volatilityTest.mq5를 사용하여 변동성 데이터에 대해서도 유사한 절차를 수행하겠습니다.
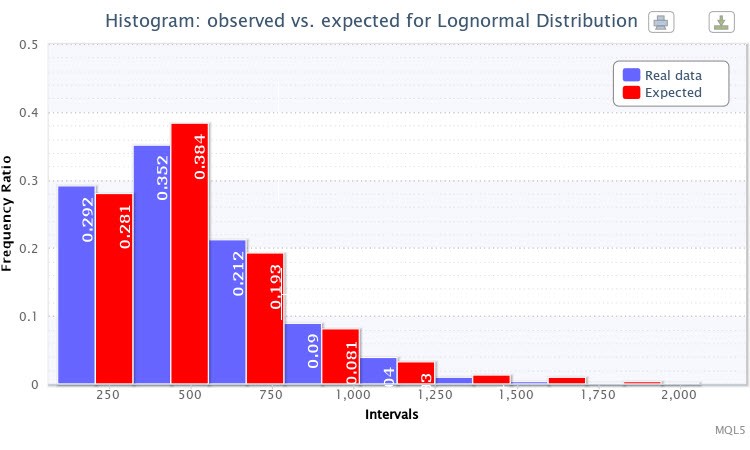
4번 그림. 관측 및 예상 빈도비 히스토그램(EURUSD H4의 절대 변동성)
저는 테스팅 용으로 대수 정규 분포 Lognormal을 선택했습니다. 그 결과, 다음과 같은 모수 추정치가 수신되었습니다:
대수 정규 분포: X~Logn(6.09, 0.53);
테스트 결과는 아래와 같습니다:
"카이-제곱 통계량: 6.17, 실제 귀무 가설을 기각할 확률: 0.4040"
경험적 분포에 대한 이론적 분포도 또한 성공적으로 선택되었습니다. 따라서 귀무 가설은 부정될 수 없습니다. (표준 신뢰도 레벨 p=0.05 기준). 그림 4에서 예상 및 관측된 빈도비의 바가 매우 유사하다는 것을 알 수 있습니다.
이제 설정된 모수가 있는 분포에서 랜덤 변수의 표본을 생성할 수 있는 또 다른 방법이 있음을 알려 드리겠습니다. 해당 작업에 관련된 클래스의 서열을 이용하기 위하여 제가 randomTest.mq5 스크립트를 작성했습니다.
그 시작 부분에서, 우리는 그림 5에 나온 것과 같은 패러미터를 입력할 필요가 있습니다.
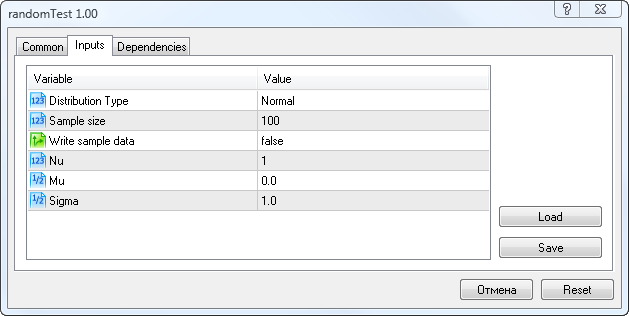
5번 그림. randomTest.mq5 스크립트의 입력 패러미터
여기에서 분포 타입 (Distribution Type), 샘플 내 랜덤 변수의 수 (Sample Size), 샘플 저장 옵션 (Write sample data), Nu 패러미터 (스튜던트 t 분포용), Mu 및 Sigma 패러미터를 선택할 수 있습니다.
만약 Write sample data 옵션 값을 true로 세팅한다면, 스크립트가Randoms.csv 파일에 랜덤 변수와 커스텀 패러미터를 저장할 것입니다. 그 외엔 이 파일에서 샘플 데이터를 읽은 다음 통계 테스트를 수행합니다.
Mu 및 Sigma 패러미터가 없는 분포들을 위하여, 제가 스크립트 시작 창의 필드에 대한 패러미터 상관 관계 표를 제공했습니다..
| 분포 | 첫 분포 패러미터 | 두번째 분포 패러미터 |
|---|---|---|
| 로그 | alph --> Mu | bet --> Sigma |
| 지수 | lambda --> Mu | -- |
| 감마 | alph --> Mu | bet --> Sigma |
| 베타 | alph --> Mu | bet --> Sigma |
| 라플라스 | alph --> Mu | bet --> Sigma |
| 이항식 | n --> Mu | pe --> Sigma |
| 푸아송 | lambda --> Mu | -- |
만약 푸아송 분포가 선택되었다면 람다(lambda) 패러미터가 뮤(Mu) 필드를 거쳐가는 식 입니다.
이 스크립트는 절대 대다수의 경우 점 추정, 신뢰 구간 구축 및 정규 분포의 통계적 표본의 알려지지 않은 평균과 관련된 가설 테스트와 같은 몇 가지 통계 절차에서만 사용되기 때문에 스튜던트 t 분포 모수를 추정하지 않습니다.
예를 들어, Write sample data=true인 경우에 패러미터로 X~Nor(3.50, 2.77)를 지정하고 표준 분포로 스크립트를 기동시켰습니다. 스크립트가 먼저 샘플을 생성했습니다. Write sample data=false인 두번째 시행에서는 6번 그림에 보이는 것 처럼 히스토그램이 만들어졌습니다.
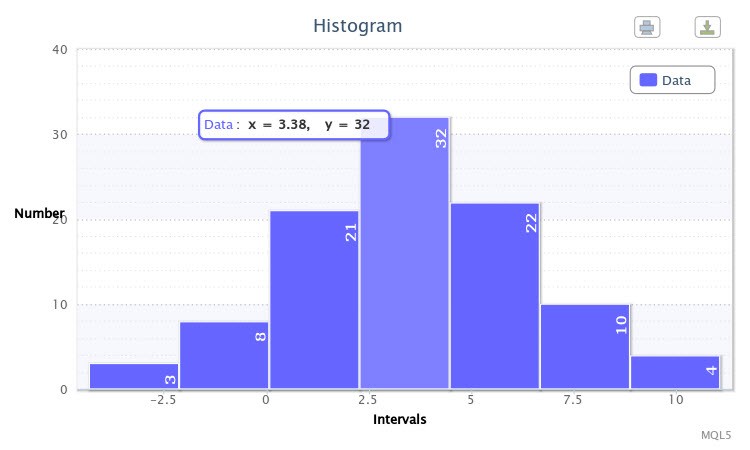
6번 그림. X~Nor(3.50,2.77)의 랜덤 변수 샘플
Terminal 창에 표시되는 나머지 정보는 다음과 같습니다:
자크-베라 테스트: "자크-베라 테스트: 참 귀무 가설을 부정할 확률은 0.9381";
모수 예상: 표준 분포: X~Nor(3.58, 2.94);
카이 제곱 테스트 결과: "카이 제곱 통계:: 0.38; 참 귀무 가설을 부정할 확률: 0.9843".
마지막으로, 표본의 관측 및 예상 주파수 비율에 대한 또 다른 이중 히스토그램이 표시되었습니다(7번 그림).
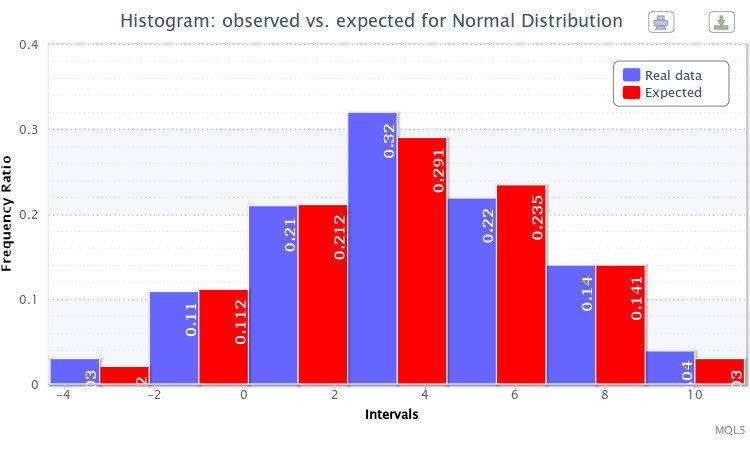
7번 그림. X~Nor에 대한 관측 및 예상 빈도비 히스토그램(3.50,2.77)
일반적으로 지정된 분포의 생성에 성공했습니다.
randomTest.mq5스크립트와 비슷한 작업을 수행하는 fitAll.mq5 스크립트 역시 작성했습니다. 유일한 차이는 두번째 스크립트에 fitDistributions 함수가 있다는 점입니다. 저는 다음 목표를 세웠습니다: 모든 가능한 분포를 랜덤 변수 샘플들에 근사하여 통계적 테스트를 시행할 것.
"베타 분포를 추정할 수 없음!"과 같이 터미널에 선이 나타나기 때문에 모수 불일치로 인해 항상 분포를 표본에 맞출 수 있는 것은 아닙니다.
또한, 이 스크립트가 "HTML의 차트와 도표" 문서에서 찾을 수 있는 작은 HTML 보고서의 형태로 통계 결과를 시각화해야 한다고 결정했습니다(8번 그림).
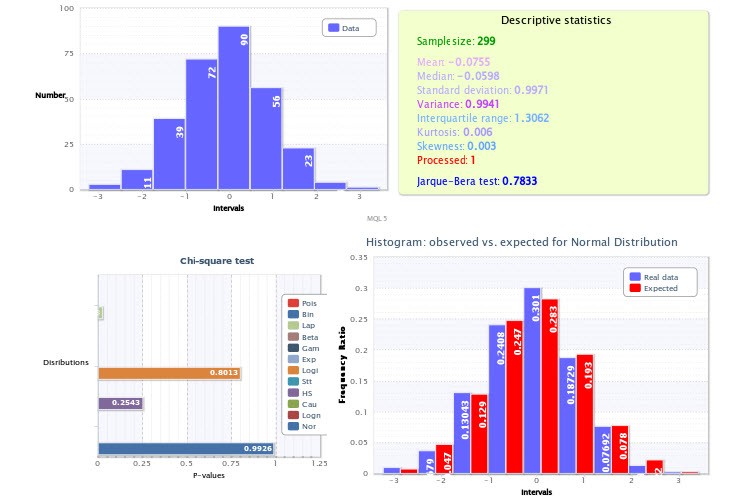
8번 그림. 표본 추정에 대한 통계적 리포트
표본의 표준 히스토그램은 왼쪽 위 분기에 표시됩니다. 오른쪽 위 분기는 기술 통계량 및 자크-베라 테스트 결과를 나타냅니다. 여기서 1과 같은 Processed 값은 아웃라이어가 삭제되었음을 의미하고 0 값은 아웃라이어가 없음을 의미합니다.
선택한 모든 분포에 대한 χ2 test의 P-값들은 좌하단에 표시되어 있습니다. 여기서 정규 분포가 적합 측면에서 가장 우수한 것으로 나타났습니다(p=0.9926). 따라서 오른쪽 아래에 관측 빈도비와 예상 빈도비 히스토그램이 그려졌습니다.
현재 갤러리에는 그다지 분포가 많지 않습니다. 하지만 분포 수가 많은 경우 이 스크립트를 사용하면 많은 시간을 절약할 수 있습니다
이제 연구 중인 샘플의 분포 모수를 정확히 알게 되었으므로 확률론적 추론으로 진행할 수 있습니다.
3.2 랜덤 변인값의 확률
이론적 분포에 대해 논한 문서에서 저는 continuousDistribution.mq5 스크립트를 예시로 삼았습니다. 이를 사용하여 알려진 모수를 가진 분포법을 표시하려고 합니다.
변동성 데이터에 저는 앞서 얻은 대수 정규 분포 모수를 입력할 것입니다.(Mu=6.09, Sigma=0.53), 대수 정규 분포 타입을 선택하고 cdf 모드를 고르십시오 (9번 그림).
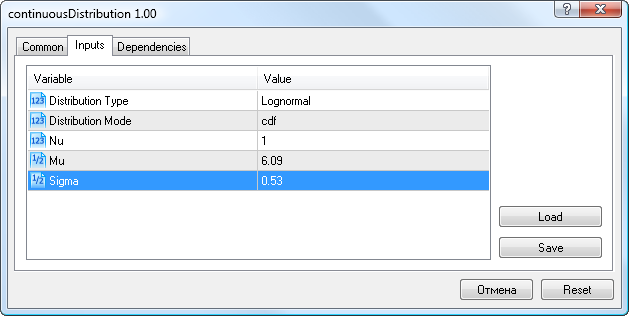
9번 그림. 대수 정규 분포 모수 X~Logn(6.09, 0.53)
그러면 스크립트가 샘플의 분포 함수를 표시합니다. 10번 그림에서처럼 보일 것입니다.
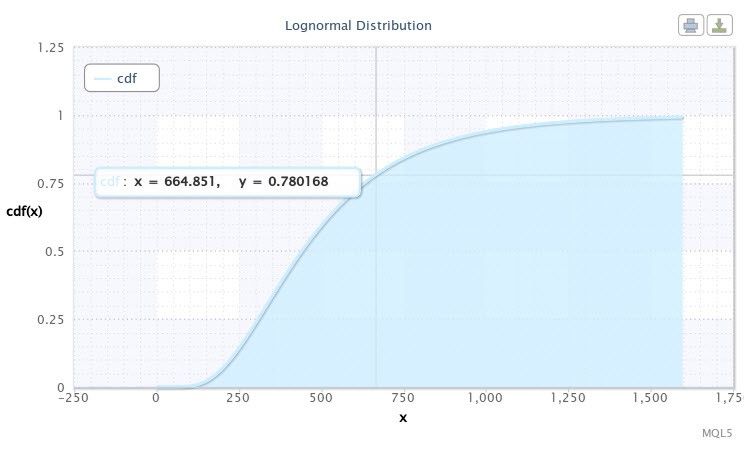
10번 그림. X~Logn (6.09, 0.53) 분포 함수
차트를 보면 커서가 대략 좌표가 [665;0.78]인 지점을 가리키고 있음을 알 수 있습니다. 이는 EURUSD H4의 변동성이 665 포인트를 넘지 않을 확률이 78% 라는 의미 입니다. 이 정보는 Expert Advisor 개발자에게는 매우 도움될 수도 있습니다. 커서를 움직이는 것 만으로 다른 값들을 커브 위로 올릴 수 있습니다.
변동성이 500에서 750 포인트 사이에 위치했을 때 우리가 이벤트가 발생할 확률이 궁금하다고 가정해봅시다. 이 목적을 위해서는 다음과 같은 작업이 수반되어야합니다:
cdf(750) - cdf(500) = 0.84 - 0.59 = 0.25.
따라서 500 에서 750포인트 사이에서 이벤트가 발생할 확률은 25% 가량입니다.
같은 분포 모수를 이용하지만 이번엔 sf만을 분포 법칙 모드로 선택하여 스크립트를 기동시켜봅시다. 신뢰성(생존) 함수는 다음과 같이 표시됩니다(11번 그림).
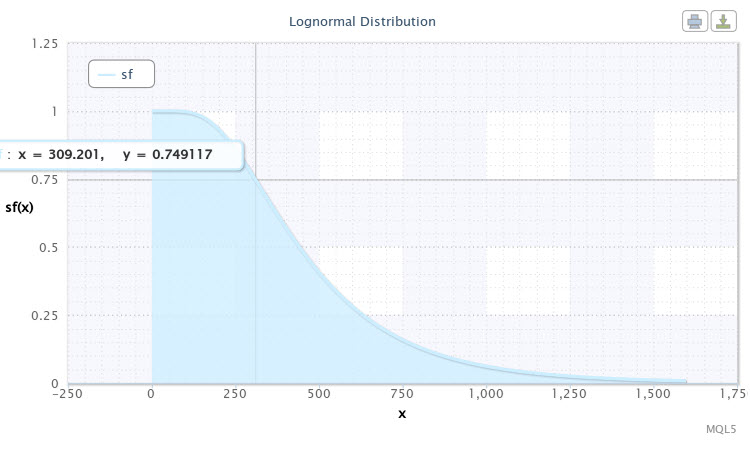
11번 그림. X~Logn의 생존 함수(6.09, 0.53)
곡선 차트에 마크된 포인트는 다음과 같이 해석될 수 있습니다: 쌍의 변동성이 310 포인트일 확률은 75%이다. 곡선에서 아래로 내려갈 수록 변동성이 올라갈 확률은 낮아집니다. 따라서 1000 포인트가 넘는 변동성은 그 자체로도 희소한 이벤트이며 발생할 확률은 5% 미만입니다.
표준화된 수익률의 표본뿐만 아니라 다른 표본에도 유사한 분포 곡선을 작성할 수 있습니다. 방법론은 나름 명료한 것 같네요.
마치며
제안된 분석은 시리즈가 다양하기 때문에 완전히 성공적이지는 않다는 점에 유의해야 합니다. 예를 들어 일련의 로그 반환과 관련이 없습니다. 그렇지만 저는 이 문서에서는 그 메소드들을 평가하지 않기로 했습니다. 이에 대해 관심있으신 분은 댓글 란에 부탁드리겠습니다.
중요한 것은 시장, 시장 상품 및 매매 전문가를 확률론적 관점에서 고려할 필요가 있다는 점입니다. 이것이 제가 보여드리고자 했던 어프로치입니다. 본 주제에 대해 독자 여러분이 관심을 갖게 되셨기를, 그리고 생산성 있는 토의로 이어지는 것을 빕니다.
파일의 위치:
| # | 파일 | 경로 | 설명 |
|---|---|---|---|
| 1 | Distribution_class.mqh | %MetaTrader%\MQL5\Include | 분포 클래스 갤러리 |
| 2 | DistributionFigure_class.mqh | %MetaTrader%\MQL5\Include | 분포의 시각적 표시 클래스 |
| 3 | Random_class.mqh | %MetaTrader%\MQL5\Include | 랜덤 숫자 샘플 생성용 클래스 |
| 4 | ExpStatistics_class.mqh | %MetaTrader%\MQL5\Include | 통계학적 특성의 예측 클래스 및 함수들 |
| 5 | volatilityTest.mq5 | %MetaTrader%\MQL5\Scripts | EURUSD H4 변동성 예측 스크립트 |
| 6 | returnsTest.mq5 | %MetaTrader%\MQL5\Scripts | EURUSD H4 반환 샘플 예측 스크립트 |
| 7 | randomTest.mq5 | %MetaTrader%\MQL5\Scripts | 랜덤 변인 샘플 예측 스크립트 |
| 8 | fitAll.mq5 | %MetaTrader%\MQL5\Scripts | 모든 분산 예측 및 근사 스크립트 |
| 9 | Volat.csv | %MetaTrader%\MQL5\Files | EURUSD H4 변동성 샘플 데이터 파일 |
| 10 | Returns_std.csv | %MetaTrader%\MQL5\Files | EURUSD H4 리턴 샘플 데이터 파일 |
| 11 | Randoms.csv | %MetaTrader%\MQL5\Files | 랜덤 변인 샘플 데이터 파일 |
| 12 | Histogram.htm | %MetaTrader%\MQL5\Files | HTML 내 샘플의 히스토그램 |
| 13 | Histogram2.htm | %MetaTrader%\MQL5\Files | HTML 내 샘플의 더블 히스토그램 |
| 14 | chi_test.htm | %MetaTrader%\MQL5\Files | 샘플 예측의 통계학적 HTML 리포트 |
| 15 | dataHist.txt | %MetaTrader%\MQL5\Files | 샘플 히스토그램 표시용 데이터 |
| 16 | dataHist2.txt | %MetaTrader%\MQL5\Files | 샘플 더블 히스토그램 표시용 데이터 |
| 17 | dataFitAll.txt | %MetaTrader%\MQL5\Files | HTML 리포트 표시용 데이터 |
| 18 | highcharts.js | %MetaTrader%\MQL5\Files | 상호작용 차트의 JavaScript 라이브러리 |
| 19 | jquery.min.js | %MetaTrader%\MQL5\Files | JavaScript 라이브러리 |
| 20 | ReturnsIndicator.mq5 | %MetaTrader%\MQL5\Indicators | 대수 리턴 인디케이터 |
레퍼런스 자료:
MetaQuotes 소프트웨어 사를 통해 러시아어가 번역됨.
원본 기고글: https://www.mql5.com/ru/articles/257
가격 상관 관계 통계 데이터를 기반으로 신호 필터링
C++ 템플릿의 대안으로 가짜 템플릿 사용
선형 회귀 예시를 통한 인디케이터 가속 그 3가지 방법
시계열 예측을 위한 ENCOG 머신 러닝 프레임워크와 함께 MetaTrader 5 지표 사용
