トレーダーの作業における統計的分布の役割
842
0
秩序は暮らしを楽にするが、でたらめから得られる恩恵にとっても重要である。
(Georgiy Aleksandrov)
はじめに
本稿は、理論的統計的分布に連携するクラスについて述べた拙著『MQL5 における統計的確率』の続編です。まずユーザーがのちに実践で使用しやすいように分布クラス形式の基礎を作る必要があることに気づきました
われわれには理論的基盤があるので、現実のデータ設定に進み、こ基盤を情報的に利用していきたいと思います。同時に、数学的統計に関連する問題も解明していきます。
1. 既定分布を用いた乱数作成
実データ設定を考える前に、たいへん重要なことは望ましい理論分布に強く関連する値のセットを取得することのように思えます。
すなわち、ユーザーは望ましい分布とサンプルサイズのパラメータのみをセットする必要があのです。プログラム（今回の場合、クラス階層）はのちの作業のためにそのような値サンプルを作成し出力する必要があります。
もうひとつ重要な事柄は、指定された規則で作成されるサンプルは数々の統計的検定をチェックします。数学的統計の分野：異なる分布法則によるランダム変数の作成、はかなり興味深く、困難ですがやりがいのあるものです。
私は目的に応じた、著書 Numerical Recipes: The Art of Scientific Computing [2]で述べられているクオリティーの高いジェネレータを使用します。その周期はおおよそ 3.138*1057です。C 言語コードは簡単にMQL5に渡されました。
よって私は以下のように Random クラスを作成しました。
//+------------------------------------------------------------------+ //| Random class definition | //+------------------------------------------------------------------+ class Random { private: ulong u, //unsigned 64-bit integers v, w; public: //+------------------------------------------------------------------+ //| The Random class constructor | //+------------------------------------------------------------------+ void Random() { randomSet(184467440737095516); } //+------------------------------------------------------------------+ //| The Random class set-method | //+------------------------------------------------------------------+ void randomSet(ulong j) { v=4101842887655102017; w=1; u=14757395258967641292; u=j^v; int64(); v = u; int64(); w = v; int64(); } //+------------------------------------------------------------------+ //| Return 64-bit random integer | //+------------------------------------------------------------------+ ulong int64() { uint k=4294957665; u=u*2862933555777941757+7046029254386353087; v^= v>> 17; v ^= v<< 31; v ^= v>> 8; w = k*(w & 0xffffffff) +(w>> 32); ulong x=u^(u<<21); x^=x>>35; x^=x<<4; return(x+v)^w; }; //+------------------------------------------------------------------+ //| Return random double-precision value in the range 0. to 1. | //+------------------------------------------------------------------+ double doub() { return 5.42101086242752217e-20*int64(); } //+------------------------------------------------------------------+ //| Return 32-bit random integer | //+------------------------------------------------------------------+ uint int32() { return(uint)int64(); } };
ここで分布からサンプルとして抽出される値に対するクラス作成が可能です。
例として、正規分布からのランダム変数を見てみます。CNormaldev クラスは以下です。
//+------------------------------------------------------------------+ //| CNormaldev class definition | //+------------------------------------------------------------------+ class CNormaldev : public Random { public: CNormaldist N; //Normal Distribution instance //+------------------------------------------------------------------+ //| The CNormaldev class constructor | //+------------------------------------------------------------------+ void CNormaldev() { CNormaldist Nn; setNormaldev(Nn,18446744073709); } //+------------------------------------------------------------------+ //| The CNormaldev class set-method | //+------------------------------------------------------------------+ void setNormaldev(CNormaldist &Nn,ulong j) { N.mu=Nn.mu; N.sig=Nn.sig; randomSet(j); } //+------------------------------------------------------------------+ //| Return Normal deviate | //+------------------------------------------------------------------+ double dev() { double u,v,x,y,q; do { u = doub(); v = 1.7156*(doub()-0.5); x = u - 0.449871; y = fabs(v) + 0.386595; q = pow(x,2) + y*(0.19600*y-0.25472*x); } while(q>0.27597 && (q>0.27846 || pow(v,2)>-4.*log(u)*pow(u,2))); return N.mu+N.sig*v/u; } }; //+------------------------------------------------------------------+
ご覧のように、クラスにはデータメンバー N of CNormaldist タイプがあります。オリジナルの C コードにはそのような分布との連携がありませんでした。クラス（ここでは CNormaldev クラスによる）によって作成されたランダム変数はその分布とロジカルかつプログラム的な関係を持つ必要があると考えました。
オリジナルでは 以下のようにNormaldev タイプが定義されています。
typedef double Doub; typedef unsigned __int64 Ullong; struct Normaldev : Ran { Doub mu,sig; Normaldev(Doub mmu, Doub ssig, Ullong i) ... }
乱数はここでuniforms メソッドのレバレッジ比率を用いた正規分布から作成されます。
さまざまな分布からのランダム変数を計算する助けとなるクラスはすべてインクルードファイル Random_class.mqh にあります。
作成は終わるので、本稿の実践部分で値配列の作成方法とサンプル検定方法をみていきます。
2. 分布パラメータ試算、統計的仮定
あきらかにわれわれが調査するのは離散変数です。ただし、実践では離散変数の数字が有意であれば、そのような変数セットを連続型変数として考えるのが便利です。これは数学的つ折形における標準的 手法です。それを分析するには、連続型変数に関連する分析式により定義される分布を使用することが可能です。
そこで 経験分布の分析にとりかかります。
メンバが代表性 の基準を満たす一般集団のサンプルは研究中だと思われます。また、セクション8.3 [9] で指定された試算への要件は満たしています。数値分布パラメータは点推定および句半法によって見つけることが可能です。
2.1CExpStatistics クラスを用いたサンプル処理
まず、サンプルからのいわゆる異常値を削除する必要があります。これらはサンプルの主要パートから著しく外れたものです。（上下どちらにも）異常値を削除する汎用メソッドは存在しません。
セクション6.3 [5にS.V.Bulashev により記述されたものを提案します。In MQL4 フォーラムでは、 統計的関数ライブラリは既定の問題が簡単に解決するということに基づき作成されています。ということは確実OOP を適用し、それに少し手を加えるということです。
私は作成された、統計的推定を行うクラスをCExpStatistics （期待される統計のクラス）と名づけました。
それは簡単に、次のようなものです。
//+------------------------------------------------------------------+ //| Expected Statistics class definition | //+------------------------------------------------------------------+ class CExpStatistics { private: double arr[]; //initial array int N; //initial array size double Parr[]; //processed array int pN; //processed array size void stdz(double &outArr_st[],bool A); //standardization public: void setArrays(bool A,double &Arr[],int &n); //set array for processing bool isProcessed; //array processed? void CExpStatistics(){}; //constructor void setCExpStatistics(double &Arr[]); //set the initial array for the class void ZeroCheckArray(bool A); //check the input array for zero elements int get_arr_N(); //get the initial array length double median(bool A); //median double median50(bool A); //median of 50% interquantile range (midquartile range) double mean(bool A); //mean of the entire initial sample double mean50(bool A); //mean of 50% interquantile range double interqtlRange(bool A); //interquartile range double RangeCenter(bool A); //range center double meanCenter(bool A); //mean of the top five estimates double expVariance(bool A); //estimated variance double expSampleVariance(bool A); //shifted estimate of sample variance double expStddev(bool A); //estimated standard deviation double Moment(int index,bool A,int sw,double xm); //moment of distribution double expKurtosis(bool A,double &Skewness); ////estimated kurtosis and skewness double censorR(bool A); //censoring coefficient int outlierDelete(); //deletion of outliers from the sample int pArrOutput(double &outArr[],bool St); //processed array output void ~CExpStatistics(){};//destructor }; //+------------------------------------------------------------------+
各メソッドの実装に関する詳細はインクルードファイル、ExpStatistics_class.mqh にあるので、ここでは扱いません。
このクラスが行う重要なことは、異常値のない配列(Parr[]),があればそれを介すことです。その上、サンプルの記述統計と推定値を取得する手助けをします。
2.2処理済みサンプルヒストグラムの作成
配列には異常値が含まれないということで、そのデータを基にヒストグラムを描画することができます。それはランダム変数分布法則を視覚的に予測するのに役立ちます。ヒストグラムを作成するには段階的手順があります。
まず、要求されるクラス数を計算する必要があります。ここで「クラス」とはグループ化、区間をいいます。クラス数はスタージェスの公式で計算されます。
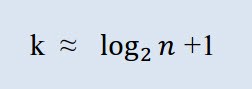
ここで k がクラス数のときn は観測数です。
MQL5 では、式は以下のように書き表されます。
int Sturges(int n) /* Function for determining the number of class intervals using Sturges' rule. Variables: y is the number of sampling observations. Returned value: number of class intervals. */ { double s; // Returned value s=1.+log2(y); if(s>15) // Empirical rule s=15; return(int) floor(s); }
要求されるクラス数（区間）がスタージェスの公式を用いて受け取られたら、配列データをクラスに落とし込みます。そのようなデータを観測値 (sing. observation)と呼びます。以下のように関数Allocate を使って行います。
void Allocate(double &data[],int n,double &f[],double &b[],int k) /* Function for allocating observations to classes. Variables: 1) data — initial sample (array) 2) n — sample size 3) f — calculated array of observations allocated to classes 4) b — array of class midpoints 5) k — number of classes */ { int i,j; // Loop counter double t,c; // Auxiliary variable t=data[ArrayMinimum(data)]; // Sample minimum t=t>0 ? t*0.99 : t*1.01; c=data[ArrayMaximum(data)]; // Sample maximum c=c>0 ? c*1.01 : c*0.99; c=(c-t)/k/2; // Half of the class interval b[0]=t+c; // Array of class interval midpoints f[0]= 0; for(i=1; i<k; i++) { b[i] = b[i - 1] + c + c; f[i] = 0; } // Grouping for(i=0; i<n; i++) for(j=0; j<k; j++) if(data[i]>b[j]-c && data[i]<=b[j]+c) { f[j]++; break; } }
見てのとおり、関数は初期観測値(data)の配列、その長さ (n)、クラス数 (k) を持ち、観測値をf 配列の特定クラスf[i] に割り当てます。それはb[i] is the f[i] クラスの中点です。これでヒストグラムデータが準備できました。
前出の記事で述べられているツールを用いたヒストグラムを表示します。これには、関数 histogramSave を書きました。これは調査中の系列に対するヒストグラムを HTML形式で表示します。この関数はパラメータを2つ取ります。クラス配列 (f) およびクラス中点の配列 (b)です。
例では、volatilityTest.mq5 スクリプトを使用したポイントにおける4時間足の時間枠でEURUSDについて500バー分の高値安値間の絶対差を表すヒストグラムを作成します。
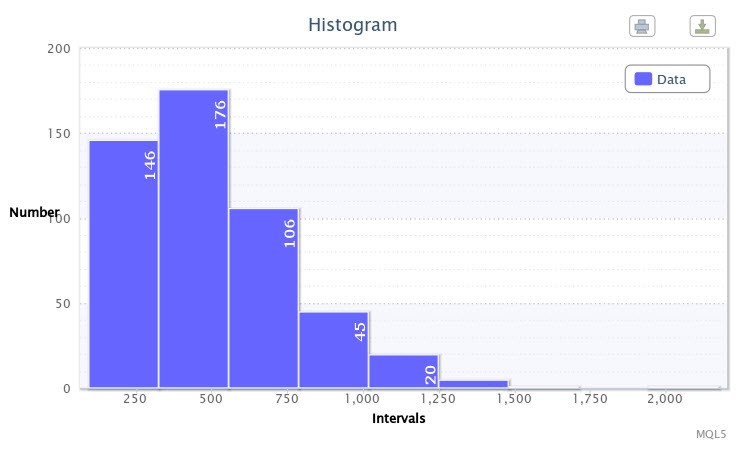
図1 データヒストグラム（EURUSD H4の絶対変動率）
ヒストグラム（図1）に表示されているように、最初のクラスは観測値 146 であり、二番目のクラスは観測値 176 等、です。ヒストグラム関数は調査対象サンプルの経験分布について視覚的な考察を提供します。
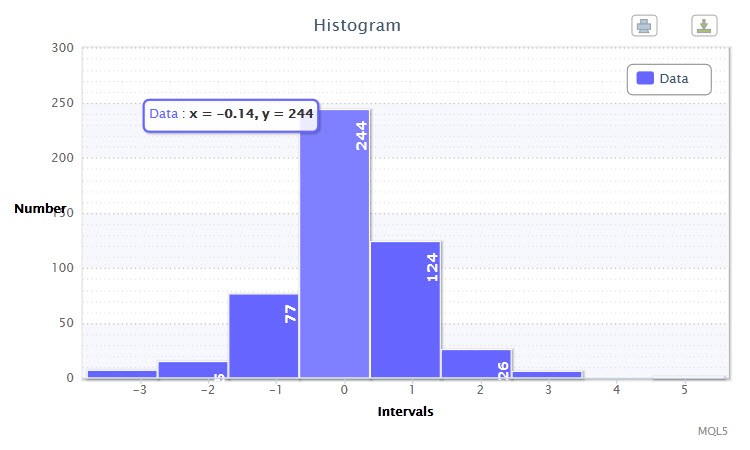
図2 データヒストグラム（EURUSD H4の標準化された戻り値）
別のヒストグラム（図2）は、EURUSD ペアの500バー分について H4 時間枠での標準化された 対数戻り値を表示します。お気づきのように、4番目および5番目のクラスがもっとも顕著な値で、それぞれ観測値 244 と 124 となっています。ヒストグラムはスクリプト returnsTest.mq5 を用いて作成されています。
よって、ヒストグラムにより、のちに推定されるパラメータの分布法則を選択することができます。どちらの分布が好ましいか視覚的に明確かどうかについては、複数の理論的分布パラメータを推定してみることです。
ここで考察した分布に関してはどちらも見た目は通常分布とは異なります。特に一番目の分布に顕著です。ただし、視覚的表現を信用するのではなく、図にも進みましょう。
2.3正常化仮定
問題の分布が正常かどうかについての仮定は、まずそれを解き、検証するのが常套手段 でしょう。そのような仮定は主要仮説と呼ばれます。サンプルの正常性を検証するのに最もよく使用される手法はジャック・べラ検定です。
そのアルゴリズムは複雑ではありませんが近似値のためにかさばるものです。C++ 言語、および別言語でいくつかのアルゴリズムバージョンがあります。もっとも有用で信頼性の高いバージョンはクロスプラットフォーム数値分析ライブラリALGLIBにあるものです。その著者[S.A.Bochkanov] は特にtest分位点テーブルのコンパイルにおいて偉業をなしました。私は MQL5にニーズに合わせてそれをちょこっと変更しました。
その主要関数jarqueberatestは以下です。
//+------------------------------------------------------------------+ // the Jarque-Bera Test | //+------------------------------------------------------------------+ void jarqueberatest(double &x[],double &p) /* The Jarque-Bera test is used to check hypothesis about the fact that a given sample xS is a sample of normal random variable with unknown mean and variance. Variables: x - sample Xs; p - p-value; */ { int n=ArraySize(x); double s; p=0.; if(n<5)//N is too small { p=1.0; return; } //N is large enough jarquebera_jarqueberastatistic(x,n,s); p=jarquebera_jarqueberaapprox(n,s); } //+------------------------------------------------------------------+
Iそれは初期データサンプル (x) を処理し р-valueを返します。たとえば帰無仮説 が実際 trueの場合、仮説を却下する可能性を特性づける値です。
関数本体には2つ予備関数があります。第一の予備関数：jarquebera_jarqueberastatisticは calculates the ジャック・ベラ統計を計算します第二の呼び関数：jarquebera_jarqueberaapproxは p 値を計算します。後者にいたってはアルゴリズムではほとんど30の近似値に関連する予備関数をアクティブにすることに注意が必要です。
それではサンプルの正常性検証をしてみます。EURUSD H4の正常化された戻り値のサンプルを処理するスクリプト returnsTest.mq5 を使います。
予想どおり、検証により真の 帰無仮説を却下する確率は 0.0000です。別の言い方をすれば、このサンプル分布は正常分布の分類には属していません。 EURUSD ペアの絶対不確実性サンプルを処理するには、volatilityTest.mq5 スクリプトを実行します。結果は似通っています。分布は正常ではありません。
3. 分布の一致
数学的統計には分散分布と正常分布を比較する手法がいくつかあります。もっとも大きな問題は、正常分布パラメータは 未知 で、調査対象データは分布の正常性を反映しないという仮説があります。
よって、非行列検証を行い、分散分布から得られた推測値を未知のパラメータに書き込む必要があります。
3.1推定および検証
今の状況でもっとも一般的でもっとも重要なのは χ2 検定です。これは>ピアソンの適合度指標に基づいています。
ここでは、関数 chsone を用いて検証を行います。
void chsone(double &f[],double &ebins[],double &df, double &chsq,double &prob,const int knstrn=1) /* 1) f — array of observations allocated to classes 2) ebins - array of expected frequencies 3) df - number of degrees of freedom 3) chsq — chi-square statistics 4) prob - probability of accepting a true null hypothesis 5) knstrn — constraint */ { CGamma gam; int j,nbins=ArraySize(bins),q,g; double temp; df=nbins-knstrn; chsq=0.0; q=nbins/2; g=nbins-1; for(j=0;j<nbins/2;j++) //passing through the left side of the distribution { if(ebins[j]<0.0 || (ebins[j]==0. && bins[j]>0.)) Alert("Bad expected number in chsone!"); if(ebins[j]<=5.0) { --df; ebins[j+1]+=ebins[j]; bins[j+1]+=bins[j]; } else { temp=bins[j]-ebins[j]; chsq+=pow(temp,2)/ebins[j]; } } for(j=nbins-1;j>nbins/2-1;j--) //passing through the right side of the distribution { if(ebins[j]<0.0 || (ebins[j]==0. && bins[j]>0.)) Alert("Bad expected number in chsone!"); if(ebins[j]<=5.0) { --df; ebins[j-1]+=ebins[j]; //starting with the last class bins[j-1]+=bins[j]; } else { temp=bins[j]-ebins[j]; chsq+=pow(temp,2)/ebins[j]; } } if(df<1)df=1; //compensate prob=gam.gammq(0.5*df,0.5*chsq); //Chi-square probability function }
リストにあるように CGamma クラスのインスタンスは、述べられているすべての分布と同様、ファイルDistribution_class.mqh にインクルードされている不完全なガンマ関数を代表して使用されます。また予想頻度の配列 (ebins) は関数estimateDistribution および expFrequency を使用して取得されます。
理論的分布に対する分析式にインクルードされる数値パラメータを選択する必要があります。パラメータ数は特定の分布に依存します。たとえば、正常分布ではパラメータが2つあり指数分布にはパラメータが1つ、などです。
分布パラメータを決定するときはモーメントのメソッド、分位点メソッド、最大尤度メソッドとして通常そのようなポイント推定メソッドを使用します。最初のメソッドは、サンプル推定（期待、バリアンス、歪度等）は一般的推定と一致することを示すため単純です。
ここでは例を用いてサンプルの理論分布を選択してみます。すでにヒストグラム作成済みの EURUSD H4 の正常化された戻り値の系列を取ります。
第一印象は正常分布はこの系列に適切ではない、というものです。というのも尖度の超過係数が見られるためです。比較のためにもうひとつ別の分布を試します。
既知のスクリプトreturnsTest.mq5 を始めるとき、その分布をHypersecとして選択してみます。また、そのスクリプトは関数 estimateDistribution を使用して選択した分布パラメータを推定し出力して、すみやかにχ2 testを実行します。選択された分布パラメータは以下のようであることが判明しました。
Hyperbolic Secant 分布： X~HS(-0.00, 1.00);
また検証結果は以下です。
"Chi-square 統計： 1.89; 真の帰無仮説を却下する確率： 0.8648"
選択された分布は χ2 統計の値がきわめて値避ければ一致します。
またhistogramSaveE 関数を使用すると正常化された戻り値の 観測 され、 期待された頻度率 （頻度率は分数またはパーセントで表される頻度）に対するヒストグラムが二重に描画されます。（図3）バーがお互いに二倍近くになっているのが確認できます。これは一致が成功した証明です。
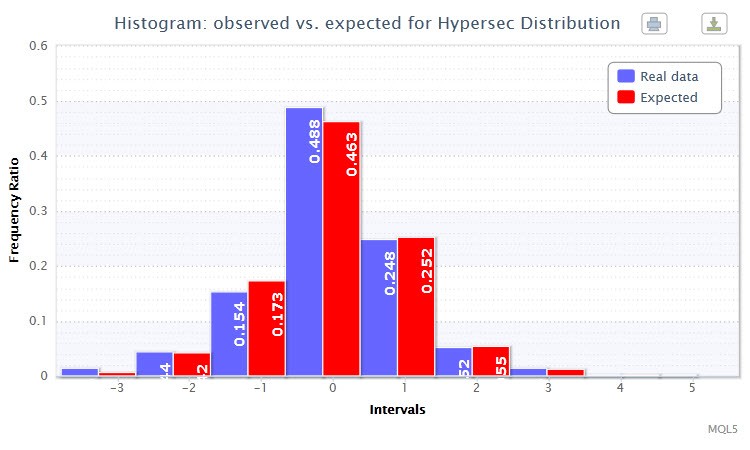
図3 観測され期待された頻度率のヒストグラム（EURUSD H4の正常化戻り値）
すでにわかっているvolatilityTest.mq5を使用し同様のデータの不確実性手順を実行します。
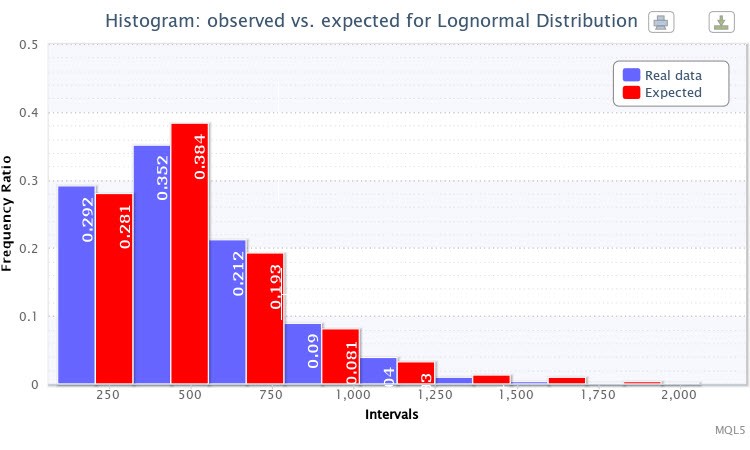
図4 観測され期待された頻度率のヒストグラム（EURUSD H4の絶対不確実性）
検証には対数分布 Lognormal を選択しました。結果、パラメータ推定の以下のような結果を得ました。
対数分布： X~Logn(6.09, 0.53);
また検証結果は以下です。
"Chi-square 統計 6.17；真の 帰無仮説を却下する確率： 0.4040"
分散分布に対する理論分布はまたきわめて成功裏に選択されました。よって、 帰無仮説は却下されないと考えられます（標準 ( confidence level p=0.05において）。図4では、期待される、観測されたバーの頻度率はまたよく似通っています。
設定されたパラメータを伴う分布から得る乱数サンプルを作成する別の機能があることを思い出していただきたいと思います。そのような処理に連携したクラスの階層を使用するために randomTest.mq5 スクリプトを書きました。
とりかかりに、図5に表示されるパラメータを入力する必要があります。
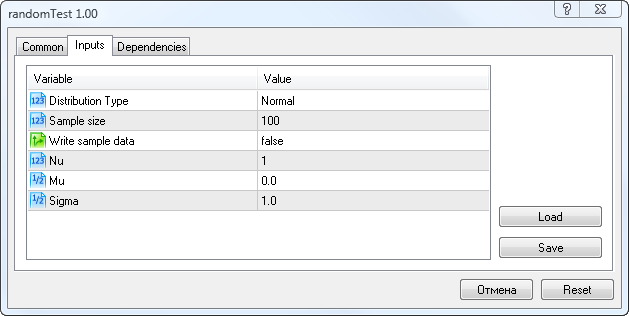
図5 スクリプト randomTest.mq5 scriptの入力パラメータ
ここで、分布タイプ (分布タイプ)サンプル内のランダム関数 (サンプルサイズ)、サンプル保存オプション (サンプルデータ記載)、Nu パラメータ（学生の t 分布）、Mu および Sigma パラメータの選択が可能です。
サンプルデータ記載 に値trueを設定したら、スクリプトはカスタムパラメータを持ちランダム変数のサンプルをRandoms.csv ファイルに保存します。それ以外なら、このファイルからサンプルデータを読み、統計検定を行います。
パラメータMu および Sigma を各分布に対しては、スクリプト開始ウィンドウ内のフィールドにパラメータを提供しました。
| 分布 | 第一分布パラメータ | 第二分布パラメータ |
|---|---|---|
| ロジック | alph --> Mu | bet --> Sigma |
| Exponential | lambda --> Mu | -- |
| Gamma | alph --> Mu | bet --> Sigma |
| Beta | alph --> Mu | bet --> Sigma |
| Laplace | alph --> Mu | bet --> Sigma |
| Binomial | n --> Mu | pe --> Sigma |
| Poisson | lambda --> Mu | -- |
たとえば、ポワソン 分布が選択されるとlambda パラメータが Mu フィールドにより入力される、など。
スクリプトは学生のt 分布パラメータを推定しません。なぜならケースの絶対的大半において、ほんの数件の統計手順で使用されるにすぎないからです。ポイント推定、信頼区間構築、正常分布の統計サンプルの道の平均に関する仮定の検証といったものです。
たとえば Write sample data=trueとなるパラメータX~Nor(3.50, 2.77)を持つ正常分布に対してスクリプトを実行します。スクリプトはまずサンプルを作成しました。Write sample data=falseでの二番目の実行ではヒストグラムは図6のように描かれました。
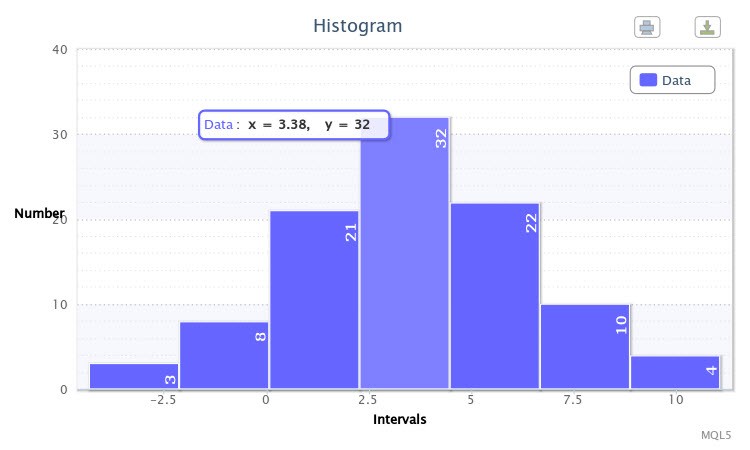
図6 ランダム変数 X~Nor(3.50,2.77)のサンプル
ターミナルウィンドウに表示される残りの情報は以下です。
ジャック・ベラ検定 「ジャック・ベラ検定：真の帰無仮説を却下する確率は 0.9381です」
パラメータ推定：正常分布： X~Nor(3.58, 2.94)
Chi-square検証結果：「Chi-square 統計： 0.38；真の帰無仮説を却下する確率は 0.9843です」
最後に、サンプルに対する観測と期待の頻度率の別の二重ヒストグラムが表示されます。（図7）
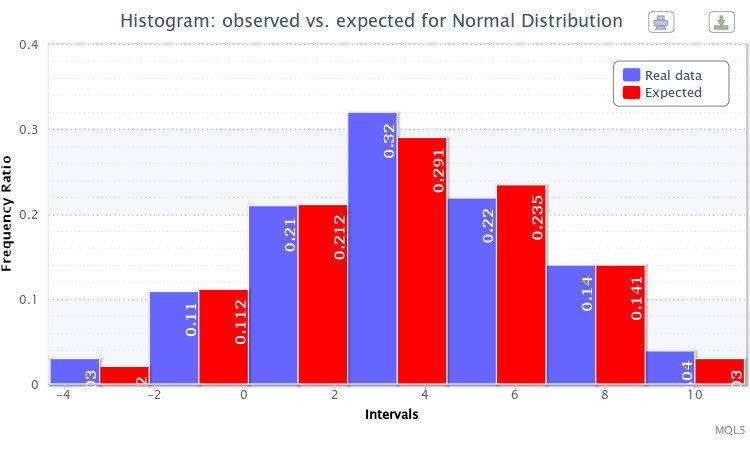
図7 X~Nor(3.50,2.77)に対する観測と期待の頻度率ヒストグラム
一般的に、指定された分布の作成は成功です。
またrandomTest.mq5 スクリプトに似た動作をするfitAll.mq5 スクリプトを書きました。違いは、最初のスクリプトが fitDistributions 関数を持っていることだけです。以下のタスクを設定しました。：すべての入手可能な分布 をランダム関数のサンプルに一致させ、統計検定を行う。
分布をサンプルと一致させるのは必ず可能ではありません。というのも推定が可能ではないと伝えるターミナルに表示される線の概観を決めるパラメータが不一致なためです。すなわち「ベータ分布は推定不可である。」
その上、このスクリプトは統計結果を小さなHTMLレポート形式に可視化しようと決めました。サンプルは『HTMLのグラフおよび図』 にあります。（図8）
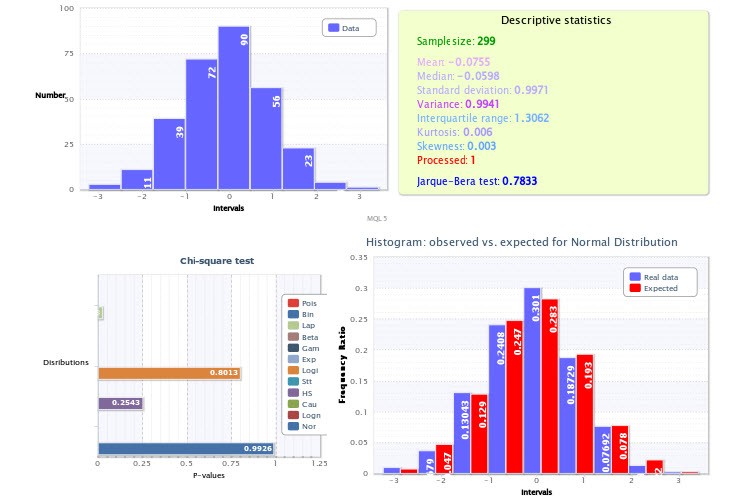
図8 サンプル推定における統計レポート
サンプルの標準ヒストグラムが左上に表示されています・右上は記述的統計とジャルク・ベラ 検定結果が表示されています。そこでProcessed 変数値が1であるのは異常値が削除あｓれたことを意味します。一方、値0は異常値がなかったことを意味します。
各選択された分布に対するχ2 test のP値が左下に表示されています。ここでは、正常分布がフィッティング (p=0.9926)に関してベストという結果になっています。観測と期待頻度率のヒストグラムは右下にあります。
このギャラリーにはそれほど多くの分布はまだありません。分布数が多ければ、このスクリプトによりかなりの時間節約ができます。
調査対象サンプルの分布パラメータについて正確にわかりました。確率確率的推論に進んでいきます。
3.2ランダム変数値の確率
理論的分布に関する 記事で例としてcontinuousDistribution.mq5スクリプトを提供しました。それを使って、興味を引かれる既知のパラメータを使い分布法則を表示してみます。
予想変動率データに対しては前に取得した対数分布パラメータ(Mu=6.09、 Sigma=0.53)を入力し、 対数 分布タイプと cdfモードを選択します。 （図9）
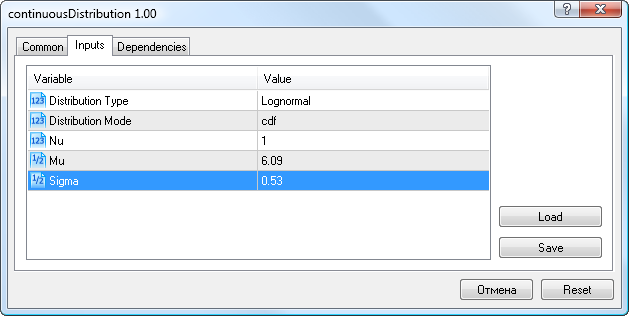
図9 対数分布パラメータ X~Logn(6.09,0.53)
それからスクリプトはサンプルに対する分布関数を表示します。それは図10のように表示されます。
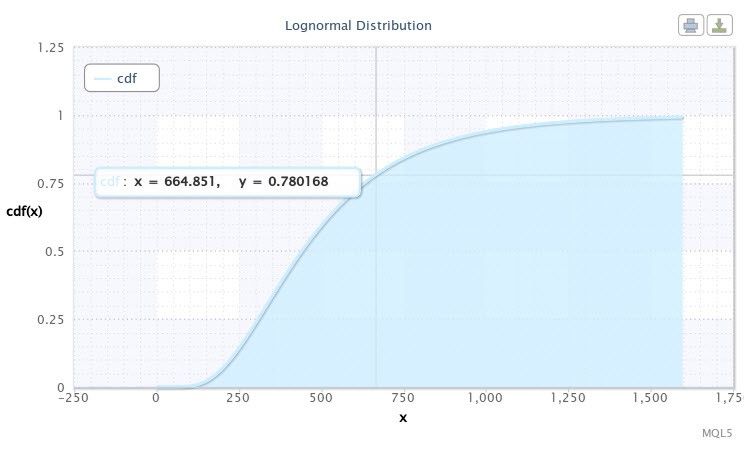
図10 X~Logn(6.09,0.53)に対する分布関数
グラフではカーするが座標がおよそ[665;0.78]の点を指しているのが判ります。それは、EURUSD H4 の予想変動率が 665 ポイントを越えない確率が 78%であることを意味しています。この情報はExpert Advisorの開発者にとってたいへん有用であると証明されるでしょう。曲線上でカーソルを移動させると別の値を取ることができます。
予想変動率値500 ～750 ポイント間の区分にあるとき、イベントの確率に興味を持つと仮定します。それには以下の処理が必要です。
cdf(750) - cdf(500) = 0.84 - 0.59 = 0.25.
4番目のイベントでは、ペアの予想変動率は 500 ～ 750 ポイントの区間で上下します。
分布法則モードとしてsf を選択し再び同じ分布パラメータでスクリプトを実行します。信頼性(survival)関数は以下のように表示されます。（図11）
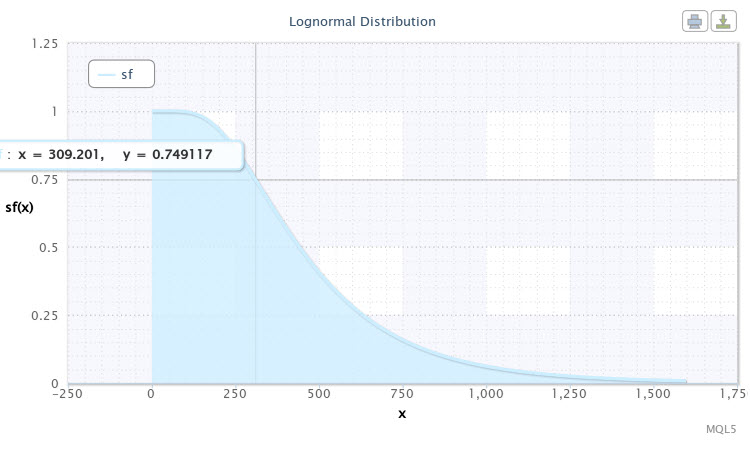
図11 X~Logn(6.09,0.53)に対するsurvival関数
グラフの曲線にマークのある点は次のように解釈できます。ペアの予想変動率が310ポイントである確率は75% である。曲線の低い場所に行くほど、変動確率は低くなります。これで 1000 ポイント以上の予想変動率は、発生確率5%以下とすでにまれなイベントであることが考えられます
正常化の戻り値サンプルに対する分布曲線は他のサンプル同様に作成可能です。方法論はこれでだいたい明確だと思います。
おわりに
提案された分析的微分 はすべて変化傾向系列として成功とはいえないことに注意が必要です。しかしながら、たとえばそれは対数戻り値系列には関連しません。ただ、メソッド判定タスクは本稿では取り上げませんでした。本件に関してご興味のある読者の方はコメントをお寄せください。
マーケット、マーケット商品、確率予測からのトレードエクスパートを考察する必要に気づくことは大切です。これが見せようとしてきた手法です。このテーマが読者の方の興味を喚起し、建設的議論につながることを願っています。
ファイル保存場所
| # | ファイル | パス | 内容 |
|---|---|---|---|
| 1 | Distribution_class.mqh | %MetaTrader%\MQL5\Include | 分布クラスのギャラリー |
| 2 | DistributionFigure_class.mqh | %MetaTrader%\MQL5\Include | 分布のグラフィカル表示用クラス |
| 3 | Random_class.mqh | %MetaTrader%\MQL5\Include | 乱数サンプル作成用クラス |
| 4 | ExpStatistics_class.mqh | %MetaTrader%\MQL5\Include | 統計特性推定のクラスおよび関数 |
| 5 | volatilityTest.mq5 | %MetaTrader%\MQL5\Scripts | EURUSD H4 予想変動率 サンプルの推定用スクリプト |
| 6 | returnsTest.mq5 | %MetaTrader%\MQL5\Scripts | EURUSD H4 戻り値サンプルの推定用スクリプト |
| 7 | randomTest.mq5 | %MetaTrader%\MQL5\Scripts | ランダム関数サンプルの推定用スクリプト |
| 8 | fitAll.mq5 | %MetaTrader%\MQL5\Scripts | 全分布の一致および推定用スクリプト |
| 9 | Volat.csv | %MetaTrader%\MQL5\Files | EURUSD H4予想変動率サンプルデータファイル |
| 10 | Returns_std.csv | %MetaTrader%\MQL5\Files | EURUSD H4 戻り値サンプルデータファイル |
| 11 | Randoms.csv | %MetaTrader%\MQL5\Files | ランダム関数サンプルデータファイル |
| 12 | Histogram.htm | %MetaTrader%\MQL5\Files | HTML形式のサンプルのヒストグラム |
| 13 | Histogram2.htm | %MetaTrader%\MQL5\Files | HTML形式のサンプルの二重ヒストグラム |
| 14 | chi_test.htm | %MetaTrader%\MQL5\Files | サンプル推定の統計的 HTML レポート |
| 15 | dataHist.txt | %MetaTrader%\MQL5\Files | サンプルのヒストグラム表示用データ |
| 16 | dataHist2.txt | %MetaTrader%\MQL5\Files | サンプルの二重ヒストグラム表示用データ |
| 17 | dataFitAll.txt | %MetaTrader%\MQL5\Files | HTML レポート表示用データ |
| 18 | highcharts.js | %MetaTrader%\MQL5\Files | 連携チャートのJavaScript ライブラリ |
| 19 | jquery.min.js | %MetaTrader%\MQL5\Files | JavaScript ライブラリ |
| 20 | ReturnsIndicator.mq5 | %MetaTrader%\MQL5\Indicators | 対数戻り値インディケータ |
参照資料
MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/257
もっとも活発な MQL5.コミュニティメンバーは iPhonesを勝ち取りました！
フィッシャートランスフォームの適用とMetaTrader5の市場分析に対するフィッシャートランスフォーム
「マーケット」でプロダクトを宣伝する方法
UML ツールを用いたExpert Advisorの開発方法
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索