Il ruolo delle distribuzioni statistiche nel lavoro del trader
198
0
Le regolarità ci semplificano la vita, ma è altrettanto importante trarre vantaggio dalla casualità.
(Georgiy Aleksandrov)
Introduzione
Questo articolo è una continuazione logica del mio articolo Statistical Probability Distributions in MQL5 che espone le classi per lavorare con alcune distribuzioni statistiche teoriche. Ho ritenuto necessario gettare prima le basi sotto forma di classi di distribuzione per rendere il tutto più conveniente per un utente che le mette successivamente in pratica.
Ora che abbiamo una base teorica, suggerisco di procedere direttamente a set di dati reali e provare a fare un uso informativo di questa base. Allo stesso tempo, metteremo in luce alcune questioni relative alla statistica matematica.
1. Generazione di numeri casuali con una distribuzione data
Ma prima di considerare i set di dati reali, sembra molto importante essere in grado di ottenere alcuni set di valori strettamente correlati a una distribuzione teorica desiderata.
In altre parole, un utente dovrebbe impostare solo i parametri della distribuzione e della dimensione del campione desiderati. Un programma (nel nostro caso, una gerarchia di classi) deve generare ed emettere tale campione di valori per ulteriori lavori.
Un altro dettaglio significativo è che i campioni generati da una legge specifica vengono utilizzati per verificare vari test statistici. L'area della statistica matematica - generazione di variabili casuali con diverse leggi di distribuzione - è piuttosto interessante e stimolante.
Per i miei scopi, ho utilizzato un generatore di alta qualità descritto nel libro Numerical Recipes: The Art of Scientific Computing [2]. Il suo periodo è approssimativamente uguale a 3,138*1057. Il codice C è stato passato abbastanza facilmente in MQL5.
E così ho creato la classe Random, come riportato di seguito:
//+------------------------------------------------------------------+ //| Random class definition | //+------------------------------------------------------------------+ class Random { private: ulong u, //unsigned 64-bit integers v, w; public: //+------------------------------------------------------------------+ //| The Random class constructor | //+------------------------------------------------------------------+ void Random() { randomSet(184467440737095516); } //+------------------------------------------------------------------+ //| The Random class set-method | //+------------------------------------------------------------------+ void randomSet(ulong j) { v=4101842887655102017; w=1; u=14757395258967641292; u=j^v; int64(); v = u; int64(); w = v; int64(); } //+------------------------------------------------------------------+ //| Return 64-bit random integer | //+------------------------------------------------------------------+ ulong int64() { uint k=4294957665; u=u*2862933555777941757+7046029254386353087; v^= v>> 17; v ^= v<< 31; v ^= v>> 8; w = k*(w & 0xffffffff) +(w>> 32); ulong x=u^(u<<21); x^=x>>35; x^=x<<4; return(x+v)^w; }; //+------------------------------------------------------------------+ //| Return random double-precision value in the range 0. to 1. | //+------------------------------------------------------------------+ double doub() { return 5.42101086242752217e-20*int64(); } //+------------------------------------------------------------------+ //| Return 32-bit random integer | //+------------------------------------------------------------------+ uint int32() { return(uint)int64(); } };
Ora possiamo creare classi per i valori campionati da una distribuzione.
Ad esempio, diamo un'occhiata a una variabile casuale della distribuzione normale. La classe CNormaldev è come di seguito:
//+------------------------------------------------------------------+ //| CNormaldev class definition | //+------------------------------------------------------------------+ class CNormaldev : public Random { public: CNormaldist N; //Normal Distribution instance //+------------------------------------------------------------------+ //| The CNormaldev class constructor | //+------------------------------------------------------------------+ void CNormaldev() { CNormaldist Nn; setNormaldev(Nn,18446744073709); } //+------------------------------------------------------------------+ //| The CNormaldev class set-method | //+------------------------------------------------------------------+ void setNormaldev(CNormaldist &Nn,ulong j) { N.mu=Nn.mu; N.sig=Nn.sig; randomSet(j); } //+------------------------------------------------------------------+ //| Return Normal deviate | //+------------------------------------------------------------------+ double dev() { double u,v,x,y,q; do { u = doub(); v = 1.7156*(doub()-0.5); x = u - 0.449871; y = fabs(v) + 0.386595; q = pow(x,2) + y*(0.19600*y-0.25472*x); } while(q>0.27597 && (q>0.27846 || pow(v,2)>-4.*log(u)*pow(u,2))); return N.mu+N.sig*v/u; } }; //+------------------------------------------------------------------+
Come si può vedere, la classe ha un membro dati N di tipo CNormaldist. Il codice C originale mancava di tale connessione con la distribuzione. Ho ritenuto necessario che una variabile casuale generata dalla classe (qui dalla classe CNormaldev) avesse una connessione logica e programmatica con la sua distribuzione.
Nella versione originale, il tipo Normaldev era definito come segue:
typedef double Doub; typedef unsigned __int64 Ullong; struct Normaldev : Ran { Doub mu,sig; Normaldev(Doub mmu, Doub ssig, Ullong i) ... }
I numeri casuali vengono generati qui dalla distribuzione normale utilizzando il metodo ratio of uniforms di Leva.
Tutte le altre classi che aiutano nel calcolo delle variabili casuali da varie distribuzioni si trovano nel file include Random_class.mqh.
Ora finiremo con la generazione e vedremo, nella parte pratica dell'articolo, come creare un array di valori e testare un campione.
2. Stima dei parametri di distribuzione, ipotesi statistiche
È chiaro che esamineremo variabili discrete. In pratica, comunque, se il numero di variabili discrete è significativo, è più conveniente considerare l'insieme di tali variabili discrete come un gruppo di variabili continue. Questo è un approccio standard nella statistica matematica. Pertanto, per la loro analisi possiamo utilizzare distribuzioni definite da formule analitiche che sono legate a variabili continue.
Quindi passiamo all'analisi della distribuzione empirica.
Si presume che sia oggetto di studio un campione di una popolazione generica i cui membri soddisfano il criterio di rappresentatività. Inoltre, sono soddisfatti i requisiti per le stime specificati nella sezione 8.3 [9]. I parametri di distribuzione numerici possono essere trovati mediante metodi di stima puntuale e di intervallo.
2.1 Esempio di gestione utilizzando la classe CExpStatistics
Si deve prima eliminare i cosiddetti outlier dal campione; si tratta di osservazioni che si discostano nettamente dalle osservazioni della maggior parte del campione (sia al rialzo che al ribasso). Non esiste un metodo universale per eliminare gli outlier.
Suggerisco di usare quello descritto da S.V. Bulashev nella Sezione 6.3 [5]. Nel forum MQL4 è stata creata una libreria di funzioni statistiche sulla base delle quali il problema può essere facilmente risolto. Detto questo, applicheremo sicuramente l'OOP e lo aggiorneremo un po'.
Ho chiamato la classe di stime delle caratteristiche statistiche CExpStatistics (Classe di statistiche previste) che è stata creata.
È approssimativamente come segue:
//+------------------------------------------------------------------+ //| Expected Statistics class definition | //+------------------------------------------------------------------+ class CExpStatistics { private: double arr[]; //initial array int N; //initial array size double Parr[]; //processed array int pN; //processed array size void stdz(double &outArr_st[],bool A); //standardization public: void setArrays(bool A,double &Arr[],int &n); //set array for processing bool isProcessed; //array processed? void CExpStatistics(){}; //constructor void setCExpStatistics(double &Arr[]); //set the initial array for the class void ZeroCheckArray(bool A); //check the input array for zero elements int get_arr_N(); //get the initial array length double median(bool A); //median double median50(bool A); //median of 50% interquantile range (midquartile range) double mean(bool A); //mean of the entire initial sample double mean50(bool A); //mean of 50% interquantile range double interqtlRange(bool A); //interquartile range double RangeCenter(bool A); //range center double meanCenter(bool A); //mean of the top five estimates double expVariance(bool A); //estimated variance double expSampleVariance(bool A); //shifted estimate of sample variance double expStddev(bool A); //estimated standard deviation double Moment(int index,bool A,int sw,double xm); //moment of distribution double expKurtosis(bool A,double &Skewness); ////estimated kurtosis and skewness double censorR(bool A); //censoring coefficient int outlierDelete(); //deletion of outliers from the sample int pArrOutput(double &outArr[],bool St); //processed array output void ~CExpStatistics(){};//destructor }; //+------------------------------------------------------------------+
L'implementazione di ciascun metodo può essere studiata in dettaglio nel file include ExpStatistics_class.mqh, quindi la tralascerò.
La cosa importante che fa questa classe è che restituisce l'array privo di outlier (Parr[]), se presente. Inoltre, aiuta a ottenere alcune statistiche descrittive del campionamento e le loro stime.
2.2 Creazione di un istogramma del campione elaborato
Ora che l'array è privo di outlier, è possibile tracciare un istogramma (distribuzione di frequenza) in base ai suoi dati. Ci aiuterà a stimare visivamente la legge di distribuzione delle variabili casuali. Esiste una procedura passo passo per la creazione di un istogramma.
Si deve prima calcolare il numero di classi richieste. In questo contesto, il termine "classe" significa raggruppamento, intervallo. Il numero di classi è calcolato dalla formula di Sturges:
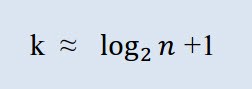
Dove k è il numero di classi e n è il numero di osservazioni.
Su MQL5 la formula può essere rappresentata come segue:
int Sturges(int n) /* Function for determining the number of class intervals using Sturges' rule. Variables: y is the number of sampling observations. Returned value: number of class intervals. */ { double s; // Returned value s=1.+log2(y); if(s>15) // Empirical rule s=15; return(int) floor(s); }
Quando il numero richiesto di classi (intervalli) è stato ricevuto utilizzando la formula di Sturges, è il momento di suddividere i dati dell'array in classi. Tali dati sono chiamati osservazioni (sing. observation). Lo faremo usando la funzione Allocate, come segue:
void Allocate(double &data[],int n,double &f[],double &b[],int k) /* Function for allocating observations to classes. Variables: 1) data — initial sample (array) 2) n — sample size 3) f — calculated array of observations allocated to classes 4) b — array of class midpoints 5) k — number of classes */ { int i,j; // Loop counter double t,c; // Auxiliary variable t=data[ArrayMinimum(data)]; // Sample minimum t=t>0 ? t*0.99 : t*1.01; c=data[ArrayMaximum(data)]; // Sample maximum c=c>0 ? c*1.01 : c*0.99; c=(c-t)/k/2; // Half of the class interval b[0]=t+c; // Array of class interval midpoints f[0]= 0; for(i=1; i<k; i++) { b[i] = b[i - 1] + c + c; f[i] = 0; } // Grouping for(i=0; i<n; i++) for(j=0; j<k; j++) if(data[i]>b[j]-c && data[i]<=b[j]+c) { f[j]++; break; } }
Come si può vedere, la funzione prende l'array di osservazioni iniziali (data), la sua lunghezza (n), il numero di classi (k) e assegna le osservazioni a una certa classe f[i] dell'array f, dove b[ i] è il punto medio della classe f[i]. I dati dell'istogramma sono ora pronti.
Visualizzeremo l'istogramma utilizzando gli strumenti descritti nell'articolo . A questo scopo ho scritto la funzione histogramSave, la quale visualizzerà l'istogramma per la serie in studio in HTML. La funzione accetta 2 parametri: array di classi (f) e array di punti medi di classe (b).
Ad esempio, ho costruito un istogramma per le differenze assolute tra massimi e minimi di 500 barre della coppia EURUSD sull'intervallo di tempo di quattro ore in punti utilizzando lo script volatilityTest.mq5.
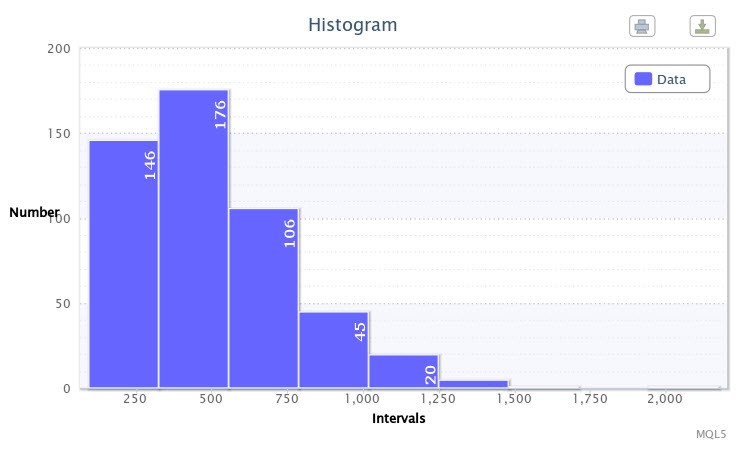
Figura 1. Istogramma dei dati (volatilità assoluta dell'EURUSD H4)
Come mostrato nell'istogramma (Fig.1), la prima classe presenta 146 osservazioni, la seconda classe 176 osservazioni, ecc. La funzione dell'istogramma è quella di dare un'idea visiva della distribuzione empirica del campione in esame.
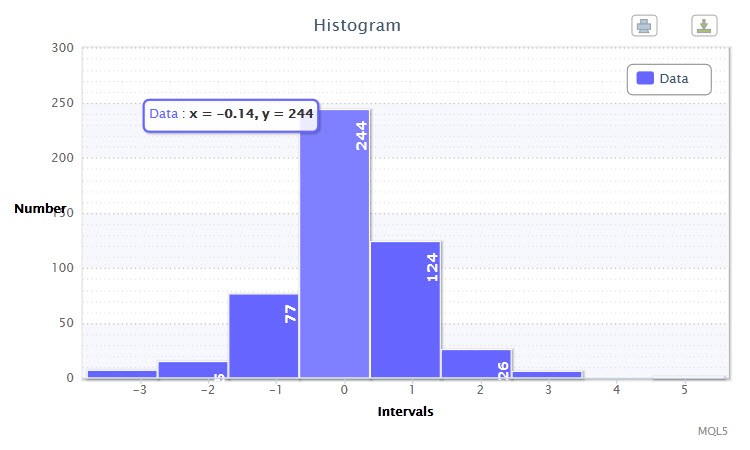
Figura 2. Istogramma dei dati (rendimenti standardizzati dell'EURUSD H4)
L'altro istogramma (Fig.2) mostra i rendimenti logaritmici standardizzati di 500 barre della coppia EURUSD sull’intervallo di tempo H4. Come puoi notare, la quarta e la quinta classe sono le più impressionanti in quanto hanno rispettivamente 244 e 124 osservazioni. Questo istogramma è stato creato utilizzando lo script returnTest.mq5.
L'istogramma ci permette quindi di scegliere la legge di distribuzione i cui parametri saranno ulteriormente stimati. Laddove non è visivamente ovvio quale distribuzione preferire, è possibile stimare i parametri di diverse distribuzioni teoriche.
Entrambe le distribuzioni che abbiamo considerato non assomigliano a quelle normali in apparenza, specialmente la prima. Tuttavia non ci fidiamo della rappresentazione visiva e procediamo con le cifre.
2.3 Ipotesi di normalità
È consuetudine risolvere e testare prima l'ipotesi (hypothesis) se la distribuzione in questione è normale. Tale ipotesi è chiamata ipotesi principale. Uno dei metodi più popolari per testare la normalità di un campione è il test Jarque-Bera.
Il suo algoritmo, sebbene non il più complesso, è piuttosto ingombrante a causa dell'approssimazione. Esistono alcune versioni dell'algoritmo in C++ e in altri linguaggi. Una delle versioni di maggior successo e collaudate è una versione situata in una libreria di analisi numerica multipiattaforma ALGLIB. Il suo autore [S.A. Bochkanov] ha svolto un lavoro enorme, in particolare nella compilazione della tabella di quantili del test. L'ho appena aggiornato un po’ per le esigenze della MQL5.
La funzione principale jarqueberatest è la seguente:
//+------------------------------------------------------------------+ // the Jarque-Bera Test | //+------------------------------------------------------------------+ void jarqueberatest(double &x[],double &p) /* The Jarque-Bera test is used to check hypothesis about the fact that a given sample xS is a sample of normal random variable with unknown mean and variance. Variables: x - sample Xs; p - p-value; */ { int n=ArraySize(x); double s; p=0.; if(n<5)//N is too small { p=1.0; return; } //N is large enough jarquebera_jarqueberastatistic(x,n,s); p=jarquebera_jarqueberaapprox(n,s); } //+------------------------------------------------------------------+
Tratta il campione di dati iniziale (x) e restituisce il valore р, cioè un valore che caratterizza la probabilità di rifiutare un'ipotesi nulla se l'ipotesi nulla è di fatto vera.
Ci sono 2 funzioni ausiliarie nel corpo della funzione. La prima funzione - jarquebera_jarqueberastatistic - calcola la statistica Jarque-Bera e la seconda - jarquebera_jarqueberaabout - calcola il valore p. Da notare che quest'ultimo, a sua volta, mette in atto funzioni ausiliarie legate all'approssimazione, che nell'algoritmo sono quasi 30.
Quindi proviamo a testare i nostri campioni per la normalità. Utilizzeremo lo script returnTest.mq5 che tratterà il campione di rendimenti standardizzati dell'EURUSD H4.
Come previsto, il test ha mostrato che la probabilità di rifiutare un'ipotesi nulla vera è 0,0000. In altre parole, la distribuzione di questo campione non appartiene alla famiglia delle distribuzioni normali. Per trattare il campione di volatilità assoluta della coppia EURUSD, esegui lo script volatilityTest.mq5. Il risultato sarà simile: la distribuzione non è normale.
3. Raccordo di distribuzione
Esistono alcuni metodi nella statistica matematica che consentono di confrontare la distribuzione empirica con la distribuzione normale. Il problema più grande è che i parametri di distribuzione normale non ci sono noti e si presume che i dati oggetto di studio non riflettano la normalità di una distribuzione.
Quindi dobbiamo usare test non parametrici e riempire i parametri incogniti con le stime ottenute dalla distribuzione empirica.
3.1 Stima e test
Uno dei test più popolari e, cosa più importante, adeguati in questa situazione è il test χ2. Si basa sulla misura della bontà di adattamento di Pearson.
Eseguiremo il test utilizzando la funzione chsone:
void chsone(double &f[],double &ebins[],double &df, double &chsq,double &prob,const int knstrn=1) /* 1) f — array of observations allocated to classes 2) ebins - array of expected frequencies 3) df - number of degrees of freedom 3) chsq — chi-square statistics 4) prob - probability of accepting a true null hypothesis 5) knstrn — constraint */ { CGamma gam; int j,nbins=ArraySize(bins),q,g; double temp; df=nbins-knstrn; chsq=0.0; q=nbins/2; g=nbins-1; for(j=0;j<nbins/2;j++) //passing through the left side of the distribution { if(ebins[j]<0.0 || (ebins[j]==0. && bins[j]>0.)) Alert("Bad expected number in chsone!"); if(ebins[j]<=5.0) { --df; ebins[j+1]+=ebins[j]; bins[j+1]+=bins[j]; } else { temp=bins[j]-ebins[j]; chsq+=pow(temp,2)/ebins[j]; } } for(j=nbins-1;j>nbins/2-1;j--) //passing through the right side of the distribution { if(ebins[j]<0.0 || (ebins[j]==0. && bins[j]>0.)) Alert("Bad expected number in chsone!"); if(ebins[j]<=5.0) { --df; ebins[j-1]+=ebins[j]; //starting with the last class bins[j-1]+=bins[j]; } else { temp=bins[j]-ebins[j]; chsq+=pow(temp,2)/ebins[j]; } } if(df<1)df=1; //compensate prob=gam.gammq(0.5*df,0.5*chsq); //Chi-square probability function }
Come si può vedere nell’elenco, viene utilizzata un'istanza della classe CGamma che rappresenta la funzione gamma incompleta che è inclusa nel file Distribution_class.mqh, così come in tutte le distribuzioni menzionate. Va inoltre notato che l'array delle frequenze che ci si aspetta (ebins) sarà ottenuto utilizzando le funzioni estimateDistribution e expFrequency.
Ora dobbiamo selezionare i parametri numerici che sono inclusi nella formula analitica per la distribuzione teorica. Il numero di parametri dipende dalla particolare distribuzione. Ad esempio, ci sono due parametri nella distribuzione normale e un parametro nella distribuzione esponenziale, ecc.
Quando si determinano i parametri di distribuzione, di solito utilizziamo metodi di stima puntuale come il metodo dei momenti, il metodo dei quantili e il metodo della massima verosimiglianza. La prima è più semplice in quanto implica che le stime campionarie (aspettativa, varianza, asimmetria, ecc.) debbano coincidere con le stime generali.
Proviamo a selezionare una distribuzione teorica per il nostro campione usando un esempio. Prenderemo una serie di rendimenti standardizzati dell'EURUSD H4 per i quali abbiamo già disegnato un istogramma.
La prima impressione è che la distribuzione normale non sia appropriata per la serie, poiché si osserva l'eccesso di coefficiente di curtosi. Per fare un confronto, proviamo ad applicare un'altra distribuzione.
Quindi, quando avvieremo lo script returnTest.mq5 già noto, proveremo a selezionare tale distribuzione come Hypersec. Inoltre, lo script stimerà e restituirà i parametri di distribuzione selezionati utilizzando la funzione estimateDistribution ed eseguirà immediatamente il test χ2. I parametri di distribuzione selezionati sono risultati essere i seguenti:
Distribuzione secante iperbolica: X~HS(-0,00, 1,00);
e i risultati del test sono stati, come segue:
"Statistica chi quadrato: 1.89; probabilità di rifiutare un'ipotesi nulla vera: 0.8648"
Va notato che la distribuzione selezionata è un buon adattamento poiché il valore della statistica χ2 è piuttosto piccolo.
Inoltre, utilizzando la funzione histogramSaveE, sarà disegnato un doppio istogramma per i rapporti osservati e previsti di frequenza (il rapporto di frequenza è una frequenza espressa in frazione o percentuale) dei rendimenti standardizzati (Fig.3). Puoi vedere che le barre si duplicano quasi a vicenda. Questa è una prova del montaggio riuscito.
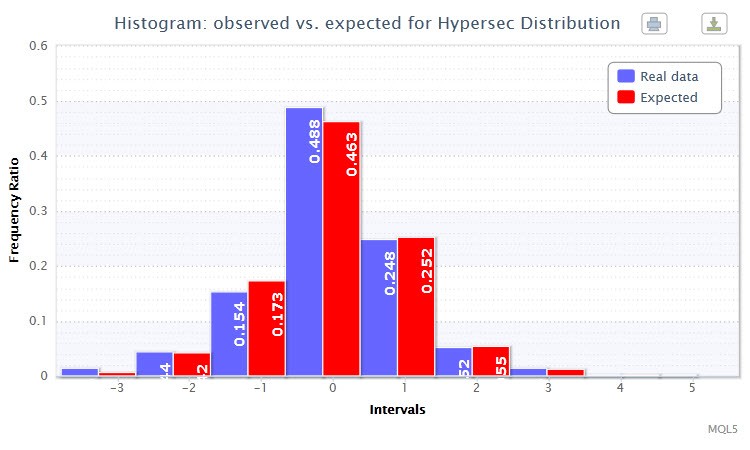
Figura 3. Istogramma dei rapporti di frequenza osservati e previsti (rendimenti standardizzati dell'EURUSD H4)
Eseguiamo una procedura simile per i dati di volatilità utilizzando il già noto volatilityTest.mq5.
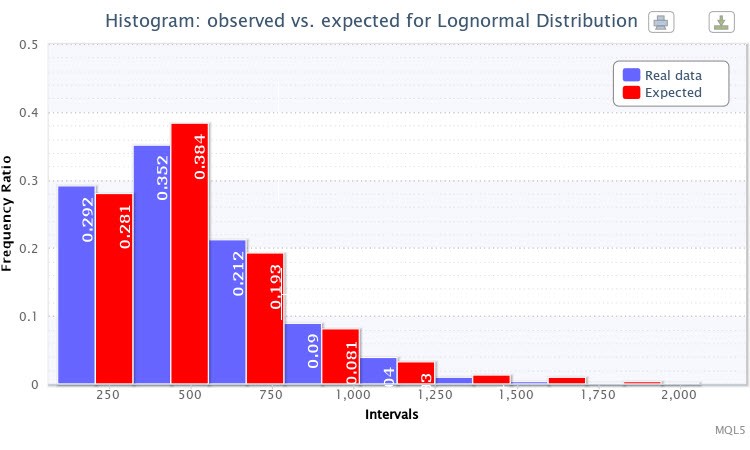
Figura 4. Istogramma dei rapporti di frequenza osservati e previsti (volatilità assoluta dell'EURUSD H4)
Ho selezionato la distribuzione lognormale Lognormal per il test. Di conseguenza, è stata ricevuta la seguente stima dei parametri:
Distribuzione lognormale: X~Logn(6.09, 0.53);
e i risultati del test sono stati, come segue:
"Statistica chi quadrato: 6.17; probabilità di rifiutare un'ipotesi nulla vera: 0.4040"
Anche la distribuzione teorica per questa distribuzione empirica è stata selezionata con successo. Quindi, si può considerare che l'ipotesi nulla non può essere rifiutata (allo standard del livello di confidence p=0.05). Si può vedere nella Fig.4 che anche le barre dei rapporti di frequenza previsti e osservati sono molto simili.
Permettetemi ora di ricordarvi che abbiamo un'altra possibilità per generare un campione di variabili casuali da una distribuzione con parametri impostati. Per utilizzare una gerarchia di classi relative a tale operazione, ho scritto lo script randomTest.mq5.
All'inizio, dobbiamo inserire i parametri come mostrato in Fig.5.
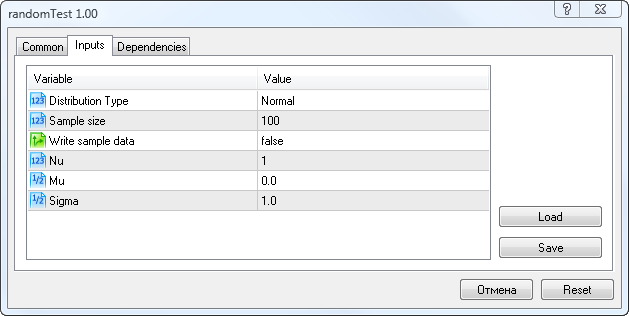
Figura 5. Parametri di input dello script randomTest.mq5
Qui puoi selezionare il tipo di distribuzione (Distribution Type), il numero di variabili casuali in un campione (Sample Size), l'opzione di salvataggio del campione (Write sample data), il parametro Nu (per la distribuzione t di Student), il Mu e i parametri Sigma.
Se si imposta per Write sample data il valore true, lo script salverà il campione di variabili casuali con i parametri personalizzati nel file Randoms.csv. Altrimenti leggerà i dati del campione da questo file e quindi eseguirà test statistici.
Per alcune distribuzioni con parametri Mu e Sigma mancanti ho fornito una tabella di correlazione dei parametri ai campi nella finestra di avvio dello script.
| Distribuzione | Primo parametro di distribuzione | Secondo parametro di distribuzione |
|---|---|---|
| Logistica | alph Mu | bet Sigma |
| Esponenziale | lambda Mu | -- |
| Gamma | alph Mu | bet Sigma |
| Beta | alph Mu | bet Sigma |
| Laplace | alph Mu | bet Sigma |
| Binomiale | n Mu | pe Sigma |
| Poisson | lambda Mu | -- |
Ad esempio, se viene selezionata la distribuzione di Poisson, il parametro lambda verrà inserito tramite il campo Mu, ecc.
Lo script non stima i parametri di distribuzione t di Student perché, nella maggioranza assoluta dei casi, viene utilizzato solo in alcune procedure statistiche: stima puntuale, costruzione di intervalli di confidenza e verifica di ipotesi che riguardano la media incognita di un campione statistico dalla distribuzione normale.
Ad esempio, ho eseguito lo script per la distribuzione normale con i parametri X~Nor(3.50, 2.77), dove Write sample data=true. Lo script ha prima generato un campione. Alla seconda esecuzione su Write sample data=false, è stato disegnato un istogramma come mostrato in Fig.6.
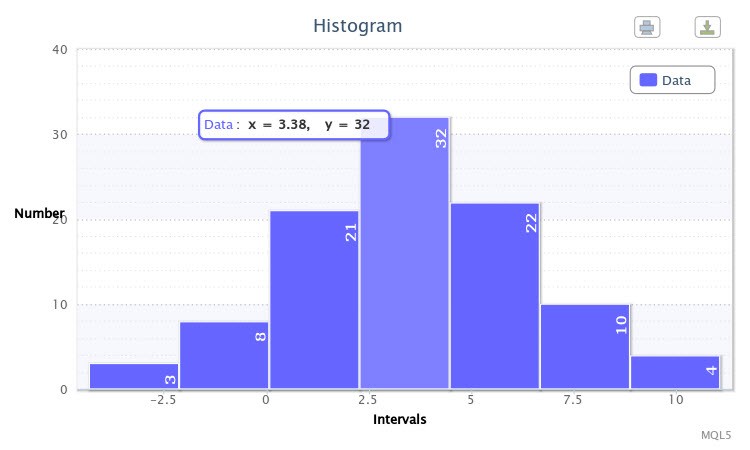
Figura 6. Il campione di variabili casuali X~Nor(3.50,2.77)
Le restanti informazioni visualizzate nella finestra Terminal sono le seguenti:
Il test di Jarque-Bera: "Il test di Jarque-Bera: la probabilità di rifiutare un'ipotesi nulla vera è 0,9381";
Stima dei parametri: Distribuzione normale: X~Nor(3.58, 2.94);
Risultati del test chi quadrato: "Statistica chi quadrato: 0,38; probabilità di rifiutare un'ipotesi nulla vera: 0.9843".
E, infine, è stato visualizzato un altro doppio istogramma dei rapporti di frequenza osservati e previsti per il campione (Fig.7).
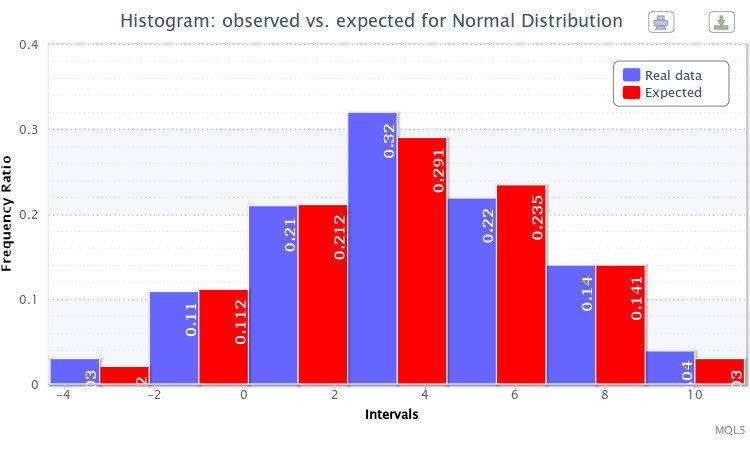
Figura 7. Istogramma dei rapporti di frequenza osservati e previsti per X~Nor (3.50,2.77)
In generale, la generazione della distribuzione specificata ha avuto successo.
Ho anche scritto lo script fitAll.mq5 che funziona in modo simile allo script randomTest.mq5. L'unica differenza è che il primo ha la funzione fitDistributions. Ho impostato il seguente compito: adattare tutte le distribuzioni disponibili a un campione di variabili casuali ed eseguire un test statistico.
Non è sempre possibile adattare una distribuzione a un campione a causa della mancata corrispondenza dei parametri che porta alla comparsa di righe nel Terminal, le quali informano che la stima non è possibile, ad es. "La distribuzione beta non può essere stimata!".
Inoltre, ho deciso che questo script dovrebbe visualizzare i risultati statistici sotto forma di un piccolo report HTML, un esempio del quale può essere trovato nell'articolo "Charts and Diagrams in HTML" (Fig.8).
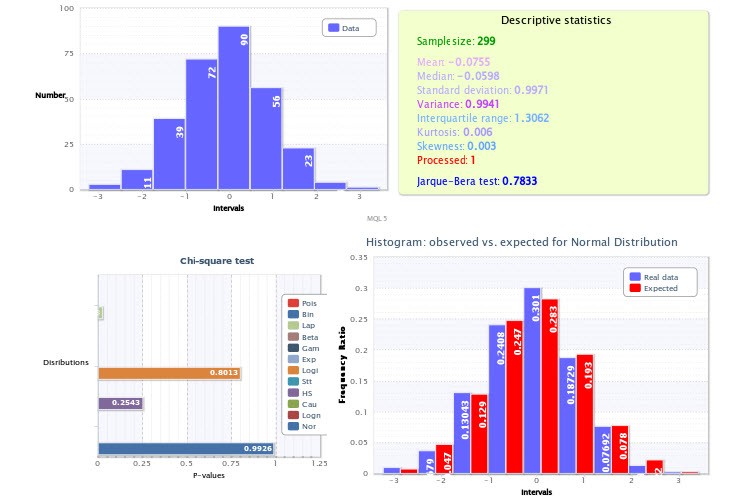
Figura 8. Report statistico sulla stima del campione
Nell’intervallo in alto a sinistra viene visualizzato un istogramma standard del campione; l’intervallo in alto a destra rappresenta le statistiche descrittive e il risultato del test Jarque-Bera, dove il valore della variabile Processed pari a 1 indica che gli outlier sono stati eliminati, mentre un valore pari a 0 significa che non c'erano outlier.
I valori P del test χ2 per ogni distribuzione selezionata sono visualizzati nell’intervallo in basso a sinistra. Qui, la distribuzione normale si è rivelata la migliore in termini di adattamento (p=0,9926). Pertanto, nell’intervallo in basso a destra è stato disegnato un istogramma dei rapporti di frequenza osservati e previsti.
Non ci sono ancora così tante distribuzioni nella mia galleria. Ma questo script ti farà risparmiare molto tempo se sono presenti un gran numero di distribuzioni.
Ora che conosciamo esattamente i parametri di distribuzione dei campioni in studio, possiamo procedere al ragionamento probabilistico.
3.2 Probabilità di valori di variabili casuali
Nell'articolo sulle distribuzioni teoriche ho fornito lo script continueDistribution.mq5 come esempio. Usandolo, cercheremo di visualizzare qualsiasi legge di distribuzione con parametri noti che possa interessarci.
Quindi, per i dati di volatilità inseriremo i parametri di distribuzione lognormali ottenuti in precedenza (Mu=6,09, Sigma=0,53), selezioneremo il tipo di distribuzione Lognormale e la modalità cdf (Fig.9).
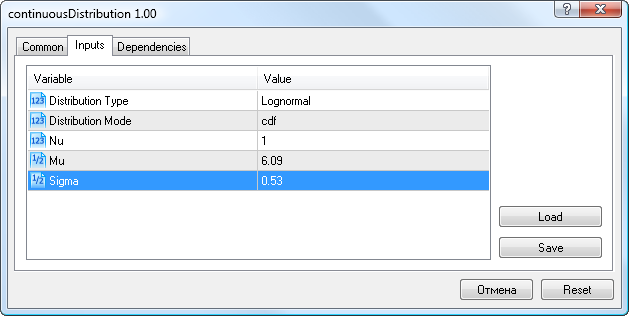
Figura 9. Parametri di distribuzione lognormale X~Logn (6,09;0,53)
Lo script visualizzerà quindi la funzione di distribuzione per il nostro esempio. Apparirà come mostrato in Fig.10.
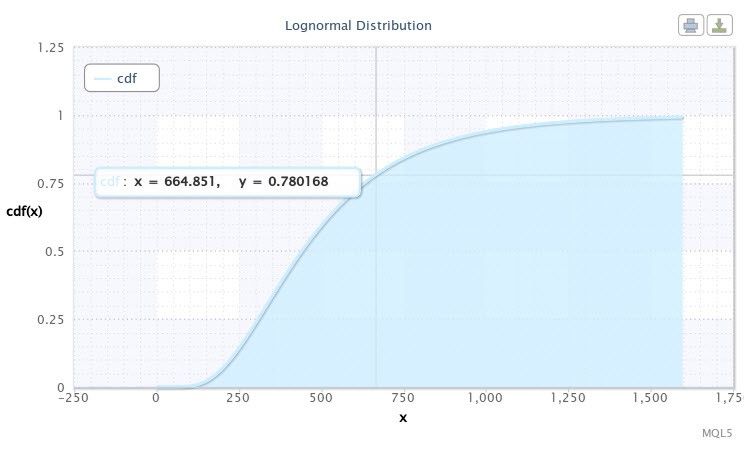
Figura 10. Funzione di distribuzione per X~Logn (6.09,0.53)
Possiamo vedere nel grafico che il cursore è puntato su un punto le cui coordinate sono approssimativamente [665;0,78]. Significa che c'è una probabilità del 78% che la volatilità dell'EURUSD H4 non superi i 665 punti. Queste informazioni possono rivelarsi molto utili per uno sviluppatore di un Expert Advisor. Si possono sicuramente assumere altri valori sulla curva spostando il cursore.
Supponiamo di essere interessati alla probabilità dell'evento quando il valore di volatilità sarà compreso nell'intervallo tra 500 e 750 punti. A tal fine è necessario eseguire la seguente operazione:
cdf(750) - cdf(500) = 0.84 - 0.59 = 0.25.
Pertanto, in un quarto degli eventi la volatilità della coppia oscilla nell'intervallo tra 500 e 750 punti.
Eseguiamo lo script con gli stessi parametri di distribuzione ancora una volta selezionando solo sf come modalità di legge di distribuzione. La funzione di affidabilità (survival) verrà mostrata, come segue (Fig.11).
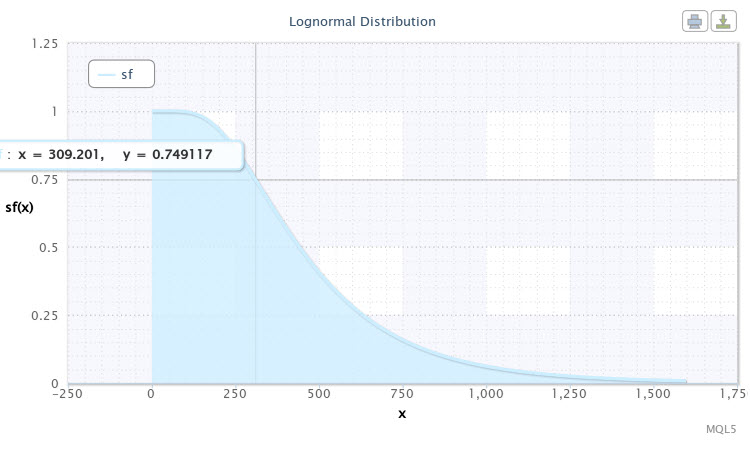
Figura 11. La funzione di sopravvivenza per X~Logn (6.09,0.53)
Il punto segnato nel grafico della curva può essere interpretato come segue: possiamo aspettarci con quasi il 75% di probabilità che la volatilità della coppia sarà di 310 punti. Più scendiamo lungo la curva, minore è la probabilità che la volatilità aumenti. Pertanto, una volatilità superiore a 1000 punti può già essere considerata un evento raro in quanto la probabilità che si verifichi è inferiore al 5%.
Curve di distribuzione simili possono essere costruite per il campione di rendimenti standardizzati così come per altri campioni. Suppongo che la metodologia sia generalmente chiara.
Conclusione
Va notato che le derivazioni analitiche proposte non hanno del tutto successo in quanto le serie tendono a variare. Anche se, ad esempio, non si tratta di serie di rendimenti logaritmici. Tuttavia, non mi sono posto il compito di valutare i metodi in questo articolo. Suggerisco al lettore interessato di commentare riguardo questo problema.
È importante notare la necessità di considerare il mercato, gli strumenti di mercato e gli esperti di trading dal punto di vista della probabilità. Questo è l'approccio che ho cercato di dimostrare. Spero che questo argomento susciti l'interesse del lettore e porti a una discussione costruttiva.
Posizione dei file:
| # | File | Path | Descrizione |
|---|---|---|---|
| 1 | Distribution_class.mqh | %MetaTrader%\MQL5\Include | Galleria delle classi di distribuzione |
| 2 | DistributionFigure_class.mqh | %MetaTrader%\MQL5\Include | Classi per la visualizzazione grafica delle distribuzioni |
| 3 | Random_class.mqh | %MetaTrader%\MQL5\Include | Classi per la generazione di un campione di numeri casuali |
| 4 | ExpStatistics_class.mqh | %MetaTrader%\MQL5\Include | Classe e funzioni delle stime delle caratteristiche statistiche |
| 5 | volatilityTest.mq5 | %MetaTrader%\MQL5\Scripts | Script per la stima del campione di volatilità EURUSD H4 |
| 6 | returnsTest.mq5 | %MetaTrader%\MQL5\Scripts | Script per la stima del campione di rendimento EURUSD H4 |
| 7 | randomTest.mq5 | %MetaTrader%\MQL5\Scripts | Script per la stima del campione di variabili casuali |
| 8 | fitAll.mq5 | %MetaTrader%\MQL5\Scripts | Script per l'adattamento e la stima di tutte le distribuzioni |
| 9 | Volat.csv | %MetaTrader%\MQL5\Files | File di dati campione di volatilità EURUSD H4 |
| 10 | Returns_std.csv | %MetaTrader%\MQL5\Files | EURUSD H4 restituisce un file di dati di esempio |
| 11 | Randoms.csv | %MetaTrader%\MQL5\Files | File di dati campione variabile casuale |
| 12 | Histogram.htm | %MetaTrader%\MQL5\Files | Istogramma del campione in HTML |
| 13 | Istogramma2.htm | %MetaTrader%\MQL5\Files | Doppio istogramma del campione in HTML |
| 14 | chi_test.htm | %MetaTrader%\MQL5\Files | Report statistico HTML della stima del campione |
| 15 | dataHist.txt | %MetaTrader%\MQL5\Files | Dati per la visualizzazione di un istogramma di campioni |
| 16 | dataHist2.txt | %MetaTrader%\MQL5\Files | Dati per la visualizzazione di un doppio istogramma dei campioni |
| 17 | dataFitAll.txt | %MetaTrader%\MQL5\Files | Dati per la visualizzazione del report HTML |
| 18 | highcharts.js | %MetaTrader%\MQL5\Files | Libreria JavaScript di grafici interattivi |
| 19 | jquery.min.js | %MetaTrader%\MQL5\Files | Libreria JavaScript |
| 20 | ReturnsIndicator.mq5 | %MetaTrader%\MQL5\Indicators | Indicatore di rendimenti logaritmici |
Materiali di riferimento:
Tradotto dal russo da MetaQuotes Ltd.
Articolo originale: https://www.mql5.com/ru/articles/257
Filtraggio dei segnali basati su dati statistici di correlazione dei prezzi
Utilizzo di pseudo-modelli come alternativa ai modelli C++
3 Metodi di accelerazione degli indicatori mediante l'esempio della regressione lineare
Utilizzo degli indicatori MetaTrader 5 con il framework di apprendimento automatico ENCOG per la previsione delle serie temporali
- App di trading gratuite
- Oltre 8.000 segnali per il copy trading
- Notizie economiche per esplorare i mercati finanziari
Accetti la politica del sito e le condizioni d’uso