Die Rolle von statistischen Verteilungen für die Arbeit eines Händlers
791
0
Regelmäßigkeiten erleichtern uns das Leben, doch es ist genauso wichtig, von der Zufälligkeit zu profitieren.
(Georgi Alexandrow)
Einleitung
Dieser Beitrag ist eine logische Fortsetzung meines Beitrags Statistische Verteilungen von Wahrscheinlichkeiten in MQL5, in dem die Klassen fr die Arbeit mit einigen theoretischen statistischen Verteilungen dargelegt wurden. Ich habe es als notwendig erachtet, erst in Form von Verteilungsklassen eine Basis zu bilden, um deren anschließende praktische Nutzung für den Benutzer zu erleichtern.
Da wir nun über die theoretische Grundlage verfügen, schlage ich vor, dass wir direkt mit realen Datensätzen fortfahren und versuchen, diese Grundlage für Informationszwecke zu nutzen. Gleichzeitig beleuchten wir einige Probleme in Bezug auf mathematische Statistik.
1. Generierung von Zufallszahlen mit einer bestimmten Verteilung
Bevor wir reale Datensätze betrachten, scheint es jedoch äußerst wichtig zu sein, einen Satz von Werten erhalten zu können, der eng mit einer gewünschten theoretischen Verteilung zusammenhängt.
In anderen Worten: Der Benutzer sollte nur Parameter der gewünschten Verteilung und Stichprobengröße festlegen. Ein Programm (in unserem Fall eine Hierarchie von Klassen) sollte eine solche Stichprobe von Werten für die weitere Arbeit generieren und ausgeben.
Ein weiteres wichtiges Detail ist, dass Stichproben, die nach einem bestimmten Gesetz generiert werden, für die Überprüfung diverser statistischer Tests genutzt werden. Dieser Bereich der mathematischen Statistik – die Generierung von zufälligen Variablen mit unterschiedlichen Verteilungsgesetzen – ist ziemlich interessant und herausfordernd.
Für meine Zwecke habe ich einen hochwertigen Generator verwendet, der im Buch Numerical Recipes: The Art of Scientific Computing [2] beschrieben wird. Sein Zeitraum beträgt in etwa 3,138*1057. Der Code in C ließ sich ziemlich einfach nach MQL5 übertragen.
Also erstellte ich auf folgende Weise die Klasse Random:
//+------------------------------------------------------------------+ //| Random class definition | //+------------------------------------------------------------------+ class Random { private: ulong u, //unsigned 64-bit integers v, w; public: //+------------------------------------------------------------------+ //| The Random class constructor | //+------------------------------------------------------------------+ void Random() { randomSet(184467440737095516); } //+------------------------------------------------------------------+ //| The Random class set-method | //+------------------------------------------------------------------+ void randomSet(ulong j) { v=4101842887655102017; w=1; u=14757395258967641292; u=j^v; int64(); v = u; int64(); w = v; int64(); } //+------------------------------------------------------------------+ //| Return 64-bit random integer | //+------------------------------------------------------------------+ ulong int64() { uint k=4294957665; u=u*2862933555777941757+7046029254386353087; v^= v>> 17; v ^= v<< 31; v ^= v>> 8; w = k*(w & 0xffffffff) +(w>> 32); ulong x=u^(u<<21); x^=x>>35; x^=x<<4; return(x+v)^w; }; //+------------------------------------------------------------------+ //| Return random double-precision value in the range 0. to 1. | //+------------------------------------------------------------------+ double doub() { return 5.42101086242752217e-20*int64(); } //+------------------------------------------------------------------+ //| Return 32-bit random integer | //+------------------------------------------------------------------+ uint int32() { return(uint)int64(); } };Nun können wir Klassen für Werte erstellen, die als Stichproben aus einer Verteilung gewählt werden. Sehen wir uns beispielsweise eine zufällige Variable aus der Normalverteilung an. Die Klasse CNormaldev sieht so aus:
//+------------------------------------------------------------------+ //| CNormaldev class definition | //+------------------------------------------------------------------+ class CNormaldev : public Random { public: CNormaldist N; //Normal Distribution instance //+------------------------------------------------------------------+ //| The CNormaldev class constructor | //+------------------------------------------------------------------+ void CNormaldev() { CNormaldist Nn; setNormaldev(Nn,18446744073709); } //+------------------------------------------------------------------+ //| The CNormaldev class set-method | //+------------------------------------------------------------------+ void setNormaldev(CNormaldist &Nn,ulong j) { N.mu=Nn.mu; N.sig=Nn.sig; randomSet(j); } //+------------------------------------------------------------------+ //| Return Normal deviate | //+------------------------------------------------------------------+ double dev() { double u,v,x,y,q; do { u = doub(); v = 1.7156*(doub()-0.5); x = u - 0.449871; y = fabs(v) + 0.386595; q = pow(x,2) + y*(0.19600*y-0.25472*x); } while(q>0.27597 && (q>0.27846 || pow(v,2)>-4.*log(u)*pow(u,2))); return N.mu+N.sig*v/u; } }; //+------------------------------------------------------------------+
Wie Sie sehen können, enthält die Klasse das Datenmitglied N des Typen CNormaldist. Dem Originalcode in C fehlte eine solche Verbindung mit der Verteilung. Ich habe es als notwendig erachtet, dass eine zufällige Variable, die durch die Klasse (hier CNormaldev) generiert wurde, eine logische und programmatische Verbindung mit ihrer Verteilung hat.
In der Originalversion war der Typ Normaldev definiert, wie folgt:
typedef double Doub; typedef unsigned __int64 Ullong; struct Normaldev : Ran { Doub mu,sig; Normaldev(Doub mmu, Doub ssig, Ullong i) ... }Zufallszahlen werden hier aus der Normalverteilung mithilfe von Levas Methode des Uniformitätskoeffizienten generiert. Alle anderen Klassen, die die Berechnung von zufälligen Variablen aus verschiedenen Verteilungen unterstützen, befinden sich in der Include-Datei Random_class.mqh. Wir schließen die Generierung nun ab und betrachten im praktischen Teil dieses Beitrags die Erstellung eines Arrays von Werten und testen eine Stichprobe.
2. Bewertung von Verteilungsparametern, statistische Hypothesen
Es ist klar, dass wir diskrete Variablen ansehen werden. In der Praxis ist es allerdings praktischer, den Satz von diskreten Variablen als Gruppe kontinuierlicher Variablen zu betrachten, wenn die Menge diskreter Variablen von Bedeutung ist. In der mathematischen Statistik ist dies eine standardmäßige Herangehensweise. Deshalb können wir für ihre Analyse Verteilungen nutzen, die durch analytische Formeln definiert sind, die sich auf kontinuierliche Variablen beziehen.
Beschäftigen wir uns also mit der Analyse der empirischen Verteilung.
2.1 Bearbeitung von Stichproben mithilfe der Klasse CExpStatistics
Als Erstes sollten sogenannte Ausreißer aus der Stichprobe entfernt werden. Dabei handelt es sich um Beobachtungen, die deutlich von den Beobachtungen des Großteils der Stichprobe abweichen (sowohl nach oben als auch nach unten). Es gibt keine universelle Methode zum Entfernen der Ausreißer.
Ich empfehle die Methode, die von S.V. Bulaschew in Abschnitt 6.3 [5] beschrieben wird. Im MQL4-Forum wurde eine Bibliothek von statistischen Funktionen geschaffen, auf deren Basis sich das vorliegende Problem einfach lösen lässt. Natürlich werden wir OOP anwenden und sie ein wenig aktualisieren.Ich habe die erstellte Klasse der Bewertung statistischer Merkmale CExpStatistics (Class of Expected Statistics) genannt.
Sie sieht in etwa so aus:
//+------------------------------------------------------------------+ //| Expected Statistics class definition | //+------------------------------------------------------------------+ class CExpStatistics { private: double arr[]; //initial array int N; //initial array size double Parr[]; //processed array int pN; //processed array size void stdz(double &outArr_st[],bool A); //standardization public: void setArrays(bool A,double &Arr[],int &n); //set array for processing bool isProcessed; //array processed? void CExpStatistics(){}; //constructor void setCExpStatistics(double &Arr[]); //set the initial array for the class void ZeroCheckArray(bool A); //check the input array for zero elements int get_arr_N(); //get the initial array length double median(bool A); //median double median50(bool A); //median of 50% interquantile range (midquartile range) double mean(bool A); //mean of the entire initial sample double mean50(bool A); //mean of 50% interquantile range double interqtlRange(bool A); //interquartile range double RangeCenter(bool A); //range center double meanCenter(bool A); //mean of the top five estimates double expVariance(bool A); //estimated variance double expSampleVariance(bool A); //shifted estimate of sample variance double expStddev(bool A); //estimated standard deviation double Moment(int index,bool A,int sw,double xm); //moment of distribution double expKurtosis(bool A,double &Skewness); ////estimated kurtosis and skewness double censorR(bool A); //censoring coefficient int outlierDelete(); //deletion of outliers from the sample int pArrOutput(double &outArr[],bool St); //processed array output void ~CExpStatistics(){};//destructor }; //+------------------------------------------------------------------+
Die Umsetzung jeder Methode kann in der Include-Datei ExpStatistics_class.mqh detailliert betrachtet werden, deshalb überspringe ich sie an dieser Stelle.
Die wichtige Handlung, die diese Klasse ausführt, ist die Ausgabe eines Arrays, das frei von Ausreißern ist (Parr[]), sofern vorhanden. Außerdem hilft sie beim Erhalten einiger beschreibender Statistiken der Stichprobe und deren Bewertungen.
2.2 Erstellen eines Histogramms für die verarbeitete Stichprobe
Da das Array nun frei von Ausreißern ist, kann auf Basis seiner Daten ein Histogramm (Häufigkeitsverteilung) gezeichnet werden. Es hilft bei der visuellen Bewertung des Verteilungsgesetztes der zufälligen Variable. Für die Erstellung eines Histogramms existiert ein Schritt-für-Schritt-Verfahren.
Zuerst sollte die Anzahl der erforderlichen Klassen berechnet werden. In diesem Kontext steht der Begriff "Klasse" für eine Gruppierung, ein Intervall. Die Anzahl der Klassen wird durch die Sturges-Formel berechnet:
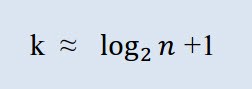
Dabei ist k die Anzahl der Klassen, n die Anzahl der Beobachtungen.
In MQL5 kann die Formel folgendermaßen dargestellt werden:
int Sturges(int n) /* Function for determining the number of class intervals using Sturges' rule. Variables: y is the number of sampling observations. Returned value: number of class intervals. */ { double s; // Returned value s=1.+log2(y); if(s>15) // Empirical rule s=15; return(int) floor(s); }Wenn die erforderliche Anzahl von Klassen (Intervallen) mithilfe der Sturges-Formel erhalten wurde, ist es an der Zeit, die Array-Daten in Klassen aufzuschlüsseln. Solche Daten werden als Beobachtungen bezeichnet (Sing. Beobachtung). Dies bewerkstelligen wir auf die folgende Weise mithilfe der Funktion Allocate:
void Allocate(double &data[],int n,double &f[],double &b[],int k) /* Function for allocating observations to classes. Variables: 1) data — initial sample (array) 2) n — sample size 3) f — calculated array of observations allocated to classes 4) b — array of class midpoints 5) k — number of classes */ { int i,j; // Loop counter double t,c; // Auxiliary variable t=data[ArrayMinimum(data)]; // Sample minimum t=t>0 ? t*0.99 : t*1.01; c=data[ArrayMaximum(data)]; // Sample maximum c=c>0 ? c*1.01 : c*0.99; c=(c-t)/k/2; // Half of the class interval b[0]=t+c; // Array of class interval midpoints f[0]= 0; for(i=1; i<k; i++) { b[i] = b[i - 1] + c + c; f[i] = 0; } // Grouping for(i=0; i<n; i++) for(j=0; j<k; j++) if(data[i]>b[j]-c && data[i]<=b[j]+c) { f[j]++; break; } }Wie Sie sehen können, nimmt die Funktion das Array der ursprünglichen Beobachtungen (data), seine Länge (n) und die Anzahl der Klassen (k) auf und ordnet die Beobachtungen einer bestimmten Klasse f[i] des Arrays f zu, wobei b[i] der Mittelpunkt der Klasse f[i] ist. Die Histogrammdaten sind nun bereit. Wir zeigen das Histogramm mithilfe der Tools an, die im vorher erwähnten Beitrag erwähnt werden. Zu diesem Zweck habe ich die Funktion histogramSave geschrieben, die das Histogramm für die beobachtete Serie in HTML darstellen wird. Die Funktion nimmt 2 Parameter auf: Array von Klassen (f) und Array von Klassenmittelpunkten (b).
Als Beispiel habe ich ein Histogramm für die absoluten Differenzen zwischen Maximal- und Minimalwerten von 500 Balken des Paares EURUSD auf dem vierstündigen Timeframe in Punkten mithilfe des Scripts volatilityTest.mq5 erstellt.
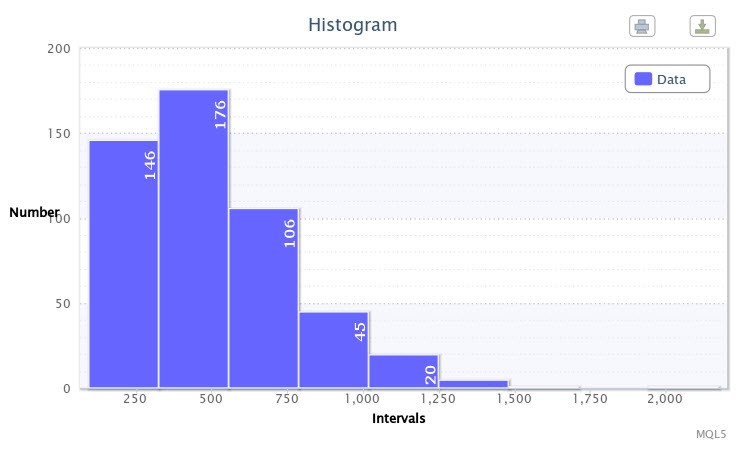
Abbildung 1. Datenhistogramm (absolute Volatilität des EURUSD H4)
Wie im Histogramm (Abb. 1) dargestellt, verfügt die erste Klasse über 146 Beobachtungen, die zweite über 176 usw. Die Funktion des Histogramms ist die Bereitstellung einer visuellen Darstellung der empirischen Verteilung der beobachteten Stichprobe.
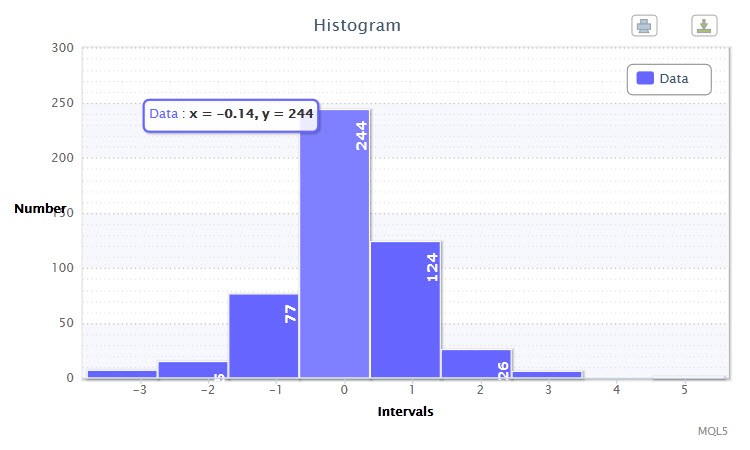
Abbildung 2. Datenhistogramm (standardisierte Erträge des EURUSD H4)
Das andere Histogramm (Abb. 2) zeigt standardisierte logarithmische Erträge von 500 Balken des Paares EURUSD auf dem H4-Timeframe. Sie haben bemerkt, dass die vierte und fünfte Klasse mit 244 bzw. 124 Beobachtungen am beeindruckendsten sind. Dieses Histogramm wurde mithilfe des Scripts returnsTest.mq5 erstellt.
Das Histogramm ermöglicht es uns also, das Verteilungsgesetz zu wählen, dessen Parameter weiter bewertet werden. In Fällen, in denen nicht visuell ersichtlich ist, welche Verteilung vorzuziehen ist, können Sie die Parameter mehrerer theoretischer Verteilungen bewerten.
Beide Verteilungen, die wir betrachtet haben, sehen nicht aus wie die normalen, insbesondere die erste. Wir möchten allerdings nicht auf die optische Darstellung vertrauen und gehen zu Zahlen über.
2.3 Normalitätshypothese
Es ist üblich, zunächst die Annahme (Hypothese) zu lösen und zu testen, dass die betrachtete Verteilung normal ist. Diese Hypothese wird als Haupthypothese bezeichnet. Eine der beliebtesten Methoden zum Testen der Normalität einer Stichprobe ist der Jarque-Bera-Test.
Sein Algorithmus ist aufgrund der Näherung ziemlich umfangreich, auch wenn er nicht der komplexeste ist. Es gibt mehrere Versionen des Algorithmus in C++ und weiteren Sprachen. Eine der erfolgreichsten und bewährtesten Versionen ist eine Situation, die sich in der plattformübergreifenden numerischen Analysebibliothek ALGLIB befindet. Ihr Autor [S.A. Botschkanow] hat eine außerordentliche Arbeit geleistet, insbesondere bei der Kompilierung der Test-Quantilstabelle. Ich habe sie nur unwesentlich an die Anforderungen von MQL5 angepasst.
Die Hauptfunktion jarqueberatest sieht so aus:
//+------------------------------------------------------------------+ // the Jarque-Bera Test | //+------------------------------------------------------------------+ void jarqueberatest(double &x[],double &p) /* The Jarque-Bera test is used to check hypothesis about the fact that a given sample xS is a sample of normal random variable with unknown mean and variance. Variables: x - sample Xs; p - p-value; */ { int n=ArraySize(x); double s; p=0.; if(n<5)//N is too small { p=1.0; return; } //N is large enough jarquebera_jarqueberastatistic(x,n,s); p=jarquebera_jarqueberaapprox(n,s); } //+------------------------------------------------------------------+Sie bearbeitet eine ursprüngliche Datenauswahl (x) und gibt den p-Wert aus, d. h. einen Wert, der die Wahrscheinlichkeit der Ablehnung einer Nullhypothese charakterisiert, wenn die Nullhypothese tatsächlich zutrifft. Im Körper der Funktion befinden sich 2 Hilfsfunktionen. Die erste Funktion – jarquebera_jarqueberastatistic – berechnet die Jarque-Bera-Statistik und die zweite – jarquebera_jarqueberaapprox – berechnet den p-Wert. Es sollte festgehalten werden, dass die letztgenannte Funktion wiederum Hilfsfunktionen in Bezug auf die Näherung auslöst, von denen knapp 30 im Algorithmus enthalten sind.
Versuchen wir also, unsere Stichproben auf Normalität zu testen. Wir verwenden das Script returnsTest.mq5, das die Stichprobe der standardisierten Erträge des EURUSD H4 bearbeiten wird.
Wie erwartet, zeigte der Test, dass die Wahrscheinlichkeit der Ablehnung einer wahren Nullhypothese 0,0000 beträgt. In anderen Worten: Die Verteilung dieser Stichprobe gehört nicht zur Familie der Normalverteilungen. Führen Sie das Script volatilityTest.mq5 aus, um die Stichprobe der absoluten Volatilität des Paares EURUSD zu bearbeiten. Das Ergebnis wird ähnlich sein: Die Verteilung ist nicht normal.
3. Anpassung der Verteilung
Die mathematische Statistik bietet eine Reihe von Methoden, die den Vergleich der empirischen Verteilung mit der Normalverteilung ermöglichen. Das größte Problem ist, dass die Parameter der Normalverteilung uns nicht bekannt sind und die Annahme herrscht, dass die betrachteten Daten die Normalität einer Verteilung nicht wiedergeben.
Deshalb müssen wir nichtparametrische Tests nutzen und die unbekannten Parameter mit den Schätzungen aus der empirischen Verteilung füllen.
3.1 Bewertung und Testing
Einer der beliebtesten und vor allem geeignetsten Tests in dieser Situation ist der χ2-Test. Er basiert auf Pearsons Messung der Anpassungsgüte.
Wir führen den Test mithilfe der Funktion chsone durch:
void chsone(double &f[],double &ebins[],double &df, double &chsq,double &prob,const int knstrn=1) /* 1) f — array of observations allocated to classes 2) ebins - array of expected frequencies 3) df - number of degrees of freedom 3) chsq — chi-square statistics 4) prob - probability of accepting a true null hypothesis 5) knstrn — constraint */ { CGamma gam; int j,nbins=ArraySize(bins),q,g; double temp; df=nbins-knstrn; chsq=0.0; q=nbins/2; g=nbins-1; for(j=0;j<nbins/2;j++) //passing through the left side of the distribution { if(ebins[j]<0.0 || (ebins[j]==0. && bins[j]>0.)) Alert("Bad expected number in chsone!"); if(ebins[j]<=5.0) { --df; ebins[j+1]+=ebins[j]; bins[j+1]+=bins[j]; } else { temp=bins[j]-ebins[j]; chsq+=pow(temp,2)/ebins[j]; } } for(j=nbins-1;j>nbins/2-1;j--) //passing through the right side of the distribution { if(ebins[j]<0.0 || (ebins[j]==0. && bins[j]>0.)) Alert("Bad expected number in chsone!"); if(ebins[j]<=5.0) { --df; ebins[j-1]+=ebins[j]; //starting with the last class bins[j-1]+=bins[j]; } else { temp=bins[j]-ebins[j]; chsq+=pow(temp,2)/ebins[j]; } } if(df<1)df=1; //compensate prob=gam.gammq(0.5*df,0.5*chsq); //Chi-square probability function }
Aus der Auflistung ist ersichtlich, dass eine Instanz der Klasse CGamma verwendet wird, die die unvollständige Gamma-Funktion repräsentiert, die in der Datei Distribution_class.mqh sowie den erwähnten Bereitstellungen enthalten ist. Es sollte auch festgehalten werden, dass das Array der erwarteten Häufigkeiten (ebins) mithilfe der Funktionen estimateDistribution und expFrequency erhalten wird.
Wir müssen nun die numerischen Parameter auswählen, die in der analytischen Formel für die theoretische Verteilung enthalten sind. Die Anzahl der Parameter hängt von der jeweiligen Verteilung ab. Beispielsweise weist die Normalverteilung zwei Parameter auf, die exponentielle Verteilung einen Parameter usw.
Bei der Bestimmung der Verteilungsparameter nutzen wir für gewöhnlich Punktschätzungsmethoden wie die Momentenmethode, die Quantilmethode und die Methode der höchsten Wahrscheinlichkeit. Die erstgenannte ist einfacher, da sie impliziert, dass die Schätzungen der Stichprobe (Erwartung, Varianz, Schiefe usw.) den allgemeinen Bewertungen entsprechen sollten.
Versuchen wir mithilfe eines Beispiels eine theoretische Verteilung für unsere Stichprobe auszusuchen. Wir nehmen eine Reihe standardisierter Erträge des EURUSD H4, für den wir bereits ein Histogramm gezeichnet haben.
Auf den ersten Blick ist die Normalverteilung für die Reihe nicht geeignet, da der Koeffizient der Kurtosis beobachtet wird. Wenden wir zum Vergleich eine andere Verteilung an.
Wenn wir also das bereits bekannte Script returntsTest.mq5 starten, versuchen wir, eine Verteilung wie Hypersec auszuwählen. Zusätzlich wird das Script die ausgewählten Verteilungsparameter mithilfe der Funktion estimateDistribution schätzen und ausgeben und unmittelbar den χ2-Test ausführen. Die Parameter der ausgewählten Verteilung haben sich als die folgenden erwiesen:
Hyperbolic Secant distribution: X~HS(-0,00, 1,00);
und die Testergebnisse waren die folgenden:
"Statistik von Chi-Quadrat: 1,89; Wahrscheinlichkeit der Ablehnung einer wahren Nullhypothese: 0,8648"
Es sollte festgehalten werden, dass die ausgewählte Verteilung gut geeignet ist, da der Wert der χ2-Statistik ziemlich gering ist.
Zudem wird mithilfe der Funktion histogramSaveE ein Doppelhistogramm der beobachteten und erwarteten Häufigkeitsverhältnisse (das Häufigkeitsverhältnis ist eine Häufigkeit, ausgedrückt als Bruchteil oder prozentualer Anteil) von standardisierten Erträgen gezeichnet (Abb. 3). Man kann erkennen, dass sich die Balken nahezu duplizieren. Dies ist ein Beweis für die erfolgreiche Anpassung.
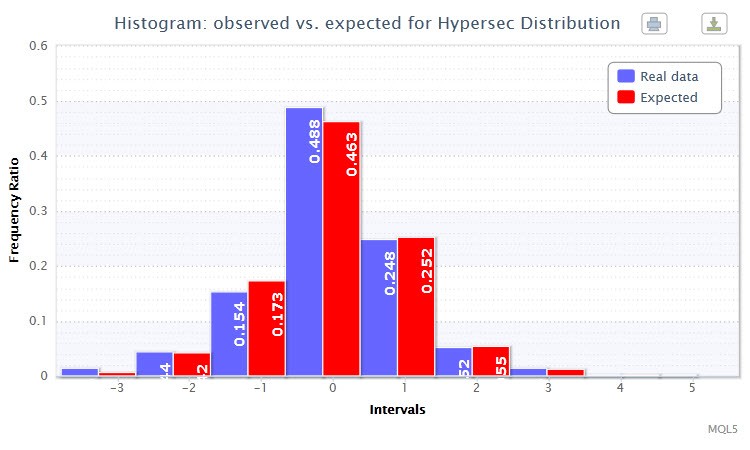
Abbildung 3. Histogramm der beobachteten und erwarteten Häufigkeitsverhältnisse (standardisierte Erträge des EURUSD H4)
Führen wir ein ähnliches Verfahren für die Volatilitätsdaten mithilfe des bereits bekannten Scripts volatilityTest.mq5 durch.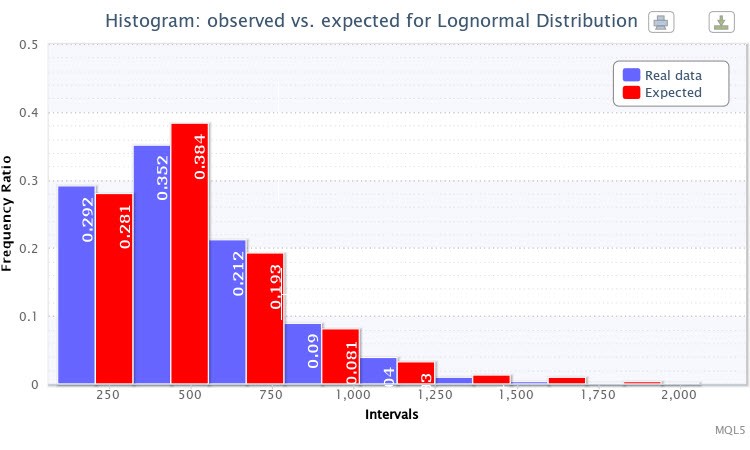
Abbildung 4. Histogramm der beobachteten und erwarteten Häufigkeitsverhältnisse (absolute Volatilität des EURUSD H4)
Ich habe für den Test die lognormale Verteilung Lognormal gewählt. Als Ergebnis habe ich die folgende Schätzung der Parameter erhalten:
Lognormal-Verteilung: X~Logn(6,09, 0,53);
und die Testergebnisse waren die folgenden:
"Statistik von Chi-Quadrat: 6,17; Wahrscheinlichkeit der Ablehnung einer wahren Nullhypothese: 0,4040"
Die theoretische Verteilung für diese empirische Verteilung wurde auch mit großem Erfolg gewählt. Somit kann man davon ausgehen, dass die Nullhypothese nicht verworfen werden kann (bei einem Standard-Konfidenzniveau p=0,05). In Abb. 4 kann man sehen, dass die Balken der erwarteten und beobachteten Häufigkeitsverhältnisse sich ebenfalls sehr ähnlich sehen.
Ich möchte Sie daran erinnern, dass wir eine weitere Möglichkeit haben, eine Stichprobe aus zufälligen Variablen aus einer Verteilung mit festgelegten Parametern zu generieren. Für die Nutzung einer Hierarchie von Klassen in Bezug auf einen solchen Vorgang habe ich das Script randomTest.mq5 geschrieben.
Bei seinem Start müssen wir die Parameter gemäß Abb. 5 festlegen.
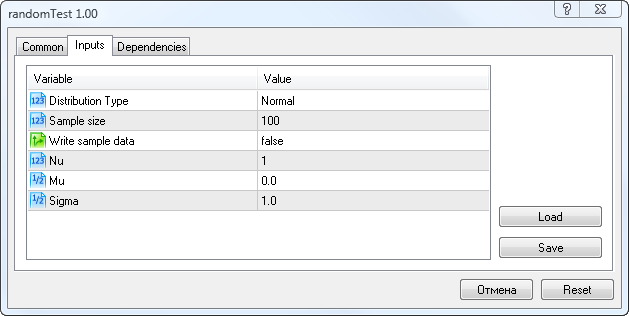
Abbildung 5. Eingabeparameter des Scripts randomTest.mq5
Hier können Sie den Verteilungstyp (Distribution Type), die Anzahl der zufälligen Variablen in einer Stichprobe (Sample Size), die Option zum Speichern der Stichprobe (Write sample data), den Parameter Nu (für die Studentsche t-Verteilung) und die Parameter Mu und Sigma auswählen.
Wenn Sie für Write sample data den Wert true festlegen, speichert das Script die Stichprobe von zufälligen Variablen mit den benutzerdefinierten Parametern in der Datei Randoms.csv. Andernfalls liest es die Daten der Stichprobe aus dieser Datei und führt anschließend statistische Tests durch.
Für einige Verteilungen mit fehlenden Parametern Mu und Sigma habe ich eine Tabelle mit der Entsprechung der Parameter mit den Feldern im Startfenster des Scripts bereitgestellt.
| Verteilung | Erster Verteilungsparameter | Zweiter Verteilungsparameter |
|---|---|---|
| Logistic | alph --> Mu | bet --> Sigma |
| Exponential | lambda --> Mu | -- |
| Gamma | alph --> Mu | bet --> Sigma |
| Beta | alph --> Mu | bet --> Sigma |
| Laplace | alph --> Mu | bet --> Sigma |
| Binomial | n --> Mu | pe --> Sigma |
| Poisson | lambda --> Mu | -- |
Wird beispielsweise die Poisson-Verteilung ausgewählt, dann wird der Parameter lambda über das Feld Mu eingegeben usw.
Als Beispiel habe ich das Script für die Normalverteilung mit den Parametern X~Nor(3.50, 2.77) mit Write sample data=true ausgeführt. Das Script generierte zuerst eine Stichprobe. Beim zweiten Durchlauf mit Write sample data=false wurde ein Histogramm gezeichnet, wie in Abb. 6 dargestellt.
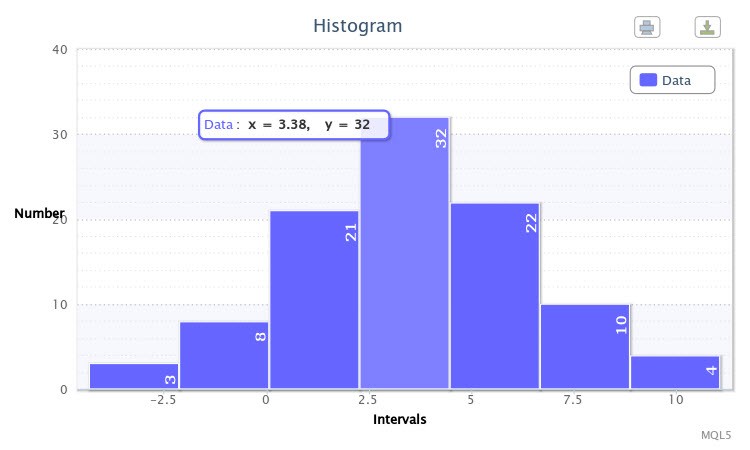
Abbildung 6. Stichprobe von zufälligen Variablen X~Nor(3.50,2.77)
Die restlichen im Terminal-Fenster dargestellten Informationen sind:
Der Jarque-Bera-Test: "Der Jarque-Bera-Test: Wahrscheinlichkeit der Ablehnung einer wahren Nullhypothese beträgt 0,9381";
Parameterschätzung: Normalverteilung: X~Nor(3.58, 2.94);
Testergebnisse Chi-Quadrat: "Statistik von Chi-Quadrat: 0,38; Wahrscheinlichkeit der Ablehnung einer wahren Nullhypothese: 0,9843 kaufen".
Letztendlich wurde ein weiteres Doppelhistogramm der beobachteten und erwarteten Häufigkeitsverhältnisse für die Stichprobe angezeigt (Abb. 7).
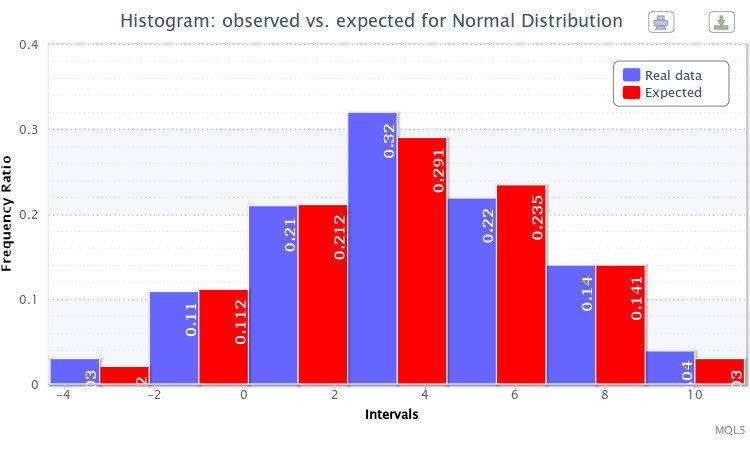
Abbildung 7. Histogramm der beobachteten und erwarteten Häufigkeitsverhältnisse für X~Nor(3.50,2.77)
Im Allgemeinen war die Generierung der angegebenen Verteilung erfolgreich.
Ich habe noch das Script fitAll.mq5 geschrieben, das ähnlich arbeitet wie randomTest.mq5. Der einzige Unterschied ist, dass das erste Script die Funktion fitDistributions enthält. Ich habe die folgende Aufgabe gestellt: Anpassung aller verfügbaren Verteilungen an eine Stichprobe von zufälligen Variablen und Durchführung eines statistischen Tests.
Aufgrund nicht zusammenpassender Parameter, die zur Anzeige von Zeilen im Terminal führen, die den Benutzer darüber informieren, dass die Schätzung nicht möglich ist, z. B. "Beta distribution cannot be estimated!" ist es nicht immer möglich, eine Verteilung an eine Stichprobe anzupassen.
Ferner habe ich beschlossen, dass dieses Script statistische Ergebnisse in Form eines kleinen HTML-Berichts visualisieren soll. Ein Beispiel davon finden Sie im Beitrag "Diagramme in HTML" (Abb. 8).
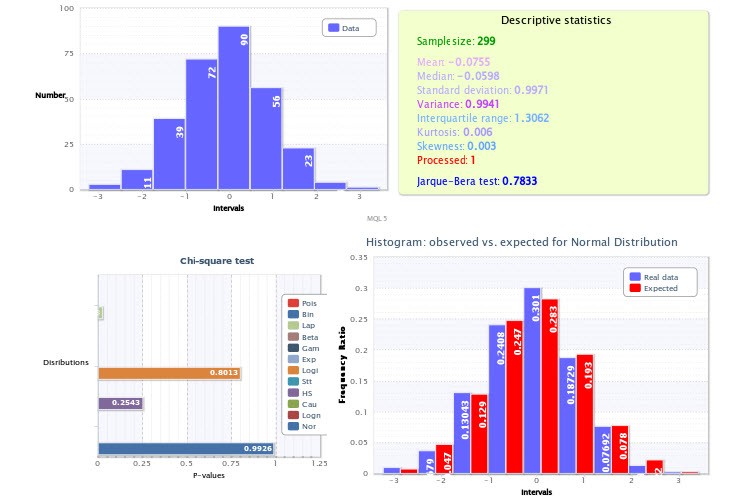
Abbildung 8. Statistischer Bericht der Schätzung einer Stichprobe
Ein Standardhistogramm der Stichprobe wird im linken oberen Viertel angezeigt. Das rechte obere Viertel stellt die beschreibende Statistik und das Ergebnis des Jarque-Bera-Tests dar, in dem der Wert der Variable Processed gleich 1 bedeutet, dass die Ausreißer gelöscht wurden, während ein Wert von 0 bedeutet, dass es keine Ausreißer gab.
P-Werte des χ2-Tests für jede ausgewählte Verteilung werden im linken unteren Viertel dargestellt. Hier erwies sich die Normalverteilung in Bezug auf ihre Anpassung (p=0,9926) als die beste. Deshalb wurde dafür ein Histogramm der beobachteten und erwarteten Häufigkeitsverhältnisse im rechten unteren Viertel gezeichnet.
Derzeit gibt es in meiner Galerie noch nicht so viele Verteilungen. Doch mit diesem Script können Sie viel Zeit sparen, wenn Sie mit einer großen Menge von Verteilungen arbeiten.
Nun, da wir die Verteilungsparameter der beobachteten Stichproben genau kennen, können wir mit probabilistischen Schlussfolgerungen fortfahren.
3.2 Wahrscheinlichkeiten von Werten zufälliger Variablen
Im Beitrag über theoretische Verteilungen führte ich das Script continuousDistribution.mq5 als Beispiel an. Mit seiner Hilfe werden wir versuchen, jedes beliebige Verteilungsgesetz mit bekannten Parametern darzustellen, das für uns von Interesse sein kann.
Für die Daten der Volatilität geben wir also die vorher erhaltenen Parameter der Lognormal-Verteilung ein (Mu=6.09, Sigma=0.53), wählen den Verteilungstyp Lognormal und den Modus cdf (Abb. 9).
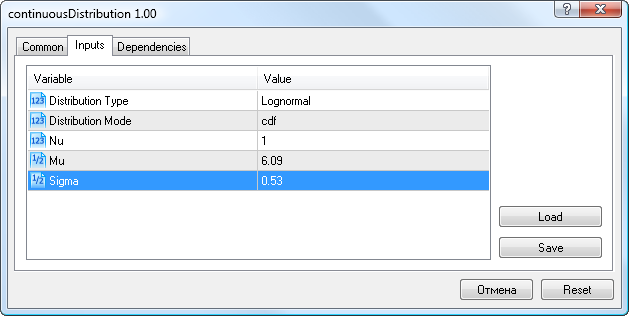
Abbildung 9. Parameter der Lognormal-Verteilung X~Logn(6.09,0.53)
Das Script zeigt anschließend die Verteilungsfunktion für unsere Stichprobe. Sie wird aussehen, wie in Abb. 10 dargestellt.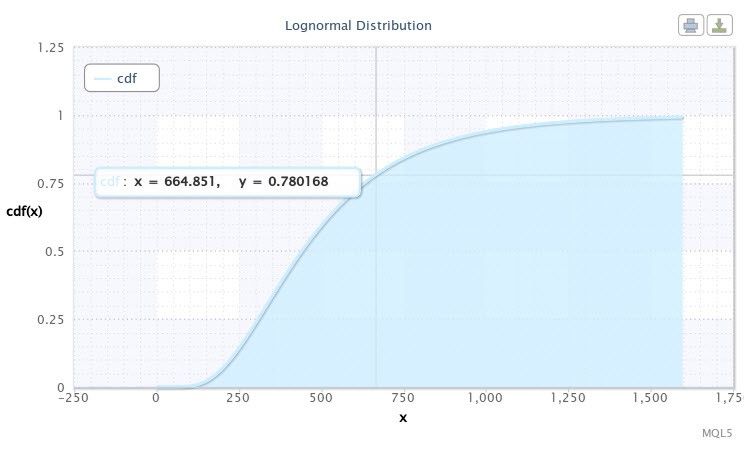
Abbildung 10. Verteilungsfunktion für X~Logn(6.09,0.53)
Im Diagramm können wir erkennen, dass der Cursor auf einen Punkt zeigt, dessen Koordinaten ungefähr [665:0.78] sind. Das bedeutet, dass die Volatilität des EURUSD H4 mit einer Wahrscheinlichkeit von 78 % nicht über 665 Punkten liegen wird. Diese Information kann sich für den Entwickler eines Expert Advisors als äußerst nützlich erweisen. Man kann sicherlich andere Werte der Kurve nehmen, indem man den Cursor bewegt.
Nehmen wir an, dass wir uns für die Wahrscheinlichkeit des Ereignisses interessieren, dass der Wert der Volatilität im Intervall zwischen 500 und 750 Punkten liegt. Zu diesem Zweck muss die folgende Operation durchgeführt werden:
cdf(750) - cdf(500) = 0.84 - 0.59 = 0.25.
Somit schwankt die Volatilität des Paares in einem Viertel der Fälle im Intervall zwischen 500 und 750 Punkten.
Führen wir das Script erneut mit den gleichen Verteilungsparametern aus, aber wählen sf als Modus des Verteilungsgesetzes. Die Funktion der Zuverlässigkeit (Überleben) wird angezeigt, wie folgt (Abb. 11).
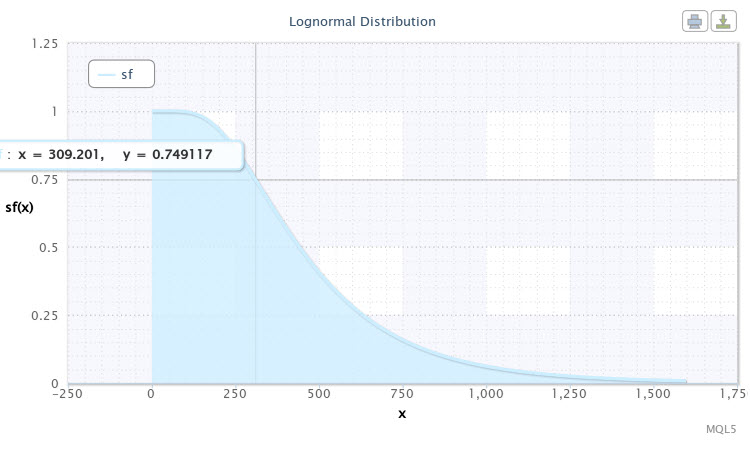
Abbildung 11. Überlebensfunktion für X~Logn(6.09,0.53)
Der im Diagramm der Kurve markierte Punkt lässt sich auf folgende Weise interpretieren: Wir können mit einer Wahrscheinlichkeit von beinahe 75 % erwarten, dass die Volatilität des Paares 310 Punkte betragen wird. Je tiefer wir mit der Kurve gehen, desto geringer ist die Wahrscheinlichkeit, dass die Volatilität steigt. Somit kann eine Volatilität von über 1000 Punkten bereits als seltenes Ereignis betrachtet werden, da die Wahrscheinlichkeit unter 5 % liegt.
Ähnliche Verteilungskurven lassen sich für die Stichprobe der standardisierten Erträge und andere Stichproben erstellen. Ich schätze, dass die Methoden dafür im Allgemeinen klar sind.
Fazit
Beachten Sie, dass die vorgestellten analytischen Ableitungen nicht vollständig erfolgreich sind, da Reihen dazu neigen, sich zu verändern. Doch dies betrifft beispielsweise nicht Reihen von logarithmischen Erträgen. Allerdings habe ich es mir nicht zur Aufgabe gemacht, die Methoden in diesem Beitrag zu bewerten. Ich schlage vor, dass interessierte Leser Kommentare zu diesem Thema hinterlassen.
Es muss festgehalten werden, dass der Markt, die Marktinstrumente und die Handelsexperten vom Standpunkt der Wahrscheinlichkeit aus betrachtet werden müssen. Das ist der Ansatz, den ich demonstrieren wollte. Ich hoffe, dass dieses Thema das Interesse der Leser wecken und zu einer konstruktiven Diskussion führen wird.
Ablageort der Dateien:
| # | Datei | Pfad | Beschreibung |
|---|---|---|---|
| 1 | Distribution_class.mqh | %MetaTrader%\MQL5\Include | Galerie von Verteilungsklassen |
| 2 | DistributionFigure_class.mqh | %MetaTrader%\MQL5\Include | Klassen für die grafische Darstellung von Verteilungen |
| 3 | Random_class.mqh | %MetaTrader%\MQL5\Include | Klassen für die Generierung von Stichproben von Zufallszahlen |
| 4 | ExpStatistics_class.mqh | %MetaTrader%\MQL5\Include | Klassen und Funktionen von Schätzungen von statistischen Merkmalen |
| 5 | volatilityTest.mq5 | %MetaTrader%\MQL5\Scripts | Script für die Schätzung der Volatilitätsstichprobe EURUSD H4 |
| 6 | returnsTest.mq5 | %MetaTrader%\MQL5\Scripts | Script für die Schätzung der Ertragsstichprobe EURUSD H4 |
| 7 | randomTest.mq5 | %MetaTrader%\MQL5\Scripts | Script für die Schätzung der Stichprobe von zufälligen Variablen |
| 8 | fitAll.mq5 | %MetaTrader%\MQL5\Scripts | Script für die Anpassung und Schätzung aller Verteilungen |
| 9 | Volat.csv | %MetaTrader%\MQL5\Files | Datendatei der Volatilitätsstichprobe EURUSD H4 |
| 10 | Returns_std.csv | %MetaTrader%\MQL5\Files | Datendatei der Ertragsstichprobe EURUSD H4 |
| 11 | Randoms.csv | %MetaTrader%\MQL5\Files | Datendatei der Stichprobe von zufälligen Variablen |
| 12 | Histogram.htm | %MetaTrader%\MQL5\Files | Histogramm der Stichprobe in HTML |
| 13 | Histogram2.htm | %MetaTrader%\MQL5\Files | Doppelhistogramm der Stichprobe in HTML |
| 14 | chi_test.htm | %MetaTrader%\MQL5\Files | Statistischer HTML-Bericht der Schätzung einer Stichprobe |
| 15 | dataHist.txt | %MetaTrader%\MQL5\Files | Daten für die Darstellung eines Histogramms von Stichproben |
| 16 | dataHist2.txt | %MetaTrader%\MQL5\Files | Daten für die Darstellung eines Doppelhistogramms von Stichproben |
| 17 | dataFitAll.txt | %MetaTrader%\MQL5\Files | Daten für die Darstellung eines HTML-Berichts |
| 18 | highcharts.js | %MetaTrader%\MQL5\Files | JavaScript-Bibliothek von interaktiven Diagrammen |
| 19 | jquery.min.js | %MetaTrader%\MQL5\Files | JavaScript-Bibliothek |
| 20 | ReturnsIndicator.mq5 | %MetaTrader%\MQL5\Indicators | Indikator von logarithmischen Erträgen |
Literatur:
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/257
Universeller Expert Advisor: Handelsmodi von Strategien (Teil 1)
Nutzung von Pseudo-Templates als Alternative für C++-Templates
Filtern von Signalen auf Basis statistischer Daten von Preiskorrelationen
Verwendung von Indikatoren in MetaTrader 5 mit dem Machine Learning Framework ENCOG für die Prognostizierung von Zeitreihen
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.