Satıcı Çalışmasında İstatistiksel Dağılımların Rolü
102
0
Düzenlilikler hayatımızı kolaylaştırır ama rasgele değerlerden faydalanmak da bir o kadar önemlidir.
(Georgiy Aleksandrov)
Tanıtım
Bu makale, bazı teorik istatistiksel dağılımlarla çalışmak için sınıfları ortaya koyan MQL5'te İstatistiksel Olasılık Dağılımları makalemin mantıksal bir devamıdır. Bir kullanıcının daha sonra pratikte kullanmasını kolaylaştırmak için önce dağıtım sınıfları şeklinde temeli atmayı gerekli buldum.
Artık teorik bir temele sahip olduğumuza göre, doğrudan gerçek veri setlerine geçmemizi ve bu temelden bilgi amaçlı yararlanmaya çalışmamızı öneriyorum. Aynı zamanda matematiksel istatistiklerle ilgili bazı konulara ışık tutacağız.
1. Verilen Bir Dağılımla Rastgele Sayıların Üretilmesi
Ancak gerçek veri kümelerini düşünmeden önce, istenen bir teorik dağılımla yakından ilgili olacak bazı değer kümelerini elde edebilmek çok önemli görünmektedir.
Başka bir deyişle, bir kullanıcı yalnızca istenen dağılımın ve numune boyutunun parametrelerini ayarlamalıdır. Bir program (bizim durumumuzda, bir sınıf hiyerarşisi), daha fazla çalışma için bu tür değer örneklerini oluşturmalı ve çıkarmalıdır.
Bir diğer önemli detay ise, belirli bir yasa ile üretilen örneklerin çeşitli istatistiksel testleri kontrol etmek için kullanılmasıdır. Farklı dağılım yasalarına sahip rasgele değişkenlerin matematiksel istatistik üretimi alanı oldukça ilginç ve zorludur.
Kendi amaçlarım için Sayısal Tarifler kitabında açıklanan yüksek kaliteli bir jeneratör kullandım: Bilimsel Hesaplama Sanatı [2]. Periyodu yaklaşık olarak 3.138*1057'ye eşittir. C kodu MQL5'e oldukça kolay bir şekilde aktarıldı.
Ve böylece Random sınıfını aşağıdaki gibi yarattım:
//+------------------------------------------------------------------+ //| Random class definition | //+------------------------------------------------------------------+ class Random { private: ulong u, //unsigned 64-bit integers v, w; public: //+------------------------------------------------------------------+ //| The Random class constructor | //+------------------------------------------------------------------+ void Random() { randomSet(184467440737095516); } //+------------------------------------------------------------------+ //| The Random class set-method | //+------------------------------------------------------------------+ void randomSet(ulong j) { v=4101842887655102017; w=1; u=14757395258967641292; u=j^v; int64(); v = u; int64(); w = v; int64(); } //+------------------------------------------------------------------+ //| Return 64-bit random integer | //+------------------------------------------------------------------+ ulong int64() { uint k=4294957665; u=u*2862933555777941757+7046029254386353087; v^= v>> 17; v ^= v<< 31; v ^= v>> 8; w = k*(w & 0xffffffff) +(w>> 32); ulong x=u^(u<<21); x^=x>>35; x^=x<<4; return(x+v)^w; }; //+------------------------------------------------------------------+ //| Return random double-precision value in the range 0. to 1. | //+------------------------------------------------------------------+ double doub() { return 5.42101086242752217e-20*int64(); } //+------------------------------------------------------------------+ //| Return 32-bit random integer | //+------------------------------------------------------------------+ uint int32() { return(uint)int64(); } };
Artık bir dağıtımdan örneklenen değerler için sınıflar oluşturabiliriz.
Örnek olarak normal dağılımdan rastgele bir değişkene bakalım. CNormaldev sınıfı aşağıdaki gibidir:
//+------------------------------------------------------------------+ //| CNormaldev class definition | //+------------------------------------------------------------------+ class CNormaldev : public Random { public: CNormaldist N; //Normal Distribution instance //+------------------------------------------------------------------+ //| The CNormaldev class constructor | //+------------------------------------------------------------------+ void CNormaldev() { CNormaldist Nn; setNormaldev(Nn,18446744073709); } //+------------------------------------------------------------------+ //| The CNormaldev class set-method | //+------------------------------------------------------------------+ void setNormaldev(CNormaldist &Nn,ulong j) { N.mu=Nn.mu; N.sig=Nn.sig; randomSet(j); } //+------------------------------------------------------------------+ //| Return Normal deviate | //+------------------------------------------------------------------+ double dev() { double u,v,x,y,q; do { u = doub(); v = 1.7156*(doub()-0.5); x = u - 0.449871; y = fabs(v) + 0.386595; q = pow(x,2) + y*(0.19600*y-0.25472*x); } while(q>0.27597 && (q>0.27846 || pow(v,2)>-4.*log(u)*pow(u,2))); return N.mu+N.sig*v/u; } }; //+------------------------------------------------------------------+
Görüldüğü gibi, sınıfın CNormaldist tipinde bir N veri üyesi vardır. Orijinal C kodu, dağıtımla böyle bir bağlantıdan yoksundu. Sınıf tarafından (burada, CNormaldev sınıfı tarafından) oluşturulan rastgele bir değişkenin, dağılımı ile mantıksal ve programatik bir bağlantısının olması gerektiğini düşündüm.
Orijinal versiyonda, Normaldev tip şu şekilde tanımlanmıştır:
typedef double Doub; typedef unsigned __int64 Ullong; struct Normaldev : Ran { Doub mu,sig; Normaldev(Doub mmu, Doub ssig, Ullong i) ... }
Rastgele sayılar burada Leva'nın üniforma oranı yöntemi kullanılarak normal dağılımdan üretilir.
Çeşitli dağılımlardan rastgele değişkenlerin hesaplanmasına yardımcı olan diğer tüm sınıflar, Random_class.mqh dosyasında bulunur.
Şimdi oluşturma işlemini bitireceğiz ve makalenin pratik bölümünde bir dizi değerin nasıl oluşturulacağını ve bir örneğin nasıl test edileceğini göreceğiz.
2. Dağılım Parametrelerinin Tahmini, İstatistiksel Hipotezler
Ayrık değişkenlere bakacağımız açıktır. Ancak uygulamada, kesikli değişkenlerin sayısı önemliyse, bu tür kesikli değişkenler kümesini bir sürekli değişkenler grubu olarak düşünmek daha uygundur. Bu, matematiksel istatistikte standart bir yaklaşımdır. Bu nedenle analizleri için sürekli değişkenlerle ilgili analitik formüllerle tanımlanan dağılımları kullanabiliriz.
Öyleyse ampirik dağılımın analizine geçelim.
Üyeleri temsil edebilirlik kriterini karşılayan genel bir popülasyon örneğinin çalışıldığı varsayılmaktadır. Ek olarak, Bölüm 8.3 [9]'da belirtilen tahminlere ilişkin gereksinimler karşılanmaktadır. Sayısal dağılım parametreleri nokta tahmini ve aralık yöntemleri ile bulunabilir.
2.1 CExpStatistics Sınıfını Kullanarak Örnek İşleme
İlk önce denen dosya örnekten silinmelidir; bunlar, örneğin büyük bölümünün (hem yukarı hem de aşağı) gözlemlerinden belirgin şekilde sapan gözlemlerdir. Aykırı değerleri silmek için evrensel bir yöntem yoktur.
SV tarafından açıklananı kullanmanızı öneririm Bulashev Bölüm 6.3 [5]. forumunda, verilen problemin kolayca çözülebileceği bir istatistiksel fonksiyonlar kütüphanesi oluşturuldu. Bununla birlikte, kesinlikle OOP uygulayacağız ve biraz güncelleyeceğiz.
Oluşturulan istatistiksel özelliklerin tahmin sınıfını CExpStatistics (Beklenen İstatistikler Sınıfı) olarak adlandırdım.
Kabaca şöyledir:
//+------------------------------------------------------------------+ //| Expected Statistics class definition | //+------------------------------------------------------------------+ class CExpStatistics { private: double arr[]; //initial array int N; //initial array size double Parr[]; //processed array int pN; //processed array size void stdz(double &outArr_st[],bool A); //standardization public: void setArrays(bool A,double &Arr[],int &n); //set array for processing bool isProcessed; //array processed? void CExpStatistics(){}; //constructor void setCExpStatistics(double &Arr[]); //set the initial array for the class void ZeroCheckArray(bool A); //check the input array for zero elements int get_arr_N(); //get the initial array length double median(bool A); //median double median50(bool A); //median of 50% interquantile range (midquartile range) double mean(bool A); //mean of the entire initial sample double mean50(bool A); //mean of 50% interquantile range double interqtlRange(bool A); //interquartile range double RangeCenter(bool A); //range center double meanCenter(bool A); //mean of the top five estimates double expVariance(bool A); //estimated variance double expSampleVariance(bool A); //shifted estimate of sample variance double expStddev(bool A); //estimated standard deviation double Moment(int index,bool A,int sw,double xm); //moment of distribution double expKurtosis(bool A,double &Skewness); ////estimated kurtosis and skewness double censorR(bool A); //censoring coefficient int outlierDelete(); //deletion of outliers from the sample int pArrOutput(double &outArr[],bool St); //processed array output void ~CExpStatistics(){};//destructor }; //+------------------------------------------------------------------+
Her yöntemin uygulanması, ExpStatistics_class.mqh dosyasında ayrıntılı olarak incelenebilir, bu yüzden burada bırakacağım.
Bu sınıfın yaptığı önemli şey, eğer varsa, aykırı değerlerden (Parr[]) diziyi döndürmesidir. Ayrıca, örneklemenin bazı tanımlayıcı istatistiklerini ve tahminlerini elde etmeye yardımcı olur.
2.2 İşlenmiş Örnek Histogram Oluşturma
Dizi artık aykırı değerler içermediğine göre, verilerine dayalı olarak bir histogram (frekans dağılımı) çizilebilir. Rastgele değişken dağılım yasasını görsel olarak tahmin etmemize yardımcı olacaktır. Bir histogram oluşturmak için adım adım bir prosedür vardır.
Önce gerekli sınıfların sayısı hesaplanmalıdır. Bu bağlamda "sınıf" terimi, gruplama, aralık anlamına gelir. Sınıfların sayısı Sturges formülüyle hesaplanır:
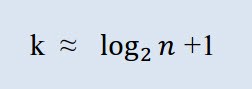
k sınıf sayısı olduğunda, n gözlem sayısıdır.
MQL5'te formül aşağıdaki gibi gösterilebilir:
int Sturges(int n) /* Function for determining the number of class intervals using Sturges' rule. Variables: y is the number of sampling observations. Returned value: number of class intervals. */ { double s; // Returned value s=1.+log2(y); if(s>15) // Empirical rule s=15; return(int) floor(s); }
Sturges formülü kullanılarak gerekli sayıda sınıf (aralık) alındığında, dizi verilerini sınıflara ayırmanın zamanı gelmiştir. Bu tür verilere gözlem denir (sing. gözlem). Bunu Tahsis Et işlevini kullanarak aşağıdaki gibi yapacağız:
void Allocate(double &data[],int n,double &f[],double &b[],int k) /* Function for allocating observations to classes. Variables: 1) data — initial sample (array) 2) n — sample size 3) f — calculated array of observations allocated to classes 4) b — array of class midpoints 5) k — number of classes */ { int i,j; // Loop counter double t,c; // Auxiliary variable t=data[ArrayMinimum(data)]; // Sample minimum t=t>0 ? t*0.99 : t*1.01; c=data[ArrayMaximum(data)]; // Sample maximum c=c>0 ? c*1.01 : c*0.99; c=(c-t)/k/2; // Half of the class interval b[0]=t+c; // Array of class interval midpoints f[0]= 0; for(i=1; i<k; i++) { b[i] = b[i - 1] + c + c; f[i] = 0; } // Grouping for(i=0; i<n; i++) for(j=0; j<k; j++) if(data[i]>b[j]-c && data[i]<=b[j]+c) { f[j]++; break; } }
Görülebileceği gibi, fonksiyon ilk gözlemler dizisini (veri), uzunluğunu (n), sınıf sayısını (k) alır ve gözlemleri f dizisinin belirli bir f[i] sınıfına tahsis eder, burada b[ i], f[i] sınıfı orta noktasıdır. Histogram verileri artık hazırdır.
Daha önce bahsedilen makalesinde açıklanan araçları kullanarak histogramı görüntüleyeceğiz. Bu amaçla, incelenen serinin histogramını HTML'de gösterecek olan histogramSave işlevini yazdım. İşlev 2 parametre alır: sınıf dizisi (f) ve sınıf orta noktaları dizisi (b).
Örnek olarak, volatilityTest.mq5 betiğini kullanarak dört saatlik zaman diliminde EURUSD çiftinin maksimum ve minimum 500 barı arasındaki mutlak farklar için bir histogram oluşturdum.
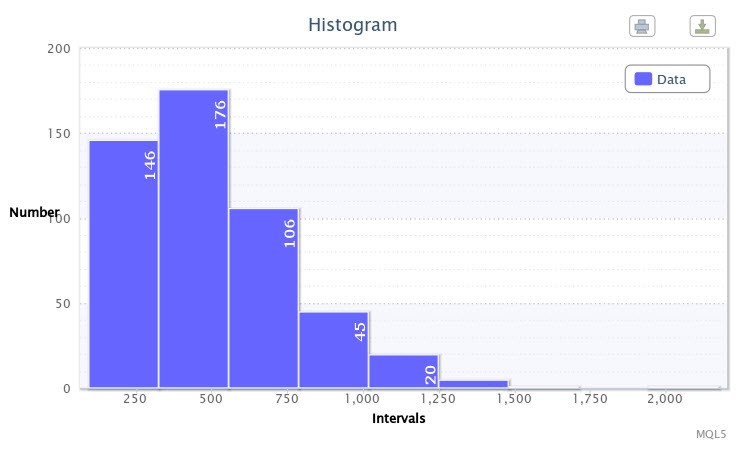
Şekil 1. Veri histogramı (EURUSD H4'ün mutlak oynaklığı)
Histogramda gösterildiği gibi (Şekil 1), birinci sınıf 146 gözleme sahiptir, ikinci sınıf 176 gözleme sahiptir, vb. Histogramın işlevi, incelenen örneğin ampirik dağılımı hakkında görsel bir fikir vermektir.
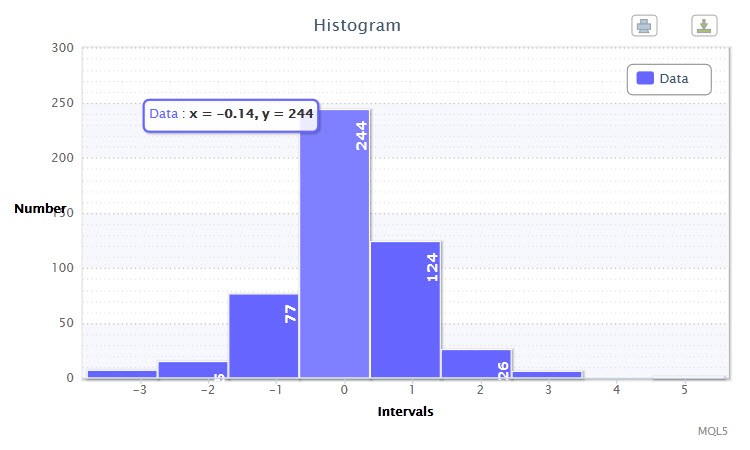
Şekil 2. Veri histogramı (EURUSD H4'ün standartlaştırılmış getirileri)
Diğer histogram (Şekil 2), H4 zaman diliminde EURUSD çiftinin 500 barlık standart logaritmik getirilerini gösterir. Fark edebileceğiniz gibi, sırasıyla 244 ve 124 gözleme sahip oldukları için dördüncü ve beşinci sınıflar en etkileyici olanlardır. Bu histogram, returnTest.mq5 betiği kullanılarak oluşturulmuştur.
Böylece histogram, parametreleri daha fazla tahmin edilecek olan dağılım yasasını seçmemizi sağlar. Hangi dağıtımın tercih edileceğinin görsel olarak açık olmadığı durumlarda, birkaç teorik dağılımın parametrelerini tahmin edebilirsiniz.
Düşündüğümüz her iki dağılım da görünüşte normal olanlara, özellikle de birincisine benzemiyor. Ancak görsel temsile güvenmeyelim ve rakamlara geçelim.
2.3 Normallik Hipotezi
İlk olarak, söz konusu dağılımın normal olup olmadığı varsayımını (hipotezi) çözmek ve test etmek adettendir. Böyle bir hipoteze ana hipotez denir. Bir örneğin normalliğini test etmek için en popüler yöntemlerden biri Jarque-Bera testidir.
Algoritması, en karmaşık olmasa da, yaklaşıklık nedeniyle oldukça hacimlidir. Algoritmanın C++ ve diğer dillerde birkaç versiyonu vardır. En başarılı ve kanıtlanmış sürümlerden biri, platformlar arası sayısal analiz kitaplığında bulunan bir sürümdür http://alglib.sources.ru/. Yazarı [SA Bochkanov], özellikle http://alglib.sources.ru/hypothesistesting/jarqueberatest.phptitletest titlenicel tablosunun derlenmesinde büyük bir iş çıkardı. Automated Trading Language Documentation'in ihtiyaçlarına göre biraz güncelledim.
Jarqueberatest'in ana işlevi aşağıdaki gibidir:
//+------------------------------------------------------------------+ // the Jarque-Bera Test | //+------------------------------------------------------------------+ void jarqueberatest(double &x[],double &p) /* The Jarque-Bera test is used to check hypothesis about the fact that a given sample xS is a sample of normal random variable with unknown mean and variance. Variables: x - sample Xs; p - p-value; */ { int n=ArraySize(x); double s; p=0.; if(n<5)//N is too small { p=1.0; return; } //N is large enough jarquebera_jarqueberastatistic(x,n,s); p=jarquebera_jarqueberaapprox(n,s); } //+------------------------------------------------------------------+
İlk veri örneğini (x) ele alır ve р-değerini, yani boş hipotez gerçekten doğru ise boş bir hipotezi reddetme olasılığını karakterize eden bir değeri döndürür.
Fonksiyon gövdesinde 2 adet yardımcı fonksiyon bulunmaktadır. İlk işlev - jarquebera_jarqueberastatistic - Jarque-Bera istatistiğini hesaplar ve ikincisi - jarquebera_jarqueberaapprox - p-değerini hesaplar. İkincisinin, algoritmada neredeyse 30 olan yaklaşıklık ile ilgili yardımcı fonksiyonları devreye soktuğuna dikkat edilmelidir.
Öyleyse örneklerimizi normallik için test etmeye çalışalım. EURUSD H4'ün standartlaştırılmış getirilerinin örneğini ele alacak returnTest.mq5 betiğini kullanacağız.
Beklendiği gibi, test, gerçek bir boş hipotezi reddetme olasılığının 0.0000 olduğunu gösterdi. Başka bir deyişle, bu örneğin dağılımı normal dağılımlar ailesine ait değildir. EURUSD çiftinin mutlak volatilite örneğini ele almak için volatilityTest.mq5 betiğini çalıştırın. Sonuç benzer olacaktır - dağılım normal değildir.
3. Dağıtım Bağlantısı
Matematiksel istatistikte, ampirik dağılımı normal dağılımla karşılaştırmaya izin veren birkaç yöntem vardır. En büyük sorun, normal dağılım parametrelerinin bizim tarafımızdan bilinmemesi ve incelenen verilerin bir dağılımın normalliğini yansıtmadığı varsayımıdır.
Bu nedenle parametrik olmayan testler kullanmalı ve bilinmeyen parametreleri ampirik dağılımdan elde edilen tahminlerle doldurmalıyız.
3.1 Tahmin ve Test Etme
Bu durumda en popüler ve en önemlisi, yeterli testlerden biri χ2 testi’dir. Pearson'ın uyum iyiliği ölçüsüne dayanmaktadır.
Testi chsone fonksiyonunu kullanarak gerçekleştireceğiz:
void chsone(double &f[],double &ebins[],double &df, double &chsq,double &prob,const int knstrn=1) /* 1) f — array of observations allocated to classes 2) ebins - array of expected frequencies 3) df - number of degrees of freedom 3) chsq — chi-square statistics 4) prob - probability of accepting a true null hypothesis 5) knstrn — constraint */ { CGamma gam; int j,nbins=ArraySize(bins),q,g; double temp; df=nbins-knstrn; chsq=0.0; q=nbins/2; g=nbins-1; for(j=0;j<nbins/2;j++) //passing through the left side of the distribution { if(ebins[j]<0.0 || (ebins[j]==0. && bins[j]>0.)) Alert("Bad expected number in chsone!"); if(ebins[j]<=5.0) { --df; ebins[j+1]+=ebins[j]; bins[j+1]+=bins[j]; } else { temp=bins[j]-ebins[j]; chsq+=pow(temp,2)/ebins[j]; } } for(j=nbins-1;j>nbins/2-1;j--) //passing through the right side of the distribution { if(ebins[j]<0.0 || (ebins[j]==0. && bins[j]>0.)) Alert("Bad expected number in chsone!"); if(ebins[j]<=5.0) { --df; ebins[j-1]+=ebins[j]; //starting with the last class bins[j-1]+=bins[j]; } else { temp=bins[j]-ebins[j]; chsq+=pow(temp,2)/ebins[j]; } } if(df<1)df=1; //compensate prob=gam.gammq(0.5*df,0.5*chsq); //Chi-square probability function }
Listede görülebileceği gibi, Distribution_class.mqh dosyasında yer alan tamamlanmamış gama işlevini ve belirtilen tüm dağıtımları temsil eden CGamma sınıfının bir örneği kullanılır. Ayrıca, beklenen frekansların (ebins) dizisinin, estimateDistribution ve expFrequency işlevleri kullanılarak elde edileceğine dikkat edilmelidir.
Şimdi teorik dağılım için analitik formülde yer alan sayısal parametreleri seçmemiz gerekiyor. Parametrelerin sayısı belirli dağılıma bağlıdır. Örneğin, normal dağılımda iki parametre ve üstel dağılımda bir parametre vb. vardır.
Dağılım parametrelerini belirlerken genellikle moment yöntemi, nicelik yöntemi ve maksimum olabilirlik yöntemi gibi nokta tahmin yöntemlerini kullanırız. İlki, örnekleme tahminlerinin (beklenti, varyans, çarpıklık vb.) genel tahminlerle örtüşmesi gerektiğini ima ettiğinden daha basittir.
Bir örnek kullanarak örneğimiz için teorik bir dağılım seçmeye çalışalım. Halihazırda bir histogram çizdiğimiz EURUSD H4'ün bir dizi standartlaştırılmış getirisini alacağız.
İlk izlenim, basıklık katsayısı fazlalığı gözlendiğinden, seriler için normal dağılımın uygun olmadığı yönündedir. Karşılaştırma olarak, başka bir dağılım uygulamaya çalışalım.
Bu nedenle, zaten bilinen returnTest.mq5 betiğini başlatırken, Hypersec gibi bir dağıtımı seçmeyi deneyeceğiz. Ek olarak, komut dosyası, estimateDistribution işlevini kullanarak seçilen dağıtım parametrelerini tahmin edip çıktısını alır ve hemen http://www.itl.nist.gov/div898/handbook/eda/section3/eda35f.htm testini çalıştırır. Seçilen dağıtım parametrelerinin aşağıdaki gibi olduğu ortaya çıktı:
Hiperbolik Sekant dağılımı: X~HS(-0.00, 1.00);
ve test sonuçları şu şekildeydi:
"Ki-kare istatistiği: 1,89; gerçek bir boş hipotezi reddetme olasılığı: 0,8648"
χ2 istatistiğinin değeri oldukça küçük olduğu için seçilen dağılımın iyi bir uyum olduğuna dikkat edilmelidir.
Ayrıca, histogramSaveE işlevini kullanarak, standartlaştırılmış getirilerin gözlemlenen ve beklenen frekans oranlarının (frekans oranı, kesir veya yüzde olarak ifade edilen bir frekanstır) bir çift histogramı çizilecektir (Şekil 3). Çubukların neredeyse birbirini kopyaladığını görebilirsiniz. Bu, başarılı montajın bir kanıtıdır.
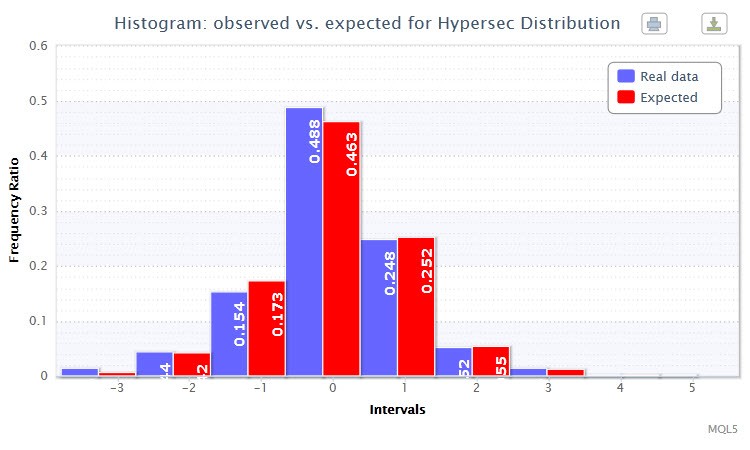
Şekil 3. Gözlemlenen ve beklenen frekans oranlarının histogramı (EURUSD H4'ün standartlaştırılmış getirileri)
Halihazırda bilinen volatiliteTest.mq5'i kullanarak istikrarsızlık verileri için benzer bir prosedür uygulayalım.
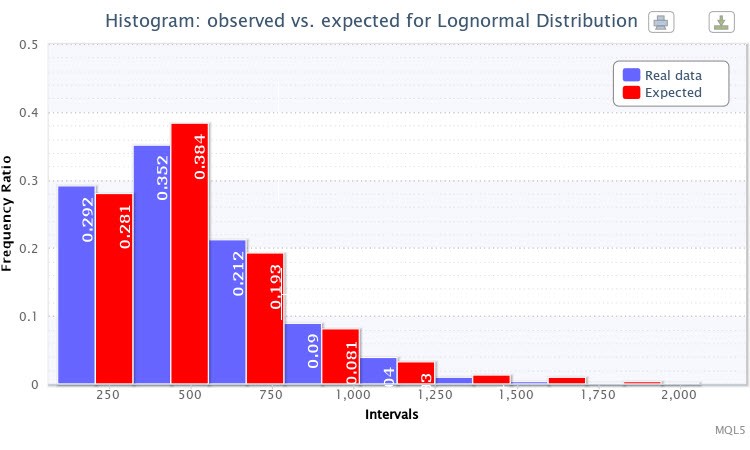
Şekil 4. Gözlenen ve beklenen frekans oranlarının histogramı (EURUSD H4'ün mutlak istikrarsızlık)
Test için lognormal dağılımı Lognormal'i seçtim. Sonuç olarak, aşağıdaki parametre tahmini alındı:
Lognormal dağılım: X~Logn(6,09, 0,53);
ve test sonuçları şu şekildeydi:
"Ki-kare istatistiği: 6,17; gerçek bir boş hipotezi reddetme olasılığı: 0,4040"
Bu ampirik dağılım için teorik dağılım da oldukça başarılı bir şekilde seçilmiştir. Bu nedenle, boş hipotezin reddedilemeyeceği düşünülebilir (standart güven düzeyi p=0,05’te). Şekil 4'te, beklenen ve gözlemlenen frekans oranlarının çubuklarının da çok benzer olduğu görülebilir.
Şimdi size, ayarlanmış parametrelere sahip bir dağılımdan rastgele değişkenlerin bir örneğini oluşturmak için başka bir olasılığımız olduğunu hatırlatmama izin verin. Böyle bir işlemle ilgili bir sınıf hiyerarşisi kullanmak için randomTest.mq5 betiğini yazdım.
Bunun başında, Şekil 5'te gösterildiği gibi parametreleri girmemiz gerekiyor.
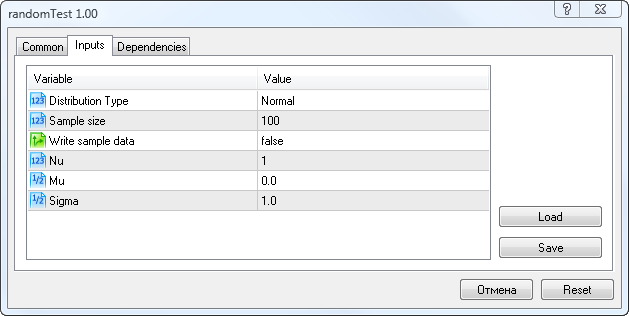
Şekil 5. randomTest.mq5 komut dosyasının giriş parametreleri
Burada dağılım türünü (Dağılım Türü), bir örnekteki rastgele değişkenlerin sayısını (Örnek Boyutu), örnek kaydetme seçeneğini (Örnek verileri yaz), Nu parametresini (Öğrencinin t-dağılımı için), Mu ve Sigma parametrelerini seçebilirsiniz.
Örnek verileri yaz için true değerini ayarlarsanız, komut dosyası rastgele değişkenlerin örneğini özel parametrelerle Randoms.csv dosyasına kaydeder. Aksi takdirde, bu dosyadan örnek verileri okuyacak ve ardından istatistiksel testler yapacaktır.
Mu ve Sigma parametrelerinin eksik olduğu bazı dağıtımlar için, komut dosyası başlatma penceresindeki alanlara bir parametre korelasyon tablosu sağladım.
| Dağılım | İlk dağıtım parametresi | İkinci dağıtım parametresi |
|---|---|---|
| Lojistik | alfa Mu | bet Sigma |
| Üstel | lambda Mu | -- |
| Gamma | alfa Mu | bet Sigma |
| Beta | alfa Mu | bet Sigma |
| Laplace | alfa Mu | bet Sigma |
| Binomial | n Mu | pe Sigma |
| Poisson | lambda Mu | -- |
Örneğin Poisson dağılımı seçilirse, lambda parametresi Mu alanı vb. üzerinden girilecektir.
Senaryo, Öğrencinin t-dağılım parametrelerini tahmin etmez çünkü vakaların mutlak çoğunluğunda sadece birkaç istatistiksel prosedürde kullanılır: normal dağılımdan istatistiksel bir örneğin bilinmeyen ortalamasını ilgilendiren nokta tahmini, güven aralıklarının oluşturulması ve hipotezlerin test edilmesi.
Örnek olarak, normal dağılım için komut dosyasını X~Nor(3.50, 2,77) parametreleriyle çalıştırdım, burada Write sample data=true. Komut dosyası önce bir örnek oluşturdu. Write sample data=false'taki ikinci çalıştırmada, Şekil 6'da gösterildiği gibi bir histogram çizildi.
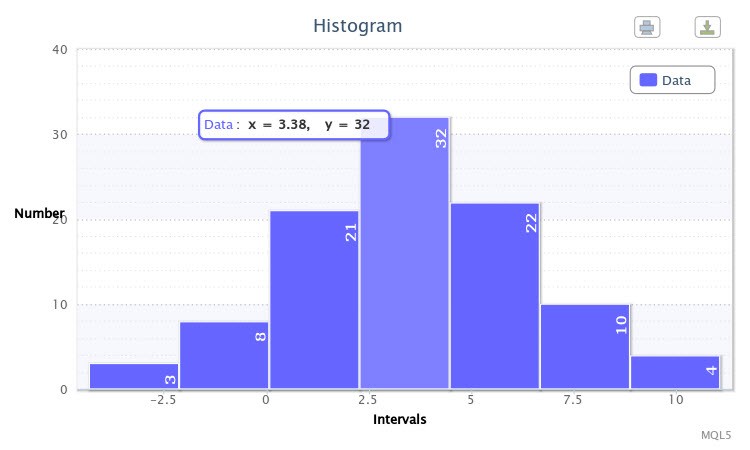
Şekil 6. Rastgele değişkenler örneği X~Nor(3.50,2.77)
Terminal penceresinde görüntülenen kalan bilgiler aşağıdaki gibidir:
Jarque-Bera testi: "Jarque-Bera testi: gerçek bir boş hipotezi reddetme olasılığı 0,9381'dir";
Parametre tahmini: Normal dağılım: X~Nor(3.58, 2.94);
Ki-kare test sonuçları: "Ki-kare istatistiği: 0,38; gerçek bir boş hipotezi reddetme olasılığı: 0,9843".
Ve son olarak, örnek için gözlemlenen ve beklenen frekans oranlarının başka bir çift histogramı görüntülendi (Şekil 7).
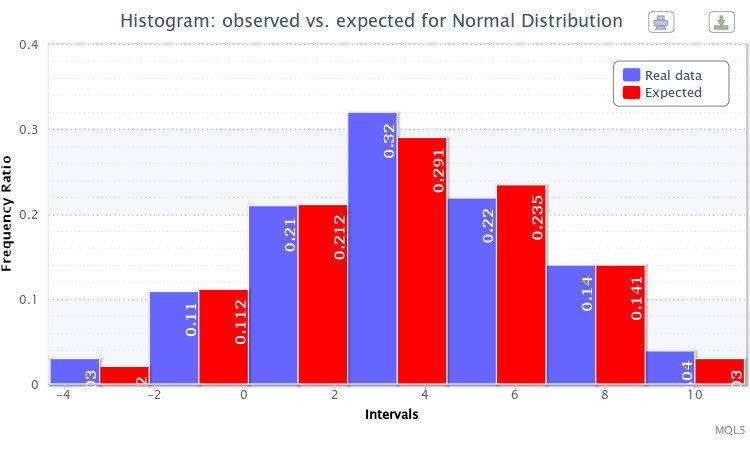
Şekil 7. X~Nor(3.50,2.77) için gözlemlenen ve beklenen frekans oranlarının histogramı
Genel olarak, belirtilen dağıtımın oluşturulması başarılı oldu.
Ayrıca randomTest.mq5 betiğine benzer şekilde çalışan fitAll.mq5 betiğini de yazdım. Tek fark, ilkinin fitDistributions işlevine sahip olmasıdır. Şu görevi belirledim: mevcut tüm dağılımları bir rastgele değişken örneğine uydurmak ve istatistiksel bir test yapmak.
Terminalde tahminin mümkün olmadığını bildiren satırların görünmesine neden olan parametre uyuşmazlığı nedeniyle bir dağılımı bir örneğe sığdırmak her zaman mümkün değildir, örn. "Beta dağılımı tahmin edilemez!".
Ayrıca, bu betiğin istatistiksel sonuçları küçük bir HTML raporu şeklinde görselleştirmesi gerektiğine karar verdim, bunun bir örneği HTML formatında Grafikler ve Diyagramlar makalesinde bulunabilir (Şekil 8).
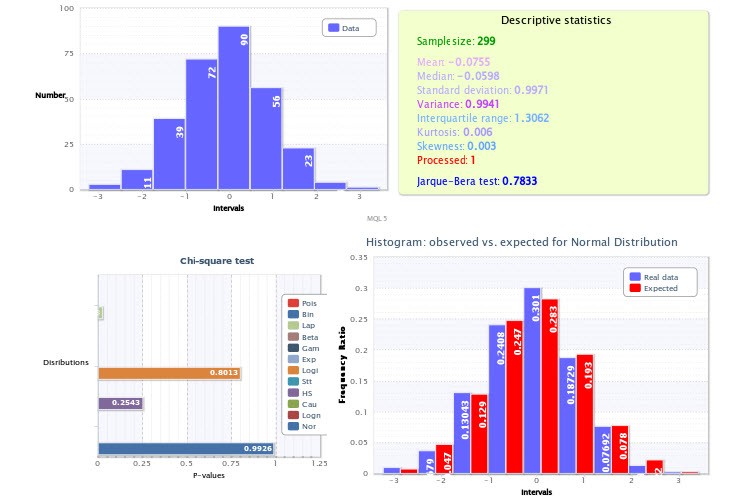
Şekil 8. Numune tahmini hakkında istatistiksel rapor
Sol üst çeyrekte örneğin standart bir histogramı görüntülenir; sağ üst çeyrek tanımlayıcı istatistikleri ve Jarque-Bera test sonucunu temsil eder, burada İşlenen değişken değeri 1'e eşittir, 0 değeri ise aykırı değerlerin silindiği anlamına gelir. aykırılar yoktu.
Seçilen her dağıtım için http://www.itl.nist.gov/div898/handbook/eda/section3/eda35f.htmtitleχ2title testinin P değerleri sol alt çeyrekte görüntülenir. Burada uyum açısından en iyi normal dağılım ortaya çıktı (p=0,9926). Bu nedenle, sağ alt çeyrekte bunun için gözlemlenen ve beklenen frekans oranlarının bir histogramı çizildi.
Henüz galerimde çok fazla dağıtım yok. Ancak çok sayıda dağıtım varsa bu komut dosyası size çok zaman kazandıracak.
Artık incelenen örneklerin dağılım parametrelerini tam olarak bildiğimize göre, olasılıksal akıl yürütmeye geçebiliriz.
3.2 Rastgele Değişken Değerlerinin Olasılıkları
makalesinde teorik dağılımlar ile ilgili olarak continuousDistribution.mq5 betiğini örnek olarak verdim. Bunu kullanarak, bizi ilgilendirebilecek bilinen parametrelerle herhangi bir dağıtım yasasını göstermeye çalışacağız.
Bu nedenle, oynaklık verileri için daha önce elde ettiğimiz lognormal dağılım parametrelerini gireceğiz (Mu=6,09, Sigma=0,53), Lognormal dağılım tipini ve cdf modunu seçeceğiz (Şekil 9).
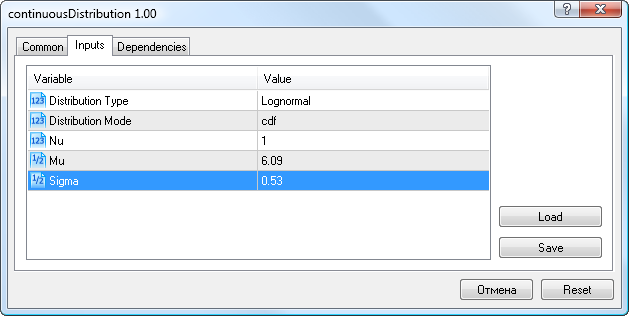
Şekil 9. Lognormal dağılım parametreleri X~Logn(6.09,0.53)
Komut dosyası daha sonra örneğimiz için dağıtım işlevini görüntüleyecektir. Şekil 10'da gösterildiği gibi görünecektir.
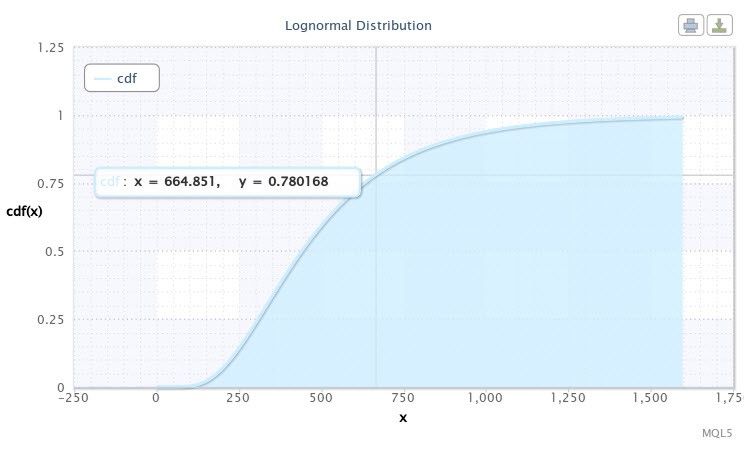
Şekil 10. X~Logn(6.09,0.53) için dağıtım fonksiyonu
İmlecin koordinatları yaklaşık [665;0.78] olan bir noktayı gösterdiğini grafikte görebiliriz. Bu, EURUSD H4'ün volatilitesinin 665 puanı geçmeme olasılığının %78 olduğu anlamına gelir. Bu bilgiler, bir Uzman Danışman geliştiricisi için çok yararlı olabilir. İmleci hareket ettirerek eğri üzerinde kesinlikle başka değerler alınabilir.
Oynaklık değerinin 500 ile 750 puan aralığında olacağı olayın olasılığı ile ilgilendiğimizi varsayalım. Bu amaçla aşağıdaki işlemin yapılması gerekir:
cdf(750) - cdf(500) = 0,84 - 0,59 = 0,25.
Böylece olayların dörtte birinde paritenin oynaklığı 500 ile 750 puan aralığında dalgalanıyor.
Bir dağıtım yasası modu olarak sadece sf'yi seçerek betiği aynı dağıtım parametreleriyle bir kez daha çalıştıralım. Güvenilirlik (hayatta kalma) işlevi aşağıdaki gibi gösterilecektir (Şekil 11).
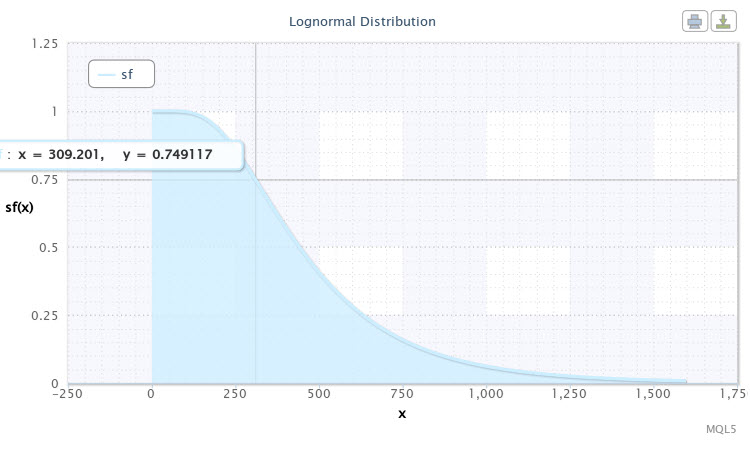
Şekil 11. X~Logn(6.09,0.53) için hayatta kalma fonksiyonu
Eğri grafiğinde işaretlenen nokta şu şekilde yorumlanabilir: Paritenin oynaklığının yaklaşık %75 olasılıkla 310 puan olmasını bekleyebiliriz. Eğride ne kadar aşağı inersek, oynaklığın artma olasılığı o kadar düşük olur. Bu nedenle, 1000 puanın üzerindeki oynaklık, meydana gelme olasılığı %5'ten az olduğu için zaten nadir bir olay olarak kabul edilebilir.
Benzer dağılım eğrileri, diğer örnekler için olduğu kadar standartlaştırılmış getiri örnekleri için de oluşturulabilir. Sanırım metodoloji genel olarak açık.
Sonuç
Seriler değişme eğiliminde olduğundan, önerilen analitik türevlerin tamamen başarılı olmadığı belirtilmelidir. Örneğin, bir dizi logaritmik getiri ile ilgili olmamasına rağmen. Ancak bu makaledeki yöntemleri değerlendirmeyi kendime bir görev belirlemedim. İlgilenen okuyucuların bu konuda yorum yapmasını öneririm.
Piyasayı, piyasa araçlarını ve ticaret uzmanlarını olasılık perspektifinden değerlendirme ihtiyacına dikkat etmek önemlidir. Benim göstermeye çalıştığım yaklaşım bu. Bu konunun okuyucunun ilgisini çekeceğini ve yapıcı bir tartışmaya yol açacağını umuyorum.
Dosyaların konumu:
| # | Dosya | Yol | Açıklama |
|---|---|---|---|
| 1 | Distribution_class.mqh | %MetaTrader%\MQL5\Include | Dağıtım sınıfları galerisi |
| 2 | DistributionFigure_class.mqh | %MetaTrader%\MQL5\Include | Dağıtımların grafiksel gösterimi için sınıflar |
| 3 | Random_class.mqh | %MetaTrader%\MQL5\Include | Rastgele sayı örneği oluşturma sınıfları |
| 4 | ExpStatistics_class.mqh | %MetaTrader%\MQL5\Include | İstatistiksel özelliklerin tahminlerinin sınıfı ve işlevleri |
| 5 | volatilityTest.mq5 | %MetaTrader%\MQL5\Scripts | EURUSD H4 volatilite örneğinin tahmini için komut dosyası |
| 6 | returnsTest.mq5 | %MetaTrader%\MQL5\Scripts | EURUSD H4 iade örneğinin tahmini için komut dosyası |
| 7 | randomTest.mq5 | %MetaTrader%\MQL5\Scripts | Rastgele değişken örneğinin tahmini için komut dosyası |
| 8 | fitAll.mq5 | %MetaTrader%\MQL5\Scripts | Tüm dağılımların montajı ve tahmini için komut dosyası |
| 9 | Volat.csv | %MetaTrader%\MQL5\Files | EURUSD H4 istikrarsızlık örnek veri dosyası |
| 10 | Returns_std.csv | %MetaTrader%\MQL5\Files | EURUSD H4, örnek veri dosyasını döndürür |
| 11 | Randoms.csv | %MetaTrader%\MQL5\Files | Rastgele değişken örnek veri dosyası |
| 12 | Histogram.htm | %MetaTrader%\MQL5\Files | HTML'deki örneğin histogramı |
| 13 | Histogram2.htm | %MetaTrader%\MQL5\Files | HTML'de örneğin çift histogramı |
| 14 | chi_test.htm | %MetaTrader%\MQL5\Files | Örnek tahminin istatistiksel HTML raporu |
| 15 | dataHist.txt | %MetaTrader%\MQL5\Files | Numunelerin histogramını görüntülemek için veriler |
| 16 | dataHist2.txt | %MetaTrader%\MQL5\Files | Örneklerin çift histogramını görüntülemek için veriler |
| 17 | dataFitAll.txt | %MetaTrader%\MQL5\Files | HTML raporu ekranı için veriler |
| 18 | highcharts.js | %MetaTrader%\MQL5\Files | Etkileşimli çizelgelerin JavaScript kitaplığı |
| 19 | jquery.min.js | %MetaTrader%\MQL5\Files | JavaScript kitaplığı |
| 20 | ReturnsIndicator.mq5 | %MetaTrader%\MQL5\Indicators | Logaritmik getiri göstergesi |
Referans Materyalleri:
MetaQuotes Ltd tarafından Rusçadan çevrilmiştir.
Orijinal makale: https://www.mql5.com/ru/articles/257
Fiyat Korelasyonunun İstatistiksel Verilerine Dayalı Sinyalleri Filtreleme
Rastgele Yürüyüş ve Trend Göstergesi
Doğrusal Regresyon Örneğiyle 3 Gösterge Hızlandırma Yöntemi
İşlem Geçmişine Dayalı Alım Satım Oynatıcısı
- Ücretsiz alım-satım uygulamaları
- İşlem kopyalama için 8.000'den fazla sinyal
- Finansal piyasaları keşfetmek için ekonomik haberler
Gizlilik ve Veri Koruma Politikasını ve MQL5.com Kullanım Şartlarını kabul edersiniz