Discusión sobre el artículo "El Papel de las Distribuciones Estadísticas en el Trabajo del Trader"
Denis, tengo este comentario sobre el artículo.
En cuanto a la teoría, no hay preguntas, todo se presenta en detalle.
En cuanto a la práctica, me gustaría llamar tu atención sobre las figuras en las que muestras histogramas empíricos, especialmente la Figura 2. La cuestión es que has cometido dos imprecisiones muy significativas en tu análisis.
En primer lugar, has fijado un número demasiado pequeño de clases para el script que genera los histogramas: sólo 9, lo que en sí mismo es un golpe enorme a la potencia del criterio de Pearson y hace ineficaz su aplicación. Para el futuro, toma 200-300 clases para estar seguro, por supuesto, si el tamaño de la muestra lo permite (y lo hace), no cometerás un error. Si hubieras hecho exactamente eso, habrías podido asegurarte de que el test de la distribución lognormal hubiera dado un resultado negativo, así como el test de rendimientos para hipersecanos. Por cierto, es muy fácil asegurarse de que dos distribuciones de este tipo no pueden representar simultáneamente un determinado valor y su módulo, basta con tomar la "mitad" de la hipersecanza y convolucionarla consigo misma (análogo a tomar el módulo de una variable aleatoria): definitivamente no obtendrás una lognormal.
La segunda inexactitud es que no utilizaste el conocimiento a priori de que la parte superior (también conocida como expectativa) de la distribución de rendimientos debe estar exactamente en 0 (de lo contrario, todos habríamos sido multimillonarios hace mucho tiempo). Por eso el histograma de la Figura 2 parece desplazado hacia la derecha, aunque no debería ser así. Una vez más, si se tuviera esto en cuenta al trazar el histograma, las pruebas serían más fiables.
P.D. Estoy escribiendo un artículo sobre los fundamentos de la modelización, de ahí tanto interés. Gracias por tu artículo, está en el tema. Saludos.
...En primer lugar, has establecido un número demasiado pequeño de clases para el script que genera los histogramas: sólo 9, lo que en sí mismo es un gran golpe para la potencia del criterio de Pearson y hace que su aplicación sea ineficaz. Para el futuro, toma 200-300 clases para estar seguro, por supuesto, si el tamaño de la muestra lo permite (y lo hace), no te equivocarás. Si lo hubieras hecho así, podrías asegurarte de que el test para la distribución lognormal daría un resultado negativo, así como el test de rendimientos para la hipersecana. Por cierto, es muy fácil asegurarse de que dos distribuciones de este tipo no pueden representar un determinado valor y su módulo al mismo tiempo, basta con tomar la "mitad" de la hipersecanza y convolucionarla consigo misma (análogo a tomar el módulo de un valor aleatorio): definitivamente no obtendrás una lognormal.
Estimado alsu, ¡gracias por tu opinión!
Vayamos por orden.
El número de clases no se fija voluntariamente, sino según alguna fórmula. En mi caso es la fórmula de Sturgis. Es una de las reglas más populares. No es perfecta, estoy de acuerdo. Pero aún así...
¿Y usted toma 200-300 clases según qué regla?
La segunda inexactitud es que no utilizaste el conocimiento a priori de que la parte superior (también conocida como expectativa) de la distribución de los rendimientos debe estar exactamente en 0 (de lo contrario todos habríamos sido multimillonarios hace mucho tiempo). Por eso el histograma de la Figura 2 parece desplazado hacia la derecha, aunque no debería ser así. Una vez más, si se tuviera en cuenta este punto a la hora de construir el histograma, las pruebas serían más fiables.
Analizo la muestra basándome en hechos. Analizo lo que tengo. ¿Y en base a qué la parte superior de la distribución del rendimiento debería estar exactamente en el punto 0? A lo mejor estoy entendiendo algo mal...
Y además, si miras la distribución a la que se aplicó el ajuste (que era X~HS(-0,00, 1,00)), es fácil ver que el primer parámetro -el parámetro de desplazamiento- es exactamente 0. De hecho, es igual al parámetro de desplazamiento. De hecho, es igual a la expectativa.
He aquí otro informe html sobre el muestreo de los valores estándar. Espero que la figura sea más o menos legible. Pero no es idéntica a la del artículo. Acabo de tomar los últimos datos.
Como puedes ver, Media =0. Y el mejor ajuste es la distribución Secante Hiperbólica: X~HS(0.00, 1.00).
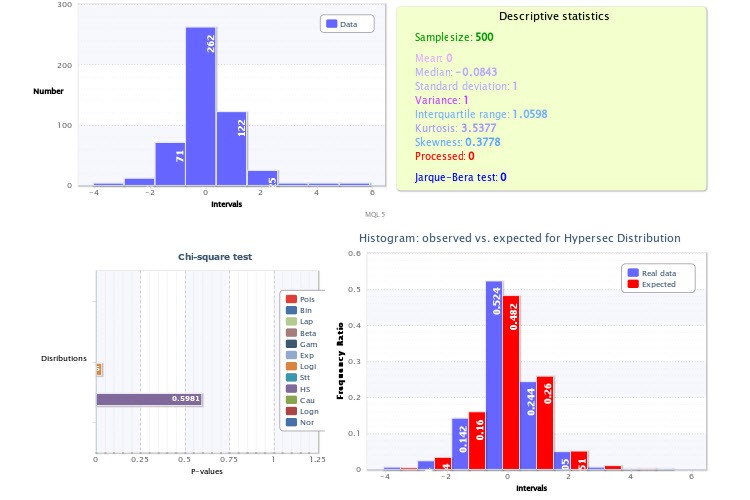
Exacto, la fórmula de Sturges daba exactamente 9 clases, pero esto es más bien una razón para pensar en aumentar el tamaño de la muestra (invirtiendo la fórmula, veo que la tienes en torno a 256...).
Además, esta fórmula sólo funciona bien para poblaciones generales de distribución normal (para las que se derivó) y, tal como se considera, el tamaño de la muestra no es superior a 200 valores. Puede utilizar fórmulas alternativas - Diakonis, Scott....
En general, ya sabes, Sturges nunca dio una justificación lógica de su fórmula - sí, se basa en la aproximación de la distribución normal por la distribución binomial, ¿y qué? ¿Cómo puede afectar esto a la cuestión de la eficacia de la elección del número de clases? El criterio de optimalidad nunca fue definido por el autor y la propia fórmula fue escrita al azar. Pero la cuestión es que durante mucho tiempo el enfoque de Sturges fue el único que se formalizó de alguna manera, y se incluyó automáticamente (¡y, en mi opinión, de forma bastante irreflexiva!) en todos los paquetes estadísticos, lo cual, por cierto, es bastante molesto precisamente porque esta fórmula casi siempre da un número de clases extremadamente subestimado.
Una vez más, existen fórmulas alternativas, pero la presencia de un ordenador personal, por paradójico que parezca, nos brinda la oportunidad de utilizar nuestra propia cabeza como dispositivo, es decir, una forma visual de determinar un número más o menos óptimo de clases para esta muestra concreta, cuando, cambiando suavemente este indicador, conseguimos un compromiso entre la suavidad del gráfico y la resolución del histograma. Por cierto, este método suele ser mejor y más rápido que cualquier fórmula.
Siempre digo a todo el mundo - antes de poner números en las fórmulas, pregunte lo que significa y cómo (y si) aplicarlo. En resumen, estoy en contra de utilizar la fórmula de Sturges, la considero anticuada e inadecuada).
Respecto a la media. La expectativa de rentabilidad debería estar en 0 porque si no fuera así, podríamos estúpidamente apostar siempre en una dirección, correspondiente al signo de esta MO, y tener garantizada la obtención de una rentabilidad de cualquier magnitud predeterminada. Pues bien, la parte superior debería coincidir con la MO puramente por razones de simetría: la mitad izquierda del gráfico debería ser una imagen especular de la derecha (el aumento y la disminución de la tasa son estadísticamente iguales, y no debería haber diferencias entre ellos), por lo que el centro de simetría coincide con el centro.
Dado que toma HS(0.00, 1.00), por lo tanto, debe centrar las clases - es decir, la clase cero debe incluir los valores de índice en algún intervalo simétrico (-x0;x0), de lo contrario introducimos en los cálculos un error sistemático asociado con el desplazamiento de las clases con respecto a cero, y finalmente se cuela en el resultado de la prueba chi^2. Tu punto 0 no está en medio de la clase cero.
De hecho, la cuestión de cómo hacer que las clases sean simétricas en datos discretos no es trivial y, de nuevo, es bueno resolverla para cada muestra en particular de forma individual y con mucho cuidado, de lo contrario corremos el riesgo de obtener un resultado inadecuado también debido a la elección incorrecta de los límites de la división en clases.
Me gusta tu opinión sobre la aplicabilidad de los conocimientos científicos en el trading.
¿Podrías decirme cuál de los libros recomendarías a una persona familiarizada con la teoría de la probabilidad y la estadística matemática?
Denis, buenas tardes.
Me gusta su opinión sobre la aplicabilidad de los conocimientos científicos en el trading.
Por favor, dígame cuál de los libros recomendaría a una persona familiarizada con la teoría de la probabilidad y la estadística matemática.
Gracias por su opinión.
Creo que entonces habría que buscar algo para principiantes, algo de literatura. Lo principal es que el texto del libro no te desanime a seguir leyendo :-))).
Me gustó algo Gaidyshev, y algo Bulashev.....
Hay un hilo interesanteaquí.
- rsdn.org
La segunda inexactitud es que no has utilizado el conocimiento a priori de que la parte superior (también conocida como expectativa) de la distribución de rendimientos debe estar exactamente en 0 (de lo contrario, todos habríamos sido multimillonarios hace mucho tiempo).
En absoluto. Un desplazamiento de la parte superior de la distribución con respecto a 0 (crecimiento/descenso de un instrumento) no significa que vaya a ser igual en el futuro. Por eso la mayoría de los traders no son multimillonarios, no porque sí.
Saludos.
...Desplazar la parte superior de la distribución con respecto a 0 (instrumento que sube/baja) no significa necesariamente que vaya a ser así en el futuro...
De acuerdo.
Pregunta para alsu. ¿Te referías a la eficiencia del mercado al hablar del punto cero?
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
Artículo publicado El Papel de las Distribuciones Estadísticas en el Trabajo del Trader:
Este artículo es una continuación lógica de mi artículo "Statistical Probability Distributions in MQL5" ("Distribuciones de Probabilidad Estadísticas en MQL5"), que presentó las clases para trabajar con algunas distribuciones estadísticas teóricas. Ahora que ya tenemos una base teórica, sugiero proceder directamente a conjuntos de datos reales para darle un uso a esta base.
Autor: Dennis Kirichenko