
集成学习模型中的门控机制
门控方法利用门控变量,基于内容信息动态调整各单个模型的影响力。这些门控变量作为监督机制,策略性地为模型输出分配权重,从而获得比任何单一模型更优的预测性能。
与传统集成方法(如平均法、投票法或堆叠法)不同,门控明确使用门控变量进行模型组合。这种方法在模型性能波动较大的场景中尤为有用,例如金融预测领域,经济趋势会影响预测准确性。通过基于内容自适应地为模型分配权重,门控机制在复杂环境中增强了预测的准确性和适应性。
门控技术一般分为两类:一类是基于门控变量选择单一模型,另一类是结合所有模型的输出,但权重取决于内容。后者通常更为稳健,能够充分利用多个模型的优势。以下部分将探讨这两种方法的实例:预先指定的专门化和学习型专门化。
预先指定的专门化
预先指定的专门化是门控的一种基本形式,其中单个变量作为决定性因素,用于在两个或多个预先训练好的专门化模型之间进行选择。这种方法有效地划分了输入空间,根据门控变量的值将实例引导至最合适的模型。为了诠释这一概念,考虑一个二维特征空间中的二分类问题,特征变量为A和B。在假设的情景中,变量B对两类别的区分能力可忽略不计,而变量A具有一定的预测能力,对某些实例能够实现准确分类,但对其他实例则产生模糊结果。
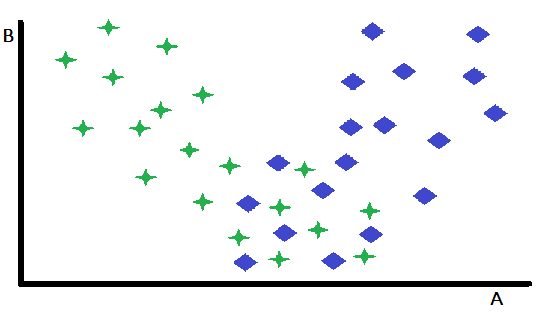
仔细审视特征散点图可以发现,变量B能够有效区分出变量A作为强分类器起作用的实例与预测能力减弱的实例。具体而言,当变量B取高值时,以变量A作为主要预测变量可获得更高的分类准确率。这一观察结果提示了一种自然的划分策略:即基于变量B的阈值对数据集进行划分。这种划分方式使得可以开发出两种不同的分类模型:一种针对变量B取高值的实例(此时变量A是强预测变量)进行优化,另一种则针对变量B取低值的实例(此时变量A的预测可靠性可能较低)进行优化。
尽管上述简化示例展示了核心原理,但必须承认,当剩余实例子集本身难以分类时,这种划分策略的益处可能有限。该方法的优势在于能够隔离并有效处理更容易分类的实例。这种简化也有助于为剩余的、更具挑战性的数据子集开发性能更优的模型。尽管前述示例仅聚焦于单个变量以阐明概念,但在实际应用中,合适模型的选择可能取决于多个变量的值,而这些变量可能包含也可能不包含在单个模型所使用的主要预测变量集中。
学习型专门化
学习型专门化代表了一种更为复杂的门控方法,其中最优的划分变量及其对应阈值并非预先确定,而是从数据中学习得到。尽管通过散点图的可视化检查有时能提供关于潜在划分变量及其阈值的初步见解,但这种直观方法在现实应用中往往效果不佳。
在实际应用中,需要采用更为系统和数据驱动的方法。这通常涉及一个严格的搜索过程,探索大量潜在的划分变量及其相关阈值。对于每个候选划分变量和阈值,数据集被划分,并在得到的子集上分别训练和评估单独的模型。这种探索、训练和评估的迭代过程可能计算量较大,特别是在处理大型数据集或复杂模型时。然而,模型性能的潜在提升往往证明增加的计算成本是合理的。
此外,寻找最优划分变量的过程不应局限于单个候选变量。相反,必须全面评估多个潜在变量,以确定最有效的门控策略。这要求对特征空间进行系统探索,以识别在确定每个数据子集的最优模型方面具有强预测能力的变量。可以通过采用神经网络或其他学习算法来确定最优门控变量,从而阐明输入与组件模型之间的关系。
使用模型输出作为门控变量的学习型专门化
学习型专门化的一种变体是采用一种独特的方法进行模型选择,即依赖于对所有竞争模型生成的预测进行分析。与需要预定义变量来选择模型的门控方法不同,这种方法利用模型自身的预测作为决策因素。本质上,这种形式的学习型专门化涉及对模型输出的元层次分析。首先,所有的竞争模型都用于生成给定输入的预测。随后,分析这些预测以确定针对该特定实例最可靠的模型。这种方法有效地将模型输出本身转变为指导选择过程的动态“门控变量”。
一个简化的示例可以在具有两个竞争模型的二分类场景中说明。当两个模型对类别标签达成一致时,选择过程很简单。然而,在出现分歧的情况下,需要采用系统的方法来解决冲突。
一种偶尔有效但较为原始的方法涉及分析训练数据,以识别解决冲突预测的最可靠决策规则。这种分析需要检查样本内性能数据,以确定在特定冲突场景中哪个模型表现出更高的准确率。例如,如果第一个模型在两个模型都产生分歧时始终优于第二个模型,则应优先考虑第一个模型的预测。
这种数据驱动的方法允许基于实证证据开发一组决策规则,以优化模型输出的组合。
应用这种简单方法存在明显的局限性。如果训练样本不能代表实际使用中遇到的大多数样本外实例,那么由此产生的集成模型将毫无价值。较复杂的方法(如后续部分将讨论的方法)具有更广泛的适用性,并且在实践中通常表现出更优越的性能。然而,当需要计算效率高且快速的算法时,此处介绍的方法可能已经足够。此外,对这种简化算法的深入分析为理解更高级的概念提供了宝贵的基础。
这种技术的完整源代码可以在本文末尾附加的oracle.mqh文件中找到。以下是声明COracle类的代码:
//+------------------------------------------------------------------+ //| Tabulated combination of component model outputs | //+------------------------------------------------------------------+ class COracle { private: ulong m_ncases; ulong m_nin; ulong m_ncats; uint m_nmodels; matrix m_thresh; ulong m_tally[]; public: COracle(void); ~COracle(void); bool fit(matrix &predictors, vector &targets, IModel* &models[],ulong ncats); double predict(vector &inputs,IModel* &models[]); };
该类定义了两个关键容器:m_thresh(矩阵)和m_tally(数组)。m_thresh矩阵存储输出阈值,用于将训练集划分为等规模的子集;而m_tally数组则标识每个子集对应的最优模型。调用fit()方法时,会基于提供的训练数据构建模型。该方法初始的部分代码如下所示:
//+------------------------------------------------------------------+ //| fit an oracle | //+------------------------------------------------------------------+ bool COracle::fit(matrix &predictors,vector &targets,IModel *&models[],ulong ncats) { if(predictors.Rows()!=targets.Size()) { Print(__FUNCTION__," ",__LINE__," invalid inputs "); return false; } m_ncases = predictors.Rows(); m_nin = predictors.Cols(); m_nmodels = models.Size(); m_ncats = ncats; ulong nthresh = m_ncats - 1; ulong nbins = 1; nbins = (ulong)pow(m_ncats,m_nmodels); m_thresh = matrix::Zeros(m_nmodels,nthresh); ZeroMemory(m_tally); if(ArrayResize(m_tally,int(nbins))<0) { Print(__FUNCTION__," ", __LINE__," error ", GetLastError()); return false; } matrix outputs(m_ncases,m_nmodels); matrix bins(nbins,m_nmodels); bins.Fill(0.0); vector inrow; for(ulong icase=0;icase<m_ncases; icase++) { inrow=predictors.Row(icase); for(uint imodel =0; imodel<m_nmodels; imodel++) outputs[icase][imodel] = models[imodel].forecast(inrow); } double frac; for(uint imodel =0; imodel<m_nmodels; imodel++) { inrow = outputs.Col(imodel); qsortd(0,long(m_ncases-1),inrow); for(ulong i = 0; i<nthresh; i++) { frac = double(i+1)/double(ncats); m_thresh[imodel][i] = inrow[ulong(frac*(m_ncases-1))]; } }
该方法首先将各组件模型的预测结果收集到outputs矩阵中。bins矩阵用于统计每个模型在各分箱内成为最优模型的次数。接下来,针对outputs矩阵的每一列,通过在排序后的列向量inrow中寻找等间距的分界点,确定阈值的数量。fit()方法的后续部分按照如下步骤推进:
vector outrow; ulong ibin,index, klow, khigh, ibest, k; k = 0; double diff,best; for(ulong icase=0;icase<m_ncases; icase++) { inrow = predictors.Row(icase); outrow = outputs.Row(icase); ibin = 0; index = 1; for(uint imodel =0; imodel<m_nmodels; imodel++) { if(outrow[imodel] <= m_thresh[imodel][0]) k = 0; else if(outrow[imodel] > m_thresh[imodel][nthresh-1]) k = nthresh; else { klow = 0; khigh = nthresh-1; while(true) { k = (klow+khigh)/2; if(k == klow) { k = khigh; break; } if(outrow[imodel]<=m_thresh[imodel][k]) khigh = k; else klow = k; } } ibin += k * index; index *= ncats; } best = DBL_MAX;
对于训练数据集中的每个样本,确定其模型预测值对应的分箱。随后,从组件模型的预测集合中找出与真实值最接近的预测值。找到后,将对应的模型与分箱的组合计数加一。fit()方法的最后部分以如下代码收尾:
for(uint imodel =0; imodel<m_nmodels; imodel++) { diff = fabs(outrow[imodel] - targets[icase]); if(diff<best) { best = diff; k = imodel; } } bins[ibin][k]+=1.0; } for(ibin =0; ibin<nbins; ibin++) { k = 0; ibest = 0; for(uint imodel = 0; imodel<m_nmodels; imodel++) { if(bins[ibin][imodel] > double(ibest)) { ibest = ulong(bins[ibin][imodel]); k = ulong(imodel); } } m_tally[ibin] = k; } return true; }
最后几步涉及遍历分箱矩阵,找出针对每个分箱被选中次数最多的模型,并将这些模型的索引保存在m_tally数组中。该分析中采用的分箱过程利用矩阵结构,根据样本在多个模型中的分类结果,高效地将训练样本归类。该矩阵可视为一个包含其他向量的向量,其长度对应于所考虑的模型数量。每个向量存储了在特定分箱类别组合下,各模型被指定为最接近目标的频率。
为说明这一点,考虑一个包含三个模型和四个类别的场景。设想一个三维空间,其中每个轴代表一个模型,并被划分为四个类别。这样将形成一个4×4×4的立方体,其中立方体内的每个唯一点代表三个模型类别分配的独特组合。
分箱过程使用一对索引变量。该对变量中的第一个直接指向矩阵中的特定分箱或行,对应于样本的类别唯一组合。第二个索引变量充当缩放因子,确保增量操作能够正确地遍历多维空间。
这种索引方案确保每次对行索引的增量操作都能将样本准确放置在矩阵中的适当分箱内,从而有效捕获所有模型的联合类别分配。
predict()方法会执行所有模型,以确定输出所属的分箱。随后检查m_tally数组,找出针对给定样本最可能适用的最优模型。
//+------------------------------------------------------------------+ //| make a prediction | //+------------------------------------------------------------------+ double COracle::predict(vector &inputs,IModel* &models[]) { ulong k, klow, khigh, ibin, index, nthresh ; nthresh = m_ncats -1; k = 0; ibin = 0; index = 1; vector otk(m_nmodels); for(uint imodel = 0; imodel<m_nmodels; imodel++) { otk[imodel] = models[imodel].forecast(inputs); if(otk[imodel]<m_thresh[imodel][0]) k = 0; else if(otk[imodel]>m_thresh[imodel][nthresh-1]) k = nthresh - 1; else { klow=0; khigh = nthresh -1 ; while(true) { k = (klow + khigh) / 2; if(k == klow) { k = khigh; break; } if(otk[imodel] <= m_thresh[imodel][k]) khigh = k; else klow = k; } } ibin += k*index; index *= m_ncats; } return otk[ulong(m_tally[ibin])]; }
代码测试
脚本Oracle_Demo.mq5用于测试COracle类的功能。该程序允许用户配置多种模拟参数,包括训练数据集的规模、分箱数量、模型数量,以及控制预测任务复杂度的噪声水平。以下为该脚本在一系列场景下的输出结果,这些场景均涉及三个预测能力相当的模型。
低预测难度,2个分箱,训练数据规模为10个样本。
PF 0 13:59:15.542 Oracle_Demo (BTCUSD,D1) ++++++ Mean raw error = 0.10777835 MQ 0 13:59:15.542 Oracle_Demo (BTCUSD,D1) Oracle error = 0.10777835
中预测难度,2个分箱,训练数据规模为10个样本。
FD 0 14:00:30.967 Oracle_Demo (BTCUSD,D1) ++++++ Mean raw error = 0.38588979 KG 0 14:00:30.967 Oracle_Demo (BTCUSD,D1) Oracle error = 0.38529990
高预测难度,2个分箱,训练数据规模为10个样本。
ES 0 14:01:11.874 Oracle_Demo (BTCUSD,D1) ++++++ Mean raw error = 1.16908710 ND 0 14:01:11.874 Oracle_Demo (BTCUSD,D1) Oracle error = 1.16824689
低预测难度,2个分箱,训练数据规模为100个样本。
LQ 0 14:02:57.441 Oracle_Demo (BTCUSD,D1) ++++++ Mean raw error = 0.10706090 NJ 0 14:02:57.441 Oracle_Demo (BTCUSD,D1) Oracle error = 0.10705483
中预测难度,2个分箱,训练数据规模为100个样本。
LL 0 14:04:24.070 Oracle_Demo (BTCUSD,D1) ++++++ Mean raw error = 0.36310507 JO 0 14:04:24.070 Oracle_Demo (BTCUSD,D1) Oracle error = 0.36303485
高预测难度,2个分箱,训练数据规模为100个样本。
RJ 0 14:06:02.290 Oracle_Demo (BTCUSD,D1) ++++++ Mean raw error = 1.12115161 PM 0 14:06:02.290 Oracle_Demo (BTCUSD,D1) Oracle error = 1.12076456
低预测难度,4个分箱,训练数据规模为100个样本。
FI 0 14:08:24.445 Oracle_Demo (BTCUSD,D1) ++++++ Mean raw error = 0.10681953 FR 0 14:08:24.445 Oracle_Demo (BTCUSD,D1) Oracle error = 0.10681329
中预测难度,4个分箱,训练数据规模为100个样本。
KG 0 14:10:29.012 Oracle_Demo (BTCUSD,D1) ++++++ Mean raw error = 0.36348921 LP 0 14:10:29.012 Oracle_Demo (BTCUSD,D1) Oracle error = 0.36363647
高预测难度,4个分箱,训练数据规模为100个样本。
MR 0 14:12:16.225 Oracle_Demo (BTCUSD,D1) ++++++ Mean raw error = 1.12231642 EE 0 14:12:16.225 Oracle_Demo (BTCUSD,D1) Oracle error = 1.12258202
后续实验引入了第四个模型,该模型被设计为生成随机预测,以此模拟存在无信息模型(即无预测价值的模型)的场景。以下呈现的实验结果表明,系统的行为发生了显著的变化。
低预测难度,2个分箱,训练数据规模为10个样本。
GH 0 14:13:47.886 Oracle_Demo (BTCUSD,D1) ++++++ Mean raw error = 0.12971017 MS 0 14:13:47.886 Oracle_Demo (BTCUSD,D1) Oracle error = 0.14153652
中预测难度,2个分箱,训练数据规模为10个样本。
JN 0 14:14:16.985 Oracle_Demo (BTCUSD,D1) ++++++ Mean raw error = 0.40381512 MI 0 14:14:16.985 Oracle_Demo (BTCUSD,D1) Oracle error = 0.40074764
高预测难度,2个分箱,训练数据规模为10个样本。
ND 0 14:14:54.040 Oracle_Demo (BTCUSD,D1) ++++++ Mean raw error = 1.16720001 OG 0 14:14:54.040 Oracle_Demo (BTCUSD,D1) Oracle error = 1.16304663
低预测难度,2个分箱,训练数据规模为100个样本。
QJ 0 14:17:05.521 Oracle_Demo (BTCUSD,D1) ++++++ Mean raw error = 0.12727773 HM 0 14:17:05.521 Oracle_Demo (BTCUSD,D1) Oracle error = 0.17687364
中预测难度,2个分箱,训练数据规模为100个样本。
QP 0 14:18:26.976 Oracle_Demo (BTCUSD,D1) ++++++ Mean raw error = 0.38337835 CK 0 14:18:26.976 Oracle_Demo (BTCUSD,D1) Oracle error = 0.39318874
高预测难度,2个分箱,训练数据规模为100个样本。
IF 0 14:20:01.925 Oracle_Demo (BTCUSD,D1) ++++++ Mean raw error = 1.13780482 IQ 0 14:20:01.925 Oracle_Demo (BTCUSD,D1) Oracle error = 1.13878032
低预测难度,4个分箱,训练数据规模为100个样本。
HL 0 14:23:03.090 Oracle_Demo (BTCUSD,D1) ++++++ Mean raw error = 0.12709947 QO 0 14:23:03.090 Oracle_Demo (BTCUSD,D1) Oracle error = 0.11975572
中预测难度,4个分箱,训练数据规模为100个样本。
CR 0 14:25:25.091 Oracle_Demo (BTCUSD,D1) ++++++ Mean raw error = 0.38314408 CE 0 14:25:25.091 Oracle_Demo (BTCUSD,D1) Oracle error = 0.37892436
高预测难度,4个分箱,训练数据规模为100个样本。
GH 0 14:27:50.024 Oracle_Demo (BTCUSD,D1) ++++++ Mean raw error = 1.13828093 CS 0 14:27:50.024 Oracle_Demo (BTCUSD,D1) Oracle error = 1.13422816
对两组实验结果的分析表明,在低噪声水平的场景下,该技术展现出卓越效能,可显著降低误差方差。相反,在高噪声的场景中,该技术不仅未能提供显著改进,甚至频繁导致性能劣化(相较于仅使用单一模型的情况)。即使所有组成模型具备相同的预测能力,这一现象仍会显现——尽管此类情况下的性能差异确实较小。
测试还揭示出,将分箱数量从2个增至4个时,性能差异既不稳定也不显著。这一结果并不意外,因为无论所有模型具有相近的预测能力,还是某个模型始终产生无价值预测,均会导致此现象。在当前的情景下,该算法的核心功能是识别并剔除无信息模型(当其存在时)。然而,可能存在某些场景,此时增加类别数量确实会带来优势。
门控广义回归集成方法
本节介绍一种基于门控变量的通用模型组合技术。该方法受广义回归神经网络(GRNN)概念的启发,允许一个或多个变量作为动态门控器,调节各组成模型的影响力。与早期门控方法(需选择单一模型输出最终结果)不同,广义回归门控通过基于门控变量的最优加权,整合所有组成模型的输出。这些门控变量可包括外部测量值以及各模型的输出结果。此方法被称为门控广义回归方法。
实施该方法需至少两个已训练的组成模型,以及一个用于训练GRNN启发式集成模型的独立数据集。训练数据集必须包含一个或多个门控变量、各组成模型的预测值,以及对应的目标值。值得注意的是,也可将组成模型的某些输出指定为门控变量,从而进一步提升方法的灵活性。
GRNN是一种专为回归任务(预测连续输出)设计的人工神经网络。GRNN基于核密度估计原理运作,并采用基于记忆的学习方法。其结构包含四层:输入层、模式层、求和层与输出层。
输入层接收预测变量,并将其传递至模式层。模式层中每个神经元代表一个训练样本,通过径向基函数计算输入与训练数据的相似度。求和层汇总模式层的加权输出,输出层则通过权重标准化生成最终预测。
GRNN在建模非线性关系方面具有显著优势,其训练时间极短,且能自动适应底层数据分布。
在此框架下,测试样本与训练样本之间的加权欧氏距离由门控变量决定。具体而言,当评估测试样本时,GRNN门控器会优先选择门控变量与测试样本高度相似的训练样本。通过利用GRNN预测模型的平方误差,各组成模型的预测平方误差可通过以下公式计算:
尽管存在无限多种将组件模型输出组合为联合预测的方法,但最简单的方式是将最终预测表示为各模型输出的线性组合。若组件模型具有无偏预测的理想特性,则仅当权重之和满足标准化条件(即权重之和为1)时,该特性才能得以保持。即使预测结果并非严格无偏,在大多数场景下这一条件仍具有优势。对于具有最小均方误差的无偏估计量线性组合,最优权重与各估计量方差的倒数成正比。通过用预测平方误差替代方差,权重可通过以下公式计算:
要生成基于GRNN门控的预测,在给定合适的σ权重值后,我们首先针对给定测试样本估计每个模型的预测误差。随后,根据预测误差计算权重,并在测试样本上评估各组件模型。最后,利用计算得到的权重将各组件模型的预测结果组合为最终估计值。
确定σ权重的最优值并非易事,因为这需要基于训练数据进行估计。评估候选σ向量质量的最有效方法是通过交叉验证。具体操作包括:从训练集中移除一个样本作为测试用例,使用指定的σ向量为该样本生成GRNN门控预测,并将预测值与真实值进行比较。随后将该样本重新放回训练集,并对数据集中的所有样本重复此过程。通过计算这些重复试验的均方误差,可衡量候选σ向量的质量。
任何无需导数的优化算法均可用于确定使交叉验证误差最小化的σ权重集合。在可选方法中,差分进化算法因其鲁棒性和广泛适用性而备受认可。不过,鲍威尔(Powell)方法提供了计算效率更高的替代方案,在大多数实际应用中的表现令人满意。鉴于其效率优势,本研究采用鲍威尔方法,尽管在涉及多个局部极值的罕见情况下,差分进化算法可能表现更优。
文件gatedreg.mqh包含CGatedReg类的源代码,该类实现了上述基于GRNN启发的门控集成方法。类声明如下:
//+------------------------------------------------------------------+ //| GRNN gating model combination | //+------------------------------------------------------------------+ class CGatedReg:public CPowellsMethod { private: ulong m_nsamples; ulong m_ngates; ulong m_nmodels; matrix m_tset; vector m_sigma; vector m_errvals; vector m_params; double criter(vector ¶ms); double trial(vector &gates, vector &contenders,long i_exclude,long n_exclude); virtual double func(vector &p) { return criter(p); } public: CGatedReg(void); ~CGatedReg(void); bool fit(matrix &gates, matrix &contenders,vector &targets); double predict(vector &gates, vector &contenders); };
组件模型的预测结果需预先计算并存储在矩阵中。每个模型必须事先完成训练,以实现对因变量的预测。门控变量(通常为单个变量)将被用于在最终预测中差异化加权各组件模型的贡献。fit()方法负责复制必要的训练数据,并确定最优的σ权重值。该方法的具体实现方式如下:
//+------------------------------------------------------------------+ //| fit a gated grnn model | //+------------------------------------------------------------------+ bool CGatedReg::fit(matrix &gates,matrix &contenders,vector &targets) { if(gates.Rows()!=contenders.Rows() || contenders.Rows()!=targets.Size() || gates.Rows()!=targets.Size()) { Print(__FUNCTION__, " ", __LINE__, " invalid training data "); return false; } m_nsamples = gates.Rows(); m_ngates = gates.Cols(); m_nmodels = contenders.Cols(); m_tset = matrix::Zeros(m_nsamples,m_ngates+m_nmodels+1); m_sigma = vector::Zeros(m_ngates); m_errvals = vector::Zeros(m_nmodels); for(ulong i = 0; i<m_nsamples; i++) { for(ulong j = 0; j<m_ngates; j++) m_tset[i][j] = gates[i][j]; for(ulong k = 0; k<m_nmodels; k++) m_tset[i][m_ngates+k] = contenders[i][k]; m_tset[i][m_ngates+m_nmodels] = targets[i]; } m_params = vector::Zeros(m_ngates); double err = criter(m_params); if(err > 0.0) Optimize(m_params); criter(m_params); return true; }
训练数据(包含fit()方法的所有输入参数)必须予以保留,因为后续预测需借助广义回归来对各模型的中间误差进行预测。此外,每次预测均需使用m_errval向量。采用鲍威尔优化算法来搜索最优的σ权重值。待最小化的目标函数由私有方法criter()定义。
//+------------------------------------------------------------------+ //| function criterion | //+------------------------------------------------------------------+ double CGatedReg::criter(vector ¶ms) { int i, ngates, nmodels, ncases; double out, diff, error, penalty ; vector inputs1,inputs2,row; ngates = int(m_ngates); ; nmodels = int(m_nmodels) ; ncases = int(m_nsamples) ; penalty = 0.0 ; for(i=0 ; i<ngates ; i++) { if(params[i] > 8.0) { m_sigma[i] = exp(8.0) ; penalty += 10.0 * (params[i] - 8.0) ; } else if(params[i] < -8.0) { m_sigma[i] = exp(-8.0) ; penalty += 10.0 * (-params[i] - 8.0) ; } else m_sigma[i] = exp(params[i]) ; } error = 0.0 ; for(i=0 ; i<ncases ; i++) { row = m_tset.Row(i); inputs1 = np::sliceVector(row,0,m_ngates); inputs2 = np::sliceVector(row,ulong(ngates),ulong(ngates+nmodels)); out = trial(inputs1, inputs2, long(i), 0) ; diff = row[ngates+nmodels] - out ; error += diff * diff ; } return error / double(ncases) + penalty ; }
该方法通过交叉验证评估候选σ向量的质量。算法不对σ本身进行优化,而是优化其对数形式(即log(σ))。将参数变化的非线性影响线性化,从而提升了稳定性。为缓解GRNN门控误差曲面在极端值处呈现的平坦性问题。准则函数首先对参数进行指数化处理,并限制其取值范围。同时引入惩罚项以抑制极端σ值。对每个训练样本,算法生成预测值并与真实值比较。累积平方误差作为误差准则。
将m_errvals数组元素初始化为0,用于累加误差方程分子。该方程分母无需直接计算,因为在权重方程分母的标准化因子中会被约去。在将每项纳入求和前,需验证测试样本与训练样本的顺序邻近性。
该方法既可用于训练集成员的预测,也可用于完全未知样本的预测。通过向trial()函数传递训练样本的序号i_exclude,可实现交叉验证。同时传递距离限制参数n_exclude。通常设为0,仅排除当前测试样本。
读者们需注意,当训练数据存在序列相关性时,该交叉验证算法存在严重局限性。训练数据通常为时间序列数据。此时可通过排除与测试样本空间邻近的训练样本来缓解问题。
//+------------------------------------------------------------------+ //| trial ( ) | //+------------------------------------------------------------------+ double CGatedReg::trial(vector &gates, vector &contenders, long i_exclude,long n_exclude) { int icase, ivar, idist, size, ncases; double psum, diff, dist, err, out ; m_errvals.Fill(0.0); int ngates = int(m_ngates); int nmodels = int(m_nmodels); size = ngates + nmodels + 1 ; ncases = int(m_nsamples); for(icase=0 ; icase<ncases ; icase++) { idist = (int)fabs(int(i_exclude) - icase) ; if(ncases - idist < idist) idist = ncases - idist ; if(idist <= int(n_exclude)) continue ; dist = 0.0 ; for(ivar=0 ; ivar<ngates ; ivar++) { diff = gates[ivar] - m_tset[icase][ivar] ; diff /= m_sigma[ivar] ; dist += diff * diff ; } dist = exp(-dist) ; for(ivar=0 ; ivar<nmodels ; ivar++) { err = m_tset[icase][ngates+ivar] - m_tset[icase][ngates+nmodels] ; m_errvals[ivar] += dist * err * err ; } } psum = 0.0 ; for(ivar=0 ; ivar<nmodels ; ivar++) { if(m_errvals[ivar] > 1.e-30) m_errvals[ivar] = 1.0 / m_errvals[ivar] ; else m_errvals[ivar] = 1.e30 ; psum += m_errvals[ivar] ; } for(ivar=0 ; ivar<nmodels ; ivar++) m_errvals[ivar] /= psum ; out = 0.0 ; for(ivar=0 ; ivar<nmodels ; ivar++) out += m_errvals[ivar] * contenders[ivar] ; return out ; }
如果某个训练样本通过交叉验证的排除检验(即未被判定为需排除的邻近样本),则计算该样本与测试样本之间的加权欧氏距离。该距离经指数化处理后,用于计算各组件模型的预测误差。随后,针对每个模型分别确定其预测误差。最后一步是利用模型权重公式,将各候选模型的输出组合为单一预测值。该值即为函数的返回值。
//+------------------------------------------------------------------+ //| infer | //+------------------------------------------------------------------+ double CGatedReg::predict(vector &gates,vector &contenders) { return trial(gates,contenders,-1,0); }
门控GRNN集成模型测试
Gating_Demo.mqh脚本提供了四种不同门控策略的全面对比。每种策略旨在展示模型选择与组合的不同维度。以下是四种策略的简要概述:
- 组件预测作为门控变量:该策略直接使用各组件模型的预测结果作为门控变量,可与基准方法(COracle类)进行直接对比。其目的是测试将模型自身输出作为模型选择决策因素的效果。
- 原始变量门控:该策略使用组件模型的原始输入变量作为门控变量。由于这些变量并非为有效门控信号设计,此策略有助于发现低效或无关门控变量对模型性能的影响。
- 随机门控:该策略采用随机生成的数值作为门控变量,模拟无有效门控信号的场景。其作用是作为基准,展示使用完全无信息信号时性能的下降情况。
- 基于比例的门控:该策略将第一与第二个模型预测误差之比的对数作为门控变量。尽管在现实场景中该方法不切实际(因模型的真实预测误差通常未知),但它为双模型场景提供了理想化参考。对于多模型情况,它仍能提供部分有价值的门控信息。
这四种策略旨在测试不同性能条件,揭示门控技术在集成学习中的优势与局限性。脚本通过评估各门控策略对整体预测准确性和误差方差的影响,帮助更清晰地理解GRNN门控机制的有效性。
实验设置:3个模型、100个样本、低预测难度。
EK 0 14:36:33.869 Gating_Demo (BTCUSD,D1) 1000 replications completed. GL 0 14:36:33.869 Gating_Demo (BTCUSD,D1) ++++++ Mean raw error = 0.10790466 JP 0 14:36:33.869 Gating_Demo (BTCUSD,D1) Component error = 0.10790458 DF 0 14:36:33.869 Gating_Demo (BTCUSD,D1) Original error = 0.10790458 HM 0 14:36:33.869 Gating_Demo (BTCUSD,D1) Random error = 0.10790458 DJ 0 14:36:33.869 Gating_Demo (BTCUSD,D1) Ratio error = 0.10790458
3个模型、100个样本、高预测难度。
GF 0 14:40:57.600 Gating_Demo (BTCUSD,D1) 1000 replications completed. LQ 0 14:40:57.600 Gating_Demo (BTCUSD,D1) ++++++ Mean raw error = 1.12143040 FE 0 14:40:57.600 Gating_Demo (BTCUSD,D1) Component error = 1.11991444 GQ 0 14:40:57.600 Gating_Demo (BTCUSD,D1) Original error = 1.11991445 QI 0 14:40:57.600 Gating_Demo (BTCUSD,D1) Random error = 1.11991443 EO 0 14:40:57.600 Gating_Demo (BTCUSD,D1) Ratio error = 1.11991443
4个模型、100个样本、低预测难度。
IO 0 14:42:58.751 Gating_Demo (BTCUSD,D1) 1000 replications completed. LK 0 14:42:58.751 Gating_Demo (BTCUSD,D1) ++++++ Mean raw error = 0.12792841 RS 0 14:42:58.751 Gating_Demo (BTCUSD,D1) Component error = 0.11516554 MK 0 14:42:58.751 Gating_Demo (BTCUSD,D1) Original error = 0.11516373 GR 0 14:42:58.751 Gating_Demo (BTCUSD,D1) Random error = 0.11516595 GE 0 14:42:58.751 Gating_Demo (BTCUSD,D1) Ratio error = 0.115165954个模型、100个样本、高预测难度。
QQ 0 14:45:15.030 Gating_Demo (BTCUSD,D1) 1000 replications completed. HE 0 14:45:15.030 Gating_Demo (BTCUSD,D1) ++++++ Mean raw error = 1.14025014 EI 0 14:45:15.030 Gating_Demo (BTCUSD,D1) Component error = 1.13144872 GM 0 14:45:15.030 Gating_Demo (BTCUSD,D1) Original error = 1.13144863 QD 0 14:45:15.030 Gating_Demo (BTCUSD,D1) Random error = 1.13144883 NL 0 14:45:15.030 Gating_Demo (BTCUSD,D1) Ratio error = 1.13144882
随机门控带来的意外性能提升,可归因于GRNN门控算法的独特工作机制。通常来说,随机门控信号本应降低模型性能,因其会引入噪声且无法为模型选择提供有效的信息。然而,GRNN算法通过计算训练样本与测试样本间的加权欧氏距离,基于样本相似性调整预测结果。
当门控信号为随机值时,算法仍会利用数据的整体结构及各组件模型的预测能力,计算加权平均预测值。由于随机门控值未对特定模型产生强烈偏向,算法将可能更依赖于数据的内在结构以及各模型本身的预测性能(这些模型本身已具备较好的预测能力)。最终结果是形成一种更稳健的模型组合,随机门控反而起到“中和作用”,避免单一模型主导决策过程。
若集成中包含三个高预测模型和一个随机预测模型,随机门控可能通过降低随机模型权重,间接实现对其的“剔除”。这种机制会显著提升集成模型性能,使得无信息随机模型的影响得以最小化。
尽管随机门控看似缺乏直观优势,但GRNN门控过程可能通过挖掘数据集与模型的内在结构,从而获得出乎意料的提升效果,尤其在那些模型本身已具备高精度的“简单”预测任务中效果更为显著。这一现象凸显了GRNN门控技术的核心优势:即使在非理想条件下,算法仍能通过动态调整各模型贡献权重,有效整合多模型潜力,提升预测效果。
算法会动态估计各模型的预测误差。当某个模型(如随机预测模型)持续产生高误差时,其误差估计值会显著增大。这会导致集成权重分配方案自动降低该模型在加权组合中的权重。
这一发现强调了GRNN门控的关键优势。即使门控变量本身缺乏预测能力,算法仍能精准识别并抑制低性能模型的贡献。因此,在门控信号信息有限或完全无效的情况下,GRNN门控仍可显著提升性能,尤其当集成中包含不同预测精度的模型时,其效果更为显著。
结论
这些技术充分展现了门控机制在提升学习算法可解释性与预测能力方面的适应性优势。具体技术选型需结合实际场景,包括任务复杂度、数据特性及计算资源限制。通常,优化算法与领域知识相结合的混合方式往往能产出兼具高效性与易解读性的成果。本文涉及的所有实现代码均附于文末。下表详细说明了配套源代码文件的作用:
| 文件名 | 描述 |
|---|---|
| MQL5/include/gatedreg.mqh | 包含实现门控GRNN集成模型的CGatedReg类定义 |
| MQL5/include/imodel.mqh | 包含封装已训练模型的接口定义 |
| MQL5/include/minimize.mqh | 提供了实现基于鲍威尔方法进行函数最小化的CPowellsMethod类定义 |
| MQL5/include/multilayerperceptron.mqh | 提供了实现多层感知器(MLP)的CMlp类定义 |
| MQL5/include/np.mqh | 用于操作向量和矩阵的通用辅助函数集合 |
| MQL5/include/oracle.mqh | 提供了COracle类定义,该类支持从一组专业组件模型中进行选择 |
| MQL5/include/qsort.mqh | 提供了用于对向量进行排序的简单函数 |
| Mql5/scripts/Gating_Demo.mq5 | 一个演示CGatedReg类功能的脚本 |
| Mql5/scripts/Oracle_Demo.mq5 | 另一个演示COracle类用法的脚本 |
本文由MetaQuotes Ltd译自英文
原文地址: https://www.mql5.com/en/articles/16995
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
本文由网站的一位用户撰写,反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责,也不对因使用所述解决方案、策略或建议而产生的任何后果负责。
 开发回放系统(第 77 部分):新 Chart Trade(四)
开发回放系统(第 77 部分):新 Chart Trade(四)
 MQL5自动化交易策略(第四部分):构建多层级区域恢复系统
MQL5自动化交易策略(第四部分):构建多层级区域恢复系统
 逆公允价值缺口(IFVG)交易策略
逆公允价值缺口(IFVG)交易策略
