Gating mechanisms in ensemble learning

Gating methods dynamically adjust the influence of individual models based on contextual information using gate variables. These variables act as supervisory mechanisms, strategically weighting model outputs to achieve superior predictive performance compared to any single model.

Unlike traditional ensemble methods that rely on averaging, voting, or stacking, gating explicitly uses gate variables for model combination. This approach is particularly valuable in scenarios with fluctuating model performance, such as financial forecasting, where economic trends impact prediction accuracy. By adaptively weighting models based on context, gating enhances accuracy and adaptability in complex environments.

Gating techniques generally fall into two categories: selecting a single model based on gate variables or combining outputs from all models with context-dependent weights. The latter is often more robust, leveraging the strengths of multiple models. The following sections explore examples of both approaches: preordained and learned specialization.

Preordained specialization

Preordained specialization constitutes a fundamental form of gating, wherein a single variable acts as a decisive factor in selecting between two or more pre-trained specialist models. This approach effectively partitions the input space, directing instances to the most suitable model based on the value of the gating variable. To illustrate this concept, consider a binary classification problem depicted in a two-dimensional feature space, with variables A and B. In this hypothetical scenario, variable B exhibits negligible discriminative power between the two classes, while variable A demonstrates moderate predictive capability, achieving accurate classifications for some instances but yielding ambiguous results for others.

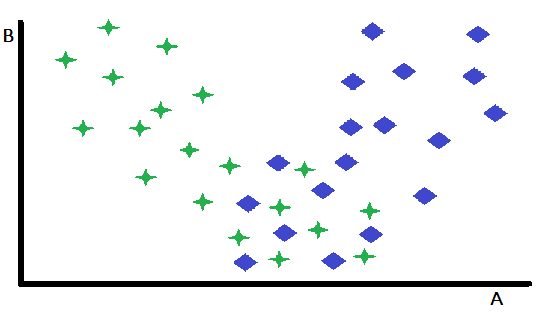
Close inspection of a scatter plot of the features reveals that variable B effectively delineates instances for which A serves as a robust classifier from those where its predictive power is diminished. Specifically, instances characterized by high values of B exhibit superior classification accuracy when using A as the primary predictor. This observation suggests a natural partitioning strategy: dividing the dataset based on a threshold value of B. This partitioning enables the development of two distinct classification models: one optimized for instances with high B values (where A is a strong predictor) and another for instances with low B values (where A may be less reliable).

While this simplified example demonstrates the core principle, it is important to acknowledge that the benefits of such partitioning may be limited when the remaining subset of instances proves inherently difficult to classify. A key advantage of this approach lies in its ability to isolate and effectively address the more easily classifiable instances. This simplification also helps in the development of more performant models for the remaining, more challenging subset of data. Although the example just described focused on a single variable to clarify the concept, in practical applications, the selection of the appropriate model can be contingent upon the values of multiple variables, which may or may not be included within the primary set of predictors used by the individual models.

Learned specialization

Learned Specialization represents a more sophisticated approach to gating, where the optimal splitting variable and its corresponding threshold are not determined a priori but rather learned from the data itself. While visual inspection of scatter plots may occasionally provide preliminary insights into potential splitting variables and their thresholds, such intuitive approaches often fall short in real-world applications.

In practice, a more systematic and data-driven approach is necessary. This typically involves a rigorous search process, exploring a wide range of potential splitting variables and their associated thresholds. For each candidate splitting variable and threshold, the dataset is partitioned, and separate models are trained and evaluated on the resulting subsets. This iterative process of exploration, training, and evaluation can be computationally demanding, particularly when dealing with large datasets or complex models. However, the potential gains in model performance often justify the increased computational cost.

Furthermore, the search for optimal splitting variables should not be limited to a single candidate. Instead, a comprehensive evaluation of multiple potential variables is essential to identify the most effective gating strategy. This necessitates a systematic exploration of the feature space to identify variables that exhibit strong predictive power in determining the optimal model for each subset of the data. The search for the optimal gate variables can be accomplished by employing neural networks or other learning algorithms to ascertain the relationship between the inputs and the component models.

Learned specialization using model outputs as gating variables

A variant of learned specialization adopts a unique approach to model selection by relying on the analysis of predictions generated by all competing models. Unlike gating methods that require predefined variables to select a model, this approach leverages the models' own predictions as decision-making factors. In essence, this form of learned specialization involves a meta-level analysis of the model outputs. All competing models are first invoked to generate predictions for a given input. Subsequently, these predictions are analyzed to determine the most reliable model for that specific instance. This approach effectively transforms the model outputs themselves into dynamic "gate variables" that guide the selection process.

A simplified example can be illustrated in a binary classification scenario with two competing models. When both models agree on the class label, the selection process is straightforward. However, in cases of disagreement, a systematic approach is required to resolve the conflict.

One occasionally effective, but primitive, method involves analyzing the training data to identify the most reliable decision rule for resolving conflicting predictions. This analysis requires examining in-sample performance data to determine which model exhibits higher accuracy in specific conflict scenarios. For instance, if a model consistently outperforms a second model when both models disagree, the first model's prediction should be prioritized.

This data-driven approach allows for the development of a set of decision rules that optimize the combination of model outputs based on empirical evidence.

There are obvious limitations to applying this simple method. If the training samples are not representative of most out-of-sample instances that will be encountered in real-world use, then the resultant ensemble model will be worthless. More sophisticated methodologies, such as the one discussed in an upcoming section, exhibit greater applicability and typically demonstrate superior performance in practical applications. Nevertheless, when a computationally efficient and expeditious algorithm is required, the method presented here may prove adequate. Also, an in-depth analysis of this simplified algorithm provides a valuable foundation for understanding more advanced concepts.

The complete source code for this technique can be found in the file oracle.mqh, which is attached at the end of this article. The following code is the declaration of the COracle class.

//+------------------------------------------------------------------+
//| Tabulated combination of component model outputs                 |
//+------------------------------------------------------------------+
class COracle
  {
private:
   ulong             m_ncases;
   ulong             m_nin;
   ulong             m_ncats;
   uint              m_nmodels;
   matrix            m_thresh;
   ulong             m_tally[];
public:
                     COracle(void);
                    ~COracle(void);
   bool              fit(matrix &predictors, vector &targets, IModel* &models[],ulong ncats);
   double            predict(vector &inputs,IModel* &models[]);

  };

The class defines two key containers, m_thresh and m_tally. The m_thresh matrix stores the output thresholds that partition the training set into equally sized subsets, while the m_tally array identifies the optimal model for each of these subsets. Invoking fit() builds a model based on the supplied training data. The initial section of this method is shown below.

//+------------------------------------------------------------------+
//| fit an oracle                                                    |
//+------------------------------------------------------------------+
bool COracle::fit(matrix &predictors,vector &targets,IModel *&models[],ulong ncats)
  {
   if(predictors.Rows()!=targets.Size())
     {
      Print(__FUNCTION__," ",__LINE__," invalid inputs ");
      return false;
     }

   m_ncases = predictors.Rows();
   m_nin = predictors.Cols();
   m_nmodels = models.Size();

   m_ncats = ncats;
   ulong nthresh = m_ncats - 1;
   ulong nbins = 1;

   nbins = (ulong)pow(m_ncats,m_nmodels);

   m_thresh = matrix::Zeros(m_nmodels,nthresh);

   ZeroMemory(m_tally);

   if(ArrayResize(m_tally,int(nbins))<0)
     {
      Print(__FUNCTION__," ", __LINE__," error ", GetLastError());
      return false;
     }

   matrix outputs(m_ncases,m_nmodels);
   matrix bins(nbins,m_nmodels);

   bins.Fill(0.0);

   vector inrow;
   for(ulong icase=0;icase<m_ncases; icase++)
     {
      inrow=predictors.Row(icase);
      for(uint imodel =0; imodel<m_nmodels; imodel++)
         outputs[icase][imodel] = models[imodel].forecast(inrow);
     }

   double frac;
   for(uint imodel =0; imodel<m_nmodels; imodel++)
     {
      inrow = outputs.Col(imodel);
      qsortd(0,long(m_ncases-1),inrow);
      for(ulong i = 0; i<nthresh; i++)
        {
         frac = double(i+1)/double(ncats);
         m_thresh[imodel][i] = inrow[ulong(frac*(m_ncases-1))];
        }
     }

The method begins by collecting the predictions of each component model in the outputs matrix. The bins matrix is used to count the number of times each model is the best within a bin. Next, for each column in the outputs matrix, the number of thresholds is determined by finding the equally spaced entries in the sorted column vector, inrow. The next section of the fit() method progresses as follows.

vector outrow;
   ulong ibin,index, klow, khigh, ibest, k;
   k = 0;
   double diff,best;
   for(ulong icase=0;icase<m_ncases; icase++)
     {
      inrow = predictors.Row(icase);
      outrow = outputs.Row(icase);
      ibin = 0;
      index = 1;
      for(uint imodel =0; imodel<m_nmodels; imodel++)
        {
         if(outrow[imodel] <= m_thresh[imodel][0])
            k = 0;
         else
            if(outrow[imodel] > m_thresh[imodel][nthresh-1])
               k = nthresh;
            else
              {
               klow = 0;
               khigh = nthresh-1;
               while(true)
                 {
                  k = (klow+khigh)/2;
                  if(k == klow)
                    {
                     k = khigh;
                     break;
                    }
                  if(outrow[imodel]<=m_thresh[imodel][k])
                     khigh = k;
                  else
                     klow = k;
                 }
              }
         ibin += k * index;
         index *= ncats;
        }
      best = DBL_MAX;

For each sample in the training dataset, the bin corresponding to its model prediction is determined. Then the prediction, from the set of component model predictions, that is closest to the true value is found. When found, the corresponding model and bin combination is incremented. The final section in the fit() method concludes with the following code.

for(uint imodel =0; imodel<m_nmodels; imodel++)
        {
         diff = fabs(outrow[imodel] - targets[icase]);
         if(diff<best)
           {
            best = diff;
            k = imodel;
           }
        }
      bins[ibin][k]+=1.0;
     }

   for(ibin =0; ibin<nbins; ibin++)
     {
      k = 0;
      ibest = 0;
      for(uint imodel = 0; imodel<m_nmodels; imodel++)
        {
         if(bins[ibin][imodel] > double(ibest))
           {
            ibest = ulong(bins[ibin][imodel]);
            k = ulong(imodel);
           }
        }
      m_tally[ibin] = k;
     }

   return true;
  }

The final steps involve traversing the bins matrix to find the model that was selected the most often for that bin, and the indices of these models are saved in m_tally. The binning process employed within this analysis utilizes a matrix structure to efficiently categorize training samples based on their classifications across multiple models. The matrix can be thought of as a vector that holds other vectors, of a length corresponding to the number of models under consideration. Each stores the frequency with which each model was designated as the closest to the target for the specific combination of categories represented by the bin.

To illustrate this, consider a scenario with three models and four categories. Visualize a three-dimensional space where each axis represents a model and is divided into four categories. This results in a 4x4x4 cube, with each unique point within this cube representing a distinct combination of category assignments across the three models.

The binning process utilizes a pair of indexing variables. The first of this pair directly addresses a specific bin or row in the matrix, corresponding to the unique combination of categories for a sample. The second indexing variable acts as a scaling factor, ensuring that increments correctly navigate through the multidimensional space.

This indexing scheme ensures that each increment to the row index correctly positions a sample within the appropriate bin within the matrix, effectively capturing the joint category assignments across all models.

The predict() method executes all models to find the bin to which the outputs belong. The m_tally array is then checked to find which model is most likely to be the most appropriate to apply for the given sample.

//+------------------------------------------------------------------+
//| make a prediction                                                |
//+------------------------------------------------------------------+
double COracle::predict(vector &inputs,IModel* &models[])
  {
   ulong k, klow, khigh, ibin, index, nthresh ;
   nthresh = m_ncats -1;
   k = 0;
   ibin = 0;
   index = 1;
   vector otk(m_nmodels);

   for(uint imodel = 0; imodel<m_nmodels; imodel++)
     {
      otk[imodel] = models[imodel].forecast(inputs);

      if(otk[imodel]<m_thresh[imodel][0])
         k = 0;
      else
         if(otk[imodel]>m_thresh[imodel][nthresh-1])
            k = nthresh - 1;
         else
           {
            klow=0;
            khigh = nthresh -1 ;
            while(true)
              {
               k = (klow + khigh) / 2;
               if(k == klow)
                 {
                  k = khigh;
                  break;
                 }
               if(otk[imodel] <= m_thresh[imodel][k])
                  khigh = k;
               else
                  klow = k;
              }
           }
      ibin += k*index;
      index *= m_ncats;
     }

   return otk[ulong(m_tally[ibin])];
  }

Testing the code

The script Oracle_Demo.mq5 tests the functionality of the COracle class. This program enables the user to configure various simulation parameters, including the size of the training dataset, the number of bins, the number of models, and a noise level that controls the complexity of the prediction task. The following output from the script presents the results obtained across a range of scenarios involving three models of equivalent predictive power.

Easy prediction difficulty, 2 bins and training data size of 10 samples.

PF      0       13:59:15.542    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.10777835
MQ      0       13:59:15.542    Oracle_Demo (BTCUSD,D1) Oracle error = 0.10777835

Moderate prediction difficulty, 2 bins and training data size of 10 samples.

FD      0       14:00:30.967    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.38588979
KG      0       14:00:30.967    Oracle_Demo (BTCUSD,D1) Oracle error = 0.38529990

Hard prediction difficulty, 2 bins and training data size of 10 samples.

ES      0       14:01:11.874    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 1.16908710
ND      0       14:01:11.874    Oracle_Demo (BTCUSD,D1) Oracle error = 1.16824689

Easy prediction difficulty, 2 bins and training data size of 100 samples.

LQ      0       14:02:57.441    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.10706090
NJ      0       14:02:57.441    Oracle_Demo (BTCUSD,D1) Oracle error = 0.10705483

Moderate prediction difficulty, 2 bins and training data size of 100 samples.

LL      0       14:04:24.070    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.36310507
JO      0       14:04:24.070    Oracle_Demo (BTCUSD,D1) Oracle error = 0.36303485

Hard prediction difficulty, 2 bins and training data size of 100 samples.

RJ      0       14:06:02.290    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 1.12115161
PM      0       14:06:02.290    Oracle_Demo (BTCUSD,D1) Oracle error = 1.12076456

Easy prediction difficulty, 4 bins and training data size of 100 samples.

FI      0       14:08:24.445    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.10681953
FR      0       14:08:24.445    Oracle_Demo (BTCUSD,D1) Oracle error = 0.10681329

Moderate prediction difficulty, 4 bins and training data size of 100 samples.

KG      0       14:10:29.012    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.36348921
LP      0       14:10:29.012    Oracle_Demo (BTCUSD,D1) Oracle error = 0.36363647

Hard prediction difficulty, 4 bins and training data size of 100 samples.

MR      0       14:12:16.225    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 1.12231642
EE      0       14:12:16.225    Oracle_Demo (BTCUSD,D1) Oracle error = 1.12258202

Subsequent experiments incorporated a fourth model, designed to produce random predictions, thereby simulating a scenario with a non-informative model. The results, presented below, demonstrate a significant alteration in the system's behavior.

Easy prediction difficulty, 2 bins and training data size of 10 samples.

GH      0       14:13:47.886    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.12971017
MS      0       14:13:47.886    Oracle_Demo (BTCUSD,D1) Oracle error = 0.14153652

Moderate prediction difficulty, 2 bins and training data size of 10 samples.

JN      0       14:14:16.985    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.40381512
MI      0       14:14:16.985    Oracle_Demo (BTCUSD,D1) Oracle error = 0.40074764

Hard prediction difficulty, 2 bins and training data size of 10 samples.

ND      0       14:14:54.040    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 1.16720001
OG      0       14:14:54.040    Oracle_Demo (BTCUSD,D1) Oracle error = 1.16304663

Easy prediction difficulty, 2 bins and training data size of 100 samples.

QJ      0       14:17:05.521    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.12727773
HM      0       14:17:05.521    Oracle_Demo (BTCUSD,D1) Oracle error = 0.17687364

Moderate prediction difficulty, 2 bins and training data size of 100 samples.

QP      0       14:18:26.976    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.38337835
CK      0       14:18:26.976    Oracle_Demo (BTCUSD,D1) Oracle error = 0.39318874

Hard prediction difficulty, 2 bins and training data size of 100 samples.

IF      0       14:20:01.925    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 1.13780482
IQ      0       14:20:01.925    Oracle_Demo (BTCUSD,D1) Oracle error = 1.13878032

Easy prediction difficulty, 4 bins and training data size of 100 samples.

HL      0       14:23:03.090    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.12709947
QO      0       14:23:03.090    Oracle_Demo (BTCUSD,D1) Oracle error = 0.11975572

Moderate prediction difficulty, 4 bins and training data size of 100 samples.

CR      0       14:25:25.091    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.38314408
CE      0       14:25:25.091    Oracle_Demo (BTCUSD,D1) Oracle error = 0.37892436

Hard prediction difficulty, 4 bins and training data size of 100 samples.

GH      0       14:27:50.024    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 1.13828093
CS      0       14:27:50.024    Oracle_Demo (BTCUSD,D1) Oracle error = 1.13422816

Analyzing both sets of results shows that, in scenarios with low noise levels, this technique demonstrates exceptional efficacy, resulting in a substantial reduction in error variance. Conversely, in high-noise scenarios, the technique not only fails to provide significant improvements but frequently leads to inferior performance compared to utilizing a single model. This phenomenon is observed even when all constituent models possess equivalent predictive power, although the performance differences in such cases are admittedly minor.

The tests also reveal that utilizing four bins instead of two yielded inconsistent and negligible performance differences. This outcome is unsurprising given that either all models exhibit comparable predictive power or one model consistently produces worthless predictions. The primary function of this algorithm, in the present context, is to identify and discard non-informative models when they are present. However, it is conceivable that scenarios exist where a larger number of categories would prove beneficial.

Gated general regression ensembles

This section introduces a broadly applicable technique for model combination that leverages gating variables. The method is inspired by concepts from General Regression Neural Networks (GRNN) and allows one or more variables to serve as dynamic gates, modulating the influence of each contributing model. In contrast to earlier gating methods, which require selecting a single model to produce the final output, general regression gating integrates the outputs of all constituent models by optimally weighting each based on the gate variables. These gating variables may include external measured values as well as the outputs of the individual models. This approach is referred to as the gated general regression method.

Implementation of this method requires at least two trained component models and a separate dataset for training the GRNN-inspired ensemble. The training dataset must contain one or more gate variables, predictions from the component models, and corresponding target values. Notably, it is also possible to designate certain outputs of the component models as gate variables, further enhancing the flexibility of the approach.

A General Regression Neural Network (GRNN) is a type of artificial neural network designed for regression tasks, which involves predicting continuous outputs. GRNN operates based on the principles of kernel density estimation and relies on a memory-based learning approach. It consists of four layers: input, pattern, summation, and output.

The input layer receives the predictor variables, which are passed to the pattern layer, where each neuron represents a training sample and computes the similarity between the input and the training data using a radial basis function. The summation layer aggregates the weighted outputs of the pattern layer, and the output layer produces the final prediction by normalizing the sum of weights.

GRNN is particularly advantageous for modeling non-linear relationships, requiring minimal training time and automatically adapting to the underlying data distribution.

In this context, the weighted Euclidean distance between a test sample and a training sample is determined by the gate variables. Specifically, when evaluating a test sample, the GRNN gate prioritizes training samples whose gate variables closely resemble those of the test sample. By employing the GRNN to predict the squared error of a model, the predicted squared error for a component model is calculated using the equation below.

While there are infinitely many ways to combine component models to produce a joint prediction, the simplest approach involves expressing the final prediction as a linear combination of the models' outputs. If the component models exhibit the desirable property of unbiased predictions, this property is preserved only if the condition that the weights sum to unity is imposed. Even when the predictions are not strictly unbiased, this condition remains advantageous in most scenarios. For a linear combination of unbiased estimators with minimum mean squared error, the optimal weights are proportional to the reciprocal of each estimator’s variance. By substituting the predicted squared error for the variance, the weights can be calculated using the following formula.

To generate a GRNN-gated prediction, given appropriate values for the sigma weights, we start by estimating the prediction error for each model on a given test sample. Subsequently, weights are calculated, and the component models are evaluated on the test sample. Finally, the individual predictions from the component models are combined into a final estimate using the calculated weights.

Determining optimal values for the sigma weights is no easy task, as it requires estimation using the training data. The most effective method for assessing the quality of a candidate sigma vector is through cross-validation. This involves removing a sample from the training set to serve as a test case, generating a GRNN-gated prediction for this sample using the specified sigma vector, and comparing the predicted value to the true value. The sample is then returned to the training set, and the process is repeated for all samples in the dataset. The mean squared error across these repetitions serves as a measure of the quality of the candidate sigma vector.

Any derivative-free optimization algorithm can be utilized to determine the set of sigma weights that minimizes the cross-validation error. Among the available options, differential evolution is recognized for its robustness and broad applicability. However, Powell's method provides a computationally efficient alternative, exhibiting satisfactory performance in the majority of practical applications. Given its efficiency, Powell's method is adopted for this study, despite the occasional superiority of differential evolution in rare cases involving multiple local extrema.

The file, gatedreg.mqh, contains the source code for the CGatedReg class, which implements the GRNN-inspired gated ensemble method just described. The class declaration is presented below.

//+------------------------------------------------------------------+
//|  GRNN gating model combination                                   |
//+------------------------------------------------------------------+
class CGatedReg:public CPowellsMethod
  {
private:
   ulong             m_nsamples;
   ulong             m_ngates;
   ulong             m_nmodels;
   matrix            m_tset;
   vector            m_sigma;
   vector            m_errvals;
   vector            m_params;

   double            criter(vector &params);
   double            trial(vector &gates, vector &contenders,long i_exclude,long n_exclude);
   virtual double    func(vector &p) {  return criter(p); }
public:
                     CGatedReg(void);
                    ~CGatedReg(void);
   bool              fit(matrix &gates, matrix &contenders,vector &targets);
   double            predict(vector &gates, vector &contenders);
  };

Predictions from component models are assumed to have been pre-computed and stored in a matrix. Each model must have undergone prior training to predict the dependent variable. Gate variables (often a single variable) will be employed to differentially weight the contributions of these component models in the final prediction. The fit() method is responsible for copying the necessary training data and determining optimal sigma weights. The method's implementation is provided next.

//+------------------------------------------------------------------+
//| fit a gated grnn model                                           |
//+------------------------------------------------------------------+
bool CGatedReg::fit(matrix &gates,matrix &contenders,vector &targets)
  {
   if(gates.Rows()!=contenders.Rows() || contenders.Rows()!=targets.Size()  || gates.Rows()!=targets.Size())
     {
      Print(__FUNCTION__, " ", __LINE__, " invalid training data ");
      return false;
     }
   m_nsamples = gates.Rows();
   m_ngates = gates.Cols();
   m_nmodels = contenders.Cols();

   m_tset = matrix::Zeros(m_nsamples,m_ngates+m_nmodels+1);
   m_sigma = vector::Zeros(m_ngates);
   m_errvals = vector::Zeros(m_nmodels);

   for(ulong i = 0; i<m_nsamples; i++)
     {
      for(ulong j = 0; j<m_ngates; j++)
         m_tset[i][j] = gates[i][j];
      for(ulong k = 0; k<m_nmodels; k++)
         m_tset[i][m_ngates+k] = contenders[i][k];
      m_tset[i][m_ngates+m_nmodels] = targets[i];
     }

   m_params = vector::Zeros(m_ngates);

   double err =  criter(m_params);
   if(err > 0.0)
      Optimize(m_params);

   criter(m_params);

   return true;

  }

The training data, comprising all inputs to the fit() method, must be preserved as subsequent predictions necessitate the use of general regression for intermediate error prediction of each model. Additionally, the m_errval vector will be required for each prediction. Powell's optimization technique is utilized to identify optimal sigma weights. The objective function to be minimized is defined as the private criter() method.

//+------------------------------------------------------------------+
//|  function criterion                                              |
//+------------------------------------------------------------------+
double CGatedReg::criter(vector &params)
  {
   int i, ngates, nmodels, ncases;
   double  out, diff, error, penalty ;
   vector inputs1,inputs2,row;

   ngates = int(m_ngates); ;
   nmodels = int(m_nmodels) ;
   ncases = int(m_nsamples) ;

   penalty = 0.0 ;
   for(i=0 ; i<ngates ; i++)
     {
      if(params[i] > 8.0)
        {
         m_sigma[i] = exp(8.0) ;
         penalty += 10.0 * (params[i] - 8.0) ;
        }
      else
         if(params[i] < -8.0)
           {
            m_sigma[i] = exp(-8.0) ;
            penalty += 10.0 * (-params[i] - 8.0) ;
           }
         else
            m_sigma[i] = exp(params[i]) ;
     }

   error = 0.0 ;

   for(i=0 ; i<ncases ; i++)
     {
      row = m_tset.Row(i);
      inputs1 = np::sliceVector(row,0,m_ngates);
      inputs2 = np::sliceVector(row,ulong(ngates),ulong(ngates+nmodels));
      out = trial(inputs1, inputs2, long(i), 0) ;
      diff = row[ngates+nmodels] - out ;
      error += diff * diff ;
     }

   return error / double(ncases) + penalty ;

  }

This method employs cross-validation to assess the quality of a trial sigma vector. Instead of directly optimizing each sigma, the logarithm of sigma is optimized. This linearizes the impact of variations, resulting in enhanced stability. To mitigate the problems, associated with the error surface of a GRNN-gate exhibiting flatness for extreme values. The criterion function initially exponentiates the parameter while imposing a bounded range. A penalty term is introduced to encourage sigma values that are not extreme. For each training sample, a prediction is made, and this prediction is compared to the true value. The squared error is accumulated to serve as the error criterion.

The m_errvals elements are initialized to zero, to cumulate the numerator of the error equation. The denominator of this equation does not require explicit computation as it cancels out when considering the normalization factor in the denominator of the weights equation. Before incorporating each term into the sum, the sequential proximity of a test sample to a training sample is verified.

This method can be utilized for prediction based on both training set members and entirely unknown samples. By passing the sequence number i_exclude of each training sample to the trial() routine, cross-validation can be implemented. A distance limit, n_exclude, is also passed. Typically, this is set to zero, excluding only the single case.

Readers, should note that the cross-validation algorithm has a serious limitation when it comes to handling training sets exhibiting serial correlation. Which is common for time series data. This can be addressed by excluding samples that are spatially proximate to the training sample being tested.

//+------------------------------------------------------------------+
//| trial ( )                                                        |
//+------------------------------------------------------------------+
double CGatedReg::trial(vector &gates, vector &contenders, long i_exclude,long n_exclude)
  {
   int icase, ivar, idist, size, ncases;
   double psum, diff, dist, err, out ;

   m_errvals.Fill(0.0);
   int ngates = int(m_ngates);
   int nmodels = int(m_nmodels);
   size = ngates + nmodels + 1 ;
   ncases = int(m_nsamples);

   for(icase=0 ; icase<ncases ; icase++)
     {

      idist = (int)fabs(int(i_exclude) - icase) ;
      if(ncases - idist < idist)
         idist = ncases - idist ;

      if(idist <= int(n_exclude))
         continue ;

      dist = 0.0 ;

      for(ivar=0 ; ivar<ngates ; ivar++)
        {
         diff = gates[ivar] - m_tset[icase][ivar] ;
         diff /= m_sigma[ivar] ;
         dist += diff * diff ;
        }

      dist = exp(-dist) ;

      for(ivar=0 ; ivar<nmodels ; ivar++)
        {
         err = m_tset[icase][ngates+ivar] - m_tset[icase][ngates+nmodels] ;
         m_errvals[ivar] += dist * err * err ;
        }

     }

   psum = 0.0 ;
   for(ivar=0 ; ivar<nmodels ; ivar++)
     {
      if(m_errvals[ivar] > 1.e-30)
         m_errvals[ivar] = 1.0 / m_errvals[ivar] ;
      else
         m_errvals[ivar] = 1.e30 ;
      psum += m_errvals[ivar] ;
     }

   for(ivar=0 ; ivar<nmodels ; ivar++)
      m_errvals[ivar] /= psum ;

   out = 0.0 ;
   for(ivar=0 ; ivar<nmodels ; ivar++)
      out += m_errvals[ivar] * contenders[ivar] ;

   return out ;
  }

If a training case passes the cross-validation exclusion test, the weighted Euclidean distance between the two cases is calculated. This distance is exponentiated for use in computing the prediction error for each component model. Subsequently, for each model, the prediction error is determined. The final step involves utilizing model weights equation to combine the outputs of each contender model into a single prediction. This constitutes the function's return value.

//+------------------------------------------------------------------+
//|  infer                                                           |
//+------------------------------------------------------------------+
double CGatedReg::predict(vector &gates,vector &contenders)
  {
   return trial(gates,contenders,-1,0);
  }

Testing a gated GRNN ensemble

The Gating_Demo.mqh script offers a comprehensive comparison of four distinct gating strategies. Each strategy serves a unique purpose in demonstrating different aspects of model selection and combination. Here is a brief overview of the four strategies:

• Component Predictions as Gating variables: This approach directly utilizes the predictions of the individual component models as gating variables, allowing for a direct comparison with the baseline method (COracle class). It tests the effect of using the models' own outputs as decision-making factors in model selection.

• Original Variable Gating: In this strategy, the original input variables (those used by the component models) serve as the gating variables. Given that these variables are not designed to act as effective gating signals, this approach helps demonstrate the impact of poor or irrelevant gating variables on model performance.

• Random Gating: This strategy employs randomly generated numbers as gating variables, simulating a scenario where no informative gating variables are available. It serves as a baseline to show the performance drop when using completely non-informative signals.

• Ratio-Based Gating: In this approach, the logarithm of the ratio between the prediction errors of the first and second models is used as the gating variable. While this method would be unrealistic in a real-world setting (as the true prediction error of the models is generally unknown), it serves as an idealized scenario for two models. For multiple models, it provides partial but still valuable gating information.

These four strategies are designed to test various performance conditions and offer insights into the strengths and limitations of different gating techniques for ensemble learning. The script evaluates how each gating strategy impacts the overall prediction accuracy and error variance, enabling a clearer understanding of the effectiveness of the GRNN gating mechanism.

Three models, 100 samples and low prediction difficulty.

EK      0       14:36:33.869    Gating_Demo (BTCUSD,D1)  1000    replications completed.
GL      0       14:36:33.869    Gating_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.10790466
JP      0       14:36:33.869    Gating_Demo (BTCUSD,D1) Component error = 0.10790458
DF      0       14:36:33.869    Gating_Demo (BTCUSD,D1) Original error = 0.10790458
HM      0       14:36:33.869    Gating_Demo (BTCUSD,D1) Random error = 0.10790458
DJ      0       14:36:33.869    Gating_Demo (BTCUSD,D1) Ratio error = 0.10790458

Three models, 100 samples and high prediction difficulty.

GF      0       14:40:57.600    Gating_Demo (BTCUSD,D1)  1000    replications completed.
LQ      0       14:40:57.600    Gating_Demo (BTCUSD,D1)  ++++++ Mean raw error = 1.12143040
FE      0       14:40:57.600    Gating_Demo (BTCUSD,D1) Component error = 1.11991444
GQ      0       14:40:57.600    Gating_Demo (BTCUSD,D1) Original error = 1.11991445
QI      0       14:40:57.600    Gating_Demo (BTCUSD,D1) Random error = 1.11991443
EO      0       14:40:57.600    Gating_Demo (BTCUSD,D1) Ratio error = 1.11991443

Four models, 100 samples and low prediction difficulty.

IO      0       14:42:58.751    Gating_Demo (BTCUSD,D1)  1000    replications completed.
LK      0       14:42:58.751    Gating_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.12792841
RS      0       14:42:58.751    Gating_Demo (BTCUSD,D1) Component error = 0.11516554
MK      0       14:42:58.751    Gating_Demo (BTCUSD,D1) Original error = 0.11516373
GR      0       14:42:58.751    Gating_Demo (BTCUSD,D1) Random error = 0.11516595
GE      0       14:42:58.751    Gating_Demo (BTCUSD,D1) Ratio error = 0.11516595

Four models, 100 samples and high prediction difficulty.

QQ      0       14:45:15.030    Gating_Demo (BTCUSD,D1)  1000    replications completed.
HE      0       14:45:15.030    Gating_Demo (BTCUSD,D1)  ++++++ Mean raw error = 1.14025014
EI      0       14:45:15.030    Gating_Demo (BTCUSD,D1) Component error = 1.13144872
GM      0       14:45:15.030    Gating_Demo (BTCUSD,D1) Original error = 1.13144863
QD      0       14:45:15.030    Gating_Demo (BTCUSD,D1) Random error = 1.13144883
NL      0       14:45:15.030    Gating_Demo (BTCUSD,D1) Ratio error = 1.13144882

The surprising performance improvement achieved through random gating can be attributed to the way the GRNN gating algorithm works. In typical scenarios, one would expect random gating signals to worsen the model's performance because they introduce noise and do not provide useful information for model selection. However, the GRNN mechanism relies on weighted Euclidean distances between training samples and adjusts its prediction based on how closely the test sample resembles training samples.

In cases where the gating signal is random, the GRNN algorithm still uses the general structure of the data and models to compute a weighted average of the component model predictions. Since the random gating values introduce no strong bias toward any particular model, the algorithm may rely more heavily on the inherent structure of the data and the performance of the individual models, which are trained to predict well. The overall result can be a more robust combination of models, with the random gating actually acting as a neutralizer, ensuring that no single model dominates the decision-making process.

In the case where three models exhibit high predictive accuracy and one model generates random predictions, the random gating approach could inadvertently act as a method of discarding the random model by reducing its influence in the ensemble. This leads to a situation where the performance of the ensemble model improves significantly, as the influence of the non-informative random model is minimized.

Thus, while random gating might not seem intuitively beneficial, the GRNN gating process may exploit the structure of the dataset and models in ways that result in unexpected improvements, especially in "easy" prediction problems where the models are already highly accurate. This behavior underscores the power of the GRNN gating technique, which, even in suboptimal situations, can harness the potential of multiple models to deliver improved predictions by effectively weighing the contribution of each model.

The algorithm effectively estimates the prediction error of each model. In the presence of a model with consistently high prediction errors, as in the case of the random prediction model, the prediction error will consistently generate large error estimates for that model. Which then results in the ensemble's weighting scheme assigning a correspondingly low weight to this model within the weighted combination.

This observation underscores the key advantage of GRNN gating. It can effectively identify and down weight models with poor predictive performance, even when the gating variables themselves lack inherent predictive power. Consequently, even in situations where the gating signals provide limited or no relevant information, GRNN gating can still yield significant performance improvements, particularly when the ensemble includes models with varying levels of predictive accuracy.

Conclusion

These techniques showcase the adaptability of gating mechanisms in enhancing the interpretability and predictive power of learning algorithms. The choice of technique depends on the specific context, including the complexity of the task, the nature of the data, and computational constraints. Often, a combination of methods, such as optimization techniques paired with domain insights, yields the most effective and interpretable results. All code referenced in the article is attached at the end. The table below describes all the accompanying source files.

File Name	Description
MQL5/include/gatedreg.mqh	Contains definition of CGatedReg class that implements a gated GRNN ensemble
MQL5/include/imodel.mqh	Contains the definition of interfaces that encapsulate a trained model
MQL5/include/minimize.mqh	Provides the definition of the CPowellsMethod which implements function minimization using Powell's method
MQL5/include/multilayerperceptron.mqh	Provides the definition of a CMlp class which is an implementation of a multilayer perceptron
MQL5/include/np.mqh	A collection of generic helper functions for manipulating vectors and matrices
MQL5/include/oracle.mqh	Provides the definition of the COracle class with enables model selection from a set of specialist component models
MQL5/include/qsort.mqh	Provides simple functions for sorting vectors
Mql5/scripts/Gating_Demo.mq5	A script demonstrating the functionality provided by CGatedReg class
Mql5/scripts/Oracle_Demo.mq5	Another script demonstrating the use of the COracle class