重构经典策略(第九部分):多时间框架分析(第二部分)
交易者可以使用许多不同的时间框架。对于社区的新成员,或者任何正在学习如何操作的交易者而言,做出选择可能会很困难。即使是经验丰富的交易者也经常争论并分享不同的观点,试图确定哪个时间框架是最优的。我们将尝试通过将最优时间框架定义为最小化我们人工智能(AI)模型误差水平的时间框架,来客观地回答这个问题。
在今天的探讨中,我们将关注模型残差在11个时间框架上的分布,我们观察到月度和小时时间框架上有两个低误差区域。然而,模型误差水平的分布并没有明显的模式,它似乎在小时框架上达到最大值和最小值。在能够明确回答古老的问题“哪个时间框架最好用?”之前,我们必须有理由确定,如果改变市场,残差的分布却不会改变。此外,未来我们应该考虑对所有可用的时间框架进行全面搜索。
交易方法概述
尽管不同时间框架上由价格K线形成的模式可能看起来截然不同,但在任何时刻,每个时间框架上只有一个价格。交易者通常同时分析不同的时间框架,以了解市场的当前状态。如果趋势逐渐减弱,我们很可能会在比我们用于开仓的时间框架更短的时间周期内,看到相互矛盾的价格走势出现。此外,这些疲软的迹象总是首先在较低的时间框架上可见,然后才在较高时间框架上变得明显。
一般来说,大多数包含多时间框架分析的策略都试图基于较高时间框架了解市场情绪。一些成功的交易者会在较高时间框架上寻找著名的价格走势模式,例如看涨吞噬蜡烛图模式。传统上,这些蜡烛图模式的存在或缺失为寻找高概率设置的交易者提供了信号。我们希望算法化地学习在预测欧元兑美元货币对时,哪个时间框架能为我们提供可靠的误差水平。
在某种程度上,我们普遍都认同这样的直观感受:您试图预测的时间越远,任务就越困难。我们今天分析的结果在根本上挑战了这一信念。在您能够理解我为什么这么说,或者这些结论是否合理之前,我们首先必须探讨所采用的方法。
方法论概述
为了使测试公平,我们必须从每个时间框架中获取相同数量的数据。在这一步中的限制因素是月度时间框架上可用的柱形图数量。仅仅400根月度数据条就涵盖了大约33年的时间。仅有少数几个市场有这么久的历史数据,这可能会使我们对所有可能市场中最优时间框架的理解产生偏差。然而,在我们探讨的范围内,欧元兑美元货币对拥有丰富的数据集,我们可以依赖这些数据。
我们从MetaTrader 5终端获取了400行月度价格报价。然后,我们又获取了400行对应的欧元兑美元货币对的未来价值数据。这两步过程在剩余的10个时间框架上重复进行。对于本次分析,我选择了:
- Weekly
- Daily
- H12
- H8
- H4
- H1
- M30
- M15
- M5
- M1
必须承认,我期望观察到强烈的相关性水平,特别是那些周期性接近的时间框架之间。然而,样本中共享的相关性水平只有中等程度。唯一可能值得进一步分析的有趣的相关性组合是:
- 当前H4价格和未来H8价格
- 当前M1价格和未来H4价格
- 当前M1价格和未来H5价格
回想一下,我们的输入数据有22列,自然我们得到的相关性矩阵很大,不会在我们的探讨中完全展示出来。到目前为止从我们的数据中,能够创建11组输入进行测试。在对数据进行建模后,我们观察到模型在月度和小时时间框架上表现最佳。此结果与直观感受大相径庭。我们的目标是预测未来20个时间步长的趋势。20个月的未来是一个1年8个月的周期。与预测20分钟内的价格变化相比,我们的模型可以更准确地预测一年内的价格变化。
由于对两个低误差的时间框架感兴趣,我们将价格数据转换为周期性收益率,并随后对收益率进行了格兰杰因果关系(Granger causality)测试。我们观察到显著的p值,表明小时收益率对月度收益率存在格兰杰因果关系。改测试证明我们可以使用向量自回归(VAR)模型,使用小时收益率来模拟月度收益率。
我们使用时间序列变形库来对齐并找到月度和小时数据之间的相似性。我们的算法能够找到数据之间的许多相似点。这带给我们对选择过程的信心,我们继续成功地调整了月度模型的参数,并将模型导出为ONNX格式。
最后,我实现了一个EA,它能够基于月度时间框架预测预期的价格水平,然后在小时时间框架上执行交易。该系统可以在基于预测的AI反转平仓,或使用移动平均线之间进行切换。我们使用技术分析来确定入场时间。
获取我们需要的数据
让我们首先导入MetaTrader 5库以及所需的其他几个库。
#Import the libraries we need import pandas as pd import numpy as np import seaborn as sns import MetaTrader5 as mt5 from sklearn.model_selection import cross_val_score,train_test_split,TimeSeriesSplit from sklearn.metrics import mean_squared_error import matplotlib.pyplot as plt from sklearn.linear_model import LinearRegression
现在测试我们是否能够连接到MetaTrader 5终端。
#Initialize the terminal
mt5.initialize()让我们定义想要测试的时间框架。
#Declare the time-frames we are interested in
time_frames = [mt5.TIMEFRAME_MN1,
mt5.TIMEFRAME_W1,
mt5.TIMEFRAME_D1,
mt5.TIMEFRAME_H12,
mt5.TIMEFRAME_H8,
mt5.TIMEFRAME_H4,
mt5.TIMEFRAME_H1,
mt5.TIMEFRAME_M30,
mt5.TIMEFRAME_M15,
mt5.TIMEFRAME_M5,
mt5.TIMEFRAME_M1
]我们应该获取多少根K线?
#How many bars should we fetch fetch = 400
让我们来预测未来20步。
#How far into the future should we forecast? look_ahead = 20
定义我们数据结构的列。
#Create our dataframe inputs = ["MN","W","D","H12","H8","H4","H1","M30","M15","M5","M1"] target = [] for i in np.arange(0,len(inputs)): target.append(inputs[i] + " Target")
创建包含我们价格的数据结构。
columns = inputs + target
prices = pd.DataFrame(columns=columns,index=np.arange(0,fetch))
图1:我们数据结构中的一些输入
图2:我们数据结构的部分目标
我们需要一个数据结构来存储我们的误差水平。
#The columns for our error levels data frame. error_columns = [] for i in np.arange(0,len(inputs)): error_columns.append(inputs[i]) #Create a dataframe to store our error levels error_levels = pd.DataFrame(columns=error_columns,index=[0]) test_error_levels = pd.DataFrame(columns=error_columns,index=[0])
获取我们需要的价格数据。
for i in np.arange(0,len(time_frames)): print(i) prices.iloc[:,i] = pd.DataFrame(mt5.copy_rates_from_pos("EURUSD",time_frames[i],look_ahead,fetch)).loc[:,"close"] prices.iloc[:,i+10] = pd.DataFrame(mt5.copy_rates_from_pos("EURUSD",time_frames[i],0,fetch)).loc[:,"close"]
探索性数据分析
让我们分析数据结构中的相关性水平。注意H12和H8时间框架之间的强相关性。还有哪些相关性水平引起了您的注意?
fig, ax = plt.subplots(figsize=(15,15)) sns.heatmap(prices.corr(),annot=True,ax=ax)
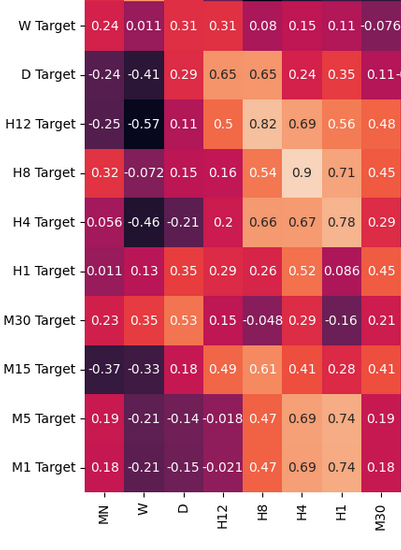
图3:我们获得的相关性矩阵中的一些值
月度收盘价和周度收盘价的散点图趋势并不明确。在大多数情况下,数据似乎呈现出一种总体上升趋势。
sns.scatterplot(data=prices,x="MN Close",y="W Close")
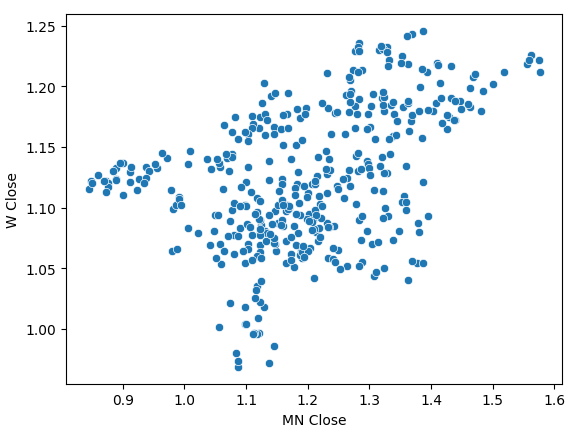
图4:月收盘价和周收盘价的散点图
我们将价格数据转换为周期性收益率,并再次绘制了散点图。这次出现了一种总体趋势,似乎我们的收益率围绕0浮动。
sns.scatterplot(data=prices.pct_change(),x="MN Close",y="W Close")
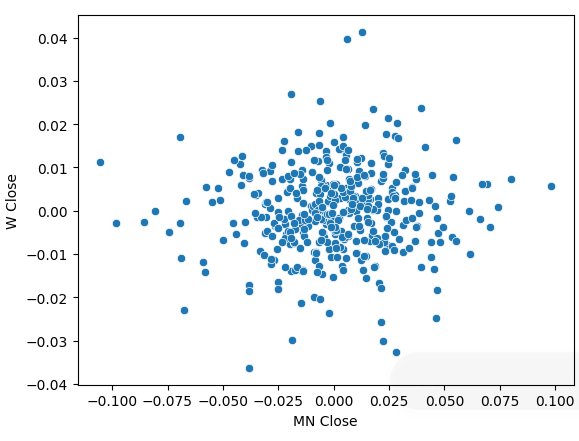
图5:不同时间框架下的收益率散点图
当我们对不同时间框架下的收益率绘制箱线图时,我们可以观察到另一种趋势。随着从月度时间框架向较低的时间框架移动,我们收益率的方差在减小。同样,所有时间框架下的平均收益率接近于0。这也告诉我们,如果试图最大化投资组合的收益率,我们应该考虑更高时间框架。
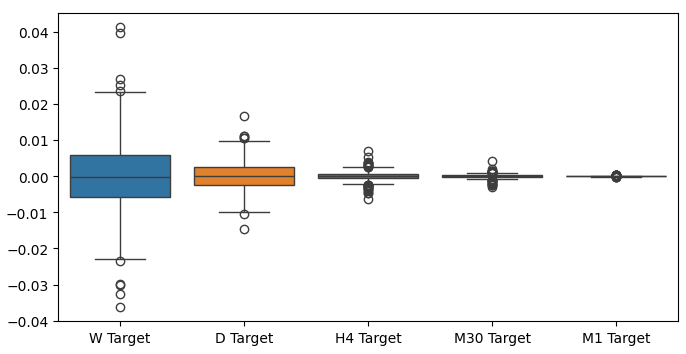
图6:不同时间框架下的收益率箱线图
准备建模数据
现在让我们开始为建模数据做准备。首先,我们需要对数据进行训练集-测试集的划分。
#Create train test splits X_train_mn,X_test_mn,y_train_mn,y_test_mn = train_test_split(prices.loc[:,["MN"]],prices.loc[:,"MN Target"],test_size=0.5,shuffle=False) X_train_w,X_test_w,y_train_w,y_test_w = train_test_split(prices.loc[:,["W"]],prices.loc[:,"W Target"],test_size=0.5,shuffle=False) X_train_d,X_test_d,y_train_d,y_test_d = train_test_split(prices.loc[:,["D"]],prices.loc[:,"D Target"],test_size=0.5,shuffle=False) X_train_h12,X_test_h12,y_train_h12,y_test_h12 = train_test_split(prices.loc[:,["H12"]],prices.loc[:,"H12 Target"],test_size=0.5,shuffle=False) X_train_h8,X_test_h8,y_train_h8,y_test_h8 = train_test_split(prices.loc[:,["H8"]],prices.loc[:,"H8 Target"],test_size=0.5,shuffle=False) X_train_h4,X_test_h4,y_train_h4,y_test_h4 = train_test_split(prices.loc[:,["H4"]],prices.loc[:,"H4 Target"],test_size=0.5,shuffle=False) X_train_h1,X_test_h1,y_train_h1,y_test_h1 = train_test_split(prices.loc[:,["H1"]],prices.loc[:,"H1 Target"],test_size=0.5,shuffle=False) X_train_m30,X_test_m30,y_train_m30,y_test_m30 = train_test_split(prices.loc[:,["M30"]],prices.loc[:,"M30 Target"],test_size=0.5,shuffle=False) X_train_m15,X_test_m15,y_train_m15,y_test_m15 = train_test_split(prices.loc[:,["M15"]],prices.loc[:,"M15 Target"],test_size=0.5,shuffle=False) X_train_m5,X_test_m5,y_train_m5,y_test_m5 = train_test_split(prices.loc[:,["M5"]],prices.loc[:,"M5 Target"],test_size=0.5,shuffle=False) X_train_m1,X_test_m1,y_train_m1,y_test_m1 = train_test_split(prices.loc[:,["M1"]],prices.loc[:,"M1 Target"],test_size=0.5,shuffle=False)
现在将这些划分结果存储到列表中。
train_X = [ X_train_mn, X_train_w, X_train_d, X_train_h12, X_train_h8, X_train_h4, X_train_h1, X_train_m30, X_train_m15, X_train_m5, X_train_m1 ] test_X = [ X_test_mn, X_test_w, X_test_d, X_test_h12, X_test_h8, X_test_h4, X_test_h1, X_test_m30, X_test_m15, X_test_m5, X_test_m1 ]
对目标值重复上述过程。
train_y = [ y_train_mn, y_train_w, y_train_d, y_train_h12, y_train_h8, y_train_h4, y_train_h1, y_train_m30, y_train_m15, y_train_m5, y_train_m1, ] test_y = [ y_test_mn, y_test_w, y_test_d, y_test_h12, y_test_h8, y_test_h4, y_test_h1, y_test_m30, y_test_m15, y_test_m5, y_test_m1, ]
交叉验证每个模型。
#Record our error for i in np.arange(0,len(train_X)): #Fit the model model = LinearRegression() cv_score = cross_val_score(model,train_X[i],train_y[i],cv=5) error_levels.iloc[0,i] = np.mean(cv_score * -1) #Record validation error model.fit(train_X[i],train_y[i]) test_error_levels.iloc[0,i] = mean_squared_error(test_y[i],model.predict(test_X[i]))
我们各自的误差水平。
error_levels
| MN | W | D | H12 | H8 | H4 | H1 | M30 | M15 | M5 | M1 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.719131 | 3.979435 | 3.897228 | 5.023601 | 5.218168 | 40.406227 | 0.196244 | 18.264356 | 3.680168 | 20.331821 | 3.540946 |
让我们可视化模型残差分布的近似情况。
fig, ax = plt.subplots(figsize=(7,4)) sns.barplot(error_levels,ax=ax)
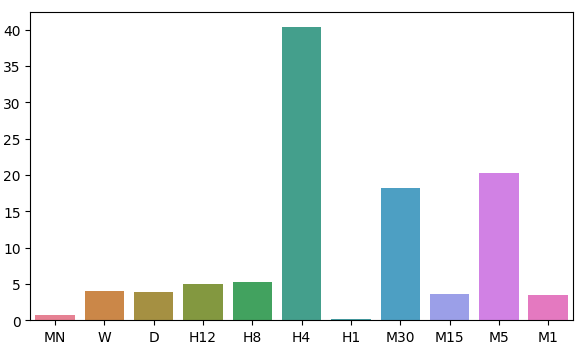
图7:可视化我们模型的误差水平
特征的重要性
既然已经确定了最优时间框架,让我们尝试检测这两个时间框架之间是否存在某种因果关系。1969年,克莱夫·格兰杰(Sir Clive Granger)爵士提出了一种检验方法,用于实证确定两个时间序列数据是否相互影响,即使在一个时间序列的过去值会影响另一个时间序列的未来值的情况下也是如此。简单来说,如果我们能将一个时间序列的值滞后,并利用它来预测第二个时间序列的未来值,且预测结果的方差没有显著下降,那么该时间序列就通过了格兰杰检验。
自提出以来,格兰杰检验经历了许多变化和改进。在现代,它已被广泛应用于从神经科学到金融等各个行业。半个多世纪以来,该检验方法在学术界一直备受争议。问题的核心在于格兰杰检验隐含地假设了线性关系。因此,如果存在真正的非线性因果关系,格兰杰检验会否定其存在。此外,在实际应用中,该检验通常仅限于二元变量问题。也就是说,我们很少在包含两个以上时间序列数据集的大型问题上使用格兰杰检验。

图8:已故的英国经济学家克莱夫·格兰杰爵士
要开始进行格兰杰因果检验,我们首先导入statsmodels库,然后运行检验。该检验是在H1收盘价的滞后版本上进行的。如果我们获得的p值小于0.05,则检验通过,而我们在第一个滞后阶上确实得到了这样的结果。所有后续滞后阶的检验均未通过,因此我们可以拒绝在第一个滞后阶之外存在任何因果关系的假设。
from statsmodels.tsa.stattools import grangercausalitytests result = grangercausalitytests(prices[['H1 Close','MN Close']].pct_change().dropna(), maxlag=4)
滞后次数(不为零)1
基于ssr的F检验:F=4.4913 , p=0.0347 , df_denom=395, df_num=1
基于ssr的chi2检验:chi2=4.5254 , p=0.0334 , df=1
似然比检验:chi2=4.4999 , p=0.0339 , df=1
参数F检验:F=4.4913 , p=0.0347 , df_denom=395, df_num=1
格兰杰因果关系
滞后次数(不为零)2
基于ssr的F检验:F=2.2706 , p=0.1046 , df_denom=392, df_num=2
基于ssr的chi2检验:chi2=4.5991 , p=0.1003 , df=2
似然比检验:chi2=4.5727 , p=0.1016 , df=2
参数F检验:F=2.2706 , p=0.1046 , df_denom=392, df_num=2
格兰杰因果关系通常只在一个方向上成立。让我们通过检查相反方向的因果关系来验证这一点。我们获得的p值均不显著,这让我们确信因果关系确实如预期的那样,是单向的。
result = grangercausalitytests(prices[['MN Close','H1 Close']].pct_change().dropna(), maxlag=4)
格兰杰因果关系
滞后次数(不为零)1
基于ssr的F检验:F=0.0188 , p=0.8909 , df_denom=395, df_num=1
基于ssr的chi2检验:chi2=0.0190 , p=0.8905 , df=1
似然比检验:chi2=0.0190 , p=0.8905 , df=1
参数F检验:F=0.0188 , p=0.8909 , df_denom=395, df_num=1
格兰杰因果关系
滞后次数(不为零)2
基于ssr的F检验:F=2.2182 , p=0.1102 , df_denom=392, df_num=2
基于ssr的chi2检验:chi2=4.4930 , p=0.1058 , df=2
似然比检验:chi2=4.4678 , p=0.1071 , df=2
参数F检验: F=2.2182 , p=0.1102 , df_denom=392, df_num=2
格兰杰因果关系
滞后次数(不为零)3
基于ssr的F检验:F=1.7310 , p=0.1601 , df_denom=389, df_num=3
基于ssr的chi2检验:chi2=5.2863 , p=0.1520 , df=3
似然比检验:chi2=5.2513 , p=0.1543 , df=3
参数F检验:F=1.7310 , p=0.1601 , df_denom=389, df_num=3
格兰杰因果关系
滞后次数(不为零)4
基于ssr的F检验:F=1.4694 , p=0.2108 , df_denom=386, df_num=4
基于ssr的chi2检验:chi2=6.0148 , p=0.1980 , df=4
似然比检验:chi2=5.9694 , p=0.2014 , df=4
参数F检验:F=1.4694 , p=0.2108 , df_denom=386, df_num=4
动态时间规整(Dynamic Time Warping,DTW)也允许我们在两个时间序列数据集之间寻找相似性。该算法还可用于对齐不同长度的序列。我们利用该算法来寻找我们数据中的月收益率和小时收益率之间的相似点。该算法通过最小化一个专门设计的成本函数来完成这一任务,该成本函数用于衡量两个序列之间的差异。我们将从导入所需的库开始。
#Let's calculate the simillarities between our time series data from dtaidistance import dtw from dtaidistance import dtw_visualisation as dtwvis
现在,让我们来找出收益率之间的相似性。
series_1 = prices["MN Close"].pct_change(periods=1).dropna().reset_index(drop=True) * 100 series_2 = prices["H1 Close"].pct_change(periods=1).dropna().reset_index(drop=True) * 100 path = dtw.warping_path(series_1, series_2) dtwvis.plot_warping(series_1, series_2, path)
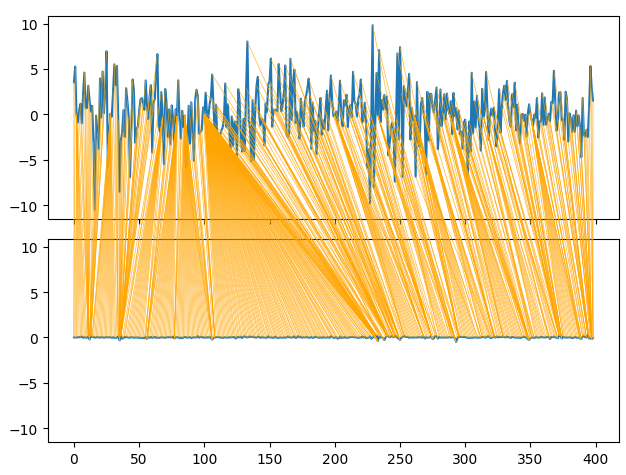
图9:可视化月收益率与小时收益率之间的相似性
参数调整
现在,让我们调整深度神经网络(Deep Neural Network,DNN)的参数,以超越线性回归模型设定的基准性能。需要注意的是,由于使用训练DNN优化过程的基本特性,本文这一部分所获得的结果可能难以复现。事实上,我运行了5次这样的测试,其中有2次未能超越线性模型的表现。
导入我们需要的库,并初始化模型。
#Let's try to outperform our linear regression model from sklearn.neural_network import MLPRegressor from sklearn.model_selection import RandomizedSearchCV #Let's tune our model model = MLPRegressor(max_iter=500)
定义参数空间。
#Tuner
tuner = RandomizedSearchCV(
model,
{
"activation" : ["relu","logistic","tanh","identity"],
"solver":["adam","sgd","lbfgs"],
"alpha":[0.1,0.01,0.001,0.0001,0.00001,0.00001,0.0000001,0.000000001,0.000000000000001],
"tol":[0.1,0.01,0.001,0.0001,0.00001,0.000001,0.0000001,0.000000001,0.000000000000001],
"learning_rate":['constant','adaptive','invscaling'],
"learning_rate_init":[1,0.1,0.0001,0.000001,100,10000,1000000,1000000000,100,1000],
"shuffle": [True,False],
"hidden_layer_sizes":[(1,4),(1,4,5),(1,8,10),(2,5),(8),(10,12),(5,10,4)]
},
n_iter=100,
cv=5,
n_jobs=-1,
scoring="neg_mean_squared_error"
)安装调整器。
tuner.fit(X_train_mn,y_train_mn)
我们找到的最优参数。
tuner.best_params_
'solver': 'lbfgs',
'shuffle': True,
'learning_rate_init': 1,
'learning_rate': 'adaptive',
'hidden_layer_sizes': (2, 5),
'alpha': 1e-05,
'activation': 'identity'}
深度优化
让我们使用SciPy库对最优参数进行更深入的搜索。
#Deeper optimization
from scipy.optimize import minimize创建数据结构以记录我们的进展。
#Create a dataframe to store our accuracy current_error_rate = pd.DataFrame(index = np.arange(0,5),columns=["Current Error"]) optimization_progress = []
定义要最小化的目标函数。我们希望最小化模型的均方根误差。
#Define the objective function def objective(x): #The parameter x represents a new value for our neural network's settings #In order to find optimal settings, we will perform 10 fold cross validation using the new setting #And return the average RMSE from all 10 tests #We will first turn the model's Alpha parameter, which controls the amount of L2 regularization model = MLPRegressor(hidden_layer_sizes=tuner.best_params_["hidden_layer_sizes"], activation=tuner.best_params_["activation"], learning_rate=tuner.best_params_["learning_rate"], solver=tuner.best_params_["solver"], shuffle=tuner.best_params_["shuffle"], alpha=x[0], tol=x[1], learning_rate_init=x[2]) #Now we will cross validate the model for i,(train,test) in enumerate(tscv.split(X_train_mn)): #Train the model model.fit(X_train_mn.loc[train[0]:train[-1],:],y_train_mn.loc[train[0]:train[-1]]) #Measure the RMSE current_error_rate.iloc[i,0] = mean_squared_error(y_train_mn.loc[test[0]:test[-1]],model.predict(X_train_mn.loc[test[0]:test[-1],:])) #Record the progress made by the optimizer optimization_progress.append(current_error_rate.iloc[:,0].mean()) #Return the Mean CV RMSE return(current_error_rate.iloc[:,0].mean())
指定优化过程的起始点,并指定较大的范围,以便我们可以近似实现全局优化。
#Define the starting point pt = [tuner.best_params_["alpha"],tuner.best_params_["tol"],tuner.best_params_["learning_rate_init"]] bnds = ((0.000000001,10000000000),(0.0000000001,10000000000),(0.000000001,10000000000))
优化我们的DNN模型。
#Searchin deeper for parameters result = minimize(objective,pt,method="TNC",bounds=bnds)
看起来我们成功地完成了优化。
结果
成功状态:True
状态:2
fun: 0.04257403904271943
x: [ 4.864e-05 1.122e-03 9.999e-01]
nit: 1
jac: [ 1.298e+04 1.806e+02 -3.371e+03]
nfev: 92
存储我们的优化值。
optima_y = result.fun
optima_x = optimization_progress.index(optima_y)
inputs = np.arange(0,len(optimization_progress))可视化优化过程所取得的进展。
plt.scatter(inputs,optimization_progress) plt.plot(optima_x,optima_y,'s',color='r') plt.axvline(x=optima_x,ls='--',color='red') plt.axhline(y=optima_y,ls='--',color='red') plt.title("Minimizing Training MSE")
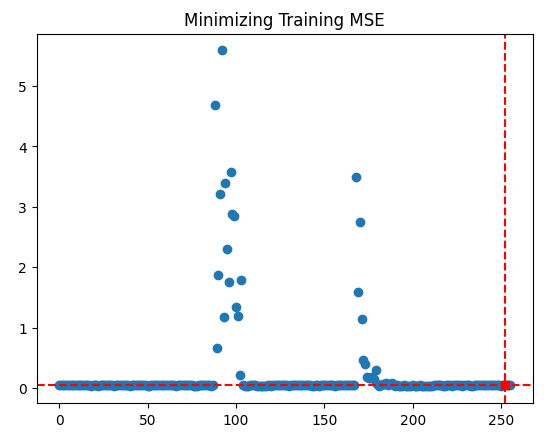
图10:我们TNC优化过程的结果
检测过拟合
让我们看一下是否真的能够超越默认线性模型。
#Test for overfitting benchmark = LinearRegression() default_model = MLPRegressor(max_iter=200) random_search_model = MLPRegressor(hidden_layer_sizes=tuner.best_params_["hidden_layer_sizes"], activation=tuner.best_params_["activation"], learning_rate=tuner.best_params_["learning_rate"], solver=tuner.best_params_["solver"], shuffle=tuner.best_params_["shuffle"], alpha=tuner.best_params_["alpha"], tol=tuner.best_params_["tol"], learning_rate_init=tuner.best_params_["learning_rate_init"], max_iter=200 ) lbfgs_model = MLPRegressor(hidden_layer_sizes=tuner.best_params_["hidden_layer_sizes"], activation=tuner.best_params_["activation"], learning_rate=tuner.best_params_["learning_rate"], solver=tuner.best_params_["solver"], shuffle=tuner.best_params_["shuffle"], alpha=result.x[0], tol=result.x[1], learning_rate_init=result.x[2], max_iter=200 )
在训练集上拟合模型。
#Fit the models
benchmark.fit(X_train_mn,y_train_mn)
default_model.fit(X_train_mn,y_train_mn)
random_search_model.fit(X_train_mn,y_train_mn)
lbfgs_model.fit(X_train_mn,y_train_mn)做好记录交叉验证分数的准备。
#Record our cross val scores
models = [benchmark,
default_model,
random_search_model,
lbfgs_model
]
val_error = pd.DataFrame(columns=["Linear Reg","Default NN","Random Search NN","TNC NN"],index=[0])交叉验证每个模型。
for i in np.arange(0,len(models)): val_error.iloc[0,i] = np.mean(cross_val_score(models[i],X_test_mn,y_test_mn,cv=5,n_jobs=-1)) * -1
我们的验证误差清楚地表明,经过TNC优化的神经网络表现最优。
val_error
| Linear Reg | 默认NN | 随机搜索NN | TNC NN |
|---|---|---|---|
| 3.323741 | 3.987083 | 3.314776 | 3.283775 |
导出为ONNX格式
现在让我们准备将模型导出为ONNX格式。ONNX代表开放神经网络交换,它是一个开源协议,用于将任何机器学习模型表示为一个由节点组成的树形结构,这些节点代表计算过程以及每次计算后的数据流。ONNX允许我们在不同的编程语言中构建和使用机器学习模型,只要这些语言实现了ONNX规范。
在开始之前,导入ONNX库。
#Preparing to export to ONNX import onnx from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType
准备模型。
#Fit the model on all the data we have model = MLPRegressor( solver= 'lbfgs', shuffle= True, activation= 'identity', learning_rate= 'adaptive', hidden_layer_sizes= (2, 5), alpha= 4.864e-05, tol= 1.122e-03, learning_rate_init= 9.999e-01, )
基于我们现有的全部数据拟合模型。
model.fit(prices[["MN Close"]],prices.loc[:,"MN Target"])
定义模型的输入形状。
#Define the input types for our ONNX model initial_types = [("float_input",FloatTensorType([1,1]))]
创建模型的ONNX表示形式。
# Create the ONNX representation onnx_model = convert_sklearn(model,initial_types=initial_types,target_opset=12)
将模型导出为ONNX格式。
# Save the ONNX model onnx.save_model(onnx_model,"EURUSD MN1 AI.onnx")
现在让我们可视化模型的ONNX格式,以确保我们的输入大小是正确的。
import netron
netron.start("EURUSD MN1 AI.onnx")
图11:可视化我们的DNN模型
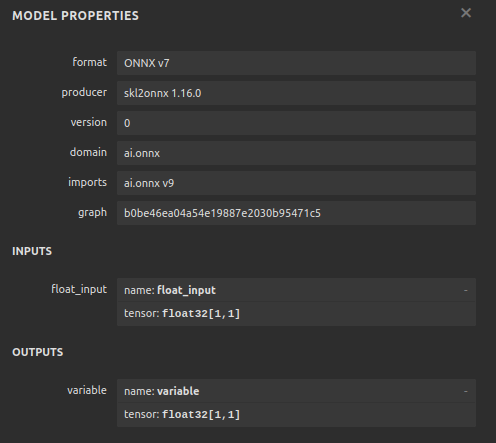
图12:我们模型的输入/输出形状
在MQL5中实现
现在我们希望在MQL5中实现交易算法。我们希望交易算法能够在使用简单移动平均线(SMA)平仓和使用AI预测之间进行切换。此外,我们还希望使用技术分析来指导我们的AI模型。开始之前,我们首先将导入上面导出的ONNX模型。
//+------------------------------------------------------------------+ //| EURUSD MTF AI.mq5 | //| Gamuchirai Zororo Ndawana | //| https://www.mql5.com/en/gamuchiraindawa | //+------------------------------------------------------------------+ #property copyright "Gamuchirai Zororo Ndawana" #property link "https://www.mql5.com/en/gamuchiraindawa" #property version "1.00" //+------------------------------------------------------------------+ //| Load the ONNX resources | //+------------------------------------------------------------------+ #resource "\\Files\\EURUSD MN1 AI.onnx" as const uchar onnx_buffer[];
现在将定义我们自定义的枚举器,以指定用户希望如何平仓。
//+-------------------------------------------------------------------+ //| Define our custom type | //+-------------------------------------------------------------------+ enum close_type { MA_CLOSE = 0, // Moving Averages Close AI_CLOSE = 1 // AI Auto Close };
让我们创建输入,以便我们可以改变应用程序的平仓方式,对比哪一种更好。
//+------------------------------------------------------------------+ //| User inputs | //+------------------------------------------------------------------+ input close_type user_close_type = AI_CLOSE; // How should we close our positions?
我们需要导入交易类。
//+------------------------------------------------------------------+ //| Libraries we need | //+------------------------------------------------------------------+ #include <Trade\Trade.mqh> CTrade Trade;
创建我们在整个程序中需要用到的全局变量。
//+------------------------------------------------------------------+ //| Global variables | //+------------------------------------------------------------------+ long onnx_model; vectorf model_input = vectorf::Zeros(1); vectorf model_output = vectorf::Zeros(1); double bid,ask; int ma_hanlder; double ma_buffer[]; int bb_hanlder; double bb_mid_buffer[]; double bb_high_buffer[]; double bb_low_buffer[]; int rsi_hanlder; double rsi_buffer[]; int system_state = 0,model_state=0;
当应用程序正在加载时,我们首先将从之前创建的缓冲区中创建ONNX模型。然后我们将分配技术指标处理器。
//+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- Load our ONNX function if(!load_onnx_model()) { return(INIT_FAILED); } //--- Load our technical indicators bb_hanlder = iBands("EURUSD",PERIOD_D1,30,0,1,PRICE_CLOSE); rsi_hanlder = iRSI("EURUSD",PERIOD_D1,14,PRICE_CLOSE); ma_hanlder = iMA("EURUSD",PERIOD_D1,20,0,MODE_EMA,PRICE_CLOSE); //--- return(INIT_SUCCEEDED); }
如果将EA从图表中移除,我们应该释放不再使用的资源。
//+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- Release the resources we don't need release_resources(); }
现在,每当收到更新的价格时,我们首先会存储新的技术数据,从模型中进行预测,然后将重要的统计数据反馈给用户。如果我们没有持仓,我们将遵循模型的预测。否则,我们将根据用户的输入来决定是否应该保持持仓或平仓。
//+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- Update market data update_market_data(); //--- Fetch a prediction from our model model_predict(); //--- Display stats display_stats(); //--- Find a position if(PositionsTotal() == 0) { if(model_state == 1) check_bullish_setup(); else if(model_state == -1) check_bearish_setup(); } //--- Manage the position we have else { //--- How should we close our positions? if(user_close_type == MA_CLOSE) { ma_close_positions(); } else { ai_close_positions(); } } } //+------------------------------------------------------------------+
现在让我们定义AI系统应该如何平仓。如果系统检测到价格水平将与头寸主张相反的方向变化,我们将平仓。
//+------------------------------------------------------------------+ //| Close whenever our AI detects a reversal | //+------------------------------------------------------------------+ void ai_close_positions(void) { if(system_state != model_state) { Alert("Reversal detected by our AI system,closing open positions"); Trade.PositionClose("EURUSD"); } }
另一方面,如果依靠移动平均线来平仓,那么如果收盘价高于移动平均线,我们就希望平掉所有卖单仓位;而对于买单仓位,情况则相反,即当收盘价低于移动平均线时平掉买单仓位 。
//+------------------------------------------------------------------+ //| Close whenever price reverses the moving average | //+------------------------------------------------------------------+ void ma_close_positions(void) { //--- Is our buy position possibly weakening? if(system_state == 1) { if(iClose("EURUSD",PERIOD_D1,0) < ma_buffer[0]) Trade.PositionClose("EURUSD"); } //--- Is our sell position possibly weakening? if(system_state == -1) { if(iClose("EURUSD",PERIOD_D1,0) > ma_buffer[0]) Trade.PositionClose("EURUSD"); } }
要开仓交易,我们首先需要看到布林带(Bollinger Band)出现突破信号,随后要得到相对强弱指标(RSI)的确认,最后,我们还希望看到移动平均线相对于价格处于右侧。
//+------------------------------------------------------------------+ //| Check bearish setup | //+------------------------------------------------------------------+ void check_bearish_setup(void) { if(iClose("EURUSD",PERIOD_D1,0) < bb_low_buffer[0]) { if(50 > rsi_buffer[0]) { if(iClose("EURUSD",PERIOD_D1,0) < ma_buffer[0]) { Trade.Sell(0.3,"EURUSD",bid,0,0,"EURUSD MTF AI"); system_state = -1; } } } } //+------------------------------------------------------------------+ //| Check bullish setup | //+------------------------------------------------------------------+ void check_bullish_setup(void) { if(iClose("EURUSD",PERIOD_D1,0) > bb_high_buffer[0]) { if(50 < rsi_buffer[0]) { if(iClose("EURUSD",PERIOD_D1,0) > ma_buffer[0]) { Trade.Buy(0.3,"EURUSD",ask,0,0,"EURUSD MTF AI"); system_state = 1; } } } }
目前,该函数只会显示模型的预测结果。
//+------------------------------------------------------------------+ //| Display account stats | //+------------------------------------------------------------------+ void display_stats(void) { Comment("Forecast: ",model_output[0]); }
从我们的模型中获取预测结果,并使用一个二进制标识位来存储。
//+------------------------------------------------------------------+ //| Fetch a prediction from our model | //+------------------------------------------------------------------+ void model_predict(void) { //--- Get inputs model_input.CopyRates("EURUSD",PERIOD_MN1,COPY_RATES_CLOSE,0,1); //--- Fetch a prediction from our model OnnxRun(onnx_model,ONNX_DEFAULT,model_input,model_output); //--- Store the model's prediction as a flag if(model_output[0] > model_input[0]) { model_state = -1; } else if(model_output[0] < model_input[0]) { model_state = 1; } }
现在,让我们来指定一个函数,该函数将用于释放不再需要的资源。
//+------------------------------------------------------------------+ //| Release the resources we don't need | //+------------------------------------------------------------------+ void release_resources(void) { OnnxRelease(onnx_model); IndicatorRelease(ma_hanlder); IndicatorRelease(rsi_hanlder); IndicatorRelease(bb_hanlder); ExpertRemove(); }
每当有新的报价出现时,就会调用这个函数来更新我们所掌握的市场数据。
//+------------------------------------------------------------------+ //| Update our market data | //+------------------------------------------------------------------+ void update_market_data(void) { //--- Update all our technical data bid = SymbolInfoDouble("EURUSD",SYMBOL_BID); ask = SymbolInfoDouble("EURUSD",SYMBOL_ASK); CopyBuffer(ma_hanlder,0,0,1,ma_buffer); CopyBuffer(rsi_hanlder,0,0,1,rsi_buffer); CopyBuffer(bb_hanlder,0,0,1,bb_mid_buffer); CopyBuffer(bb_hanlder,1,0,1,bb_high_buffer); CopyBuffer(bb_hanlder,2,0,1,bb_low_buffer); }
最后,让我们来定义一个函数,该函数将从之前定义的缓冲区中创建ONNX模型。
//+------------------------------------------------------------------+ //| Load our ONNX model | //+------------------------------------------------------------------+ bool load_onnx_model(void) { //--- Create the ONNX model from our buffer onnx_model = OnnxCreateFromBuffer(onnx_buffer,ONNX_DEFAULT); //--- Validate the model if(onnx_model == INVALID_HANDLE) { //--- Give feedback Comment("Failed to create the ONNX model"); //--- We failed to create the model return(false); } //--- Specify the I/O shapes ulong input_shape[] = {1,1}; ulong output_shape[] = {1,1}; //--- Validate the I/O shapes if(!(OnnxSetInputShape(onnx_model,0,input_shape)) || !(OnnxSetOutputShape(onnx_model,0,output_shape))) { //--- Give feedback Comment("We failed to define the correct input shapes"); //--- We failed to define the correct I/O shape return(false); } return(true); } //+------------------------------------------------------------------+
图13:我们的EA输入
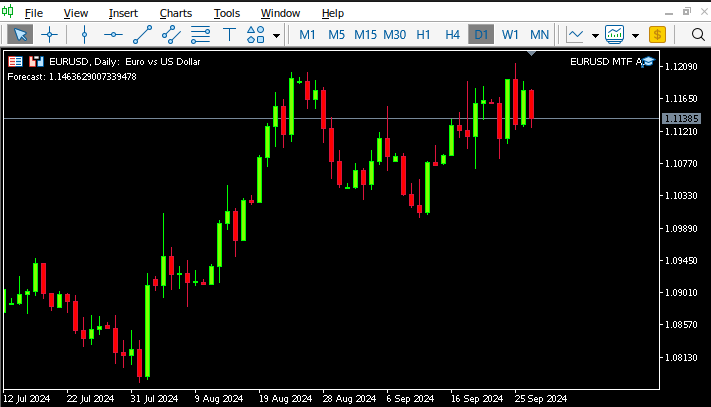
图14:我们运行中的EA
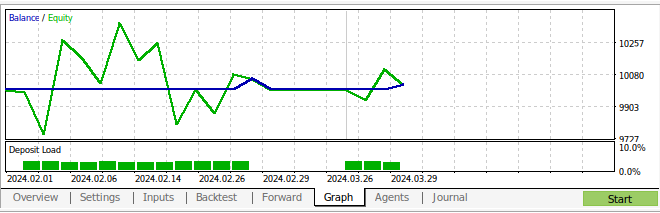
图15:我们策略的回测结果
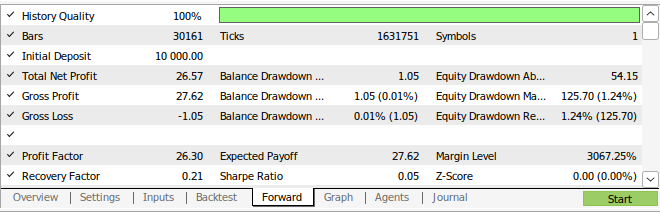
图16:我们策略的前瞻性测试结果
结论
在本文中,我们展示了月度和小时时间框架,似乎是预测欧元兑美元货币对最稳定的框架。我们不能确信这一点适用于所有现有的市场。同样,我们也必须在未来考虑搜索更多可能的时间框架,以确保我们没有忽视任何最优的时间框架。此外,还可以对我们的方法进行进一步的调整,以寻找更低的误差指标。例如,我们可能好奇是否有一种时间框架的组合可以进一步降低误差水平。
本文由MetaQuotes Ltd译自英文
原文地址: https://www.mql5.com/en/articles/15972
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
本文由网站的一位用户撰写,反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责,也不对因使用所述解决方案、策略或建议而产生的任何后果负责。
 MQL5 简介(第 9 部分):理解和使用 MQL5 中的对象
MQL5 简介(第 9 部分):理解和使用 MQL5 中的对象
 基于MQL5和Python的自优化EA(第五部分):深度马尔可夫模型
基于MQL5和Python的自优化EA(第五部分):深度马尔可夫模型
 大气云模型优化(ACMO):实战
大气云模型优化(ACMO):实战
