Klassische Strategien neu interpretieren (Teil IX): Analyse mehrerer Zeitrahmen (II)
140
0
Es gibt viele Zeitrahmen, die Händler nutzen können. Für ein neues Mitglied der Gemeinschaft oder für jeden, der den Handel erlernen möchte, kann die Entscheidung schwierig sein. Selbst erfahrene Händler diskutieren häufig und tauschen unterschiedliche Standpunkte aus, um herauszufinden, welcher Zeitrahmen optimal ist. Wir werden versuchen, diese Frage objektiv zu beantworten, indem wir den optimalen Zeitrahmen als denjenigen definieren, der die Fehlerquote unseres KI-Modells minimiert.
In der heutigen Diskussion werden wir uns mit der Verteilung der Residuen unseres Modells über 11 Zeitrahmen befassen. Wir haben 2 Regionen mit geringen Fehlern im monatlichen und stündlichen Zeitrahmen beobachtet. Es gibt jedoch kein offensichtliches Muster in der Verteilung der Fehlerwerte des Modells, sie scheinen ein Maximum und ein Minimum im stündlichen Rahmen zu erreichen. Bevor wir die uralte Frage "Welcher Zeitrahmen ist der beste?" endgültig beantworten können, müssen wir einigermaßen sicher sein, dass sich die Verteilung der Residuen nicht ändert, wenn wir die Märkte wechseln. Außerdem sollten wir in Zukunft eine erschöpfende Suche über alle verfügbaren Zeiträume in Betracht ziehen.
Überblick über die Handelsmethodik
Während das von den Preiskerzen erzeugte Muster in allen Zeitrahmen sehr unterschiedlich erscheinen kann, gibt es in jedem Moment nur einen Preis, der in allen Zeitrahmen angeboten wird. Händler analysieren oft verschiedene Zeitrahmen gleichzeitig, um einen Einblick in die aktuelle Marktlage zu erhalten. Wenn der Trend schwächer wird, werden wir wahrscheinlich widersprüchliche Kursbewegungen auf Zeitrahmen sehen, die niedriger sind als der, den wir zur Eröffnung unseres Handels verwendet haben. Außerdem werden diese Anzeichen von Schwäche immer zuerst auf dem unteren Zeitrahmen sichtbar, bevor sie auf höheren Zeitrahmen erkennbar werden.
Im Allgemeinen versuchen die meisten Strategien, die eine Analyse mehrerer Zeitrahmen beinhalten, die Marktstimmung in höheren Zeitrahmen zu verstehen. Einige erfolgreiche Händler achten auf die Bildung von bekannten Preisaktionsmustern auf höheren Zeitrahmen, wie z. B. „Bullish Engulfing“. Traditionell diente das Vorhandensein oder Nichtvorhandensein dieser Kerzenmuster als Signal für Händler, die auf der Suche nach hochwahrscheinlichen Setups waren. Wir wollten algorithmisch lernen, welcher Zeitrahmen bei der Vorhersage des EURUSD-Paares zuverlässige Fehlerwerte liefert.
Auf einer gewissen Ebene schätzen wir alle die Intuition, dass die Aufgabe umso schwieriger wird, je weiter in die Zukunft man versucht, sie vorherzusagen. Die Ergebnisse unserer heutigen Analyse stellen diese Annahme grundlegend in Frage. Bevor Sie vielleicht verstehen können, warum ich dies sage oder ob diese Schlussfolgerungen stichhaltig sind, müssen wir zunächst die angewandte Methodik erörtern.
Überblick über die Methodik
Damit unser Test fair ist, mussten wir aus jedem Zeitrahmen die gleiche Menge an Daten abrufen. Der einschränkende Faktor bei diesem Schritt war die Anzahl der für den Zeitrahmen Monat verfügbaren Balken. Nur 400 Balken monatlicher Daten umfassen etwa 33 Jahre. Es gibt nur eine Handvoll so alter Märkte, was unser Verständnis des besten Zeitrahmens für alle möglichen Märkte verzerren kann. Für den Rahmen unserer Diskussion verfügt das EURUSD-Paar jedoch über umfangreiche Datensätze, auf die wir uns stützen können.
Wir haben 400 Zeilen mit monatlichen Kursnotierungen vom MetaTrader 5-Terminal abgerufen. Wir haben dann 400 entsprechende Zeilen für den zukünftigen Wert des EURUSD-Paares abgerufen. Dieser zweistufige Prozess wurde in den verbleibenden 10 Zeitfenstern wiederholt. Für diese Analyse habe ich ausgewählt:
- Wöchentlich
- Täglich
- H12
- H8
- H4
- H1
- M30
- M15
- M5
- M1
Ich muss zugeben, dass ich starke Korrelationsniveaus erwartet habe, vor allem zwischen Zeiträumen, die periodisch nahe beieinander liegen. Allerdings war die Korrelation in der gesamten Stichprobe nur mäßig ausgeprägt. Die einzigen interessanten Korrelationspaare, die eine weitere Analyse verdienen könnten, waren:
- Aktueller H4-Preis und zukünftiger H8-Preis
- Aktueller M1-Preis und zukünftiger H4-Preis
- Aktueller M1-Preis und zukünftiger M5-Preis
Da unsere Eingabedaten 22 Spalten hatten, war die Korrelationsmatrix, die wir erhielten, natürlich sehr groß und wird in unserer Diskussion nicht vollständig dargestellt. Aus unseren bisherigen Daten konnten wir 11 Sätze von zu testenden Eingaben erstellen. Nach der Modellierung unserer Daten haben wir festgestellt, dass unsere Modelle im monatlichen und stündlichen Zeitrahmen am besten funktionieren. Dieses Ergebnis war ziemlich kontraintuitiv. Unser Ziel waren 20 Zeitschritte in die Zukunft. 20 Monate in die Zukunft ist ein Zeitraum von 1 Jahr und 8 Monaten. Unser Modell konnte die Preisveränderungen über ein Jahr genauer vorhersagen als die Preisveränderungen über 20 Minuten.
Aus Interesse an den beiden Zeitrahmen mit geringem Fehler transformierten wir die Kursdaten in periodische Renditen und führten anschließend Granger-Kausalitätstests für die Renditen durch. Wir haben signifikante p-Werte festgestellt, die darauf hindeuten, dass die stündlichen Renditen die monatlichen Renditen aufgrund der Granger-Kausalität beeinflussen. Dieser Test beweist, dass wir die monatlichen Renditen anhand der stündlichen Renditen mit einem Vektor-Autoregressions-Modell (VAR) modellieren können.
Wir haben eine Bibliothek für „Time Series Warping“ verwendet, um die monatlichen und stündlichen Daten aufeinander abzustimmen und Ähnlichkeiten zu finden. Unser Algorithmus war in der Lage, viele Ähnlichkeiten zwischen den Daten zu finden. Dies gab uns Vertrauen in unseren Auswahlprozess, und wir fuhren fort, die Parameter unseres Monatsmodells erfolgreich abzustimmen und unser Modell in das ONNX-Format zu exportieren.
Schließlich habe ich einen Expert Advisor implementiert, der Vorhersagen zu den erwarteten Kursniveaus auf dem monatlichen Zeitrahmen macht und dann seine Handelsgeschäfte auf dem stündlichen Zeitrahmen ausführt. Das System kann zwischen der Schließung seiner Positionen auf der Grundlage von vorhergesagten KI-Umkehrungen oder der Verwendung gleitender Durchschnitte wechseln. Wir nutzten die technische Analyse, um den Zeitpunkt für den Einstieg in unsere Positionen zu bestimmen.
Abrufen der benötigten Daten
Beginnen wir mit dem Import der MetaTrader 5-Bibliothek und einiger anderer Bibliotheken, die wir benötigen.
#Import the libraries we need import pandas as pd import numpy as np import seaborn as sns import MetaTrader5 as mt5 from sklearn.model_selection import cross_val_score,train_test_split,TimeSeriesSplit from sklearn.metrics import mean_squared_error import matplotlib.pyplot as plt from sklearn.linear_model import LinearRegression
Nun testen wir, ob wir das Terminal erreichen können.
#Initialize the terminal
mt5.initialize()Legen wir die Zeiträume fest, die wir testen möchten.
#Declare the time-frames we are interested in
time_frames = [mt5.TIMEFRAME_MN1,
mt5.TIMEFRAME_W1,
mt5.TIMEFRAME_D1,
mt5.TIMEFRAME_H12,
mt5.TIMEFRAME_H8,
mt5.TIMEFRAME_H4,
mt5.TIMEFRAME_H1,
mt5.TIMEFRAME_M30,
mt5.TIMEFRAME_M15,
mt5.TIMEFRAME_M5,
mt5.TIMEFRAME_M1
]Wie viele Datenbalken sollten wir abrufen?
#How many bars should we fetch fetch = 400
Blicken wir 20 Schritte in die Zukunft.
#How far into the future should we forecast? look_ahead = 20
Definition der Spalten unseres Datenrahmens.
#Create our dataframe inputs = ["MN","W","D","H12","H8","H4","H1","M30","M15","M5","M1"] target = [] for i in np.arange(0,len(inputs)): target.append(inputs[i] + " Target")
Wir erstellen den Datenrahmen, der unsere Preise enthält.
columns = inputs + target
prices = pd.DataFrame(columns=columns,index=np.arange(0,fetch))
Abb. 1: Einige der Eingaben in unserem Daten-Frame
Abb. 2: Einige der Ziele in unserem Daten-Frame
Wir brauchen einen Datenrahmen, um unsere Fehlerstufen zu speichern.
#The columns for our error levels data frame. error_columns = [] for i in np.arange(0,len(inputs)): error_columns.append(inputs[i]) #Create a dataframe to store our error levels error_levels = pd.DataFrame(columns=error_columns,index=[0]) test_error_levels = pd.DataFrame(columns=error_columns,index=[0])
Holen wir uns die benötigten Preisdaten.
for i in np.arange(0,len(time_frames)): print(i) prices.iloc[:,i] = pd.DataFrame(mt5.copy_rates_from_pos("EURUSD",time_frames[i],look_ahead,fetch)).loc[:,"close"] prices.iloc[:,i+10] = pd.DataFrame(mt5.copy_rates_from_pos("EURUSD",time_frames[i],0,fetch)).loc[:,"close"]
Explorative Datenanalyse
Analysieren wir nun die Korrelationsniveaus in unserem Datenrahmen. Beachten Sie die starken Korrelationsniveaus zwischen dem H12- und dem H8-Zeitrahmen. Welche anderen Korrelationsstufen fallen Ihnen auf?
fig, ax = plt.subplots(figsize=(15,15)) sns.heatmap(prices.corr(),annot=True,ax=ax)
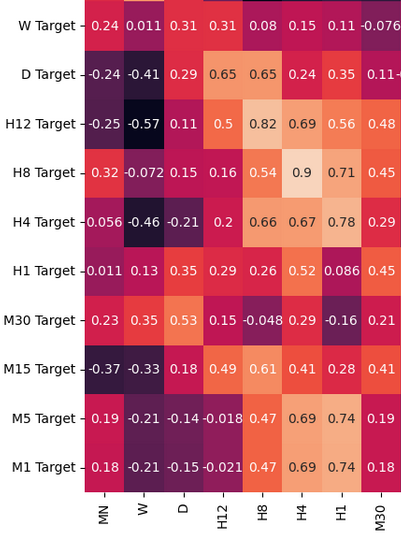
Abb. 3: Einige der Werte aus der Korrelationsmatrix, die wir erhalten haben
Ein Streudiagramm der monatlichen und wöchentlichen Schlusskurse zeigte einen unklaren Trend. Im Großen und Ganzen scheinen die Daten einen allgemeinen Aufwärtstrend zu zeigen.
sns.scatterplot(data=prices,x="MN Close",y="W Close")
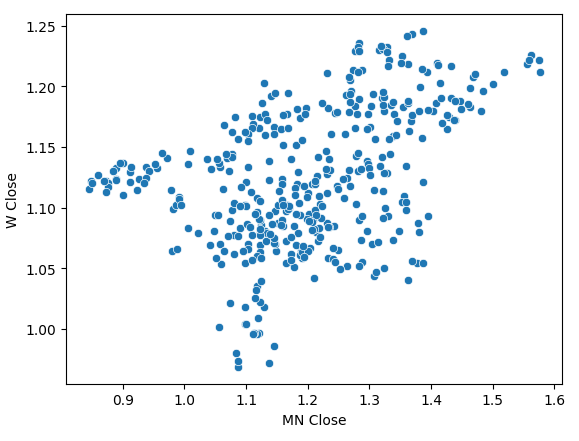
Abb. 4: Ein Streudiagramm unserer monatlichen und wöchentlichen Schlusskurse
Wir haben unsere Kursdaten in periodische Renditen umgewandelt und das Streudiagramm erneut erstellt. Diesmal zeigt sich ein allgemeiner Trend, es scheint, dass sich unsere Renditen um 0 herum gruppieren.
sns.scatterplot(data=prices.pct_change(),x="MN Close",y="W Close")
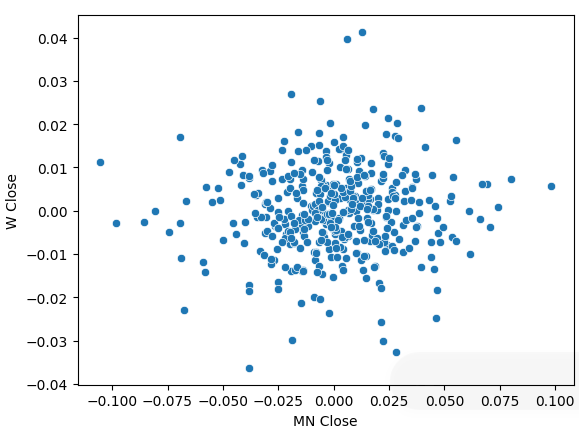
Abb. 5: Ein Streudiagramm unserer Renditen für verschiedene Zeiträume
Wenn wir Boxplots unserer Renditen über verschiedene Zeiträume erstellen, können wir einen weiteren Trend beobachten. Die Varianz unserer Renditen nimmt ab, je weiter wir uns vom monatlichen Zeitrahmen entfernen und zu niedrigeren Zeitrahmen übergehen. Auch die durchschnittliche Rendite über alle Zeiträume liegt nahe bei 0. Dies kann auch so interpretiert werden, dass wir, wenn wir versuchen, die Rendite eines Portfolios zu maximieren, höhere Zeitrahmen in Betracht ziehen sollten.
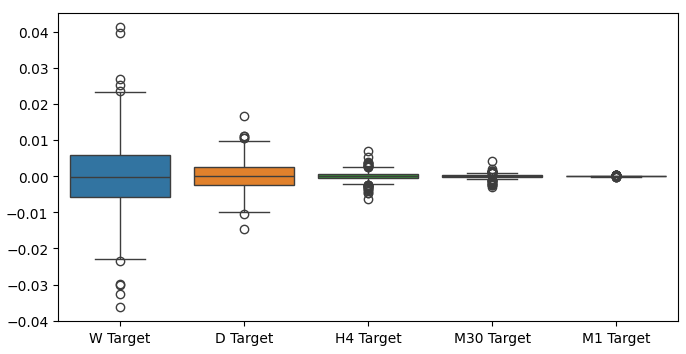
Abb. 6: Ein Boxplot unserer Renditen über verschiedene Zeiträume
Vorbereiten der Datenmodellierung
Treffen wir nun die notwendigen Vorbereitungen, um mit der Modellierung der Daten zu beginnen. Zunächst müssen wir unsere Daten in Trainings- und Testdaten aufteilen.
#Create train test splits X_train_mn,X_test_mn,y_train_mn,y_test_mn = train_test_split(prices.loc[:,["MN"]],prices.loc[:,"MN Target"],test_size=0.5,shuffle=False) X_train_w,X_test_w,y_train_w,y_test_w = train_test_split(prices.loc[:,["W"]],prices.loc[:,"W Target"],test_size=0.5,shuffle=False) X_train_d,X_test_d,y_train_d,y_test_d = train_test_split(prices.loc[:,["D"]],prices.loc[:,"D Target"],test_size=0.5,shuffle=False) X_train_h12,X_test_h12,y_train_h12,y_test_h12 = train_test_split(prices.loc[:,["H12"]],prices.loc[:,"H12 Target"],test_size=0.5,shuffle=False) X_train_h8,X_test_h8,y_train_h8,y_test_h8 = train_test_split(prices.loc[:,["H8"]],prices.loc[:,"H8 Target"],test_size=0.5,shuffle=False) X_train_h4,X_test_h4,y_train_h4,y_test_h4 = train_test_split(prices.loc[:,["H4"]],prices.loc[:,"H4 Target"],test_size=0.5,shuffle=False) X_train_h1,X_test_h1,y_train_h1,y_test_h1 = train_test_split(prices.loc[:,["H1"]],prices.loc[:,"H1 Target"],test_size=0.5,shuffle=False) X_train_m30,X_test_m30,y_train_m30,y_test_m30 = train_test_split(prices.loc[:,["M30"]],prices.loc[:,"M30 Target"],test_size=0.5,shuffle=False) X_train_m15,X_test_m15,y_train_m15,y_test_m15 = train_test_split(prices.loc[:,["M15"]],prices.loc[:,"M15 Target"],test_size=0.5,shuffle=False) X_train_m5,X_test_m5,y_train_m5,y_test_m5 = train_test_split(prices.loc[:,["M5"]],prices.loc[:,"M5 Target"],test_size=0.5,shuffle=False) X_train_m1,X_test_m1,y_train_m1,y_test_m1 = train_test_split(prices.loc[:,["M1"]],prices.loc[:,"M1 Target"],test_size=0.5,shuffle=False)
Speichern wir nun diese Aufteilung in Listen.
train_X = [ X_train_mn, X_train_w, X_train_d, X_train_h12, X_train_h8, X_train_h4, X_train_h1, X_train_m30, X_train_m15, X_train_m5, X_train_m1 ] test_X = [ X_test_mn, X_test_w, X_test_d, X_test_h12, X_test_h8, X_test_h4, X_test_h1, X_test_m30, X_test_m15, X_test_m5, X_test_m1 ]
Wir wiederholen das obige Verfahren für die Zielwerte.
train_y = [ y_train_mn, y_train_w, y_train_d, y_train_h12, y_train_h8, y_train_h4, y_train_h1, y_train_m30, y_train_m15, y_train_m5, y_train_m1, ] test_y = [ y_test_mn, y_test_w, y_test_d, y_test_h12, y_test_h8, y_test_h4, y_test_h1, y_test_m30, y_test_m15, y_test_m5, y_test_m1, ]
Machen wir eine Kreuzvalidierung von jedem Modell.
#Record our error for i in np.arange(0,len(train_X)): #Fit the model model = LinearRegression() cv_score = cross_val_score(model,train_X[i],train_y[i],cv=5) error_levels.iloc[0,i] = np.mean(cv_score * -1) #Record validation error model.fit(train_X[i],train_y[i]) test_error_levels.iloc[0,i] = mean_squared_error(test_y[i],model.predict(test_X[i]))
Unsere jeweiligen Fehlerquoten.
error_levels
| MN | W | D | H12 | H8 | H4 | H1 | M30 | M15 | M5 | M1 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.719131 | 3.979435 | 3.897228 | 5.023601 | 5.218168 | 40.406227 | 0.196244 | 18.264356 | 3.680168 | 20.331821 | 3.540946 |
Veranschaulichen wir unsere Annäherung an die Verteilung der Residuen unseres Modells.
fig, ax = plt.subplots(figsize=(7,4)) sns.barplot(error_levels,ax=ax)
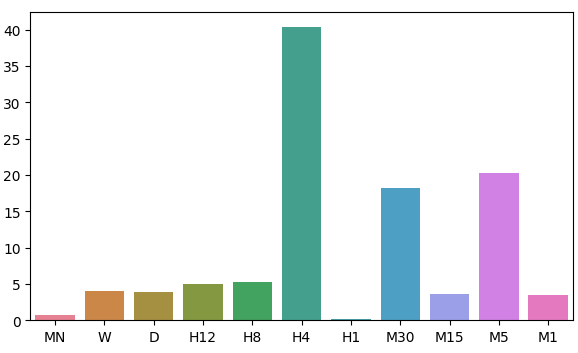
Abb. 7: Visualisierung der Fehlerniveaus unseres Modells
Die Bedeutung der Merkmale
Nachdem wir nun unsere optimalen Zeitrahmen ermittelt haben, wollen wir versuchen herauszufinden, ob zwischen den beiden Zeitrahmen möglicherweise eine Kausalität besteht. 1969 schlug Sir Clive Granger einen Test vor, mit dem empirisch festgestellt werden kann, ob zwei Zeitreihendaten einander bedingen, oder ob vergangene Werte der einen Zeitreihe die zukünftigen Werte einer anderen beeinflussen. Vereinfacht ausgedrückt, ist der Granger-Test bestanden, wenn wir die Werte einer Zeitreihe verzögern und sie zur Vorhersage des künftigen Wertes der zweiten Zeitreihe verwenden können, ohne dass die Varianz unserer Vorhersagen signifikant abnimmt.
Seit seiner Einführung hat der Granger-Test zahlreiche Änderungen und Verbesserungen erfahren. In der heutigen Zeit wird sie in vielen Bereichen eingesetzt, von den Neurowissenschaften bis zum Finanzwesen. Die Verwendung des Tests steht seit über einem halben Jahrhundert im Mittelpunkt vieler Debatten in akademischen Kreisen. Das Hauptproblem liegt in der Annahme der Linearität, die der Granger-Test implizit voraussetzt. Wenn es also tatsächlich eine nichtlineare Kausalbeziehung gibt, wird der Granger-Test diese widerlegen. Außerdem ist der Test in der Praxis in der Regel auf bivariate Probleme beschränkt. Das heißt, dass wir den Granger-Test bei großen Problemen mit mehr als zwei Zeitreihendatensätzen nur selten anwenden.
Abb. 8: Der verstorbene britische Wirtschaftswissenschaftler Sir Clive Granger
Zunächst importieren wir die statsmodels-Bibliothek und führen dann den Test durch. Der Test wird für verzögerte Versionen des H1 Close durchgeführt. Der Test ist bestanden, wenn wir p-Werte < 0,05 erhalten, was bei der ersten Verzögerung der Fall war. Alle nachfolgenden Verzögerungen haben den Test nicht bestanden, und wir können jegliche Granger-Kausalität nach der ersten Verzögerung ablehnen.
from statsmodels.tsa.stattools import grangercausalitytests result = grangercausalitytests(prices[['H1 Close','MN Close']].pct_change().dropna(), maxlag=4)
Anzahl der Verzögerungen (keine Null) 1
ssr-basierter F-Test: F=4,4913 , p=0,0347 , df_denom=395, df_num=1
ssr-basierter chi2-Test: chi2=4,5254 , p=0,0334 , df=1
Likelihood-Verhältnistest: chi2=4,4999 , p=0,0339 , df=1
Parameter F-Test: F=4,4913 , p=0,0347 , df_denom=395, df_num=1
Granger-Kausalität
Anzahl der Verzögerungen (keine Null) 2
ssr-basierter F-Test: F=2,2706 , p=0,1046 , df_denom=392, df_num=2
ssr-basierter chi2-Test: chi2=4,5991 , p=0,1003 , df=2
Likelihood-Verhältnistest: chi2=4,5727 , p=0,1016 , df=2
Parameter F-Test: F=2,2706 , p=0,1046 , df_denom=392, df_num=2
Die Granger-Kausalität funktioniert normalerweise in eine Richtung. Um dies sicherzustellen, müssen wir die Kausalität in umgekehrter Richtung prüfen. Keiner der erhaltenen p-Werte war signifikant, was uns beruhigt, dass die Kausalität tatsächlich in eine Richtung geht, wie wir erwarten.
result = grangercausalitytests(prices[['MN Close','H1 Close']].pct_change().dropna(), maxlag=4)
Granger-Kausalität
Anzahl der Verzögerungen (keine Null) 1
ssr-basierter F-Test: F=0,0188 , p=0,8909 , df_denom=395, df_num=1
ssr-basierter chi2-Test: chi2=0,0190 , p=0,8905 , df=1
Likelihood-Verhältnistest: chi2=0,0190 , p=0,8905 , df=1
Parameter F-Test: F=0,0188 , p=0,8909 , df_denom=395, df_num=1
Granger-Kausalität
Anzahl der Verzögerungen (keine Null) 2
ssr-basierter F-Test: F=2,2182 , p=0,1102 , df_denom=392, df_num=2
ssr-basierter chi2-Test: chi2=4,4930 , p=0,1058 , df=2
Likelihood-Verhältnistest: chi2=4,4678 , p=0,1071 , df=2
Parameter F-Test: F=2,2182 , p=0,1102 , df_denom=392, df_num=2
Granger-Kausalität
Anzahl der Verzögerungen (keine Null) 3
ssr-basierter F-Test: F=1,7310 , p=0,1601 , df_denom=389, df_num=3
ssr-basierter chi2-Test: chi2=5,2863 , p=0,1520 , df=3
Likelihood-Verhältnistest: chi2=5,2513 , p=0,1543 , df=3
Parameter F-Test: F=1,7310 , p=0,1601 , df_denom=389, df_num=3
Granger-Kausalität
Anzahl der Verzögerungen (keine Null) 4
ssr-basierter F-Test: F=1,4694 , p=0,2108 , df_denom=386, df_num=4
ssr-basierter chi2-Test: chi2=6,0148 , p=0,1980 , df=4
Likelihood-Verhältnistest: chi2=5,9694 , p=0,2014 , df=4
Parameter F-Test: F=1,4694 , p=0,2108 , df_denom=386, df_num=4
Mit dem „Dynamic Time Series Warping“ können wir auch Ähnlichkeiten zwischen zwei Zeitreihendatensätzen finden. Der Algorithmus kann auch für die Angleichung von Reihen unterschiedlicher Länge verwendet werden. Wir haben den Algorithmus eingesetzt, um Ähnlichkeiten zwischen den monatlichen und stündlichen Renditen unserer Daten zu finden. Der Algorithmus erfüllt diese Aufgabe, indem er eine spezielle Kostenfunktion minimiert, die die Differenz zwischen 2 Reihen misst. Wir beginnen damit, die benötigten Bibliotheken zu importieren.
#Let's calculate the simillarities between our time series data from dtaidistance import dtw from dtaidistance import dtw_visualisation as dtwvis
Lassen Sie uns nun Gemeinsamkeiten zwischen den Renditen finden.
series_1 = prices["MN Close"].pct_change(periods=1).dropna().reset_index(drop=True) * 100 series_2 = prices["H1 Close"].pct_change(periods=1).dropna().reset_index(drop=True) * 100 path = dtw.warping_path(series_1, series_2) dtwvis.plot_warping(series_1, series_2, path)
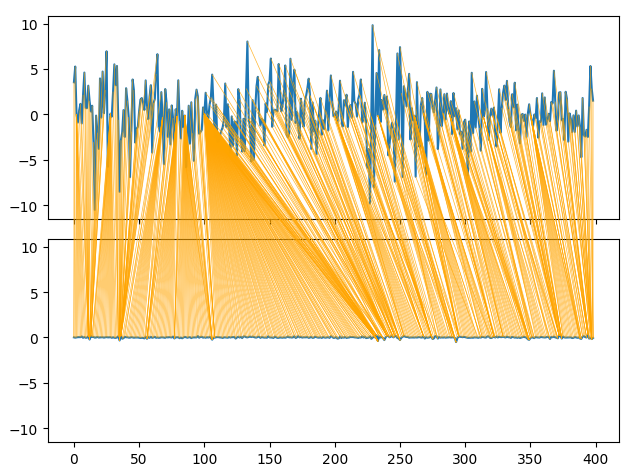
Abb. 9: Visualisierung der Ähnlichkeiten zwischen den monatlichen und stündlichen Renditen
Einstellung der Parameter
Stellen wir nun die Parameter unseres tiefen neuronalen Netzes so ein, dass es die von der linearen Regression vorgegebene Benchmark-Leistung übertrifft. Beachten Sie, dass aufgrund der Art der Optimierungsverfahren, die zum Trainieren von DNN verwendet werden, die in diesem Abschnitt des Artikels erzielten Ergebnisse schwer zu reproduzieren sein könnten. Tatsächlich habe ich diesen Test 5 Mal durchgeführt, und bei 2 Tests ist es uns nicht gelungen, das lineare Modell zu erfüllen.
Importieren wir die benötigten Bibliotheken, und initialisieren das Modell.
#Let's try to outperform our linear regression model from sklearn.neural_network import MLPRegressor from sklearn.model_selection import RandomizedSearchCV #Let's tune our model model = MLPRegressor(max_iter=500)
Definieren des Parameterraums
#Tuner
tuner = RandomizedSearchCV(
model,
{
"activation" : ["relu","logistic","tanh","identity"],
"solver":["adam","sgd","lbfgs"],
"alpha":[0.1,0.01,0.001,0.0001,0.00001,0.00001,0.0000001,0.000000001,0.000000000000001],
"tol":[0.1,0.01,0.001,0.0001,0.00001,0.000001,0.0000001,0.000000001,0.000000000000001],
"learning_rate":['constant','adaptive','invscaling'],
"learning_rate_init":[1,0.1,0.0001,0.000001,100,10000,1000000,1000000000,100,1000],
"shuffle": [True,False],
"hidden_layer_sizes":[(1,4),(1,4,5),(1,8,10),(2,5),(8),(10,12),(5,10,4)]
},
n_iter=100,
cv=5,
n_jobs=-1,
scoring="neg_mean_squared_error"
)und Anpassen des Tuners:
tuner.fit(X_train_mn,y_train_mn)
Die besten Parameter, die wir gefunden haben.
tuner.best_params_
'solver': 'lbfgs',
'shuffle': True,
'learning_rate_init': 1,
'learning_rate': 'adaptive',
'hidden_layer_sizes': (2, 5),
'alpha': 1e-05,
'activation': 'identity'}
Tiefergehende Optimierung
Wir wollen die Suche nach den optimalen Parametern mit Hilfe der SciPy-Bibliothek vertiefen.
#Deeper optimization
from scipy.optimize import minimizeWir erstellen Datenstrukturen, um unseren Fortschritt festzuhalten,
#Create a dataframe to store our accuracy current_error_rate = pd.DataFrame(index = np.arange(0,5),columns=["Current Error"]) optimization_progress = []
definieren die Zielfunktion, die minimiert werden soll. Wir wollen den mittleren quadratischen Fehler unseres Modells minimieren.
#Define the objective function def objective(x): #The parameter x represents a new value for our neural network's settings #In order to find optimal settings, we will perform 10 fold cross validation using the new setting #And return the average RMSE from all 10 tests #We will first turn the model's Alpha parameter, which controls the amount of L2 regularization model = MLPRegressor(hidden_layer_sizes=tuner.best_params_["hidden_layer_sizes"], activation=tuner.best_params_["activation"], learning_rate=tuner.best_params_["learning_rate"], solver=tuner.best_params_["solver"], shuffle=tuner.best_params_["shuffle"], alpha=x[0], tol=x[1], learning_rate_init=x[2]) #Now we will cross validate the model for i,(train,test) in enumerate(tscv.split(X_train_mn)): #Train the model model.fit(X_train_mn.loc[train[0]:train[-1],:],y_train_mn.loc[train[0]:train[-1]]) #Measure the RMSE current_error_rate.iloc[i,0] = mean_squared_error(y_train_mn.loc[test[0]:test[-1]],model.predict(X_train_mn.loc[test[0]:test[-1],:])) #Record the progress made by the optimizer optimization_progress.append(current_error_rate.iloc[:,0].mean()) #Return the Mean CV RMSE return(current_error_rate.iloc[:,0].mean())
Wir geben den Ausgangspunkt für das Optimierungsverfahren an und legen große Grenzen fest, damit wir die globale Optimierung annähern können.
#Define the starting point pt = [tuner.best_params_["alpha"],tuner.best_params_["tol"],tuner.best_params_["learning_rate_init"]] bnds = ((0.000000001,10000000000),(0.0000000001,10000000000),(0.000000001,10000000000))
Optimieren unseres DNN-Modells.
#Searchin deeper for parameters result = minimize(objective,pt,method="TNC",bounds=bnds)
Es scheint, dass wir die Optimierung erfolgreich durchgeführt haben.
result
success: True
status: 2
fun: 0.04257403904271943
x: [ 4.864e-05 1.122e-03 9.999e-01]
nit: 1
jac: [ 1.298e+04 1.806e+02 -3.371e+03]
nfev: 92
Wir speichern unsere optimalen Werte
optima_y = result.fun
optima_x = optimization_progress.index(optima_y)
inputs = np.arange(0,len(optimization_progress))und visualisieren den Fortschritt des Optimierungsverfahrens.
plt.scatter(inputs,optimization_progress) plt.plot(optima_x,optima_y,'s',color='r') plt.axvline(x=optima_x,ls='--',color='red') plt.axhline(y=optima_y,ls='--',color='red') plt.title("Minimizing Training MSE")
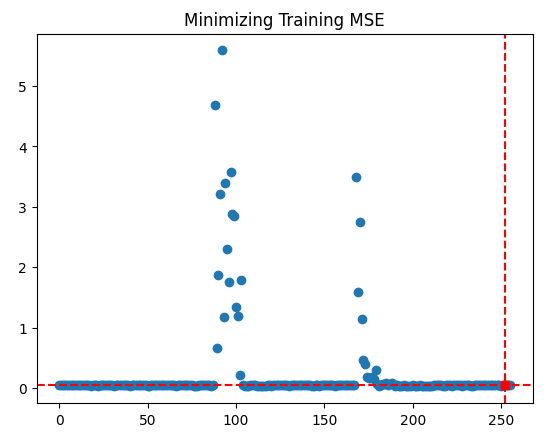
Abb. 10: Die Ergebnisse unseres TNC-Optimierungsverfahrens
Test auf Überanpassung
Wir wollen sehen, ob wir unser lineares Standardmodell tatsächlich übertreffen können.
#Test for overfitting benchmark = LinearRegression() default_model = MLPRegressor(max_iter=200) random_search_model = MLPRegressor(hidden_layer_sizes=tuner.best_params_["hidden_layer_sizes"], activation=tuner.best_params_["activation"], learning_rate=tuner.best_params_["learning_rate"], solver=tuner.best_params_["solver"], shuffle=tuner.best_params_["shuffle"], alpha=tuner.best_params_["alpha"], tol=tuner.best_params_["tol"], learning_rate_init=tuner.best_params_["learning_rate_init"], max_iter=200 ) lbfgs_model = MLPRegressor(hidden_layer_sizes=tuner.best_params_["hidden_layer_sizes"], activation=tuner.best_params_["activation"], learning_rate=tuner.best_params_["learning_rate"], solver=tuner.best_params_["solver"], shuffle=tuner.best_params_["shuffle"], alpha=result.x[0], tol=result.x[1], learning_rate_init=result.x[2], max_iter=200 )
Passen wir die Modelle an die Trainingsmenge an
#Fit the models
benchmark.fit(X_train_mn,y_train_mn)
default_model.fit(X_train_mn,y_train_mn)
random_search_model.fit(X_train_mn,y_train_mn)
lbfgs_model.fit(X_train_mn,y_train_mn)und treffen die Vorbereitungen für die Aufzeichnung unserer Kreuzvalidierungsergebnisse.
#Record our cross val scores
models = [benchmark,
default_model,
random_search_model,
lbfgs_model
]
val_error = pd.DataFrame(columns=["Linear Reg","Default NN","Random Search NN","TNC NN"],index=[0])Machen wir eine Kreuzvalidierung von jedem Modell.
for i in np.arange(0,len(models)): val_error.iloc[0,i] = np.mean(cross_val_score(models[i],X_test_mn,y_test_mn,cv=5,n_jobs=-1)) * -1
Unser Validierungsfehler zeigt deutlich, dass unser TNC-optimiertes neuronales Netz die beste Leistung erbrachte.
val_error
| Linear Reg | Standard NN | Zufällige Suche NN | TNC NN |
|---|---|---|---|
| 3.323741 | 3.987083 | 3.314776 | 3.283775 |
Exportieren ins ONNX-Format
Bereiten wir nun den Export unseres Modells in das ONNX-Format vor. ONNX steht für Open Neural Network Exchange und ist ein Open-Source-Protokoll zur Darstellung eines beliebigen Modells für maschinelles Lernen als Baum von Knoten, die Berechnungen und den Datenfluss nach jeder Berechnung darstellen. ONNX ermöglicht es uns, Modelle für maschinelles Lernen in verschiedenen Programmiersprachen zu erstellen und zu verwenden, sofern diese Sprachen die ONNX-Spezifikation implementieren.
Importieren wir die ONNX-Bibliothek, um loszulegen,
#Preparing to export to ONNX import onnx from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType
bereiten das Modell vor.
#Fit the model on all the data we have model = MLPRegressor( solver= 'lbfgs', shuffle= True, activation= 'identity', learning_rate= 'adaptive', hidden_layer_sizes= (2, 5), alpha= 4.864e-05, tol= 1.122e-03, learning_rate_init= 9.999e-01, )
passen das Modell an alle Daten an, die wir haben,
model.fit(prices[["MN Close"]],prices.loc[:,"MN Target"])
definieren die Eingabeform unseres Modells,
#Define the input types for our ONNX model initial_types = [("float_input",FloatTensorType([1,1]))]
erstellen die ONNX-Darstellung des Modells und
# Create the ONNX representation onnx_model = convert_sklearn(model,initial_types=initial_types,target_opset=12)
exportieren das Modell in das ONNX-Format.
# Save the ONNX model onnx.save_model(onnx_model,"EURUSD MN1 AI.onnx")
Nun wollen wir unser Modell im ONNX-Format visualisieren, um sicherzustellen, dass unsere Eingaben die richtige Größe haben.
import netron
netron.start("EURUSD MN1 AI.onnx")
Abb. 11: Visualisierung unseres DNN-Modells
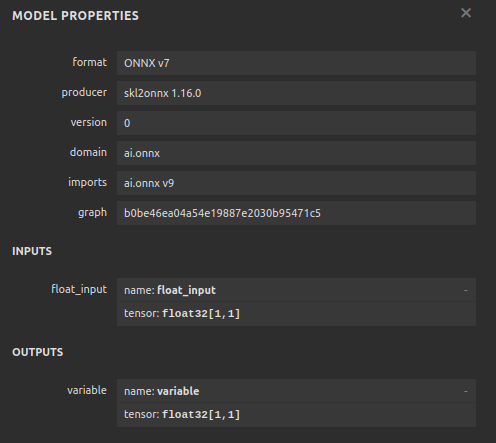
Abb. 12: Die E/A-Form unseres Modells
Implementierung in MQL5
Wir wollen nun unseren Handelsalgorithmus in MQL5 implementieren. Wir möchten, dass unser Handelsalgorithmus in der Lage ist, zwischen der Schließung seiner Positionen anhand einfacher gleitender Durchschnitte und der Verwendung von KI-Prognosen zu wechseln. Außerdem wollen wir unser KI-Modell mit Hilfe der technischen Analyse steuern. Um zu beginnen, importieren wir zunächst das ONNX-Modell, das wir oben exportiert haben.
//+------------------------------------------------------------------+ //| EURUSD MTF AI.mq5 | //| Gamuchirai Zororo Ndawana | //| https://www.mql5.com/en/gamuchiraindawa | //+------------------------------------------------------------------+ #property copyright "Gamuchirai Zororo Ndawana" #property link "https://www.mql5.com/en/gamuchiraindawa" #property version "1.00" //+------------------------------------------------------------------+ //| Load the ONNX resources | //+------------------------------------------------------------------+ #resource "\\Files\\EURUSD MN1 AI.onnx" as const uchar onnx_buffer[];
Nun werden wir unseren eigenen Enumerator definieren, um anzugeben, wie der Nutzer Positionen schließen möchte.
//+-------------------------------------------------------------------+ //| Define our custom type | //+-------------------------------------------------------------------+ enum close_type { MA_CLOSE = 0, // Moving Averages Close AI_CLOSE = 1 // AI Auto Close };
Lassen Sie uns Eingaben erstellen, damit wir die Art und Weise, wie unsere Anwendung ihre Positionen schließt, ändern können, um zu sehen, was besser ist.
//+------------------------------------------------------------------+ //| User inputs | //+------------------------------------------------------------------+ input close_type user_close_type = AI_CLOSE; // How should we close our positions?
Wir müssen die Handelsklasse importieren.
//+------------------------------------------------------------------+ //| Libraries we need | //+------------------------------------------------------------------+ #include <Trade\Trade.mqh> CTrade Trade;
Erstellen wir die globalen Variablen, die wir in unserem Programm benötigen.
//+------------------------------------------------------------------+ //| Global variables | //+------------------------------------------------------------------+ long onnx_model; vectorf model_input = vectorf::Zeros(1); vectorf model_output = vectorf::Zeros(1); double bid,ask; int ma_hanlder; double ma_buffer[]; int bb_hanlder; double bb_mid_buffer[]; double bb_high_buffer[]; double bb_low_buffer[]; int rsi_hanlder; double rsi_buffer[]; int system_state = 0,model_state=0;
Wenn unsere Anwendung geladen wird, erstellen wir zunächst unser ONNX-Modell aus dem Puffer, den wir zuvor erstellt haben. Dann werden wir unsere technischen Indikator-Handler zuweisen.
//+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- Load our ONNX function if(!load_onnx_model()) { return(INIT_FAILED); } //--- Load our technical indicators bb_hanlder = iBands("EURUSD",PERIOD_D1,30,0,1,PRICE_CLOSE); rsi_hanlder = iRSI("EURUSD",PERIOD_D1,14,PRICE_CLOSE); ma_hanlder = iMA("EURUSD",PERIOD_D1,20,0,MODE_EMA,PRICE_CLOSE); //--- return(INIT_SUCCEEDED); }
Wenn unser Expert Advisor aus dem Chart entfernt wird, sollten wir die Ressourcen freigeben, die wir nicht mehr verwenden.
//+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- Release the resources we don't need release_resources(); }
Wenn wir nun aktualisierte Preise erhalten, speichern wir zunächst die neuen technischen Daten, erstellen eine Vorhersage auf der Grundlage unseres Modells und zeigen dem Nutzer dann die wichtigsten Daten an. Wenn wir keine offenen Positionen haben, folgen wir den Vorhersagen unseres Modells. Andernfalls folgen wir den Eingaben des Nutzers, um festzustellen, ob wir unsere Positionen offen oder geschlossen halten sollen.
//+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- Update market data update_market_data(); //--- Fetch a prediction from our model model_predict(); //--- Display stats display_stats(); //--- Find a position if(PositionsTotal() == 0) { if(model_state == 1) check_bullish_setup(); else if(model_state == -1) check_bearish_setup(); } //--- Manage the position we have else { //--- How should we close our positions? if(user_close_type == MA_CLOSE) { ma_close_positions(); } else { ai_close_positions(); } } } //+------------------------------------------------------------------+
Lassen Sie uns nun festlegen, wie unser KI-System seine Geschäfte abschließen soll. Wenn unser KI-System feststellt, dass sich die Preisniveaus in einer Weise ändern, die der Annahme unserer Position widerspricht, schließen wir unsere Handelsgeschäfte.
//+------------------------------------------------------------------+ //| Close whenever our AI detects a reversal | //+------------------------------------------------------------------+ void ai_close_positions(void) { if(system_state != model_state) { Alert("Reversal detected by our AI system,closing open positions"); Trade.PositionClose("EURUSD"); } }
Wenn wir uns hingegen auf den gleitenden Durchschnitt stützen, um unsere Positionen zu schließen, wollen wir alle Verkaufsgeschäfte schließen, wenn der Schlusskurs über dem gleitenden Durchschnitt liegt, und umgekehrt für unsere Kaufgeschäfte.
//+------------------------------------------------------------------+ //| Close whenever price reverses the moving average | //+------------------------------------------------------------------+ void ma_close_positions(void) { //--- Is our buy position possibly weakening? if(system_state == 1) { if(iClose("EURUSD",PERIOD_D1,0) < ma_buffer[0]) Trade.PositionClose("EURUSD"); } //--- Is our sell position possibly weakening? if(system_state == -1) { if(iClose("EURUSD",PERIOD_D1,0) > ma_buffer[0]) Trade.PositionClose("EURUSD"); } }
Damit wir einen Handel eröffnen können, benötigen wir zunächst einen Ausbruch aus dem Bollinger Band, gefolgt von einer Bestätigung durch den RSI-Indikator, und schließlich möchten wir auch den gleitenden Durchschnitt auf der rechten Seite im Verhältnis zum Preis sehen.
//+------------------------------------------------------------------+ //| Check bearish setup | //+------------------------------------------------------------------+ void check_bearish_setup(void) { if(iClose("EURUSD",PERIOD_D1,0) < bb_low_buffer[0]) { if(50 > rsi_buffer[0]) { if(iClose("EURUSD",PERIOD_D1,0) < ma_buffer[0]) { Trade.Sell(0.3,"EURUSD",bid,0,0,"EURUSD MTF AI"); system_state = -1; } } } } //+------------------------------------------------------------------+ //| Check bullish setup | //+------------------------------------------------------------------+ void check_bullish_setup(void) { if(iClose("EURUSD",PERIOD_D1,0) > bb_high_buffer[0]) { if(50 < rsi_buffer[0]) { if(iClose("EURUSD",PERIOD_D1,0) > ma_buffer[0]) { Trade.Buy(0.3,"EURUSD",ask,0,0,"EURUSD MTF AI"); system_state = 1; } } } }
Diese Funktion zeigt derzeit nur die Vorhersage des Modells an.
//+------------------------------------------------------------------+ //| Display account stats | //+------------------------------------------------------------------+ void display_stats(void) { Comment("Forecast: ",model_output[0]); }
Abruf einer Vorhersage aus unserem Modell und Speicherung unter Verwendung einer binären Markierung.
//+------------------------------------------------------------------+ //| Fetch a prediction from our model | //+------------------------------------------------------------------+ void model_predict(void) { //--- Get inputs model_input.CopyRates("EURUSD",PERIOD_MN1,COPY_RATES_CLOSE,0,1); //--- Fetch a prediction from our model OnnxRun(onnx_model,ONNX_DEFAULT,model_input,model_output); //--- Store the model's prediction as a flag if(model_output[0] > model_input[0]) { model_state = -1; } else if(model_output[0] < model_input[0]) { model_state = 1; } }
Geben wir nun die Funktion an, mit der die nicht benötigten Ressourcen freigegeben werden sollen.
//+------------------------------------------------------------------+ //| Release the resources we don't need | //+------------------------------------------------------------------+ void release_resources(void) { OnnxRelease(onnx_model); IndicatorRelease(ma_hanlder); IndicatorRelease(rsi_hanlder); IndicatorRelease(bb_hanlder); ExpertRemove(); }
Immer wenn ein neuer Kurs notiert wird, wird diese Funktion aufgerufen, um die uns vorliegenden Marktdaten zu aktualisieren.
//+------------------------------------------------------------------+ //| Update our market data | //+------------------------------------------------------------------+ void update_market_data(void) { //--- Update all our technical data bid = SymbolInfoDouble("EURUSD",SYMBOL_BID); ask = SymbolInfoDouble("EURUSD",SYMBOL_ASK); CopyBuffer(ma_hanlder,0,0,1,ma_buffer); CopyBuffer(rsi_hanlder,0,0,1,rsi_buffer); CopyBuffer(bb_hanlder,0,0,1,bb_mid_buffer); CopyBuffer(bb_hanlder,1,0,1,bb_high_buffer); CopyBuffer(bb_hanlder,2,0,1,bb_low_buffer); }
Zum Schluss definieren wir die Funktion, die unser ONNX-Modell aus dem zuvor definierten Puffer erstellt.
//+------------------------------------------------------------------+ //| Load our ONNX model | //+------------------------------------------------------------------+ bool load_onnx_model(void) { //--- Create the ONNX model from our buffer onnx_model = OnnxCreateFromBuffer(onnx_buffer,ONNX_DEFAULT); //--- Validate the model if(onnx_model == INVALID_HANDLE) { //--- Give feedback Comment("Failed to create the ONNX model"); //--- We failed to create the model return(false); } //--- Specify the I/O shapes ulong input_shape[] = {1,1}; ulong output_shape[] = {1,1}; //--- Validate the I/O shapes if(!(OnnxSetInputShape(onnx_model,0,input_shape)) || !(OnnxSetOutputShape(onnx_model,0,output_shape))) { //--- Give feedback Comment("We failed to define the correct input shapes"); //--- We failed to define the correct I/O shape return(false); } return(true); } //+------------------------------------------------------------------+
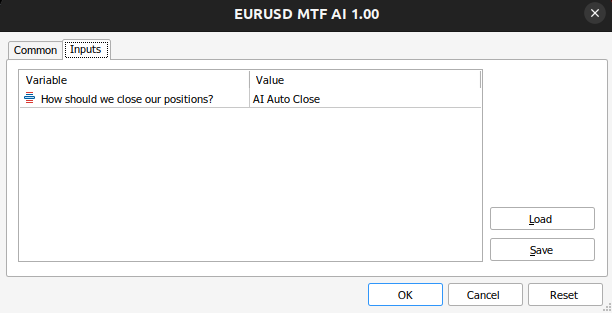
Abb. 13: Die Beiträge unseres Expertenberaters
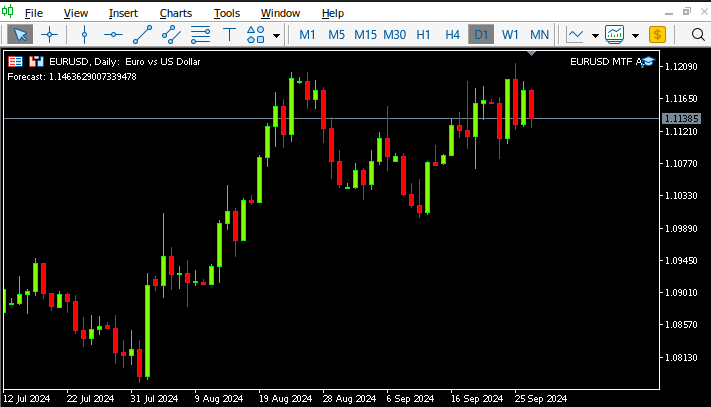
Abb. 14: Unser Expert Advisor in Aktion
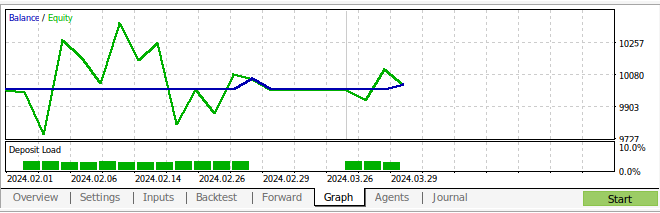
Abb. 15: Die Ergebnisse des Backtests unserer Strategie
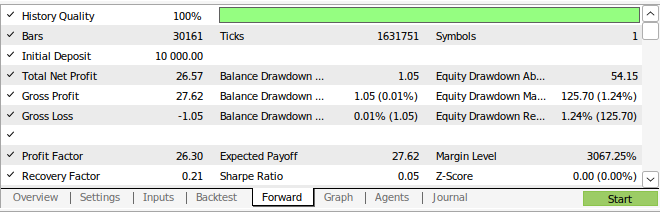
Abb. 16: Die Ergebnisse der Vorwärtsprüfung unserer Strategie
Schlussfolgerung
In diesem Artikel haben wir gezeigt, dass der monatliche und der stündliche Zeitrahmen für die Vorhersage des EURUSD-Paares am stabilsten zu sein scheinen. Wir können nicht davon ausgehen, dass dies für jeden bestehenden Markt gilt. Ebenso müssen wir in Zukunft in Betracht ziehen, mehr mögliche Zeitrahmen zu suchen, um sicherzustellen, dass wir keine optimalen Zeitrahmen übersehen. Darüber hinaus gibt es weitere Anpassungen, die wir an unserem Ansatz vornehmen können, um nach niedrigeren Fehlermetriken zu suchen. Wir möchten zum Beispiel wissen, ob es eine Kombination von Zeitrahmen gibt, die unsere Fehlerquote noch weiter senken könnte.
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/15972
Der Header im Connexus (Teil 3): Die Verwendung von HTTP-Headern für Anfragen beherrschen
MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 41): Deep-Q-Networks
Erstellen eines MQL5 Expert Advisors basierend auf der PIRANHA Strategie unter Verwendung von Bollinger Bändern
Wie man ein Handelsjournal mit MetaTrader und Google-Tabellen erstellt
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.