古典的な戦略を再構築する(第9回):多時間枠分析(II)
トレーダーが利用できる時間枠は数多く存在します。取引の方法を学び始めたばかりの初心者や、コミュニティに新しく参加したメンバーにとって、どの時間枠を選べばよいかという問題は非常に難しいものです。経験豊富なトレーダーでさえも、最適な時間枠を巡って意見を交わし、異なる視点を共有することがよくあります。本稿では、AIモデルの誤差レベルを最小化する時間枠を「最適」と定義することで、この問いに客観的に答えることを試みます。
本日のディスカッションでは、モデルの残差の分布に注目します。11種類の時間枠を調べた結果、月次および時間足の時間枠で誤差が低い領域が観察されました。ただし、モデルの誤差レベルの分布には明確なパターンは見られず、時間足のフレームでは誤差が最大値と最小値を示します。どの時間枠を使うべきかという長年の疑問に答えるためには、市場を変更しても残差の分布が変わらないことを確認する必要があります。さらに、将来的には利用可能なすべての時間枠を網羅的に調べるべきです。
取引手法の概要
ローソク足のパターンは、時間枠ごとに大きく異なるように見えるかもしれませんが、任意の時点で提示されている価格はどの時間枠でも1つだけです。トレーダーは市場の状態を把握するために、複数の時間枠を同時に分析することがよくあります。たとえば、トレンドが弱まりつつある場合、取引を開始した時間枠よりも低い時間枠で矛盾する値動きが見られる可能性があります。また、このような弱まりの兆候は、常に低い時間枠で最初に現れ、それが高い時間枠で明らかになるよりも先に見られます。
一般的に、複数の時間枠を用いた分析を含む戦略は、高い時間枠から市場のセンチメントを理解しようとします。成功しているトレーダーの中には、高い時間枠で形成される強気の包み足パターンのような、よく知られた価格アクションパターンを探す人もいます。これまで、これらのローソク足パターンの有無は、高確率の取引セットアップを探しているトレーダーにとってシグナルとして機能してきました。私たちは、EURUSDペアを予測する際に、どの時間枠が信頼できる誤差レベルを提供するのかをアルゴリズム的に学習したいと考えました。
ある程度、未来を予測しようとするほど困難になるという直感は、私たちが一般的に共有しているものです。しかし、今回の分析結果は、その信念を根本から覆すものでした。この結論が妥当であるかどうかを理解するためには、まず採用した方法論を説明する必要があります。
方法論の概要
テストが公平であるためには、各時間枠から同じ量のデータを収集する必要がありました。このステップの制限要因は、月次時間枠で利用可能なバーの数でした。400バー分の月次データは約33年分に相当します。これほど古い市場は非常に限られているため、すべての市場における最適な時間枠に関する理解に偏りが生じる可能性があります。しかし、今回の議論の範囲では、EURUSDペアは信頼できる豊富なデータセットを提供してくれます。
MetaTrader 5端末から400行の月次価格を取得しました。その後、EURUSDペアの将来の値に対応する400行を取得しました。この2ステップのプロセスを残りの10種類の時間枠についても繰り返しました。この分析のために選択した時間枠は次の通りです。
- 週次
- 日次
- H12
- H8
- H4
- H1
- M30
- M15
- M5
- M1
正直に言えば、特に周期的に近い時間枠間で強い相関が見られることを期待していました。しかし、全体的に観察された相関レベルは中程度でした。さらなる分析が必要だと思われる興味深い相関ペアは以下だけでした。
- 現在のH4価格と将来のH8価格
- 現在のM1価格と将来のH4価格
- 現在のM1価格と将来のM5価格
入力データには22列があり、相関行列は非常に大きくなるため、ここではすべてを表示しません。しかし、これまでのデータに基づいて11の入力セットを作成し、それぞれをテストしました。モデリングの結果、モデルは月次および1時間足の時間枠で最も高い性能を発揮することがわかりました。この結果は非常に直感に反するものでした。20ステップ先を予測することを目標にしました。20カ月先とは1年8カ月先のことです。私たちのモデルは、1年8カ月先(20カ月先)の価格変化を予測するほうが、20分後の価格変化を予測するよりも正確でした。
低い誤差を示した2つの時間枠(月次と1時間足)に興味を引かれ、価格データを周期的リターンに変換し、そのリターンについてグレンジャー因果性検定を実施しました。その結果、1時間足のリターンが月次リターンに対してグレンジャー因果を示す有意なp値が観測されました。この検定の結果、1時間足のリターンを用いて月次リターンをベクトル自己回帰(VAR)モデルでモデリングできることが確認されました。
さらに、Time Series Warpingライブラリを活用し、月次データと1時間足データを整列させ、それぞれの間に存在する類似点を特定しました。このアルゴリズムにより、データ間の多くの類似点を見つけることができました。この結果に自信を深め、月次モデルのパラメータを調整し、モデルをONNX形式にエクスポートすることに成功しました。
最後に、月次時間枠で予測される価格水準を用いて、1時間足時間枠で取引を実行するエキスパートアドバイザー(EA)を実装しました。このシステムでは、AIが予測した反転ポイントに基づいてポジションを閉じるか、移動平均を活用するかを切り替えることができます。また、ポジションエントリーのタイミングを決定するためにテクニカル分析を採用しました。
必要なデータの取得
最初に、MetaTrader 5ライブラリおよびその他の必要なライブラリをインポートすることから始めます。
#Import the libraries we need import pandas as pd import numpy as np import seaborn as sns import MetaTrader5 as mt5 from sklearn.model_selection import cross_val_score,train_test_split,TimeSeriesSplit from sklearn.metrics import mean_squared_error import matplotlib.pyplot as plt from sklearn.linear_model import LinearRegression
次に、端末にアクセスできるか確認します。
#Initialize the terminal
mt5.initialize()次に、テスト対象とする時間枠を定義します。
#Declare the time-frames we are interested in
time_frames = [mt5.TIMEFRAME_MN1,
mt5.TIMEFRAME_W1,
mt5.TIMEFRAME_D1,
mt5.TIMEFRAME_H12,
mt5.TIMEFRAME_H8,
mt5.TIMEFRAME_H4,
mt5.TIMEFRAME_H1,
mt5.TIMEFRAME_M30,
mt5.TIMEFRAME_M15,
mt5.TIMEFRAME_M5,
mt5.TIMEFRAME_M1
]取得するバーの数を設定します。
#How many bars should we fetch fetch = 400
20歩先の未来を予想しましょう。
#How far into the future should we forecast? look_ahead = 20
データフレームの列を定義します。
#Create our dataframe inputs = ["MN","W","D","H12","H8","H4","H1","M30","M15","M5","M1"] target = [] for i in np.arange(0,len(inputs)): target.append(inputs[i] + " Target")
価格を格納するデータフレームを作成します。
columns = inputs + target
prices = pd.DataFrame(columns=columns,index=np.arange(0,fetch))
図1:データフレームの入力の一部
図2:データフレームのターゲットの一部
誤差レベルを保存するデータフレームが必要です。
#The columns for our error levels data frame. error_columns = [] for i in np.arange(0,len(inputs)): error_columns.append(inputs[i]) #Create a dataframe to store our error levels error_levels = pd.DataFrame(columns=error_columns,index=[0]) test_error_levels = pd.DataFrame(columns=error_columns,index=[0])
必要な価格データを取得します。
for i in np.arange(0,len(time_frames)): print(i) prices.iloc[:,i] = pd.DataFrame(mt5.copy_rates_from_pos("EURUSD",time_frames[i],look_ahead,fetch)).loc[:,"close"] prices.iloc[:,i+10] = pd.DataFrame(mt5.copy_rates_from_pos("EURUSD",time_frames[i],0,fetch)).loc[:,"close"]
探索的データ分析
データフレームの相関レベルを分析してみましょう。H12とH8の時間枠の間に強い相関水準があることに注目してください。その他の相関関係で目立ったものは何でしょうか。
fig, ax = plt.subplots(figsize=(15,15)) sns.heatmap(prices.corr(),annot=True,ax=ax)
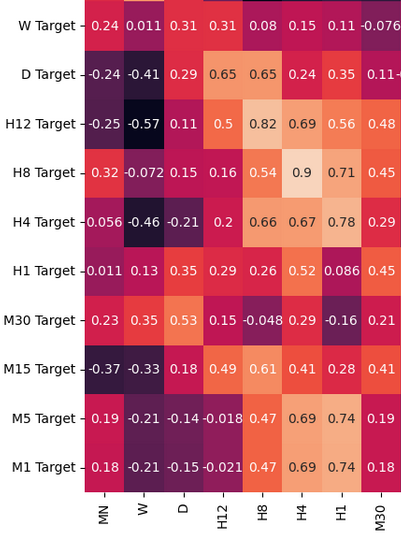
図3:相関行列から得られたいくつかの値
月足と週足の終値を散布図にすると、トレンドがはっきりしません。ほとんどの場合、データは全般的に上昇トレンドにあるようです。
sns.scatterplot(data=prices,x="MN Close",y="W Close")
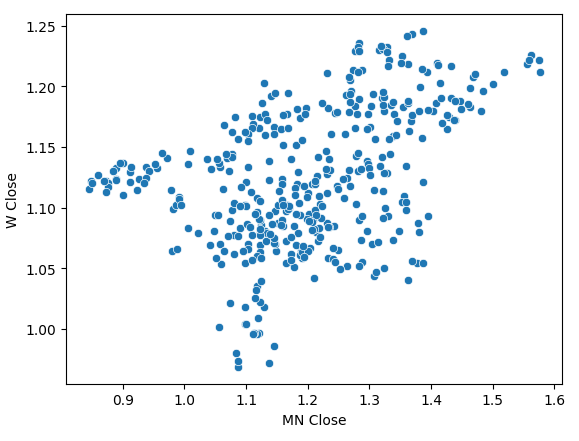
図4:月間終値と週間終値の散布図
価格データを周期的リターンに変換し、再度散布図を作成しました。今回は一般的なトレンドが現れ、リターンは0を中心に集まっているように見えます。
sns.scatterplot(data=prices.pct_change(),x="MN Close",y="W Close")
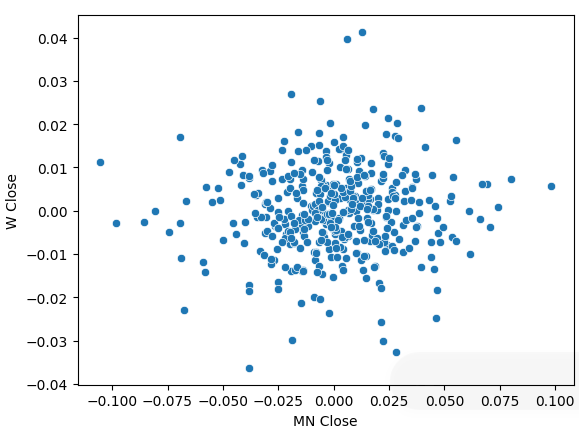
図5:異なる時間枠でのリターンの散布図
異なる時間枠のリターンを箱ひげ図にすると、別の傾向が見られます。リターンのばらつきは、月次の時間枠を離れ、下位の時間枠に移るにつれて小さくなります。同様に、すべての時間枠の平均リターンは0に近くなります。これは、ポートフォリオのリターンを最大化しようとするならば、より高い時間枠を考慮すべきであると解釈することもできます。
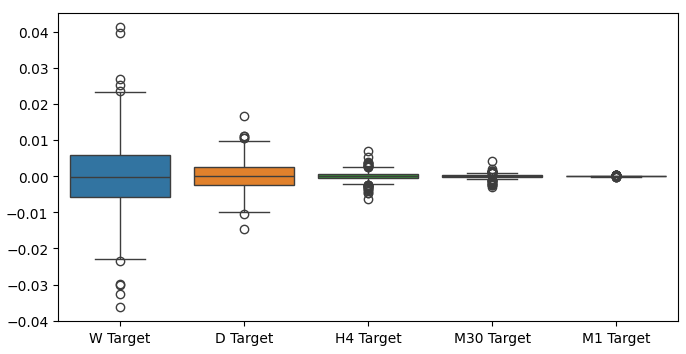
図6:異なる時間枠にわたるリターンの箱ひげ図
データモデル化の準備
では、データのモデリングを始めるために必要な準備をしましょう。まず、データを訓練用とテスト用に分ける必要があります。
#Create train test splits X_train_mn,X_test_mn,y_train_mn,y_test_mn = train_test_split(prices.loc[:,["MN"]],prices.loc[:,"MN Target"],test_size=0.5,shuffle=False) X_train_w,X_test_w,y_train_w,y_test_w = train_test_split(prices.loc[:,["W"]],prices.loc[:,"W Target"],test_size=0.5,shuffle=False) X_train_d,X_test_d,y_train_d,y_test_d = train_test_split(prices.loc[:,["D"]],prices.loc[:,"D Target"],test_size=0.5,shuffle=False) X_train_h12,X_test_h12,y_train_h12,y_test_h12 = train_test_split(prices.loc[:,["H12"]],prices.loc[:,"H12 Target"],test_size=0.5,shuffle=False) X_train_h8,X_test_h8,y_train_h8,y_test_h8 = train_test_split(prices.loc[:,["H8"]],prices.loc[:,"H8 Target"],test_size=0.5,shuffle=False) X_train_h4,X_test_h4,y_train_h4,y_test_h4 = train_test_split(prices.loc[:,["H4"]],prices.loc[:,"H4 Target"],test_size=0.5,shuffle=False) X_train_h1,X_test_h1,y_train_h1,y_test_h1 = train_test_split(prices.loc[:,["H1"]],prices.loc[:,"H1 Target"],test_size=0.5,shuffle=False) X_train_m30,X_test_m30,y_train_m30,y_test_m30 = train_test_split(prices.loc[:,["M30"]],prices.loc[:,"M30 Target"],test_size=0.5,shuffle=False) X_train_m15,X_test_m15,y_train_m15,y_test_m15 = train_test_split(prices.loc[:,["M15"]],prices.loc[:,"M15 Target"],test_size=0.5,shuffle=False) X_train_m5,X_test_m5,y_train_m5,y_test_m5 = train_test_split(prices.loc[:,["M5"]],prices.loc[:,"M5 Target"],test_size=0.5,shuffle=False) X_train_m1,X_test_m1,y_train_m1,y_test_m1 = train_test_split(prices.loc[:,["M1"]],prices.loc[:,"M1 Target"],test_size=0.5,shuffle=False)
次に、これらの分割をリストに格納します。
train_X = [ X_train_mn, X_train_w, X_train_d, X_train_h12, X_train_h8, X_train_h4, X_train_h1, X_train_m30, X_train_m15, X_train_m5, X_train_m1 ] test_X = [ X_test_mn, X_test_w, X_test_d, X_test_h12, X_test_h8, X_test_h4, X_test_h1, X_test_m30, X_test_m15, X_test_m5, X_test_m1 ]
目標値に対して上記の手順を繰り返します。
train_y = [ y_train_mn, y_train_w, y_train_d, y_train_h12, y_train_h8, y_train_h4, y_train_h1, y_train_m30, y_train_m15, y_train_m5, y_train_m1, ] test_y = [ y_test_mn, y_test_w, y_test_d, y_test_h12, y_test_h8, y_test_h4, y_test_h1, y_test_m30, y_test_m15, y_test_m5, y_test_m1, ]
各モデルを交差検証します。
#Record our error for i in np.arange(0,len(train_X)): #Fit the model model = LinearRegression() cv_score = cross_val_score(model,train_X[i],train_y[i],cv=5) error_levels.iloc[0,i] = np.mean(cv_score * -1) #Record validation error model.fit(train_X[i],train_y[i]) test_error_levels.iloc[0,i] = mean_squared_error(test_y[i],model.predict(test_X[i]))
それぞれの誤差レベル
error_levels
| MN | W | D | H12 | H8 | H4 | H1 | M30 | M15 | M5 | M1 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.719131 | 3.979435 | 3.897228 | 5.023601 | 5.218168 | 40.406227 | 0.196244 | 18.264356 | 3.680168 | 20.331821 | 3.540946 |
モデルの残差分布の近似を視覚化してみましょう。
fig, ax = plt.subplots(figsize=(7,4)) sns.barplot(error_levels,ax=ax)
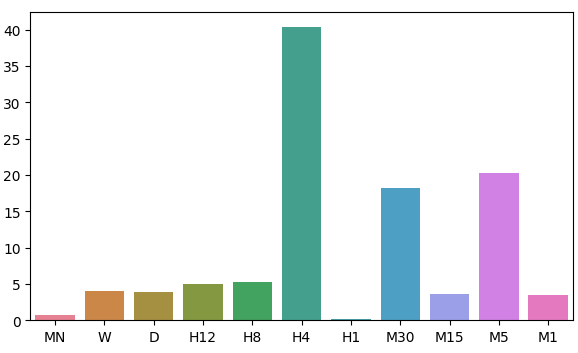
図7:モデルの誤差レベルの視覚化
特徴量の重要性
さて、最適な時間枠を特定したところで、これらの時間枠間に因果関係が存在するかどうかを確認してみましょう。1969年に英国の経済学者クライブ・グレンジャー卿は、2つの時系列データの間に因果関係があるかを実証的に判断する検定を提案しました。この検定は、1つの時系列データの過去の値がもう1つの時系列データの将来の値に影響を与えるかを評価します。簡単に言えば、時系列データをラグさせてその値を使用し、もう1つの時系列データの将来の値を予測する際に、予測の分散が著しく低下しなければ、グレンジャー検定は因果関係を肯定します。
グレンジャー検定はその後、多くの変更と改良を経てきました。現在では、神経科学から金融分野まで、幅広い業界で広く使用されています。このテストの使用については、半世紀以上にわたって学界で多くの議論の的となってきました。主な課題は、グレンジャー検定が暗黙的に仮定する線形性にあります。もし因果関係が非線形である場合、グレンジャー検定はその存在を否定してしまいます。また、このテストは通常、2つの時系列データに限定されるため、2つ以上の時系列データセットを持つ大規模な問題でグレンジャーの検定を使うことはほとんどありません。

図8:英国人エコノミスト、故クライブ・グレンジャー卿
手始めに、statsmodelsライブラリをインポートして、テストを実行します。このテストでは、1時間足の終値データのラグを利用します。pp値が0.05未満であれば、テストは合格です。初期のラグでこの条件を満たしましたが、それ以降のラグでは条件を満たさなかったため、1つ目のラグ以降には因果関係が存在しないと結論づけました。
from statsmodels.tsa.stattools import grangercausalitytests result = grangercausalitytests(prices[['H1 Close','MN Close']].pct_change().dropna(), maxlag=4)
number of lags (no zero) 1
ssr based F test: F=4.4913 , p=0.0347 , df_denom=395, df_num=1
ssr based chi2 test: chi2=4.5254 , p=0.0334 , df=1
likelihood ratio test: chi2=4.4999 , p=0.0339 , df=1
parameter F test: F=4.4913 , p=0.0347 , df_denom=395, df_num=1
Granger Causality
number of lags (no zero) 2
ssr based F test: F=2.2706 , p=0.1046 , df_denom=392, df_num=2
ssr based chi2 test: chi2=4.5991 , p=0.1003 , df=2
likelihood ratio test: chi2=4.5727 , p=0.1016 , df=2
parameter F test: F=2.2706 , p=0.1046 , df_denom=392, df_num=2
グレンジャーの因果関係は通常一方向に働きます。このことを、逆方向の因果関係をチェックすることで確かめましょう。どのp値も有意ではなかったので、因果関係は予想通り一方通行であることが確認できました。
result = grangercausalitytests(prices[['MN Close','H1 Close']].pct_change().dropna(), maxlag=4)
Granger Causality
number of lags (no zero) 1
ssr based F test: F=0.0188 , p=0.8909 , df_denom=395, df_num=1
ssr based chi2 test: chi2=0.0190 , p=0.8905 , df=1
likelihood ratio test: chi2=0.0190 , p=0.8905 , df=1
parameter F test: F=0.0188 , p=0.8909 , df_denom=395, df_num=1
Granger Causality
number of lags (no zero) 2
ssr based F test: F=2.2182 , p=0.1102 , df_denom=392, df_num=2
ssr based chi2 test: chi2=4.4930 , p=0.1058 , df=2
likelihood ratio test: chi2=4.4678 , p=0.1071 , df=2
parameter F test: F=2.2182 , p=0.1102 , df_denom=392, df_num=2
Granger Causality
number of lags (no zero) 3
ssr based F test: F=1.7310 , p=0.1601 , df_denom=389, df_num=3
ssr based chi2 test: chi2=5.2863 , p=0.1520 , df=3
likelihood ratio test: chi2=5.2513 , p=0.1543 , df=3
parameter F test: F=1.7310 , p=0.1601 , df_denom=389, df_num=3
Granger Causality
number of lags (no zero) 4
ssr based F test: F=1.4694 , p=0.2108 , df_denom=386, df_num=4
ssr based chi2 test: chi2=6.0148 , p=0.1980 , df=4
likelihood ratio test: chi2=5.9694 , p=0.2014 , df=4
parameter F test: F=1.4694 , p=0.2108 , df_denom=386, df_num=4
Dynamic Time Series Warpingは、2つの時系列データセット間の類似点を特定するための手法です。このアルゴリズムは、異なる長さの時系列データを整列させることもできます。私たちは、このアルゴリズムを用いて月次リターンと1時間足リターンの類似点を特定しました。アルゴリズムは、2つの時系列間の差を測定する特殊なコスト関数を最小化することで、このタスクを達成します。まず、必要なライブラリをインポートします。
#Let's calculate the simillarities between our time series data from dtaidistance import dtw from dtaidistance import dtw_visualisation as dtwvis
次に、リターンの類似性を見つけます。
series_1 = prices["MN Close"].pct_change(periods=1).dropna().reset_index(drop=True) * 100 series_2 = prices["H1 Close"].pct_change(periods=1).dropna().reset_index(drop=True) * 100 path = dtw.warping_path(series_1, series_2) dtwvis.plot_warping(series_1, series_2, path)
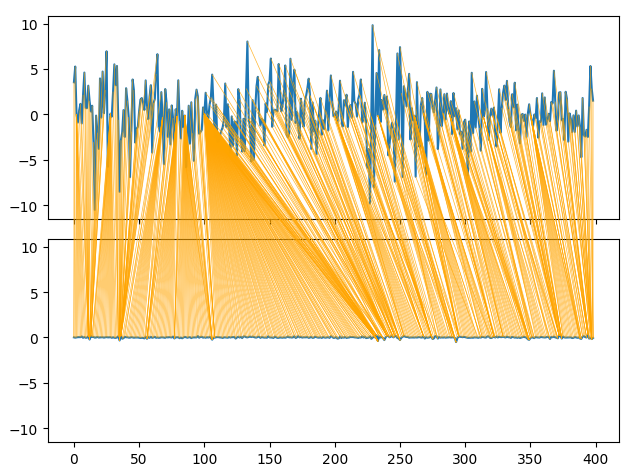
図9:月次リターンと毎時リターンの類似性の視覚化
パラメータチューニング
ここで、ディープニューラルネットワークのパラメータをチューニングして、線形回帰で設定されたベンチマークパフォーマンスを上回るようにしましょう。DNNの訓練に使用される最適化手順の性質上、このセクションで得られた結果を再現するのは難しいかもしれないことに注意してください。実のところ、このテストを5回おこないましたが、2回で Linearモデルを実行できませんでした。
必要なライブラリをインポートし、モデルを初期化します。
#Let's try to outperform our linear regression model from sklearn.neural_network import MLPRegressor from sklearn.model_selection import RandomizedSearchCV #Let's tune our model model = MLPRegressor(max_iter=500)
パラメータ空間を定義します。
#Tuner
tuner = RandomizedSearchCV(
model,
{
"activation" : ["relu","logistic","tanh","identity"],
"solver":["adam","sgd","lbfgs"],
"alpha":[0.1,0.01,0.001,0.0001,0.00001,0.00001,0.0000001,0.000000001,0.000000000000001],
"tol":[0.1,0.01,0.001,0.0001,0.00001,0.000001,0.0000001,0.000000001,0.000000000000001],
"learning_rate":['constant','adaptive','invscaling'],
"learning_rate_init":[1,0.1,0.0001,0.000001,100,10000,1000000,1000000000,100,1000],
"shuffle": [True,False],
"hidden_layer_sizes":[(1,4),(1,4,5),(1,8,10),(2,5),(8),(10,12),(5,10,4)]
},
n_iter=100,
cv=5,
n_jobs=-1,
scoring="neg_mean_squared_error"
)チューナーを適合させます。
tuner.fit(X_train_mn,y_train_mn)
以下が、見つかった最高のパラメータです。
tuner.best_params_
'solver': 'lbfgs',
'shuffle':True,
'learning_rate_init':1
'learning_rate': 'adaptive',
'hidden_layer_sizes':(2, 5),
'alpha':1e-05,
'activation': 'identity'}
より深い最適化
SciPyライブラリを使って最適なパラメータをより深く検索してみましょう。
#Deeper optimization
from scipy.optimize import minimize進捗状況を記録するためのデータ構造を作成します。
#Create a dataframe to store our accuracy current_error_rate = pd.DataFrame(index = np.arange(0,5),columns=["Current Error"]) optimization_progress = []
最小化する目的関数を定義します。モデルの平均二乗誤差を最小化したい。
#Define the objective function def objective(x): #The parameter x represents a new value for our neural network's settings #In order to find optimal settings, we will perform 10 fold cross validation using the new setting #And return the average RMSE from all 10 tests #We will first turn the model's Alpha parameter, which controls the amount of L2 regularization model = MLPRegressor(hidden_layer_sizes=tuner.best_params_["hidden_layer_sizes"], activation=tuner.best_params_["activation"], learning_rate=tuner.best_params_["learning_rate"], solver=tuner.best_params_["solver"], shuffle=tuner.best_params_["shuffle"], alpha=x[0], tol=x[1], learning_rate_init=x[2]) #Now we will cross validate the model for i,(train,test) in enumerate(tscv.split(X_train_mn)): #Train the model model.fit(X_train_mn.loc[train[0]:train[-1],:],y_train_mn.loc[train[0]:train[-1]]) #Measure the RMSE current_error_rate.iloc[i,0] = mean_squared_error(y_train_mn.loc[test[0]:test[-1]],model.predict(X_train_mn.loc[test[0]:test[-1],:])) #Record the progress made by the optimizer optimization_progress.append(current_error_rate.iloc[:,0].mean()) #Return the Mean CV RMSE return(current_error_rate.iloc[:,0].mean())
最適化手順の開始点を指定し、大域的最適化を近似できるように大きな境界を指定します。
#Define the starting point pt = [tuner.best_params_["alpha"],tuner.best_params_["tol"],tuner.best_params_["learning_rate_init"]] bnds = ((0.000000001,10000000000),(0.0000000001,10000000000),(0.000000001,10000000000))
DNNモデルを最適化します。
#Searchin deeper for parameters result = minimize(objective,pt,method="TNC",bounds=bnds)
最適化は成功したようです。
result
success:True
status:2
fun:0.04257403904271943
x:[4.864e-05 1.122e-03 9.999e-01].
nit:1
JAC: [ 1.298e+04 1.806e+02 -3.371e+03 ]。
nfev:92
最適値を保存します。
optima_y = result.fun
optima_x = optimization_progress.index(optima_y)
inputs = np.arange(0,len(optimization_progress))最適化手順の進捗状況を可視化します。
plt.scatter(inputs,optimization_progress) plt.plot(optima_x,optima_y,'s',color='r') plt.axvline(x=optima_x,ls='--',color='red') plt.axhline(y=optima_y,ls='--',color='red') plt.title("Minimizing Training MSE")
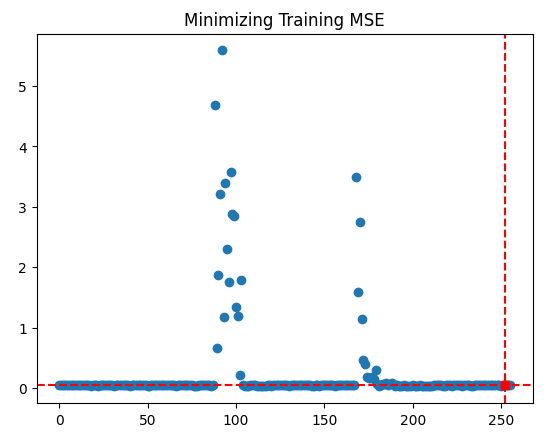
図10:TNC最適化手順の結果
過剰適合のテスト
デフォルトの線形モデルを本当に上回ることができるか見てみましょう。
#Test for overfitting benchmark = LinearRegression() default_model = MLPRegressor(max_iter=200) random_search_model = MLPRegressor(hidden_layer_sizes=tuner.best_params_["hidden_layer_sizes"], activation=tuner.best_params_["activation"], learning_rate=tuner.best_params_["learning_rate"], solver=tuner.best_params_["solver"], shuffle=tuner.best_params_["shuffle"], alpha=tuner.best_params_["alpha"], tol=tuner.best_params_["tol"], learning_rate_init=tuner.best_params_["learning_rate_init"], max_iter=200 ) lbfgs_model = MLPRegressor(hidden_layer_sizes=tuner.best_params_["hidden_layer_sizes"], activation=tuner.best_params_["activation"], learning_rate=tuner.best_params_["learning_rate"], solver=tuner.best_params_["solver"], shuffle=tuner.best_params_["shuffle"], alpha=result.x[0], tol=result.x[1], learning_rate_init=result.x[2], max_iter=200 )
訓練セットにモデルを適合します。
#Fit the models
benchmark.fit(X_train_mn,y_train_mn)
default_model.fit(X_train_mn,y_train_mn)
random_search_model.fit(X_train_mn,y_train_mn)
lbfgs_model.fit(X_train_mn,y_train_mn)交差検証のスコアを記録する準備をします。
#Record our cross val scores
models = [benchmark,
default_model,
random_search_model,
lbfgs_model
]
val_error = pd.DataFrame(columns=["Linear Reg","Default NN","Random Search NN","TNC NN"],index=[0])各モデルを交差検証します。
for i in np.arange(0,len(models)): val_error.iloc[0,i] = np.mean(cross_val_score(models[i],X_test_mn,y_test_mn,cv=5,n_jobs=-1)) * -1
検証の結果、TNCに最適化されたニューラルネットワークが最も優れていることが明らかになりました。
val_error
| Linear Reg | デフォルトNN | ランダムサーチNN | TNC NN |
|---|---|---|---|
| 3.323741 | 3.987083 | 3.314776 | 3.283775 |
ONNX形式へのエクスポート
モデルをONNX形式にエクスポートする準備をしましょう。ONNXはOpen Neural Network Exchangeの略で、あらゆる機械学習モデルを、計算と各計算後のデータの流れを表すノードのツリーとして表現するためのオープンソースのプロトコルです。ONNXは、ONNX仕様を実装している言語であれば、さまざまなプログラミング言語で機械学習モデルを構築し、使用することを可能にします。
ONNXライブラリをインポートして開始します。
#Preparing to export to ONNX import onnx from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType
モデルを準備します。
#Fit the model on all the data we have model = MLPRegressor( solver= 'lbfgs', shuffle= True, activation= 'identity', learning_rate= 'adaptive', hidden_layer_sizes= (2, 5), alpha= 4.864e-05, tol= 1.122e-03, learning_rate_init= 9.999e-01, )
保有するすべてのデータにモデルを適合させます。
model.fit(prices[["MN Close"]],prices.loc[:,"MN Target"])
モデルの入力形状を定義します。
#Define the input types for our ONNX model initial_types = [("float_input",FloatTensorType([1,1]))]
モデルのONNX表現を作成します。
# Create the ONNX representation onnx_model = convert_sklearn(model,initial_types=initial_types,target_opset=12)
モデルをONNX形式でエクスポートします。
# Save the ONNX model onnx.save_model(onnx_model,"EURUSD MN1 AI.onnx")
ここで、入力が適切なサイズであることを確認するために、ONNX形式でモデルを可視化してみましょう。
import netron
netron.start("EURUSD MN1 AI.onnx")
図11:DNNモデルの視覚化
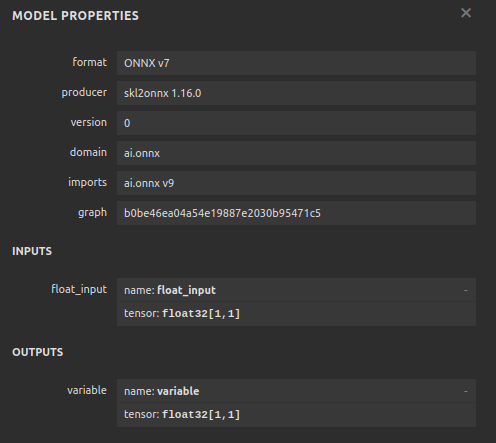
図12:モデルのI/O形状
MQL5での実装
MQL5で取引アルゴリズムを実装したいと思います。アルゴリズムが、単純な移動平均を使ったポジションの決済と、AIの予測を使ったポジションの決済を切り替えられるようにしたいと考えています。さらに、テクニカル分析を用いてAIモデルを導きたいです。まず始めに、上でエクスポートしたONNXモデルをインポートします。
//+------------------------------------------------------------------+ //| EURUSD MTF AI.mq5 | //| Gamuchirai Zororo Ndawana | //| https://www.mql5.com/ja/gamuchiraindawa | //+------------------------------------------------------------------+ #property copyright "Gamuchirai Zororo Ndawana" #property link "https://www.mql5.com/ja/gamuchiraindawa" #property version "1.00" //+------------------------------------------------------------------+ //| Load the ONNX resources | //+------------------------------------------------------------------+ #resource "\\Files\\EURUSD MN1 AI.onnx" as const uchar onnx_buffer[];
次に、ユーザーがどのようにポジションを閉じたいかを指定するために、カスタム列挙子を定義します。
//+-------------------------------------------------------------------+ //| Define our custom type | //+-------------------------------------------------------------------+ enum close_type { MA_CLOSE = 0, // Moving Averages Close AI_CLOSE = 1 // AI Auto Close };
入力を作成し、アプリケーションがポジションを閉じる方法を変更し、どちらが良いかを調べてみましょう。
//+------------------------------------------------------------------+ //| User inputs | //+------------------------------------------------------------------+ input close_type user_close_type = AI_CLOSE; // How should we close our positions?
取引クラスをインポートする必要があります。
//+------------------------------------------------------------------+ //| Libraries we need | //+------------------------------------------------------------------+ #include <Trade\Trade.mqh> CTrade Trade;
プログラム全体で必要となるグローバル変数を作成します。
//+------------------------------------------------------------------+ //| Global variables | //+------------------------------------------------------------------+ long onnx_model; vectorf model_input = vectorf::Zeros(1); vectorf model_output = vectorf::Zeros(1); double bid,ask; int ma_hanlder; double ma_buffer[]; int bb_hanlder; double bb_mid_buffer[]; double bb_high_buffer[]; double bb_low_buffer[]; int rsi_hanlder; double rsi_buffer[]; int system_state = 0,model_state=0;
アプリケーションがロードされると、まず、先に作成したバッファからONNXモデルを作成します。次に、テクニカルインジケーターハンドラを割り当てます。
//+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- Load our ONNX function if(!load_onnx_model()) { return(INIT_FAILED); } //--- Load our technical indicators bb_hanlder = iBands("EURUSD",PERIOD_D1,30,0,1,PRICE_CLOSE); rsi_hanlder = iRSI("EURUSD",PERIOD_D1,14,PRICE_CLOSE); ma_hanlder = iMA("EURUSD",PERIOD_D1,20,0,MODE_EMA,PRICE_CLOSE); //--- return(INIT_SUCCEEDED); }
エキスパートアドバイザー(EA)がチャートから削除された場合、使用しなくなったリソースを解放する必要があります。
//+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- Release the resources we don't need release_resources(); }
現在、更新された価格を受け取るたびに、まず新しい技術データを保存し、モデルから予測をおこない、そして重要な統計情報をユーザーに表示します。ポジションがなければ、モデルの予測に従います。そうでない場合は、ユーザーの入力に従って、ポジションをオープンにしておくかクローズしておくかを決定します。
//+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- Update market data update_market_data(); //--- Fetch a prediction from our model model_predict(); //--- Display stats display_stats(); //--- Find a position if(PositionsTotal() == 0) { if(model_state == 1) check_bullish_setup(); else if(model_state == -1) check_bearish_setup(); } //--- Manage the position we have else { //--- How should we close our positions? if(user_close_type == MA_CLOSE) { ma_close_positions(); } else { ai_close_positions(); } } } //+------------------------------------------------------------------+
それでは、AIシステムがどのように取引を終了するかを定義してみましょう。AIシステムが、価格水準がポジションの主張と矛盾する形で変化することを検知した場合、取引を終了します。
//+------------------------------------------------------------------+ //| Close whenever our AI detects a reversal | //+------------------------------------------------------------------+ void ai_close_positions(void) { if(system_state != model_state) { Alert("Reversal detected by our AI system,closing open positions"); Trade.PositionClose("EURUSD"); } }
一方、ポジションの決済を移動平均線に頼るのであれば、終値が移動平均線を上回ったら売りポジションを決済し、逆に移動平均線を下回ったら売りポジションを決済します。
//+------------------------------------------------------------------+ //| Close whenever price reverses the moving average | //+------------------------------------------------------------------+ void ma_close_positions(void) { //--- Is our buy position possibly weakening? if(system_state == 1) { if(iClose("EURUSD",PERIOD_D1,0) < ma_buffer[0]) Trade.PositionClose("EURUSD"); } //--- Is our sell position possibly weakening? if(system_state == -1) { if(iClose("EURUSD",PERIOD_D1,0) > ma_buffer[0]) Trade.PositionClose("EURUSD"); } }
取引を開始するには、まずボリンジャーバンドのブレイクアウトとそれに続くRSIインジケーターの確認が必要であり、最後に価格との関係で正しい側の移動平均も確認する必要があります。
//+------------------------------------------------------------------+ //| Check bearish setup | //+------------------------------------------------------------------+ void check_bearish_setup(void) { if(iClose("EURUSD",PERIOD_D1,0) < bb_low_buffer[0]) { if(50 > rsi_buffer[0]) { if(iClose("EURUSD",PERIOD_D1,0) < ma_buffer[0]) { Trade.Sell(0.3,"EURUSD",bid,0,0,"EURUSD MTF AI"); system_state = -1; } } } } //+------------------------------------------------------------------+ //| Check bullish setup | //+------------------------------------------------------------------+ void check_bullish_setup(void) { if(iClose("EURUSD",PERIOD_D1,0) > bb_high_buffer[0]) { if(50 < rsi_buffer[0]) { if(iClose("EURUSD",PERIOD_D1,0) > ma_buffer[0]) { Trade.Buy(0.3,"EURUSD",ask,0,0,"EURUSD MTF AI"); system_state = 1; } } } }
この関数は現在、モデルの予測だけを表示します。
//+------------------------------------------------------------------+ //| Display account stats | //+------------------------------------------------------------------+ void display_stats(void) { Comment("Forecast: ",model_output[0]); }
モデルから予測値を取得し、バイナリフラグを使って保存します。
//+------------------------------------------------------------------+ //| Fetch a prediction from our model | //+------------------------------------------------------------------+ void model_predict(void) { //--- Get inputs model_input.CopyRates("EURUSD",PERIOD_MN1,COPY_RATES_CLOSE,0,1); //--- Fetch a prediction from our model OnnxRun(onnx_model,ONNX_DEFAULT,model_input,model_output); //--- Store the model's prediction as a flag if(model_output[0] > model_input[0]) { model_state = -1; } else if(model_output[0] < model_input[0]) { model_state = 1; } }
ここで、不要なリソースを解放する関数を指定してみましょう。
//+------------------------------------------------------------------+ //| Release the resources we don't need | //+------------------------------------------------------------------+ void release_resources(void) { OnnxRelease(onnx_model); IndicatorRelease(ma_hanlder); IndicatorRelease(rsi_hanlder); IndicatorRelease(bb_hanlder); ExpertRemove(); }
新しい価格が提示されるたびに、この関数が呼び出され、マーケットデータが更新されます。
//+------------------------------------------------------------------+ //| Update our market data | //+------------------------------------------------------------------+ void update_market_data(void) { //--- Update all our technical data bid = SymbolInfoDouble("EURUSD",SYMBOL_BID); ask = SymbolInfoDouble("EURUSD",SYMBOL_ASK); CopyBuffer(ma_hanlder,0,0,1,ma_buffer); CopyBuffer(rsi_hanlder,0,0,1,rsi_buffer); CopyBuffer(bb_hanlder,0,0,1,bb_mid_buffer); CopyBuffer(bb_hanlder,1,0,1,bb_high_buffer); CopyBuffer(bb_hanlder,2,0,1,bb_low_buffer); }
最後に、先ほど定義したバッファからONNXモデルを作成する関数を定義しましょう。
//+------------------------------------------------------------------+ //| Load our ONNX model | //+------------------------------------------------------------------+ bool load_onnx_model(void) { //--- Create the ONNX model from our buffer onnx_model = OnnxCreateFromBuffer(onnx_buffer,ONNX_DEFAULT); //--- Validate the model if(onnx_model == INVALID_HANDLE) { //--- Give feedback Comment("Failed to create the ONNX model"); //--- We failed to create the model return(false); } //--- Specify the I/O shapes ulong input_shape[] = {1,1}; ulong output_shape[] = {1,1}; //--- Validate the I/O shapes if(!(OnnxSetInputShape(onnx_model,0,input_shape)) || !(OnnxSetOutputShape(onnx_model,0,output_shape))) { //--- Give feedback Comment("We failed to define the correct input shapes"); //--- We failed to define the correct I/O shape return(false); } return(true); } //+------------------------------------------------------------------+
図13:エキスパートアドバイザーの入力
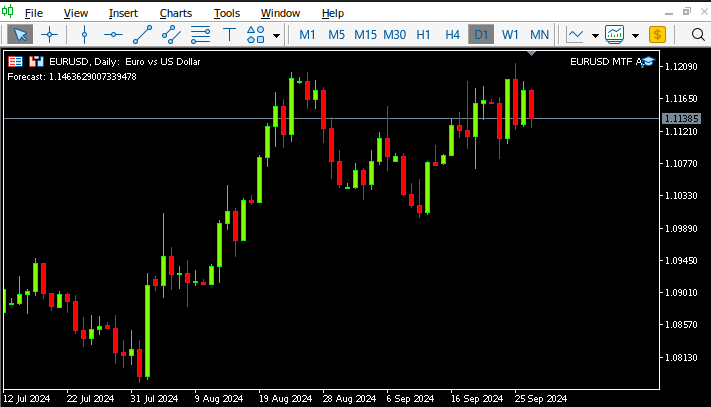
図14:EAの動作
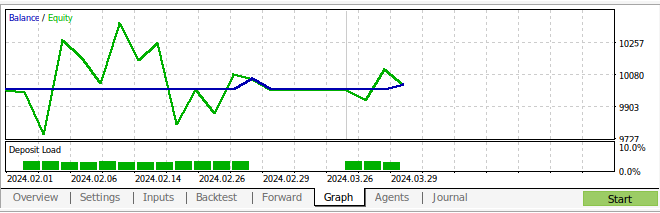
図15:戦略のバックテスト結果
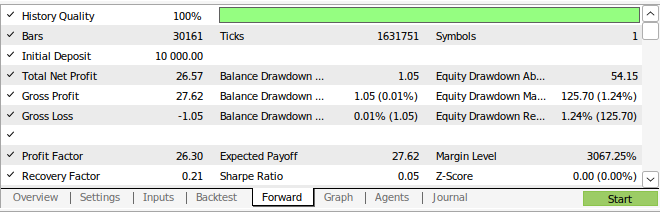
図16:戦略のウォークフォワードテストの結果
結論
この記事では、EURUSDペアの予測には月足と時間足が最も安定しているように見えることを示しました。これがすべての既存市場に当てはまるとは断言できません。同様に、最適な時間枠を見落とさないよう、今後はより多くの可能な時間枠を探索することも検討しなければなりません。さらに、より低い誤差メトリックを探すために、アプローチにさらなる調整を加えることができます。たとえば、誤差レベルをさらに下げることができる時間枠の組み合わせがあるかどうかを理解したいと思うかもしれません。
MetaQuotes Ltdにより英語から翻訳されました。
元の記事: https://www.mql5.com/en/articles/15972
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。
この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。
 知っておくべきMQL5ウィザードのテクニック(第41回):DQN (Deep-Q-Network)
知っておくべきMQL5ウィザードのテクニック(第41回):DQN (Deep-Q-Network)
 MQL5-Telegram統合エキスパートアドバイザーの作成(第7回):チャート上のインジケーター自動化のためのコマンド解析
MQL5-Telegram統合エキスパートアドバイザーの作成(第7回):チャート上のインジケーター自動化のためのコマンド解析
 MQL5とPythonで自己最適化エキスパートアドバイザーを構築する(第5回):深層マルコフモデル
MQL5とPythonで自己最適化エキスパートアドバイザーを構築する(第5回):深層マルコフモデル
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索
