
重思经典策略(第八部分):基于美元兑加元(USDCAD)探讨外汇市场与贵金属
通过本系列文章,我们旨在探索人工智能在交易策略中可能的应用领域。我们的目标是为您提供所需的信息,以便您在使用基于人工智能的策略投资资金之前能够做出明智的决策。希望您能够找到一种适合您特定风险承受水平的策略。
交易策略概览
在今天的讨论中,我们将探讨货币市场与贵金属市场之间的关系。贵金属是任何现代经济体系中不可或缺的一部分。这归因于它们广泛的工业用途,从电子到医疗保健,无所不涉及。贵金属价格的波动会导致制成品生产商面临通胀压力,这可能会降低国内生产水平,或者另一方面,对于出口这些金属的国家来说,可能会导致需求下降。
黄金是加拿大和美国的主要矿物出口产品之一。黄金天然的抗腐蚀性使其在敏感电子设备开发商和珠宝商中都备受青睐。相比之下,钯金则受到众多行业的青睐,尤其是汽车行业。汽车中有超过20个不同的部件需要催化转换器,其中最广为人知的是安装在排气管中的催化转换器。这些转换器中都含有相当数量的钯金。加拿大和美国都是汽车的主要出口国。因此,这些贵金属的价格将对这两个国家的国内出产造成一定的影响。
在过去,黄金价格与美元汇率呈反向关系。每当美元表现不佳时,投资者往往会平仓他们对美元的看好预期,转而将资金投入黄金以对冲风险。然而,在如今的量化宽松时代,这种相关性已不再那么明显。
方法论概述
我们希望让计算机从这三大市场的价格中自行学习交易策略。自然地,我们可能会倾向于相信那些对我们有吸引力或符合直觉的策略,而不是那些不符合的策略。然而,通过算法学习策略,计算机也许能够发现我们一生都难以发现的关系。或者,它也可能会揭示我们策略的准确度存在的局限性。为了评估贵金属市场在预测外汇市场领域的可靠性,我们尝试使用三组预测因子来预测美元兑加元(USDCAD)的汇率:
- 美元兑加元(USDCAD)报价
- 黄金兑美元(XAUUSD)和钯金兑美元(XPDUSD)报价
- 上述两组数据的组合。
我们通过在MetaTrader 5终端上运行我们用MQL5编写的定制脚本,直接获取了所有数据。我们将数据导出为CSV格式,并在Python中进行处理。此外,我们观察到显著的负相关性:XAUUSD与USDCAD之间的相关系数为-0.5,XPDUSD与USDCAD之间的相关系数为-0.66。然而,两种金属之间的直接相关性仅为0.37,属于中等水平。
我们尝试对数据进行可视化。然而,却未能从数据中发现任何明显的关联关系。我们还尝试使用3D散点图在更高维度上绘制数据,但同样没有成功。这些数据似乎很难被有效地分离开。
之前,我们训练了几个模型,使用前面提到的三组预测因子来预测美元兑加元(USDCAD)的汇率。表现最佳的模型是使用第一组预测因子的线性模型。然而,由于线性模型没有可调整的参数,我们选择了表现第二的模型——线性支持向量回归器(Linear Support Vector Regressor,LSVR)作为我们的最佳模型。
我们成功地调整了LSVR模型的超参数,而没有过度拟合训练集,这体现在我们在未见数据上的表现超过了默认的LSVR模型。遗憾的是,我们在相同的验证数据上未能超过线性模型。无论是训练还是验证阶段,我们都采用5折时间序列交叉验证(不进行随机打乱)计算平均均方根误差(RMSE)来进行模型选择。
之后,我们将定制的LSVR模型导出为ONNX格式,并使用MQL5构建了我们自己的带有集成人工智能的EA。
数据收集
我为您准备了一个便捷的脚本,用于从您的MetaTrader 5终端获取数据。只需将该脚本附加到您想要分析的任何图表上,即可开始。
该脚本将获取您在输入中指定的多根柱线,并将它们以CSV格式导出。写入时间是至关重要的,因为稍后当我们希望在Python中将CSV文件并入成为一个合并的数据帧时,我们会用到它。我们只会在它们共有的日期上合并数据。
请注意,我们包含了属性:“#property script_show_inputs”,如果您的脚本中没有包含这个属性,那么您将无法调整脚本的输入。
//+------------------------------------------------------------------+ //| ProjectName | //| Copyright 2020, CompanyName | //| http://www.companyname.net | //+------------------------------------------------------------------+ #property copyright "Gamuchirai Zororo Ndawana" #property link "https://www.mql5.com/en/users/gamuchiraindawa" #property version "1.00" #property script_show_inputs //---Amount of data requested input int size = 100000; //How much data should we fetch? //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void OnStart() { //---File name string file_name = "Market Data " + Symbol() + ".csv"; //---Write to file int file_handle=FileOpen(file_name,FILE_WRITE|FILE_ANSI|FILE_CSV,","); for(int i= size;i>=0;i--) { if(i == size) { FileWrite(file_handle,"Time","Open","High","Low","Close"); } else { FileWrite(file_handle,iTime(Symbol(),PERIOD_CURRENT,i), iOpen(Symbol(),PERIOD_CURRENT,i), iHigh(Symbol(),PERIOD_CURRENT,i), iLow(Symbol(),PERIOD_CURRENT,i), iClose(Symbol(),PERIOD_CURRENT,i)); } } } //+------------------------------------------------------------------+
现在我们的数据已经准备好,可以在Python中开始清理数据。
数据清理
首先,我们将导入我们需要的标准库。
#Import the libraries we need import pandas as pd import numpy as np
这是我们在这次演示中使用的库的版本。
#Display library versions print(f"Pandas version {pd.__version__}") print(f"Numpy version {np.__version__}")
Numpy 1.26.4版
现在,读取我们获得的CSV数据。
#Read in the data we need usdcad = pd.read_csv("\\home\\volatily\\.wine\\drive_c\\Program Files\\MetaTrader 5\\MQL5\\Files\\Market Data USDCAD.csv") usdcad = usdcad[::-1] xauusd = pd.read_csv("\\home\\volatily\\.wine\\drive_c\\Program Files\\MetaTrader 5\\MQL5\\Files\\Market Data XAUUSD.csv") xauusd = xauusd[::-1] xpdusd = pd.read_csv("\\home\\volatily\\.wine\\drive_c\\Program Files\\MetaTrader 5\\MQL5\\Files\\Market Data XPDUSD.csv") xpdusd = xpdusd[::-1]
使用时间列作为索引。
#Set the time column as the index usdcad.set_index("Time",inplace=True) xauusd.set_index("Time",inplace=True) xpdusd.set_index("Time",inplace=True)
合并数据。
#Let's merge the data
merged_data = usdcad.merge(xauusd,suffixes=('',' XAU'),left_index=True,right_index=True)
merged_data = merged_data.merge(xpdusd,suffixes=('',' XPD'),left_index=True,right_index=True)
这就是我们的数据。
merged_data
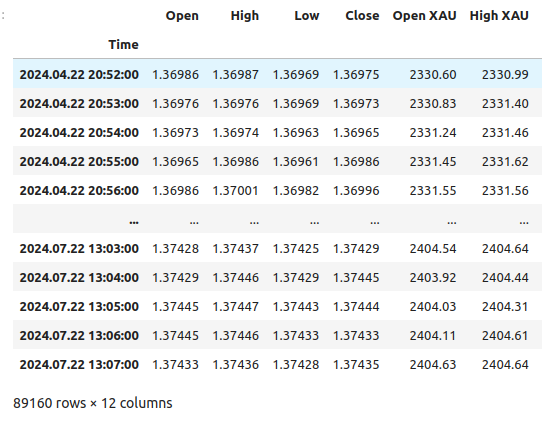
图1:我们合并后的数据帧
让我们定义希望预测多久之后的未来。
#Define the forecast horizon look_ahead = 20
定义我们想要测试的3组预测因子。
#Define the predictors and target ohlc_predictors = ['Open','High','Low','Close'] new_predictors = ['Open XAU','High XAU','Low XAU','Close XAU','Open XPD','High XPD','Low XPD','Close XPD'] predictors = ohlc_predictors + new_predictors
标记数据。
#Let's add labels to the data merged_data["Target"] = merged_data["Close"].shift(-look_ahead)
让我们也来创建标签,这些标签在我们可视化数据时会很有帮助。标签将总结每次市场的变化。
#Let's also add labels to help us visualize the relationships merged_data["Binary Target"] = np.nan merged_data["XAU Target"] = np.nan merged_data["XPD Target"] = np.nan #Define the target values #Changes in the USDCAD Exchange rate merged_data.loc[merged_data["Close"] > merged_data["Target"],"Binary Target"] = 0 merged_data.loc[merged_data["Close"] < merged_data["Target"],"Binary Target"] = 1 #Changes in the price of Gold merged_data.loc[merged_data["Close XAU"] > merged_data["Close XAU"].shift(-look_ahead),"XAU Target"] = 0 merged_data.loc[merged_data["Close XAU"] < merged_data["Close XAU"].shift(-look_ahead),"XAU Target"] = 1 #Changes in the price of Palladium merged_data.loc[merged_data["Close XPD"] > merged_data["Close XPD"].shift(-look_ahead),"XPD Target"] = 0 merged_data.loc[merged_data["Close XPD"] < merged_data["Close XPD"].shift(-look_ahead),"XPD Target"] = 1 #Drop any NA values merged_data.dropna(inplace=True)
探索性数据分析
为了可视化我们的数据,我们首先需要导入必要的库。
#Explorartory data analysis import seaborn as sns import matplotlib.pyplot as plt
显示库的版本。
#Display library version print(f"Seaborn version: {sns.__version__}")
首先,让我们重置合并数据帧的索引。
#Reset the index
merged_data.reset_index(inplace=True)
现在,让我们创建一个相关性热力图。正如我们所见,两种贵金属与美元兑加元(USDCAD)货币对之间存在显著的强相关性。这与我们对这两种金属在两国国内生产总值(GDP)中所起作用的基本分析是一致的。遗憾的是,在尝试预测美元兑加元(USDCAD)汇率时,这并没有带来更好的表现。#Correlation heatmap fig , ax = plt.subplots(figsize=(7,7)) sns.heatmap(merged_data.loc[:,predictors].corr(),annot=True,ax=ax)
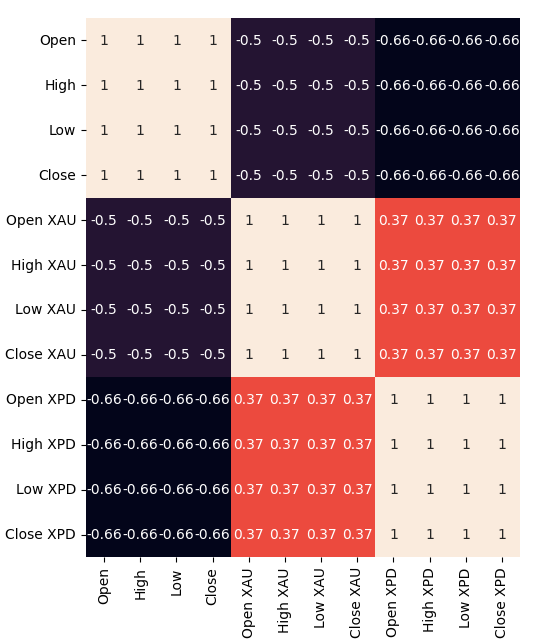
图2:我们的相关性热力图
我们创建了两个分类图,总结了黄金或钯金价格上涨(第1列)或下跌(第2列)的所有情况。然后,我们用颜色标记每个点,以表示美元兑加元汇率是上涨(用橙色点表示)还是下跌(用蓝色点表示)。正如所见,两列中都包含了这两种结果的混合。这可能表明,美元兑加元汇率的变化与我们所选贵金属的变化是独立的。
#Let's create categorical plots sns.catplot(data=merged_data,x="XAU Target",y="Close",hue="Binary Target")

图3:黄金价格和美元兑加元收盘价的分类图
#Let's create categorical plots sns.catplot(data=merged_data,x="XPD Target",y="Close",hue="Binary Target")
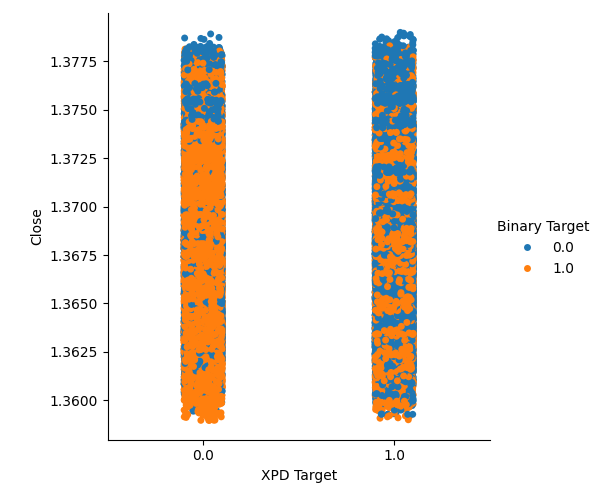
图4:钯金价格与美元兑加元价格的分类图
随后,我们创建了散点图,用于可视化钯金收盘价与美元兑加元市场之间的差异。遗憾的是,这并没有产生我们可以利用的任何明显关系。我们使用上述相同的橙色和蓝色配色方案来标记每个点。
#Let's visualize scatter plots sns.scatterplot(data=merged_data,x="Close XPD",y="Close",hue="Binary Target")
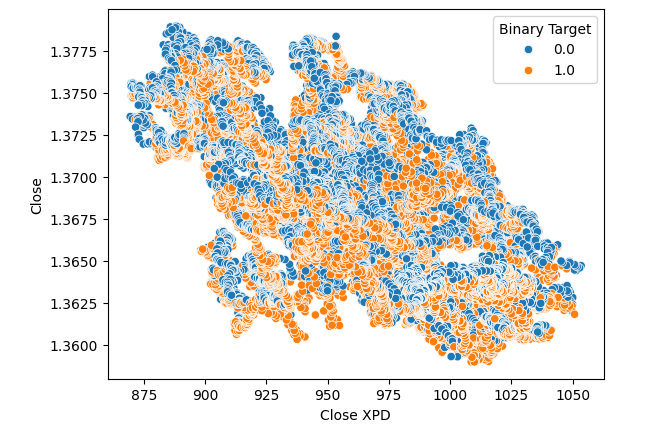
图5:钯金兑美元与美元兑加元散点图
当我们在散点图中用黄金价格替换钯金价格时,并没有取得任何改进。
#Let's visualize scatter plots sns.scatterplot(data=merged_data,x="Close XAU",y="Close",hue="Binary Target")
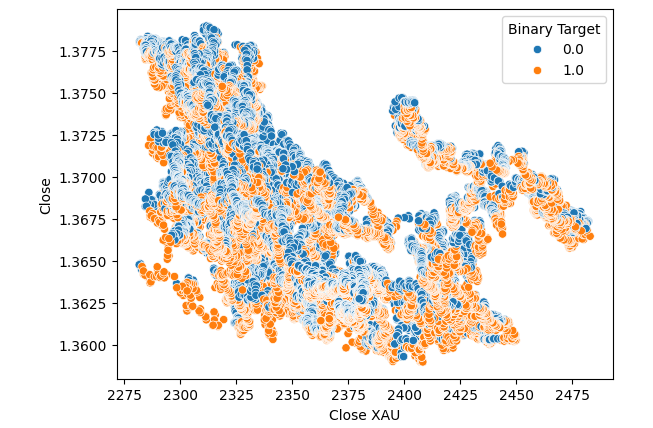
图6:黄金兑美元对美元兑加元收盘价的散点图
我们考虑尝试测试这两种金属之间的关系。然而,这种关系对我们来说仍然不明显。我们创建了一个黄金价格与钯金价格的散点图,并使用美元兑加元货币对的变化来标记每个点,但这样也并没有带来任何改进。
#Let's visualize scatter plots sns.scatterplot(data=merged_data,x="Close XPD",y="Close XAU",hue="Binary Target")
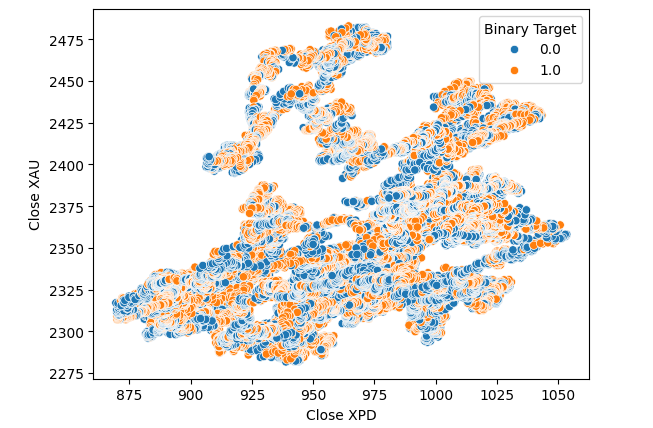
图7:黄金兑美元与钯金对美元散点图
关系有时候可能被隐藏起来,因为我们没有同时查看足够多的变量来观察到其影响。我们创建了一个3D散点图,使用钯金、黄金的收盘价以及美元兑加元。遗憾的是,结果图强调了数据中似乎存在聚集,但这些聚集的分离度很差,基本上重申了我们到目前为止已经知晓的内容。
#Visualizing 3D data fig = plt.figure(figsize=(7,7)) ax = fig.add_subplot(111,projection='3d') colors = ['blue' if movement == 0 else 'orange' for movement in merged_data.loc[0:1100,"Binary Target"]] ax.scatter(merged_data.loc[0:1100,"Close"],merged_data.loc[0:1100,"Close XAU"],merged_data.loc[0:1100,"Close XPD"],c=colors) #Set labels ax.set_xlabel('USDCAD') ax.set_ylabel('XAUUSD') ax.set_zlabel('XPDUSD')
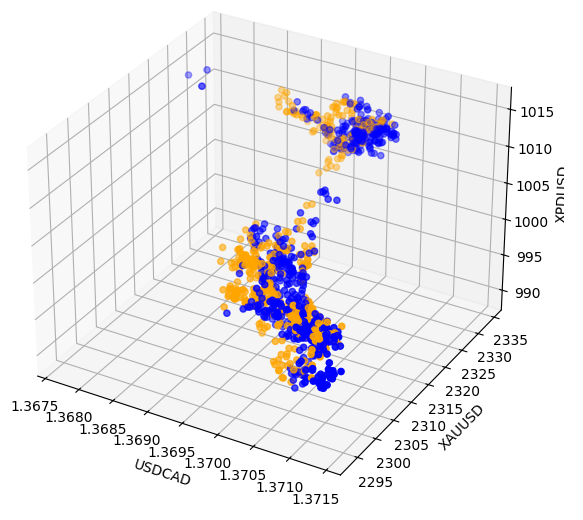
图8:以3D方式可视化我们的市场数据
数据建模
让我们开始准备对数据进行建模。首先,我们将导入标准库。
#Modelling the data
import sklearn
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import RobustScaler
显示库的版本。
#Print library version print(f"Sklearn version {sklearn.__version__}")
Sklearn 1.4.1.post1版
在开始训练任何模型之前,我们需要先对数据进行缩放和标准化处理。
#Scale the data
scaled_data = pd.DataFrame(RobustScaler().fit_transform(merged_data.loc[:,predictors]),columns=predictors)
现在,我们将把数据分成两部分,一部分用于训练和优化,另一部分用于验证和测试过拟合。
#Split the data train_X,test_X,train_y,test_y = train_test_split(scaled_data,merged_data.loc[:,"Target"],shuffle=False,test_size=0.5)
现在导入模型。
#Preparing to model the data from sklearn.model_selection import TimeSeriesSplit from sklearn.linear_model import LinearRegression from sklearn.ensemble import RandomForestRegressor , GradientBoostingRegressor , BaggingRegressor from sklearn.svm import LinearSVR from sklearn.neighbors import KNeighborsRegressor from sklearn.neural_network import MLPRegressor from sklearn.metrics import root_mean_squared_error
创建时间序列拆分对象。
#Create the time series split object tscv = TimeSeriesSplit(gap=look_ahead,n_splits=5)
将模型存储在列表中,以便我们可以进行迭代。
#Create a list of models models = [ LinearRegression(), RandomForestRegressor(), GradientBoostingRegressor(), BaggingRegressor(), LinearSVR(), KNeighborsRegressor(), MLPRegressor(hidden_layer_sizes=(100,10)) ]
创建一个数据帧来存储我们的准确度。
#List of models columns = [ "Linear Regression", "Random Forest", "Gradient Boost", "Bagging", "Linear SVR", "K-Neighbors", "Neural Network" ] #Create a dataframe to store our error metrics ohlc_error = pd.DataFrame(columns=columns,index=np.arange(0,5)) new_error = pd.DataFrame(columns=columns,index=np.arange(0,5)) all_error = pd.DataFrame(columns=columns,index=np.arange(0,5))
定义要使用的预测器。
#Setting the current predictors
current_predictors = predictors
使用上面定义的预测器交叉验证每个模型。
#Perform cross validation for j in np.arange(0,len(models)): model = models[j] for i,(train,test) in enumerate(tscv.split(train_X)): model.fit(train_X.loc[train[0]:train[-1],current_predictors],train_y.loc[train[0]:train[-1]]) all_error.iloc[i,j] = root_mean_squared_error(train_y.loc[test[0]:test[-1]],model.predict(train_X.loc[test[0]:test[-1],current_predictors]))
让我们使用普通的OHLC(开盘价、最高价、最低价、收盘价)数据来观察误差水平。从我们的可视化和汇总统计数据来看,线性回归模型在这项任务上的表现最佳。
ohlc_error
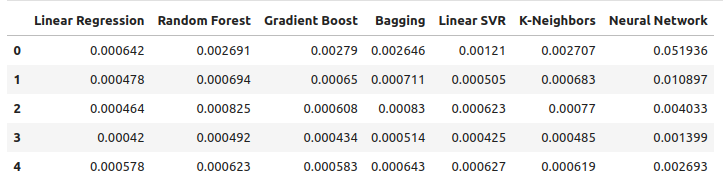
图9:使用OHLC美元兑加元数据进行预测时的误差水平
绘图数据。
ohlc_error.plot()
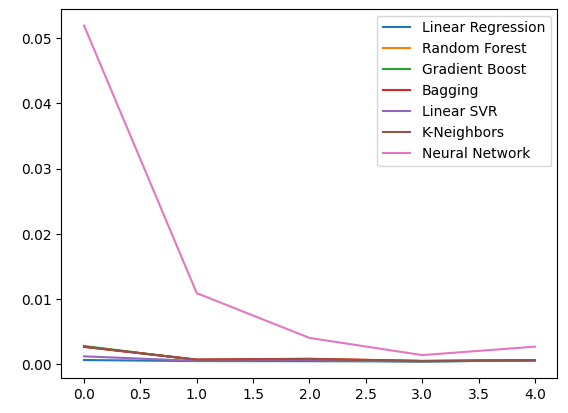
图10:使用第一组预测因子时的模型准确性
创建箱线图。
fig = plt.figure(figsize=(5,5)) plt.boxplot(ohlc_error)
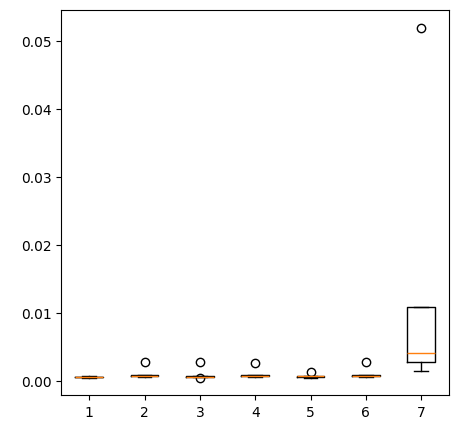
图11:使用第一组预测因子预测时的模型准确性
让我们观察使用贵金属预测美元兑加元汇率时的误差水平。线性回归仍然是表现最佳的模型,但优势不再明显。
new_error
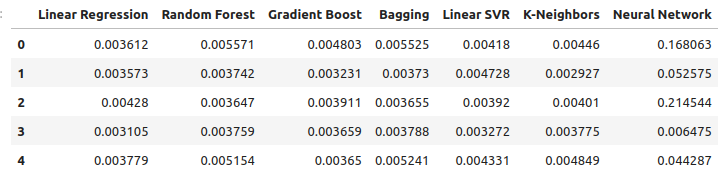
图12:新的误差水平
绘制新的误差水平。
new_error.plot()
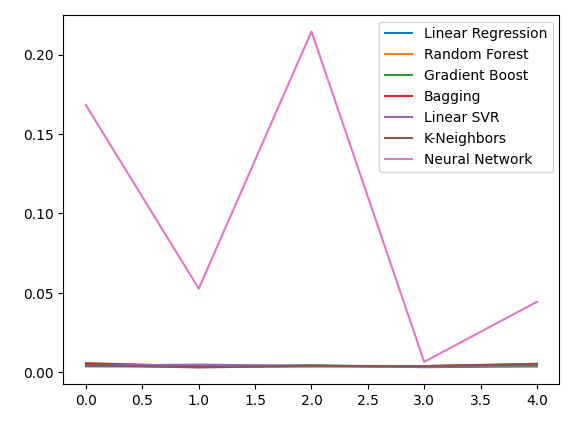
图13:新的误差水平
创建新结果的箱线图。
fig = plt.figure(figsize=(5,5)) plt.boxplot(new_error)
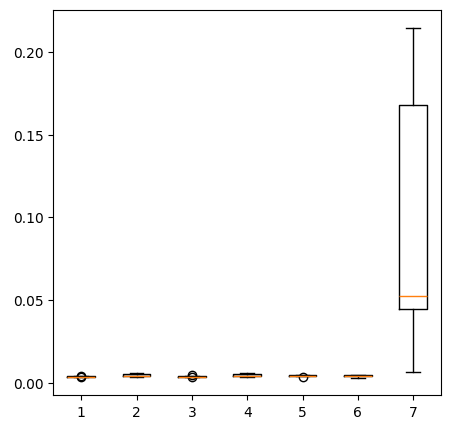
图14:使用贵金属市场数据时的误差水平
现在,让我们考查一下使用所有可用数据时的表现。我们仍然观察到线性模型的表现远远超过了所有的其他模型。让我们尝试优化表现第二的模型——线性支持向量回归器(LinearSVR),使其超越线性回归模型。
all_error
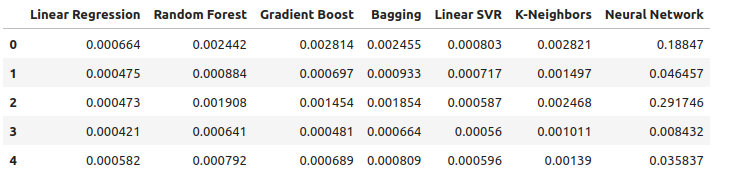
图15:使用我们所有数据时的准确性
绘制误差水平。
all_error.plot()
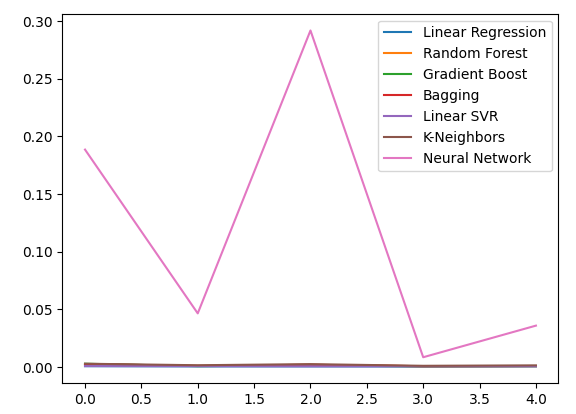
图16:使用我们所有数据时的准确性折线图
当我们使用所有数据时,根据创建的误差水平箱线图显示,简单的线性回归仍然是我们的最佳选择。
fig = plt.figure(figsize=(5,5)) plt.boxplot(all_error)
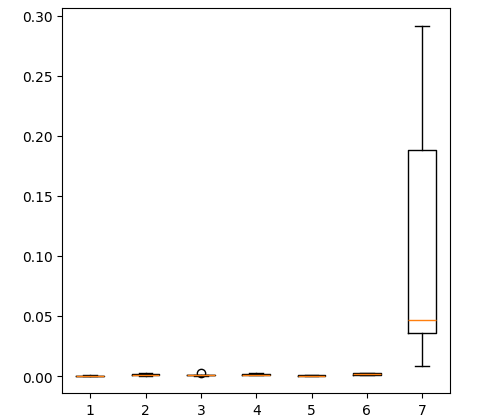
图17:使用我们所有数据时的准确性箱线图
我们所有5个验证集的模型平均误差水平清楚地表明,线性模型到目前为止仍然是我们的最佳选择。线性支持向量回归器(LinearSVR)紧随其后。
all_error.mean()
线性回归 0.000523
随机森林 0.001333
梯度提升 0.001227
Bagging 0.001343
线性支持向量回归 0.000653
K-近邻 0.001837
神经网络 0.114188
数据类型:对象
特征的重要性
在我们开始优化模型之前,让我们首先评估哪些特征显得重要,希望与贵金属市场相关的数据能在此次测试中显示其价值。我们将首先测试互信息(Mutual Information,MI)水平。互信息是衡量您通过了解其中一个预测因子的值,能获得关于目标值多少确定性的一种度量。互信息采用对数尺度,因此在实践中,互信息分数超过2的情况较为罕见。
我们将从导入所需的库开始。
#Mutual information score
from sklearn.feature_selection import mutual_info_regression
现在我们计算每个预测因子的MI评分。
#Prepare the data for plotting mi = mutual_info_regression(train_X,train_y) mi = mi.reshape(1,12) mi_scores = pd.DataFrame(mi,columns=predictors)
根据绘制的MI分数表明,美元兑加元市场的数据可能比贵金属市场的所有数据更具有信息量。这一观点得到了我们的交叉验证测试的验证,在该测试中,我们观察到仅使用美元兑加元市场报价的线性模型产生了最低的误差。
#Prepare the data for plotting mi = mutual_info_regression(train_X,train_y) mi = mi.reshape(1,12) mi_scores = pd.DataFrame(mi,columns=predictors) #Plot the scores mi_scores.plot.bar()
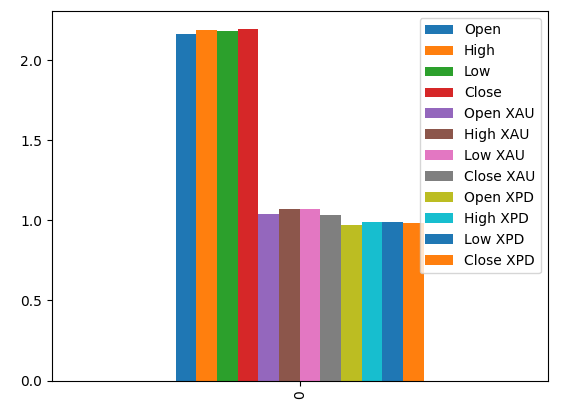
图18:我们三个数据集上的互信息分数
接下来,我们将计算SHAP值。SHAP值是黑箱解释器,帮助我们识别机器学习模型中的全局特征重要性。
导入SHAP库。
#The Linear SVR appears to be performing second best
import shap
初始化LSVR模型。
#Initialize the model
model = LinearSVR()
model.fit(train_X,train_y)
计算SHAP值。
#Compute SHAP values
explainer = shap.Explainer(model,train_X)
explanations = explainer(train_X)
展示全局特征的重要性。
#Plot SHAP values
shap.plots.violin(explanations)
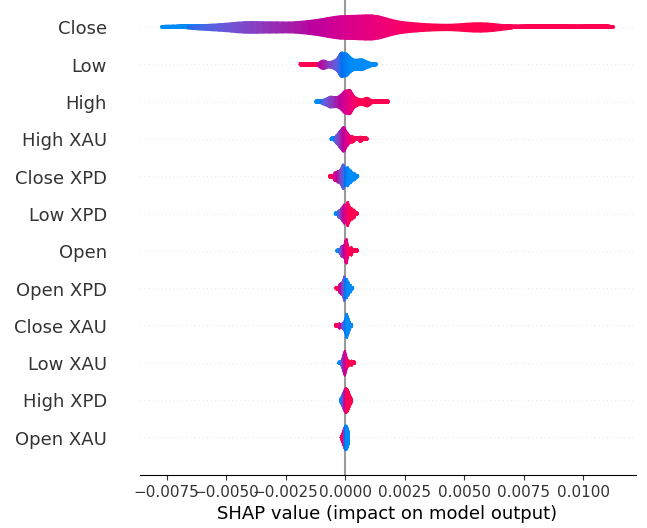
图19:我们的SHAP重要性水平
我们的SHAP解释与我们的互信息评估不一致。我们在以前的文章中广泛探讨了这种不一致的问题,最好的说法是,特征重要性的评估可能具有挑战性,需要谨慎对待。然而,两种解释都表明贵金属市场中包含一些有用的信息。
超参数调整
调整模型可能使我们能够在未见数据上表现得比使用默认模型时更好。为了调整我们的模型,让我们首先导入需要的库。
#Parameter tuning
from sklearn.model_selection import RandomizedSearchCV
现在初始化模型。
#Reinitialize the model
model = LinearSVR()
然后我们来定义调整参数。我们将模型以及一个可能的参数值字典传递进去,随后是我们希望执行的总迭代次数。我们希望执行5折交叉验证来衡量负均方误差,这意味着我们将选择验证误差最低的模型。最后,将n_jobs设置为-1,允许在所有可用的CPU内核上并行执行搜索。
#Define the tuner
tuner = RandomizedSearchCV(
model,
{
"epsilon" : [0,10,100,1000],
"tol":[0.01,0.001,0.0001,0.00001,0.0000001],
"C":[1,10,100,1000,10000],
"loss":['epsilon_insensitive', 'squared_epsilon_insensitive']
},
n_iter=1000,
cv=5,
n_jobs=-1,
scoring="neg_mean_squared_error"
)
安装调整器。
#Let's fit the tuner tuner_results = tuner.fit(train_X,train_y)
我们找到的最佳参数。
#Let's see the best parameters we found tuner_results.best_params_
{'tol': 1e-05, 'loss': 'squared_epsilon_insensitive', 'epsilon': 0, 'C': 10000}
过拟合测试
为了测试是否过拟合,我们首先需要初始化模型。#Testing for overfitting benchmark = LinearRegression() default_lsvr = LinearSVR() customized_lsvr = LinearSVR(tol=1e-05,loss='squared_epsilon_insensitive',epsilon=0,C=10000)
现在重置索引,以便我们可以执行交叉验证。
#Reset the indexes
test_y = test_y.reset_index()
test_X = test_X.reset_index()
格式化数据。
#Format the data test_y = test_y.loc[:,"Target"] test_X = test_X.loc[:,predictors]
创建数据帧来存储我们的误差级别。
#Create dataframes to store our error levels test_error = pd.DataFrame(columns=["Linear Regression","LSVR","Customized LSVR"],index=[0,1,2,3,4])
在训练集上训练模型。
#Fit the models on the training set
benchmark.fit(train_X,train_y)
default_lsvr.fit(train_X,train_y)
customized_lsvr.fit(train_X,train_y)
将模型存储在列表中。
models = [benchmark,default_lsvr,customized_lsvr]
交叉验证测试集上的每个模型。
for j in np.arange(0,len(models)): model = models[j] for i,(train,test) in enumerate(tscv.split(test_X)): model.fit(test_X.loc[train[0]:train[-1],:],test_y.loc[train[0]:train[-1]]) test_error.iloc[i,j] = root_mean_squared_error(test_y.loc[test[0]:test[-1]],model.predict(test_X.loc[test[0]:test[-1],:]))
我们的测试误差。
test_error
| 线性回归 | LSVR | 定制LSVR |
|---|---|---|
| 0.000598 | 0.000542 | 0.000743 |
| 0.000472 | 0.000573 | 0.000722 |
| 0.000318 | 0.000451 | 0.000333 |
| 0.000341 | 0.000366 | 0.000499 |
| 0.00043 | 0.000839 | 0.00043 |
根据在所有5折上的平均表现,我们的线性模型仍然是表现最佳的模型。并且,我们成功地超越了默认模型。
#Let's calculate our mean performances test_error.mean()
线性回归 0.000432
LSVR 0.000554
定制LSVR 0.000545
数据类型:对象
可视化我们的测试误差。
#Let's visualize our error test_error.plot()
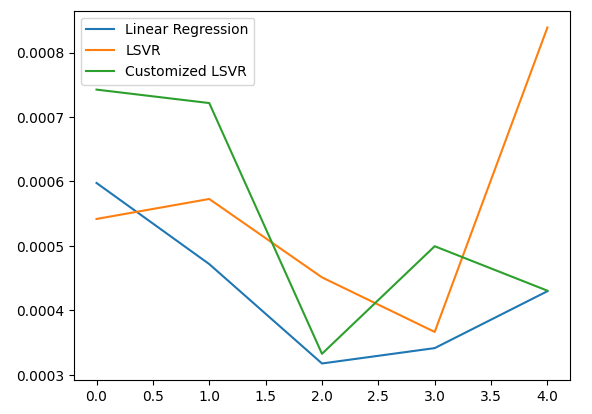
图20:可视化我们的测试误差
创建我们测试误差率的箱线图。
#Create a boxplot of the error
sns.boxplot(data=test_error)

图21:可视化我们的测试误差
为导出ONNX格式准备模型
在我们将模型导出为ONNX格式之前,我们首先需要通过减去均值并除以标准差来对数据进行缩放和标准化,然后我们将把缩放因子写入CSV,以便我们可以在MQL5中重现这个过程。
首先,创建一个数据帧来存储我们的缩放因子。
#Let's scale our data scaling_factors = pd.DataFrame(columns=predictors,index=['mean','standard deviation']) X = merged_data.loc[:,predictors] y = merged_data.loc[:,"Target"]
然后存储均值和标准差,最后执行缩放流程。
#Let's fill each column for i in np.arange(0,len(predictors)): scaling_factors.iloc[0,i] = X.iloc[:,i].mean() scaling_factors.iloc[1,i] = X.iloc[:,i].std() X.iloc[:,i] = ( ( X.iloc[:,i] - scaling_factors.iloc[0,i] ) / scaling_factors.iloc[1,i])
保存缩放因子。
#Save the scaling factors as a CSV scaling_factors.to_csv("/home/volatily/.wine/drive_c/Program Files/MetaTrader 5/MQL5/Files/usd_cad_xau_xpd_scaling_factors.csv")
将模型导出到ONNX
ONNX代表开放神经网络交换(Open Neural Network Exchange),它是一个开源的、可互操作的机器学习框架,允许开发人员在与语言无关的框架中创建、共享和部署机器学习模型。这是通过将每个机器学习模型表示为节点和图形的树结构来实现的,任何支持ONNX API的语言都可以将这些节点和图形重新组装回原始模型。
首先,我们将导入我们需要的库。
#Let's prepare to export our model to ONNX format import onnx import netron import skl2onnx from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType
显示库的版本。
#Display library versions print(f"Onnx version: {onnx.__version__}") print(f"Netron version: {netron.__version__}") print(f"Skl2onnx version: {skl2onnx.__version__}")
Onnx 版本:1.15.0
Netron 版本:7.8.0
Skl2onnx版本:1.16.0
接下来,我们需要定义模型的输入类型。
#Define the input type
initial_types = [('float_input',FloatTensorType([1,12]))]
让我们用所有的数据来训练这个模型。
#Train the model on all the data we have customized_lsvr = LinearSVR(tol=1e-05,loss='squared_epsilon_insensitive',epsilon=0,C=10000) customized_lsvr.fit(X,y)
将模型转换为ONNX格式。
#Covert the sklearn model
onnx_model = convert_sklearn(customized_lsvr,initial_types=initial_types)
保存ONNX模型。
#Save the onnx model onnx_name = "USDCAD XAUUSD XPDUSD M1 Float.onnx" onnx.save(onnx_model,onnx_name)
查看ONNX模型。
#View the onnx model
netron.start(onnx_name)
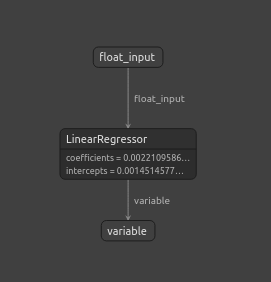
图22:在Netron中可视化我们的ONNX模型
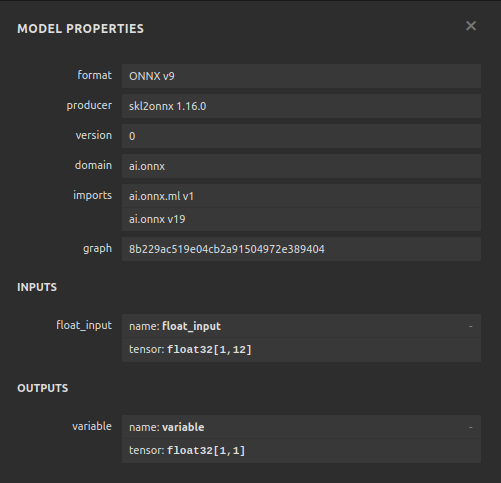
图23:我们的ONNX模型参数与对模型输入和输出的预期一致
在MQL5中的实现
为了在MQL5中实现一个集成人工智能的EA,我们首先需要加载之前导出的ONNX模型。
//+------------------------------------------------------------------+ //| USDCAD AI.mq5 | //| Gamuchirai Zororo Ndawana | //| https://www.mql5.com/en/gamuchiraindawa | //+------------------------------------------------------------------+ #property copyright "Gamuchirai Zororo Ndawana" #property link "https://www.mql5.com/en/gamuchiraindawa" #property version "1.00" //+------------------------------------------------------------------+ //| Resources | //+------------------------------------------------------------------+ #resource "\\Files\\USDCAD XAUUSD XPDUSD M1 Float.onnx" as const uchar onnx_buffer[];
接下来,我们需要加载交易库,以便我们可以开仓和平仓。
//+------------------------------------------------------------------+ //| Libraries we need | //+------------------------------------------------------------------+ #include <Trade/Trade.mqh> CTrade Trade;
让我们同时定义一些全局变量,这些变量将在程序中被多次使用。
//+------------------------------------------------------------------+ //| Global variables | //+------------------------------------------------------------------+ long onnx_model; double mean_values[12],std_values[12]; vectorf model_output = vectorf::Zeros(1); int model_forecast,state; double ask,bid;
让我们定义程序中将要使用的辅助函数,需要一个负责加载ONNX模型并设置其输入和输出形状的函数。我们将通过一个函数来实现,如果成功则返回true,否则返回false。我们的函数首先从之前创建的缓冲区中创建模型,然后尝试设置并验证输入和输出的形状。
//+------------------------------------------------------------------+ //| This function is responsible for loading our ONNX model | //+------------------------------------------------------------------+ bool load_onnx(void) { //--- First we must create the model from the buffer onnx_model = OnnxCreateFromBuffer(onnx_buffer,ONNX_DEFAULT); //--- Now we shall define our I/O shape ulong input_shape [] = {1,12}; ulong output_shape [] = {1,1}; if(!OnnxSetInputShape(onnx_model,0,input_shape)) { Comment("Failed to set ONNX input shape!"); return(false); } if(!OnnxSetOutputShape(onnx_model,0,output_shape)) { Comment("Failed to set ONNX output shape!"); return(false); } //--- Everything went fine return(true); } //+------------------------------------------------------------------+
该函数负责读取包含我们缩放值的CSV文件,并将它们存储到定义的全局作用域数组中。
//+------------------------------------------------------------------+ //| This function will read our scaling factors and store them | //+------------------------------------------------------------------+ bool load_scaling_factors(void) { //--- Read in the file string file_name = "usd_cad_xau_xpd_scaling_factors.csv"; //--- Try open the file int result = FileOpen(file_name,FILE_READ|FILE_CSV|FILE_ANSI,","); //Strings of ANSI type (one byte symbols). //--- Check the result if(result != INVALID_HANDLE) { Print("Opened the file"); //--- Store the values of the file int counter = 0; string value = ""; while(!FileIsEnding(result) && !IsStopped()) //read the entire csv file to the end { if(counter > 100) //if you aim to read 10 values set a break point after 10 elements have been read break; //stop the reading progress value = FileReadString(result); Print("Trying to read string: ",value," count value: ",counter); //--- Check where we are if((counter >= 14) && (counter < 26)) { mean_values[counter - 14] = (float) value; } //--- Check where we are if((counter >= 27) && (counter < 39)) { std_values[counter - 27] = (float) value; } //--- Reading a new row if(FileIsLineEnding(result)) { Print("row++"); } counter++; } //---Close the file ArrayPrint(mean_values); ArrayPrint(std_values); FileClose(result); return(true); } //--- We failed to find the file else { Comment("Failed to find the file containing scaling factors"); return(false); } }
我们还需要一个负责从市场获取最新价格报价的函数。
//+------------------------------------------------------------------+ //| Update market prices | //+------------------------------------------------------------------+ void update_market_prices(void) { ask = SymbolInfoDouble(_Symbol,SYMBOL_ASK); bid = SymbolInfoDouble(_Symbol,SYMBOL_BID); }
最后,我们需要一个从模型中获取预测的函数。我们的预测函数首先会对数据进行缩放,然后才将其传递给模型。
//+------------------------------------------------------------------+ //| Model predict | //+------------------------------------------------------------------+ void model_predict(void) { //--- First fetch the market data vectorf model_input = { iOpen("USDCAD",PERIOD_CURRENT,0),iHigh("USDCAD",PERIOD_CURRENT,0),iLow("USDCAD",PERIOD_CURRENT,0),iClose("USDCAD",PERIOD_CURRENT,0), iOpen("XAUUSD",PERIOD_CURRENT,0),iHigh("XAUUSD",PERIOD_CURRENT,0),iLow("XAUUSD",PERIOD_CURRENT,0),iClose("XAUUSD",PERIOD_CURRENT,0), iOpen("XPDUSD",PERIOD_CURRENT,0),iHigh("XPDUSD",PERIOD_CURRENT,0),iLow("XPDUSD",PERIOD_CURRENT,0),iClose("XPDUSD",PERIOD_CURRENT,0) }; //--- Now standardize and scale the data for(int i =0; i < 12; i++) { model_input[i] = ((model_input[i] - mean_values[i]) / std_values[i]); } //--- Now fetch a prediction from our model OnnxRun(onnx_model,ONNX_DEFAULT,model_input,model_output); //--- Store our model's forecat if(model_output[0] > iClose("USDCAD",PERIOD_CURRENT,0)) { model_forecast = 1; } else if(model_output[0] < iClose("USDCAD",PERIOD_CURRENT,0)) { model_forecast = -1; } }
在初始化EA时,我们首先会加载ONNX文件,然后读取缩放值。如果这两个步骤中的任何一个失败,我们将终止整个过程。
//+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- This function will load our ONNX model if(!load_onnx()) { return(INIT_FAILED); } //--- This function will load our scaling factors if(!load_scaling_factors()) { return(INIT_FAILED); } //--- return(INIT_SUCCEEDED); }
每当EA从图表中移除时,让我们释放不再需要的资源。
//+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- Free up the resources we do not need OnnxRelease(onnx_model); ExpertRemove(); }
最后,每当我们收到买入价和卖出价的更新时,会把更新后的价格存储在内存中,并从我们的人工智能模型中获取新的预测。如果尚未开仓,我们将按照人工智能模型建议的方向开仓,然而如果已有开仓,我们将检查以确保人工智能模型的预测并没有与我们当前的头寸方向相反。
void OnTick() { //--- Update the market prices update_market_prices(); //--- Fetch a forecast from our model model_predict(); //--- Find a trading oppurtunity if(PositionsTotal() == 0) { if(model_forecast == -1) { Trade.Sell(0.2,_Symbol,ask,0,0,"USDCAD AI"); state = -1; } else if(model_forecast == 1) { Trade.Buy(0.2,_Symbol,ask,0,0,"USDCAD AI"); state = 1; } } //--- Check for reversals if(PositionsTotal() > 0) { if(state != model_forecast) { Alert("Reversal detected by our AI system, closing all positions now!"); Trade.PositionClose(_Symbol); } } } //+------------------------------------------------------------------+
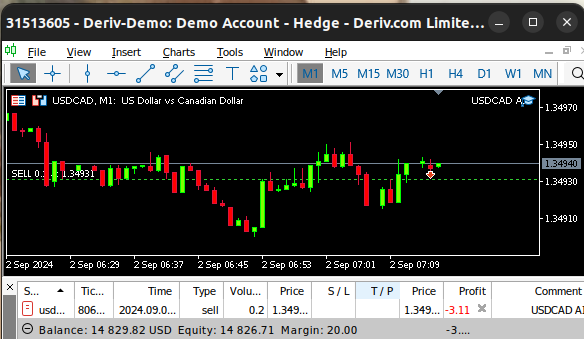
图24:我们运行中的EA
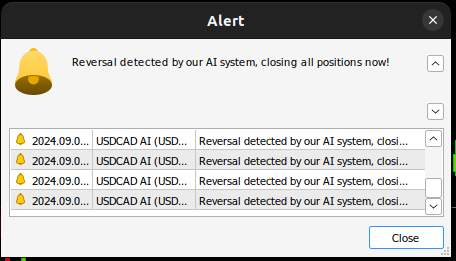
图25:我们的人工智能系统检测到可能的逆转
结论
在今天的文章中,我们展示了如何揭示可能存在于相互关联的市场之间的隐藏关系。然而,值得注意的是,我们的实证分析表明,可能只需要使用普通的市场数据和更简单的线性模型就足够了。正如我们所熟知的,这可能是因为市场数据具有噪声。在数据存在噪声的情况下,简单的模型往往比复杂的模型表现得更好,因为复杂模型对输入数据的变化更为敏感。
本文由MetaQuotes Ltd译自英文
原文地址: https://www.mql5.com/en/articles/15762
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
本文由网站的一位用户撰写,反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责,也不对因使用所述解决方案、策略或建议而产生的任何后果负责。
 在 MQL5 中重新构想经典策略(第二部分):富时 100 指数(FTSE100)与英国国债(UK Gilts)
在 MQL5 中重新构想经典策略(第二部分):富时 100 指数(FTSE100)与英国国债(UK Gilts)
 从基础到中级:操作符
从基础到中级:操作符
 您应当知道的 MQL5 向导技术(第 30 部分):聚焦机器学习中的批量归一化
您应当知道的 MQL5 向导技术(第 30 部分):聚焦机器学习中的批量归一化

再次感谢 Gamuchirai,又一个出色的文档模板。关于如何使用不同的数据模型确定特征重要性、相关性和可视化结果的实用示例非常有帮助。在阅读的过程中,我们了解了机器学习,谢谢。今天给我上的一课是 "SHAP "值。再次感谢你的工作,我一直对 Python 提供的工具感到惊讶。