
Recetas para "Neuronets"
Introducción
No hace mucho, en el amanecer del análisis técnico, cuando no todos los traders tenían ordenadores, apareció gente que intentó predecir los precios futuros utilizando fórmulas y regularidades inventadas por ellos. A menudo se les llamaba "charlatanes". Pasó el tiempo, se complicaron los métodos de proceso de información, y ahora es difícil encontrar traders para los que el análisis técnico sea indiferente. Cualquier trader principiante puede utilizar gráficos fácilmente, varios indicadores, búsqueda de regularidades.
En número de traders-forex crece a diario. Junto con que sus requisitos para los métodos de análisis del mercado crecen. Uno de estos métodos "relativamente" nuevos es el uso de lógicas teóricamente confusas y redes neuronales. Vemos que los temas dedicados a estas preguntas se están discutiendo cada vez más en varios foros temáticos. Existen, y seguirán existiendo. Alguien que entre en el mercado, difícilmente saldrá de él. Al mismo tiempo, es un reto para la inteligencia, el cerebro, y la fuerza de voluntad de uno. Por eso un trader nunca deja de estudiar cosas nuevas, ni de utilizar varios métodos en la práctica.
En este artículo, se analizan las bases para a creación de un "neuronet", se aprenderá la noción de la red neuronal de Kohonen, y se hablará un poco sobre la optimización de métodos de trading. Este artículo está destinado, antes que nada, a los traders que se encuentran al principio del estudio de las "neuronets" y de los principios de procesamiento de información.
Cocinar una red neuronal con la primera capa de Kohonen necesitará:
1) 10 000 barras de historial de cualquier par de divisas;
2) 5 gramos de movimiento promedio (o cualquier otro indicador, es elección suya);
3) 2-3 capas de distribución inversa;
4) métodos de optimización como relleno;
5) las verduras del crecimiento de balance y el número de las direcciones de trade adivinadas que han sido correctas.
Sección l. Receta de la Capa Kohonen
Vamos a empezar con la sección para los que están en el principio del todo. Vamos a hablar de varios acercamientos a la capa de Kohonen o, para ser más exacto, a su versión básica, porque hay muchas variantes. No hay nada de original en este capítulo, todas las explicaciones se han cogido de referencias clásicas de este tema. Sin embargo, la ventaja de este capítulo es la gran cantidad de números de imágenes explicativas para cada sección.
En este capítulo, trataremos con las siguientes preguntas:
- la manera en la que se ajustan los vectores de peso de Kohonen;
- preparación preliminar de los vectores de entrada;
- selección de los pesos iniciales de las neuronas Kohonen.
Por eso, según Wikipedia, la red neuronal de Kohonen representa un tipo de redes neuronales cuyo elemento principal es la capa de Kohonen. La capa de Kohonen consiste en complementos lineales adaptables ("neuronas lineales formales"). Por regla general, las señales de salidas de la capa de Kohonen se procesan según la norma: "el ganador se lo lleva todo": las señales más grandes se convierten en una, todas las otras pasan a cero.
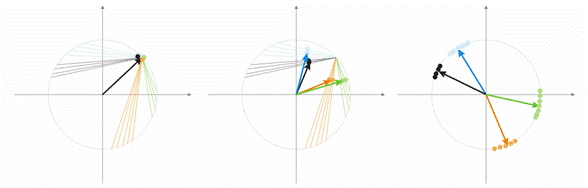
Vamos a hablar de esto con un ejemplo. Con el objetivo de visualizar todos los cálculos que se darán para los vectores de entrada de dos dimensiones. En la img alt="". 1 el vector de entrada se muestra en color. Cada neurona de la capa Kohonen (como de cualquier otra capa), sólo hay que sumar la entrada, multiplicándola por sus pesos. De hecho, todos los pesos de la capa Kohonen son vectores coordinados por esta neurona.
Por lo tanto, la salida de cada neurona de la capa Kohonen es el producto escalar de dos vectores. Por la geometría, sabemos que el producto escalar máximo aparecerá si el ángulo entre los vectores tiende a cero (el coseno del ángulo tiende a 1). Por lo que el valor máximo será el de la neurona de la capa de Kohonen que esté más cerca del vector de entrada.
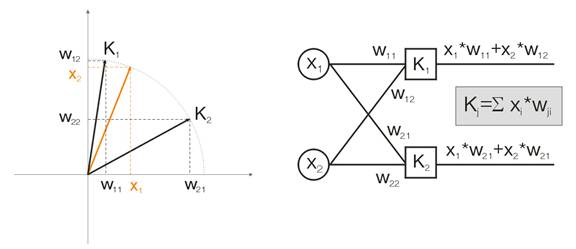
img alt="". 1 La ganadora es la neurona cuyo vector está más cerca de la señal de entrada.
En cuanto a la definición, hay que encontrar el valor máximo de salida entre todas las neuronas, asignando su salida a una y asignando cero al resto. Y la capa de Kohonen nos "responderá" en qué zona está el vector de entrada.
Ajusto de los vectores de peso de Kohonen
El objetivo de la formación en capas, como se dice arriba, es precisar la clasificación del espacio en los vectores de entrada. Esto quiere decir que cada neurona tiene que ser responsable de su zona en concreto, en la que está la ganadora. El error de desviación de la neurona ganadora de la neurona de entrada debe ser más pequeño que el de las otras neuronas. Para conseguirlo, la neurona ganadora "gira" hacia el lado del vector de entrada.
La img alt="". 2 muestra la división de dos neuronas (neuronas negras) de dos vectores de entrada (los de colores).

img alt="".2 Cada neurona se acerca a su señal de entrada más cercana.
Con cada iteración, la neurona ganadora se acerca a "su propio" vector de entrada. Sus nuevas coordenadas se calculan según la siguiente fórmula:
![]()
en la que A(t) es el parámetro de velocidad de training, dependiendo del tiempo t. Esta es una función no creciente que se reduce en cada iteración de 1 a 0. Si el valor iniciar es A=1, se hace la corrección de peso en una etapa. Esto es posible cuando para cada vector de entrada hay una neurona Kohonen (por ejemplo, 10 vectores de entrada y 10 neuronas en la capa Kohonen).
Pero en la práctica, estos casos no se ven casi nunca, porque normalmente el volumen más grande de entrada de datos necesita dividirse en grupos de similares, para reducir así la diversidad de datos de entrada. Por eso es indeseable el valor A=1. La práctica muestra que el valor inicial óptimo debe ser por debajo de 0,3.
Además, A es inversamente proporcional al número de vectores de entrada. Es decir, cuando más grande es la selección, es mejor hacer correcciones pequeñas, para que la neurona ganadora no "surfee" a lo largo de todo el espacio en sus correcciones. Como funcionalidad de A, normalmente se elige cualquier función monotónicamente decreciente. Por ejemplo, hipérbola o disminución lineal, o función Gaussiana.
La img alt="". 3 muestra el paso de la corrección de los pesos de neurona a velocidad A=0,5. La neurona se ha acercado al vector de entrada, el error es más pequeño.
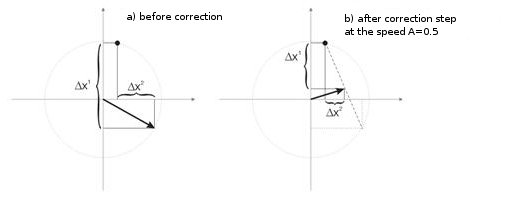
img alt="". 3. La corrección del peso de la neurona bajo la influencia de la señal de entrada.
Pequeño número de neuronas con una muestra más amplia
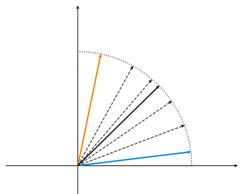
img alt="". 4. Las fluctuaciones de la neurona entre dos vectores de entrada.
En la img alt="". 4 (izquierda) hay dos vectores de entrada (en color) y sólo una neurona de Kohonen. En el proceso de corrección, a neurona cambiará de un vector a otro (líneas de puntos). Conforme el valor disminuye hasta 0, se estabiliza entre ellos. Los cambios de tiempo coordinados por la neurona se pueden caracterizar por una línea en zigzag (img alt="". 4 derecha).
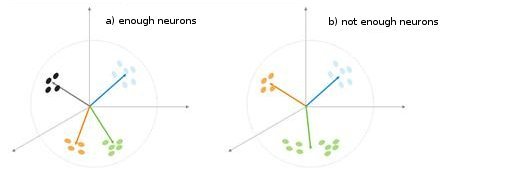
Fig. 5. Dependencia del tipo de clasificación en el número de neuronas.
Se muestra una situación más en la img alt="". 5. En el primero caso de la adecuación de neuronas, divida la muestra en cuatro áreas de hypersphere. En el segundo caso, el número insuficiente de neuronas resulta en el aumento del error y la reclasificación de la muestra. Aunque se puede concluir que la capa Kohonen debe contener el número suficiente de tres neuronas que dependen en el volumen de la muestra clasificada.
Preparación preliminar de los vectores de entrada
Como escribe Philip D. Wasserman en su libro, es conveniente (pero no obligatorio) normalizar los vectores de entrada antes de introducirlo en la red. Esto se hace dividiendo cada componente del vector de entrada entre la longitud del vector. Esta longitud se encuentra con la extracción de una raíz cuadrada de la suma de los cuadrados de los componentes del vector. Esta es la presentación algebraica.
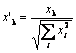
Esto transforma el vector de entrada en un vector de unidad con la misma dirección, es decir, un vector con la longitud de unidad en el espacio dimensión-n. El significado de esta operación está claro: proyectar todos los vectores de entrada en la superficie de hypersphere, simplificando así la tarea de búsqueda de la capa Kohonen. En otras palabras, para buscar el ángulo entre los vectores de entrada y los vectores de las neuronas Kohonen, hay que eliminar los factores como la longitud del vector, igualando las oportunidades de todas las neuronas.
Muy a menudo los elementos de los vectores de muestra son valores no negativos (por ejemplo, valores de movimientos promedios, precios). Todos se concentran en el espacio cuadrante positivo. Como resultado de la normalización de esta muestra "positiva" se obtiene la acumulación de vectores sólo del área positiva, que no es muy buena para la cualificación. Por eso, antes de la normalización se pueden realizar la suavización de la muestra. Si la muestra es más bien grande, se puede asumir que los vectores están colocados aproximadamente en una zona sin "extraños", que están lejos de la muestra principal. Por lo tanto, una muestra se puede centrar relativamente a sus coordinadas "extremas".
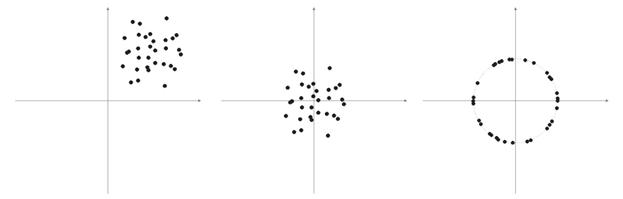
Fig. 6. Normalización de los vectores de entrada.
Como se ha escrito arriba, es conveniente la normalización de los vectores. Simplifica la corrección de la capa de Kohonen. Sin embargo, debería representarse claramente una muestra y decidir si debe proyectarse en una sphere o no.
Enumerado 1. Contracción de los vectores de entrada en el rango [-1, 1]
for (N=0; N<nNeuron[0]; N++) // for all neurons of the input layer { min=in[N][0]; // finding minimum in the whole sample for (pat=0; pat<nPattern; pat++) if (in[N][pat]<min) min=in[N][pat]; for (pat=0; pat<nPattern; pat++) in[N][pat]-=min; // shift by the value of the minimal value max=in[N][0]; // finding maximum in the whole sample for (pat=0; pat<nPattern; pat++) if (in[N][pat]>max) max=in[N][pat]; for (pat=0; pat<nPattern; pat++) in[N][pat]=2*(in[N][pat]/max)-1; // narrowing till [-1,1] }
Si se normalizan los vectores de entradas, deberían normalizarse todos los pesos de neuronas.
Selección de pesos iniciales de neurona
Son muchas las posibles variantes.
1) Se asignan valores aleatorios a los pesos, como se hace normalmente con las neuronas (aleatorización);
2) Inicialización por ejemplos, cuando se seleccionan los ejemplos seleccionados aleatoriamente de una muestra de training como valores iniciales;
3) Inicialización lineal. En este caso, los pesos se inician por un valor de vector que se ordenan linealmente junto con el espacio lineal completo ubicado entre dos vectores desde el conjunto de datos inicial;
4) Todos los pesos tienen el mismo valor: método de combinación convexa.
Vamos a analizar el primer y el último caso.
1) Se asignan valores aleatorios a los pesos.
Durante la aleatorización, todos las neuronas-vectores se distribuyen sobre la superficie de una hypershpere. Mientras que los vectores de entrada tienen tendencia a agruparse. En este caso, puede ocurrir que algunos vectores de peso están tan distanciados de los vectores de entrada que nunca podrán dar una mejor correlación y, como consecuencia, no podrán aprender: figuras "grises" en la img alt="". 7 (derecha). Además, las neuronas que quedan no serán suficiente para minimizar el error y dividir las clases similares: la clase "roja" se incluye en la neurona "verde".
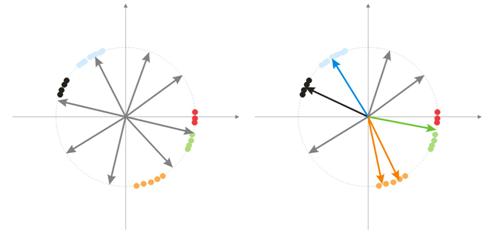
Fig. 7. Resultado del training de las neuronas aleatorizadas.
Y si hay una acumulación más grande de neuronas en una zona, pueden entrar varias neuronas en la zona de una clase y dividirla en subclases: zona naranja en la img alt="". 7. Esto no es muy importante, porque los procesos siguientes de procesamiento de señales de capas pueden arreglar la situación, pero necesita el tiempo de training.
Una de las variantes para resolver estos problemas es el método en el que se hace una corrección inicial no sólo para los vectores de una neurona ganadora, sino también para el grupo de vectores cercanos. Luego el número del grupo disminuye gradualmente y finalmente sólo una neurona se corrige. Se puede seleccionar un grupo de una gama almacenada de salidas de neuronas. Se corregirán las neuronas de las primas salidas máximas de K.
El siguiente método es otro enfoque más en el ajuste del grupo de peso de vectores.
a) Se define la longitud de corrección del vector para cada neurona:
![]()
.
b) Una neurona con la misma distancia mínima se vuelve ganadora: Wn Después, la correlación de un grupo de neuronas (si se encuentra) está en el límite de la distancia C*Ln de Wn.
c) Los pesos de estas neuronas se corrigen con una regla simple ![]() . De este modo se hace la corrección de la muestra completa.
. De este modo se hace la corrección de la muestra completa.
El parámetro C cambia en el proceso de training de algún número (normalmente de 1) a 0.
El tercer método interesante implica que cada neurona se puede corregir sólo N/k veces para una que pasa por la muestra. Aquí N es el tamaño de la muestra, y k- el número de neuronas. Es decir, si alguna de las neuronas se vuelve ganadora más a menudo que otras, "deja el juego" hasta que termine de pasar por la muestra. De este modo también pueden aprender otras neuronas.
2) método de combinación convexa
El significado del método implica que tanto los vectores de peso como de entrada se colocan inicialmente en una zona. El cálculo de las fórmulas para las coordenadas actuales de vectores de entrada y de peso inicial será el siguiente:
![]()
,
![]()
en el que n es la dimensión de un vector de entrada, a(t)- función no decreciente en tiempo, en el que cada iteración aumenta su valor de 0 a 1, resultando en la coincidencia de todos los vectores de entrada con los vectores de peso, y finalmente se colocan. Además, los vectores de peso "alcanzarán" sus clases.
Esto es todo material de la versión básica de la capa Kohonen que se aplicará en esta red neuronal.
II. Spoons, ladles y scripts
El primer script del que vamos a hablar recopilará datos de las barras y creará un archivo de vectores de entradas. Como ejemplo de trading vamos a utilizar MA:
Enumerado 2. Crear un archivo de vectores de entrada
// input parameters #define NUM_BAR 10000 // number of bars for training (number of training patterns) #define NUM_MA 5 // number of movings #define DEPTH_MA 3 // number of values of a moving // creating a file hFile = FileOpen(FileName, FILE_WRITE|FILE_CSV); FileSeek(hFile, 0, SEEK_END); // Creating an array of inputs int i, ma, depth; double MaIn; for (i=NUM_BAR; i>0; i--) // going through bars and collecting values of MA fan { for (depth=0; depth<DEPTH_MA; depth++) //calculating moving values for (ma=0; ma<NUM_MA; ma++) { MaIn=iMA(NULL, 0, 2+MathSqrt(ma*ma*ma)*3, 0, 1, 4, i+depth*depth)- ((High[i+depth*depth] + Low[i+depth*depth])/2); FileWriteDouble(hFile, MaIn); } }
El archivo de datos se crea con la intención de transmitir la información entre las aplicaciones. Cuando se familiarice con los algoritmos de trading, se recomienda revisar los resultados provisional de su funcionamiento, los valores de varias variables y, si es necesario, el cambio en las condiciones de training.
Por eso se recomienda utilizar el lenguaje de programación de nivel alto (VB, VC++ etc.), mientras que los objetivos actuales de depuración de MQL4 no son suficientes (espero que esta situación mejore en MQL5). Más tarde, cuando descubra todos los errores de sus algoritmos y funciones, puede empezar a utilizar MQL4. Además, tendrá que escribir el objetivo principal (indicador o Asesor Experto) en MQL4.
Estructura generalizada de clases
Enumerado 3. Clases de red neuronal
class CNeuroNet : public CObject { public: int nCycle; // number of learning cycles until stop int nPattern; // number of training patterns int nLayer; // number of training layers double Delta; // required minimal output error int nNeuron[iMaxLayer]; // number of neurons in a layer (by layers) int LayerType[iMaxLayer]; // types of layers (by layers) double W[iMaxLayer][iMaxNeuron][iMaxNeuron];// weights by layers double dW[iMaxLayer][iMaxNeuron][iMaxNeuron];// correction of weight double Thresh[iMaxLayer][iMaxNeuron]; // threshold double dThresh[iMaxLayer][iMaxNeuron]; // correction of threshold double Out[iMaxLayer][iMaxNeuron]; // output value double OutArr[iMaxNeuron]; // sorted output values of Kohonen layer int IndexWin[iMaxNeuron]; // sorted neuron indexes of Kohonen layer double Err[iMaxLayer][iMaxNeuron][iMaxNeuron];// error double Speed; // Speed of training double Impuls; // Impulse of training double in[100][iMaxPattern]; // Vector of input values double out[10][iMaxPattern]; // vector of output values double pout[10]; // previous vector of output values double bar[4][iMaxPattern]; // bars, on which we learn int TradePos; // order direction double ProfitPos; // obtained profit/loss of an order public: CNeuroNet(); virtual ~CNeuroNet(); // functions void Init(int aPattern=1, int aLayer=1, int aCycle=10000, double aDelta=0.01, double aSpeed=0.1, double aImpuls=0.1); // learning functions void CalculateLayer(); // Calculation of layer output void CalculateError(); // Error calculation /for Target array/ void ChangeWeight(); // Correction of weights bool TrainNetwork(); // Network training void CalculateLayer(int L); // Output calculation of Kohonen layer void CalculateError(int L); // Error calculation of Kohonen layer void ChangeWeight(int L); // Correction of weights for layer indication bool TrainNetwork(int L); // Training of Kohonen layer bool TrainMPS(); // Network training for getting the best profit // variables for internal interchange bool bInProc; // flag for entering the TrainNetwork function bool bStop; // flag for the forced termination of the TrainNetwork function int loop; // number of the current iteration int pat; // number of the current processed pattern int iMaxErr; // pattern with the maximal error double dMaxErr; // maximal error double sErr; // square of pattern error int iNeuron; // maximal number of neurons in Kohonen layer correction int iWinNeuron; // number of winner neurons in Kohonen layer int WinNeuron[iMaxNeuron]; // array of active neurons (ordered) int NeuroPat[iMaxPattern][iMaxNeuron]; // array of active neurons void LinearCovariation(); // normalization of the sample void SaveW(); // Analysis of neuron activity };
En realidad la clase no es compleja. Contiene el conjunto necesario principal + variables de servicio.
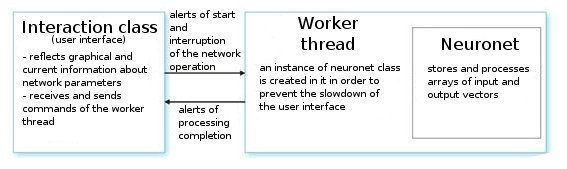
Vamos a analizarlo. Sobre petición del usuario, la clase de interfaz crea una rama de trabajo e inicia un temporizador para las lecturas de los valores de la red. También recibe los índices de lectura de información de los parámetros "neuronet". La rama de trabajo en sí vuelve las primeras gamas de lecturas de vectores de entrada/salida del archivo preliminar preparado y establece los parámetros de las capas (tipos de capas y números de neuronas en cada capa). Esta es la etapa de preparación.
Después de llamar a la función CNeuroNet::Init, en la que se inician los pesos, la muestra se normaliza y se establecen los parámetros de trainign (velocidad, impulso, error necesario y número de ciclos de training). Y sólo después de eso, se llama a la función de "caballo de batalla": CNeuroNet::TrainNetwork (oTrainMPS o TrainNetwork(int L), dependiendo de lo que se quiera obtener). Cuando finaliza en training, la rama de trabajo guarda los pesos de red en un archivo para la implementación del último en un indicador o Asesor Experto.
III. Cocinando la red
Ahora pasemos a las cuestiones de training. La práctica normal en training es configurar el par "patrón-profesor". Esto quiere decir que un objetivo determinado corresponde con cada patrón de entrada. Se realiza en base a las diferencias entre la entrada actual y la corrección de valor objetivo de los pesos. Por ejemplo, si un investigador quiere la red prediga el precio de la barra siguiente en base a los precios de las 10 barras anteriores presentadas en la red. En este caso, después de colocar 10 valores por entrada, hay que comparar la salida obtenida y el valor instructor y luego corregir los pesos por las diferencias entre ellos.
En el modelo que se ofrece, no habrá vectores "instruyendo" en el sentido usual porque no se sabe con antelación en qué barras se debería entrar o salir del mercado. Quiere decir que nuestra red corregirá sus vectores de salida basándose en sus propios valores de salida anteriores. Quiere decir que la red intentará obtener el beneficio máximo (maximización del número de direcciones de trade predichas correctamente). Vamos a considerar un ejemplo en la img alt="".8.
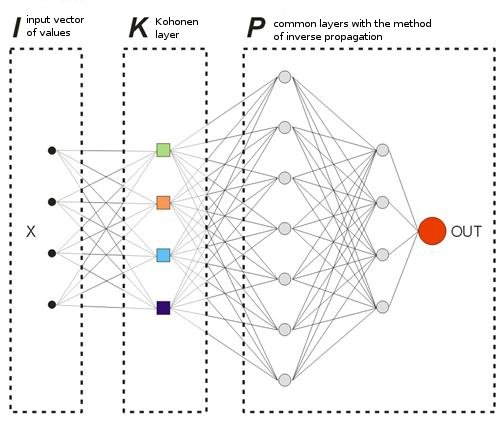
Fig. 8. Esquema de una red neuronal entrenada.
La capa Kohonen preentrenada en una muestra envía su vector más adelante a la red. En la salida de la última capa de la red, se tendrá el valor OUT, que se interpreta de la siguiente manera. Si OUT>0,5, introduzca Buy; si OUT<0,5, introduzca Sell (los valores sigmoideos se cambian en límites [0, 1]).
![]()
Suponga que a algún vector de entrada X1 la red respondió con la salida OUT1>0,5. Significa que en la barra a la que pertenece el patrón se abre una posición Buy. Después de eso, en la presentación cronológica de los vectores de entrada en alguna Xk la señal OUTk se gira a la "contraria". Como consecuencia, se cierra la posición Buy y se abre una posición Sell.
Exactamente en este momento, se necesitan ver los resultados de la orden cerrada. Si se obtiene beneficio, se puede reforzar esta alerta. O se puede considerar que no hay ningún error y no se corregirá nada. Si se obtienen pérdidas, se corrigen los pesos de las capas de manera que al entrar por la alerta de X1 los vectores muestran OUT1<0,5.
Ahora vamos a calcular el valor de una salida instructora (objetivo). Para ello se coge el valor de una forma sigmoideo de las pérdidas obtenidas (en puntos) multiplicado por la señal de la dirección del trade. Como consecuencia, cuanto más grande sea la pérdida, se castigará más estrictamente a la red y se corregirá sus pesos por el valor más grande. Por ejemplo, si hay una pérdida =50 puntos en Buy, la corrección de la capa de salida se calculará como se muestra a continuación:
![]() ,
, ![]() ,
, ![]()
Se pueden delimitar las reglas de trading introduciendo en el trade los parámetros del análisis de los procesos de TakeProfit (TP) y StopLoss(SL) en puntos. Por lo que hay que trazar 3 eventos: 1) cambio de la señal OUT; 2) cambios de precio del precio de apertura por el valor de TP; 3) cambios de precio del precio de apertura del valor SL.
Cuando ocurra alguno de estos eventos, la corrección de los pesos se realiza de forma análoga. Si se obtienen beneficios, los pesos o se quedan sin cambiar o se corrigen (señal fuerte). Si se obtienen pérdidas, se corrigen los pesos para hacer la entrada por la alerta X1 el vector muestra OUT1 con la señal "deseada".
El único inconveniente de esta limitación es el hecho de que se utilizan valores absolutos de TP y SL, que no es tan bueno para la optimización de una red en un periodo de tiempo grande en las condiciones del mercado actuales. Según me he dado cuenta, TP y SL no deberían ser muy diferentes la una de la otra.
Significa que el sistema tiene que ser simétrico para evitar la desviación en la dirección de una tendencia de Buy o Sell más global durante el training. También hay una opinión según la que TP debería ser 2-4 veces más grande que SL: de este modo se aumenta artificialmente la proporción de los trades rentables y no rentables. Pero en este caso, se arriesga el training de la red con un cambio de la tendencia. Estas variantes pueden existir, por supuesto, pero debería comprobar ambas en sus investigaciones.
Enumerado 4. Una iteracción de configuración de peso de red.
int TradePos; int pat=0; // open an order for the first pattern for(i=0;i<nNeuron[0];i++) Out[0][i]=in[i][pat]; // take the training pattern CalculateLayer(); // calculate the network output TradePos=TradeDir(Out[nLayer-1][0]); // if exit is larger than 0.5, then buy. Otherwise - sell ipat=pat; // remember the pattern for(pat=1;pat<nPattern;pat++) // go through the pattern and train the network { for(i=0;i<nNeuron[0];i++) Out[0][i]=in[i][pat]; // take the training pattern CalculateLayer(); // calculate the network output ProfitPos=1e4*TradePos*(bar[3][pat]-bar[3][ipat]); // calculate profit/loss at close prices [3] // if trade direction has changed or stop order has triggered if (TradeDir(Out[nLayer-1][0])!=TradePos || ProfitPos>=TP || ProfitPos<=-SL) { // correcting weights Out[nLayer][0]=Sigmoid(0.1*TradePos*ProfitPos); // set the desired output of the network for(i=0;i<nNeuron[0];i++) Out[0][i]=in[i][ipat];// take the pattern by which // CalculateLayer() were opened; // calculate the network output CalculateError(); // calculate the error ChangeWeight(); // correct weights for(i=0;i<nNeuron[0];i++) Out[0][i]=in[i][pat]; // go to the new order CalculateLayer(); // calculate the new output of the network TradePos=TradeDir(Out[nLayer-1][0]); // if output is > 0.5, then buy //otherwise sell ipat=pat; // remember the pattern } }
Con estos simples pasos la red distribuirá finalmente las clases obtenidas de la capa Kohonen de manera que haya una alerta de entrada de mercado con el máximo número de beneficios correspondiente a cada uno de ellos. Desde el punto de vista de las estadísticas, la red ajusta cada patrón de entrada para el grupo de trabajo.
Mientras que un solo vector de entrada puede ofrecer las alertas en diferentes direcciones durante el proceso de ajuste de peso, obteniendo gradualmente el número máximo de predicciones verdaderas, este método puede llamarse dinámico. El meto utilizando se conoce como MPS: Sistema de maximización de beneficio (SMB).
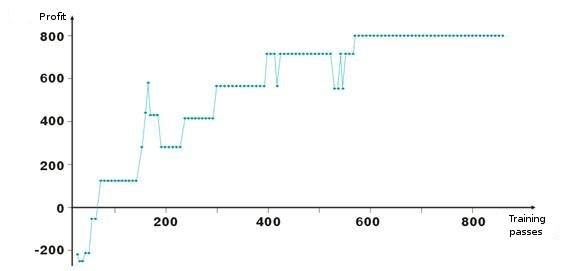
Aquí están los resultados del ajuste de pesos de la red. Cada punto del gráfico es el valor del beneficio obtenido en puntos durante un pase del periodo de training. El sistema está siempre en el mercado: TakeProfit = StoplLoss = 50 puntos, se hace el arreglo sólo con una orden de stop, los pesos se corrigen en caso de beneficio y pérdida.
Después de un inicio negativo, los pesos de las capas se ajustan para que sobre la iteración número cien, el beneficio sea positivo. Es interesante el hecho de que el sistema se ralentiza en algunos niveles. Esto está conectado con los parámetros de la velocidad de training.
Como puede ver en la enumeración 2, el beneficio ProfitPos se calcula cerrando precios de una barra en la que se ha entrado, y en la que se consiguió una de las condiciones (orden de stop o alerta de cambio). Este método es duro, por supuesto, especialmente para los casos con órdenes de stop. Se le puede añadir una complicación analizando los precios High y Low de una barra r (bar[1][ipat] y bar[2][ipat] respectivamente). Puede intentar hacerlo usted mismo.
¿Cambiar o buscar entradas?
Hemos estudiado el método dinámico de training que entrena la red a través de sus propios errores. Ha debido darse cuenta de que según el algoritmo con el que siempre estamos en el mercado, arreglar beneficio/pérdida y va más allá. Por lo que hay que delimitar las entradas e intentar entrar en el mercado sólo con los vectores de entrada "favorables". Esto quiere decir que hay que definir la dependencia del nivel de alerta de entrada a la red en el número de trades rentables/no rentables.
Se puede hacer fácilmente. Vamos a introducir la variable 0<M<0,5, que será el criterio de la entrada que se necesita. De Out>0,5+M, buy; si Out<0,5-M, sell. Seleccionamos entre las entradas y salidas los vectores que estén entre 0,5-M<Out<0,5+M.
Otro método para seleccionar los vectores innecesarios, es recopilar información estadística sobre la rentabilidad de una orden desde los valores de salidas concretas de la red. Vamos a llamarlo análisis visual. Antes de eso, hay que definir el método de cierre de posiciones: alcanzar la orden stop, cambio de señal de la salida de red. Luego se crea una table Out | ProfitPos. Los valores de Out y ProfitPos se calculan para cada vector de salida (es decir, para cada barra).
Luego vamos a hacer una tabla resumen del campo ProfitPos. Como resultado, veremos la dependencia de los valores Out y el beneficio obtenido. Seleccione el rango Out=[MLo, MHi], en el que está el mejor beneficio y utilice sus valores en el trading.
De vuelta a MQL4
Una vez que ha empezado el desarrollo en VC++, no se intentaron amortizar las posibilidades de MQL4. No se hizo por el bien de la comodidad. Voy a hablarle de un incidente. Recientemente, un conocido mío intentó obtener una base de datos de compañías de nuestra ciudad. Hay muchos directorios en Internet, pero ninguno quería vender la base.
Y escribimos un script en MQL4 que escanea una página html y selecciona una zona con información sobre una empresa, y la guarda en un archivo. Luego editamos el archivo en Excel y ya estaba lista la base de datos de tres páginas amarillas con todos los teléfonos, direcciones y actividades empresariales. Era la base de datos más completa de la ciudad; yo me sentí orgulloso de la facilidad y las posibilidades de MQL4.
Naturalmente, cada uno puede manejar una sola tarea en varias lenguas, pero es mejor seleccionar la que será mejor en términos de proporción de posibilidad/dificultad para ciertas tareas.
Por lo que, después de la formación de la red, deberían guardarse todos sus parámetros en un archivo para transferirlo a MQL4.
- tamaño del vector de entrada
- tamaño de vector de salida
- número de capas
- número de neuronas por capas - de entrada a salida
- pesos de las neuronas por capas
El indicador utilizará sólo una función del arsenal de la claseCNeuroNet – CalculateLayer. Vamos a formar un vector de entrada para cada barra, calcular el valor de la salida de la red, y construir el indicador [6].
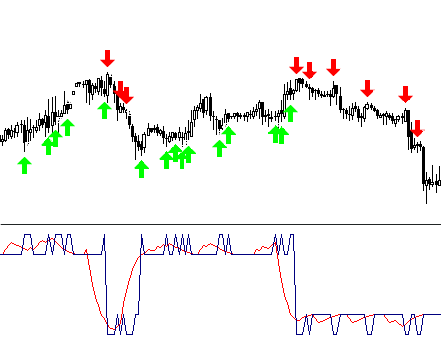
Si ya se han decidido los niveles de entrada, se pueden pintar las partes de la curva obtenida en diferentes colores.
En el artículo se adjunta el ejemplo del código !NeuroInd.mq4
IV. Método creativo
Para una buena implementación hay que tener un punto de vista amplio. Las redes neuronales no son la excepción. No creo que la variante que se ofrece sea ideal y pueda adaptarse a cualquier tarea. Por eso debería buscar siempre sus propias soluciones, dibujar las imágenes generales, sistematizar y comprobar las ideas. A continuación encontrará varios avisos y recomendaciones.
- Adaptación de la red. Una red neuronal es un aproximador. Un "neuronet" restaura una curva cuando obtiene puntos nodales. Si la cantidad de puntos es muy grande, la construcción futura dará malos resultados. Los datos viejos de historial deben eliminarse de la formación y se deben añadir nuevos. Así es como se realiza la aproximación a un nuevo polinomio.
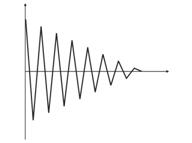
- Sobreentrenamiento Ocurre en el ajuste "ideal" (o cuando se entrena una red el ruido de los valores de entrada. Como resultado, cuando se da el valor de prueba a una red, mostrará un resultado erróneo (img alt="". 9).
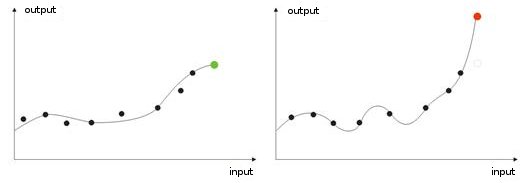
Fig. 9. Resultado de una red "sobreentrenada": diagnóstico erróneo.
- Complejidad, repetibilidad, inconsistencia de una muestra de entrenamiento En los trabajos [8, 9] los autores analizan la dependencia entre los parámetros enumerados. Supongo que está claro que si diferentes vectores instructores (o, peor, contradictorios) corresponden a un único vector de aprendizaje, la red nunca aprenderá a clasificarlos correctamente. Para este fin, se deben crear vectores de entrada mayores, para que contengan los datos que permitan delimitarlos en espacio de clases. La img alt="". 10 muestra esta dependencia. Cuando más alta sea la complejidad de un vector, más baja es la repetibilidad y la inconsistencia de los patrones.
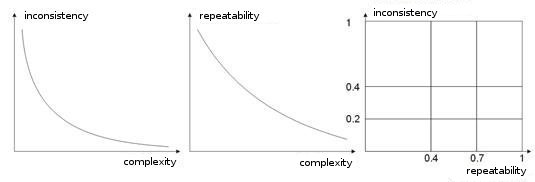
Fig. 10. La dependencia de las características de los vectores de entrada.
- Entrenamiento de red mediante el modelo de Boltzmann. Este método es similar al intento de varias variantes de peso posibles. La InteligenciaArtificial del Asesor Experto trabaja en función al principio similar en su aprendizaje. Cuando se entrena a una red, pasa por absolutamente todas las variantes de valores de peso (como el craqueo de la contraseña de un correo electrónico) y selecciona la mejor combinación.
Esta tarea es intensa para un ordenador, por eso el número de pesos de todas las redes está limitado a 10. Por ejemplo, si el peso cambia de 0 a 1 en el paso 0,01, necesitaremos 100 pasos. Para 5 pesos, esto significa 5 100 combinaciones. Es un número muy grande, por lo que esta tarea sobrepasa la potencia de un ordenador. La única manera de construir una red mediante este método, es utilizar un gran número de ordenadores, cada uno procesando una parte concreta.
Esta tarea la pueden realizar 10 ordenadores. Cada uno procesará 510 combinaciones, por lo que la red se puede hacer más compleja utilizando un número más grande de pesos, capas, y pasos.
A diferencia del "Ataque de fuerza bruta", el método de Boltzmann actúa de forma más suave y más rápida. En cada iteración, se establece un cambio sobre un peso. Si con el nuevo peso el sistema mejora sus características de entrada, se acepta ese peso y se hace una nueva iteración.
Si el peso aumenta el error de salida, se acepta con la probabilidad calculada mediante la fórmula de distribución de Boltzmann. Por lo tanto, al principio de la red, la salida puede tener valores completamente diferentes, "enfriando" gradualmente la red hasta el mínimo global necesario [10, 11].
Por supuesto, esta no es una lista completa de sus próximos estudios, también hay algoritmos genéricos, métodos de mejora de aproximación, redes con memoria, redes radiales, máquinas de asociación, etc.
Conclusión
Me gustaría añadir que una "neuronet" no es una cura universal de todos sus problemas en trading. Cada uno selecciona trabajo independiente y la creación de sus propios algoritmos, otra persona preferirá utilizar paquetes de neuronas ya preparados, de los que se pueden encontrar más en el mercado.
Lo único que tiene que hacer es no tener miedo de los experimentos. ¡Buena suerte y grandes beneficios!
Referencias
1. Baestaens, Dirk-Emma; Van Den Bergh, Willem Max; Wood, Douglas. Soluciones de redes neuronales para el trading en mercados financieros.
2. Voronovskii G.K. y otros. Geneticheskie algoritmy, iskusstvennye neironnye seti i problemy virtualnoy realnosti (Algoritmos genéricos, Redes neuronales artificiales, y Problemas de la realidad virtual).
3. Galushkin A.I. Teoriya Neironnyh setei (Teoría de las Redes neuronales).
4. Debok G., Kohonen T. Analyzing Datos financieros utilizando mapas de autoorganización.
5. Ezhov A.A., Shumckii S.A. Neirokompyuting i ego primeneniya v ekonomike i biznese (Informática neuronal y su uso en economía y negocios).
6. Ivanov D.V. Prognozirovanie finansovyh rynkov s ispolzovaniem neironnyh setei (Previsión de los mercados financieros utilizando redes neuronales artificiales) (Trabajo de grado)
7. Osovsky S. Redes neuronales para el procesamiento de datos.
8. Tarasenko R.A., Krisilov V.A., Vybor razmera opisaniya situatsii pri formirovanii obuchayushchey vyborki dlya neironnyh setei v zadachah prognozirovaniya vremennyh ryadov (Elección del tamaño de la descripción de la situación cuando se crea una muestra de entrenamiento para la serie de redes neuronales en tareas de previsión del tiempo).
9. Tarasenko R.A., Krisilov V.A., Predvaritelnaya otsenka kachestva obuchayushchey vyborki dlya neironnyh setei v zadachah prognozirovaniya vremennyh ryadov (Estimación preliminar de la calidad de una muestra de entrenamiento para la serie de redes neuronales en tareas de previsión de tiempo).
10. Philip D. Wasserman. Informática neuronal: teoría y práctica.
11. Simon Haykin. Redes neuronales Una base completa.
12. www.wikipedia.org
13. Internet.
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/1562
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Promediación efectiva de algoritmos con retraso mínimo: Uso en indicadores y en Asesores Expertos
Promediación efectiva de algoritmos con retraso mínimo: Uso en indicadores y en Asesores Expertos
 Carpeta de programa de la Terminal de cliente de MetaTrader4
Carpeta de programa de la Terminal de cliente de MetaTrader4
 Canales. Modelos avanzados. Ondas Wolfe
Canales. Modelos avanzados. Ondas Wolfe
 ¿Dormir, o no dormir?
¿Dormir, o no dormir?
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso