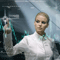神经网络诀窍
简介
曾几何时,技术分析尚在襁褓之中,那时并不是所有交易者都拥有计算机 - 人们开始试着用他们发明的公式和规律来预测未来的价格。 他们通常都被人蔑称为江湖骗子。 时间流逝,各种信息处理方法变得愈加复杂,现在几乎没有对技术分析漠不关心的交易者了。 任何新手交易者都可轻松利用图表、各种指标来寻找规律。
外汇交易者与日俱增。 与此同时,他们对市场分析方法的要求也在不断提高。 此类“相对”较新的方法之一是使用理论模糊逻辑和神经网络。 我们看到,各大专题论坛上有关这些问题的主题引发了大量活跃的讨论。 它们确实存在,并将继续存在下去。 进入市场的用户很难离得开它。 而这对个人的智力、大脑和意志力来说是一个挑战。 因此,交易者孜孜不倦地学习新东西,在实践中使用各种方法。
本文中我们将分析神经网络创建的基础实施,了解 Kohonen 神经网络的概念,并谈一谈交易优化方法。 本文是第一篇面向神经网络和信息处理原则初学者的文章。
要用 Kohonen 层构建一个神经网络,需要:
1) 任意货币对的 10 000 个历史条柱;
2) 5 克移动平均线(或任何其他指标 - 全看你的选择);
3) 逆向分布的 2 到 3 层;
4) 以优化方法作为内容;
5) 不断增长的余额量和正确猜出的交易方向的数量。
第 I 节. Kohonen 层的诀窍
为新手考虑,让我们从这一节开始。 我们将讨论各种练习 Kohonen 层的方法,更确切地说,是其基本版本,因为它有很多版本。 本节中没有什么原创内容,所有说明都取自本主题的经典参考内容。 但是,本节的优点在于针对各节的大量说明性图片。
在本节中,我们将讨论以下问题:
- Kohonen 权向量的调整方式;
- 输入向量的前期准备工作;
- 选择 Kohonen 神经元的初始权值。
因此,根据维基百科,Kohonen 神经网络是一类神经网络,其主要元素为 Kohonen 层。 Kohonen 层包含自适应线性加法器(“线性形式神经元”)。 通常,Kohonen 层的输出信号的处理依据是“赢家通吃”规则:最大的信号变为 1,其他信号统统变为 0。
现在让我们举个例子来讨论此概念。 为了能够看得见,将对二维输入向量给出所有计算值。 图 1 中,输入向量以彩色显示。 Kohonen 层(像任何其他层一样)的各个神经元只是计算输入内容的总和,将其乘以其权值。 实际上,Kohonen 层的所有权值都是此神经元的向量坐标。
因此,各个 Kohonen 神经元的输出是两个向量的点积。 从几何学中我们了解到,如果向量之间的角度趋于 0(角度余弦趋于 1),点积将达到最大值。因此,最大值将是最接近于输入向量的 Kohonen 层神经元的最大值。
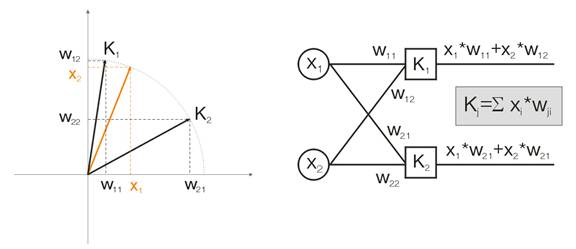
图 1 赢家是向量最接近输入信号的神经元。
根据定义,现在我们应该找到所有神经元中的最大输出值,向其输出赋值 1,向所有其他神经元赋值 0。 Kohonen 层将在输入向量所在空间区域“回复”我们。
Kohonen 权向量的调整
如上所述,层训练的目的是对输入向量进行精确的空间分类。 这意味着各个神经元必须对其获胜的特定区域负责。 获胜神经元与输入神经元之间的偏差必须小于其他神经元的偏差。 为了达到这一目的,获胜神经元“拐入”了输入向量侧。
图 2 显示两个神经元(黑色神经元)针对两个输入向量(彩色的向量)的划分。

图 2. 各个神经元都向最近的输入信号靠近。
每次迭代时,获胜神经元都会靠近“其自己的”输入向量。 它的新坐标根据以下公式计算得出:
![]()
其中,A(t) 是训练速度参数,取决于时间 t。这是一个非增函数,每次迭代时都会从 1 降至 0。 如果初始值为 A=1,则将在某个阶段执行权值校正。 当每个输入向量都有一个 Kohonen 神经元时(例如,Kohonen 层中有 10 个输入向量和 10 个神经元),就有可能出现这种情况。
但实际上,这种情况几乎不可能出现,因为我们通常需要把大量输入数据划分为多个包含类似数据的组,从而减少了输入数据的多样性。 这就是值 A=1 不可取的原因。 实践表明,最佳初始值应小于 0.3。
此外,A 与输入向量的数量成反比。 即,如果 A 较大,最好进行小规模校正,使获胜神经元不会“穿过”其整个校正空间。 作为 A 的功能,通常会选择任意单调递减函数。 例如,双曲线下降或线性下降,或 Gaussian 函数。
图 3 显示速度 A=0.5 时的神经元权值修正步骤。 神经元越靠近输入向量,误差越小。
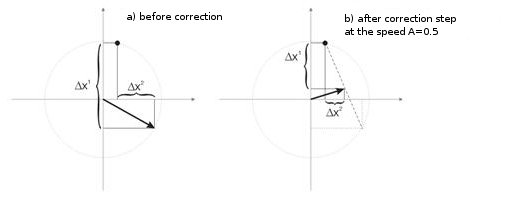
图 3. 神经元权值校正受输入信号的影响。
宽样本时的少量神经元
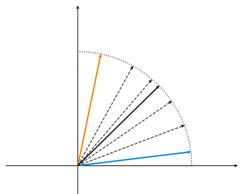
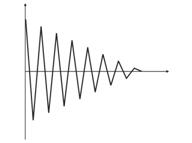
图 4. 两个输入向量之间的神经元波动。
图 4(左)中有两个输入向量(以彩色显示)和仅仅一个 Kohonen 神经元。 在校正期间,神经元将从一个向量转至另一个向量(点线)。 当 A 值减小至 0 时,它在两者之间稳定下来。 神经元坐标随时间的变动可以锯齿形波浪线表示(图 4 右)。
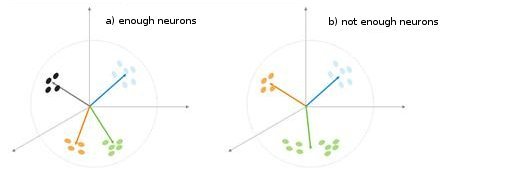
图 5 分类类型对神经元数量的依赖关系。
图 5 中显示了另一种情况。 在第一种情况中,四个神经元把样本充分地划分为四个超球体区域。 在第二种情况中,神经元数量不足,导致误差增大且样本重新分类。 因此,我们可以得出以下结论:Kohonen 层必须包含足够数量的可用神经元,这取决于已分类样本的容量。
输入向量情况下的预先准备
Philip D. Wasserman 在他的书中写道,在将输入向量放到网上之前,最好(虽然不是必须的)将它们标准化。 方法是将输入向量的各个分量除以向量长度。 此长度是通过从向量分量平方和中提取平方根得出的。 以下是代数表示法:
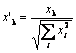
这可将输入向量转换为同一方向的单位向量,即 n 维空间中单位长度的向量。 此操作的含义很明显 - 投射超球体表面上的所有输入向量,从而简化搜索 Kohonen 层的任务。 换句话说,为了搜索输入向量与向量-Kohonen 神经元之间的角度,我们应该消除向量长度等因素,使所有神经元的几率等同。
样本向量的元素通常是非负值(例如,移动平均线的值、价格)。 它们都集中于正象限空间。 此类“正”样本标准化的结果是,大量向量累积在仅仅一个正区域内,这种情况对于获取资格来说并不有利。 所以我们才能在标准化之前执行样本平滑处理。 如果样本相当大,我们可以假设向量基本上聚集于一个区域,没有远离主样本的“局外人”。 因此,可将样本相对于其“极值”坐标居中放置。
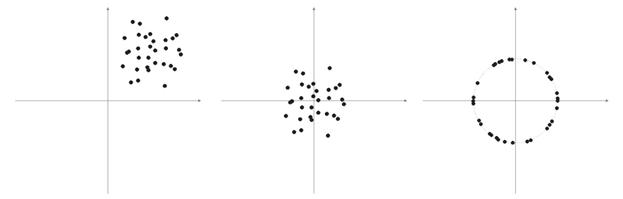
图 6 输入向量的标准化。
如上所述,向量标准化是有必要的。 它能够简化 Kohonen 层的校正工作。 但是,我们应该明确给出一个样本,并确定是否将其映射到球体上。
列表 1. 将输入向量的范围缩小至 [-1, 1]
for (N=0; N<nNeuron[0]; N++) // for all neurons of the input layer { min=in[N][0]; // finding minimum in the whole sample for (pat=0; pat<nPattern; pat++) if (in[N][pat]<min) min=in[N][pat]; for (pat=0; pat<nPattern; pat++) in[N][pat]-=min; // shift by the value of the minimal value max=in[N][0]; // finding maximum in the whole sample for (pat=0; pat<nPattern; pat++) if (in[N][pat]>max) max=in[N][pat]; for (pat=0; pat<nPattern; pat++) in[N][pat]=2*(in[N][pat]/max)-1; // narrowing till [-1,1] }
如果我们要标准化输入向量,我们应该相应地将所有神经元权值都标准化。
选择初始神经元权值
这有无数的可能。
1) 像平常对神经元所做的那样(随机化),将随机值分配给权值;
2) 按示例初始化,将从训练样本中随机选择的示例的值指派为初始值;
3) 线性初始化。 在这种情况下,权值是由沿整个线性空间线性排序,并介于初始数据集中的两个向量之间的向量值发出的;
4) 所有权值具有相同的值 - 凸组合方法。
让我们分析第一种和最后一种情况。
1) 将随机值分配给权值。
随机化期间,所有向量神经元都分布在超球体的表面上。 而输入向量有分组的趋势。 在这种情况下,有些权向量可能与输入向量相距太远,它们绝无可能提供较好的关联,因此它们无法学习 - 图 7(右)中的“灰色”数字。 此外,剩余的神经元将不足以最大程度减小误差并划分类似的类 -“红色”类包括在“绿色”神经元中。
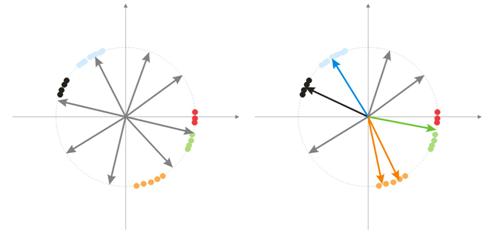
图 7 随机化神经元的训练结果。
如果一个区域内聚集了大量神经元,多个神经元可以进入一个类的区域,并将其划分为多个子类 - 图 7 中的橙色区域。 这并不重要,因为之后对层信号的进一步处理可以修复此问题,但这需要占用训练时间。
解决这些问题的方法之一 是在初始阶段,对一个获胜神经元的向量进行校正,同时也对最接近此神经元的向量组进行校正。 然后组的数量逐渐减小,最终仅校正一个神经元。 可从已排序的神经元输出数组中选择一个组。 将矫正前 K 个最大输出中的神经元。
另一个 权向量的组调整方法是以下方法。
a) 为各个神经元定义校正向量的长度:
![]()
.
b) 距离最短的神经元成为获胜者 - Wn. 之后,如果找到一组神经元,其关联限制在距离 Wn 的 C*Ln 处。
c) 根据一个简单的规则 ![]() 来校正这些神经元的权值。 这样就完成了整个样本的校正。
来校正这些神经元的权值。 这样就完成了整个样本的校正。
C 参数在训练过程中从某个数字(通常是 1)更改为 0。
第三个 有趣的方法表明每个神经元在一次完整的样本流程中仅可校正 N/k 次。 这里,N 是样本的大小,k 是神经元数量。 即,如果任意神经元成为获胜者的次数比其他神经元多,它会“退出游戏”直至完成样本流程。 这样,其他神经元也可学习。
2) 凸组合方法
此方法意味着权向量和输入向量初始时都放置于同一区域内。 输入向量和初始权向量的当前坐标的计算公式如下:
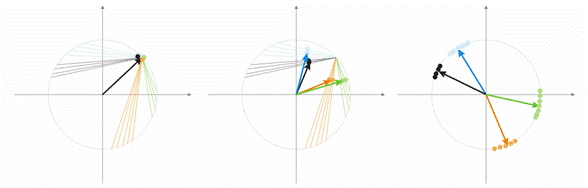
![]()
,
![]()
其中,n 是输入向量的维数,a(t) 是时间的非减函数,各个迭代将其值从 0 增加到 1,结果,所有输入向量与权向量一致,最终取代了它们。 此外,权向量将“达到”其类。
这些就是此神经网络中应用的 Kohonen 层基础版本的所有资料了。
II. 汤匙、长柄勺和脚本
我们要讨论的第一个脚本将采集有关条柱的数据并创建一个输入向量文件。 让我们以 MA 为练习用例。
列表 2. 创建输入向量文件
// input parameters #define NUM_BAR 10000 // number of bars for training (number of training patterns) #define NUM_MA 5 // number of movings #define DEPTH_MA 3 // number of values of a moving // creating a file hFile = FileOpen(FileName, FILE_WRITE|FILE_CSV); FileSeek(hFile, 0, SEEK_END); // Creating an array of inputs int i, ma, depth; double MaIn; for (i=NUM_BAR; i>0; i--) // going through bars and collecting values of MA fan { for (depth=0; depth<DEPTH_MA; depth++) //calculating moving values for (ma=0; ma<NUM_MA; ma++) { MaIn=iMA(NULL, 0, 2+MathSqrt(ma*ma*ma)*3, 0, 1, 4, i+depth*depth)- ((High[i+depth*depth] + Low[i+depth*depth])/2); FileWriteDouble(hFile, MaIn); } }
创建的数据文件用作应用程序之间的信息传递手段。 如果你正在熟悉训练算法,强烈建议查看其操作的中期结果和一些变量的值,并在必要时更改训练条件。
因此我们推荐你使用高级编程语言(VB、VC++ 等),而 MQL4 的当前调试手段尚有不足(我希望这种情况在 MQL5 中能够有所改善)。 之后,当你了解你的算法和函数的所有误区后,你可以开始使用 MQL4。 此外,你必须在 MQL4 中编写最终目标(指标或 Expert Advisor)。
广义的类结构
列表 3. 神经网络的类
class CNeuroNet : public CObject { public: int nCycle; // number of learning cycles until stop int nPattern; // number of training patterns int nLayer; // number of training layers double Delta; // required minimal output error int nNeuron[iMaxLayer]; // number of neurons in a layer (by layers) int LayerType[iMaxLayer]; // types of layers (by layers) double W[iMaxLayer][iMaxNeuron][iMaxNeuron];// weights by layers double dW[iMaxLayer][iMaxNeuron][iMaxNeuron];// correction of weight double Thresh[iMaxLayer][iMaxNeuron]; // threshold double dThresh[iMaxLayer][iMaxNeuron]; // correction of threshold double Out[iMaxLayer][iMaxNeuron]; // output value double OutArr[iMaxNeuron]; // sorted output values of Kohonen layer int IndexWin[iMaxNeuron]; // sorted neuron indexes of Kohonen layer double Err[iMaxLayer][iMaxNeuron][iMaxNeuron];// error double Speed; // Speed of training double Impuls; // Impulse of training double in[100][iMaxPattern]; // Vector of input values double out[10][iMaxPattern]; // vector of output values double pout[10]; // previous vector of output values double bar[4][iMaxPattern]; // bars, on which we learn int TradePos; // order direction double ProfitPos; // obtained profit/loss of an order public: CNeuroNet(); virtual ~CNeuroNet(); // functions void Init(int aPattern=1, int aLayer=1, int aCycle=10000, double aDelta=0.01, double aSpeed=0.1, double aImpuls=0.1); // learning functions void CalculateLayer(); // Calculation of layer output void CalculateError(); // Error calculation /for Target array/ void ChangeWeight(); // Correction of weights bool TrainNetwork(); // Network training void CalculateLayer(int L); // Output calculation of Kohonen layer void CalculateError(int L); // Error calculation of Kohonen layer void ChangeWeight(int L); // Correction of weights for layer indication bool TrainNetwork(int L); // Training of Kohonen layer bool TrainMPS(); // Network training for getting the best profit // variables for internal interchange bool bInProc; // flag for entering the TrainNetwork function bool bStop; // flag for the forced termination of the TrainNetwork function int loop; // number of the current iteration int pat; // number of the current processed pattern int iMaxErr; // pattern with the maximal error double dMaxErr; // maximal error double sErr; // square of pattern error int iNeuron; // maximal number of neurons in Kohonen layer correction int iWinNeuron; // number of winner neurons in Kohonen layer int WinNeuron[iMaxNeuron]; // array of active neurons (ordered) int NeuroPat[iMaxPattern][iMaxNeuron]; // array of active neurons void LinearCovariation(); // normalization of the sample void SaveW(); // Analysis of neuron activity };
实际上,这个类并不复杂。 它包含必要的主要设置和服务变量。
让我们分析一下。 根据用户的命令,接口类创建一个工作线程并初始化一个定时器,用于定期读出网络值。 它还接收用于从神经网络参数中读取信息的索引。 工作线程先从初步制备的文件中读取输入/输出向量的数组,并设置层的参数(层的类型以及各个层中的神经元数量)。 这是准备阶段。
之后,我们调用函数 CNeuroNet::Init,并在其中初始化权值,标准化样本,并设置训练参数(速度、脉冲、必要误差和训练循环次数)。 上述工作完成后,才可调用“主力军”- CNeuroNet::TrainNetwork 函数(或 TrainMPS或 TrainNetwork(int L),这取决于我们想要获得什么。 训练结束后,工作线程将网络权值保存到一个文件中,以在指标或 Expert Advisor 中实施最后一个权值。
III. 烘培网络
现在让我们转到训练问题。 训练中的习惯做法是设置“模式-教师”对。 这是与各个输入模式对应的特定目标。 基于当前输入与目标值之间的差异,执行权值校正。 例如,某研究人员想要让网络基于前十个传到网络上的条柱价格来预测下一个条柱的价格。 在这种情况下,在放置了 10 个值作为输入之后,我们需要比较所获输出与教学值,然后根据它们之间的差异校正权值。
我们提供的模型中并没有一般意义上的“教学”向量,因为我们事先并不知道我们应该在哪些条柱上入场或离场。 这意味着我们的网络将基于自己之前的输出值来校正其输出向量。 同时还意味着网络将尝试获取最大利润(将正确预测交易方向的数量最大化)。 让我们考虑图 8 的例子。
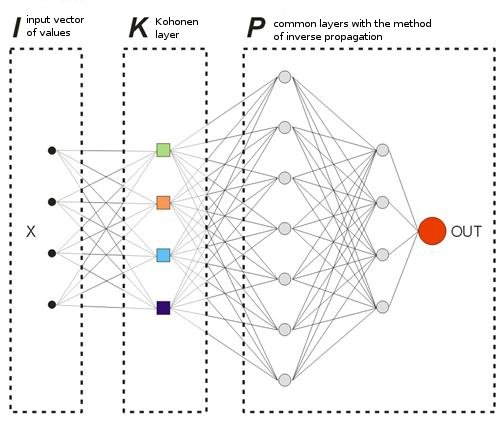
图 8 已训练神经网络的方案。
已在样本上预先训练过的 Kohonen 层将其向量进一步转发给网络。 输出网络的最后一层时,我们将获得值 OUT,其意义如下。 如果 OUT>0.5,执行买入交易;如果 OUT<0.5,执行卖出交易(sigmoid 值的变化范围为 [0, 1])。
![]()
假设网络以输出 OUT1 >0.5 来回复某个输入向量 OUT1。 这意味着我们在此模式所属的条柱上建了一个买入仓位。 之后,在输入向量在某个 Xk 上的时间表示形式上,符号 OUTk 转变为“反方向”。 结果,我们关闭了买入仓位并打开了卖出仓位。
就在此时,我们需要查看已结订单的结果。 如果我们获利,我们可以强化这一提示。 或者我们可以认为没有误差并将无需进行任何校正。 如果我们亏损,我们将校正层的权值,以使 X1 向量的提示的输入显示 OUT1<0.5。.
现在让我们计算教学(目标)输出的值。 同样地,让我们将发生的损失(以点数计算)中的 sigmoid 乘以交易方向信号得到一个值。 结果,亏损越大,对网络的惩罚越严厉,对其权值的校正值就越大。 例如,如果我买入仓位有 =50 个亏损点,则将按以下方式计算对输出层的校正:
![]() ,
, ![]() ,
, ![]()
我们可以界定引入交易分析流程参数 TakeProfit (TP) 和 StopLoss (SL)(以点数计算)的交易规则。 所以我们需要跟踪 3 个事件: 1) 更改 OUT OUT 信号,2) 价格从建仓价格改变了 TP 的值,3) 价格从建仓价格改变了值 -SL。
出现以下事件之一时,将以类似方式修正权值。 如果我们获利,权值可保持不变或进行校正(更强信号)。 如果我们亏损,则校正权值以使 X1 向量的提示的输入显示 向量的提示的输入显示 OUT1 和“期望”信号。
此限制唯一的缺陷是我们使用绝对 TP 和 SL 值,在当前市场条件下,这些值在很长一段时间内不利于网络的优化。 在我看来,TP 和 SL 不应相差太大。
这表示系统必须对称,以避免训练期间在更全局的买入或卖出趋势的方向上发生偏离。 还有一个观点是,TP 应比 SL 大 2 到 4 倍 - 这样我们就人为地增大了获利交易与亏损交易的比率。 但这种情况的风险是训练的网络有转向趋势。 当然,这两种方法都是可行的,但你应该自己对它们进行一番研究。
列表 4. 网络权值设置的一个迭代
int TradePos; int pat=0; // open an order for the first pattern for(i=0;i<nNeuron[0];i++) Out[0][i]=in[i][pat]; // take the training pattern CalculateLayer(); // calculate the network output TradePos=TradeDir(Out[nLayer-1][0]); // if exit is larger than 0.5, then buy. Otherwise - sell ipat=pat; // remember the pattern for(pat=1;pat<nPattern;pat++) // go through the pattern and train the network { for(i=0;i<nNeuron[0];i++) Out[0][i]=in[i][pat]; // take the training pattern CalculateLayer(); // calculate the network output ProfitPos=1e4*TradePos*(bar[3][pat]-bar[3][ipat]); // calculate profit/loss at close prices [3] // if trade direction has changed or stop order has triggered if (TradeDir(Out[nLayer-1][0])!=TradePos || ProfitPos>=TP || ProfitPos<=-SL) { // correcting weights Out[nLayer][0]=Sigmoid(0.1*TradePos*ProfitPos); // set the desired output of the network for(i=0;i<nNeuron[0];i++) Out[0][i]=in[i][ipat];// take the pattern by which // CalculateLayer() were opened; // calculate the network output CalculateError(); // calculate the error ChangeWeight(); // correct weights for(i=0;i<nNeuron[0];i++) Out[0][i]=in[i][pat]; // go to the new order CalculateLayer(); // calculate the new output of the network TradePos=TradeDir(Out[nLayer-1][0]); // if output is > 0.5, then buy //otherwise sell ipat=pat; // remember the pattern } }
通过这些简单的流程,网络最终将分配从 Kohonen 层中获取的类,使入市提示中的最大获利交易数对应于各个类。 从统计学的角度来看 - 各个输入模式由网络进行调整,用于小组工作。
而同一个输入向量在权值调整过程中可以在不同方向上提供提示,逐渐获得最大真实预测数,这种方法可称为动态方法。 此方法以 MPS(利润最大化系统)著称。
以下是网络权值调整的结果。 图中的每个点都是一次训练周期内所获利润的值(以点数计算)。 此系统始终存在于市场上,TakeProfit = StopLoss = 50 个点,仅由止损订单来进行固定,并在获利和亏损情况下校正权值。
看,在开局不利的情况下,层的权值被调整,使利润在大约第 100 个迭代上变为正值。 一个有趣的事实是,系统某种程度上减慢了速度。 这与训练速度的参数相关。
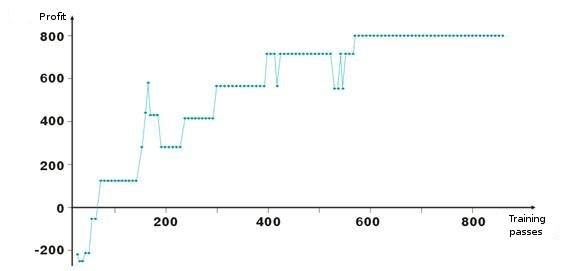
如列表 2 中所示,利润 ProfitPos 是按满足某一条件(止损订单或提示更改)的入市条柱的收盘价来计算的。 当然,这是一个比较粗糙的方法,尤其是在使用止损订单的情况下。 我们可以通过分析条柱的最高价和最低价(对应于 bar[1][ipat] 和 bar[2][ipat])来添加较复杂的方法。 你可以试着自己做做看。
寻求或寻找入市?
我们研究动态训练方法,即让网络自己从失败中吸取教训。 你肯定已经注意到,根据此算法,我们始终在市场中,固定利润/损失,然后再做进一步的打算。 所以,我们需要限制我们的入市,并试着仅在使用“有利”的输入向量时才入市。 这意味着我们需要定义入市网络提示级别与获利/亏损交易数的依赖关系。
这个任务相当简单。 让我们引入变量 0<M<0.5,它将是所需入市的标准。 如果 Out>0.5+M,则买入,如果 Out<0.5-M,则卖出。 我们根据 0.5-M<Out<0.5+M 之间的向量来筛选入市和退市。
另一个筛选不必要向量的方法是从网络的某些输出项的值中收集有关订单盈利能力的统计信息。 让我们称其为可视化分析。 在此之前,我们应定义平仓方法 - 触及止损订单,网络输出信号更改。 然后让我们创建一个表格 Out | ProfitPos。 Out 和 ProfitPos 的值是针对各个输入向量(即针对各个条柱)而计算的。
然后让我们制作 ProfitPos 字段的汇总表。 结果,我们将看到 Out 值与所获利润的依赖关系。 选择范围 Out=[MLo, MHi],在此范围内,我们会得到最高利润,并在交易中使用其值。
返回 MQL4
开始进行 VC++ 开发后,为了方便起见, 我们并未试着减少 MQL4 的使用。 我告诉你一件事。 最近我的一个熟人想获取我们城市的公司数据库。 网上有很多公司名录,但没人愿意卖数据库。
我们在 MQL4 中编写了一个能够扫描 html 页面并选择包含公司信息的区域的脚本,然后将其保存到一个文件中。 然后我们在 Excel 中编辑了此文件,这样,包含所有电话号码、地址和公司活动的三大黄页的数据库就完成了。 这就是这个城市最完整的数据库了;而对于我来说,MQL4 的易用性和功能性让我深以为豪。
当然,你可以用不同的语言来完成同样的任务,但最好还是选一个对于特定任务来说具有最佳的功能性/难度比的语言。
因此,在网络训练之后,我们应该将其所有参数保存到一个文件中,然后传输至 MQL4。
- 输入向量的大小
- 输出向量的大小
- 层数
- 神经元数量(按层) - 从输入到输出
- 神经元权值(按层)
此指标将仅使用类库 CNeuroNet 中的一个函数 - CalculateLayer。 让我们为各个条柱构建一个输入向量,计算网络输出的值并构建指标 [6]。
如果我们已确定输入价位,我们可以为所得曲线的各个部分涂上不同的颜色。
本文随附了代码 !NeuroInd.mq4 的示例。
IV. 创新方法
要获得良好的实施成果,就得开阔我们的思路。 神经网络也不例外。 我觉得提供给我们的方式并不理想,也不通用于所有任务。 所以你才应不断寻求自己的解决方案,勾勒概貌,将你的想法系统化并进行检验。 以下你会看到一些警告和建议。
- 网络自适应性。 神经网络是一个逼近器。 神经网络在获得节点时会恢复曲线。 如果点数太多,未来的结构不会有好结果。 应从训练中移除旧历史数据,然后添加新数据。 这就是逼近新多项式的方法。
- 训练过度。 这种情况出现在执行“理想”调整时(或对网络进行输入值噪声方面的训练时)。 结果,当某个测试值被提供给网络时,它将显示错误的结果(图 9)。
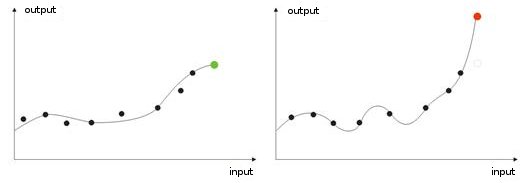
图 9 网络“训练过度”的结果 - 预测错误。
- 训练样本的复杂性、可重复性、不一致性。 在文章 [8, 9] 中,作者分析了枚举参数之间的依赖关系。 如果不同的教学向量(或是更糟糕的对立的教学向量)对应于同一个学习向量,则网络将永远无法学会正确将它们分类,我想这一点是显而易见的。 为此,我们应创建大输入向量,使它们包含允许在类空间中界定它们的数据。 图 10 显示了这种依赖关系。 向量的复杂性越高,模式的可重复性和不一致性越低。
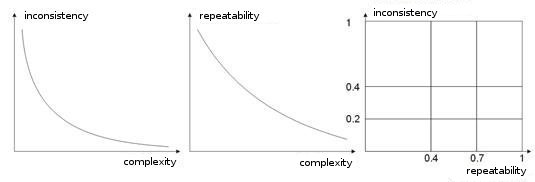
图 10 输入向量的特性的依赖关系。
- 用 Boltzmann 方法执行的网络训练。 此方法类似于尝试使用各种可能的权值类型。 Expert Advisor ArtificialIntelligence 在其学习过程中也遵循类似的原理。 在训练一个网络时,它遍历所有类型的权值(例如破解邮箱密码)并选择最佳组合。
这对计算机来说是个劳动密集型任务,所以一个网络的所有权值数限制为 10 个。 例如,如果权值以 0.01 的步长从 0 更改为 1,我们需要 100 步。 如果有 5 个权值,那就有 5100 种组合。 这是个很大的数字,这个任务超出了计算机的能力范围。 用此法构建网络的唯一途径是使用大量计算机,每台计算机处理一个部分。
这个任务可以用 10 台计算机来执行。 每台处理 510 个组合,那么在使用更大的权值数、层数和步骤数之后,网络会变得愈加复杂。
与这种“蛮力破解”法不同的是,Boltzmann 方法更柔和也更快捷。 每次迭代时,都将针对权值设置一个随机移动。 如果使用新权值时,系统的输入特性得以改善,则将接受此权值并进行新的迭代。
如果权值增大了输出误差,则其被接受的可能性由 Boltzmann 分配公式进行计算。 因此,开始时网络输出可以有完全不同的值,然后逐渐“冷却”,缩减至必要的全局最小值 [10, 11]。
当然,这并不是全部的后续学习内容,还有 遗传算法、提高收敛性法、带内存的网络、径向网络、关联机器等。
总结
我想再说一句,神经网络并非能够解决交易中所有问题的灵丹妙药。 有人选择独立工作并创建自己的算法,有人更愿意使用现成的神经元包,其中大部分都可在市场上找到。
唯一要注意的是别嫌做实验麻烦! 祝你好运,财源广进!
参考文献
1. Baestaens, Dirk-Emma; Van Den Bergh, Willem Max; Wood, Douglas. 金融市场交易的神经网络解决方案。
2. Voronovskii G.K. 等人。 Geneticheskie algoritmy, iskusstvennye neironnye seti i problemy virtualnoy realnosti(遗传算法、人工神经网络和虚拟现实的问题)。
3. Galushkin A.I. Teoriya Neironnyh setei(神经网络理论)。
4. Debok G., Kohonen T. 使用自组织映射分析金融数据。
5. Ezhov A.A., Shumckii S.A. Neirokompyuting i ego primeneniya v ekonomike i biznese(神经计算及其在经济和商业中的应用)。
6. Ivanov D.V. Prognozirovanie finansovyh rynkov s ispolzovaniem neironnyh setei(使用人工神经网络预测金融市场)(毕业作品)
7. Osovsky S. 用于数据处理的神经网络。
8. Tarasenko R.A., Krisilov V.A., Vybor razmera opisaniya situatsii pri formirovanii obuchayushchey vyborki dlya neironnyh setei v zadachah prognozirovaniya vremennyh ryadov(时序预测任务中在构建神经网络训练样本时选择情况描述大小)。
9. Tarasenko R.A., Krisilov V.A., Predvaritelnaya otsenka kachestva obuchayushchey vyborki dlya neironnyh setei v zadachah prognozirovaniya vremennyh ryadov(时序预测任务中对神经网络训练样本质量的初步评估)。
10. Philip D. Wasserman. 神经计算: 理论与实践。
11. Simon Haykin. 神经网络: 综合基础。
12. www.wikipedia.org
13. 互联网。
本文由MetaQuotes Ltd译自俄文
原文地址: https://www.mql5.com/ru/articles/1562
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
本文由网站的一位用户撰写,反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责,也不对因使用所述解决方案、策略或建议而产生的任何后果负责。
 具有最小延迟的有效平均算法: 在指标和 Expert Advisor 中使用
具有最小延迟的有效平均算法: 在指标和 Expert Advisor 中使用