Rezepte für neuronale Netzwerke

Einleitung

Es ist noch nicht so lange her, als Händler noch keine Computer für die technische Analyse hatten und versucht haben mit Hilfe von Formeln und Regelmäßigkeiten, die durch sie erfunden wurden, die zukünftigen Kurse zu prognostizieren. Sie wurden oft als Scharlatane bezeichnet. Die Zeit verging, die Methoden der Informationsverarbeitung sind komplizierter geworden, und es gibt kaum noch Händler, denen die technische Analyse gleichgültig ist. Jeder Anfänger kann ganz einfach Chart, verschiedene Indikatoren sowie die Suche nach Regelmäßigkeiten nutzen.

Die Zahl der Forex-Händler wächst täglich. Damit steigen auch die Anforderungen für die Methoden zur Marktanalyse. Eine dieser "relativ" neuen Methoden ist die Verwendung von theoretischen Fuzzy-Logiken und neuronalen Netzwerken. Wir stellen fest, dass Fragen zu diesem Thema aktiv in verschiedenen thematischen Foren diskutiert werden. Es gibt sie und es wird sie weiterhin geben. Ein Mensch, der den Markt einmal betreten hat, wird ihn kaum mehr verlassen. Es ist eine Herausforderung für die Intelligenz, das Gehirn und die Willensstärke. Deshalb hört ein Händler nie auf, etwas Neues zu lernen und verschiedene Ansätze in die Praxis umzusetzen.

In diesem Artikel werden wir die Grundlagen zur Erstellung neuronaler Netze analysieren und mehr über den Begriff des Kohonen neuronalen Netz erfahren. Außerdem werden wir ein wenig über die Methoden der Handelsoptimierung sprechen. Dieser Artikel ist vor allem für Händler gedacht, die am Anfang sind beim Studieren der neuronalen Netze und der Prinzipien der Informationsverarbeitung.

Um ein neuronales Netzwerk mit der Kohonen-Schicht zu kochen, benötigt man:

1) 10.000 historische Balken eines Währungspaars;
2) 5 Gramm gleitende Durchschnitte (Moving Averages) oder andere Indikatoren - dies ist Ihre Entscheidung;
3) 2-3 Schichten der inversen Verteilung;
4) Methoden der Optimierung als Füllung;
5) wachsender Saldo und eine steigende Zahl an richtig erratenen Richtungen beim Handel.

Abschnitt I. Rezept der Kohonen-Schicht

Beginnen wir mit dem Abschnitt für diejenigen, die ganz am Anfang stehen. Wir werden verschiedene Ansätze zum Einarbeiten der Kohonen-Schicht oder um genauer zu sein, dessen Basisversion diskutieren, denn es gibt viele Varianten davon. Es gibt eigentlich nichts Besonderes an diesem Kapitel, alle Erklärungen stammen von den klassischen Referenzen zu diesem Thema. Der Vorteil dieses Kapitels ist jedoch die große Anzahl von erläuternden Abbildungen zu jedem Abschnitt.

In diesem Kapitel werden wir auf folgende Fragen eingehen:
- die Art und Weise wie Kohonen Wichtungsvektoren eingestellt werden;
- vorläufige Vorbereitung von Eingabevektoren;
- Auwahl der ursprünglichen Gewichtungen der Kohonen Neuronen.

Laut Wikipedia repräsentiert ein Kohonen neuronales Netzwerk eine Klasse von neuronalen Netzwerken, wobei das Hauptelement von ihnen die Kohonen-Schicht ist. Die Kohonen-Schicht besteht aus adaptiven linearen Addierern ("lineare formale Neuronen"). In der Regel werden die Ausgangssignale der Kohonen-Schicht nach der Regel "der Gewinner bekommt alles" verarbeitet: die größten Signale verwandeln sich in Einser, alle anderen Signale werden zu Nullen.

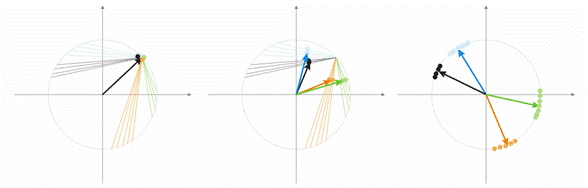
Nun wollen wir diesen Gedanken mit Hilfe eines Beispiels erörtern. Zum Zwecke der Visualisierung werden alle Berechnungen für zweidimensionale Eingabevektoren angegeben. In der Abb. 1 wird der Eingabevektor in Farbe dargestellt. Jedes Neuron der Kohonen-Schicht (wie auch bei jeder anderen Schicht) summiert einfach die Eingabe und multipliziert diese mit der Gewichtung. Eigentlich sind alle Gewichtungen der Kohonen-Schicht Vektor-Koordinaten für dieses Neuron.

Daher ist Ausgabe eines jeden Kohonen Neurons das Punktprodukt von zwei Vektoren. Von der Geometrie wissen wir, dass das maximale Punktprodukt entseht, wenn der Winkel zwischen Vektoren Richtung Null tendiert (der Kosinus-Winkel tendiert zu 1). Der maximale Wert wird also jener des Kohonen-Schicht Neurons sein, das am nähesten zum Eingabevektor ist.

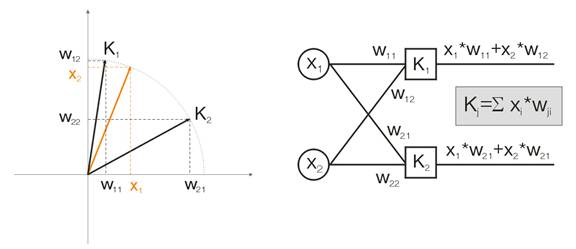
Abb.1 Der Gewinner ist das Neuron, dessen Vektor am nähesten zum Eingangssignal ist.

Entsprechend der Definition sollten wir jetzt den maximalen Ausgabewert unter allen Neuronen finden, dessen Ausgabe eine Eins und allen anderen Neuronen eine Null zuweisen. Und die Kohonen-Schicht wird uns "antworten", in welchem Raumbereich der Eingabevektor liegt.

Anpassung der Kohonen Gewichtungsvektoren

Der Zweck der Einarbeitung mit der Kohonen-Schicht ist wie bereits oben geschrieben, die präzise Raumklassifizierung der Eingabevektoren. Dies bedeutet, dass jedes Neuron für seinen ganz bestimmten Bereich verantwortlich sein muss, in dem es der Gewinner ist. Der Abweichungsfehler des Gewinner-Neurons vom Eingabeneuron muss kleiner sein als jener der anderen Neuronen. Um das zu erreichen, "verwandelt" sich das Gewinner-Neuron in die Seite des Eingabevektors.
Abb. 2 zeigt die Teilung von zwei Neuronen (schwarze Neuronen) für zwei Eingabevektoren (die farbigen).

Abb. 2: Jedes der Neuronen nähert sich seinem nächsten Eingangssignal.

Mit jeder Wiederholung nähert sich das Gewinner-Neuron "seinem eigenen" Eingabevektor. Seine neuen Koordinaten werden entsprechend der folgenden Formel berechnet:

wobei A(t) der Parameter der Einarbeitunsgeschwindigkeit ist und von der Zeit tabhängt. Dies ist eine nicht ansteigende Funktion, die bei jeder Wiederholung von 1 auf 0 reduziert wird. Wenn der Anfangswert A=1 ist, wird die Gewichtungskorrektur in einem Schritt vorgenommen. Dies ist möglich, wenn es für jeden Einangsvektor ein Kohonen-Neuron gibt (zum Beispiel 10 Eingabevektoren und 10 Neuronen in der Kohonen-Schicht).

In der Praxis tritt so ein Fall aber fast nie ein, da in der Regel das große Volumen von Eingabedaten in Gruppen aufgeteilt werden muss, wodurch sich die Vielfalt der Eingabedaten verringert. Deshalb ist der Wert A=1 unerwünscht. Die Praxis zeigt, dass der optimale Anfangswert unter 0,3 sein sollte.

Außerdem ist A umgekehrt proportional zu der Anzahl der Eingabevektoren. Das heißt bei einer großen Auswahl ist es besser, kleine Korrekturen vorzunehmen, so dass das Gewinner-Neuron nicht durch den ganzen Raum in seinen Korrekturen "surft". Als A-Funktionalität wird in der Regel jede monoton fallende Funktion gewählt. Zum Beispiel Hyperbel oder lineare Abnahme oder die Gauß-Funktion.
Abb. 3 zeigt den Schritt der Neuronengewichtungskorrektur bei der Geschwindigkeit A=0,5. Das Neuron hat sich dem Eingabevektor genähert, der Fehler ist kleiner.

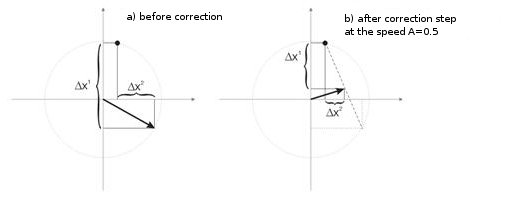
Abb. 3: Neuronengewichtungskorrektur unter dem Einfluss des Eingangssignals.

Kleine Anzahl von Neuronen in einem breiten Beispiel

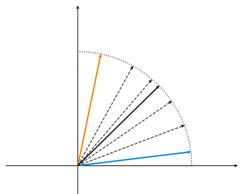
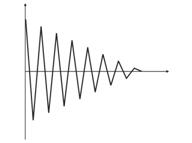
Abb. 4: Neuron Schwankungen zwischen zwei Eingabevektoren.

In der Abb. 4 (links) gibt es zwei Eingabevektoren (in Farbe angezeigt) und nur ein Kohonen Neuron. Im Prozess der Korrektur wird das Neuron von einem Vektor zu einem anderen schwingen (gepunktete Linien). Da der A-Wert sich bis 0 verringert, stabilisiert es sich zwischen ihnen. Die Neuron-Koordinaten, die sich von Zeit zu Zeit ändern, können durch eine Zick-Zack-Linie charakterisiert werden (Abb. 4 rechts).

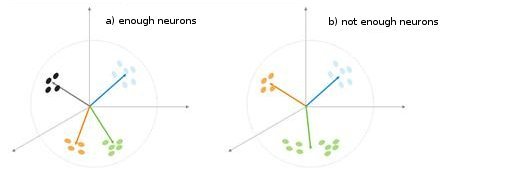
Abb. 5: Abhängigkeit des Klassifikationstyps hinsichtlich der Anzahl von Neuronen.

Eine weitere Situation wird in Abb 5. gezeigt. Im ersten Fall teilen vier Neuronen die Probe ausreichend in vier Bereiche der Hyperkugel. Im zweiten Fall führt die ungenügende Anzahl von Neuronen zu einem Fehler und zur Neuklassifizierung der Probe. Wir können somit daraus schließen, dass die Kohonen-Schicht eine ausreichende Anzahl von freien Neuronen erhalten muss, die vom Volumen der klassifizierten Probe abhängt.

Vorläufige Vorbereitung der Eingabevektoren
Wie Philip D. Wasserman in seinem Buch schreibt, ist es wünschenswert (wenn auch nicht obligatorisch), die Eingabevektoren zu normalisieren, bevor Sie sie in das Netz einführen. Dies wird durch das Aufteilen einer jeden Komponenten des Eingabevektors durch die Vektorlänge erledigt. Diese Länge wird durch die Extraktion der Quadratwurzel aus der Summe der Quadrate der Vektorkomponenten gefunden. Dies ist die algebraische Darstellung:

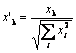
Dies wandelt den Eingabevektor in einen Einheitsvektor mit der gleichen Richtung um, das heißt einen Vektor mit der Längeneinheit im n-dimensionalen Raum. Die Bedeutung dieser Operation ist klar - das Pojizieren aller Eingabevektoren auf der Oberfläche der Hyperkugel, wodurch die Aufgabe, die Kohonen-Schicht zu suchen, erleichtert wird. Mit anderen Worten, für die Suche nach dem Winkel zwischen den Eingabevektoren und den Vektoren-Kohonen-Neuronen, sollten wir solch einen Faktor wie die Vektorlänge eliminieren, um die Chancen aller Neuronen auszugleichen.

Sehr oft haben die Elemente von Probevektoren keine negativen Werte (zum Beispiel Werte von Moving Averages, Kursen). Sie alle konzentrieren sich auf den positiven Quadranten im Raum. Als Ergebnis der Normalisierung einer solchen "positiven" Probe erhalten wir die große Ansammlung von Vektoren in nur einem positiven Bereich, was nicht sehr gut für die Qualifikation ist. Deshalb kann vor der Normalisierung der Probe eine Glättung durchgeführt werden. Wenn die Probe ziemlich groß ist, können wir davon ausgehen, dass sich die Vektoren in etwa in einem Bereich befinden, ohne "Außenseiter", die weit entfernt von der Hauptprobe sind. Deshalb kann eine Probe relativ zu ihren "extremen" Koordinaten zentriert werden.

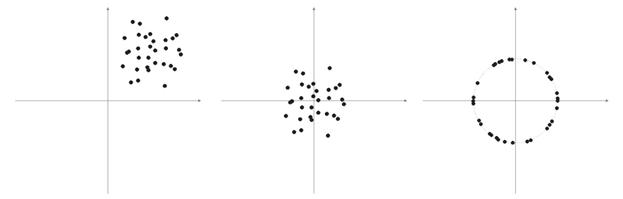
Abb. 6: Normalisierung der Eingabevektoren.

Wie oben geschrieben, ist die Normalisierung der Vektoren wünschenswert. Sie vereinfacht die Korrektur der Kohonen-Schicht. Wir sollten jedoch deutlich eine Probe darstellen und entscheiden, ob sie auf einer Kugel projiziert werden soll oder nicht.

Liste 1. Verschmälerung der Eingabevektoren im Bereich [-1, 1]

for (N=0; N<nNeuron[0]; N++) // for all neurons of the input layer
 {
  min=in[N][0]; // finding minimum in the whole sample
  for (pat=0; pat<nPattern; pat++) if (in[N][pat]<min) min=in[N][pat];
  for (pat=0; pat<nPattern; pat++) in[N][pat]-=min; // shift by the value of the minimal value 
  max=in[N][0]; // finding maximum in the whole sample
  for (pat=0; pat<nPattern; pat++) if (in[N][pat]>max) max=in[N][pat];
  for (pat=0; pat<nPattern; pat++) in[N][pat]=2*(in[N][pat]/max)-1; // narrowing till [-1,1]
 }

Wenn wir die Eingabevektoren normalisieren, sollten wir auch dementsprechend alls Neuronen-Gewichtungen normalisieren.


Auswählen der ursprünglichen Neuronen-Gewichtungen
Die möglichen Varianten sind zahlreich.
1) Zufällige Werte werden den Gewichtungen zugeordnet, wie es üblich mit Neuronen gemacht wird (Randomisierung);
2) Initialisierung durch Beispiele, wenn Werte von zufällig ausgewählten Beispielen aus einer Einarbeitungsprobe als Anfangswerte zugeordnet sind;
3) Lineare Initialisierung. In diesem Fall werden die Gewichtungen durch Vektorwerte initiiert, die linear entlang des gesamten linearen Raums zwischen zwei Vektoren aus dem ursprünglichen Datensatz angeordnet sind.;
4) Alle Gewichtungen haben den gleichen Wert - Methode der konvexen Kombination.

Lassen Sie uns den ersten und letzten Fall analysieren.
1) Zufallswerte werden den Gewichtungen zugeordnet.

Während der Randomisierung werden alle Vektor-Neuronen auf der Oberfläche einer Hyperkugel verteilt. Während die Eingabevektoren eine Tendenz zur Gruppierung haben. In diesem Fall kann es vorkommen, dass einige Gewichtungsvektoren so viel Abstand von Eingabevektoren haben, dass sie niemals eine bessere Korrelation geben und daher nicht lernen können - "graue" Objekte in Abb. 7 (rechts). Darüber hinaus werden die verbleibenden Neuronen nicht ausreichen, um den Fehler zu minimieren und ähnliche Klassen zu unterteilen - die "rote" Klasse ist im "grünen" Neuron enthalten.

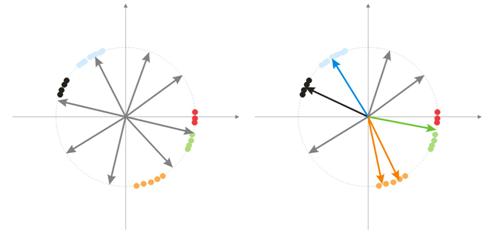
Abb. 7: Einarbeitungsergebnis von randomisierten Neuronen.

Und wenn es eine große Ansammlung von Neuronen in einem Bereich gibt, können mehrere Neuronen in den Bereich einer Klasse eindringen und diesen in Unterklassen teilen - orangefarbener Bereich in Abb. 7. Dies ist nicht kritisch, da die Weiterverarbeitung der Schichtsignale die Situation beheben kann. Dies dauert jedoch die Einarbeitungszeit über.

Eine der Varianten zum Lösen dieser Probleme ist die Methode, wenn bei den Anfangsstufen die Korrektur nicht nur für Vektoren eines gewinnenden Neurons gemacht wird, sondern auch für die Gruppe von Vektoren, die am nächsten liegt. Dann wird sich die Anzahl der Neuronen in der Gruppe allmählich verringern und letztendlich wird nur ein Neuron korrigiert. Eine Gruppe kann aus einem sortierten Array von Neuronen-Ausgängen ausgewählt werden. Neuronen von den ersten K Maximal-Ausgangssignalen werden korrigiert.

Eine weitere Vorgehensweise zur gruppierten Anpassung der Gewichtungsvektoren ist das folgende Verfahren.

a) Für jedes Neuron wird die Länge des Korrekturvektors definiert:

.
b) Ein Neuron mit minimalem Abstand wird zum Gewinner – Wn. Danach wird eine Gruppe von Neuronen gefunden, die in Korrelation zu den Grenzen der Distanz C*Ln von Wn stehen.
c) Gewichtungen dieser Neuronen werden durch eine einfache Regel korrigiert. . Somit wird die Korrektur der gesamten Probe gemacht.

Der Parameter C ändert sich im Prozess der Einarbeitung von einer Nummer (üblicherweise 1) auf 0.

Die dritte interessante Methode bedeutet, dass jedes Neuron nur N/k Mal korrigiert werden wann, wenn es durch die Probe kommt. N ist hier die Größe der Probe, k- die Anzahl der Neuronen. Das heißt, eines der Neuronen wird öfter zum Gewinner als andere. Es "beendet das Spiel" wenn das Passieren der Probei vorbei ist. Dadurch können auch andere Neuronen lernen.

2) Methode der Konvexkombination

Die Bedeutung des Verfahrens beinhaltet, dass sowohl die Gewichtung als auch die Eingabevektoren zunächst in einem Bereich angeordnet sind. Die Berechnungsformeln für die aktuellen Koordinaten der Eingabe- und ursprünglichen Gewichtungsvektoren sind die folgenden:

,

wobei n die Dimension eines Eingabevektors, a(t)- die nicht abnehmende Funktion der Zeit ist. Mit jeder Wiederholung erhöht sich dessen Wert von 0 auf 1, wodurch alle Eingabevektoren mit den Gewichtungsvektoren übereinstimmen und schließlich ihre Plätze einnehmen. Außerdem werden die Gewichtungsvektoren nach ihren Klassen "greifen".

Dies sind alle Materialien zur Basisversion der Kohonen-Schicht, die in diesem neuronalen Netzwerk angewendet werden.

II. Löffel, Schöpfkellen und Skripte

Das erste Skript, das wir diskutieren werden, sammelt Daten über Balken und erstellt eine Datei von Eingabevektoren. Lassen Sie uns MA als Traininsbeispiel verwenden.

Liste 2. Erstellen einer Datei von Eingabevektoren

// input parameters
 #define NUM_BAR 10000 // number of bars for training (number of training patterns)
 #define NUM_MA 5 // number of movings
 #define DEPTH_MA 3 // number of values of a moving
 // creating a file
 hFile = FileOpen(FileName, FILE_WRITE|FILE_CSV);
 FileSeek(hFile, 0, SEEK_END); 
 // Creating an array of inputs
 int i, ma, depth;
 double MaIn;
 for (i=NUM_BAR; i>0; i--) // going through bars and collecting values of MA fan 
 {
  for (depth=0; depth<DEPTH_MA; depth++) //calculating moving values
   for (ma=0; ma<NUM_MA; ma++) 
   {
   MaIn=iMA(NULL, 0, 2+MathSqrt(ma*ma*ma)*3, 0, 1, 4, 
                    i+depth*depth)- ((High[i+depth*depth] + Low[i+depth*depth])/2);
   FileWriteDouble(hFile, MaIn);
   }
  }

Die Datendatei wird als Mittel zur Übertragung von Informationen zwischen Anwendungen geschaffen. Wenn Sie die Einarbeitungs-Algorithmen kennenlernen, wird dringend empfohlen, dass Sie die Zwischenergebnisse ihrer Aktivitäten, die Werte einiger Variablen und falls notwendig, die Änderungen der Traininsbedingungen beobachten.

Deshalb empfehlen wir Ihnen, die Programmiersprache eines hohen Niveaus (VB, VC++ etc.) zu verwenden, während das Debuggen mit MQL4 nicht genug ist (ich hoffe, diese Situation wird in MQL5 verbessert). Später, wenn Sie über alle Tücken Ihrer Algorithmen und Funktionen erfahren haben, können Sie beginnen, MQL4 zu verwenden. Außerdem müssen Sie das endgültige Ziel (Indikator oder Expert Advisor) in MQL4 schreiben.

Verallgemeinerte Struktur der Klassen

Liste 3. Klasse des neuronalen Netzwerks

class CNeuroNet : public CObject  
 {
 public:
  int nCycle; // number of learning cycles until stop
  int nPattern; // number of training patterns
  int nLayer; // number of training layers
  double Delta; // required minimal output error
  int nNeuron[iMaxLayer]; // number of neurons in a layer (by layers)
  int LayerType[iMaxLayer]; // types of layers (by layers)
  double W[iMaxLayer][iMaxNeuron][iMaxNeuron];// weights by layers
  double dW[iMaxLayer][iMaxNeuron][iMaxNeuron];// correction of weight
  double Thresh[iMaxLayer][iMaxNeuron]; // threshold
  double dThresh[iMaxLayer][iMaxNeuron]; // correction of threshold
  double Out[iMaxLayer][iMaxNeuron]; // output value
  double OutArr[iMaxNeuron]; // sorted output values of Kohonen layer
  int IndexWin[iMaxNeuron]; // sorted neuron indexes of Kohonen layer
  double Err[iMaxLayer][iMaxNeuron][iMaxNeuron];// error

  double Speed; // Speed of training
  double Impuls; // Impulse of training

  double in[100][iMaxPattern]; // Vector of input values
  double out[10][iMaxPattern]; // vector of output values
  double pout[10]; // previous vector of output values
  double bar[4][iMaxPattern]; // bars, on which we learn
  int TradePos; // order direction
  double ProfitPos; // obtained profit/loss of an order

 public:
  CNeuroNet();
  virtual ~CNeuroNet();
  // functions
  void Init(int aPattern=1, int aLayer=1, int aCycle=10000, double aDelta=0.01, double aSpeed=0.1, 
                                                                               double aImpuls=0.1);
  // learning functions
  void CalculateLayer(); // Calculation of layer output
  void CalculateError(); // Error calculation /for Target array/
  void ChangeWeight(); // Correction of weights
  bool TrainNetwork(); // Network training
  void CalculateLayer(int L); // Output calculation of Kohonen layer
  void CalculateError(int L); // Error calculation of Kohonen layer
  void ChangeWeight(int L); // Correction of weights for layer indication
  bool TrainNetwork(int L); // Training of Kohonen layer

  bool TrainMPS(); // Network training for getting the best profit

  // variables for internal interchange
  bool bInProc; // flag for entering the TrainNetwork function
  bool bStop; // flag for the forced termination of the TrainNetwork function
  int loop; // number of the current iteration
  int pat; // number of the current processed pattern
  int iMaxErr; // pattern with the maximal error
  double dMaxErr; // maximal error
  double sErr; // square of pattern error
  int iNeuron; // maximal number of neurons in Kohonen layer correction
  int iWinNeuron; // number of winner neurons in Kohonen layer

  int WinNeuron[iMaxNeuron]; // array of active neurons (ordered)
  int NeuroPat[iMaxPattern][iMaxNeuron]; // array of active neurons

  void LinearCovariation(); // normalization of the sample
  void SaveW(); // Analysis of neuron activity
 };

Eigentlich ist die Klasse nicht komplex. Sie enthält den wichtigsten Satz + Service Variable.

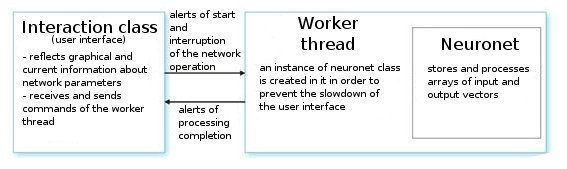
Lassen Sie uns sie analysieren. Auf Anweisung eines Befehls vom Benutzer, erstellt die Interface-Klasse einen Arbeits-Thread und initialisiert einen Timer für das periodische Auslesen der Netzwerkwerte. Sie empfängt auch Indexe zum Auslesen der Informationen aus Parametern neuronaler Netzwerke. Der Arbeits-Thread wiederum liest die Arrays von Eingabe-/Ausgabevektoren aus der vorläufig ausgearbeiteten Datei aus und stellt die Parameter für die Schichten ein (die Schichttypen und die Anzahl der Neuronen in jeder Schicht). Dies ist die Vorbereitungsphase.

Danach rufen wir die Funktion CNeuroNet::Init auf, in der die Gewichtungen initialisiert werden, die Probe normalisiert wird und die Einarbeitungsparameter eingestellt werden (Geschwindigkeit, Impuls, erforderlicher Fehler und die Anzahl der Traininszyklen). Und erst danach rufen wir die " Arbeitspferd" Funktion - CNeuroNet::TrainNetwork (oder TrainMPS, oder TrainNetwork(int L) auf, je nachdem, was wir erhalten wollen). Wenn die Einarbeitung vorbei ist, speichert der Arbeits-Thread die Netzwerkgewichtungen in eine Datei für die Implementierung der letzten in einen Indikator oder Expert Advisor.

III. Backen des Netzwerks

Kommen wir nun zu den Problemen beim Einarbeiten. Die übliche Praxis in der Einarbeitung legt das Paar "Muster-Lehrer" fest. Das ist ein bestimmtes Ziel, das jedem einzelnen Eingabemuster entspricht. Auf der Grundlage der Differenz zwischen der aktuellen Eingabe und dem Sollwert wird die Korrektur der Gewichtungen durchgeführt. Zum Beispiel möchte ein Researcher haben, dass das Netz den Kurs des darauffolgenden Balkens anhand der vorherigen 10 Balken prognostiziert. In diesem Fall müssen wir nach der Eingabe der 10 Werte das erhaltene Ergebnis mit dem Lernwert vergleichen und dann die Gewichtungen für den Unterschied zwischen ihnen korrigieren.

In dem Modell, das wir anbieten, gibt es keine "Lern"-Vektoren im üblichen Sinne, da wir nicht im Voraus wissen, bei welchen Balken wir den Markt betreten oder verlassen sollten. Das bedeutet, dass unser Netzwerk seine Ausgabevektoren auf der Grundlage seiner eigenen früheren Ausgabewerte korrigieren wird. Das bedeutet, dass das Netzwerk versuchen wird, den maximalen Gewinn zu erhalten (Maximierung der Anzahl der richtig vorhergesagten Richtungen im Markt). Betrachten wir das Beispiel in Abb. 8.

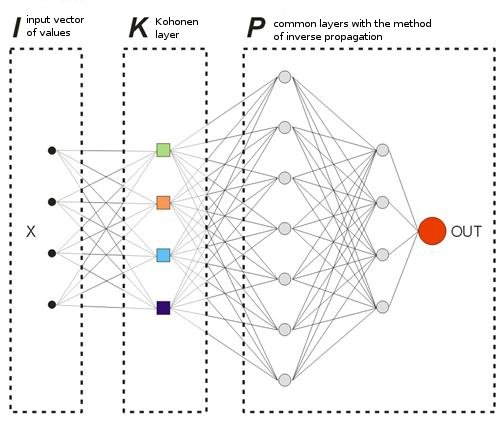
Abb. 8: Schema des eingearbeiteten neuronalen Netzwerks.

Die Kohonen-Schicht, die anhand einer Probe voreingearbeitet ist, gibt seinen Vektor an das Netzwerk weiter. Bei der Ausgabe der letzten Schicht des Netzwerks, haben wir den Wert OUT, der auf folgende Weise interpretiert wird. Wenn OUT>0,5 ist, gehen Sie eine Kaufposition ein; wenn OUT<0,5 ist, gehen Sie eine Verkaufsposition ein (die sigmoiden Werte werden in Grenzen verändert [0, 1]).

Angenommen zu einem gewissen Eingabevektor X1 hat das Netzwerk durch die Ausgabe OUT1>0,5 geantwortet. Das bedeutet, dass wir auf dem Balken, zum dem das Muster gehört, wir eine Kaufposition öffnen. Danach verwandelt sich bei der chronologischen Darstellung der Eingabevektoren nach einigen Xk das Zeichen OUTk in das "Gegenteil". Folglich schließen wir die Kaufposition und öffnen eine Verkaufsposition.

Genau in diesem Moment müssen wir das Ergebnis der geschlossenen Order betrachten. Wenn wir einen Gewinn erhalten, können wir diesn Alarm stärken. Oder wir können erachten, dass es keinen Fehler gibt und wir nichts korrigieren werden. Wenn wir einen Verlust erhalten, korrigieren wir die Gewichtungen der Schichten in einer solchen Weise, dass die Eingabe durch den Alarm des X1 Vektors OUT1<0,5 anzeigt.

Nun wollen wir den Wert der Lern-(Ziel)-Ausgabe berechnen. Lassen Sie uns daher den Wert eines Sigmoiden aus dem erhaltenen Verlust (in Punkten) nehmen und multiplizieren ihn mit dem Zeichen der Handelsrichtung. Folglich gilt, dass je größer der Verlust ist, desto strenger das Netzwerk bestraft und seine Gewichtungen durch den größeren Wert korrigieren werden wird. Wenn wir zum Beispiel =50 Verlustpunkte bei einer Kaufposition haben, dann wird die Korrektur für die Ausgabeschicht wie unten dargestellt berechnet:

, ,

Wir können die Handelsregeln für die Handelsanalyseprozessparameter von TakeProfit (TP) und StopLoss (SL) in Punkten begrenzen. Wir müssen also 3 Ereignisse verfolgen: 1) Änderung des OUT Zeichens, 2) Kursänderungen vom Eröffnungspreis durch den Wert von TP, 3) Kursänderungen vom Eröffnungskurs durch den Wert -SL.

Wenn eines dieser Ereignisse auftritt, wird die Korrektur der Gewichtungen auf analoge Weise durchgeführt. Wenn wir einen Gewinn erhalten, bleiben die Gewichtungen entweder unverändert oder sie werden korrigiert (stärkeres Signal). Wenn wir einen Verlust haben, werden die Gewichtungen korrigiert, damit die Eingabe durch den Alarm vom X1 Vektor OUT1 mit dem "gewünschten" Zeichen anzeigt.

Der einzige Nachteil dieser Begrenzung ist die Tatsache, dass wir absolute TP und SL Werte verwenden, was bei einem langen Zeitraum unter aktuellen Marktbedingungen nicht so gut für die Optimierung eines Netzwerks ist. Meine persönliche Bemerkung dazu ist, dass TP und SL nicht weit voneinander entfernt sein sollten.

Das bedeutet, dass das System symmetrisch sein muss, um während der Einarbeitung eine Abweichung hinsichtlich der Richtung eines globaleren Kauf-oder Verkaufstrend zu vermeiden. Es gibt auch eine Meinung, dass der TP 2-4 mal größer als der SL sein sollte - so erhöhen wir künstlich das Verhältnis von profitablen und verlustbringenden Trades. Aber in solch einem Fall besteht die Gefahr, dass die Einarbeitung des Netzwerks mit einer Verschiebung in Richtung Trend erfolgt. Natürlich können beide Varianten existieren, aber Sie sollten beide bei Ihren Untersuchungen überprüfen.

Liste 4. Eine Wiederholung des Setups für die Netzwerkgewichtung

int TradePos;
 int pat=0; // open an order for the first pattern
 for(i=0;i<nNeuron[0];i++) Out[0][i]=in[i][pat]; // take the training pattern
 CalculateLayer(); // calculate the network output
 TradePos=TradeDir(Out[nLayer-1][0]); // if exit is larger than 0.5, then buy. Otherwise - sell
 ipat=pat; // remember the pattern
 for(pat=1;pat<nPattern;pat++) // go through the pattern and train the network
 {
  for(i=0;i<nNeuron[0];i++) Out[0][i]=in[i][pat]; // take the training pattern
  CalculateLayer(); // calculate the network output
  ProfitPos=1e4*TradePos*(bar[3][pat]-bar[3][ipat]); // calculate profit/loss at close prices [3]
  // if trade direction has changed or stop order has triggered
  if (TradeDir(Out[nLayer-1][0])!=TradePos || ProfitPos>=TP || ProfitPos<=-SL) 
  {
   // correcting weights
   Out[nLayer][0]=Sigmoid(0.1*TradePos*ProfitPos); // set the desired output of the network
   for(i=0;i<nNeuron[0];i++) Out[0][i]=in[i][ipat];// take the pattern by which
                                                   // CalculateLayer() were opened;  
                                                   // calculate the network output
   CalculateError(); // calculate the error
   ChangeWeight(); // correct weights
   for(i=0;i<nNeuron[0];i++) Out[0][i]=in[i][pat]; // go to the new order CalculateLayer(); 
                                                   // calculate the new output of the network
   TradePos=TradeDir(Out[nLayer-1][0]);            // if output is > 0.5, then buy 
                                                   //otherwise sell ipat=pat; 
                                                   // remember the pattern
  }
 }

Durch diese einfachen Arbeitsgänge wird das Netzwerk letztendlich die erhaltenen Klassen aus der Kohonen-Schicht in einer solchen Weise verteilen, dass es für jede einen Alarm zum Markteinstieg mit dem entsprechenden Maximalgewinn gibt. Aus der Sicht der Statistik - wird jedes Eingabemuster durch das Netz für die Gruppenarbeit angepasst.

Während ein und derselbe Eingabevektor während des Vorgangs zur Gewichtungsanpassung Alarme in verschiedenen Richtungen geben kann, wird allmählich die maximale Anzahl der richtigen Vorhersagen erhalten. Diese Methode kann als dynamisch beschrieben werden. Das verwendete Verfahren wird auch als MPS (Profit Maximizing System) bezeichnet.

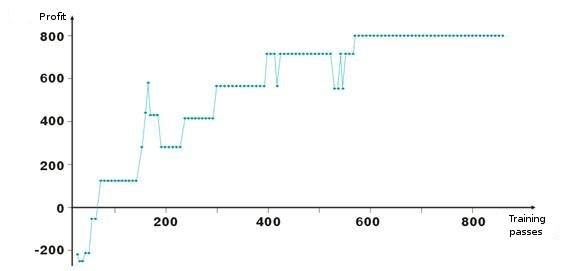
Hier sind Ergebnisse der Anpassung von Netzwerkgewichtungen. Jeder Punkt im Diagramm ist der Wert des erhaltenen Gewinns in Punkten während des Einarbeitungszeitraums. Das System ist immer Marktaktuell, TakeProfit = StopLoss = 50 Punkte, Fixierung erfolgt nur durch eine Stop-Order, Gewichtungen werden bei Gewinn oder Verlust korrigiert.

Sie sehen, nach dem negativen Start werden die Gewichtungen der Schichten angepasst, so dass nach etwas hundert Wiederholungen, der Gewinn positiv wird. Interessant ist die Tatsache, dass das System bei einigen Niveaus etwas langsamer wird. Dies hängt mit den Parametern der Einarbeitungsgeschwindigkeit zusammen.

Wie Sie in der Liste 2 sehen können, wird der Gewinn ProfitPos durch die Schlusskurse der Balken berechnet, auf denen wir die Position eröffnet und auf welchem die Bedingungen (Stop-Order oder Alarmänderung) eingetroffen sind. Natürlich ist dies ein grobes Verfahren, insbesondere im Fall von Stop-Orders. Wir können durch das Analysieren von Hochs und Tiefs des Balkens (bar[1][ipat] und bar[2][ipat]) eine Verfeinerung hinzufügen. Sie können versuchen, dies selbst zu tun.

Suche nach Einstiegen?
Wir haben also das dynamische Einarbeitungsverfahren studiert, welches das Netzwerk durch seine eigenen Fehler einarbeitet. Sie haben sicher bemerkt, dass wir entsprechend dem Algorithmus immer den Markt betreten mit fixem Gewinn/Verlust. Wir müssen daher unsere Einstiege begrenzen und versuchen, nur bei "günstigen" Eingabevektoren den Markt zu betreten. Das bedeutet, dass wir die Netzwerk-Alarmstufe zum Einstieg in den Markt von den profitablen/verlustbringenden Trades abhängig machen müssen.

Dies kann sehr leicht durchgeführt werden. Lassen Sie uns die Variable 0<M<0,5 vorstellen, die das Kriterium eines Markteintritts sein wird. Wenn Out>0,5+M, dann kaufen Sie, wenn Out<0,5-M, dann verkaufen Sie. Wir kristallisieren Ein-und Ausstiege mit Hilfe von Vektoren heraus, die zwischen 0,5-M<Out<0,5+M liegen.

Ein weiteres Verfahren zum Aussieben von unnötigen Vektoren ist das Sammeln von statistischen Daten über die Rentabilität einer Order anhand von den Werten bestimmter Ausgaben des Netzwerks. Nennen wir es eine visuelle Analyse. Davor sollten wir das Verfahren zur Positionsschließung definieren - Erreichen der Stop-Order, Änderung des Netzwerk-Ausgabesignals. Lassen Sie uns eine Tabelle erstellen Out | ProfitPos. Die Werte von Out und ProfitPos werden für jeden Eingabevektor (das heißt für jeden Balken) berechnet.

Dann lassen Sie uns eine Übersichtstabelle zum ProfitPos Feld machen. Als Ergebnis werden wir die Abhängigkeit zwischen dem Out Wert und dem erhaltenen Gewinn sehen. Wählen Sie den Bereich Out=[MLo, MHi], in dem wir den besten Gewinn haben und verwenden Sie seine Werte für den Handel.

Zurück zu MQL4
Nachdem wir mit der Entwicklung in VC++ begonnen haben, haben wir nicht versucht, die Möglichkeiten von MQL4 zu würdigen. Dies war aus Gründen der Bequemlichkeit. Ich werde Ihnen ein Erlebnis erzählen. Vor kurzem hat einer meiner Bekannten versucht, eine Datenbank über Firmen in unserer Stadt anzulegen. Es gibt eine Menge von Verzeichnissen im Internet, aber niemand wollte die Datenbank verkaufen.

Wir schrieben also ein Skript in MQL4, das die HTML-Seite scannt und einen Bereich mit Informationen über ein Unternehmen auswählt und diesen in einer Datei speichert. Danach haben wir die Datei in Excel bearbeitet und die Datenbank von drei großen gelben Seiten mit allen Telefonnummern, Adressen und Firmenaktivitäten war fertig. Dies war die vollständigste Datenbank der ganzen Stadt; für mich war es das Gefühl von Stolz und Leichtigkeit, was die Möglichkeiten von MQL4 betrifft.

Natürlich kann man ein und dieselbe Aufgabe in verschiedenen Programmiersprachen lösen, aber es ist besser die eine zu wählen, die hinsichtlich Möglichkeiten/Schwierigkeit für eine bestimmte Aufgabe die optimale ist.

Nach dem Einarbeiten des Netzwerks sollten wir jetzt alle seine Parameter in einer Datei speichern, um sie nach MQL4 zu transferieren.
- Größe des Eingabevektors
- Größe des Ausgabevektors
- Anzahl der Schichten
- Anzahl der Neuronen nach Schichten - von Eingabe zur Ausgabe
- Gewichtungen der Neuronen nach Schichten
Der Indikator wird nur eine Funktion aus dem Arsenal der Klasse CNeuroNet verwenden – CalculateLayer. Lassen Sie uns einen Eingabevektor für jeden Balken bilden, den Wert der Netzwerkausgabe berechnen und den Indikator [6] bauen.

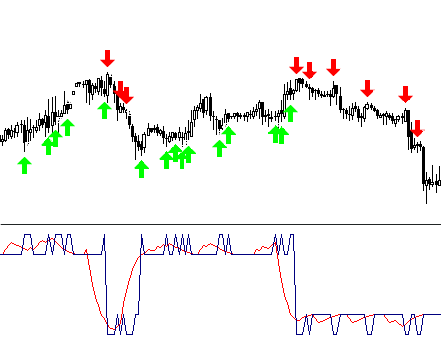
Wenn wir uns bereits für Eingabepegel entschieden haben, können wir Teile der erhaltenen Kurve in verschiedenen Farben malen.
Ein Beispiel des Codes !NeuroInd.mq4 ist dem Artikel angehängt.

IV. Kreativer Ansatz

Für eine gute Umsetzung sollten wir einen breiten Verstand haben. Neuronale Netzwerke sind nicht die Ausnahme. Ich denke nicht, dass die angebotene Variante ideal ist und für jede Aufgabe geeignet ist. Deshalb sollten Sie immer nach Ihren eigenen Lösungen suchen, das allgemeine Bild aufzeichnen, systematisieren und Ideen überprüfen. Nachfolgend finden Sie einige Warnungen und Empfehlungen.
- Netzwerk-Anpassung. Ein neuronales Netzwerk ist ein Annäherer. Ein neuronales Netzwerk stellt eine Kurve her, wenn es Knotenpunkte bekommt. Wenn die Menge der Punkte zu groß ist, wird der zukünftige Aufbau schlechte Ergebnisse liefern. Alte Verlaufsdaten sollten von der Einarbeitung entfernt und neue sollten hinzugefügt werden. Dies ist, wie die Annäherung an ein neues Polynom durchgeführt wird.
- Übereinarbeiten. Dies kommt bei der "idealen" Anpassung vor (oder wenn es bei der Einarbeitung zu viele Eingabewerte gibt). Wenn einem Netzwerk ein Testwert gegeben wird, erhalten wir als Ergebnis ein falsches Resultat (Abb. 9).

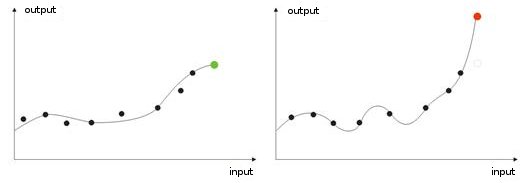
Abb. 9: Ergebnis einer "übereingearbeiteten" Netzwerks - falsche Prognose.

- Komplexität, Wiederholbarkeit, Widersprüchlichkeit einer Einarbeitungsprobe. In den Arbeiten [8, 9] analysieren Autoren die Abhängigkeit zwischen den aufgezählten Parametern. Ich nehme an, es ist klar, dass wenn verschiedene Lernvektoren (oder falls noch schlimmer, widersprüchliche) ein und demselben Lernvektor entsprechen, ein Netzwerk nie lernen wird, sie richtig zu klassifizieren. Zu diesem Zweck sollten große Eingabevektoren erzeugt werden, so dass sie Daten enthalten, mit denen Sie den Raum der Klassen abgrenzen können. Abb. 10 zeigt diese Abhängigkeit. Je höher die Komplexität eines Vektors ist, desto geringer ist die Wiederholbarkeit und Widersprüchlichkeit von Mustern.

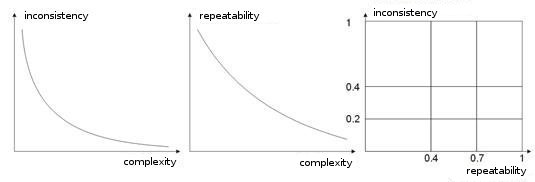
Abb. 10: Abhängigkeit der Eigenschaften von Eingabevektoren.

- Einarbeiten des Netzwerks nach der Methode von Boltzmann. Diese Methode ist ähnlich wie verschiedene mögliche Gewichtungsvarianten zu versuchen. Die künstliche Intelligenz eines Expert Advisors arbeitet hinsichtlich des Lernens nach einem ähnlichen Prinzip. Beim Einarbeiten eines Netzwerks geht sie durch alle Varianten der Gewichtungswerte (wie beim Knacken eines Mailgox-Passworts) und wählt die beste Kombination aus.

Dies ist eine arbeitsintensive Aufgabe für einen Computer. Daher ist die Anzahl aller Gewichtungen eines Netzwerks auf zehn begrenzt. Wenn sich die Gewichtung zum Beispiel von 0 auf 1 (mit einem Schritt von 0,01) ändert, benötigen wir dafür 100 Schritte. Für 5 Gewichtungen bedeutet dies 5100 Kombinationen. Dies ist eine große Zahl und diese Aufgabe geht über die Leistung eines Computers hinaus. Der einzige Weg, um ein Netzwerk nach dieser Methode zu bauen ist, eine große Anzahl von Computern zu verwenden, wobei jeder davon einen bestimmten Teil verarbeitet.

Diese Aufgabe kann von 10 Computern ausgeführt werden. Jeder wird 510 Kombinationen verarbeiten, so dass ein Netzwerk komplexer gemacht werden kann, denn es kann eine größere Anzahl von Gewichtungen, Schichten und Schritten verwendet werden.

Im Unterschied zu einem solchen "Brachialen Angriff", wirkt die Methode von Boltzmann sanfter und schneller. Bei jeder Wiederholung wird eine zufällige Verschiebung auf die Gewichtung eingestellt. Wenn das System mit der neuen Gewichtung seine Eingabecharakteristik verbessert, wird die Gewichtung akzeptiert und eine neue Wiederholung durchgeführt.

Wenn eine Gewichtung den Ausgabefehler erhöht, wird sie akzeptiert, wenn sie durch die Boltzmann Verteilungsformel berechnet wurde. Somit kann die Netzwerkausgabe am Anfang absolut unterschiedliche Werte haben. Eine allmähliche "Abkühlung" bringt das Netzwerk zum erforderlichen globalen Minimum [10, 11].

Natürlich ist dies nicht die vollständige Liste Ihrer weiteren Studien. Es gibt auch genetische Algorithmen, Methoden zur Verbesserung der Konvergenz, Netzwerke mit Speicher, Radialnetzwerke, Verbund von Rechern, usw.

Fazit

Ich möchte hinzufügen, dass ein neuronales Netzwerk kein Heilmittel für alle Probleme beim Handeln ist. Der eine wählt eine unabhängige Arbeit und die Erstellung seiner eigenen Algorithmen und eine andere Person bevorzugt das Verwenden von bereiten Neuro-Paketen, von denen eine große Anzahl im Markt gefunden werden kann.

Haben Sie nur keine Angst vor Experimenten! Viel Glück und große Gewinne!

Der Markt ist ein Intellekt, das Finanzportfolio ist ein neuronales Netzwerk.

Referenzen

1. Baestaens, Dirk-Emma; Van Den Bergh, Willem Max; Wood, Douglas. Neural Network Solutions for Trading in Financial Markets.
2. Voronovskii G.K. and others. Geneticheskie algoritmy, iskusstvennye neironnye seti i problemy virtualnoy realnosti (Genetische Algorithmen, künstliche neuronale Netzwerke und Probleme der virtuellen Realität).
3. Galushkin A.I. Teoriya Neironnyh setei (Theorie von neuronalen Netzwerken).
4. Debok G., Kohonen T. Analyzing Financial Data using Self-Organizing Maps.
5. Ezhov A.A., Shumckii S.A. Neirokompyuting i ego primeneniya v ekonomike i biznese (Neuronale Datenverarbeitung und ihre Verwendung in der Wirtschaft und Unternehmen).
6. Ivanov D.V. Prognozirovanie finansovyh rynkov s ispolzovaniem neironnyh setei (Prognose der Finanzmärkte mit künstlichen neuronalen Netzwerken) (Diplomarbeit)
7. Osovsky S. Neural Networks for Data Processing .
8. Tarasenko R.A., Krisilov V.A., Vybor razmera opisaniya situatsii pri formirovanii obuchayushchey vyborki dlya neironnyh setei v zadachah prognozirovaniya vremennyh ryadov (Die Wahl der Situation, Beschreibung, Größe beim Formen einer Einarbeitungsprobe für neuronale Netzwerke zur Prognose bei Zeitreihen).
9. Tarasenko R.A., Krisilov V.A., Predvaritelnaya otsenka kachestva obuchayushchey vyborki dlya neironnyh setei v zadachah prognozirovaniya vremennyh ryadov (Vorläufige Schätzung der Qualität einer Einarbeitungsprobe für neuronale Netzwerke zur Prognose bei Zeitreihen).
10. Philip D. Wasserman. Neral Computing: Theory and Practice.
11. Simon Haykin. Neural Networks: A Comprehensive Foundation.
12. www.wikipedia.org
13. Das Internet.