Comercio con portafolio en MetaTrader 4
Magnus
ab integro saeclorum nascitur ordo
Publius
Vergilius Maro, Eclogues
Introducción
El concepto de portafolio o cartera de inversiones es conocido desde hace muchísmo tiempo. Distribuyendo los recursos en varias direcciones, el propietario crea al mismo tiempo un portafolio, reduciendo de esa forma el riesgo de pérdidas gracias a la diversificación y haciendo el crecimiento de las ganancias más suave. La teoría del portafolio se desarrolló de forma significativa después de que en 1950, Harry Markowitz formulase el primer modelo matemático del portafolio. Después, en los años 80, un grupo de investigadores de Morgan Stanley creó la primera estrategia de spread-trading, lo que abrió una nueva rama de investigación: las estrategias de mercado neutras. La actual teoría del portafolio es muy diversa y compleja, el número de variantes de estrategias de portafolio es difícil de describir. En este artículo se analizará solo un pequeño espectro de estrategias especulativas y un ejemplo de implementación en la plataforma MetaTrader 4.
Algunas definiciones que se aplican en este artículo:
- Portafolio (cesta, herramienta sintética): es un conjunto de posiciones de varios instrumentos comerciales, con volúmenes óptimos calculados. Las posiciones se mantienen durante cierto tiempo, se las sigue como a una sola unidad y se cierran con un resultado financiero común.
- Corrección del portafolio (cesta, herramienta sintética): cambio de la composición de los instrumentos y/o sus volúmenes en el portafolio para minimizar las pérdidas o para bien fijar un resultado intermedio.
- Volumen sintético: número de posiciones sintéticas (cuántas veces se ha comprado o vendido el portafolio).
- Beneficio/pérdida virtual: resultado financiero que podría obtenerse al mantener la posición en un cierto intervalo de tiempo.
En el mercado de valores normalmente se trabaja con los portafolios de inversión clásicos. En el mercado de divisas este enfoque no se puede usar, y aquí los portafolios tienen un carácter especulativo, se crean y se comercia con ellos de una manera un poco distinta. Aplicado al mercado Fórex, el comercio con portafolio podría llamarse comercio multidivisa, pero, estrictamente, no todas las estrategias multidivisa son estrategias de portafolio. Si los instrumentos se comercian independientemente unos de otros y sin realizar un seguimiento de la dinámica del resultado total, entonces estaremos ante el comercio multi-instrumental. Asimismo, existe un enfoque en el que en una cuenta comercial se negocia con varios sistemas independientes, este sistema se puede llamar portafolio de estrategias. En el marco del artículo, analizaremos el comercio con portafolio en un sentido más restringido, cuando a partir de varios instrumentos se forma una posición sintética y a continuación se gestiona esta posición.
Principios
La construcción del portafolio incluye dos etapas: la elección de instrumentos y el cálculo de lotes y direcciones para los instrumentos elegidos. Existen muchos métodos para formar los portafolios, pero como el artículo no aspira a la universalidad, aquí se analizarán varios métodos sencillos, además de ejemplos de algoritmos. En particular, se propone como base utilizar el método de los mínimos cuadrados (MMC) y el análisis de componentes pricipales (ACP). Podrá leer más información sobre estos métodos aquí:
Al crear un portafolio, normalmente se determina el comportamiento deseado del gráfico del portafolio. Gráfico del portafolio: gráfico en el que se muestran los cambios del beneficio sumario de todas las posiciones que entran en el portafolio en un intervalo de tiempo. Optimización del portafolio: búsqueda de los lotes y direcciones que se corresponden de mejor forma con el comportamiento deseado del portafolio. Por ejemplo, dependiendo de la tarea, se puede pedir que el portafolio tenga retorno al valor inicial, o bien que tenga rasgos claros de tendencia, o bien que su gráfico sea parecido al gráfico de una cierta función.
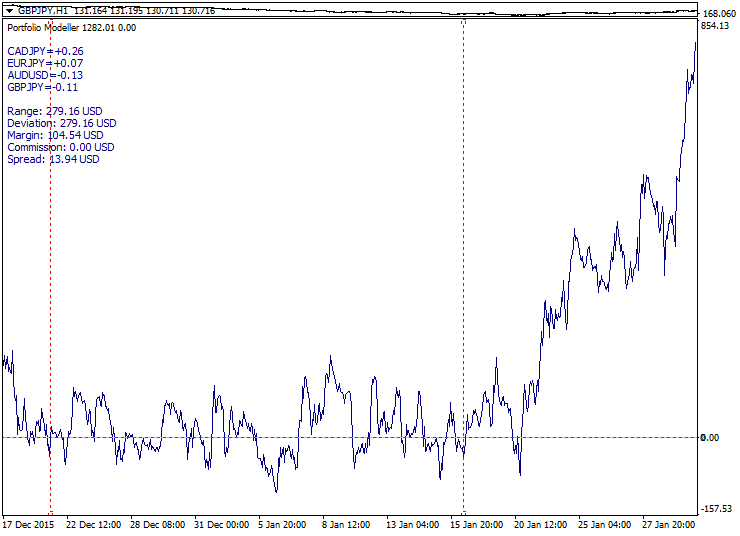
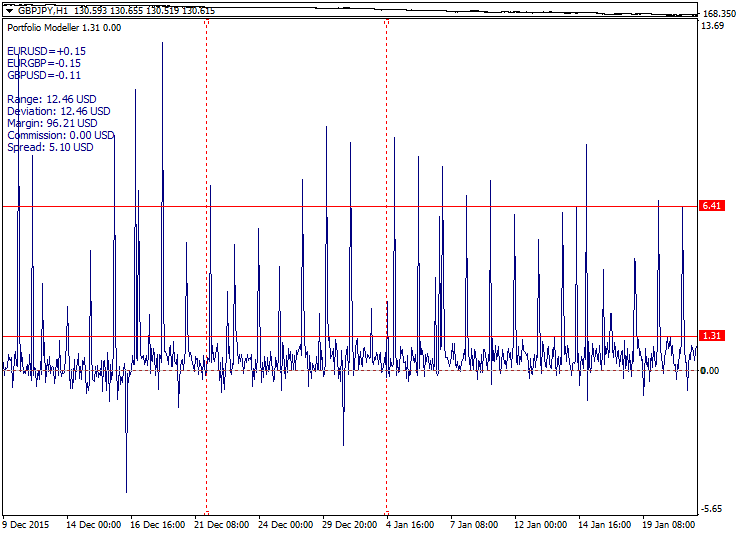
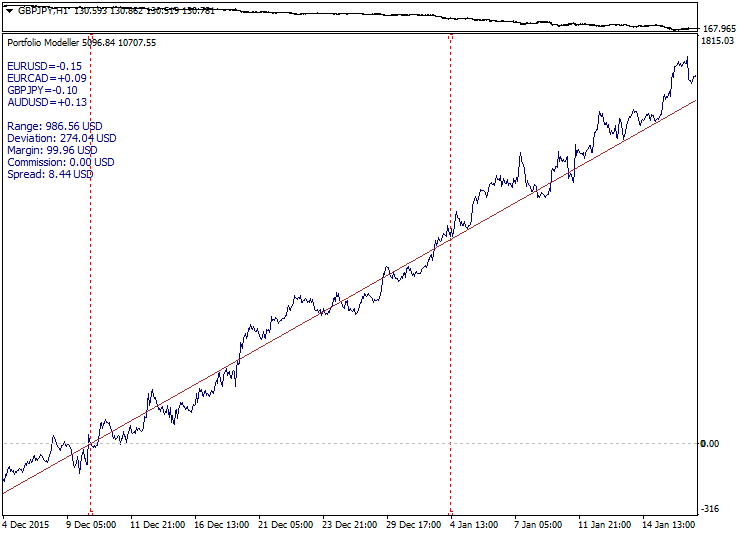
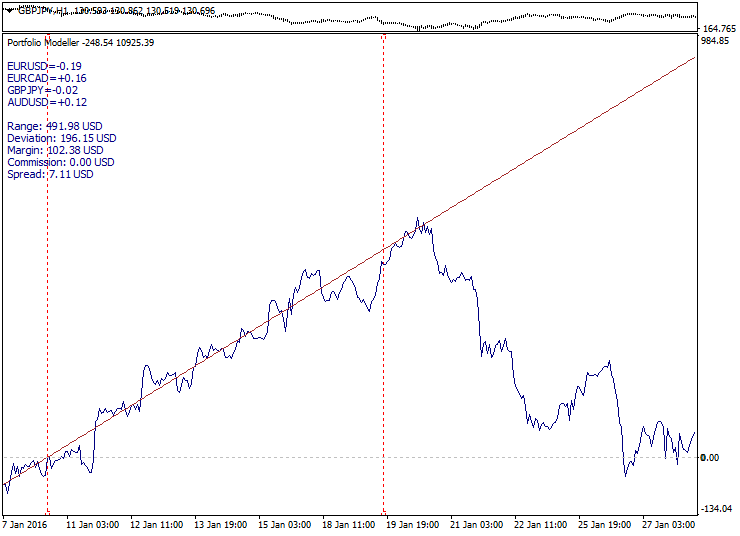
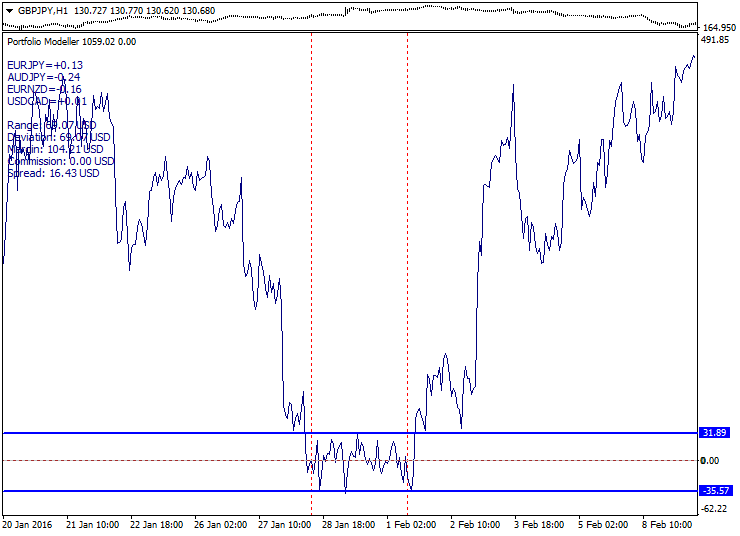
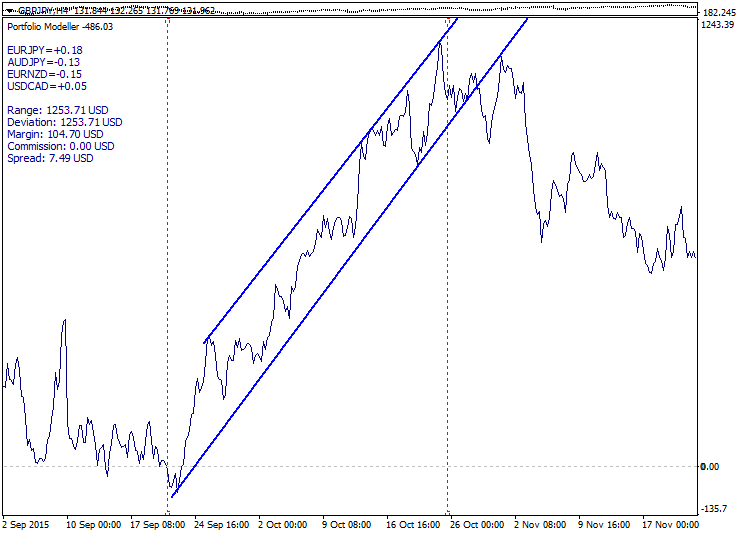
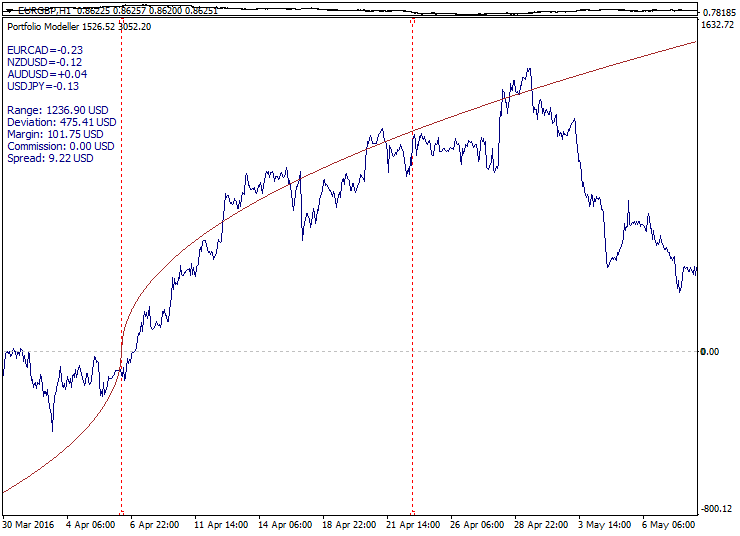
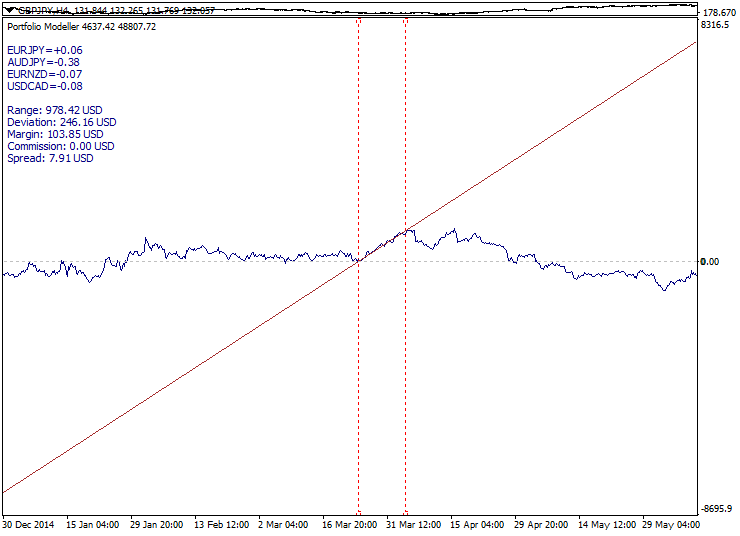
Ilustración de los tres tipos de portafolio (tendencia, flat, función):

El portafolio se puede presentar como una ecuación del siguiente tipo:
A*k1 + B*k2 + C*k3 + ... = F
donde
A, B, C ... — son las series temporales que corresponden a los instrumentos en el portafolio
k1, k2, k3 ... — son los lotes de los instrumentos (positivos - compra, negativos - venta)
F — función meta (se establece con los valores en puntos de la serie temporal)
Es una ecuación de regresión lineal de factor múltiple con un miembro libre cero, y sus raíces se pueden encontrar con facilidad usando el MMC. Preliminarmente será necesario hacer comparables las series temporales, es decir, traducir los puntos de precio a la divisa del depósito. Entonces cada elemento de cada serie temporal será un valor del beneficio virtual de un lote único del instrumento correspondiente en un momento determinado. Normalmente, en las tareas de estadística aplicada se recomienda realizar una logaritmación preliminar de los precios, o bien tomar las diferencias de los precios, pero esto, de hecho, será no solo innecesario, sino también perjudicial, puesto que eliminará información importante sobre la dinámica conjunta de los instrumentos.
La función meta determina el aspecto del gráfico al que deberá parecerse el gráfico del portafolio. El valor de la función meta se debe calcular de forma preliminar en cada punto de la forma correspondiente. Por ejemplo, cuando se crea un portafolio creciente sencillo (portafolio de tendencia), la función meta tendrá los valores: 0, 1*S, 2*S, 3*S etc, donde S será el salto del crecimiento, la magnitud monetaria en la que debe crecer el portafolio con cada barra en el intervalo establecido. El algoritmo de MMC suma las series temporales A, B, C, ... de tal forma que su suma total tienda a repetir el gráfico de la función meta. Para ello, el algoritmo MMC minimiza la suma de los cuadrados de las desviaciones entre la suma de las series y la función meta. Se trata de una tarea estadística estándar, no es obligatorio conocer al detalle el funcionamiento del algoritmo, ya que se puede usar una biblioteca ya preparada.
Se da una situación especial cuando la función meta contiene solo valores cero (portafolio flat). En este caso, son imprescindibles limitaciones adicionales en la suma de coeficientes, por ejemplo: k1 + k2 + k3 + ... = 1, para evitar la solución degenerada de la ecuación regresiva con raíz cero. Enfoque alternativo: trasladar un miembro de la ecuación al lado derecho, que se convertirá por sí mismo en función meta y recibirá el coeficiente -1, y los miembros restantes se optimizarán de la forma habitual. En este caso, igualamos la cesta de instrumentos con el instrumento elegido, es decir, creamos un portafolio de tipo spread. En conclusión, podemos usar para formar estos portafolios un algoritmo de ACP más avanzado, que a través de la matriz de covariación de instrumentos calcula el vector de coeficientes correspondiente a la hipersuperficie de cruce de la nube de puntos con la dispersión mínima restante del portafolio. Aquí tampoco debemos preocuparnos por entender al detalle el algoritmo, puesto que podemos usar una biblioteca preparada.
Algoritmos
Ahora, las ideas descritas debemos implementarlas en el lenguaje MQL. Para el trabajo se usará la conocida biblioteca matemática ALGLIB, adaptada para MT4. A veces surgen preguntas relacionadas con su instalación, por eso merece la pena que nos detengamos en ello con más tiempo. Si en la computadora hay varios terminales instalados, entonces es muy importante que determinemos la carpeta de datos correcta, puesto que el indicador no verá la biblioteca si esta se encuentra en la carpeta de datos de otro terminal.
Instalación de la biblioteca ALGLIB:
- descargamos la biblioteca (https://www.mql5.com/es/code/11077), descomprimimos el archivo zip;
- abrimos la carpeta include, dentro estará la carpeta Math;
- iniciamos el terminal МetaТrader 4 en el que necesitamos poner la biblioteca;
- elegimos el comando menú: archivo — Abrir catálogo de datos, se abrirá la carpeta de datos del terminal;
- Abrimos en esta carpeta la subcarpeta MQL4 y después la subcarpeta Include;
- desde la biblioteca descomprimida, copiamos la carpeta Math en la carpeta Include del terminal;
- comprobamos qué ha sucedido: los archivos *.mhq deberán estar dentro de MQL4\Include\Math\Alglib.
Más abajo se muestra un ejemplo de la función que calcula el precio del contrato:
double ContractValue(string symbol,datetime time,int period) { double value=MarketInfo(symbol,MODE_LOTSIZE); // obtenemos el tamaño del lote string quote=SymbolInfoString(symbol,SYMBOL_CURRENCY_PROFIT); // obtenemos la divisa de los cálculos if(quote!="USD") // si la divisa de los cálculos no es USD, entonces realizamos la conversión { string direct=FX_prefix+quote+"USD"+FX_postfix; // formamos una cotización directa para la divisa de los cálculos if(MarketInfo(direct,MODE_POINT)!=0) // comprobamos su existencia { int shift=iBarShift(direct,period,time); // encontramos la barra por la hora double price=iClose(direct,period,shift); // obtenemos la cotización de esta barra if(price>0) value*=price; // calculamos el precio } else { string indirect=FX_prefix+"USD"+quote+FX_postfix; // formamos la cotización inversa para la divisa de los cálculos int shift=iBarShift(indirect,period,time); // encontramos la barra por la hora double price=iClose(indirect,period,shift); // obtenemos la cotización de esta barra if(price>0) value/=price; // calculamos el precio } } if(Chart_Currency!="USD") // si la divisa meta no es USD, entonces realizamos la conversión { string direct=FX_prefix+Chart_Currency+"USD"+FX_postfix; // formamos una cotización directa para la divisa meta if(MarketInfo(direct,MODE_POINT)!=0) // comprobamos su existencia { int shift=iBarShift(direct,period,time); // encontramos la barra por la hora double price=iClose(direct,period,shift); // obtenemos la cotización de esta barra if(price>0) value/=price; // calculamos el precio } else { string indirect=FX_prefix+"USD"+Chart_Currency+FX_postfix; // formamos la cotización inversa para la divisa meta int shift=iBarShift(indirect,period,time); // encontramos la barra por la hora double price=iClose(indirect,period,shift); // obtenemos la cotización de esta barra if(price>0) value*=price; // calculamos el precio } } return(value); }
Usaremos esta función constantemente en lo sucesivo. Funciona no solo con las parejas de divisas, sino también con índices, futuros y con CFD, también tiene en cuenta los prejifos y sufijos para las parejas de divisas (FX_prefix, FX_postfix) que usan ciertos brókeres. El resultado se transforma a la divisa meta Chart_Currency. Si multiplicamos el valor retornado de la función por el precio actual del instrumento, entonces obtendremos el coste de un lote de este instrumento. Sumando el coste de todos los contratos del portafolio, teniendo en cuenta los lotes, obtenemos el coste de todo el portafolio. Si multiplicamos el valor de la función por la diferencia de los precios en el tiempo, entonces obtendremos el beneficio o las pérdidas recibidas como resultado de este cambio de precio.
Siguiente paso: cálculo del beneficio virtual para todos los contratos para los lotes únicos. Será una matriz bidemensional cuya primera dimensión será el índice del punto en el intervalo de cálculo, y cuya segunda dimensión será el índice del instrumento (la dimensionalidad para la segunda dimensión se puede reducir a un cierto número, sabiendo de antemano que la cantidad de instrumentos en el portafolio no lo va a superar):
double EQUITY[][100]; // primera dimensión para las barras, segunda dimensión para los instrumentos
Primero recordamos los precios iniciales para todos los instrumentos (en el límite izquierdo del intervalo de cálculo), después en cada punto del intervalo de cálculo calculamos la diferencia entre los precios iniciales y finales, luego la multiplicamos por el precio del contrato. Cada vez en el ciclo, nos desplazamos en un intervalo de tiempo a la derecha:
for(int i=0; i<variables+constants; i++) // ciclo de instrumentos del portafolio (variables y constantes del modelo) { int shift=iBarShift(SYMBOLS[i],Timeframe,zero_time); // obtenemos el número de la barra por la hora para el punto cero opening[i]=iClose(SYMBOLS[i],Timeframe,shift); // obtenemos el precio de esta barra y lo guardamos en la matriz } points=0; // calcularemos los puntos en esta variable datetime current_time=zero_time; // comenzamos el ciclo a partir del punto cero while(current_time<=limit_time) // pasamos por las etiquetas de tiempo en el intervalo de optimización { bool skip_bar=false; for(int i=0; i<variables+constants; i++) // ciclo de instrumentos del portafolio (variables y constantes del modelo) if(iBarShift(SYMBOLS[i],Timeframe,current_time,true)==-1) // comprobamos la existencia de la barra para el instrumento skip_bar=true; // si la barra no existe, entonces la saltamos para los demás instrumentos if(!skip_bar) // continuamos el trabajo si la barra está sincronizada entre todos los instrumentos { points++; // multiplicamos el número de puntos por la unidad TIMES[points-1]=current_time; // recordamos la etiqueta de la hora for(int i=0; i<variables+constants; i++) // ciclo principal del cálculo del beneficio de todos los instrumentos en el punto { int shift=iBarShift(SYMBOLS[i],Timeframe,current_time); // obtenemos el número de la barra por la hora closing[i]=iClose(SYMBOLS[i],Timeframe,shift); // obtenemos el precio de esta barra double CV=ContractValue(SYMBOLS[i],current_time,Timeframe); // calculamos el coste del contrato profit[i]=(closing[i]-opening[i])*CV; // calculamos el beneficio según la diferencia de los precios y el coste EQUITY[points-1,i]=profit[i]; // guardamos el valor del beneficio } } current_time+=Timeframe*60; // nos desplazamos al siguiente intervalo de tiempo }
En este fragmento de código: zero_time — es la hora del límite izquierdo del intervalo de cálculo, limit_time — es la hora del límite derecho del intervalo de cálculo, Timeframe — es el número de minutos en una barra del marco temporal de trabajo, points — es el número total de puntos encontrados en el intervalo calculado. En este ejemplo se usa la regla de la correspondencia estricta de las etiquetas de tiempo, y si aunque sea en un instrumento no hay una barra para una etiqueta determinada de tiempo, entonces la posición se salta y se desplaza a la siguiente posición. El control de las etiquetes es muy importante para la preparación preliminar de los datos, puesto que la desincronización de datos en diferentes instrumentos puede provocar desviaciones importantes en el portafolio.
Ejemplo de datos preparados para un portafolio de tres instrumentos y una función independiente (parábola de la raíz cuadrada):
DATE/TIME AUDJPY GBPUSD EURCAD MODEL 03.08.16 14:00 0 0 0 0 03.08.16 15:00 -61,34 -155 -230,06 10,21 03.08.16 16:00 -82,04 -433 -219,12 14,43 03.08.16 17:00 -39,5 -335 -356,68 17,68 03.08.16 18:00 147,05 -230 -516,15 20,41 03.08.16 19:00 169,73 -278 -567,1 22,82 03.08.16 20:00 -14,81 -400 -703,02 25 03.08.16 21:00 -109,76 -405 -753,15 27 03.08.16 22:00 -21,74 -409 -796,49 28,87 03.08.16 23:00 51,37 -323 -812,04 30,62 04.08.16 00:00 45,43 -367 -753,36 32,27 04.08.16 01:00 86,88 -274 -807,34 33,85 04.08.16 02:00 130,26 -288 -761,16 35,36 04.08.16 03:00 321,92 -194 -1018,51 36,8 04.08.16 04:00 148,58 -205 -927,15 38,19 04.08.16 05:00 187 -133 -824,26 39,53 04.08.16 06:00 243,08 -249 -918,82 40,82 04.08.16 07:00 325,85 -270 -910,46 42,08 04.08.16 08:00 460,02 -476 -907,67 43,3 04.08.16 09:00 341,7 -671 -840,46 44,49
Ahora que tenemos los datos preparatorios, podemos enviarlos al modelo de optimización. Ejecutaremos la optimización con la ayuda de las funciones LRBuildZ, LSFitLinearC y PCABuildBasis de la biblioteca ALGLIB. La descripción de estas funciones (bastante modesta, pero clara) se puede encontrar dentro de la propia biblioteca y en la página oficial del proyecto, aquí: http://www.alglib.net/dataanalysis/linearregression.php y aquí: http://www.alglib.net/dataanalysis/principalcomponentsanalysis.php.
Para comenzar a trabajar con la biblioteca, primero hay que conectarla:
#include <Math\Alglib\alglib.mqh>A continuación, para cada modelo de optimización hay que escribir su propio fragmento de código, teniendo en cuenta las peculiaridades del modelo. Veamos primero un ejemplo de construcción del modelo de tendencia:
if(Model_Type==trend) { int info,i,j; // definimos las variables para trabajar CLinearModelShell LM; // determinamos el objeto-modelo especial CLRReportShell AR; // determinamos el objeto-informe especial CLSFitReportShell report; // determinamos un objeto más CMatrixDouble MATRIX(points,variables+1); // determinamos la matriz para guardar todos los datos if(Model_Growth==0) { Alert("Zero model growth!"); error=true; return; } // comprobamos que los parámetros del modelo sean correctos for(j=0; j<points; j++) // calculamos la función meta según los puntos del intervalo de optimización { double x=(double)j/(points-1)-Model_Phase; // calculamos el valor de la abcisa if(Model_Absolute) x=MathAbs(x); // hacemos simétrico el modelo, de ser necesario MODEL[j]=Model_Growth*x; // calculamos el valor de la ordenada } double zero_shift=-MODEL[0]; if(zero_shift!=0) for(j=0; j<points; j++) MODEL[j]+=zero_shift; // desplazamos el modelo por la vertical hacia el punto cero for(i=0; i<variables; i++) for(j=0; j<points; j++) MATRIX[j].Set(i,EQUITY[j,i]); // cargamos los datos de los instrumentos en la matriz for(j=0; j<points; j++) MATRIX[j].Set(variables,MODEL[j]); // cargamos los datos del modelo en la matriz CAlglib::LRBuildZ(MATRIX,points,variables,info,LM,AR); // iniciamos el cálculo de la regresión if(info<0) { Alert("Error in regression model!"); error=true; return; } // comprobamos el resultado CAlglib::LRUnpack(LM,ROOTS,variables); // obtenemos las raíces de la ecuación }
En una primera lectura esto puede parecer complicado, pero básicamente todo es sencillo. Primero se calcula la función de tendencia lineal y sus valores se colocan en la matriz MODEL, además, el parámetro Model_Growth define la magnitud para todo el intervalo de cálculo (cuánto tiene que crecer el portafolio en la divisa del depósito). Los parámetros Model_Absolute y Model_Phase son opcionales y no son importantes por ahora en esta etapa. Para los cálculos se crea la matriz MATRIX, en la que se cargan los datos del beneficio virtual de todos los contratos de la matriz EQUITY, así como los valores de la función meta MODEL en la última fila de esta matriz. El número de variables independientes de la ecuación regresiva se guardan en la variable "variables". A continuación, se llama la función LRBuildZ, que ejecuta el cálculo, después de lo cual, las raíces de la ecuación regresiva se anotan en la matriz ROOTS con la ayuda de la función LRUnpack. Todas las matemáticas complejas se encuentran dentro de la biblioteca, podemos usar las funciones ya preparadas. Aquí la complejidad es puramente técnica y reside en la necesidad de registrar correctamente todas las llamadas y no perder los datos durante la preparación.
Este fragmento de código se puede usar para cualquier función definida aleatoriamente, basta con sustiruir el contenido de la matriz MODEL por su función meta. Por ejemplo, el cálculo de la función parabólica de la raíz cuadrada:
for(j=0; j<points; j++) // calculamos la función meta por los puntos del intervalo de optimización { double x=(double)j/(points-1)-Model_Phase; // calculamos el valor de la abcisa int sign=(int)MathSign(x); // definimos el singo del número if(Model_Absolute) sign=1; // hacemos simétrico el modelo, si es necesario MODEL[j]=sign*Model_Growth*MathSqrt(MathAbs(x)); // calculamos el valor de la ordenada }
Aquí tenemos un ejemplo de una función más complicada, la suma de la tendencia y las oscilaciones armónicas:
for(j=0; j<points; j++) // calculamos la función meta por los puntos del intervalo de optimización { double x=(double)j/(points-1)*Model_Cycles-Model_Phase; // calculamos el valor de la abcisa if(Model_Absolute) x=MathAbs(x); // hacemos simétrico el modelo, de ser necesario MODEL[j]=Model_Amplitude*MathSin(2*M_PI*x); // calculamos el valor de la ordenada }
En el último ejemplo se puede regular la magnitud de la tendencia con la ayuda del parámetro Model_Growth y la amplitud de las oscilaciones con la ayuda del parámetro Model_Amplitude, además, es posible establecer el ciclo de oscilaciones con la ayuda del parámetro Model_Cycles y desplazar la fase de oscilaciones con la ayuda del parámetro Model_Phase.
Para que los cálculos sean correctos, será necesario desplazarse en vertical, para que la función adopte el valor cero en el punto cero:
double zero_shift=-MODEL[0]; // calculamos el valor del modelo en el punto cero if(zero_shift!=0) // comprobamos que no sea cero for(j=0; j<points; j++) // pasamos por todos los puntos del intervalo MODEL[j]+=zero_shift; // desplazamos todos los puntos del modelo
Usando estos ejemplos, no resulta complicado crear nuestro propia función de tipo aleatorio. El aspecto de la función puede ser absolutamente cualquiera, dependiendo de la tarea descrita y de la configuración comercial. Está claro que cuanto más complejo sea el tipo de la función, más difícil será elegir la mejor solución, puesto que el mercado no está obligado a comportarse de acuerdo con alguna función concreta, se trata solo de una aproximación.
Para construir portafolios inversos de flat y portafolios de spread, no es necesaria una función meta. Por ejemplo, para construir el spread entre dos cestas de instrumentos, la cesta optimizada se carga en la parte principal de la matriz, y la cesta modelo actúa en lugar de la función meta y se carga en la última fila de la matriz de la suma total:
for(i=0; i<variables; i++) // ciclo de los instrumentos de la cesta optimizada for(j=0; j<points; j++) // ciclo de puntos del intervalo calculado MATRIX[j].Set(i,EQUITY[j,i]); // cargamos los valores de los instrumentos de la cesta optimizada en las columnas de la matriz for(i=variables; i<variables+constants; i++) // ciclo por los instrumentos de la cesta modelo for(j=0; j<points; j++) // ciclo de puntos del intervalo calculado MODEL[j]+=EQUITY[j,i]*LOTS[i]; // cargamos los valores de los instrumentos de la cesta modelo en la última columna de la matriz
Ejemplo de cálculo de un portafolio de flat, donde la función LSFitLinearC hace el portafolio simétrico al máximo alrededor del cero en los límites del intervalo calculado:
if(Model_Type==fitting) { int info,i,j; // definimos las variables para trabajar CLSFitReportShell report; // definimos el objeto-modelo especial CMatrixDouble CONSTRAIN(1,variables+1); // definimos la matriz de limitaciones lineales CMatrixDouble MATRIX(points,variables); // determinamos la matriz para guardar todos los datos ArrayInitialize(MODEL,0); // rellenamos el modelo con ceros CONSTRAIN[0].Set(variables,1); // establecemos una limitación única for(i=0; i<variables; i++) CONSTRAIN[0].Set(i,1); // la suma de las raíces deberá ser igual a la unidad for(i=0; i<variables; i++) for(j=0; j<points; j++) MATRIX[j].Set(i,EQUITY[j,i]); // cargamos los datos de los instrumentos en la matriz CAlglib::LSFitLinearC(MODEL,MATRIX,CONSTRAIN,points,variables,1,info,ROOTS,report); // calculamos el modelo de optimización por MMC if(info<0) { Alert("Error in linear fitting model!"); error=true; return; } // comprobamos el resultado }
Veamos otro ejemplo importante de cálculo del portafolio de flat con dispersión mínima según el método ACP. Aquí la función PCABuildBasis calcula los coeficientes de tal forma que el gráfico del portafolio esté comprimido al máximo en el intervalo calculado:
if(Model_Type==principal) { int info,i,j; // definimos las variables para trabajar double VAR[]; // definimos la matriz de dispersión ArrayResize(VAR,variables); // convertimos la matriz al tamaño necesario CMatrixDouble VECTOR(variables,variables); // determinamos la matriz de los vectores de los coeficientes CMatrixDouble MATRIX(points,variables); // determinamos la matriz para guardar todos los datos for(i=0; i<variables; i++) for(j=0; j<points; j++) MATRIX[j].Set(i,EQUITY[j,i]); // cargamos los datos de los instrumentos en la matriz CAlglib::PCABuildBasis(MATRIX,points,variables,info,VAR,VECTOR); // calculamos la base ortogonal con ACP if(info<0) { Alert("Error in principal component model!"); error=true; return; } // comprobamos el resultado for(i=0; i<variables; i++) ROOTS[i]=VECTOR[i][variables-1]; // descargamos los coeficientes óptimos }
Si al leer este apartado del artículo ya se siente confuso, como ya hemos recordado más arriba, no es obligatorio comprender los detalles matemáticos para construir un portafolio y comerciar con él. La secuencia general de las etapas tiene el aspecto siguiente:
| 1 | Cálculo del beneficio virtual para los instrumentos del portafolio con lotes únicos |
| 2 | Cálculo de los valores de la función meta |
| 3 | Algoritmo de optimización de los lotes |
| 4 | Normalización de los volúmenes del portafolio |
| 5 | Cálculo del gráfico y operaciones comerciales con el portafolio |
Hasta este momento, con la ayuda de una serie de procedimientos ya hemos obtenido la matriz de coeficientes óptimos ROOTS. Ahora tenemos que transformar los coeficientes en lotes. Para ello, es necesario un procedimiento de normalización: escalado y redondeo. El escalado es necesario para hacer que los lotes sean cómodos para comerciar, es decir, para seleccionar la escala necesaria. El redondeo es imprescindible para que el rango dinámico de los lotes coincida con las exigencias del bróker. A veces se recomienda ejecutar la normalización conforme al margen general del portafolio, pero este método tiene desventajas sustanciales (puesto que el margen de instrumentos aparte no tiene el mismo valor y puede cambiar), es mucho mejor hacer la normalización según el coste del portafolio o bien según su volatilidad.
Ejemplo sencillo del algoritmo de normalización según el coste del portafolio:
double total_value=0; // definimos la variable para el coste del portafolio for(int i=0; i<variables+constants; i++) // pasamos por todos los instrumentos del portafolio total_value+=closing[i]*ContractValue(SYMBOLS[i],limit_time,Timeframe)*MathAbs(LOTS[i]); // Calculamos y sumamos los componentes del coste if(total_value==0) { Alert("Zero portfolio value!"); error=true; return; } // comprobamos que no hayamos obtenido cero scale_volume=Portfolio_Value/total_value; // encontramos el coeficiente de escalado for(int i=0; i<variables+constants; i++) // pasamos de nuevo por todos los instrumentos del portafolio LOTS[i]=NormalizeDouble(LOTS[i]*scale_volume,Lots_Digits); // convertimos los lotes al coste sumario necesario
Aquí el coste del portafolio se iguala al necesario con la ayuda de la proporción. Portfolio_Value — coste necesario del portafolio, total_value — coste total del portafolio con los coeficientes por defecto, scale_volume — coeficiente de escalado, Lots_Digits — dígitos de los lotes, LOTS — matriz de los valores de los lotes aptos para el comercio.
Los valores de los lotes constituyen la estructura final del portafolio. Los lotes positivos corresponden a una posición larga, los negativos a una posición corta. Conociendo la estructura del portafolio, se puede construir su gráfico y ejecutar operaciones comerciales con el portafolio. Ejemplos de la estructura del portafolio después de la normalización:
| Instrumento | AUDJPY | GBPUSD | EURCAD |
| Lote | -0,07 | -0,11 | -0,11 |
El gráfico del portafolio se formará solo conforme a los precios de cierre, y por motivos comprensibles se construirá en una subventana de indicador aparte. Para construir el gráfico del portafolio es necesario calcular cada barra del gráfico exactamente de la misma forma que se calculó antes el beneficio virtual de los instrumentos por separado, pero ahora se sumarán teniendo en cuenta los lotes adjudicados:
for(int j=draw_begin; j>=draw_end; j--) // ciclo por las barras del gráfico en el intervalo de dibujado { double profit=0; // comenzamos desde el valor cero for(int i=0; i<variables; i++) // pasamos por todos los instrumentos { if(Fast_Period>0 && Slow_Period>0 && number!=N_TOTAL) // realizamos las comprobaciones secundarias { int shift=iBarShift(SYMBOLS[i],Period(),Time[j]); // obtenemos el número de la barra según la hora double CV=ContractValue(SYMBOLS[i],Time[j],Period()); // calculamos el coste del contrato double fast=iMA(SYMBOLS[i],Period(),Fast_Period,0,MODE_SMA,PRICE_CLOSE,shift); // calculamos la media lenta double slow=iMA(SYMBOLS[i],Period(),Slow_Period,0,MODE_SMA,PRICE_CLOSE,shift); // calculamos la media rápida profit+=(fast-slow)*CV*LOTS[i]; // calculamos el modelo de oscilación } else { int shift=iBarShift(SYMBOLS[i],Period(),Time[j]); // obtenemos el número de la barra según la hora double closing=iClose(SYMBOLS[i],Period(),shift); // obtenemos el precio del instrumento en el punto double CV=ContractValue(SYMBOLS[i],Time[j],Period()); // calculamos el coste del contrato profit+=(closing-OPENINGS[i])*CV*LOTS[i]; // calculamos el beneficio según la diferencia de los precios y el coste } } BUFFERS[number].buffer[j]=NormalizeDouble(profit,2); // guardamos el valor del beneficio en la matriz de indicador }
En este fragmento de código se puede ver que el gráfico se construye en el segmento entre la barra inicial y la final: draw_begin y draw_end. En este sentido, el valor del portafolio es la suma de los beneficios/pérdidas de todos los instrumentos, que se calculan como la diferencia de los precios multiplicada por el coste del contrato y por el lote anteriormente calculado. Hemos omitido aquí los momentos técnicos referidos a los búferes de indicador, el formateo, etc. Tenemos un ejemplo de un indicador de portafolio preparado en el apartado que sigue más abajo.
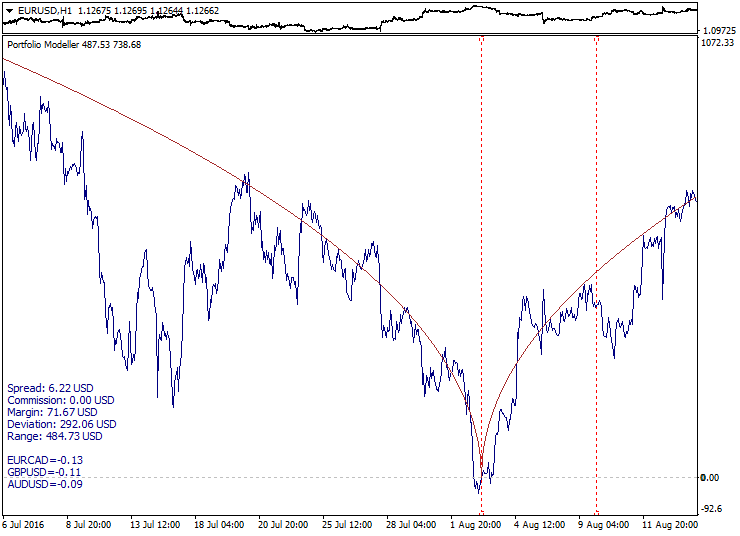
Ejemplo de construcción del gráfico del portafolio (subventana del indicador) con gráfico superpuesto de la función meta:
En este ejemplo, como función meta se usa la parábola de la raíz cuadrada, que se ha hecho de forma simétrica con respecto al comienzo de las coordenadas (parámetro Model_Absolute=true). Los límites del intervalo de cálculo se marcan en el gráfico con líneas rojas punteadas, el gráfico del portafolio tiende a moverse a lo largo de la línea de la función meta, además, como se nota fácilmente, tanto dentro como fuera del intervalo de cálculo.
Los gráficos de los portafolios pueden someterse a análisis técnico de la misma forma que los gráficos de los instrumentos comerciales normales: se pueden superponer medias móviles, líneas de tendencia y líneas de niveles. Esto amplía las posibilidades de análisis y comercio, da la posibilidad de seleccionar la estructura del portafolio de tal forma que en el gráfico del portafolio se forme una configuración comercial determinada a elección del usuario, por ejemplo: corrección tras el impulso de tendencia, ruptura de la tendencia, salida de flat, sobrecompra-sobreventa, convergencia-divergencia, ruptura y consolidación del nivel y otras configuraciones. En la calidad de las configuraciones comerciales influyen: los componentes del portafolio, el método de optimización, la función meta y el segmento de historia elegido.
Al trabajar con el portafolios es muy importante conocer su volatilidad, para elegir el volumen adecuado para el comercio. Puesto que el gráfico del portafolio desde un principio se construye en la divisa del depósito, entonces usando el modo de cursor "en cruz", es posible mediante el "estiramiento" valorar el alcance de las oscilaciones y la profundidad potencial de la reducción del portafolio directamente en la divisa del depósito.
El sistema comercial deberá apoyarse en las propiedades del comportamiento de los portafolios y la estadística de las configuraciones. Hasta el momento actual no se ha mencionado que el comportamiento del portafolio puede cambiar significativamente más allá del límite del intervalo de optimización. el flat puede cambiar hacia una tendencia, y la tendencia puede virar. El sistema comercial deberá tener en cuenta el hecho de que no es posible garantizar de forma fiable la conservación de las propiedades del portafolio en el futuro. Esta cuestión se discutirá más tarde.
Las operaciones comerciales con el portafolios constituyen la compra/venta en un momento de todos los instrumentos en el portafolio con los volúmenes calculados. Para mayor comodidad, es aconsejable disponer de un asesor especial que se haga cargo de todo el trabajo de rutina: la obtención de información sobre la estructura del portafolio y la preparación de las posiciones sintéticas, el seguimiento de los niveles de entrada, la fijación de las ganancias y la limitación de pérdidas. En el contexto del funcionamiento del asesor, tendrá sentido el término: posición sintética larga de la cartera y posición sintética corta de la cartera (en la que las largas se cambian a cortas y al revés). El asesor debe saber acumular posiciones, seguir volúmenes sintéticos, ejecutar compensación y transformar la cartera. Veremos un ejemplo de un asesor semejante en el siguiente apartado, pero su construcción no se comenta aquí para ahorrar espacio.
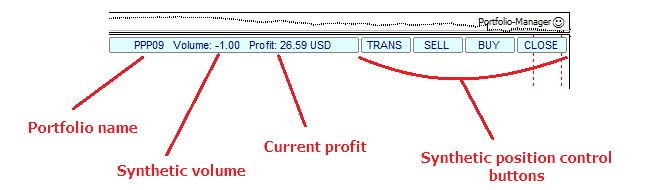
Ejemplo de una sencilla interfaz minimalista para el asesor de portafolio:
A veces resulta necesario construir no un portafolio, sino varios. En el caso más sencillo, se trata de comparar dos portafolios. Algunas tareas exigen de la construcción de una serie entera de portafolios en un intervalo de la historia, y como resultado de estas construcciones, tendremos un montón de portafolios en el que pueden existir ciertas leyes. Para implementar tareas semejantes es necesario un algoritmo que genere los portafolios según una plantilla determinada. En el siguiente apartado tenemos un ejemplo de la implementación completa de un indicador semejante, aquí se describen solo los momentos esenciales de su funcionamiento.
Para guardar los datos de multitud de portafolios es necesario organizar una matriz de estructura, por ejemplo:
struct MASSIVE // definimos la estructura con multitud de tipos de datos dentro { string symbol[MAX_SYMBOLS]; // matriz de texto para los instrumentos del portafolio double lot[MAX_SYMBOLS]; // matriz numérica para los lotes string formula; // línea con la fórmula del portafolio double direction; // signo de dirección del portafolio double filter; // signo de filtrado }; MASSIVE PORTFOLIOS[DIM_SIZE]; // creamos la matriz de estructuras para el grupo de portafolios
En este fragmento de código DIM_SIZE establece el tamaño máximo para guardar los portafolios. La propia estructura está construida de la siguiente forma: symbol — matriz de instrumentos del portafolio, lot — matriz de los lotes para los instrumentos del portafolio, formula — línea de texto con la fórmula del portafolio, direction — dirección para el portafolio (long o short), filter — signo del filtro (activado/desactivado). El uso de la matriz de estructuras es más cómodo y lógico que las matrices aparte.
Para guardar las matrices de búfer para los gráficos del portafolio también es cómodo crear una matriz de estructuras:
struct STREAM{double buffer[];}; // definimos la estructura que contiene la matriz numérica STREAM BUFFERS[DIM_SIZE]; // creamos la matriz de estructuras
Los portafolios se diferencian por su composición, es decir, por las combinaciones de instrumentos. Estas combinaciones pueden ser escritas de antemano o bien generarse según ciertas reglas. El trabajo con el grupo de portafolios puede incluir varias etapas, dependiendo de la tarea a resolver. En este caso, estudiaremos la siguiente secuencia de etapas:
| 1 | Cálculo de los gráficos de los portafolios aparte |
| 2 | Coincidencia del haz de portafolios en el punto cero |
| 3 | Viraje de los portafolios con respecto al nivel cero |
| 4 | Uso del filtro para el haz de portafolios |
| 5 | Sumarización - formación de un súper-portafolio |
La siguiente figura ilustra estas operaciones:
La coincidencia de los portafolios se consigue gracias al desplazamiento vertical. El viraje del portafolio se consigue multiplicando por -1. El uso del filtro se implementa mediante la clasificación y el muestreo por valores. No vamos a adjuntar una descripción detallada de estos algoritmos, puesto que contendría mucho código rutinario.
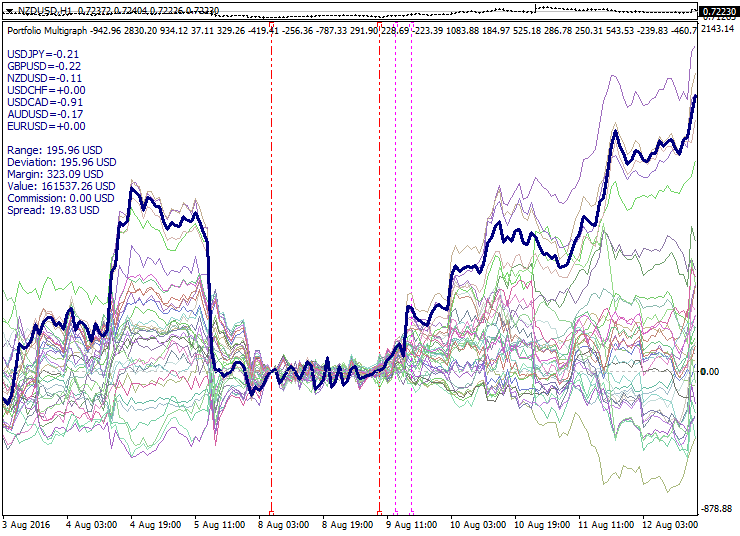
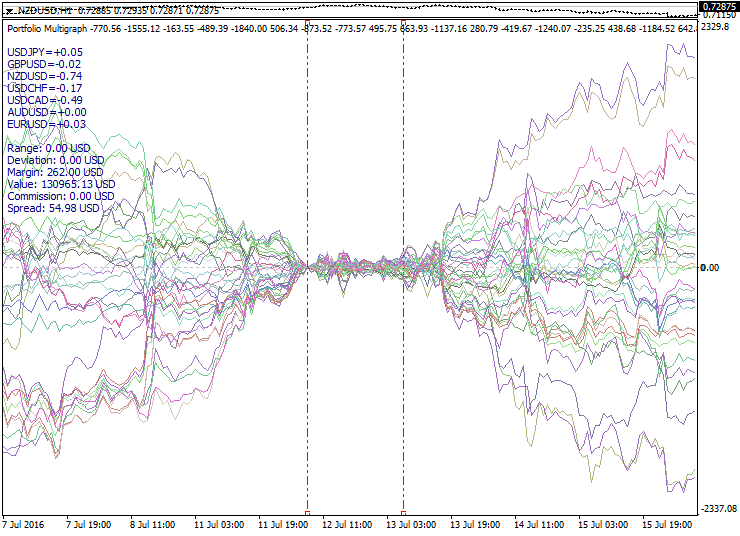
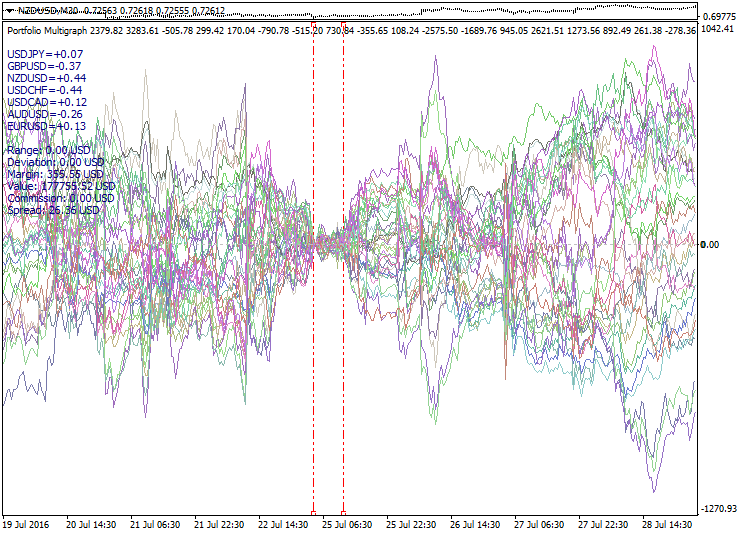
Ejemplo de un haz de portafolios construido según los principios descritos más arriba:
Aquí en el gráfico se ha formado un haz de portafolios calculados conforme a los modelos del ACP con un periodo corto. Los límites del intervalo de cálculo se marcan con líneas discontinuas. En el gráfico se ve la ampliación del haz de portafolios a ambos lados del intervalo de optimización. El punto cero se ha elegido en el límite izquierdo del intervalo de optimización, el momento del viraje con respecto al cero y el momento de uso del filtro se marcan con líneas punteadas violetas. Con una línea gruesa se indica el portafolio formado de portafolios más móviles, que debido a ello se desvían significativamente del cero.
La combinación de portafolios abre posibilidades adicionales para el análisis y creación de estrategias comerciales, por ejemplo: la diversificación entre portafolios, los spreads entre portafolios, la convergencia-divergencia del haz de portafolios, la espera de que el haz de portafolios se retuerza, el paso de un portafolios a otro, además de otros enfoques.
Ejemplos de implementación
Los métodos descritos en este artículo han sido implementados en forma de indicador de portafolio y de asesor para el comercio semi-automático. Aquí podemos familiarizarnos con las instrucciones, descargar las fuentes, estudiar y adaptar el material a nuestras tareas:
Portfolio Modeller es un constructor-optimizador de portafolios. Tiene varios tipos de modelos de optimización con parámetros ajustables, es posible detallar modelos propios y funciones meta, dispone de recursos básicos para el análisis técnico de portafolios y diferentes opciones de formateo del gráfico.
Portfolio Multigraph es un generador de haces de portafolios con los mismos modelos y parámetros, con opciones adicionales para transformar y filtrar portafolios y para componer súper-portafolios.
Portfolio Manager es un asesor para trabajar con portafolios y súper-portafolios, funciona en conjunto con el indicador de portafolio, permite abrir y controlar posiciones sintéticas, tiene la funcionalidad de corrección de portafolios, y un modo de auto-comercio basado en las líneas gráficas de las órdenes virtuales.
Enlace para la descarga: https://www.mql5.com/es/code/11859
Estrategias comerciales
Existe una gran multitud de estrategias comerciales basadas en el uso de instrumentos sintéticos. Vamos a estudiar algunas ideas básicas que pueden ser útiles al crear una estrrategia comercial con portafolio. Además, en este caso no deberemos olvidarnos de los riesgos y limitaciones que conllevan.
Enfoque clásico con la composición del portafolio: identificar los activos infravalorados con perspectiva de crecimiento y conectarlos al portafolio, esperando el crecimiento del precio. La volatilidad del portafolio siempre es menor que la suma de la volatilidad de los instrumentos incluidos en él. Este enfoque servirá para el mercado de valores. En el mercado de divisas tiene un uso muy limitado, puesto que las divisas no tienen un crecimiento progresivo, como sucede con las acciones.
Portafolio a largo plazo de Warren Buffet:
Para trabajar con los portafolios de inversión clásicos hay que valorar con mucho cuidado el estado actual de los activos para no comprarlo en su pico de crecimiento, sino en el descenso.
La primera variante y la más sencilla de comercio especulativo con un portafolio era el trading por pares: crear el spread de dos instrumentos correlativos. En el mercado Fórex este enfoque se ve limitado sustancialemnte, puesto que incluso las parejas con una fuerte correlación no tienen cointegración, y como consecuencia, pueden dispersarse significativamente transcurrido cierto tiempo. Esta situación se llama "el spread se ha rasgado". Además, como en el spread normalmente entran parejas con una divisa común, entonces el trading de pares se transforma en comercio con cambio cruzado sintético. El trading de pares en esta forma es una idea muy mala. Al abrir posiciones de spread opuestas, a veces tendremos que esperar mucho antes de que las curvas coincidan de nuevo.
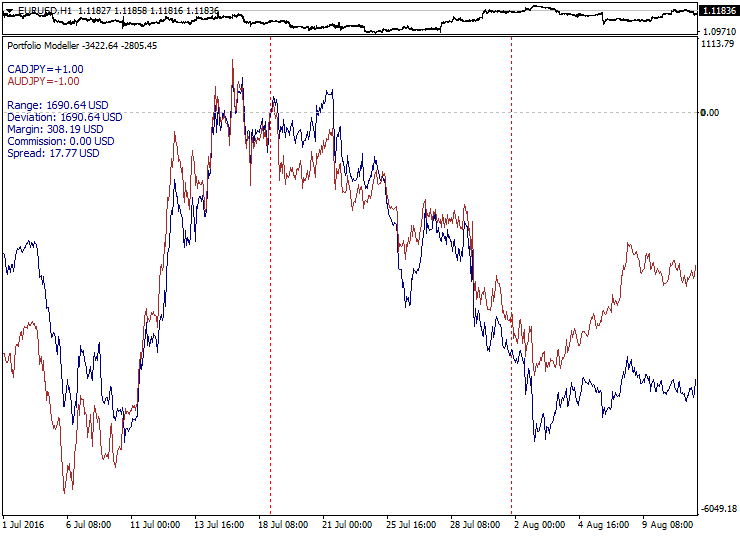
Ejemplo de parejas bien correlacionadas y su divergencia gradual e inevitable:
El desarrollo de este enfoque consiste en el spread trading multilateral, cuando en el spread se incluyen tres parejas de divisas o más. Esto ya está mejor que el trading de pares, dado que con varias parejas es más sencillo componer un spread más regular, y hay más variantes para combinar. Sin embargo, aquí existen los mismos riesgos que en el trading de pares: el spread puede diverger y no converger de nuevo. En un mercado tranquilo es sencillo lograr que el spread retorne bien, pero transcurrido cierto tiempo, las noticias fundamentales intensas provocan una desviación rápida e irreversible. Es curioso, pero al aumentar el número de instrumentos en el spread, la probabilidad de desviación aumenta, puesto que cuantas más divisas haya implicadas, mayor será la probabilidad de que "suceda algo" tras las noticias de turno. Esperar que el spread converja de nuevo puede ser algo extremadamente perjudicial. Esto solo funciona en condiciones de mercado con flat estable.
Ejemplo del comportamiento del spread multilateral con las noticias:
El spread trading tiene mayores perspectivas en el mercado de valores o de futuros si entre activos existe una conexión fundamental. Pero incluso en ese caso pueden surgir rupturas de spread al llegar las fechas de los dividendos al finalizar los contratos de futuros. Es posible, además, reunir los spreads de los índices bursátiles y los futuros, pero todo esto exige tener en cuenta las peculiaridades del comercio bursátil.
El callejón sin salida del spread-trading es el bloqueo multilateral, cuando se eligen parejas de divisas interrelacionadas de forma cíclica (por ejemplo, EURUSD-GBPUSD-EURGBP) y se compone con ellas un spread equilibrado. El spread resultará ideal, pero no será posible comerciar con él, puesto que los spread sumarios y las comisiones serán demasiado grandes. Cualquier intento de equilibrar ligeramente los lotes causará que el gráfico comience a adquirir componentes de tendencia, lo que contradice el comercio con spread, y los costes seguirán siendo elevados. Un enfoque semejante carece totalmente de sentido.
Ejemplo de bloqueo multidivisa equilibrado, el spread sumario se muestra con dos líneas rojas:
Los defectos del srpread-trading lógicamente nos obligan a pasarnos a los modelos de tendencia. Aquí todo parece muy armonioso a primera vista: identificamos la tendencia, entramos en la corrección y salimos en niveles más elevados ya con beneficio, un clásico del trading.
Ejemplo de un buen modelo de tendencia:
Pero no siempre, ni mucho menos, resulta todo tan sencillo con los modelos de tendencia. En una serie de casos, el portafolio no quiere ir más arriba, y a veces no vira hacia abajo. Esta situación se llama "la tendencia se ha roto". En los modelos a corto y medio palzo estas situaciones suceden con bastante frecuencia. La efectividad de este comercio dependerá mucho de las fases del mercado. Cuando en los mercados hay tendencia, el sistema funcionará bien, y en el mercado flat tranquilo o de oscilación reversa, serán muchas las pérdidas.
Ejemplo de finalización brusca de la tendencia:
Estas desventajas nos obligan a reevaluar los enfoques tradicionales. Ahora vamos a estudiar el comercio con ruptura del spread y el comercio con viraje de tendencia. La premisa general es la siguiente: dado que no podemos librarnos de la inestabilidad en los portafolios, es imprescindible aprender a manejarla.
Para crear una configuración de la ruptura de spread, se crea un spread muy comprimido de periodo corto con una volatilidad mínima, a la espera de algún movimiento grande. Cuanto más comprimamos la volatilidad del portafolio, más fuerte "se disparará". Para acelerar la ruptura del spread, se puede formar la configuración antes del comienzo de las sesiones comerciales y antes de las noticias, eligiendo los segmentos locales del mercado tranquilo. El método de optimización de ACP viene mejor que ninguno para comprimir la volatilidad. En esta configuración no se sabe de antemano en qué lado será el despegue, por eso la entrada se presupone ya en el movimento desde los límites del spread.
Ejemplo de la salida del corredor de spread a corto plazo, se marcan los límites del corredor de spread:
Ventajas de este método: los spreads de periodo corto se encuentran constantemente en los gráficos, la volatilidad después de la ruptura con frecuencia supera la anchura del corredor de spread. Defectos del método: la ampliación de los spreads con las noticias y la posibilidad de obtener una "sierra" cuando los precios vayan hacia arriba y hacia abajo varias veces. Como alternativa, podemos proponer una entrada conservadora después de la salida del corredor de spread durante la corrección hacia el límite del corredor, si disponemos de tal posibilidad.
Para crear una configuración con viraje de tendencia, se crea un modelo de tendencia y se hace un seguimiento de los movimientos decisivos y los niveles de precio del portafolio. En este sentido, la dirección del movimiento está definida unívocamente, pero conocemos de antemano en qué momento tendrá lugar la ruptura de la tendencia. Para una entrada conservadora hay que hacer un seguimiento del cruce de la línea interior de tendencia, la correlación inversa y el rebote. Para una entrada agresiva, se sigue el contacto de la línea interior de tendencia y el rebote.
Ejemplo de viraje del portafolio de tendencia, se muestran las líneas de tendencia interior y exterior:
Ventajas de este método: buen precio de entrada, tecnicidad, la inestabilidad de los precios extremos trabaja a favor de la configuración. Defectos del método: el precio del portafolio puede irse más arriba en la tendencia por motivos fundamentales. Como mejora de la situación, podemos proponer la entrada con volúmenes fraccionados con varios niveles.
Se puede implementar una configuración análoga con un modelo de función parabólica de la raíz cuadrada. La base de esta configuración será una propiedad conocida: cuando el precio alcance un límite teórico, el límite del capullo de la distribución de mercado, su avance posterior se verá dificultado. Aquí, como en otros casos, la función meta de optimización se selecciona dependiendo de la distribución de mercado actual. Si los mercados tuvieran una distribución de Gauss normal, entonces la ley de la raíz cuadrada del tiempo funcionaría siempre de forma ideal, pero como la distribución del mercado es fractal e inestable, se necesita una afinación situacional.
Podrá leer información más detallada sobre las propiedades de las distribuciones de mercado en los siguientes libros de Edgar Peters:
- "Caos y orden en los mercados de capitales"
- "Análisis fractal de los mercados financieros"
Ejemplo de salida del portafolio de la función parabólica:
Esta configuración viene bien para adaptarse a la volatilidad a medio plazo. Pero aquí, como con la configuración de tendencia, existe el riesgo de que el precio del portafolio suba debido a factores fundamentales. En general, el mercado no está obligado a seguir el comportamiento definido de la función meta, al mismo tiempo que no está obligado a infringirlo. En este aspecto, siempre existe cierta libertad y ambigüedad. Todas las configuraciones comerciales no son mercantilmente neutrales en un sentido absoluto, sino que se basan en esta o aquella forma de análisis.
Ilustración de la naturaleza ambigua de la tendencia y el flat, el modelo de tendencia a gran escala recuerda a un flat irregular:
A la hora de crear un portafolio, aparte de la combinación de instrumentos y del tipo del modelo, tiene una gran importancia la posición de los límites del intervalo calculado. Al realizar el ajuste puede ser útil mover los límites y observar qué resultados se obtienen. Una elección adecuada de los límites permite encontrar portafolios más adecuados desde el punto de vista de la configuración. Si la posición del portafolio sale hacia la zona de pérdidas, existe la posibilidad de corregir el portafolio sin cerrar las posiciones existentes. El desplazamiento de los límites cambia la curva del portafolio y lo adapta a la situación cambiante. Después de reconstruir el portafolio, hay que ejecutar la corrección correspondiente de la posición. Esto no significa que la reducción disminuya al instante, pero un portafolio corregido puede tener más éxito que el inicial.
A continuación, veremos algunas propiedades de los haces de portafolios y su posible uso en los sistemas comerciales.
La primera propiedad de los haces de portafolios que salta a la vista es la expansión del haz, la desviación (divergencia) de los portafolios a medida que se alejan del punto cero. La verdad es que resulta bastante natural y justificado el uso de esta propiedad para el comercio: comprar los portafolios crecientes y vender los decrecientes.
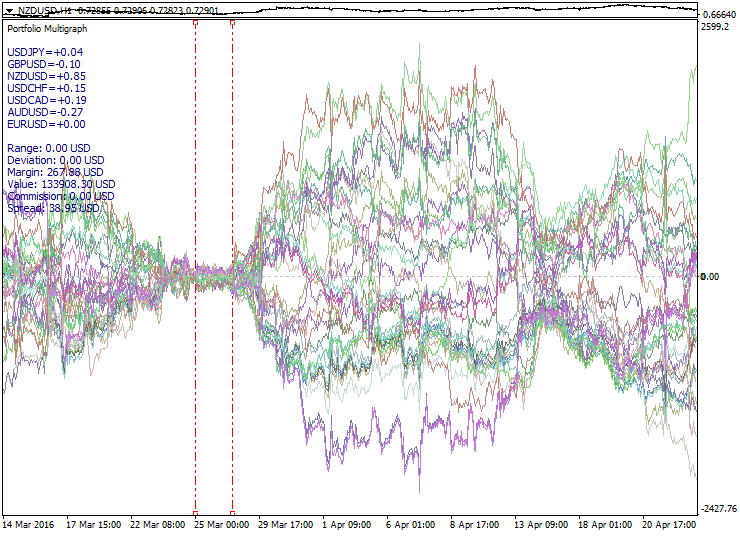
Ejemplo de un haz de portafolios en expansión:
La segunda propiedad de los haces de portafolios se opone a la primera, la compresión del haz, el encauzamiento (convergencia) de los portafolios después de la expansión. Los ciclos de expansión y compresión nos sugieren que podríamos intentar usar este comportamiento abriendo posiciones sintéticas de retorno al centro del haz después de la supuesta expansión máxima del mismo. Pero el máximo de la expansión es difernte cada vez, el límite de la desviación de las curvas del haz nos es de antemano desconocido.
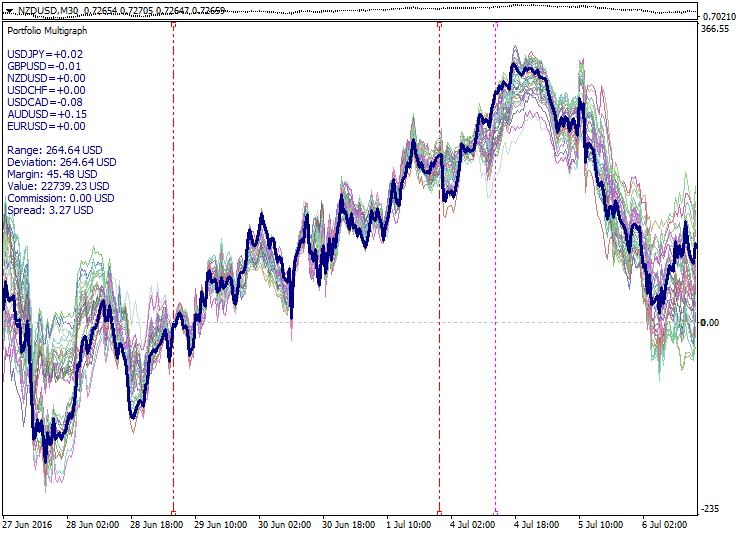
Ejemplo de un haz de portafolios en convergencia:
El uso de diferentes funciones meta, los parámetros de filtrado, el viraje y la coincidencia abren amplias posibilidades en la experimentación y búsqueda de configuraciones comerciales originales. En general, todas las configuraciones se pueden dividir en dos clases: el comercio con continuación del movimiento y el comercio con viraje.
Ejemplo de configuración comercial con continuación del movimiento con viraje y coincidencia del haz:
Ejemplo de configuración comercial con viraje según el modelo multidivisa:
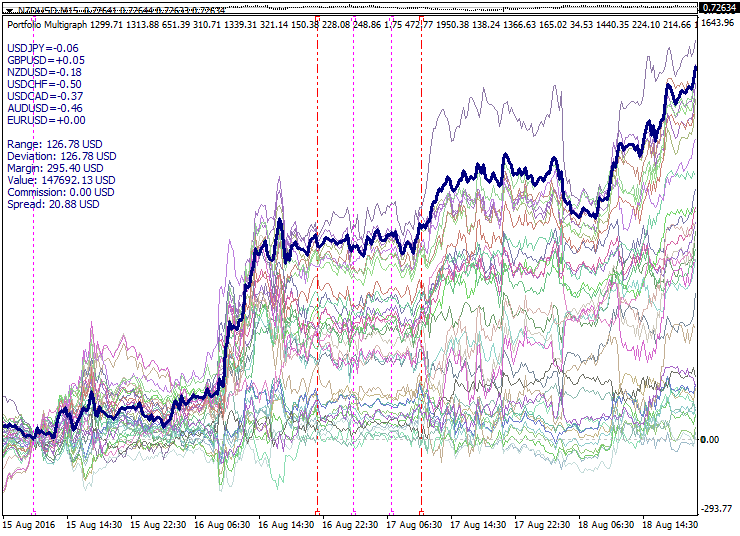
Otra propiedad que se repite en los portafolios es la torsión del haz (auto-cruzamiento). Normalmente, este fenómeno se corresponde con el cambio de tendencia en el mercado. Para comerciar con la dispersión de los portafolios, la torsión es fatídica y exige de una recostrucción del haz. Para otras estrategias, el cruce de algunas curvas de portafolio se puede usar para identificar los portafolios que funcionan y tienen perspectivas. Además de esto, hay que tener en cuenta el recorrido (distancia recorrida) del nivel, la posición del haz y la posición con respecto a la función meta.
Ejemplo de torsión múltiple del haz:
Hemos dejado fuera de plano las cuestiones de control de los volúmenes, y esta es una parte importante de cualquier sistema comercial. Aquí, basándonos en ideas generales, podemos señalar los siguientes enfoques:
- comercio con una posición sintética (el caso más sencillo)
- fraccionamiento de los volúmenes (entrada creciente conforme a los niveles)
- adición al portafolio creciente (pyramiding según la tendencia)
- adición al portafolio con reducción (promediación de las posiciones)
- adición al portafolio después de la corrección (método de remate)
- adición al portafolio después del viraje (estrategia expansiva)
- adición a nuevos portafolios (consolidación de los portafolios)
- enfoque combinado (combinación de varios enfoques)
Un enfoque concreto de gestión de volúmenes debe trabajarse teniendo en cuenta las peculiaridades del sistema comercial. Al planear los beneficios y pérdidas es necesario apoyarse en la magnitud de la volatilidad del portafolio. En el caso más sencillo se puede valorar la volatilidad del portafolio como la amplitud de los movimientos de su gráfico en un cierto sector. Es deseable valorar la volatilidad no solo en el intervalo de optimización, sino también en la historia pasada. Conociendo la volatilidad del portafolio es posible calcular el valor teórico de la reducción sumaria máxima de una serie de posiciones. Tradicionalmente conviene tener cuidado con la adición demasiado agresiva de volúmenes. La suma de los recursos en la cuenta comercial, asignada bajo la cobertura del portafolio, deberá soportar el movimiento adverso teniendo en cuenta todas las posiciones añadidas.
El comercio multi-portafolio consiste en la selección sistemática y la consolidación de los portafolios. Si se ha comprado un portafolio y se le añade otro, esto puede tener un efecto positivo de diversificación si los portafolios tienen diferencias notables. Pero si ambos portafolios están correlacionados, esto puede tener también un efecto negativo, puesto que en el caso de que los acontecimientos se desarrollen de forma adversa, ambos entrarán en pérdidas. Normalmente conviene evitar la adición de portafolios correlacionados. El comercio con spread entre dos portafolios correlacionadas, a priera vista, puede parecer que tiene muchas perpectivas, pero un estudio más atento nos hará entender que estos spreads no se diferencian en nada de los spreads normales, puesto que no tiene estabilidad.
En el comercio multi-portafolio, pueden emplearse diferentes estrategias de salida, concretamente:
- el cierre según el resultado total de todos los portafolios
- el cierre de un grupo de portafolios según el resultado común del grupo
- el cierre según los objetivos y los límites para portafolios aparte.
Para ciertas estrategias, el punto de entrada tiene especial significado. Por ejemplo, si la estrategia usa precios extremos antes de la ruptura de la tendencia o la corrección antes de la continuación de la tendencia, entonces el tiempo para la entrada será muy corto. Para otras estrategias, la precisión de entrada es menos importante, lo clave es el cálculo óptimo del esquema de adición de posiciones y el principio de selección de los portafolios. En este caso, algunos portafolios aparte pueden tener reducción, pero otros portafolios con beneficios en la serie de consolidación corrigen el resultado total.
Conclusión
Ventajas del trading de portafolio: usando la optimización, el tráder puede crear una curva de portafolio conforme a sus preferencias, formar la configuración comercial deseada y comerciar con ella en un gráfico normal, al tiempo que, con respecto a los instrumentos comerciales normales, la posición del tráder es muy pasiva (se acepta el gráfico como es o se rechaza). Asimismo, a medida que se desarrolla la situación, el tráder puede corregir el portafolio, adaptándolo a las nuevas condiciones del mercado.
Defectos del trading de portafolio: no se pueden aplicar las órdenes pendientes estándar, más exigencias con respecto al volumen mínimo, más spreads en los gráficos М30 e inferiores, el scalping intradía se complica, en el gráfico del portafolio no hay datos de OHLC, no todos los indicadores pueden aplicarse a los portafolios.
En resumen, esta tendencia en el trading es muy específica y podríamos decir que "para elegidos". En el artículo se ha dado una panorámica de las propiedades de los portafolios y los métodos de trabajo con ellos. Es conveniente realizar las investigaciones más profundas de los sistemas comerciales con portafolios en la plataforma MT5, y estudiar las propiedades de las distribuciones de mercado en paquetes estadísticos especializados.
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/2646
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Valoración rápida de señales: actividad comercial, gráficos de reducción/carga y distribuciones MFE/MAE
Valoración rápida de señales: actividad comercial, gráficos de reducción/carga y distribuciones MFE/MAE
 Trabajando con cestas de parejas de divisas en el mercado fórex
Trabajando con cestas de parejas de divisas en el mercado fórex
 Comparando MQL5 y QLUA - ¿Por qué las operaciones comerciales en MQL5 son hasta 28 veces más rápidas?
Comparando MQL5 y QLUA - ¿Por qué las operaciones comerciales en MQL5 son hasta 28 veces más rápidas?
 Red Neuronal: EA autooptimizable
Red Neuronal: EA autooptimizable
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso