古典的な戦略を再構築する（第4回）：SP500と米財務省中期証券

MetaTrader 5 — 例 | 21 10月 2024, 12:21

110

Gamuchirai Zororo Ndawana

はじめに

前回の記事では、S&P 500の高い重みを持つ銘柄選定に基づく潜在的な取引戦略について議論しました。今回の記事では、米財務省中期証券の利回りを活用してS&P500を取引する別のアプローチに焦点を当てます。ここ数年、投資家がリスク回避の姿勢をとる際には、通常リスクの高い株式から資金を引き上げ、代わりに債券や国債などのより安全な投資に資金を移す傾向があります。逆に、市場への信頼が高まると、投資家は債券などの安全資産から資金を引き上げ、株式市場に資金を投じる傾向があります。

ファンダメンタルアナリストは、S&P500の動きと国債利回りの動きとの間に見られる逆相関に長年にわたり気づいてきました。具体的には、投資家が株式投資を増やす際には債券や米財務省中期証券への投資が減少する傾向があります。

取引戦略の概要

S&P500は、アメリカの産業経済のパフォーマンスを幅広く示す重要なベンチマークです。一方、米財務省中期証券は、地球上で最も安全な投資の１つとされています。投資家が債券や米財務省中期証券を購入する際は、実質的にそれを発行した政府に資金を貸していることになります。それぞれの米財務省中期証券は、債券に記載された利子のクーポンを支払います。それぞれの米財務省中期証券は、債券の表面に記載されている利子のクーポンを支払います。

債券の需要が低いと、債券の利回りは上昇します。これは需要を再燃させるためにおこなわれます。つまり、債券を買う投資家が減れば、利回りは上昇します。一般的に、ファンダメンタル分析をおこなうアナリストたちは、この関係を長年にわたり活用してきました。S&P500の取引であれば、トレンドが弱まる兆候を探すでしょう。

例えば、債券利回りが上昇し始めた場合、ファンダメンタルズアナリストは、投資家が債券を買っているのではなく、株式のような高い収益率を得られる証券に資金を回している可能性があることを知るでしょう。

しかし、債券の利回りが低下していることにファンダメンタルズアナリストが気づいたとすれば、それは債券に対する需要が非常に高いというサインです。これはファンダメンタルアナリストにとって、一般的な市場センチメントはリスク回避的であり、ファンダメンタル戦略はこれを利用してポジションを出し入れするため、現時点では株式市場に投資すべきではないことを示唆することになります。

今日の記事では、この関係が統計的に有意かどうか、そしてこの関係を軸に取引戦略を構築することが信頼できるかどうかを確認します。始めましょう。

方法論の概要

この戦略のメリットを経験的に精査するために、インデックス自体の通常のOHLCデータを使用してSP500の終値を予測するさまざまなモデルを適合させます。そこから、同じターゲットを予測するようにモデル訓練しようとしたときの精度の変化を観察しますが、今回はモデルがアクセスできるのは米国 5 年国債のOHLCデータのみです。私たちの観察から、投資家はSP500指数のデータを利用した方がよいのではないかと考えるようになりました。私たちのモデルのパフォーマンスレベルは全体的に低下し、さらに、財務省のデータを使用しようとしたときにエラーレベルの分散が増加しました。異なる複雑さのモデルを比較するために、ランダムシャッフルを用いない時系列交差検証を採用しました。

誤差レベルの変化を観察した後、SGD回帰(SGD Regressor)を最もパフォーマンスの良いモデルとして特定し、そのモデルに対して特徴量選択をおこないました。米財務省中期証券に関連するデータは、特徴量セレクタによって選択されなかったことから、この関係は統計的に有意ではない可能性があります。この時点で、米財務省中期証券のデータを削除できる十分な証拠が揃っていましたが、あえてデータを保持し、モデルの構築を続けました。

モデルをONNX形式にエクスポートする前の最後の手順では、モデルのハイパーパラメータのチューニングを試みました。モデルの最適なパラメーター設定を見つけるために、L-BFGS-B（Limited-Memory Broyden-Fletcher-Goldfarb-Shanno）アルゴリズムを使用しました。目標は、デフォルトのモデル設定のパフォーマンスを上回ることでした。残念ながら、モデルは訓練データに過剰適合してしまい、デフォルトモデルを上回ることはできませんでした。

Pythonによる探索的データ分析

MetaTrader 5端末からデータを取得するために、過去のマーケットデータをCSV形式に書き出すスクリプトを作成しました。スクリプトは添付してあります。チャート上にドラッグ＆ドロップするだけで、データを書き出してくれます。

データが準備できたら、まずは必要なライブラリをインポートします。

#Import the libraries we need 
import pandas as pd
import numpy as np
import seaborn as sns

それが終わったら、データを読み込みます。

#Read in the data
SP500 = pd.read_csv("/home/volatily/market_data/Market Data US SP 500.csv")
T5Y = pd.read_csv("/home/volatily/market_data/Market Data UST05Y_U4.csv")

どの程度先の未来を予測したいのかを明確にする必要があります。この例では、20ステップ先の未来を予測します。

#How far into the future should we forecast?
look_ahead = 20

ここで、データが最も古い日から始まり、データ全体の中で最も新しい日が失われることも確認しなければなりません。

#Make sure the data starts with the oldest day first
SP500 = SP500[::-1].reset_index().set_index("Time").drop(columns=["index"])
T5Y = T5Y[::-1].reset_index().set_index("Time").drop(columns=["index"])

それが終わったら、今度はデータにラベルを付けます。S&P500の20ステップ先の終値のラベルを1つ用意します。そして、2つ目のバイナリターゲットは、プロットのためだけに作成されています。

#Insert the label
SP500["Target SP500"] = SP500["Close"].shift(-look_ahead)
SP500["Binary Target SP500"] = 0
SP500.loc[SP500["Close"] < SP500["Target SP500"],"Binary Target SP500"] = 1
SP500.dropna(inplace=True)

これで、2つのデータを統合することができます。S&P500と5年物国債利回りのデータを1つのデータフレームに統合します。

#Merge the data
merged_df = pd.merge(SP500,T5Y,how="inner",left_index=True,right_index=True,suffixes=(" SP500"," T5Y"))

そして、結合されたデータフレームを見ることができます。

#Let's observe the merged dataframe
merged_df

結合されたデータフレーム

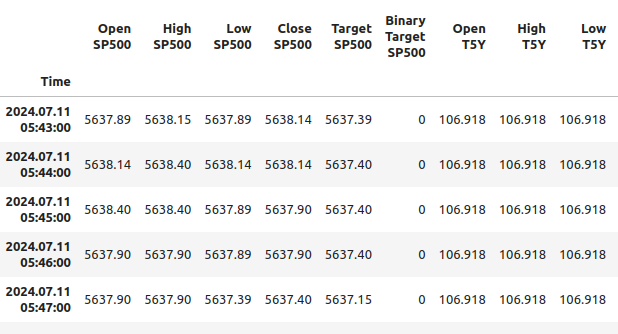
図1：結合されたデータフレーム

また、結合されたデータフレームの相関関係を分析することもできます。相関関係は0.1程度であり、強いとは言えません。

#Merged data frame correlation
merged_df.corr()

相関レベル

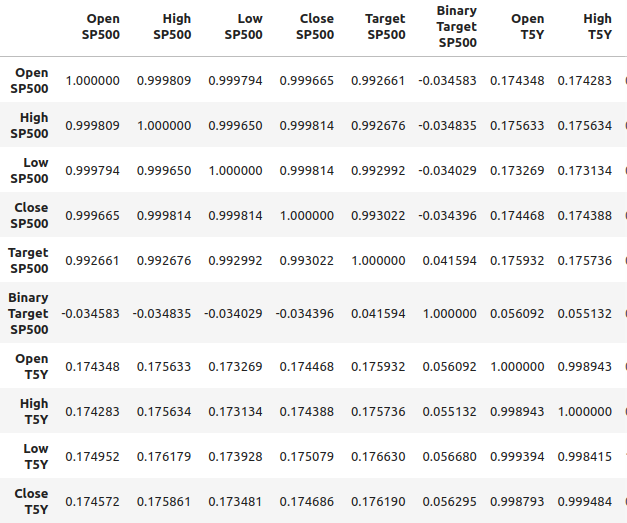
図2：結合されたデータフレームにおける相関レベル

しかし、強い相関水準は、見ている2つの変数の間に明確な関係があることを必ずしも意味しません。また、一方の変数が他方の変数を引き起こしているということを意味するものでもありません。強い相関水準は、この2つの市場に影響を及ぼしている共通の原因があることを示唆しているのかもしれません。

X軸に時間、Y軸にS&P500の始値をとって散布図を作成しました。そして、バイナリターゲットを使って散布図に沿った点に色をつけました。青とオレンジの点が自然に集まっていることに注目してください。これは、時間がデータをうまく分離していることを示しているのかもしれません。青い点は、次の20ステップで価格が下落したことを意味し、オレンジの点は、その反対のことが起こったことを意味します。

#It appears that one variable that separates the data well is time
sns.scatterplot(data=merged_df,x="Candle",y="Open SP500",hue="Binary Target SP500")

時間の経過がデータを分ける

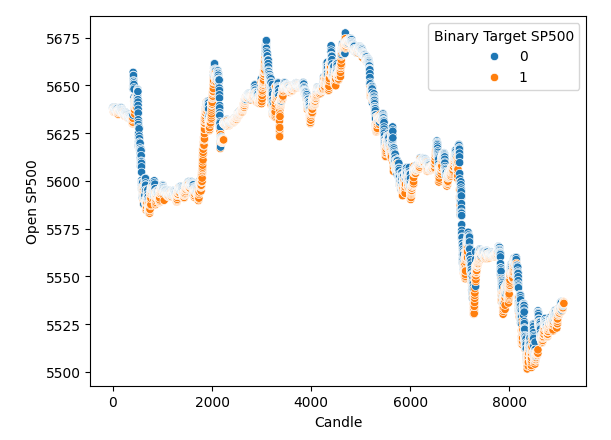
図3：データは時間的によく分離している

時間でデータをうまく分離しているようです。しかし、他の変数を使ってデータを分離しようとすると、例えばここでは、SP500の始値と5年物国債の利回りの始値を対にした散布図を作成します。そうすると、このようにあまり分離されていない散布図が得られ、多くの点が重なり合っていて、明確な分離が全く見られません。

#It appears that one variable that separates the data well is time
sns.scatterplot(data=merged_df,x="Open T5Y",y="Open SP500",hue="Binary Target SP500")

不十分な分離

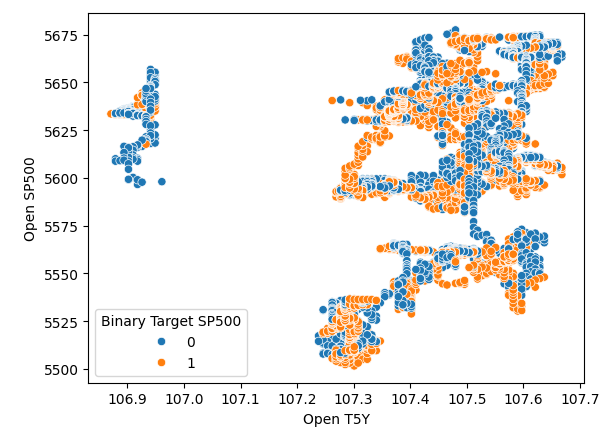
図4：不十分な分離

モデルの選択

それでは、SP500と国債利回りの関係をモデル化することにしましょう。scikit-learnから必要なモジュールをインポートします。

#Import the libraries we need
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Lasso
from sklearn.linear_model import SGDRegressor
from sklearn.svm import LinearSVR
from sklearn.ensemble import RandomForestRegressor
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.ensemble import BaggingRegressor
from sklearn.ensemble import AdaBoostRegressor
from sklearn.neural_network import MLPRegressor
from sklearn.model_selection import TimeSeriesSplit
from sklearn.metrics import root_mean_squared_error
from sklearn.preprocessing import RobustScaler
import time
from numpy.random import rand,randn
from scipy.optimize import minimize

そして、時系列分割オブジェクトを作る準備をします。まず、必要な分割数を定義し、時系列分割オブジェクト自体を作成します。

#Define the number of splits we want
splits = 10

#Create the time series split object
tscv = TimeSeriesSplit(n_splits = splits, gap=look_ahead)

多数のモデルがあるので、それらをリストに格納します。

#Store the models in a list
models = [LinearRegression(),
         Lasso(),
         SGDRegressor(),
         LinearSVR(),
         RandomForestRegressor(),
         GradientBoostingRegressor(),
         BaggingRegressor(),
         AdaBoostRegressor(),
         MLPRegressor(hidden_layer_sizes=(10,4),early_stopping=True),
         ]

モデルを初期化する関数を定義し、その関数を initialize_modelsと呼びます。

#Define a function to initialize our models
def initialize_models():
    models = [LinearRegression(),
         Lasso(),
         SGDRegressor(),
         LinearSVR(),
         RandomForestRegressor(),
         GradientBoostingRegressor(),
         BaggingRegressor(),
         AdaBoostRegressor(),
         MLPRegressor(hidden_layer_sizes=(10,4),early_stopping=True),
         ]

そして、誤差レベルを保存するためのデータフレームも必要です。データフレームは3つ必要です。最初のデータフレームは、S&P500の通常の始値オ高値と安値、終値のデータだけを使う場合の誤差レベルを格納します。2番目のデータフレームは、S&P500を国庫利回りに頼って予測しようとする場合の誤差レベルを格納します。そして最後のデータフレームは、私たちが持っているすべてのデータを使用した場合の誤差レベルを格納します。

#Create 3 dataframes to measure our performance
#Before we do that, we will define the columns and idexes
columns = ["Linear Regression",
          "Lasso",
          "SGD Regressor",
          "Linear SVR",
          "Random Forest Regressor",
          "Gradient Boosting Regressor",
          "Bagging Regressor",
          "Ada Boost Regressor",
          "MLP Regressor"]
indexes = np.arange(0,10)


#First dataframe stores our error levels using just the ordinary SP500 OHCL
SP500_error = pd.DataFrame(columns=columns,index=indexes)
#Second dataframe stores our error levels using just the ordinary Treasury Yield OHCL
TY5_error = pd.DataFrame(columns=columns,index=indexes)
#Last dataframe stores our error levels using all the data we have
total_error = pd.DataFrame(columns=columns,index=indexes)

これから入力とターゲットを定義します。

#Now we will define the inputs and target
target = "Target SP500"
predictors = ["Open T5Y",
              "Close T5Y",
              "High T5Y",
              "Low T5Y",
              "Open SP500",
              "Close SP500",
              "High SP500",
              "Low SP500"
             ]

そして、結合したデータフレームのインデックスをリセットします。

#Reset the index
merged_df.reset_index(inplace=True)

Robust Scalerを使ってデータをスケーリングします。そこで、単純にRobust Scalerをインスタンス化し、変換関数を呼び出し、 fit_transform関数に結合データフレームを渡します。これらすべては、pandasを使って作成する新しいデータフレームオブジェクトの中に包まれます。

#Scale the data
scaled_data = pd.DataFrame(RobustScaler().fit_transform(merged_df.loc[:,predictors]),columns=predictors,index=np.arange(0,merged_df.shape[0]))

さて、ここまで来たら、次は交差検証を実施しましょう。最も簡単な方法は、ネストされたループを使うことでした。したがって、最初のforループは、今あるすべてのモデルを繰り返し、次に2番目のループで各モデルを個別に交差検証します。線形回帰モデルを適合し、次にラッソ回帰を適合します。

#Now we will perform cross validation
#First we iterate over all the models we have
for j in np.arange(0,len(models)):
    for i,(train,test) in enumerate(tscv.split(merged_df)):
        #Prepare the models
        initialize_models()
        #Prepare the data
        X_train = scaled_data.loc[train[0]:train[-1],predictors]
        X_test = scaled_data.loc[test[0]:test[-1],predictors]
        y_train = merged_df.loc[train[0]:train[-1],target]
        y_test = merged_df.loc[test[0]:test[-1],target]
        #Now fit each model and measure its accuracy
        models[j].fit(X_train,y_train)
        SP500_error.iloc[i,j] = root_mean_squared_error(y_test,models[j].predict(X_test))
        print(f"Completed fitting model {models[j]}")

Completed fitting model LinearRegression()
Completed fitting model LinearRegression()
Completed fitting model LinearRegression()
Completed fitting model LinearRegression()
Completed fitting model LinearRegression()

そこから、S&P500の誤差レベルを見ることができます。線形回帰はこのケースで最も良いパフォーマンスのモデルの1つであり、SGD回帰がそれに続いているように見えます。ニューラルネットワークのパフォーマンスが良くありませんでした。実際、パラメータのチューニングから多くの恩恵を受けることができるでしょう。

SP500_error

SP500誤差レベル

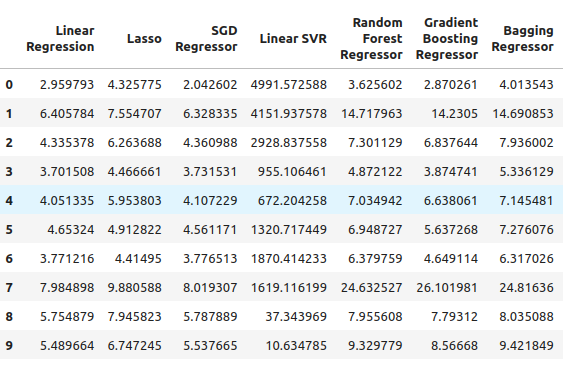
図5：通常のOHLC SP500データを使用した場合の誤差レベル

次に5年物国債利回りを見てみましょう。この場合、すべてのモデルのパフォーマンスが良くありませんでした。しかし、Random Forest Regressorはかなり良い結果を出しているようです。

TY5_error

国債利回りの誤差レベル

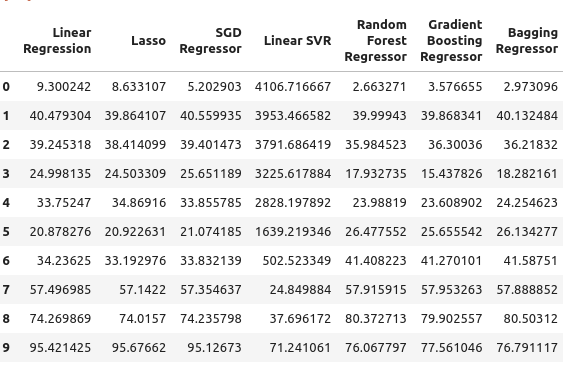
図6：国債利回りに依存した場合の誤差レベル

そして最後に、利用可能なすべてのデータを使用した場合の合計誤差があります。確率的勾配降下回帰がかなりうまく機能しているように見えるため、これらの理由から、SGD回帰を最もパフォーマンスの高いモデルとして選択しました。

total_error

合計誤差レベル

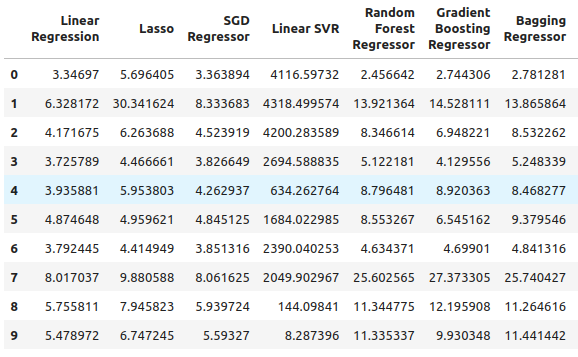
図7：入手可能なすべてのデータを使用した場合の誤差レベル

特徴量の選択

これから特徴選択をおこない、コンピューターが国庫利回りのデータも重要だと考えているかどうかを確認します。もし特徴選択器が国債利回りに関連するデータを除外すると、私たちの戦略にとって懸念材料となる可能性があります。なぜなら、その関係が信頼できないように見えるからです。しかし、もし特徴選択器が宝の歩留まりデータを保持しているなら、それは良い兆候かもしれません。

#Feature selection
from mlxtend.feature_selection import SequentialFeatureSelector as SFS

#Get the best model
model = SGDRegressor()

逐次特徴選択器オブジェクトを作成し、使用したいモデルを渡します。そこから、必要なだけの特徴を選択できるようにアルゴリズムに指示しました。5つの特徴量を選ぶように指定することもできましたが、重要だと計算された特徴量をいくつでも選びました。forwardをtrueに設定したので、これは前方選択を実行することを意味し、そこから「cv=5」を渡して、つまり5倍の交差検証を採用することを意味します。ここから「n_jobs=-1」を渡すと、特徴選択器はこのタスクを並行して実行できるようになります。

#Let us perform feature selection for the best model we have
sfs_sgd_regressor = SFS(model,
                            (1,8),
                            forward=True,
                            cv=5,
                            n_jobs=-1,
                            scoring="neg_mean_squared_error"
                           )

そこから特徴量選択器を適合します。

#Fit the feature selector
sfs_1 = sfs_sgd_regressor.fit(scaled_data.loc[:,predictors],merged_df.loc[:,target])

次に、どの特徴量がモデルにとって最も重要であったかを見てみると、残念ながら国庫に関連する特徴量は皆無でした。利回りはS&P500の終値の高値と安値のみを選択しました。したがって、この関係はそれほど安定していないことを示している可能性があります。国債利回りとS&P 500の相関関係が時々崩れることはよく知られています。

#Which features were most important to our model?
sfs_1.k_feature_names_

('Close SP500', 'High SP500', 'Low SP500')

まだモデルを最適化し、どれだけのパフォーマンスが得られるか試してみるつもりです。

#None the less, let us attempt to optimize the model
from scipy import optimize

そこから、2つの専用データセットを作成します。1つはモデルの訓練と最適化のため、もう1つは検証のためです。検証セット上で、最適化したモデルの性能を、デフォルト設定を使用しただけのデフォルトモデルの性能と比較します。デフォルトの誤差レベルを上回るよう努力します。

#Create a training and validation set
scaled_data = merged_df.loc[:,predictors]
scaled_data = (scaled_data - scaled_data.mean()) / (scaled_data.std())
#Create the two datasets
train_data , test_data = scaled_data.loc[:(scaled_data.shape[0]//2),:],scaled_data.loc[(scaled_data.shape[0]//2):,:]

最初はRobustScalarを使いましたが、今回は別のスケーリングテクニックを使っています。今回は、各列から平均を引き、各列を標準偏差で割るという、ごく一般的なスケーリング手法を採用しました。

#Let's write out the column mean and standard deviations
#We'll store the mean first 
#Then the standard deviation
scale_factors = pd.DataFrame(columns=predictors,index=(0,1))
#Save the mean and std value of each respective column
for i in (np.arange(0,len(predictors))):
    #Calculate and store the values of each column mean and std
    scale_factors.iloc[0,i] = merged_df.loc[:,predictors[i]].mean()
    scale_factors.iloc[1,i] = merged_df.loc[:,predictors[i]].std()

#Inspect the data
scale_factors

スケールファクター

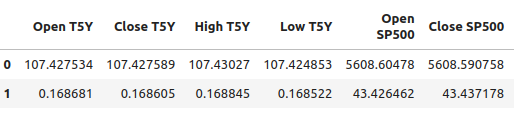
図8：各列の平均と標準偏差

各列について計算した平均値と標準偏差は重要で、MQL5で再び作業するときにそのデータが必要になるので、データをCSV形式に書き出しています。

#Write it out to csv format
scale_factors.to_csv("/home/volatily/.wine/drive_c/Program Files/MetaTrader 5/MQL5/Files/sp500_treasury_yields_scale.csv")

SGD回帰モデルの調整

モデルの調整を試みます。まず目的関数を定義します。この場合の目的関数は訓練のRMSEレベルであり、訓練データのRMSEレベルを最小化します。しかし、この処置は諸刃の剣です。どのハイパーパラメータが訓練セットでの誤差を最小化しても、検証セットでの誤差を最小化できる保証はありません。

#Define the objective function 
def objective(x):
    #Initialize the model with the new parameters
    model = SGDRegressor(alpha=x[0],shuffle=False,eta0=x[1])
    #We need a dataframe to store our current model accuracy levels
    current_accuracy = pd.DataFrame(index=np.arange(0,splits),columns=["Error"])
    #Now we perform cross validation
    for i,(train,test) in enumerate(tscv.split(train_data)):
        #Split the data into a training set and test set
        X_train = train_data.loc[train[0]:train[-1],predictors]
        X_test  = train_data.loc[test[0]:test[-1],predictors]
        y_train = merged_df.loc[train[0]:train[-1],target]
        y_test  = merged_df.loc[test[0]:test[-1],target]
        #Fit the model
        model.fit(X_train,y_train)
        #Record the accuracy
        current_accuracy.iloc[i,0] = root_mean_squared_error(y_test,model.predict(X_test))
    #Return the model accuracrcy
    return(current_accuracy.iloc[:,0].mean())

そこで、いつものように、まずは直線探索をおこない、最適値がどこにあるのかを探ります。そこで、まずは通常のライン検索をおこなったところ、ライン検索を完了するのに41秒かかりました。

#Let's optimize our model
#Let us measure how much time this takes.
start = time.time()

#Create a dataframe to measure the error rates
starting_point_error = pd.DataFrame(index=np.arange(0,21),columns=["Average CV RMSE"])
starting_point_error["Iteration"] = np.arange(0,21)

#Let us first find a good starting point for our optimization algorithm
for i in np.arange(0,21):
    #Set a new starting point
    new_starting_point = (10.0 ** -i)
    #Store error rates
    starting_point_error.iloc[i,0] = objective([new_starting_point  ,new_starting_point]) 

#Record the time stamp at the end
stop = time.time()

#Report the amount of time taken
print(f"Completed in {stop - start} seconds")

Completed in 41.863527059555054 seconds

直線探索の結果から、最初の反復で最適点を越えているように見えます。

starting_point_error["alpha"] = 0
starting_point_error["eta0"] = 0

for i in np.arange(0,21):
    starting_point_error.loc[i,"alpha"] = (10.0 ** -i)
    starting_point_error.loc[i,"eta0"] = (10.0 ** -i)

starting_point_error

直線探索結果

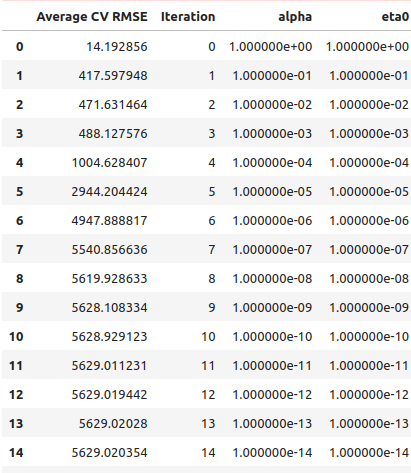
図9：直線探索結果

また、この情報を視覚的にプロットすることもできます。ご覧のように、ほとんど逆ホッケースティックのような形をしており、一番最初の誤差が最も小さく、その後は誤差が増え続けています。

#Let's visualize our error levels
sns.lineplot(data=starting_point_error,x="Iteration",y="Average CV RMSE").set(title="Optimizing our SGD Regressor on Training Data")

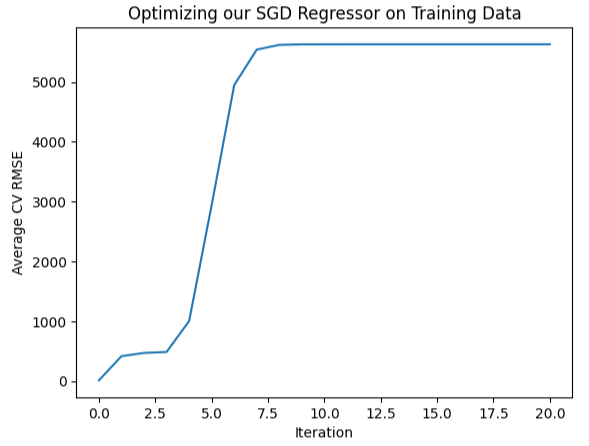
図10：誤差レベルの可視化

最適と思われる領域がわかったので、最適と思われる権利の周辺を局所的に探索することができます。L-BGFS-Bアルゴリズムを使って最適点を見つけます。まず、最適と思われる領域からランダムに点を選びます。

#Now let us perform a local search in the space that appears optimal
pt = abs(((10 ** -2) + rand(2) * ((1) - (10 ** -2))))
pt

array([0.94169659, 0.33068772])

次に、訓練データに対してモデルを最適化してみます。

#Let's try optimize our model
start = time.time()
bounds = ((0.01,1),(0.01,1))
result = minimize(objective,pt,bounds=bounds,method="L-BFGS-B")
stop = time.time()
print(f"Task completed in {stop - start} seconds")

Task completed in 106.46932244300842 seconds

その結果は？

#What are the results?
result

メッセージ：CONVERGENCE:REL_REDUCTION_OF_F_<=_FACTR*EPSMCH
success:True
   status:0
      fun:11.428966326221078
        x: [ 1.040e-01 3.193e-01]
      nit:24
      jac: [ 9.160e+00 -1.475e+01]
     nfev:351
     njev:117
hess_inv: <2x2 LbfgsInvHessProduct with dtype=float64>

成功したようです。得られた最小の誤差は 11.43 でした。ただし、真のテストは、カスタマイズされたモデルをテストセットのデフォルトモデルと比較したときにおこなわれます。

過剰適合のテスト

訓練データに過剰適合しているかどうかを検出するために、カスタマイズしたモデルの誤差レベルと、デフォルト設定のモデルの誤差レベルを比較してみましょう。パラメータチューニングを始める前に、データセットを2つに分割したことを思い出してください。

#Now let us compare the default model and the customized model
default_model = SGDRegressor()
customized_model = SGDRegressor(alpha=result.x[0],shuffle=False,eta0=result.x[1])

まず、デフォルトモデルとテストセットの誤差レベルを評価します。

#Default model accuracy
default_model.fit(train_data.loc[:,predictors],merged_df.loc[:(merged_df.shape[0]//2),target])
root_mean_squared_error(merged_df.loc[(merged_df.shape[0]//2):,target],default_model.predict(test_data.loc[:,predictors]))

5.793428451043455

次に、カスタマイズしたモデルの誤差レベルと比較します。

#Customized model accuracy
customized_model.fit(train_data.loc[:,predictors],merged_df.loc[:(merged_df.shape[0]//2),target])
root_mean_squared_error(merged_df.loc[(merged_df.shape[0]//2):,target],customized_model.predict(test_data.loc[:,predictors]))

63.45882351828459

確かに訓練データに対して過剰適合していたようで、デフォルト設定を上回ることはできませんでした。この場合、デフォルトのモデルで作業を続け、ONNX形式にエクスポートします。

ONNX形式へのエクスポート

必要なライブラリをインポートすることから始めましょう。

#Let's convert the regression model to ONNX format
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx import convert_sklearn
import onnxruntime as ort
import onnx

次に、入力を正規化し、スケーリングします。

for i in predictors:
    merged_df.loc[:,i] = (merged_df.loc[:,i] - merged_df.loc[:,i].mean()) / merged_df.loc[:,i].std()

次に、データセット全体でモデルを訓練します。

#Prepare the model
model = SGDRegressor()
model.fit(merged_df.loc[:,predictors],merged_df.loc[:,"Target SP500"])

ここで、入力形状とタイプを定義しておきます。

#Define the input types
initial_type_float = [("float_input",FloatTensorType([1,len(predictors)]))]
onnx_model_float = convert_sklearn(model,initial_types=initial_type_float,target_opset=12)

ONNXモデルを保存します。

#ONNX file name
onnx_file_name = "SP500_ONNX_FLOAT_M1.onnx"
#ONNX file
onnx.save_model(onnx_model_float,onnx_file_name)

次に、ONNXモデルの入力と出力の形状を素早く調べます。

# load the ONNX model and inspect input and ouput shapes
onnx_session = ort.InferenceSession(onnx_file_name)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

モデルの入力形状が1×8であることを確認します。

#Display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

以下は、ONNXの入力テンソルに関する情報です。
1. Name: float_input, Data Type: tensor(float), Shape：[1, 8]

最後に、出力形状は1×1でなければなりません。

#Display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

以下は、ONNXの出力テンソルに関する情報です。
1. Name: variable, Data Type: tensor(float), Shape: [1, 1]

Netronを使ってONNXモデルを可視化することもできます。

#Visualize the model
import netron

netronのstart関数によって、ONNXモデルを可視化することができます。

#Call netron 
netron.start(onnx_file_name)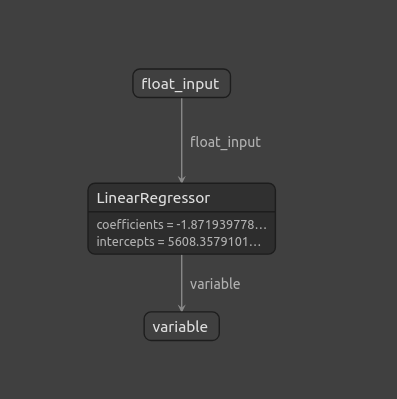

Netronを使ったONNXモデルの可視化

図11：Netronを使ったONNXモデルの可視化

ONNXモデルのメタデータ

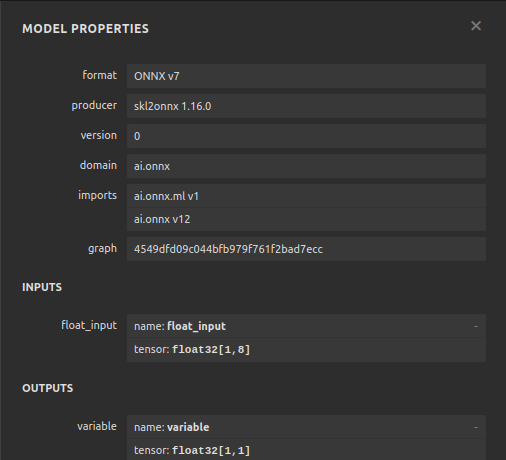
図12：ONNXモデルの特性

MQL5での実装

ONNXモデルの構築が完了し、エクスポートしたので、エキスパートアドバイザー(EA)の構築を開始します。EAで最初にすることは、エクスポートしたONNXモデルをロードすることです。

//+------------------------------------------------------------------+
//|                                      SP500 X Treasury Yields.mq5 |
//|                                        Gamuchirai Zororo Ndawana |
//|                          https://www.mql5.com/ja/gamuchiraindawa |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Zororo Ndawana"
#property link      "https://www.mql5.com/ja/gamuchiraindawa"
#property version   "1.00"
#property tester_file "sp500_treasury_yields_scale.csv"

//+------------------------------------------------------------------+
//| Require the ONNX model                                           |
//+------------------------------------------------------------------+
#resource "\\Files\\SP500_ONNX_FLOAT_M1.onnx" as const uchar ModelBuffer[];

ここから、取引ライブラリをインクルードします。このライブラリは、ポジションのオープン、クローズ、修正をサポートしてくれます。

//+------------------------------------------------------------------+
//| Libraries we need                                                |
//+------------------------------------------------------------------+
#include <Trade/Trade.mqh>
CTrade Trade;

また、エンドユーザーからの入力も必要で、例えば、ロット倍率はどのくらいにすべきか、ストップロスの幅はどのくらいにすべきか、などです。

//+------------------------------------------------------------------+
//| Inputs for our EA                                                |
//+------------------------------------------------------------------+
input int lot_multiple = 1; //How many times bigger than minimum lot?
input double sl_width = 1;  //How wide should our stop loss be?

EA全体で使用されるグローバル変数が必要です。ONNXモデルを表すグローバル変数と、モデルの予測値を格納するベクトルが必要です。

//+------------------------------------------------------------------+
//| Global variables                                                 |
//+------------------------------------------------------------------+
long model;                              //Our ONNX SGDRegressor model
vectorf prediction(1);                   //Our model's prediction
float mean_values[8],variance_values[8]; //We need this data to normalise and scale model inputs
double trading_volume;                   //How big should our positions be?
int state = 0;

次に、先ほど定義したCSV設定ファイルを読み込む関数も必要です。このファイルには、各列の平均値と標準偏差の値が含まれているので、重要であることを覚えておいてください。この関数は、ONNXモデルに与えるすべての入力が正規化されていることを保証します。この関数はまず、ファイルを開くコマンドを使ってファイルを開こうとします。もし成功し、ファイルを開くことができたら、CSVファイルをパースし、平均値と分散値をそれぞれ独立した配列に格納します。そうでない場合は、ファイルの読み込みに失敗したと表示され、falseが返され、初期化プロシージャは失敗します。

//+------------------------------------------------------------------+
//| A function responsible for reading the CSV config file           |
//+------------------------------------------------------------------+
bool read_configuration_file(void)
  {
//--- Read the config file
   Print("Reading in the config file");

//--- Config file name
   string file_name = "sp500_treasury_yields_scale.csv";

//--- Try open the file
   int result = FileOpen(file_name,FILE_READ|FILE_CSV|FILE_ANSI,",");

//--- Check the result
   if(result != INVALID_HANDLE)
     {
      Print("Opened the file");
      //--- Prepare to read the file
      int counter = 0;
      string value = "";
      //--- Make sure we can proceed
      while(!FileIsEnding(result) && !IsStopped())
        {
         if(counter > 60)
            break;
         //--- Read in the file
         value = FileReadString(result);
         Print("Reading: ",value);
         //--- Have we reached the end of the line?
         if(FileIsLineEnding(result))
            Print("row++");
         counter++;
         //--- The first few lines will contain the title of each columns, we will ingore that
         if((counter >= 11) && (counter <= 18))
           {
            mean_values[counter - 11] = (float) value;
           }
         if((counter >= 20) && (counter <= 27))
           {
            variance_values[counter - 20] = (float) value;
           }
        }
      //--- Close the file
      FileClose(result);
      Print("Mean values");
      ArrayPrint(mean_values);
      Print("Variance values");
      ArrayPrint(variance_values);
      return(true);
     }

   else
      if(result == INVALID_HANDLE)
        {
         Print("Failed to read the file");
         return(false);
        }

   return(false);
  }

モデルから予測を取得する関数も必要です。入力データを格納するために、最初にベクトルを用意しました。必要な価格をすべて取得したら、その列の平均値を引き、その列の分散で割ります。そうすれば、モデルから予測を得ることができます。

//+------------------------------------------------------------------+
//| A function responsible for getting a forecast from our model     |
//+------------------------------------------------------------------+
void predict(void)
  {
//--- Let's prepare our inputs
   vectorf input_data = vectorf::Zeros(8);
//--- Select the symbol
   input_data[0] = ((iOpen("UST05Y_U4",PERIOD_M1,0) - mean_values[0]) / variance_values[0]);
   input_data[1] = ((iClose("UST05Y_U4",PERIOD_M1,0) - mean_values[1]) / variance_values[1]);
   input_data[2] = ((iHigh("UST05Y_U4",PERIOD_M1,0) - mean_values[2]) / variance_values[2]);
   input_data[3] = ((iLow("UST05Y_U4",PERIOD_M1,0) - mean_values[3]) / variance_values[3]);;
   input_data[4] = ((iOpen("US500",PERIOD_M1,0) - mean_values[4]) / variance_values[4]);;
   input_data[5] = ((iClose("US500",PERIOD_M1,0) - mean_values[5]) / variance_values[5]);;
   input_data[6] = ((iHigh("US500",PERIOD_M1,0) - mean_values[6]) / variance_values[6]);
   input_data[7] = ((iLow("US500",PERIOD_M1,0) - mean_values[7]) / variance_values[7]);;
//--- Show the inputs
   Print("Inputs: ",input_data);
//--- Obtain a prediction from our model
   OnnxRun(model,ONNX_DEFAULT,input_data,prediction);
  }

モデルが予測を出したら、行動を起こす必要があります。つまり、この特別なケースでは、モデルが予測した方向にポジションを建てるかどうかを決めることができます。あるいは、モデルが、価格が私たちに不利に反転すると予測した場合、ポジションをクローズすることを決定するかもしれません。

//+------------------------------------------------------------------+
//| This function will decide if we should open or close our trades  |                                                                  |
//+------------------------------------------------------------------+
void intepret_prediction(void)
  {
   if(PositionsTotal() == 0)
     {
      double ask = SymbolInfoDouble("US500",SYMBOL_ASK);
      double bid = SymbolInfoDouble("US500",SYMBOL_BID);
      double close = iClose("US500",PERIOD_M1,0);
      if(prediction[0] > close)
        {
         Trade.Buy(trading_volume,"US500",ask,(ask - sl_width),(ask + sl_width),"SP500 X Treasury Yields");
         state = 1;
        }

      if(prediction[0] < iClose("US500",PERIOD_M1,0))
        {
         Trade.Sell(trading_volume,"US500",bid,(bid + sl_width),(bid - sl_width),"SP500 X Treasury Yields");
         state = 2;
        }
     }
   else
      if(PositionsTotal() > 0)
        {
         if((state == 1) && (prediction[0] > iClose("US500",PERIOD_M1,0)))
           {
            Alert("Reversal predicted, consider closing your buy position");
           }

         if((state == 2) && (prediction[0] < iClose("US500",PERIOD_M1,0)))
           {
            Alert("Reversal predicted, consider closing your buy position");
           }
        }

  }

モデルのヘルパー関数の定義が終わったので、EAの初期化関数の定義に移ります。まずONNXモデルを作成し、そのモデルが有効であることを確認します。

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {

//--- Create the ONNX model from the model buffer we have
   model = OnnxCreateFromBuffer(ModelBuffer,ONNX_DEFAULT);

//--- Ensure the model is valid
   if(model == INVALID_HANDLE)
     {
      Comment("[ERROR] Failed to initialize the model: ",GetLastError());
      return(INIT_FAILED);
     }

モデルが有効であると確信したら、モデルの入力形状を定義し、次にモデルの出力形状を定義します。

//--- Define the model parameters, input and output shapes
   ulong input_shape[] = {1,8};

//--- Check if we were defined the right input shape
   if(!OnnxSetInputShape(model,0,input_shape))
     {
      Comment("[ERROR] Incorrect input shape specified: ",GetLastError(),"\nThe model's inputs are: ",OnnxGetInputCount(model));
      return(INIT_FAILED);
     }

   ulong output_shape[] = {1,1};

//--- Check if we were defined the right output shape
   if(!OnnxSetOutputShape(model,0,output_shape))
     {
      Comment("[ERROR] Incorrect output shape specified: ",GetLastError(),"\nThe model's outputs are: ",OnnxGetOutputCount(model));
      return(INIT_FAILED);
     }

これらすべてが完了したら、設定ファイルを読み込むことができます。これは初期化時におこなう必要があり、設定ファイルの読み込みに失敗した場合は、正規化されていないデータに対して予測をおこなうことができないため、EA全体が終了する必要があります。

//--- Read the configuration file
   if(!read_configuration_file())
     {
      Comment("Failed to find the configuration file, ensure it is stored here: ",TerminalInfoString(TERMINAL_DATA_PATH));
      return(INIT_FAILED);
     }

銘柄を選択し、気配値表示に追加する必要があります。

//--- Select the symbols
   SymbolSelect("US500",true);
   SymbolSelect("UST05Y_U4",true);

最後に、市場データを取得する必要があります。

//--- Calculate the lotsize
   trading_volume = SymbolInfoDouble(Symbol(),SYMBOL_VOLUME_MIN) * lot_multiple;

//--- Return init succeeded
   return(INIT_SUCCEEDED);
  }

EAが使用されていないときは常に、割り当てられていたリソースを解放する必要があります。

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//--- Free up the resources we used for our ONNX model
   OnnxRelease(model);
//--- Remove the expert advisor
   ExpertRemove();
  }

最後に、OnTickイベントハンドラで、ONNXモデルを使って予測をおこない、その予測をアクションにマッピングします。

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//--- Get a prediction
   predict();
//--- Interpret the forecast
   intepret_prediction();
   Comment("Model forecast",prediction[0]);
  }

EAの動作