Klassische Strategien neu interpretieren (Teil IV): SP500 und US-Staatsanleihen
117
0
Einführung
In unserem letzten Artikel haben wir eine mögliche Handelsstrategie für den S&P 500 erörtert, die sich auf eine Auswahl von Aktien stützt, die innerhalb des Index eine hohe Gewichtung haben. Im heutigen Artikel werden wir einen alternativen Ansatz für den Handel mit dem S&P 500 anhand der Rendite von Staatsanleihen untersuchen. Seit vielen Jahren ziehen Anleger, wenn sie sich risikoscheu fühlen, normalerweise ihr Geld aus risikoreichen Anlagen wie Aktien ab und sparen es lieber in sichereren Anlagen wie Anleihen und Staatsanleihen. Umgekehrt würden die Anleger, wenn sie Vertrauen in die Märkte gewännen, dazu neigen, ihr Geld aus sicheren Anlagen wie Anleihen abzuziehen und lieber in den Aktienmarkt zu investieren.
Fundamentalanalysten haben im Laufe der Jahre festgestellt, dass diese Korrelation zwischen der Entwicklung des S&P 500 und der Entwicklung der Staatsanleihen-Renditen gegenläufig zu sein scheint. Es scheint sich um eine negative Korrelation zu handeln, d. h. je mehr Anleger in Aktien investieren, desto weniger investieren sie in Anleihen und Staatsanleihen.
Überblick über die Handelsstrategie
Der S&P 500 ist ein bedeutender Maßstab für die Leistung der amerikanischen Industriewirtschaft auf einer sehr breiten Ebene. Andererseits gelten Staatsanleihen als die sichersten Anlagen der Welt. Wenn ein Anleger eine Anleihe oder einen Staatsanleihen erwirbt, leiht er dem Staat, der den Schatzbrief ausgegeben hat, im Wesentlichen Geld. Jede Staatsanleihe zahlt Zinskupons aus, die auf der Vorderseite der Anleihe angegeben sind.
Wenn die Nachfrage nach Anleihen gering ist, steigt die Rendite der Anleihe an. Dies geschieht, um die Nachfrage wieder zu beleben. Da also weniger Anleger Anleihen kaufen, wird die Rendite steigen. Im Allgemeinen nutzen die Fundamentalanalysten diese Beziehung schon seit langem zu ihrem Vorteil. Würden sie mit dem S&P 500 handeln, würden sie auf Anzeichen für eine Abschwächung des Trends achten.
Wenn beispielsweise die Anleiherenditen zu steigen beginnen, wissen die Fundamentalanalysten, dass die Anleger keine Anleihen kaufen, sondern ihr Geld in Wertpapiere investieren, die ihnen eine höhere Rendite bringen, wie etwa Aktien.
Wenn ein Fundamentalanalyst jedoch feststellt, dass die Rendite der Anleihen gesunken ist, ist dies ein Zeichen dafür, dass die Nachfrage nach Anleihen sehr hoch ist. Dies würde dem Fundamentalanalysten sagen, dass er wahrscheinlich noch nicht in den Aktienmarkt investieren sollte, da die allgemeine Marktstimmung risikoscheu ist und die Fundamentalstrategien dies nutzen würden, um in ihre Positionen ein- und auszusteigen.
Im heutigen Artikel wollen wir herausfinden, ob diese Beziehung statistisch signifikant ist und ob wir auf dieser Beziehung eine zuverlässige Handelsstrategie aufbauen können. Lassen Sie uns beginnen.
Überblick über die Methodik
Um die Vorzüge dieser Strategie empirisch zu untersuchen, werden wir verschiedene Modelle zur Vorhersage des Schlusskurses des SP500 unter Verwendung gewöhnlicher OHLC-Daten aus dem Index selbst anpassen. Anschließend werden wir die Veränderung der Genauigkeit beobachten, wenn wir versuchen, die Modelle zur Vorhersage desselben Ziels zu trainieren, wobei die Modelle dieses Mal nur Zugang zu OHLC-Daten aus der 5-jährigen US-Staatsanleihen haben werden. Unsere Beobachtungen haben uns zu der Überzeugung gebracht, dass Anleger besser beraten sind, wenn sie die Daten des SP500-Index verwenden. Die Leistung unseres Modells sank auf breiter Front, und außerdem nahm die Varianz unserer Fehlerwerte zu, als wir versuchten, Daten der Staatsanleihen zu verwenden. Wir haben die Zeitserien-Kreuzvalidierung ohne zufälliges Verschieben (shuffling) eingesetzt, um Modelle unterschiedlicher Komplexität zu vergleichen.
Nach der Beobachtung der Veränderungen in den Fehlerniveaus identifizierten wir den SGD-Regressor als das Modell mit der besten Leistung und führten dann eine Merkmalsauswahl für das Modell durch. Keine der Daten, die sich auf die Staatsanleihen beziehen, wurden von unserer Merkmalsauswahl ausgewählt, was darauf hindeutet, dass die Beziehung möglicherweise nicht statistisch signifikant ist. Obwohl wir zu diesem Zeitpunkt genügend Beweise dafür hatten, dass wir die Daten der Staatsanleihen weglassen können, haben wir die Daten beibehalten und unser Modell weiter aufgebaut.
In unserem letzten Schritt vor dem Export des Modells in das ONNX-Format haben wir versucht, die Hyperparameter des Modells zu optimieren. Wir haben mit dem L-BFGS-B-Algorithmus (Limited-Memory Broyden-Fletcher-Goldfarb-Shanno) versucht, optimale Parametereinstellungen für unser Modell zu finden. Unser Ziel war es, die Leistung der Standardmodelleinstellungen zu übertreffen. Leider passten wir unser Modell zu stark an die Trainingsdaten an, sodass wir das Standardmodell nicht übertreffen konnten.
Explorative Datenanalyse in Python
Um Daten von unserem MetaTrader 5 Terminal zu holen, habe ich ein Skript erstellt, um historische Marktdaten in das CSV-Format für uns zu schreiben, ich habe das Skript beigefügt. Ziehen Sie es einfach auf das Chart und lassen Sie es dort fallen, damit es die Daten für uns ausschreibt.
Sobald die Daten vorbereitet sind, beginnen wir mit dem Import der benötigten Bibliotheken.
#Import the libraries we need import pandas as pd import numpy as np import seaborn as sns
Sobald das geschehen ist, werden wir unsere Daten einlesen.
#Read in the data SP500 = pd.read_csv("/home/volatily/market_data/Market Data US SP 500.csv") T5Y = pd.read_csv("/home/volatily/market_data/Market Data UST05Y_U4.csv")
Wir müssen festlegen, wie weit wir in die Zukunft schauen wollen. In diesem Beispiel werden wir also 20 Schritte in die Zukunft prognostizieren.
#How far into the future should we forecast? look_ahead = 20
Jetzt müssen wir auch sicherstellen, dass die Daten mit dem ältesten Tag beginnen und der jüngste Tag in den gesamten Daten verloren gehen soll.
#Make sure the data starts with the oldest day first SP500 = SP500[::-1].reset_index().set_index("Time").drop(columns=["index"]) T5Y = T5Y[::-1].reset_index().set_index("Time").drop(columns=["index"])
Danach werden wir die Daten beschriften. Wir werden ein Label haben, das der zukünftige Schlusskurs des S&P 500 ist, 20 Schritte in die Zukunft. Und das zweite binäre Ziel wird nur zu Darstellungszwecken erstellt.
#Insert the label SP500["Target SP500"] = SP500["Close"].shift(-look_ahead) SP500["Binary Target SP500"] = 0 SP500.loc[SP500["Close"] < SP500["Target SP500"],"Binary Target SP500"] = 1 SP500.dropna(inplace=True)
Nachdem wir dies getan haben, werden wir die beiden Daten zusammenführen. Wir werden die Daten über den S&P 500 und die fünfjährige Staatsanleihen-Rendite in einem Datenrahmen zusammenführen.
#Merge the data merged_df = pd.merge(SP500,T5Y,how="inner",left_index=True,right_index=True,suffixes=(" SP500"," T5Y"))
Und wir können den zusammengeführten Datenrahmen beobachten.
#Let's observe the merged dataframe merged_df
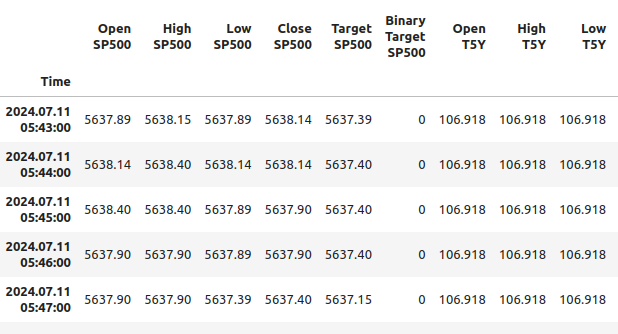
Abb. 1: Unser zusammengeführter Datenrahmen
Wir können auch die Korrelation im zusammengeführten Datenrahmen analysieren. Wir können feststellen, dass die Korrelationswerte bei etwa 0,1 liegen, was nicht sehr stark ist.
#Merged data frame correlation
merged_df.corr()
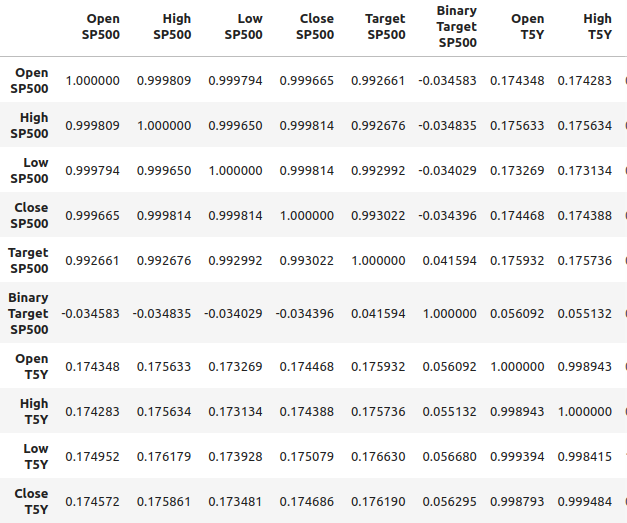
Abb. 2: Korrelationsniveaus in unserem fusionierten Datenrahmen
Starke Korrelationswerte bedeuten jedoch nicht unbedingt, dass eine eindeutige Beziehung zwischen den beiden betrachteten Variablen besteht. Es bedeutet auch nicht, dass die eine Variable die andere Variable verursacht. Starke Korrelationsniveaus können darauf hindeuten, dass es eine gemeinsame Ursache gibt, die sich auf diese beiden Märkte auswirkt.
Ich habe ein Streudiagramm erstellt, bei dem auf der x-Achse die Zeit und auf der y-Achse der Eröffnungskurs des S&P 500 steht. Und dann habe ich die binären Ziele verwendet, um die Punkte entlang des Streudiagramms einzufärben. Beachten Sie, dass sich die blauen und orangenen Punkte natürlich häufen, was darauf hindeutet, dass die Zeit die Daten gut trennt. Erinnern Sie sich daran, dass unser binäres Ziel uns sagt, was in 20 Schritten in der Zukunft passieren wird. Die blauen Punkte bedeuten, dass der Preis in den nächsten 20 Schritten gefallen ist, und die orangefarbenen Punkte sagen uns, dass das Gegenteil passiert ist.
#It appears that one variable that separates the data well is time sns.scatterplot(data=merged_df,x="Candle",y="Open SP500",hue="Binary Target SP500")
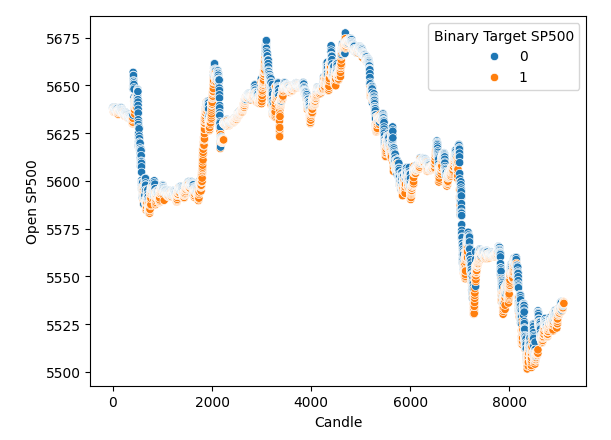
Abb. 3: Unsere Daten scheinen zeitlich gut getrennt zu sein
Es scheint also, dass die Zeit die Daten sehr gut trennt. Wenn wir jedoch versuchen, die Daten mit anderen Variablen zu trennen, wie z. B. hier, erstellen wir ein Streudiagramm des Eröffnungskurses des SP500 gegen den Eröffnungskurs der fünfjährigen Schatzrendite. Wir sehen, dass wir dieses schlecht getrennte Streudiagramm erhalten, bei dem so viele Punkte übereinander liegen, dass es überhaupt keine klare Trennung gibt.
#It appears that one variable that separates the data well is time sns.scatterplot(data=merged_df,x="Open T5Y",y="Open SP500",hue="Binary Target SP500")
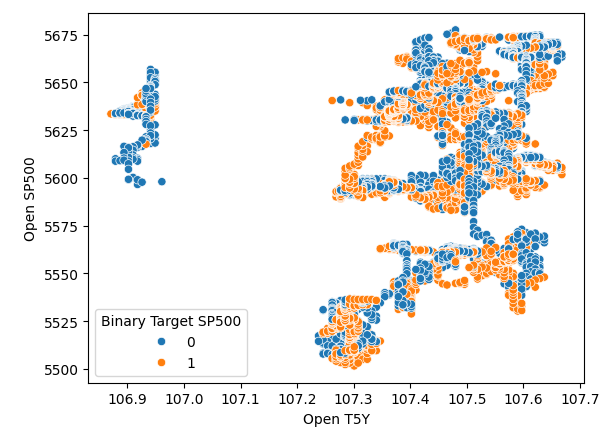
Abb. 4: Schlechte Trennung
Auswahl des Modells
Nachdem wir dies getan haben, werden wir uns nun der Modellierung der Beziehung zwischen dem SP500 und den Renditen der Staatsanleihen zuwenden. Wir werden die Module, die wir benötigen, aus scikit-learn importieren.
#Import the libraries we need from sklearn.linear_model import LinearRegression from sklearn.linear_model import Lasso from sklearn.linear_model import SGDRegressor from sklearn.svm import LinearSVR from sklearn.ensemble import RandomForestRegressor from sklearn.ensemble import GradientBoostingRegressor from sklearn.ensemble import BaggingRegressor from sklearn.ensemble import AdaBoostRegressor from sklearn.neural_network import MLPRegressor from sklearn.model_selection import TimeSeriesSplit from sklearn.metrics import root_mean_squared_error from sklearn.preprocessing import RobustScaler import time from numpy.random import rand,randn from scipy.optimize import minimize
Und dann werden wir uns darauf vorbereiten, ein geteiltes Zeitreihenobjekt zu erstellen. Zunächst legen wir also die Anzahl der gewünschten Splits fest und erstellen dann das Zeitreihen-Split-Objekt selbst.
#Define the number of splits we want splits = 10
#Create the time series split object
tscv = TimeSeriesSplit(n_splits = splits, gap=look_ahead) Und da wir zahlreiche Modelle haben, werden wir sie in einer Liste speichern.
#Store the models in a list models = [LinearRegression(), Lasso(), SGDRegressor(), LinearSVR(), RandomForestRegressor(), GradientBoostingRegressor(), BaggingRegressor(), AdaBoostRegressor(), MLPRegressor(hidden_layer_sizes=(10,4),early_stopping=True), ]
Ich werde eine Funktion definieren, um unsere Modelle zu initialisieren, und die Funktion heißt „initialize_models“.
#Define a function to initialize our models def initialize_models(): models = [LinearRegression(), Lasso(), SGDRegressor(), LinearSVR(), RandomForestRegressor(), GradientBoostingRegressor(), BaggingRegressor(), AdaBoostRegressor(), MLPRegressor(hidden_layer_sizes=(10,4),early_stopping=True), ]
Und dann brauchen wir noch Datenrahmen, um unsere Fehlerstufen zu speichern. Wir benötigen also drei Datenrahmen. Der erste Datenrahmen speichert unsere Fehlerniveaus, wenn wir nur gewöhnliche Eröffnungs-, Höchst-, Tiefst- und Schlussdaten des S&P 500 verwenden, der zweite Datenrahmen speichert unsere Fehlerniveaus, wenn wir versuchen, den S&P 500 zu prognostizieren, indem wir uns nur auf Staatsanleihen-Renditen stützen. Und der letzte Datenrahmen speichert unsere Fehlerniveaus bei Verwendung aller Daten, die wir haben.
#Create 3 dataframes to measure our performance #Before we do that, we will define the columns and idexes columns = ["Linear Regression", "Lasso", "SGD Regressor", "Linear SVR", "Random Forest Regressor", "Gradient Boosting Regressor", "Bagging Regressor", "Ada Boost Regressor", "MLP Regressor"] indexes = np.arange(0,10) #First dataframe stores our error levels using just the ordinary SP500 OHCL SP500_error = pd.DataFrame(columns=columns,index=indexes) #Second dataframe stores our error levels using just the ordinary Treasury Yield OHCL TY5_error = pd.DataFrame(columns=columns,index=indexes) #Last dataframe stores our error levels using all the data we have total_error = pd.DataFrame(columns=columns,index=indexes)
Wir werden nun unsere Eingaben und unser Ziel definieren.
#Now we will define the inputs and target target = "Target SP500" predictors = ["Open T5Y", "Close T5Y", "High T5Y", "Low T5Y", "Open SP500", "Close SP500", "High SP500", "Low SP500" ]
Und dann setzen wir den Index unseres zusammengeführten Datenrahmens zurück.
#Reset the index
merged_df.reset_index(inplace=True) Und wir werden die Daten mit robusten Skalaren skalieren. Wir instanziieren also einfach den robusten Skalierer, rufen die Transformationsfunktion auf und übergeben den zusammengeführten Datenrahmen an die Fit-Transformationsfunktion. All dies wird in ein neues Datenrahmenobjekt verpackt, das wir mit Pandas erstellen werden.
#Scale the data scaled_data = pd.DataFrame(RobustScaler().fit_transform(merged_df.loc[:,predictors]),columns=predictors,index=np.arange(0,merged_df.shape[0]))
Nachdem wir nun so weit gekommen sind, können wir nun eine Kreuzvalidierung durchführen. Am einfachsten war es also, eine verschachtelte Schleife zu verwenden. Daher durchläuft die erste for-Schleife alle Modelle, die wir haben, und in der zweiten Schleife wird dann jedes Modell einzeln überprüft. Daher werden wir das lineare Regressionsmodell anpassen, dann das Lasso und so weiter.
#Now we will perform cross validation #First we iterate over all the models we have for j in np.arange(0,len(models)): for i,(train,test) in enumerate(tscv.split(merged_df)): #Prepare the models initialize_models() #Prepare the data X_train = scaled_data.loc[train[0]:train[-1],predictors] X_test = scaled_data.loc[test[0]:test[-1],predictors] y_train = merged_df.loc[train[0]:train[-1],target] y_test = merged_df.loc[test[0]:test[-1],target] #Now fit each model and measure its accuracy models[j].fit(X_train,y_train) SP500_error.iloc[i,j] = root_mean_squared_error(y_test,models[j].predict(X_test)) print(f"Completed fitting model {models[j]}")
Completed fitting model LinearRegression()
Completed fitting model LinearRegression()
Completed fitting model LinearRegression()
Completed fitting model LinearRegression()
Von dort aus können wir unsere S&P 500-Fehlerniveaus sehen, und es scheint, dass die lineare Regression in diesem Fall eines der besten Modelle war, gefolgt von dem SGD-Regressor. Das neuronale Netz schnitt recht schlecht ab. In der Tat könnte sie wahrscheinlich sehr von einer Anpassung der Parameter profitieren.
SP500_error
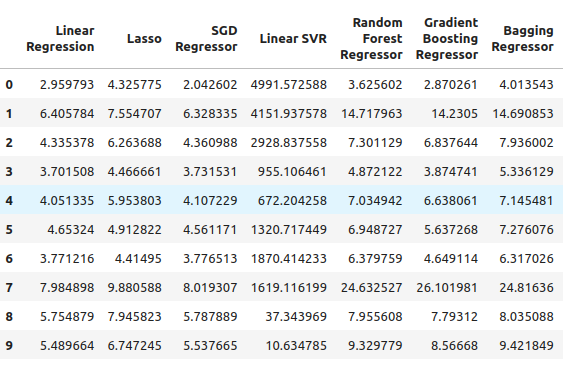
Abb. 5: Unsere Fehlerquoten bei der Verwendung gewöhnlicher OHLC SP500-Daten
Weiter geht es mit der Rendite fünfjähriger Staatsanleihen. In diesem speziellen Fall haben alle unsere Modelle schlecht abgeschnitten. Der Random Forest Regressor scheint jedoch recht gut zu funktionieren.
TY5_error
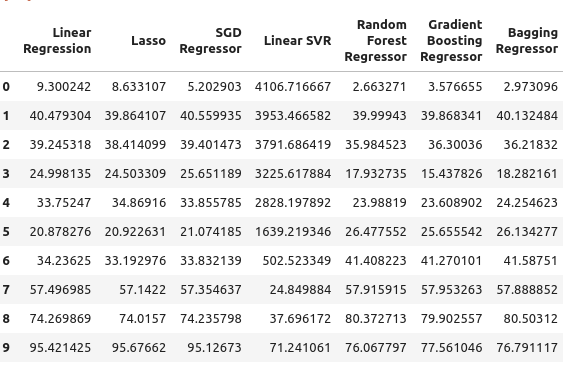
Abb. 6: Unsere Fehlerquote, wenn wir uns auf die Renditen von Staatsanleihen verlassen
Und schließlich haben wir den Gesamtfehler, wenn wir alle verfügbaren Daten verwenden. Es scheint, dass der stochastische Gradientenabstiegsregressor recht gut abschneidet, und aus diesen Gründen habe ich den SGD-Regressor als das Modell mit der besten Leistung ausgewählt.
total_error
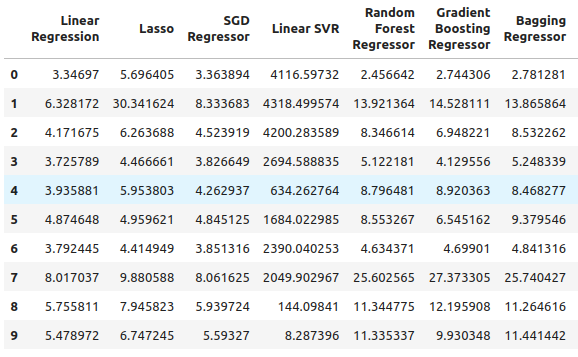
Abb. 7: Unsere Fehlerquoten, wenn wir alle verfügbaren Daten verwenden
Auswahl der Merkmale
Wir werden nun eine Merkmalsauswahl durchführen, um zu sehen, ob unser Computer die Daten zu den Staatsanleihen ebenfalls für wichtig hält. Wenn die Merkmalsauswahl die Daten, die sich auf die Staatsanleihen beziehen, fallen lässt, dann könnte das für unsere Strategie ein Grund zur Sorge sein, weil es den Anschein hat, dass die Beziehung nicht zuverlässig ist. Wenn unsere Merkmalsauswahl jedoch die Ertragsdaten der Staatsanleihen beibehält, dann könnte das ein gutes Zeichen sein.
#Feature selection from mlxtend.feature_selection import SequentialFeatureSelector as SFS #Get the best model model = SGDRegressor()
Wir erstellen das Objekt für die sequentiellen Merkmalsauswahl und übergeben ihm das Modell, das wir verwenden möchten. Von dort aus habe ich den Algorithmus angewiesen, dass er so viele Merkmale wie nötig auswählen kann. Wir hätten angeben können, dass fünf Merkmale ausgewählt werden sollen, aber ich wollte so viele auswählen, wie es für wichtig erachtet. Wir setzen Forward auf true, das heißt, es wird eine Vorwärtsselektion durchgeführt, und dann haben wir CV gleich fünf gesetzt, was bedeutet, dass wir eine fünffache Kreuzvalidierung durchführen. Von dort aus haben wir n-jobs gleich minus 1 übergeben, sodass die Merkmalsauswahl diese Aufgabe parallel ausführen kann.
#Let us perform feature selection for the best model we have sfs_sgd_regressor = SFS(model, (1,8), forward=True, cv=5, n_jobs=-1, scoring="neg_mean_squared_error" )
Von dort aus passen wir die Merkmalsauswahl an.
#Fit the feature selector
sfs_1 = sfs_sgd_regressor.fit(scaled_data.loc[:,predictors],merged_df.loc[:,target]) Wenn wir uns nun ansehen, welche Merkmale für unser Modell am wichtigsten waren, stellen wir fest, dass sich leider keines der Merkmale auf den Staatsanleihen bezog. Bei der Auswahl der Renditen wurden nur die Höchst- und Tiefststände des S&P 500 ausgewählt. Dies kann also darauf hindeuten, dass die Beziehung nicht so stabil ist, und es ist bekannt, dass die Korrelation zwischen den Renditen von Staatsanleihen und dem S&P 500 von Zeit zu Zeit abbricht.
#Which features were most important to our model?
sfs_1.k_feature_names_ Wir werden weiterhin versuchen, unser Modell zu optimieren und zu sehen, wie viel Leistung wir erreichen können.
#None the less, let us attempt to optimize the model
from scipy import optimize Und von dort aus werden wir zwei spezielle Datensätze erstellen. Eine zum Trainieren und Optimieren des Modells und die andere zur Validierung. In der Validierungsgruppe vergleichen wir die Leistung unseres optimierten Modells mit der Leistung eines Standardmodells, das nur die Standardeinstellungen verwendet. Wir wollen versuchen, die Standardfehlergrenzen zu übertreffen.
#Create a training and validation set scaled_data = merged_df.loc[:,predictors] scaled_data = (scaled_data - scaled_data.mean()) / (scaled_data.std()) #Create the two datasets train_data , test_data = scaled_data.loc[:(scaled_data.shape[0]//2),:],scaled_data.loc[(scaled_data.shape[0]//2):,:]
Beachten Sie, dass ich dieses Mal eine andere Skalierungstechnik verwende als beim ersten Mal, als ich nur einen robusten Skalar verwendete. Diesmal haben wir eine sehr gängige Skalierungstechnik angewandt, bei der wir den Mittelwert von jeder Spalte abziehen und dann jede Spalte durch ihre Standardabweichung teilen.
#Let's write out the column mean and standard deviations #We'll store the mean first #Then the standard deviation scale_factors = pd.DataFrame(columns=predictors,index=(0,1)) #Save the mean and std value of each respective column for i in (np.arange(0,len(predictors))): #Calculate and store the values of each column mean and std scale_factors.iloc[0,i] = merged_df.loc[:,predictors[i]].mean() scale_factors.iloc[1,i] = merged_df.loc[:,predictors[i]].std() #Inspect the data scale_factors
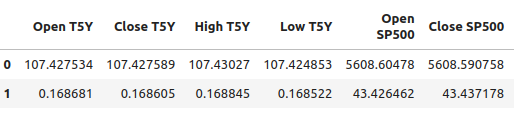
Abb. 8: Unser Mittelwert und die Standardabweichung für jede Spalte
Die Mittelwerte und die Standardabweichungen, die wir für jede Spalte berechnet haben, sind aussagekräftig, und wir werden diese Daten brauchen, wenn wir wieder in MQL5 arbeiten, also schreibe ich die Daten ins CSV-Format.
#Write it out to csv format scale_factors.to_csv("/home/volatily/.wine/drive_c/Program Files/MetaTrader 5/MQL5/Files/sp500_treasury_yields_scale.csv")
Abstimmung des SGD-Regressor-Modells
Wir werden nun versuchen, das Modell abzustimmen, indem wir zunächst die Zielfunktion definieren. Die Zielfunktion ist in diesem Fall der RMSE-Wert für das Training, und wir wollen den RMSE-Wert für die Trainingsdaten minimieren. Dieses Verfahren ist jedoch ein zweischneidiges Schwert. Die Hyperparameter, die unseren Fehler in der Trainingsmenge minimieren, garantieren nicht, dass sie auch unseren Fehler in der Validierungsmenge minimieren!
#Define the objective function def objective(x): #Initialize the model with the new parameters model = SGDRegressor(alpha=x[0],shuffle=False,eta0=x[1]) #We need a dataframe to store our current model accuracy levels current_accuracy = pd.DataFrame(index=np.arange(0,splits),columns=["Error"]) #Now we perform cross validation for i,(train,test) in enumerate(tscv.split(train_data)): #Split the data into a training set and test set X_train = train_data.loc[train[0]:train[-1],predictors] X_test = train_data.loc[test[0]:test[-1],predictors] y_train = merged_df.loc[train[0]:train[-1],target] y_test = merged_df.loc[test[0]:test[-1],target] #Fit the model model.fit(X_train,y_train) #Record the accuracy current_accuracy.iloc[i,0] = root_mean_squared_error(y_test,model.predict(X_test)) #Return the model accuracrcy return(current_accuracy.iloc[:,0].mean())
Wie immer werden wir also zunächst eine Zeilensuche durchführen, um eine Vorstellung davon zu bekommen, wo die optimalen Werte liegen könnten. Wir begannen also mit einer normalen Zeilensuche und brauchten 41 Sekunden, um die Zeilensuche abzuschließen.
#Let's optimize our model #Let us measure how much time this takes. start = time.time() #Create a dataframe to measure the error rates starting_point_error = pd.DataFrame(index=np.arange(0,21),columns=["Average CV RMSE"]) starting_point_error["Iteration"] = np.arange(0,21) #Let us first find a good starting point for our optimization algorithm for i in np.arange(0,21): #Set a new starting point new_starting_point = (10.0 ** -i) #Store error rates starting_point_error.iloc[i,0] = objective([new_starting_point ,new_starting_point]) #Record the time stamp at the end stop = time.time() #Report the amount of time taken print(f"Completed in {stop - start} seconds")
Aus den Ergebnissen unserer Liniensuche geht hervor, dass wir die optimalen Punkte gleich in der ersten Iteration überschritten haben.
starting_point_error["alpha"] = 0 starting_point_error["eta0"] = 0 for i in np.arange(0,21): starting_point_error.loc[i,"alpha"] = (10.0 ** -i) starting_point_error.loc[i,"eta0"] = (10.0 ** -i) starting_point_error
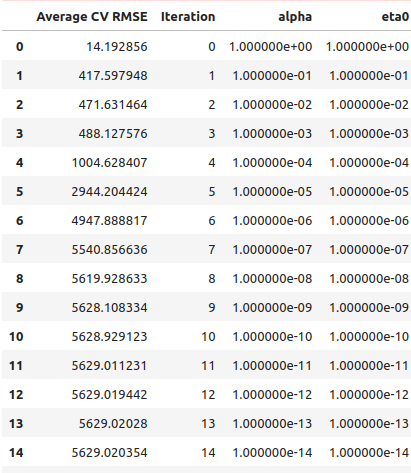
Abb. 9: Unsere Suchergebnisse nach Linien
Wir können diese Informationen auch visuell darstellen, wie Sie an der Form eines fast umgekehrten Hockeyschlägers sehen können, bei dem der Fehler ganz am Anfang am geringsten ist und dann immer weiter ansteigt,
#Let's visualize our error levels sns.lineplot(data=starting_point_error,x="Iteration",y="Average CV RMSE").set(title="Optimizing our SGD Regressor on Training Data")
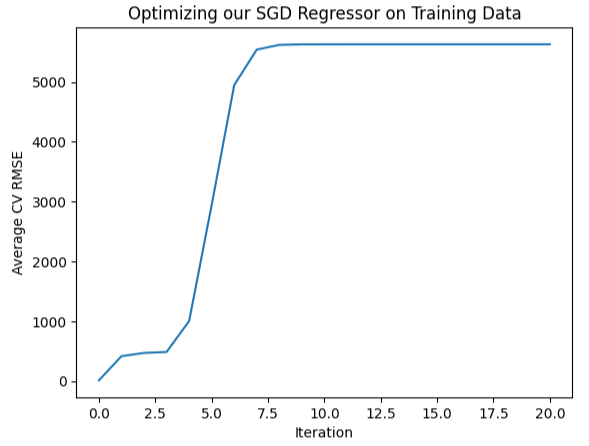
Abb. 10: Visualisierung unserer Fehlerquoten
Da wir nun eine Vorstellung davon haben, was optimal erscheint, können wir eine lokale Suche um die Region herum durchführen, die optimal richtig zu sein scheint. Wir werden den L-BGFS-B-Algorithmus verwenden, um diese optimalen Punkte zu finden. Zunächst wählen wir zufällige Punkte aus der Region aus, die optimal erscheint.
#Now let us perform a local search in the space that appears optimal pt = abs(((10 ** -2) + rand(2) * ((1) - (10 ** -2)))) pt
Nun werden wir versuchen, unser Modell für die Trainingsdaten zu optimieren.
#Let's try optimize our model
start = time.time()
bounds = ((0.01,1),(0.01,1))
result = minimize(objective,pt,bounds=bounds,method="L-BFGS-B")
stop = time.time()
print(f"Task completed in {stop - start} seconds") Was sind die Ergebnisse?
#What are the results?
result success: True
status: 0
fun: 11.428966326221078
x: [ 1.040e-01 3.193e-01]
nit: 24
jac: [ 9.160e+00 -1.475e+01]
nfev: 351
njev: 117
hess_inv: <2x2 LbfgsInvHessProduct with dtype=float64>
Es scheint, dass wir erfolgreich waren. Der niedrigste Fehler, den wir erreichen konnten, war 11,43, aber der wahre Test kommt, wenn wir das angepasste Modell mit dem Standardmodell auf dem Testsatz vergleichen.
Testen auf Überanpassung
Um festzustellen, ob wir die Trainingsdaten zu stark anpassen, vergleichen wir die Fehlerwerte unseres angepassten Modells mit den Fehlerwerten eines Modells mit Standardeinstellungen. Erinnern Sie sich daran, dass wir den Datensatz in zwei Hälften geteilt haben, bevor wir mit der Parameteroptimierung begannen.#Now let us compare the default model and the customized model default_model = SGDRegressor() customized_model = SGDRegressor(alpha=result.x[0],shuffle=False,eta0=result.x[1])
Lassen Sie uns zunächst die Fehlerquoten des Standardmodells und der Testdaten bewerten.
#Default model accuracy default_model.fit(train_data.loc[:,predictors],merged_df.loc[:(merged_df.shape[0]//2),target]) root_mean_squared_error(merged_df.loc[(merged_df.shape[0]//2):,target],default_model.predict(test_data.loc[:,predictors]))
Vergleichen wir dies nun mit den Fehlerniveaus des angepassten Modells.
#Customized model accuracy customized_model.fit(train_data.loc[:,predictors],merged_df.loc[:(merged_df.shape[0]//2),target]) root_mean_squared_error(merged_df.loc[(merged_df.shape[0]//2):,target],customized_model.predict(test_data.loc[:,predictors]))
Es scheint, dass wir die Trainingsdaten tatsächlich zu stark angepasst haben und die Standardeinstellungen nicht übertroffen haben. In diesem Fall werden wir mit dem Standardmodell weiterarbeiten und es in das ONNX-Format exportieren.
Exportieren ins ONNX-Format
Wir beginnen mit dem Import der benötigten Bibliotheken.
#Let's convert the regression model to ONNX format from skl2onnx.common.data_types import FloatTensorType from skl2onnx import convert_sklearn import onnxruntime as ort import onnx
Dann werden wir unsere Eingaben normalisieren und skalieren.
for i in predictors:
merged_df.loc[:,i] = (merged_df.loc[:,i] - merged_df.loc[:,i].mean()) / merged_df.loc[:,i].std() Trainieren wir nun das Modell mit dem gesamten Datensatz.
#Prepare the model model = SGDRegressor() model.fit(merged_df.loc[:,predictors],merged_df.loc[:,"Target SP500"])
Wir werden nun die Eingabeform und -typen definieren.
#Define the input types initial_type_float = [("float_input",FloatTensorType([1,len(predictors)]))] onnx_model_float = convert_sklearn(model,initial_types=initial_type_float,target_opset=12)
Speichern wir das ONNX-Modell
#ONNX file name onnx_file_name = "SP500_ONNX_FLOAT_M1.onnx" #ONNX file onnx.save_model(onnx_model_float,onnx_file_name)
und untersuchen nun schnell die Form der Ein- und Ausgänge unseres ONNX-Modells.
# load the ONNX model and inspect input and ouput shapes onnx_session = ort.InferenceSession(onnx_file_name) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name
Stellen wir sicher, dass unsere Modelleingabeform 1 x 8 ist.
#Display information about input tensors in ONNX print("Information about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
1. Name: float_input, Data Type: tensor(float), Shape: [1, 8]
Schließlich sollte unsere Ausgabeform 1 mal 1 sein.
#Display information about output tensors in ONNX print("Information about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
1. Name: variable, Data Type: tensor(float), Shape: [1, 1]
Wir können unser ONNX-Modell auch mit Netron visualisieren.
#Visualize the model
import netron
Die Startfunktion in netron ermöglicht es uns, unser ONNX-Modell zu visualisieren.
#Call netron
netron.start(onnx_file_name)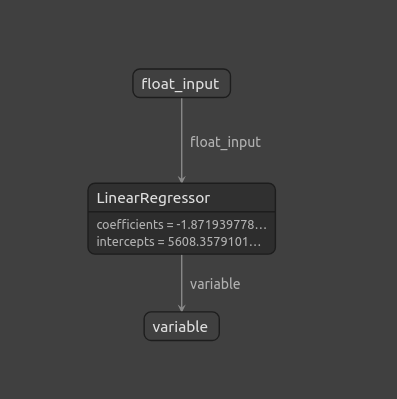 
Abb. 11: Visualisierung unseres ONNX-Modells mit Netron
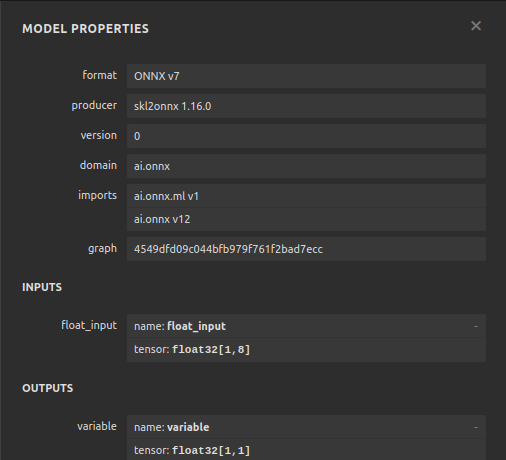
Abb. 12: Eigenschaften unseres ONNX-Modells
Implementation in MQL5
Nachdem wir die Erstellung unseres ONNX-Modells abgeschlossen und es exportiert haben, können wir nun mit der Erstellung unseres Expert Advisors beginnen. Als erstes laden wir in unserem Expert Advisor das ONNX-Modell, das wir gerade exportiert haben.
//+------------------------------------------------------------------+ //| SP500 X Treasury Yields.mq5 | //| Gamuchirai Zororo Ndawana | //| https://www.mql5.com/en/gamuchiraindawa | //+------------------------------------------------------------------+ #property copyright "Gamuchirai Zororo Ndawana" #property link "https://www.mql5.com/en/gamuchiraindawa" #property version "1.00" #property tester_file "sp500_treasury_yields_scale.csv" //+------------------------------------------------------------------+ //| Require the ONNX model | //+------------------------------------------------------------------+ #resource "\\Files\\SP500_ONNX_FLOAT_M1.onnx" as const uchar ModelBuffer[];
Von dort aus werden wir auch die Handelsbibliothek einbinden, die uns beim Öffnen, Schließen und Ändern unserer Positionen hilft.
//+------------------------------------------------------------------+ //| Libraries we need | //+------------------------------------------------------------------+ #include <Trade/Trade.mqh> CTrade Trade;
Es müssen auch einige Eingaben des Endnutzers berücksichtigt werden, z. B. wie groß sollte ein Lot-Multiple sein und wie groß sollte der Stop-Loss sein, wenn das erledigt ist?
//+------------------------------------------------------------------+ //| Inputs for our EA | //+------------------------------------------------------------------+ input int lot_multiple = 1; //How many times bigger than minimum lot? input double sl_width = 1; //How wide should our stop loss be?
Wir benötigen globale Variablen, die im gesamten Expert Advisor verwendet werden. Wir benötigen eine globale Variable, um das ONNX-Modell darzustellen, und einen weiteren Vektor, um die Vorhersagen unseres Modells zu speichern.
//+------------------------------------------------------------------+ //| Global variables | //+------------------------------------------------------------------+ long model; //Our ONNX SGDRegressor model vectorf prediction(1); //Our model's prediction float mean_values[8],variance_values[8]; //We need this data to normalise and scale model inputs double trading_volume; //How big should our positions be? int state = 0;
Weiter geht es mit der Funktion, die für das Lesen der zuvor definierten CSV-Konfigurationsdatei verantwortlich ist. Denken Sie daran, dass diese Datei von Bedeutung ist, weil sie die Mittelwerte und die Standardabweichung jeder Spalte enthält. Diese Funktion stellt sicher, dass alle Eingaben, die wir in unser ONNX-Modell eingeben, normalisiert sind. Die Funktion versucht zunächst, die Datei mit dem Befehl FileOpen zu öffnen. Wenn es uns gelungen ist, die Datei zu öffnen, analysieren wir unsere CSV-Datei und speichern die Mittelwerte und die Varianzwerte in ihren eigenen separaten Arrays. Andernfalls, wenn wir nicht erfolgreich sind, dann wird die Funktion ausgeben, dass sie die Datei nicht lesen konnte, und sie wird false zurückgeben, und die Initialisierungsprozedur wird fehlschlagen.
//+------------------------------------------------------------------+ //| A function responsible for reading the CSV config file | //+------------------------------------------------------------------+ bool read_configuration_file(void) { //--- Read the config file Print("Reading in the config file"); //--- Config file name string file_name = "sp500_treasury_yields_scale.csv"; //--- Try open the file int result = FileOpen(file_name,FILE_READ|FILE_CSV|FILE_ANSI,","); //--- Check the result if(result != INVALID_HANDLE) { Print("Opened the file"); //--- Prepare to read the file int counter = 0; string value = ""; //--- Make sure we can proceed while(!FileIsEnding(result) && !IsStopped()) { if(counter > 60) break; //--- Read in the file value = FileReadString(result); Print("Reading: ",value); //--- Have we reached the end of the line? if(FileIsLineEnding(result)) Print("row++"); counter++; //--- The first few lines will contain the title of each columns, we will ingore that if((counter >= 11) && (counter <= 18)) { mean_values[counter - 11] = (float) value; } if((counter >= 20) && (counter <= 27)) { variance_values[counter - 20] = (float) value; } } //--- Close the file FileClose(result); Print("Mean values"); ArrayPrint(mean_values); Print("Variance values"); ArrayPrint(variance_values); return(true); } else if(result == INVALID_HANDLE) { Print("Failed to read the file"); return(false); } return(false); }
Wir brauchen auch eine Funktion, die für die Abfrage einer Prognose aus unserem Modell verantwortlich ist. Am Anfang steht ein Vektor, in dem die Eingabedaten gespeichert werden. Sobald wir alle benötigten Preise abgerufen haben, ziehen wir den Mittelwert für diese Spalte ab und dividieren ihn durch die Varianz für diese bestimmte Spalte. Sobald dies geschehen ist, können wir mit unserem Modell eine Vorhersage treffen.
//+------------------------------------------------------------------+ //| A function responsible for getting a forecast from our model | //+------------------------------------------------------------------+ void predict(void) { //--- Let's prepare our inputs vectorf input_data = vectorf::Zeros(8); //--- Select the symbol input_data[0] = ((iOpen("UST05Y_U4",PERIOD_M1,0) - mean_values[0]) / variance_values[0]); input_data[1] = ((iClose("UST05Y_U4",PERIOD_M1,0) - mean_values[1]) / variance_values[1]); input_data[2] = ((iHigh("UST05Y_U4",PERIOD_M1,0) - mean_values[2]) / variance_values[2]); input_data[3] = ((iLow("UST05Y_U4",PERIOD_M1,0) - mean_values[3]) / variance_values[3]);; input_data[4] = ((iOpen("US500",PERIOD_M1,0) - mean_values[4]) / variance_values[4]);; input_data[5] = ((iClose("US500",PERIOD_M1,0) - mean_values[5]) / variance_values[5]);; input_data[6] = ((iHigh("US500",PERIOD_M1,0) - mean_values[6]) / variance_values[6]); input_data[7] = ((iLow("US500",PERIOD_M1,0) - mean_values[7]) / variance_values[7]);; //--- Show the inputs Print("Inputs: ",input_data); //--- Obtain a prediction from our model OnnxRun(model,ONNX_DEFAULT,input_data,prediction); }
Nachdem unser Modell eine Vorhersage gemacht hat, müssen wir Maßnahmen ergreifen. In diesem speziellen Fall können wir uns also entscheiden, eine Position in der Richtung zu eröffnen, die unser Modell vorhergesagt hat. Oder wenn unser Modell vorhersagt, dass sich der Kurs gegen uns wenden wird, könnten wir beschließen, unsere offenen Positionen zu schließen.
//+------------------------------------------------------------------+ //| This function will decide if we should open or close our trades | | //+------------------------------------------------------------------+ void intepret_prediction(void) { if(PositionsTotal() == 0) { double ask = SymbolInfoDouble("US500",SYMBOL_ASK); double bid = SymbolInfoDouble("US500",SYMBOL_BID); double close = iClose("US500",PERIOD_M1,0); if(prediction[0] > close) { Trade.Buy(trading_volume,"US500",ask,(ask - sl_width),(ask + sl_width),"SP500 X Treasury Yields"); state = 1; } if(prediction[0] < iClose("US500",PERIOD_M1,0)) { Trade.Sell(trading_volume,"US500",bid,(bid + sl_width),(bid - sl_width),"SP500 X Treasury Yields"); state = 2; } } else if(PositionsTotal() > 0) { if((state == 1) && (prediction[0] > iClose("US500",PERIOD_M1,0))) { Alert("Reversal predicted, consider closing your buy position"); } if((state == 2) && (prediction[0] < iClose("US500",PERIOD_M1,0))) { Alert("Reversal predicted, consider closing your buy position"); } } }
Wir haben die Definition der Hilfsfunktionen für unser Modell abgeschlossen und gehen nun dazu über, die Initialisierungsfunktion unseres Expert Advisors zu definieren. Zunächst müssen wir unser ONNX-Modell erstellen und dann sicherstellen, dass das Modell gültig ist.
//+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- Create the ONNX model from the model buffer we have model = OnnxCreateFromBuffer(ModelBuffer,ONNX_DEFAULT); //--- Ensure the model is valid if(model == INVALID_HANDLE) { Comment("[ERROR] Failed to initialize the model: ",GetLastError()); return(INIT_FAILED); }
Sobald wir sicher sind, dass das Modell gültig ist, definieren wir die Eingabeformen unseres Modells und dann die Ausgabeformen unseres Modells.
//--- Define the model parameters, input and output shapes ulong input_shape[] = {1,8}; //--- Check if we were defined the right input shape if(!OnnxSetInputShape(model,0,input_shape)) { Comment("[ERROR] Incorrect input shape specified: ",GetLastError(),"\nThe model's inputs are: ",OnnxGetInputCount(model)); return(INIT_FAILED); } ulong output_shape[] = {1,1}; //--- Check if we were defined the right output shape if(!OnnxSetOutputShape(model,0,output_shape)) { Comment("[ERROR] Incorrect output shape specified: ",GetLastError(),"\nThe model's outputs are: ",OnnxGetOutputCount(model)); return(INIT_FAILED); }
Wenn das alles erledigt ist, können wir die Konfigurationsdatei einlesen. Dies muss bei der Initialisierung geschehen, und wenn wir die Konfigurationsdatei nicht einlesen können, sollte der gesamte Expert Advisor abbrechen, da wir keine Prognosen für Daten erstellen können, die nicht normalisiert sind.
//--- Read the configuration file if(!read_configuration_file()) { Comment("Failed to find the configuration file, ensure it is stored here: ",TerminalInfoString(TERMINAL_DATA_PATH)); return(INIT_FAILED); }
Nun müssen wir die Symbole auswählen und sie zur Marktbeobachtung hinzufügen.
//--- Select the symbols SymbolSelect("US500",true); SymbolSelect("UST05Y_U4",true);
Schließlich müssen wir noch einige Marktdaten abrufen.
//--- Calculate the lotsize trading_volume = SymbolInfoDouble(Symbol(),SYMBOL_VOLUME_MIN) * lot_multiple; //--- Return init succeeded return(INIT_SUCCEEDED); }Immer wenn unser Expert Advisor nicht in Gebrauch ist, müssen wir die uns zugewiesenen Ressourcen freigeben.
//+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- Free up the resources we used for our ONNX model OnnxRelease(model); //--- Remove the expert advisor ExpertRemove(); }
Schließlich werden wir in unserem OnTick-Ereignishandler mithilfe unseres ONNX-Modells Vorhersagen treffen und diese Vorhersagen dann in Aktionen umsetzen.
//+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- Get a prediction predict(); //--- Interpret the forecast intepret_prediction(); Comment("Model forecast",prediction[0]); }
Abb. 13: Unser Expertenratgeber in Aktion
Schlussfolgerung
In diesem Artikel haben wir die klassische SP500-Handelsstrategie, die sich auf die Rendite von Staatsanleihen stützt, erneut untersucht. Unsere Analyse hat gezeigt, dass die Beziehung nicht immer stabil ist, und darüber hinaus scheint es, dass Anleger besser dran sind, wenn sie die gewöhnlichen Marktdaten des SP500-Index selbst verwenden.
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/15531
Erstellen eines Handelsadministrator-Panels in MQL5 (Teil I): Aufbau einer Nachrichtenschnittstelle
Nachrichtenhandel leicht gemacht (Teil 3): Ausführen des Handels
Mustererkennung mit dynamischer Zeitnormierung in MQL5
Integration von MQL5 in Datenverarbeitungspakete (Teil 2): Maschinelles Lernen und prädiktive Analytik
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.