Discusión sobre el artículo "Herramientas econométricas para la previsión de la volatilidad: el modelo GARCH"
Muy buen trabajo.
Lo leí en un santiamén.
Gracias.
Buen artículo. Sería interesante conocer su opinión sobre el artículo de Stepanov, en el que plantea una hipótesis sobre la naturaleza no estocástica de las fluctuaciones de la volatilidad.
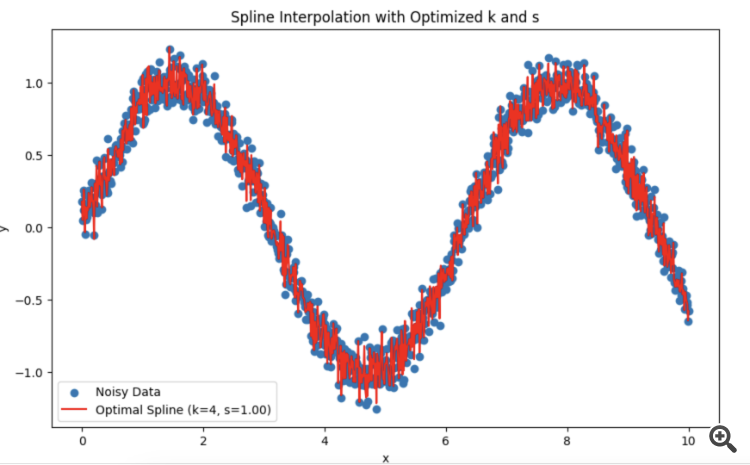
Me has dado de lleno en mi TS. Estoy probando con splines en lugar de HP.
Me preguntaba qué es mejor para elegir el período y el grado de suavizado.
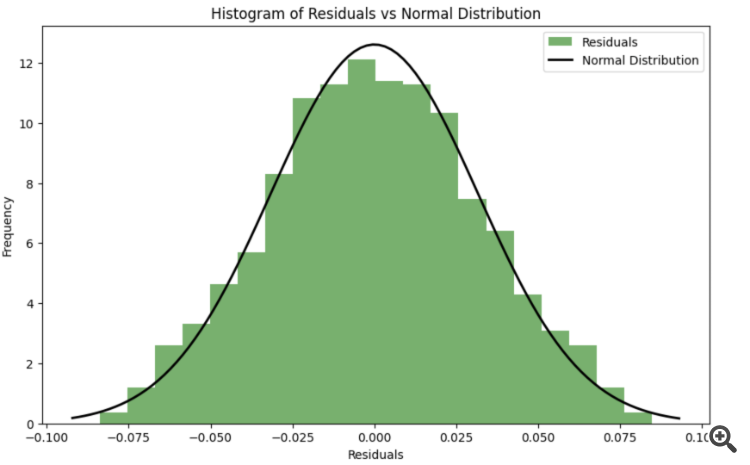
Resulta que es mejor confiar en la prueba de distribución normal de los residuos?
Me has dado justo en el TC. En lugar de HP, estoy tratando de splines.
Me preguntaba qué es mejor elegir el período y el grado de suavizado.
Resulta que es mejor confiar en la prueba de distribución normal de los residuos?
Buen artículo. Sería interesante conocer su opinión sobre el artículo de Stepanov, en el que plantea una hipótesis sobre la naturaleza no estocástica de las fluctuaciones de la volatilidad.
El artículo es complejo y contradictorio. Por un lado, el autor utiliza terminología probabilística, herramientas estadísticas, caracteriza el incremento de los precios y la volatilidad como variables aleatorias, construye distribuciones de diferentes medidas de volatilidad, etc., por otro lado, no le gustan los modelos estocásticos de volatilidad.
En mi opinión, sí, si se construyen modelos para incrementos en intervalos de tiempo constantes, al final hay que reducirlo todo a ruido gaussiano. Ese es probablemente el objetivo de la econometría: todos los factores que no se tienen en cuenta en el modelo deberían comportarse como ruido suave.
Interesante, aún no lo he hecho. En el artículo, el autor seleccionaba empíricamente los parámetros. Pero es posible optimizarlos mediante la función de verosimilitud.
Tema de investigación :)
Interesante, aún no lo he hecho. En el artículo, el autor seleccionó empíricamente los parámetros. Pero es posible hacer la optimización a través de la función de verosimilitud.
Tema de investigación :)
Hice LLM DeepSeek con la ayuda de Dios. Usted puede sustituir sus propios datos.
Explicación:
Para que los residuos se aproximen lo más posible a una distribución normal durante el proceso de optimización, se puede utilizar un criterio de concordancia (por ejemplo, el criterio de Shapiro-Wilk o el criterio de Kolmogorov-Smirnov) para evaluar la normalidad de los residuos. Los parámetros k k y s spueden optimizarse para minimizar la desviación de los residuos respecto a la distribución normal.
-
Función de error que tiene en cuenta la normalidad de los residuos: Se introduce una nueva función spline_error_with_normality , que calcula los residuos y utiliza el criterio de Shapiro-Wilk para evaluar su normalidad. El valor p negativo se minimiza para maximizar la normalidad de los residuos.
-
Optimización: Se utiliza para optimizar los parámetros k k y s s basándose en una nueva función de error.
Este enfoque permite ajustar los parámetros del spline para que los residuos maximicen la distribución normal, lo que puede mejorar la calidad del modelo y la interpretabilidad de los resultados.
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
Artículo publicado Herramientas econométricas para la previsión de la volatilidad: el modelo GARCH:
El presente artículo describe las propiedades de un modelo de heteroscedasticidad condicional no lineal (GARCH). Sobre esta base se construye el indicador iGARCH para predecir la volatilidad un paso por delante. Para estimar los parámetros del modelo se usará la biblioteca de análisis numérico ALGLIB.
La volatilidad supone una medida importante a la hora de evaluar la volatilidad de los precios de los activos financieros. Al analizar las cotizaciones, se ha observado desde hace tiempo que las grandes variaciones de precios suelen conllevar cambios aún mayores, sobre todo en tiempos de crisis financiera. A su vez, los pequeños cambios suelen ir seguidos de pequeñas variaciones de precio. Así, a periodos tranquilos de volatilidad siguen otros de relativa inestabilidad.
El primer modelo que intentó explicar este fenómeno fue el modelo ARCH, desarrollado por Engle, la Heteroscedasticidad condicional autorregresiva (heterogeneidad). Además del efecto de agrupamiento (agrupación de los rendimientos en conjuntos de valores grandes y pequeños), este modelo también explicaba la aparición de colas pesadas y curtosis positiva, característica de todas las distribuciones de incrementos de precio. El éxito del modelo gaussiano condicional ARCH ha dado lugar a la aparición de una serie de generalizaciones del modelo ARCH para explicar otros fenómenos observados en el análisis de series temporales financieras. Históricamente, una de las primeras generalizaciones del modelo ARCH es el modelo GARCH, (Generalized ARCH).
La principal ventaja de GARCH en comparación con ARCH es que es más parsimonioso y no requiere una estructura long-lag al ajustar los datos de muestra. En este artículo, queremos ofrecer una descripción de lo que es un GARCH y, lo que es más importante, ofrecer una herramienta de previsión de la volatilidad basada en él, ya que la previsión es uno de los principales objetivos del análisis de datos financieros.
Autor: Evgeniy Chernish