
Matemáticas de trading. Cómo evaluar los resultados de las transacciones comerciales
Nassim N. Taleb
Introducción: Las matemáticas son las reinas de la ciencia
Cualquier trader necesita cierto nivel de base de matemáticas, y esto no necesita prueba alguna. El tema es: ¿Cómo se puede definir el nivel mínimo requerido? Para ampliar su experiencia en trading, los traders a menudo amplían sus perspectivas leyendo sólo publicaciones en foros o algunos libros. Algunos libros requieren un nivel de matemáticas más bajo, sin embargo, otros inspiran al estudio o actualización de los conocimientos en un campo u otro de las ciencias puras. Intentaremos dar algunas previsiones y sus interpretaciones en este artículo.
De lo malo, elije lo menos malo
Hay más matemáticos que traders exitosos en el mundo. Esto es un argumento utilizado a menudo por los que se oponen a cálculos o métodos complicados en trading. Para rebatirlo, decimos que el trading no es sólo la capacidad de desarrollar reglas de trading (habilidades de análisis), sino también la capacidad de observar esas reglas (disciplina). Además, todavía no se ha creado una teoría que describa exactamente la fijación de los precios en el mercado financiero (y creo que nunca se creará). La creación una teoría (de naturaleza matemática) de los propios mercados financieros, significaría la muerte de los mismos, que es una paradoja indeseable filosóficamente hablando. Sin embargo, si hacemos frente a la pregunta de si accedemos al mercado con una descripción matemática poco satisfactoria o sin descripción alguna, elegimos lo menos malo.: elegimos métodos de estimación de sistemas de trading.
¿Qué es la anormalidad de la distribución normal?
Una de las nociones básicas en la teoría de la probabilidad es la de distribución normal (Gauss). ¿Por qué se llama así? Muchos procesos naturales resultaron ser distribuidos normalmente. Para ser más exactos, los procesos más naturales, al final, reducen la distribución normal. Vamos a considerar un ejemplo simple. Imagine que tenemos una distribución uniforme en el intervalo de 0 a 100. La distribución uniforme significa que la probabilidad de caída de cualquier valor en el intervalo y la probabilidad de que 3. 14 (Pi) caiga es la misma que la de caer de 77 (mi número favorito, con dos sietes). Los ordenadores modernos ayudan a generar una secuencia bastante buena de números pseudoaleatorios.
¿Cómo se puede obtener la distribución normal de esta distribución uniforme? Resulta que si, si cogemos siempre varios números aleatorios (por ejemplo, 5 números) de una distribución única, encontramos el valor principal de esos números (lo que se conoce como "coger una muestra"), y la cantidad de esas muestras es muy buena, la distribución recién obtenida tenderá a ser normal. El teorema límite centras dice que esto está relacionado no sólo con las muestras cogidas de la distribución única, sino también con una gran variedad de otras distribuciones. Como las propiedades de la distribución normal se han estudiado bastante bien, será muvho más fácil analizar el proceso si se representan como procesos con distribución normal. Pero como ver es creer, podemos ver la confirmación de este teorema límite central utilizando un indicador MQL4 simple.
Vamos a lanzar el indicador en cualquier gráfico con diferentes valores N (cantidad de muestras) y vamos a ver que la frecuencia empírica de distribución se vuelve cada vez más suave.
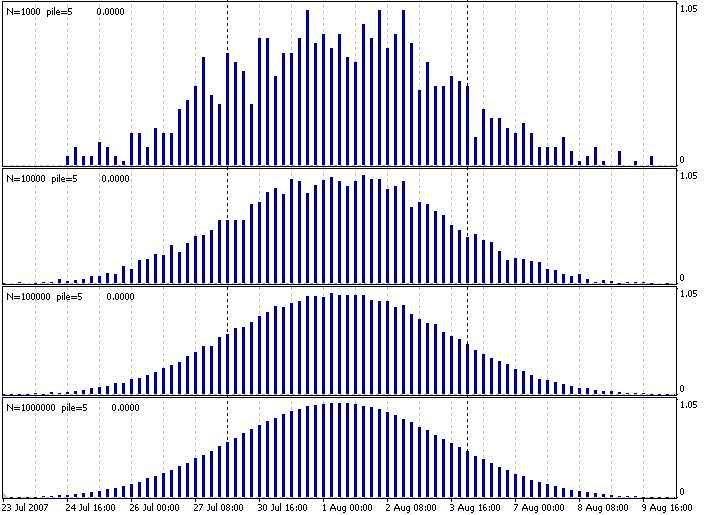
Fig. 1. El indicador crea una distribución normal de una uniforme.
En este caso, N es para las veces que se coge la cantidad promedia de montones=5 de números distribuidos de forma uniforme en el intervalo de 0 a 100. Se obtienen cuatro gráficos con apariencias muy similares. Si se normalizan de alguna manera al final (adjuntos a una escala simple), se obtendrán varias realizaciones de la distribución normal estándar. El único "pero" aquí es que fijar los precios en los mercados financieros (para ser más exactos, el incremento de precios y otras cosas derivadas de esos incrementos), en general, no encajan en la distribución normal. La probabilidad de un evento más bien raro (por ejemplo, una bajada de precios del 50%) en el mercado financiero, aunque es baja, sigue siendo considerablemente más alta que en la distribución normal. Es por eso por lo que hay que recordarlo cuando se estiman los riesgos en las bases de la distribución normal.
La cantidad se transforma en calidad
Incluso este simple ejemplo de modejale de distribución normal muestra que la cantidad de datos a procesar cuenta mucho. Cuanto más datos iniciales haya, más preciso y válido será el resultado. Se considera que el número más pequeño de la muestra debe ser superior a 30. Esto quiere decir que, si se quieren estimar los resultados de los trades (por ejemplo, un Asesor experto en el Tester), una cantidad de trades por debajo de 30 es insuficiente para sacar conclusiones estadísticamente fiables sobre algún parámetro del sistema. Cuantos más trades se analicen, menos probabilidad habrá de que esos trades sólo sean elementos arrebatados de un sistema de trading poco fiable. Por lo tanto, el beneficio final en una serie de 150 trades, permite más terreno para poner el sistema en servicio que un sistema estimado sólo en 15 trades.
Esperanza matemática y dispersión como riesgo estimado
Las dos características más importantes de una distribución son la esperanza matemática (promedia) y la dispersión. La distribución normal estándar tiene una esperanza matemática igual a cero. En ese punto, el centro de distribución se coloca también en cero. La llanura o la inclinación de la distribución normal se caracteriza por la medida de extensión de un valor aleatorio dentro del área de esperanza matemática. Es la dispersión lo que muestra cómo se extienden los valores sobre la expecativa matemática del valor aleatorio.
La esperanza matemática se puede encontrar de forma muy simple: Para los grupos contables, se pueden sumar todos los valores de distribución; la cantidad obtenida se divide por la cantidad de valores. Por ejemplo, un grupo de números naturales es infinito, pero contable, ya que cada valor se puede cotejar con su índice (número de orden). Para los grupos incontables, se aplicará la integración. Para estimar la esperanza matemática de una serie de trades, se sumarán todos los resultados del trade y se dividirá el resultado por la cantidad de trades. El valor obtenido mostrará el resultado promedio esperado de cada trade. Si la esperanza matemática es positiva, se obtendrán beneficios promedios. Si es negativa, se producirán pérdidas promedias.
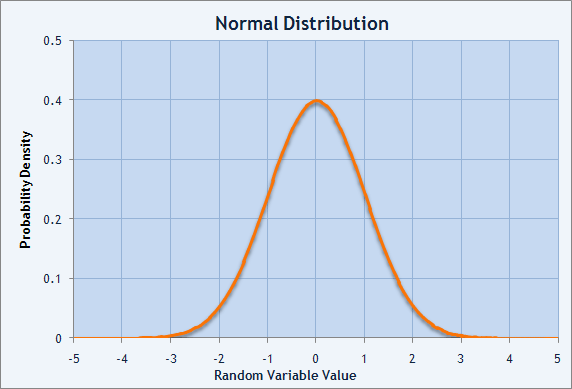
Img. 2. Gráfico de la densidad de probabilidad de la distribución normal.
La medida de la expansión de la distribución es la suma de la desviación elevada al cuadrado del valor aleatorio desde su esperanza matemática. Esta característica de la distribución es conocida como dispersión. Normalmente, a la esperanza matemática de un valor distribuido aleatoriamente se la conoce como M(X). Luego, la dispersión puede describirse como D(X) = M((X-M(X))^^2). La raíz cuadrada de la dispersión es conocida como desviación estándar. También se define como sigma (σ). Es una distribución normal (o distribución de Gauss) cuando se tiene una esperanza matemática igual a cero y una desviación estándar igual 1.
Cuanto más alto sea el valor de la desviación estándar, más variable será el capital de trading, y más alto será el riesgo. Si la esperanza matemática es positiva (una estrategia rentable), y es igual a 100 dólares; y si la desviación estándar es igual a 500 dólares, se arriesga un total varias veces más grande de ganar cada dólar. Por ejemplo, se tienen los resultados de 30 trades:
|
|
|---|
Para obtener la esperanza matemática de esta secuencia de trades, se suman todos los resultados y se dividen entre 30. Se obtendrá el valor principal M(X), igual a 4,26 dólares. Para obtener la desviación estándar, se resta el promedio del resultado de cada trade, se eleva al cuadrado, y se suman los resultados de cada promedio elevado al cuadrado. El resultado se divide entre 29 (la cantidad de trades menos uno). Se obtendrá una dispersión D igual a 9 353,623. Una vez generada la raíz cuadrada de la dispersión, se obtiene la desviación estándar, sigma, igual a 96,71 dólares.
Los datos comprobados están en la siguiente tabla:
| Número de trade | X (Resultado) | X-M(X) (Diferencia) | (X-M(X))^2 (Cuadrado de diferencia) |
|---|---|---|---|
| 1 | -17,08 | -21,34 | 455,3956 |
| 2 | -41,00 | -45,26 | 2 048,4676 |
| 3 | 147,80 | 143,54 | 20 603,7316 |
| 4 | -159,96 | -164,22 | 26 968,2084 |
| 5 | 216,97 | 212,71 | 45 245,5441 |
| 6 | 98,30 | 94,04 | 8 843,5216 |
| 7 | -87,74 | -92,00 | 8 464,00 |
| 8 | -27,84 | -32,10 | 1 030,41 |
| 9 | 12,34 | 8,08 | 65,2864 |
| 10 | 48,14 | 43,88 | 1 925,4544 |
| 11 | -60,91 | -65,17 | 4 247,1289 |
| 12 | 10,63 | 6,37 | 40,5769 |
| 13 | -125,42 | -129,68 | 16 816,9024 |
| 14 | -27,81 | -32,07 | 1 028,4849 |
| 15 | 88,03 | 83,77 | 7 017,4129 |
| 16 | 32,93 | 28,67 | 821,9689 |
| 17 | 54,82 | 50,56 | 2 556,3136 |
| 18 | -160,10 | -164,36 | 27 014,2096 |
| 19 | -83,37 | -87,63 | 7 679,0169 |
| 20 | 118,40 | 114,14 | 13 027,9396 |
| 21 | 145,65 | 141,39 | 19 991,1321 |
| 22 | 48,44 | 44,18 | 1 951,8724 |
| 23 | 77,39 | 73,13 | 5 347,9969 |
| 24 | 57,48 | 53,22 | 2 832,3684 |
| 25 | 67,75 | 63,49 | 4 030,9801 |
| 26 | -127,10 | -131,36 | 17 255,4496 |
| 27 | -70,18 | -74,44 | 5 541,3136 |
| 28 | -127,61 | -131,87 | 17 389,6969 |
| 29 | 31,31 | 27,05 | 731,7025 |
| 30 | -12,55 | -16,81 | 282,5761 |
Lo que se ha obtenido es la esperanza matemática igual a 4,26 dólares y la desviación estándar de 96,71 dólares. No es la mejor proporción entre el riesgo y el trade promedio. El siguiente gráfico de beneficios lo confirma:
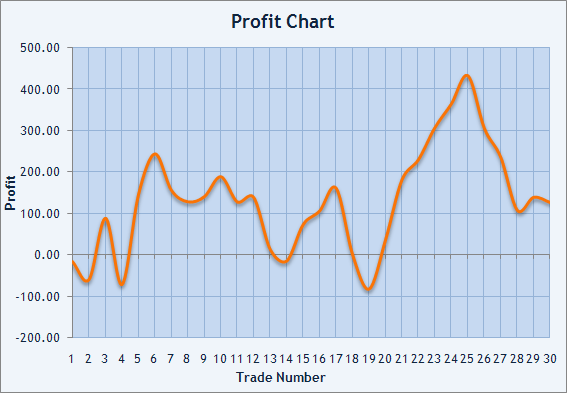
Img.3. Gráfico de balance de los trades realizados.
¿Hago trading de forma aleatoria? Puntuación-Z
La propia suposición de que el beneficio obtenido como resutado de una serie de trades es aleatorio, suena sarcástica para la mayoría de los trades. Después de pasar mucho tiempo buscando un sistema de trading eficaz y de observar que el sistema encontrado ya ha resultado en beneficios reales en un periodo de tiempo más bien limitado, el trader supone que ha encontrado un método apropiado para el mercado. ¿Cómo puede asumir que todo esto fha sido simplemente algo aleatorio? Es muy denso, incluso para los más inexpertos. Sin embargo, es esencial estimar los resultados de forma objetiva. En este caso, la distribución normal viene al rescate, una vez más.
No se sabe cuál será el resultado de cada trade. Sólo se puede decir que o se obtienen beneficios (+), o pérdidas (-). Los beneficios y las pérdidas se alternan de diferentes formas según los sistemas de trading. Por ejemplo, si se espera un beneficio 5 veces menor que la pérdida que se espera al lanzar Stop Loss, sería razonable presumir de que los trades rentables (trades +) predominarán bastante sobre los trades con pérdidas (trades -) La Puntuación-Z permite estimar con qué frecuencia se van a alternar los trades rentables con los no rentables.
En un sistema de trading, Z se calcula con la siguiente fórmula:
en la que: |
Una serie es una secuencia de positivos uno detrás de otro (por ejemplo, +++) o de negativos uno detrás de otro (por ejemplo, --). R cuenta la cantidad de estas series.

Img. 4. Comparación de dos series de beneficios y pérdidas.
En la Img. 4, se muestra en azul una parte de la secuencia de beneficios y pérdidas del Asesor experto que se alzó con el cuarto puesto en el Campeonato de trading automático de 2006. La Puntuación-Z de la cuenta de competición tiene el valor de -3,85, en los paréntesis se muestra la probabilidad de 99,74%. Esto quiere decir que, con una probabilidad del 99,74%, los trades de esta cuenta tuvieron una dependencia positiva entre ellos (la Puntuación-Z es negativa): había un beneficio seguido de otro beneficio, una pérdida seguida de una pérdida. ¿Es este e caso? Aquellos que estuvieron viendo el Campeonato, seguramente recordarán que Roman Rich colocó su versión MACD del Asesor experto que había abierto frecuentemente tres trades en la misma dirección.
En rojo se muestra una secuencia típica de valores positivos y negativos del valor aleatorio en una distribución normal. Se puede ver que son secuencias diferentes. Sin embargo, ¿cómo puede medirse la diferencia? La Puntuación-Z da la respuesta: ¿Su secuencia de beneficios y pérdidas contiene más o menos franjas (series rentables o no rentables) de las que puede esperar para una secuencia realmente aleatoria sin ninguna dependencia entre trades? Si la Puntuación-Z está cercana a cero, no se puede decir que la distribución de los trades sea diferente de la distribución normal. La Puntuación-Z de una secuencia trading puede informar sobre la posible dependencia entre trades consecutivos.
En ese momento, los valor de Z se interpretan de la misma manera que la probabilidad de desviación de cero a un valor aleatorio distribuido según el estándar de distribución normal (promedio=0, sigma=1). Si la probabilidad de caída de un valor aleatorio distribuido de manera normal en el rango de ±3σ es 99,74%, la caída de este valor fuera de este intervalo con la misma probabilidad, informa que este valor aleatorio no pertenece a esta distribución normal. Por esto, "la regla 3-sigma" se lee de la siguiente manera: un valor aleatorio normal se desvía de su promedio no más de una distancia 3-sigma.
El signo de Z informa sobre el tipo de dependencia. Positivo quiere decir que es más probable que el trade rentable esté seguido de uno no rentable. Negativo dice que el beneficio irá seguido de un beneficio, una pérdida irá seguida de nuevo por una pérdida. La siguiente tabla ilustra el tipo y la probabilidad de dependencia entre los trades al compararlos con la distribución normal.
| Puntuación-Z | Probabilidad de dependencia % | Tipo de dependencia % |
|---|---|---|
| -3 | 99,73 | Positiva |
| -2,9 | 99,63 | Positiva |
| -2,8 | 99,49 | Positiva |
| -2,7 | 99,31 | Positiva |
| -2,6 | 99,07 | Positiva |
| -2,5 | 98,76 | Positiva |
| -2 | 95,45 | Positiva |
| -1,5 | 86,64 | Indeterminada |
| -1,0 | 68,27 | Indeterminada |
| 0,0 | 0,00 | Indeterminada |
| 1,0 | 68,27 | Indeterminada |
| 1,5 | 86,64 | Indeterminada |
| 2,0 | 95,45 | Negativa |
| 2,5 | 98,76 | Negativa |
| 2,6 | 99,07 | Negativa |
| 2,7 | 99,31 | Negativa |
| 2,8 | 99,49 | Negativa |
| 2,9 | 99,63 | Negativa |
| 3,0 | 99,73 | Negativa |
Una dependencia positiva entre trades, quiere decir que un beneficio producirá otro beneficio, mientras que una pérdida causará una nueva pérdida. Una dependencia negativa quiere decir que un beneficio irá seguido de una pérdida, mientras que la pérdida irá seguida de un beneficio. La dependencia que se encuentre permite regular los tamaños de las posiciones que han de ser abiertas (idealmente) o incuso saltar algunas de ellas y abrirlas sólo de forma virtual para ver las secuencias de trade.
Rentabilidad del Periodo de tenencia (RPT)
En su libro Las matemáticas de la gestión monetaria, Ralph Vince utiliza el término RPT (Rentabilidad del Periodo de tenencia). Un trade que resulte en un beneficio del 10%, tiene la RPT=1+0. 10=1,10. Un trade que resulte en una pérdida del 10%, tiene la RPT=1-0. 10=0,90. También se puede obtener el valor de la RPT de un trade dividiendo el valor de balance después de haber cerrado el trade (BalanceClose) entre el valor de balance en la apertura del detrade (BalanceOpen). RPT=BalanceCose/BalanceOpen. Sin embargo, cada trade tiene tanto resultados en términos monetarios como resultados en RPT. Esto permite que se comparen los sistemas independientemente al tamaño de los contratos negociados. Uno de los índices utilizados en estas comparaciones, es el promedio aritmético, RPPT (rentabilidad promedia del periodo de tenencia).
Para averiguarlo, se suman todas las RPTs y se divide el resultado entre la cantidad de trades. Vamos a probar estos cálculos con el ejemplo anterior de 30 trades. Suponga que se empieza el trading con 500 dólares en la cuenta. Vamos a hacer una tabla nueva:
| Número de trade | Balance, en dólares | Resultado, en dólares | Balance en el cierre, en dólares | RPT |
|---|---|---|---|---|
| 1 | 500,00 | -17,08 | 482,92 | 0,9658 |
| 2 | 482,92 | -41,00 | 441,92 | 0,9151 |
| 3 | 441,92 | 147,8 | 589,72 | 1,3344 |
| 4 | 589,72 | -159,96 | 429,76 | 0,7288 |
| 5 | 429,76 | 216,97 | 646,73 | 1,5049 |
| 6 | 646,73 | 98,30 | 745,03 | 1,1520 |
| 7 | 745,03 | -87,74 | 657,29 | 0,8822 |
| 8 | 657,29 | -27,84 | 629,45 | 0,9576 |
| 9 | 629,45 | 12,34 | 641,79 | 1,0196 |
| 10 | 641,79 | 48,14 | 689,93 | 1,0750 |
| 11 | 689,93 | -60,91 | 629,02 | 0,9117 |
| 12 | 629,02 | 10,63 | 639,65 | 1,0169 |
| 13 | 639,65 | -125,42 | 514,23 | 0,8039 |
| 14 | 514,23 | -27,81 | 486,42 | 0,9459 |
| 15 | 486,42 | 88,03 | 574,45 | 1,1810 |
| 16 | 574,45 | 32,93 | 607,38 | 1,0573 |
| 17 | 607,38 | 54,82 | 662,20 | 1,0903 |
| 18 | 662,20 | -160,10 | 502,10 | 0,7582 |
| 19 | 502,10 | -83,37 | 418,73 | 0,8340 |
| 20 | 418,73 | 118,4 | 537,13 | 1,2828 |
| 21 | 537,13 | 145,65 | 682,78 | 1,2712 |
| 22 | 682,78 | 48,44 | 731,22 | 1,0709 |
| 23 | 731,22 | 77,39 | 808,61 | 1,1058 |
| 24 | 808,61 | 57,48 | 866,09 | 1,0711 |
| 25 | 866,09 | 67,75 | 933,84 | 1,0782 |
| 26 | 933,84 | -127,10 | 806,74 | 0,8639 |
| 27 | 806,74 | -70,18 | 736,56 | 0,9130 |
| 28 | 736,56 | -127,61 | 608,95 | 0,8267 |
| 29 | 608,95 | 31,31 | 640,26 | 1,0514 |
| 30 | 640,26 | -12,55 | 627,71 | 0,9804 |
La RPPT se averiguará como el promedio aritmético. Es igual a 1,0217. En otras palabras, se gana un promedio de (1.0217-1)*100%=2.17% en cada trade. ¿Es este e caso? Si se multiplica 2,1 entre 30, se verá que el resultado debería llegar al 65,1%. Vamos a multiplicar la cantidad inicial de 500 dólares por 65,1% y se obtendrá 325,50 dólares. Al mismo tiempo, el beneficio real es de (627.71-500)/500*100%=25.54%. Sin embargo, el promedio aritmético de la RPT no siempre permite estimar un sistema correctamente.
Junto con el promedio aritmético, Ralph Vince introduce el término de promedio geométrico, al que llamaremos RPTG (rentabilidad del periodo de tenencia geométrico), que es casi siempre menor que la RPPT. El promedio geométrico es el factor de crecimiento por juego y se consigue con la siguiente fórmula:
en la que: |
El sistema que tenga la mayor RPTG hará los mejores beneficios si se hace trade en bases de reinversión. La RPTG baja quiere decir que el sistema perderá dinero si se hace trade en bases de reinversión. En el historial de la cuenta de sashken se puede encontrar una buena ilustración de la diferencia entre la RPPT y la RPTG. Fue el lider del campeonato durante mucho tiempo. La RPPT=9,98% impresiona, pero la RPTG final=27,68% lo pone todo en perspectiva.
Índice de Sharpe
La eficiencia de inversiones se estima a menudo en términos de dispersión de beneficios. Uno de estos índices es el Índice de Sharpe. Este índice muestra cómo la disminución de la RPPT por la tasa sin riesgo (TsR) está relacionada a la desviación estándar (DE) de la secuencia RPT. El valor de la TsR suele ser igual que la tasa de interés en el depósito del banco o la tasa de interés en las obligaciones del tesoro. En este ejemplo, RPPT=1,0217, DE(RPT)=0,17607, TsR=0
en la que: |
Índice de Sharpe=(1,0217-(1+0))/0,17607=0,0217/0,17607=0,1232. Para la distribución normal, más del 99% de los valores aleatorios están en el rango de ±3σ (sigma=ED) sobre el valor principal M(X). Resulta que el valor del Índice de Sharpe superior a 3 es muy bueno. En la Img. 5 a continuación, se puede ver que, si el resultado de los trades se distribuyen normalmente y el Índice de Sharpe=3, la probabilidad de perder está por debajo del 1% por trade, según la regla sigma-3.
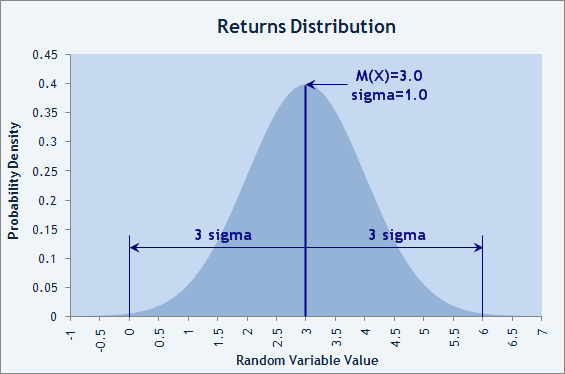
Img. 5. La distribución normal del trade resulta con una probabilidad de pérdida menor al 1%.
La cuenta del participante RobinHood lo confirma: si AE hizo 26 trades sin pérdidas en el Campeonato de Trading Automático de 2006. Índice de Sharpe=3,07.
Regresión lineal (RL) y Coeficiente de correlación lineal (CCL)
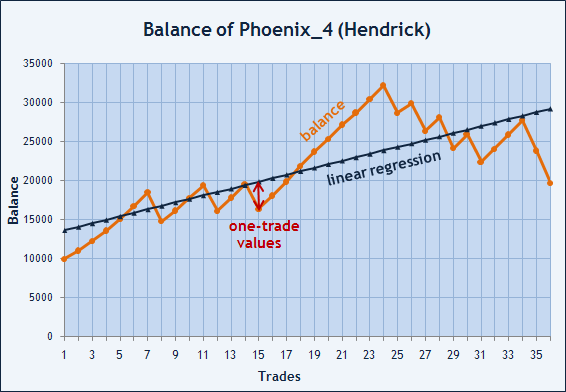
También hay otra manera de estimar la estabilidad de los resultados de trade. El Índice de Sharpe permite estimar el riesgo que corre el capital, pero se puede intentar estimar también la curva de balance de grado suave. Si se imponen los valores del balance al cierre de cada trade, podremos dibujar una línea discontinua. Estos puntos se puede fijar con una línea recta que mostrará la dirección principal de los cambios del capital. Consideremos un ejemplo de esta oportunidad utilizando el gráfico de balance del Asesor experto Phoenix_4 desarrollado por Hendrick.
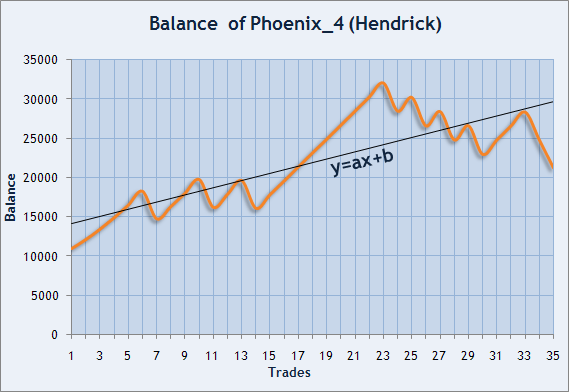
Img. 6. El balance del gráfico de Hendric, el participante del Campeonato de Trading Automático de 2006.
Hay que encontrar los coeficientes a y b lo más cercanos posibles a los puntos que se han establecido. En este caso, x es el número de trade, y es el valor de balance al cerrar el trade.
|
|
|---|
Normalmente los coeficientes de una línea recta aproximada se encuentran por el método menos justo (método MJ). Suponga que tiene la línea recta con los coeficientes conocidos a y b. Para cada x, hay dos valores: y(x)=a*x+b y balance(x). La desviación del balance(x) de y(x) será d(x)=y(x)-balance(x). SDC (suma de desviaciones al cuadrado) se puede calcuar como DE=suma{d(n)^2}. Encontrar la línea recta con el método MJ quiere decir buscar un a y b que tengan una DE mínima. Esta línea también se conoce como regresión lineal (RL) para esta secuencia.
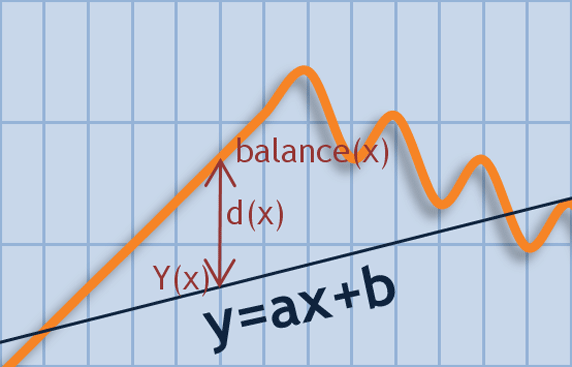
Img. 7. Desviación del valor de balance para la línea y=ax+b
Al haber obtenido los coeficientes de la línea de y=a*x+b utilizando el método MJ, se puede estimar la desviación del valor de balance del fondo de línea en términos monetarios. Si se calcula el promedio aritmético de la secuencia d(x), se asegurará que М(d(x)) está cerca de cero (para ser más exactos, es igual a cero en algunos grados de cálculo de precisión). Al mismo tiempo, la SDC de la DE no es igual a cero y tiene un valor algo limitado. La raíz cuadrada de DE(N-2) muestra los valores expandidos en el gráfico de balance sobre la línea recta y permite estimar los sistemas de trading con valores idénticos al estado inicial de la cuenta. A este parámetro se le conoce como Error estándar de RL.
A continuación se muestran los valores de estos parámetros para las primeras 15 cuentas en el Campeonato de Trading Automático de 2006:
| # | Iniciar sesión | Error estándar de RL, en dólares | Beneficio, en dólares |
|---|---|---|---|
| 1 | Rich | 6 582,66 | 25 175,60 |
| 2 | ldamiani | 5 796,32 | 15 628,40 |
| 3 | GODZILLA | 2 275,99 | 11 378,70 |
| 4 | valvk | 3 938,29 | 9 819,40 |
| 5 | Hendrick | 3 687,37 | 9 732,30 |
| 6 | bvpbvp | 9 208,08 | 8 236,00 |
| 7 | Flame | 2 532,58 | 7 676,20 |
| 8 | Berserk | 1 943,72 | 7 383,70 |
| 9 | vgc | 905,10 | 6 801,30 |
| 10 | RobinHood | 109,11 | 5 643,10 |
| 11 | alexgomel | 763,76 | 5 557,50 |
| 12 | LorDen | 1 229,40 | 5 247,90 |
| 13 | systrad5 | 6 239,33 | 5 141,10 |
| 14 | emil | 2 667,76 | 4 658,20 |
| 15 | payday | 1 686,10 | 4 588,90 |
Sin embargo, el grado de aproximación del gráfico de balance a una línea recta se puede medir tanto en términos monetarios como en términos absolutos. Para esto se puede utilizar una tasa de correación. La tasa de correlación, r, mide el grado de correlación entre dos secuencias de números. Su valor puede estar entre -1 y +1. Si r=+1, significa que hay dos secuencias que tienen un comportamiento idéntico y la correlación es positiva.
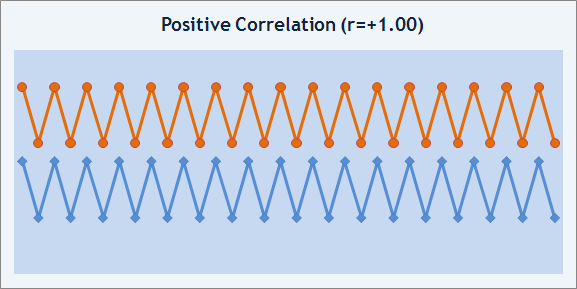
Img. 8. Ejemplo de correlación positiva.
Si r=-1, las dos sencuentas tienen posiciones diferentes, la correlación es negativa.
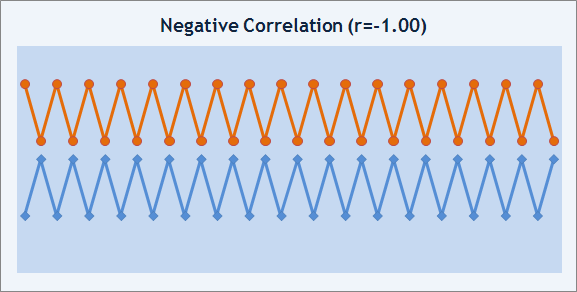
Img. 9. Ejemplo de correlación negativa.
Si r=0, quiere decir que no se ha encontrado dependencia entre las secuencias. Hay que enfatizar que r=0 no significa que no hay correlación entre las secuencias, simplemente quiere decir que no se ha encontrado la correlación. Esto hay que recordarlo. En este caso, hay que comparar dos secuencias de números: una del balance del esquema, y la segunda el punto correpondiente en la regresión lineal.
Img. 10. Valores de balance y puntos de regresiones lineales.
A continuación hay una tabla con la representación de estos datos:
|
|
Vamos a indicar los valores de balance como X y la secuencia de puntos en la línea recta de regresión como Y. Para calcular el coeficiente de la correlation lineal entre las secuencias X e Y, es necesario encontrar los valores principales M(X) y M(Y) primero. Luego se creará una nueva secuencia T=(X-M(X))*(Y-M(Y)) y se calcularán su valor principal M(T)=cov(X, Y)=M((X-M(X))*(Y-M(Y))). El valor que resulte de cov(X,Y) es la covarianza de X e Y y es la esperanza matemática del resultado (X-M(X))*(Y-M(Y)). Para este ejemplo, el valor de la covarianza es 21 253 775,08. Tenga en cuenta que M(X) y M(Y) son iguales y tienen un valor de 21 382,26 cada uno. Quiere decir que el valor principal del Balance y el promedio de la línea recta son iguales.
en la que: |
Lo único que que queda por hacer es el cálculo de Sx y Sy. Para calcular Sx, hay que obtener la suma de los valores de (X-M(X))^2, es decir, la SDC de X desde su valor principal. Recuerde cómo se calculó la dispersión y el algoritmo del método MJ. Como puede ver, está todo relacionado. La SDC obtenida se dividirá entre la cantidad de números en la secuencia, en este caso 36 (de cero a 35), y se hará la raíz cuadrada del valor resultante. Ya se ha obtenido el valor de Sx. El valor de Sy se calculará de la misma manera. En este ejemplo, Sx=5839. 098245 y Sy=4610. 181675.
en la que: |
Ahora se puede averiguar el valor de la correlación como r=21 253 775,08/(5839, 098245*4610 181675)=0,789536583. Es bajo, pero está lejos del cero. Por lo tanto, se puede decir que el gráfico de balance está correlacionado con la línea de tendencia con valor 0,79. En comparación con otros sistemas, se irá aprendiendo poco a poco cómo interpretar los valores del coeficiente de correlación. En la página "Informes" del Campeonato, este parámetro aparece como Correlación RL. La única diferencia al calcular este parámetro dentro del marco del Campeonato, es que la señal de la RL indica que el trade es rentable.
El tema es que se puede calcular el coeficiente de la correlación entre el gráfico de balance y cualquier línea recta. Para el Campeonato se calculó para una línea de tendencia ascendente, por lo que, si la correlación RL está por encima de cero, el trading es rentable. Si está por debajo de cero, es una pérdida. A veces ocurre un efecto interesante cuando la correlación muestra beneficios, pero la correlación RL es negativa. Esto puede significar que el trading está perdiendo. En Aver puede verse un ejemplo de una situación así. El beneficio total neto es de 2 642 dólares, mientras que la correlación RL es -0,11. En este caso es probable que no haya correlación. Simplemente quiere decir que no se puede juzgar el futuro de una cuenta.
EAM y EFM dirán mucho
A menudo nos advierten: "Corta las pérdidas y deja que crezcan los beneficios". Viendo los resultados finales del trade, no se puede llegar a ninguna conclusión sobre si las paradas protectoras (Stop Loss) están disponibles o si la fijación de los beneficios es efectiva. Sólo vemos la fecha de apertura de la posición, la fecha de cierre y el resultado final: beneficio o pérdida. Es como juzgar a una persona por su fecha de nacimiento y de muerte. Sin conocer los beneficios flotantes durante la duración de cada trade, ni todas las posiciones en total, no se puede juzgar la naturaleza de un sistema de trading. ¿Cómo es de arriesgado? ¿Cómo se consiguió el beneficio? ¿Se perdió el beneficio de papel? Las respuestas a estas preguntas pueden obtenerse con los parámetros EAM (Excursión Adversa Máxima) y EFM (Excursión Favorable Máxima).
Cada posición abierta (hasta que se cierre) sufre continuamente fluctuaciones de los beneficios. Cada trade alcanza su beneficio máximo y su pérdida máxima durante el periodo entre su apertura y su cierre. EFM muestra el movimiento máximo de los precios en dirección favorable. Respectivamente, EAM muestra el movimiento máximo de los precios en dirección adversa. Sería lógico medir ambos índices en puntos. Sin embargo, si se negocian dos pares diferentes de divisas, habrá que expresarlo en términos monetarios.
Cada trade cerrado se corresponde con su resultado (retorno) y dos índices: EFM y EAM. Si el trade dio un resultado con un beneficio de 100 dólares, y EAM llegó a -1 000 dólares, no es lo mejor para el trade. La capacidad de tener muchos trades con resultados rentables, pero con muchos valores negativos para EAM por trade, muestra que el sistema sólo "se queda" con las posiciones no rentables. Un trading así está destinado a fracasar tarde o temprano.
Igualmente, los valores para EFM pueden ofrecer alguna infomación útil. Si se abrió una posición en la dirección correcta, EFM alcanza 3 000 dólares por trade, pero el trade se cerró con 500 dólares de beneficio como resultado, se puede decir que estaría bien elaborar el sistema de protección de beneficios no fijada. Esta puede ser la Trailing Stop que se puede mover después del precio si los más tardíos se mueven en una dirección favorable. Si siempre se producen pocos beneficios, el sistema puede mejorarse mucho. EFM dirá mucho sobre esto.
Para que el análisis visual sea más cómodo, sería mejor utilizar representación gráfica de la distribución de los valores de EAM y EFM. Si se impone cada trade en un gráfico, se verá cómo se obtiene el resultado. Por ejemplo, si se le echa otro vistazo a "Informes" de RobinHood, que no tuvo ningún trade no rentable, se podrá ver que cada trade tiene una reducción (EAM) de -120 dólares a - 2500 dólares.
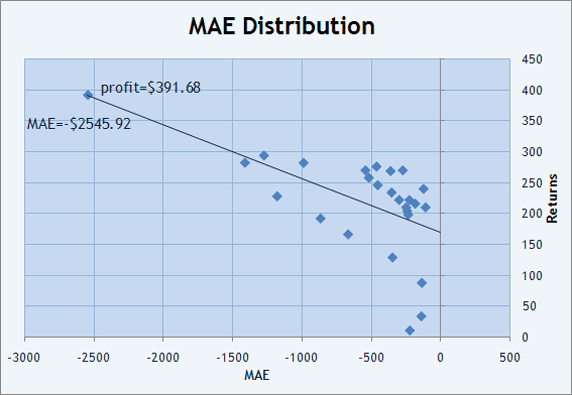
Img. 11. La distribución de los trades en el plano de EAMxRetorno
Además, se puede dibujar una línea recta para que encaje la distribución Retorno x EAM utilizando el método MJ. En la Img. 11 se muestra en rojo y tiene una pendiente negativa (los valores rectos descienden cuando se mueven de izquierda a derecha). El parámetro de la correlación (beneficios, EAM)=0,59, permite estimar la distancia a la que están distribuidos los puntos en el gráfico con respecto a la línea recta. El valor negativo muestra una pendiente negativa para la línea de ajuste.
Si busca por cuentas de otros participantes, verá que el coeficiente de correlación es generalmente positivo. En el ejemplo anterior, la pendiente descendente de la línea avisa de que tiende a ser cada vez más reducidas para no permitir los trades no rentables. Ahora se puede entender qué precio se ha pagado para el valor ideal del parámetro Correlación RL=1.
Igualmente, se puede crear un gráfico de distribución de Retornos y EFM, así como buscar los valores de Correlación(Beneficios, EFM)=0,79 y Correlación (EFM, EAM)=0,59. La Correlación(Beneficios, EFM) es positiva y tiende a uno (0,77). Esto muestra que la estrategia intenta no permitir "quedarse" mucho tiempo con beneficios flotantes. Es más probable que no se permita que el beneficio crezca lo suficiente y que Take Profit cierre los trades. Como puede ver, las dietribuciónes de EAM y EFM, dan una estimación visual y unos valores de Correlación(Beneficios, EFM) y Correlación(Beneficios, EAM) que pueden informar sobre la naturaleza del trading, incluso sin usar gráficos.
Los valores de Correlación(EFM, EAM), Correlación(BeneficiosNormalizados, EAM) y Correlación(BeneficiosNormalizados EFM) en los "Informes" de los participantes del Campeonato se han dado como información adicional.
Normalización del resultado del trade
En el desarrollo de los sistemas de trading, normalmente se usan tamaños fijos para las posiciones. Esto permite una optimización del sistema más sencilla, para poder encontrar los mejores en ciertos criterios. Sin embargo, tras encontrar las entradas, aparece la pregunta lógica: ¿Qué sistema de gestión de tamaño (Gestión monetaria, GM) debería aplicarse? El tamaño de las posiciones abiertas está directamente relacionado con la cantidad de dinero en la cuenta, por lo que no sería razonable hacer trade en una cuenta con 5 000 dólares de la misma manera que hacerlo en una con 50 000. Además, el sistema GM puede abrir posiciones que no son directamente proporcionales. Me refiero a que una cuenta abierta con 50 000 dólares no tiene por qué ser necesariamente 10 veces más que la que se abrió con un depósito de 5 000 dólares.
El tamaño de la posición también puede variar según a la fase actual del mercado, según los resultados de los últimos análisis de trades, etc. Por lo que el sisitema de gestión monetaria que se aplice puede cambiar esencialmente la aparición inicial de un sistema de trading. ¿Cómo se puede estimar el impacto del sistema de gestión monetaria aplicado? ¿Fue útil o sólo empeoró los lados negativos del método de trading? ¿Cómo se pueden comparar los resultados del trade en varias cuentas teniendo el mismo tamaño de depósito que al principio? Una posible solución sería la normalización de los resultados de trade.
en la que: |
La normalización se realizará de la siguiente manera: Se dividirá cada resultado del trade (rentable o no) entre el volumen de la posición y luego se multiplicará por el tamaño mínimo permitido de la posición. Por ejemplo, la orden #4399142 BUY 2,3 lotes USDJPY, se cerró con un beneficio de 4 056 dólares. 20 + 118,51 dólares (canjea) = 4 174,71 dólares. Este ejemplo se obtuvo de la cuenta de GODZILLA (Nikolay Kositsin). Se divide el resultado entre 2,3 y se multiplica por 0,1 (el tamaño mínimo permitido de la posición), y se obtiene un beneficio de 4 056,20 dólares/2,3 * 0,1 = 176,36 dólares y canjea = 5,15 dólares. Estos serían los resultados para la orden del tamaño de lote 0,1. Vamos a hacer lo mismo con los resultados de todos los trades y se obtendrán los beneficios normalizados (BN).
Lo primero que se piensa es en encontrar los valores de la Correlación(BeneficiosNormalizados, EAM) y Correlación(BeneficiosNormalizados, EFM) y compararlos con la Correlación(Beneficios, AEM) y Correlación(Beneficios, EFM) iniciales. Si la diferencia entre los parámetros es muy grande, los métodos que se han aplicado probablemente hayan cambiado el sistema inicial. Se dice que aplicar la GM puede "matar" a un sistema rentable, pero no puede convertir un sistema no rentable en uno rentable. En el campeonato, la cuenta de TMR es una excepción en la que cambiar el valor de Correlación(BeneficiosNormalizados, EFM) de 0,23 a 0,63 permitió al trader "cerrar en negro".
¿Cómo se puede estimar la agresión de a estrategia?
Se pueden obtener más beneficios de los trades normalizados en medida a cómo el método GM aplicado influencia la estrategia. Es obvio que aumentar los tamaños de las posiciones 10 veces, provocará que el resultado final sea 10 veces diferente al inicial. ¿Y qué pasa si se cambia el tamaño del trade, no por un cierto número de veces, sino dependiendo de los desarrollos actuales? Los resultados obtenidos por las compañías de gestión de fondos se comparan a menudo con cierto modelo, normalmente a un índice de acciones. Beta Coefficient muestra cuántas veces cambia el depósito de la cuenta comparado con el índice. Si se cogen los trades normalizados como índices, se podrá saber cuánto más volátiles son los resultados si se comparan con el sistema inicial (lote de trades 0,1).
Por lo tanto, lo primero es calcular la covarianza: cov(Beneficios, BeneficiosNormalizados). Luego se calcula la dispersión de los trades normalizados, nombrando BN a la secuencia de trades nomalizados. Para esto, se calcula la esperanza matemática de los trades normalizados con nombre M(BN). M(BN) muestra el resultado promedio del trade para los trades normalizados. Luego se busca la SDC de los trades normalizadso desde M(BN), es decir, se suman BN-M(BN))^2). El resultado que se obtenga se vidide entre la cantidad de trades y se le nombra D(BN). Esta es la dispersión de los trades normalizados. Se divide la covarianza entre el sistema bajo medida, Beneficios, y el índice ideal, BeneficiosNormalizados cov(Beneficios, BeneficiosNormalizados), entre la dispersión del índice D(BN). El resultado será el valor del parámetro que permitirá estimar cuántas veces el capital es más volátil que los resultados de los trades originales (trades en el Campeonato) comparados con los trades normalizados. Este parámetro se llama Capitalización de fondos en los "Informes". Muestra el nivel de agresión de trading para algunas medidas.
en la que: |
Ahora se puede revisar la manera en la que se lee la tabla de los participantes en el Campeonato de Trading Automático de 2006:
| # | Iniciar sesión | Error estándar de RL, en dólares | Correlación RL | Mejorar | RPTG | Puntuación-Z (%) | Capitalización de fondos | Beneficio, en dólares |
|---|---|---|---|---|---|---|---|---|
| 1 | Rich | 6 582,66 | 0,81 | 0,41 | 2,55 | -3,85(99,74) | 17,27 | 25 175,60 |
| 2 | ldamiani | 5 796,32 | 0,64 | 0,21 | 2,89 | -2,47 (98.65) | 28,79 | 15 628,40 |
| 3 | GODZILLA | 2 275,99 | 0,9 | 0,19 | 1,97 | 0,7(51,61) | 16,54 | 11 378,70 |
| 4 | valvk | 3 938,29 | 0,89 | 0,22 | 1,68 | 0,26(20,51) | 40,17 | 9 819,40 |
| 5 | Hendrick | 3 687,37 | 0,79 | 0,24 | 1,96 | 0,97(66,8) | 49,02 | 9 732,30 |
| 6 | bvpbvp | 9 208,08 | 0,58 | 0,43 | 12,77 | 1,2(76,99) | 50,00 | 8 236,00 |
| 7 | Flame | 2 532,58 | 0,75 | 0,36 | 3,87 | -2,07(96,06) | 6,75 | 7 676,20 |
| 8 | Berserk | 1 943,72 | 0,68 | 0,20 | 1,59 | 0,69(50,98) | 17,49 | 7 383,70 |
| 9 | vgc | 905,10 | 0,95 | 0,29 | 1,63 | 0,58(43,13) | 8,06 | 6 801,30 |
| 10 | RobinHood | 109,11 | 1,00 | 3,07 | 1,74 | N/A (N/A) | 41,87 | 5 643,10 |
| 11 | alexgomel | 763,76 | 0,95 | 0,43 | 2,63 | 1,52(87,15) | 10,00 | 5 557,50 |
| 12 | LorDen | 1229,40 | 0,8 | 0,33 | 3,06 | 1,34(81,98) | 49,65 | 5 247,90 |
| 13 | systrad5 | 6 239,33 | 0,66 | 0,27 | 2,47 | -0,9(63,19) | 42,25 | 5 141,10 |
| 14 | emil | 2 667,76 | 0,77 | 0,21 | 1,93 | -1,97(95,12) | 12,75 | 4 658,20 |
| 15 | payday | 1686,10 | 0,75 | 0,16 | 0,88 | 0,46(35,45) | 10,00 | 4 588,90 |
El error de RL Estándar en las cuentas de los ganadores no era el más pequeño. Al mismo tiempo, los gráficos de balance de los Asesores expertos más rentables eran más bien suaves, ya que los valores de la Correlación RL no están lejos de 1,0. El Índice de Sharp estuvo básicamente en el rango de 0,20 a 0,40. El único AE con un Índice de Sharp extremo= 3,07 resultó no tener muy buenos valores de EAM y EFM.
La RTPG por trade está ubicada básicamente en el rango de 1,5 a 3%. En ese momento, los ganadores no tuvieron los valores más grandes para RTPG, sino los más pequeños. El valor extremo de RPTG=12,77% informa de que hubo una anormalidad en el trading, y se puede ver que esta cuenta experimentó las fluctuaciones más grandes con el error estándar de RL= 9 208,08 dólares.
La Puntuación-Z no da ninguna generalización sobre los primeros 15 participantes en el Campeonato, pero los valores de |Z|>2,0 pueden llamar la atención en el historial de trading, para poder entender la naturaleza de dependencia entre los trades en la cuenta. Por lo tanto, se sabe que para la cuenta de Rich, Z=3,85 se alcanzó prácticamente por la apertura simultánea de tres posiciones. ¿Y cómo están las cosas en la cuenta de ldamiani's?
Finalmente, la última columna de la tabla anterior, Capitalización de fondos, también tiene un gran rango de valores de 8 a 50, siendo 50 el valor máximo para este Campeonato, ya que el tamaño máximo pertimitido de trade hizo 5,0 lotes, que es 50 veces más que el tamaño mínimo del lote 0,1. Sin embargo, por curioso que parezca, este parámetro no es el más grande en los granadores. Los tres mejores valores son 17,27, 28,79 y 16,54. ¿Acaso no usaron los ganadores el tamaño máximo permitido de las posiciones? Sí, sí lo hicieron. Lo que pasa es que, quizás, los métodos GM no influenciaron mucho los riesgos de trading en el aumento general de los tamaños de los contratos. Es una evidencia clara de que la gestión monetaria es muy importante en un sistema de trading.
El puesto número 15 fue para payday. El AE de este participante no pudo abrir trades con tamaños superiores a 1. Lote 0 por un pequeño error en el código. ¿Qué hubiera pasado si el error no se hubiera producido y los tamaños de las posiciones hubieran aumentado 5 veces hasta los lotes 5,0? ¿Hubiera aumentado proporcionalmente el beneficio de 588,99 dólares a 22 944,50 dólares? ¿Habría conseguido el participante el segundo puesto o habría experimentado una reducción de la que no se hubiera podido recuperar por el aumento de los riesgos? ¿Habría estado alexgomel en el primer lugar? Su AE también negoció sólo con un lote de trades 0,1. O vgc podría haber ganado, cuyo AE abrió trades casi siempre de un tamaño inferior a 1,0. Los tres tienen un gráfico de balance bueno y suave. Como puede ver, la trama del Campeonato continua aunque ya haya acabado.
Conclusión: No confunda la hierba con maleza
Hay diferentes opiniones. Este artículo ofrece algunos métodos muy generales para la estimación de las estrategias de trading. Se pueden crear muchos más criterios para estimar los resultados de un trade. Cada característica por separado no proporcionará una estimación objetiva, pero al juntarse pueden ayudar a evitar métodos desequilibrados en este tema.
Se puede decir que cualquier resultado (ganancia de beneficios en una secuencia suficiente de trades) se puede someter a un "contrainterrogatorio" para detectar los puntos negativos. Esto quiere decir que todas estas características no se caracterizan mucho por la eficiencia de una estrategia de trading en particular mientras informan de puntos débiles a los que se debe prestar atención, sin ser satisfactorias sólo con un resultado final: el beneficio neto adquirido en la cuenta.
No se puede crear el sistema de trading ideal, todos los sistemas tienen sus beneficios y sus consecuencias. Las pruebas de estimación se utilizan para no rechazar un método de trading dogmáticamente, sino para saber cómo realizar un desarrollo futuro de los sistemas de trading y de los Asesores expertos. En este sentido, los datos estadísticos acumulados durante el Campeonato de Trading Automático de 2006 servirán mucho de ayuda a todos los traders.
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/1492
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
 Desarrollo del tester de estrategia limit para probar un AE hedge
Desarrollo del tester de estrategia limit para probar un AE hedge
 El tester en la terminal MetaTrader 4: Debería saberse
El tester en la terminal MetaTrader 4: Debería saberse
 Plantilla universal de Asesor experto
Plantilla universal de Asesor experto
 Interacción entre MetaTrader 4 y Matlab a través de archivos CSV
Interacción entre MetaTrader 4 y Matlab a través de archivos CSV
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso