
Matemática na negociação: Como estimar resultados de trading
Nassim N. Taleb
Introdução: A matemática é a rainha das ciências
Um certo nível de formação matemática é exigida de qualquer operador esta declaração não precisa de provas. A questão é: Como podemos definir este nível mínimo exigido? No crescimento de sua experiência de trading, o operador, muitas vezes amplia sua visão "sozinho", lendo postagens em fóruns ou vários livros. Alguns livros exigem menor nível de formação matemática de leitores, outros, pelo contrário, inspiram o leitor para estudar ou retocar o conhecimento em algum campo das ciências. Vamos tentar fornecer algumas estimativas e suas interpretações neste único artigo.
De dois males escolha o menor
Há mais matemáticos no mundo do que operadores bem sucedidos. Este fato é muitas vezes usado como um argumento por aqueles que se opõem a cálculos ou métodos complexos no trading. Podemos dizer contra isso que o trading não é só a capacidade de desenvolver regras de negociação (análise de habilidades), mas também a capacidade de observar essas regras (disciplina). Além disso, uma teoria que descreve exatamente os preços nos mercados financeiros ainda não foi criada (acho que nunca vai ser criada). A criação da própria teoria (descoberta de natureza matemática) de mercados financeiros significaria a morte destes mercados, o que é um paradoxo, em termos de filosofia. No entanto, se nos depararmos com a questão de saber para onde ir com o mercado sem uma descrição matemática completamente satisfatória do mercado ou sem qualquer descrição, podemos escolher o menor dos males: Nós escolhemos métodos de estimativa de sistemas de trading.
O que é anomalia da distribuição normal?
Uma das noções básicas na teoria das probabilidades é a noção de distribuição normal (Gaussiana). Por que é chamada assim? Muitos processos naturais acabam sendo distribuídos normalmente. Para ser mais exato, os processos mais naturais, no limite, reduzem a distribuição normal. Vamos considerar um exemplo simples: Suponha que temos uma distribuição uniforme no intervalo de 0 a 100. Uma distribuição uniforme significa que a probabilidade de cair qualquer valor no intervalo e a probabilidade de 3. 14 (Pi) cairá é a mesma que a de cair 77 (meu número favorito com dois 7). Os computadores modernos ajudam a gerar uma boa sequência de números pseudo aleatória.
Como podemos obter uma distribuição normal desta distribuição uniforme? Acontece que, se tomarmos cada vez números aleatórios (por exemplo, 5 números) de uma distribuição única e encontrar o valor médio destes números (isto é chamado de "colher uma amostra") e se a quantidade de tais amostras for grande, a distribuição recém obtida tenderá ao normal. O teorema do limite central diz que isso se relaciona não apenas com amostras colhidas de distribuições únicas, mas também para uma classe muito grande de outras distribuições. Se as propriedades de distribuição normal forem muito bem estudadas, será muito mais fácil de analisar processos se eles forem representados como um processo com distribuição normal. No entanto, é ver para crer, para que possamos ver a confirmação deste teorema do limite central utilizando um indicador MQL4 simples.
Vamos lançar este indicador em qualquer gráfico com diferente N (quantidade de amostras) e ver que a distribuição de frequência empírica torna-se cada vez mais suave.
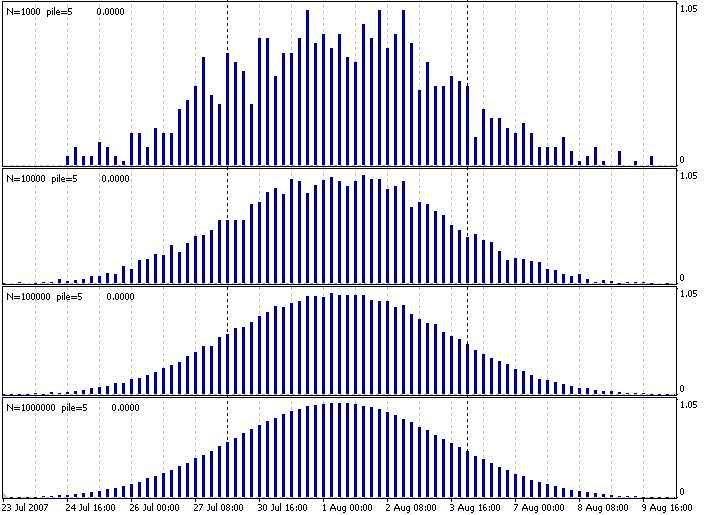
Figura 1. Indicador que cria uma distribuição normal de uma distribuição uniforme.
Aqui, N significa quantas vezes nós tomamos a média de acúmulo=5 números uniformemente distribuídos no intervalo de 0 a 100. Obtivemos quatro gráficos, muito semelhantes na aparência. Se normalizá-los de alguma forma no limite (em conjunto com uma única escala), obteremos várias realizações da distribuição normal padrão. O único problema é que os preços nos mercados financeiros (para ser mais exato, os incrementos de preços e outros derivados desses incrementos), de modo geral, não se encaixam na distribuição normal. A probabilidade de um evento bastante raro (por exemplo, diminuição do preço em 50%) em mercados financeiros é, mesmo baixa, consideravelmente mais elevada do que uma distribuição normal. É por isso que se deve lembrar disso quando estimar os riscos com base na distribuição normal.
Quantidade transforma em qualidade
Mesmo neste exemplo simples de modelagem de distribuição normal, vemos que a quantidade de dados a serem processados conta muito. Quanto maior a existência de dados iniciais, mais preciso e válido o resultado. O menor número na amostra é considerado ter que exceder 30. Isso significa que, se quisermos estimar resultados de trades (por exemplo, um Expert Advisor no verificador), a quantidade de trades abaixo de 30 é insuficiente para tirar conclusões estatisticamente confiáveis sobre alguns parâmetros do sistema. Quanto mais trades analisarmos, menor é a probabilidade de que esses trades sejam apenas coincidências felizes de um sistema de trading não muito confiável. Assim, o lucro final de uma série de 150 trades dá mais motivos para colocar o sistema em operação do que um sistema estimado em apenas 15 trades.
Expectativa matemática e Dispersão como Estimativa de Risco
As duas características mais importantes de uma distribuição são expectativa matemática (média) e dispersão. A distribuição normal padrão tem uma expectativa matemática igual a zero. No que, o centro de distribuição também é localizado no zero. O nivelamento ou a inclinação da distribuição normal são caracterizados pela medida da expansão de um valor aleatório dentro da área da expectativa matemática. É a dispersão que nos mostra como os valores estão espalhados sobre a valores aleatórios da expectativa matemática.
A expectativa matemática pode ser encontrada de uma maneira muito simples: Para conjuntos contáveis, todos os valores de distribuição são somados, a soma obtida sendo dividida pela quantidade de valores. Por exemplo, um conjunto de números naturais é infinito, mas contábil, desde que cada valor possa ser coletado com seu índice (número de ordem). Para conjuntos incontáveis, a integração será aplicada. Para estimar a expectativa matemática de uma série de trades, vamos resumir todos os resultados de trade e dividir o montante obtido pela quantidade de trades. O valor obtido irá mostrar o resultado médio esperado de cada trade. Se a expectativa matemática for positiva, lucramos na média. Se for negativa, perdemos na média.
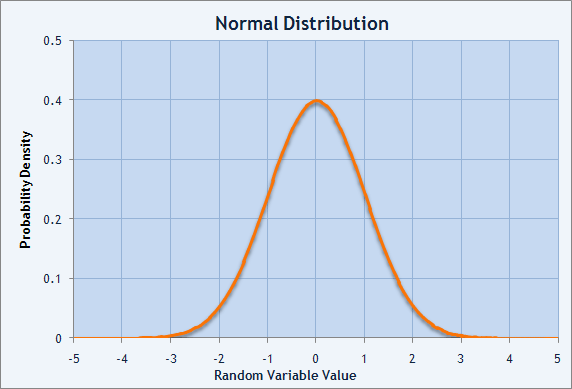
Figura 2. Gráfico de densidade de probabilidade de distribuição normal.
A medida de propagação da distribuição é a soma dos desvios quadrados do valor aleatório de sua expectativa matemática. Esta característica da distribuição é chamada dispersão. Normalmente, a expectativa matemática para um valor distribuído aleatoriamente é chamada M(X). Então, a dispersão pode ser descrita como D(X) = M((X-M(X))^2 ). A raiz quadrada da dispersão é chamada desvio padrão. Também é definida como sigma (σ). É uma distribuição normal que possui expectativa matemática igual a zero e desvio padrão igual a 1 que é chamada de distribuição normal ou Gaussiana.
Quanto maior o valor do desvio padrão, mais mutável é o capital de trading, e também, maior é o risco. Se a expectativa matemática for positiva (uma estratégia rentável) e igual a $100 e se o desvio padrão for igual a $500, corremos o risco de uma soma, que é várias vezes maior, para ganhar cada dólar. Por exemplo, temos os resultados de 30 trades:
|
|
|---|
Para encontrar a expectativa matemática para esta sequência de trades, vamos resumir todos os resultados e dividir por 30. Obteremos o valor médio M(X) igual a $ 4,26. Para encontrar o desvio padrão, vamos subtrair a média do resultado de cada trade, elevá-los ao quadrado, e encontrar a soma dos quadrados. O valor obtido será dividido por 29 (a quantidade de trades menos um). Então, vamos obter dispersão D igual a 9.353,623. Tendo gerado a raiz quadrada da dispersão, obtém-se o desvio padrão sigma, igual a $96,71.
Os dados de verificação são fornecidos na tabela abaixo:
| Número do trade |
X (Resultado) |
X-M(X) (Diferença) |
(X-M(X))^2 (Quadrado da Diferença) |
|---|---|---|---|
| 1 | -17,08 | -21,34 | 455,3956 |
| 2 | -41,00 | -45,26 | 2 048.4676 |
| 3 | 147,80 | 143,54 | 20 603.7316 |
| 4 | -159,96 | -164,22 | 26 968.2084 |
| 5. | 216,97 | 212,71 | 45 245.5441 |
| 6 | 98,30 | 94,04 | 8 843.5216 |
| 7 | -87,74 | -92,00 | 8 464.00 |
| 8 | -27,84 | -32,10 | 1 030.41 |
| 9 | 12,34 | 8,08 | 65,2864 |
| 10 | 48,14 | 43,88 | 1 925.4544 |
| 11 | -60,91 | -65,17 | 4 247.1289 |
| 12 | 10,63 | 6,37 | 40,5769 |
| 13 | -125,42 | -129,68 | 16 816.9024 |
| 14 | -27,81 | -32,07 | 1 028.4849 |
| 15 | 88,03 | 83,77 | 7 017.4129 |
| 16 | 32,93 | 28,67 | 821,9689 |
| 17 | 54,82 | 50,56 | 2 556.3136 |
| 18 | -160,10 | -164,36 | 27 014.2096 |
| 19 | -83,37 | -87,63 | 7 679.0169 |
| 20 | 118,40 | 114,14 | 13 027.9396 |
| 21 | 145,65 | 141,39 | 19 991.1321 |
| 22 | 48,44 | 44,18 | 1 951.8724 |
| 23 | 77,39 | 73,13 | 5 347.9969 |
| 24 | 57,48 | 53,22 | 2 832.3684 |
| 25 | 67,75 | 63,49 | 4 030.9801 |
| 26 | -127,10 | -131,36 | 17 255.4496 |
| 27 | -70,18 | -74,44 | 5 541.3136 |
| 28 | -127,61 | -131,87 | 17 389.6969 |
| 29 | 31,31 | 27,05 | 731,7025 |
| 30 | -12,55 | -16,81 | 282,5761 |
O que obtivemos é a expectativa matemática igual a $4,26 e desvio padrão de $96,71. Não é a melhor relação entre o risco e a média de trade. O gráfico de lucro abaixo confirma isso:
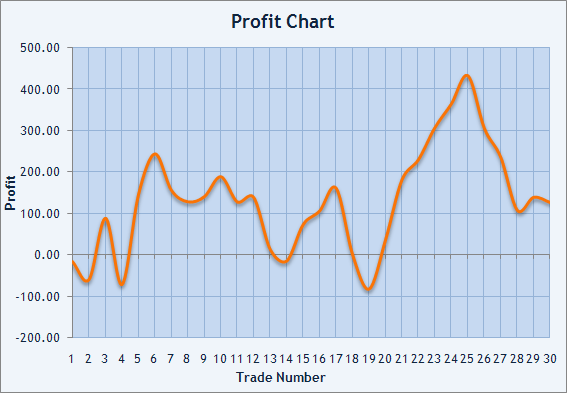
Figura 3. Gráfico de balanço de trades realizados.
Efetuo trade aleatoriamente? Z-Score
A suposição por si só se de que o lucro obtido como resultado de uma série de trades é aleatório soa sardonicamente para a maioria dos operadores. Depois de ter passado muito tempo à procura de um sistema de trading bem sucedido e observar que o sistema encontrado já resultou em alguns lucros reais em um período limitado de tempo, o operador supõe ter encontrado uma abordagem adequada ao mercado. Como ele poderia pensar que tudo isso foi apenas por acaso? Isso é um pouco complicado, especialmente para iniciantes. No entanto, é essencial estimar os resultados objetivamente. Neste caso, a distribuição normal, novamente, vem para o resgate.
Nós não sabemos se cada trade vai dar resultado. Só podemos dizer que lucramos (+) ou perdemos (-). Os ganhos e perdas alternam de maneiras diferentes para diferentes sistemas de trading. Por exemplo, se o lucro esperado é 5 vezes menor do que a perda esperada no desencadeamento de Stop Loss, seria razoável presumir que trades rentáveis (trades +) prevalecerão significativamente em relação aos trades com perdas (trades -). Z-Score nos permite estimar a frequência com que trades rentáveis alternam com os trades de perda.
O Z para um sistema de trading é calculado pela seguinte fórmula:
Z=(N*(R-0.5)-P)/((P*(P-N))/(N-1))^(1/2) em que: |
Uma série é uma sequência de prós(por exemplo, +++) ou contras (por exemplo, --). R conta a quantidade de tal série.

Figura 4. Comparação de duas séries de lucros e perdas.
Na Figura 4, uma parte da sequência de lucros e perdas do Expert Advisor que levou o primeiro lugar no Campeonato de Trading Automatizado de 2006, é mostrada em azul. O Z-score desta competição tem o valor de -3,85, a probabilidade de 99,74% é fornecida entre parênteses. Isto significa que, com uma probabilidade de 99,74%, os trades nesta conta possuem uma dependência positiva entre eles (Z-score é negativo): um lucro foi seguido por um lucro, uma perda foi seguida por uma perda. É este o caso? Aqueles que estavam assistindo o Campeonato provavelmente lembram que Roman Rich colocou a sua versão do Expert Advisor MACD que tem aberto frequentemente três trades que funcionam na mesma direção.
Uma sequência típica de valores positivos e negativos do valor aleatório na distribuição normal é mostrada em vermelho. Podemos ver que estas sequências são diferentes. No entanto, como podemos medir esta diferença? O Z-score responde esta pergunta: A sua sequência de lucros e perdas contêm mais ou menos faixas (série rentável ou de perda) do que você pode esperar para uma seqüência realmente aleatória sem qualquer dependência entre trades? Se o Z-score estiver próximo de zero, não podemos dizer que a distribuição do trade difere da distribuição normal. O Z-score de uma sequência de trading pode nos informar sobre uma possível dependência entre trades consecutivos.
No que, os valores de Z são interpretados do mesmo modo que a probabilidade de desvio de zero de um valor aleatório com uma distribuição de acordo com a distribuição normal padrão (média=0, sigma=1). Se a probabilidade de cair um valor aleatório distribuído normalmente dentro do intervalo de ± 3σ é 99,74%, a queda deste valor fora deste intervalo, com a mesma probabilidade de 99,74% nos informa que este valor aleatório não pertence a esta distribuição normal fornecida. É por isso que a "regra 3-sigma '' é lida da seguinte forma: um valor aleatório normal desvia em não mais que 3-sigma de distância.
Sinal de Z nos informa sobre o tipo de dependência. Além disso, significa que é mais provável que o trade rentável seja seguido por um de perda. Menos diz que um lucro será seguido por um lucro, uma perda será seguida novamente por uma perda. Uma pequena tabela abaixo ilustra o tipo e a probabilidade de dependência entre trades em comparação com distribuição normal.
| Z-Score | Probabilidade de dependência, % | Tipo de dependência |
|---|---|---|
| -3 | 99,73 | Positiva |
| -2,9 | 99,63 | Positiva |
| -2,8 | 99,49 | Positiva |
| -2,7 | 99,31 | Positiva |
| -2,6 | 99,07 | Positiva |
| -2,5 | 98,76 | Positiva |
| -2 | 95,45 | Positiva |
| -1,5 | 86,64 | Intermediária |
| -1,0 | 68,27 | Intermediária |
| 0,0 | 0,00 | Intermediária |
| 1,0 | 68,27 | Intermediária |
| 1,5 | 86,64 | Intermediária |
| 2,0 | 95,45 | Negativa |
| 2,5 | 98,76 | Negativa |
| 2,6 | 99,07 | Negativa |
| 2,7 | 99,31 | Negativa |
| 2,8 | 99,49 | Negativa |
| 2,9 | 99,63 | Negativa |
| 3,0 | 99,73 | Negativa |
Uma dependência positiva entre trades significa que um lucro causará um novo lucro, enquanto que uma perda causará uma nova perda. Uma dependência negativa significa que um lucro será seguido por uma perda, enquanto que uma perda será seguida por um lucro. A dependência encontrada nos permite regular a dimensão das posições a serem abertas (idealmente) ou mesmo ignorar algumas delas e abri-las apenas virtualmente para assistir sequências de trade.
Segurar período de retorno (HPR)
Em seu livro, The Mathematics of Money Management, Ralph Vince utiliza a noção de HPR (segurar período de retorno). Um trade que resultou em um lucro de 10% possui HPR=1+0,10=1,10. Um trade que resultou em uma perda de 10% possui HPR=1-0. 10=0,90. Você também pode obter o valor de HPR para um trade dividindo o valor de balanço após o fechamento do trade (Fechamento de Balanço) pelo valor de balanço na abertura do trade (Abertura de Balanço). HPR=Fechamento de Balanço/Abertura de Balanço. Assim, cada trade possui tanto um resultado em termos de dinheiro, quanto um resultado expresso em HPR. Isto nos permitirá comparar os sistemas independentemente do tamanho dos contratos de trade. Um dos índices utilizados para tal comparação é a média aritmética, AHPR (segurar média do período de retorno).
Para encontrar a AHPR, devemos resumir todas as HPRs e dividir o resultado pela quantidade de trades. Vamos considerar esses cálculos usando o exemplo acima de 30 trades. Suponha que começamos o trade com $500 na conta. Vamos fazer uma nova tabela:
| Número do trade | Saldo, $ | Resultado, $ | Balanço no fechamento, $ | HPR |
|---|---|---|---|---|
| 1 | 500,00 | -17,08 | 482,92 | 0,9658 |
| 2 | 482,92 | -41,00 | 441,92 | 0,9151 |
| 3 | 441,92 | 147,8 | 589,72 | 1,3344 |
| 4 | 589,72 | -159,96 | 429,76 | 0,7288 |
| 5. | 429,76 | 216,97 | 646,73 | 1,5049 |
| 6 | 646,73 | 98,30 | 745,03 | 1,1520 |
| 7 | 745,03 | -87,74 | 657,29 | 0,8822 |
| 8 | 657,29 | -27,84 | 629,45 | 0,9576 |
| 9 | 629,45 | 12,34 | 641,79 | 1,0196 |
| 10 | 641,79 | 48,14 | 689,93 | 1,0750 |
| 11 | 689,93 | -60,91 | 629,02 | 0,9117 |
| 12 | 629,02 | 10,63 | 639,65 | 1,0169 |
| 13 | 639,65 | -125,42 | 514,23 | 0,8039 |
| 14 | 514,23 | -27,81 | 486,42 | 0,9459 |
| 15 | 486,42 | 88,03 | 574,45 | 1,1810 |
| 16 | 574,45 | 32,93 | 607,38 | 1,0573 |
| 17 | 607,38 | 54,82 | 662,20 | 1,0903 |
| 18 | 662,20 | -160,10 | 502,10 | 0,7582 |
| 19 | 502,10 | -83,37 | 418,73 | 0,8340 |
| 20 | 418,73 | 118,4 | 537,13 | 1,2828 |
| 21 | 537,13 | 145,65 | 682,78 | 1,2712 |
| 22 | 682,78 | 48,44 | 731,22 | 1,0709 |
| 23 | 731,22 | 77,39 | 808,61 | 1,1058 |
| 24 | 808,61 | 57,48 | 866,09 | 1,0711 |
| 25 | 866,09 | 67,75 | 933,84 | 1,0782 |
| 26 | 933,84 | -127,10 | 806,74 | 0,8639 |
| 27 | 806,74 | -70,18 | 736,56 | 0,9130 |
| 28 | 736,56 | -127,61 | 608,95 | 0,8267 |
| 29 | 608,95 | 31,31 | 640,26 | 1,0514 |
| 30 | 640,26 | -12,55 | 627,71 | 0,9804 |
<
AHPR será encontrada através da média aritmética. É igual a 1,0217. Em outras palavras, nós ganhamos em média (1,0217-1)*100%=2,17% em cada trade. É este o caso? Se multiplicarmos 2,17 por 30, veremos que a renda deve alcançar 65,1%. Vamos multiplicar o montante inicial de $500 por 65,1% e obter $325,50. Ao mesmo tempo, o lucro real (627,71-500) /500*100%=25,54%. Assim, a média aritmética do HPR nem sempre nos permite estimar corretamente um sistema.
Junto com média aritmética, Ralph Vince introduz a noção de média geométrica que chamaremos GHRP (período de retenção de retornos geométrico), que é praticamente sempre inferior ao AHPR. A média geométrica é o fator de crescimento por jogo e é encontrada através da seguinte fórmula:
GHPR=(BalanceClose/BalanceOpen)^(1/N) em que: |
O sistema que possuir o maior GHPR terá os maiores lucros se negociarmos com base no reinvestimento. O GHPR abaixo significa que o sistema perderá dinheiro se negociarmos com base no reinvestimento. Um bom exemplo da diferença entre o AHPR e o GHPR pode ser o histórico de conta do sashken . Ele foi líder do campeonato por um bom tempo. AHPR=9,98% impressiona, mas o final GHPR=-27,68% coloca tudo em perspectiva.
Taxa de Sharpe
A eficiência dos investimentos é frequentemente estimada em termos de dispersão dos lucros. Um desses índices é a taxa de sharpe. Este índice mostra como o AHPR diminuiu devido a taxa livre de risco (RFR) relaciona-se com p desvio padrão (SD) da sequência HPR. O valor da RFR é geralmente tomado igual à taxa de juros depositados no banco ou taxa de juros sobre obrigações do tesouro. No nosso exemplo, AHPR=1,0217, SD(HPR)=0,17607, RFR=0.
Sharpe Ratio=(AHPR-(1+RFR))/SD em que: |
Taxa de sharpe=(1,0217-(1+0))/0,17607=0,0217/0,17607=0,1232. Para distribuição normal, mais de 99% dos valores aleatórios estão dentro do intervalo de ± 3σ (sigma= SD) sobre o valor médio M(X). Isto resulta que o valor do taxa de Sharpe superior a 3 é muito bom. Na Fig. 5 abaixo, podemos ver que, se os resultados dos trades forem distribuídos normalmente e a taxa de Sharpe=3, a probabilidade de perda será inferior a 1% por trade de acordo com a regra 3-sigma.
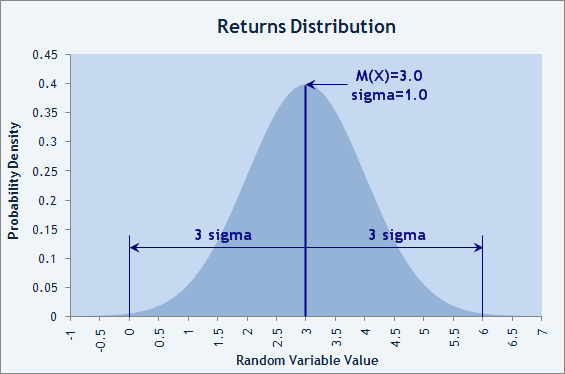
Fig.5. A distribuição normal dos resultados de trade com probabilidade perda é menor que 1%.
A conta do participante chamado RobinHood confirma isto: o EA dele fez 26 trades no Campeonato de Trading Automatizado de 2006 sem perdas entre eles. Taxa de Sharpe=3,07!
Regressão Linear(R) e Coeficiente de Correlação Linear (CLC)
Há também uma outra maneira de estimar a estabilidade de trades comerciais. A taxa de Sharpe nos permite estimar o risco do capital que está em execução, mas também podemos tentar estimar o grau de suavização da curva de balanço. Se impusermos os valores de equilíbrio no fechamento de cada trade, vamos ser capazes de desenhar uma linha quebrada. Estes pontos podem ser equipados com uma certa linha reta que vai nos mostrar a direção média das alterações de capital. Vamos considerar um exemplo desta oportunidade através do gráfico de balanço do Expert Advisor Phoenix_4 desenvolvido por Hendrick.
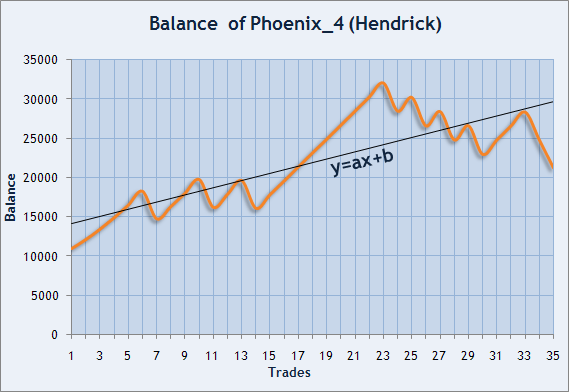
Figura 6. O balanço gráfico do Hendrick, o participante do Campeonato de Trading Automatizado 2006.
Temos de encontrar tais coeficientes a e b que esta linha vai o mais próximo possível dos pontos que estão sendo ajustados. No nosso caso, x é o número do trade, y é o valor de balanço no fechamento do trade.
|
|
|---|
Coeficientes de uma reta de aproximação são normalmente encontrados pelo método dos quadrados mínimos (método LS). Suponhamos que temos esta reto com coeficientes conhecidos a e b. Para cada x, temos dois valores: y(x)=a*x+b e balanço(x). Desvio do balanço (x) de y(x) será denotado como d(x)=y(x)-balanço(x). A SSD (soma dos desvios quadrados) pode ser calculada como SD=Summ{d(n)^2}. Encontrar a reta pelo método LS significa procurar por tais a e b em que SD é mínima. Esta reta também é chamado de regressão linear (LR) para a sequência dada.
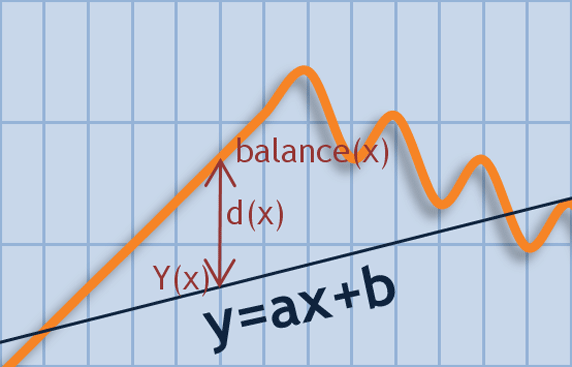
Figura 7. Valor de balanço de desvio da reta de y=ax+b
Tendo obtido coeficientes da reta de y=a*x+b usando o método LS, podemos estimar o valor de balanço de desvio da reta encontrada em termos financeiros. Se calcularmos a média aritmética para a sequência d (x), vamos ter certeza de que М(d(x)) está perto de zero (para ser mais exato, em algum grau de precisão de cálculo, é igual a zero). Ao mesmo tempo, o SSD de SD não é igual a zero e tem um certo valor limitado. A raiz quadrada de SD/(N-2) mostra a propagação de valores no gráfico de balanço sobre a linha reta e permite estimar sistemas de negociação em valores idênticos do estado inicial da conta. Chamaremos este parâmetro de Erro Padrão LR.
A seguir estão os valores deste parâmetro para as primeiras 15 contas no Campeonato de Trading Automatizado 2006:
| # | Login | Erro padrão LR, $ | Lucro, $ |
|---|---|---|---|
| 1 | Rich | 6 582.66 | 25 175.60 |
| 2 | ldamiani | 5 796.32 | 15 628.40 |
| 3 | GODZILLA | 2 275.99 | 11 378.70 |
| 4 | valvk | 3 938.29 | 9 819.40 |
| 5. | Hendrick | 3 687.37 | 9 732.30 |
| 6 | bvpbvp | 9 208.08 | 8 236.00 |
| 7 | Flame | 2 532.58 | 7 676.20 |
| 8 | Berserk | 1 943.72 | 7 383.70 |
| 9 | vgc | 905,10 | 6 801.30 |
| 10 | RobinHood | 109,11 | 5 643.10 |
| 11 | alexgomel | 763,76 | 5 557.50 |
| 12 | LorDen | 1 229.40 | 5 247.90 |
| 13 | systrad5 | 6 239.33 | 5 141.10 |
| 14 | emil | 2 667.76 | 4 658.20 |
| 15 | payday | 1 686.10 | 4 588.90 |
No entanto, o grau de aproximação do gráfico de balanço para uma sequência pode ser medido em termos financeiros e termos absolutos. Para isso, podemos usar taxa de correlação. A taxa de correlação, r, mede o grau de correlação entre duas sequências de números. O seu valor pode situar-se na taxa de -1 a +1. Se r=+1, isto significa que duas sequências têm um comportamento idêntico e a correlação é positiva.
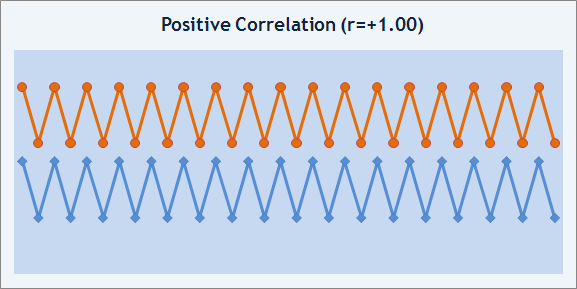
Figura 8. Exemplo de correlação positiva.
Se r=-1, as duas sequências mudam na oposição, a correlação é negativa.
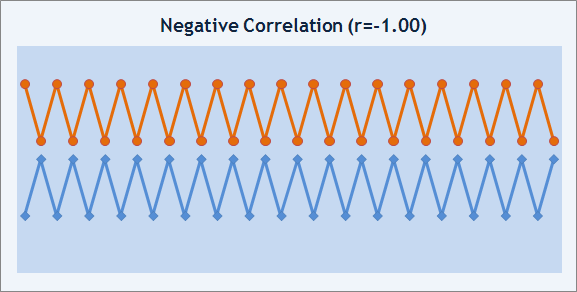
Figura 9. Exemplo de correlação negativa.
Se r=0, isso significa que não há nenhuma dependência encontrada entre as sequências. Deve ser enfatizado que r=0 não significa que não existe uma correlação entre as sequências, significa que tal correlação não foi encontrada. Isto deve ser lembrado. No nosso caso, temos que comparar duas sequências de números: одна последовательность из графика баланса, а вторая - соответствующие точки на прямой линейной регрессии.
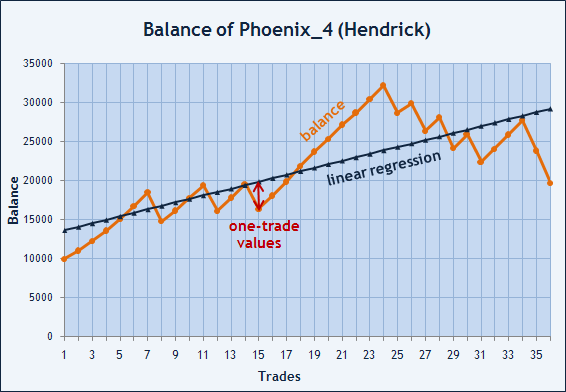
Figura 10. Valores de balanço e pontos na regressão linear.
A seguir está a representação da tabela com os mesmos dados:
|
|
Vamos denotar valores de balanço como X e a sequência dos pontos da linha de regressão linear como Y. Para calcular o coeficiente de correlação linear entre as sequências X e Y, é necessário encontrar valores médios M(X) e M(Y) em primeiro lugar. Em seguida, vamos criar uma nova seqüência T=(X-M(X))*(Y-M(Y)) e calcular sua média como M(T)=cov(X, Y)=M((X-M(X))*(Y-M(Y))). O valor encontrado de cov(X, Y) é chamado de covariância de X e Y e significa expectativa matemática do produto (X-M(X))*(Y-M(Y)). No nosso exemplo, o valor de covariância é 21 253 775.08. Por favor note que M(X) e M(Y) são iguais e têm o valor de 21 382.26 cada. Isso significa que o valor médio do Balanço e a média da reta de ajuste são iguais.
T=(X-M(X))*(Y-M(Y)) M(T)=cov(X,Y)=M((X-M(X))*(Y-M(Y))) em que: |
A única coisa que resta a ser feita é o cálculo de Sx e Sy. Para calcular Sx, vamos encontrar a soma dos valores de (X-M(X))^2, ou seja, encontrar o SSD de X do seu valor médio. Lembre-se de como calculamos dispersão e o algoritmo do método LS. Como você pode ver, eles estão todos relacionados. O SSD encontrado será dividido pela quantidade de números na sequência - no nosso caso, 36 (de zero a 35) - e extrairemos a raiz quadrada do valor resultante. Assim, obtemos o valor de Sx. O valor de Sy será calculado da mesma maneira. No nosso exemplo, Sx=5839. 098245 e Sy=4610. 181675.
Sx=Summ{(X-M(X))^2}/N
Sy=Summ{(Y-M(Y))^2}/N
r=cov(X,Y)/(Sx* Sy)
em que: |
Agora podemos encontrar o valor do coeficiente de correlação como r=21 253 775.08/(5839. 098245*4610. 181675)=0.789536583. Isto é inferior a um, mas longe de zero. Assim, podemos dizer que o gráfico do balanço correlaciona-se com a linha de tendência valorizada como 0,79. Em comparação a outros sistemas, vamos gradualmente aprender a interpretar os valores do coeficiente de correlação. Na página "Relatórios" do campeonato, este parâmetro é chamado de correlação LR. A única diferença feita para calcular esse parâmetro no âmbito do Campeonato é que o sinal da correlação LR indica a rentabilidade do trade.
A questão é que poderíamos calcular o coeficiente de correlação entre o gráfico de balanço e qualquer reta. Para fins do campeonato, foi calculado para a linha ascendência de tendência, portanto, se a correlação LR estiver acima de zero, a negociação é rentável. Se estiver abaixo de zero, temos perdas. Às vezes, um efeito interessante ocorre quando a conta mostra lucro, mas a correlação LR é negativa. Isto pode significar que o trading está perdendo, de qualquer maneira. Um exemplo de tal situação pode ser visto em Aver's. O Lucro Líquido total faz $2.642, enquanto a correlação LR é -0,11. Não é provável que haja nenhuma correlação, neste caso. Isso significa que apenas não poderíamos julgar sobre o futuro da conta.
MAE e MFE nos dirão muita coisa.
Muitas vezes somos avisados: "Corte as perdas e deixe o lucro crescer". Olhando para os resultados finais do trade, não podemos tirar quaisquer conclusões sobre se as paragens de proteção (Stop Loss) estão disponíveis ou se a fixação de lucro é eficaz. Apenas vemos a data de abertura da posição, a data de fechamento e o resultado final - lucro ou perda. Isto é como julgar uma pessoa baseado em sua data de nascimento ou de morte. Sem saber sobre a flutuação dos lucros durante toda a vida do trade e sobre todas as posições como um total, não podemos julgar sobre a natureza do sistema de trading. O quão arriscado é isto? Como o lucro foi alcançado? O lucro do papel foi perdido? As respostas a estas perguntas podem ser bem fornecidas pelos parâmetros MAE (Excursão adversa máxima) e MFE (Excursão favorável máxima).
Cada posição aberta (até que seja fechada) experimenta continuamente flutuações de lucro. Todo o trade atinge seu lucro máximo e sua perda máxima durante o período entre a sua abertura e seu fechamento. MFE mostra o movimento de preço máximo em uma direção favorável. Respectivamente, MAE mostra o movimento de preço máximo em uma direção adversa. Seria lógico medir ambos os índices em pontos. No entanto, se diferentes pares de moedas foram negociados, vamos ter que expressar isto em termos financeiros.
Todo trade fechado corresponde ao seu resultado (regresso) e dois índices - MFE e MAE. Se o trade resultou em lucro de $100, atingindo MAE - $1000, este não fala por esta melhora do trade. A disponibilidade de muitos trades resultou em lucros, mas ter grandes valores negativos de MAE por trade, nos informa que o sistema apenas "aguarda" perder posições. Este trading está fadado ao fracasso, mais cedo ou mais tarde.
Da mesma forma, os valores de MFE podem fornecer informações úteis. Se uma posição foi aberta na direção certa, o MFE por trade chega a $3000, mas o trade foi então fechado resultando no lucro de $500, podemos dizer que seria bom para elaborar o sistema de proteção de lucro não fixo. Isto pode parar de seguir o que podemos mover após o preço, se o último se mover em uma direção favorável. Se lucros curtos forem sistemáticos, o sistema pode ser significativamente melhorado. O MFE nos informará sobre isto.
Para a análise visual ser mais conveniente, seria melhor usar uma representação gráfica da distribuição dos valores de MAE e MFE. Se impusermos cada trade em um gráfico, veremos como o resultado foi obtido. Por exemplo, se olharmos os "Relatórios" do RobinHood novamente,que não teve nenhum trade com perdas, veremos que cada trade teve um levantamento de crédito (MAE) de -$120 a -$2500.
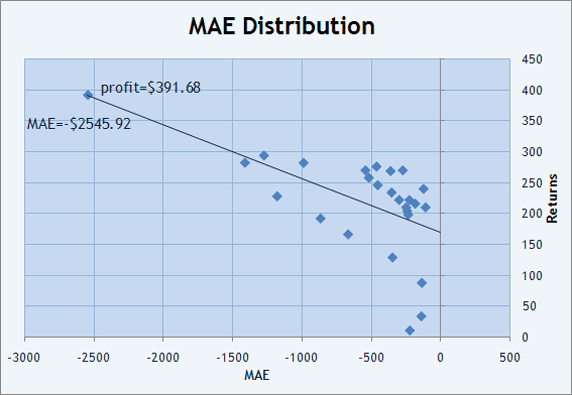
Figura 11. Distribuição de trades no plano de MAExReturns
Além disso, podemos traçar uma linha reta adequar a distribuição dos Retornos x MAE utilizando o método LS. Na Fig. 11, isto é mostrado em vermelho e tem uma inclinação negativa (os valores retos diminuem quando se movem da esquerda para a direita). A correlação de parâmetros (lucros, MAE) =-0,59 nos permite estimar o quão perto da reta os pontos estão distribuídos no gráfico. O valor negativo mostra inclinação negativa da linha de ajuste.
Se você olhar através das contas de outros participantes, você verá que o coeficiente de correlação é geralmente positivo. No exemplo acima, a inclinação descendente da linha nos diz que ela tende a receber mais e mais levantamentos de crédito a fim de não permitir a perda de trades. Agora podemos entender qual preço foi pago pelo valor ideal do parâmetro de correlação LR=1!
Da mesma forma, podemos construir um gráfico de distribuição dos retornos e MFE, bem como encontrar os valores de correlação (lucros, MFE)=0,77 e Correlação(MFE, MAE)=-0,59. A correlação (lucros, MFE) é positiva e tende a um (0,77). Isso nos informa que a estratégia tenta não permitir que lucros flutuantes "esperem". É mais provável que o lucro não seja permitido de crescer o suficiente e que os trades sejam fechados pelo Take Profit. Como você pode ver, as distribuições de MAE e MFE д nos dá uma estimativa visual e os valores de correlação (lucros, MFE) podem nos informar sobre a natureza do trading, mesmo sem os gráficos.
Os valores de correlação (MFE, MAE), correlação (lucros normalizados, MAE) e correlação (lucros normalizados, MFE) nos "Relatórios" dos participantes do campeonato são fornecidos como informação adicional.
Normalização dos resultados do trade
No desenvolvimento de sistemas de trading, eles costumam usar tamanhos fixos para posições. Isto permite uma optimização mais fácil dos parâmetros do sistema, a fim de encontrar os mais otimizados em determinados critérios. No entanto, após as entradas serem encontradas, a pergunta lógica ocorre: Qual dimensionamento do sistema de gestão (Gestão financeira, MM) deve ser aplicado? O tamanho das posições abertas se relacionam diretamente com a quantidade de dinheiro na conta, portanto, não seria razoável negociar na conta com $5000 da mesma forma que naquela com $50000. Além disso, um sistema de gerenciamento financeiro (ММ) pode abrir posições que não sejam diretamente proporcionais. Quero dizer que uma posição aberta na conta com $50000 não deve ser necessariamente 10 vezes mais do que a aberta em um depósito de $5000.
Os tamanhos da posição também podem variar de acordo com a fase atual do mercado, para os resultados da última análise de vários trades e assim por diante. Assim, o sistema de gestão financeira aplicado pode alterar essencialmente a aparência inicial de um sistema de trading. Como podemos, então, estimar o impacto do sistema de gestão financeiro aplicado? Seria útil ou se ele apenas agravaria os lados negativos da nossa abordagem de trading? Como podemos comparar os resultados de trade em várias contas com o mesmo tamanho do depósito inicial? Uma possível solução seria a normalização dos resultados de trade.
NP=TradeProfit/TradeLots*MinimumLots em que: |
A normalização será realizada da seguinte forma: Vamos dividir o resultado de cada trade (lucro ou prejuízo) pelo volume da posição e, em seguida, multiplicaremos pelo tamanho da posição mínima permitida. Por exemplo, ordem #4399142 COMPRA 2,3 lotes USDJPY foi fechada com lucro de $4056. 20 + $118,51 (troca) = $4.174.71. Este exemplo foi pego da conta do GODZILLA (Nikolay Kositsin). Vamos dividir o resultado por 2,3 e multiplicar por 0,1 (o tamanho mínimo permitido de posição), e obter um lucro de $ 4.056,20/2,3*0, = $176,36 e trocas = $ 5,15. Estes seriam resultados para a ordem de grandeza de 0,1-lote. Vamos fazer o mesmo com os resultados de todos os trades e vamos então obter lucros normalizados (NP).
A primeira coisa que pensamos é encontrar valores de correlação (lucros normalizados, MAE) e Correlação (lucros normalizados, MFE) e compará-los com a correlação inicial (lucros, MAE) e correlação (lucros, MFE). Se a diferença entre os parâmetros for significativa, o método aplicado provavelmente alterou essencialmente o sistema inicial. Eles dizem que a aplicação do ММ pode "matar" um sistema rentável, mas não pode transformar um sistema de perdas em um sistema rentável. No Campeonato, a conta do TMR é uma rara exceção onde a mudança de correlação (Lucros normalizados, MFE) de 0,23 a 0,63 permitiu que o operador "fechasse no preto".
Como podemos estimar a agressão da estratégia?
Podemos nos beneficiar ainda mais a partir de trades normalizados na medição de como o método MM aplicado influência a estratégia. É evidente que o aumento da dimensão das posições em 10 vezes causará diferenças no resultado em relação ao resultado inicial de 10 vezes. E se mudarmos os tamanhos dos trades não por um determinado número de vezes, mas dependendo dos desenvolvimentos atuais? Os resultados obtidos por empresas de gestão de confiança são geralmente comparados a um determinado modelo, geralmente a um índice de ações. OCoeficiente Beta nos mostra quantas vezes as mudanças de depósito mudam em comparação com o índice Se tomarmos trades normalizados como um índice, seremos capazes de saber quão mais volátil os resultados tornaram-se em comparação com o sistema inicial (0,1-lote trades).
Assim, em primeiro lugar, calculamos a covariância - cov (lucros, lucros normalizados), em seguida, calcula-se a dispersão de trades normalizados nomeando a sequência de trades normalizados como NP. Para isso, vamos calcular a expectativa matemática de trades normalizadas nomeados M(NP). M(NP) mostra o resultado médio do trade para trades normalizados. Então, encontraremos o SSD dos trades normalizados a partir de M(NP), ou seja, vamos resumir (NP-M(NP))^2. O resultado obtido será então dividido pela quantidade de trades e nome D(NP). Esta é a dispersão dos trades normalizados. Vamos dividir a covariância entre o sistema em medição, lucros, e o índice ideal, lucros normalizados cov (lucros, lucros normalizados), pelo índice de dispersão D(NP). O resultado será o valor do parâmetro que nos permitirá estimar quantas vezes mais volátil o capital está em relação aos resultados dos trades originais (Trades no campeonato) em comparação com os trades normalizados. Este parâmetro é chamado de Composto financeiro nos "Relatórios". Ele mostra o nível de agressão do trading até certo ponto.
MoneyCompounding=cov(Profits, NP)/D(NP)= M((Profits-M(Profits))*(NP-M(NP)))/M((NP-M(NP))^2) em que: |
Agora, podemos rever a maneira que lemos a tabela de participantes do Campeonato de Trading Automatizado 2006:
| # | Login | Erro padrão LR, $ | Correlação LR | Sharpe | GHPR | Z-score (%) | Composto financeiro | Lucro, $ |
|---|---|---|---|---|---|---|---|---|
| 1 | Rich | 6 582.66 | 0,81 | 0,41 | 2,55 | -3.85(99.74) | 17,27 | 25 175.60 |
| 2 | ldamiani | 5 796.32 | 0,64 | 0,21 | 2,89 | -2,47 (98.65) | 28,79 | 15 628.40 |
| 3 | GODZILLA | 2 275.99 | 0,9 | 0,19 | 1,97 | 0.7(51.61) | 16,54 | 11 378.70 |
| 4 | valvk | 3 938.29 | 0,89 | 0,22 | 1,68 | 0.26(20.51) | 40,17 | 9 819.40 |
| 5. | Hendrick | 3 687.37 | 0,79 | 0,24 | 1,96 | 0.97(66.8) | 49,02 | 9 732.30 |
| 6 | bvpbvp | 9 208.08 | 0,58 | 0,43 | 12,77 | 1.2(76.99) | 50,00 | 8 236.00 |
| 7 | Flame | 2 532.58 | 0,75 | 0,36 | 3,87 | -2.07(96.06) | 6,75 | 7 676.20 |
| 8 | Berserk | 1 943.72 | 0,68 | 0,20 | 1,59 | 0.69(50.98) | 17,49 | 7 383.70 |
| 9 | vgc | 905,10 | 0,95 | 0,29 | 1,63 | 0.58(43.13) | 8,06 | 6 801.30 |
| 10 | RobinHood | 109,11 | 1,00 | 3,07 | 1,74 | N/A (N/A) | 41,87 | 5 643.10 |
| 11 | alexgomel | 763,76 | 0,95 | 0,43 | 2,63 | 1.52(87.15) | 10,00 | 5 557.50 |
| 12 | LorDen | 1229,40 | 0,8 | 0,33 | 3,06 | 1.34(81.98) | 49,65 | 5 247.90 |
| 13 | systrad5 | 6 239.33 | 0,66 | 0,27 | 2,47 | -0.9(63.19) | 42,25 | 5 141.10 |
| 14 | emil | 2 667.76 | 0,77 | 0,21 | 1,93 | -1.97(95.12) | 12,75 | 4 658.20 |
| 15 | payday | 1686,10 | 0,75 | 0,16 | 0,88 | 0.46(35.45) | 10,00 | 4 588.90 |
O erro padrão LR nas contas dos vencedores não era o menor. Ao mesmo tempo, os gráficos de equilíbrio dos Expert Advisors mais rentáveis eram suavizados já que os valores de correlação LR não estavam longe de 1,0. A taxa Sharpe estava praticamente entre 0,20 e 0,40. O único EA com taxa Sharpe extrema=3,07 não obteve valores muito bons de MAE e MFE.
O GHPR por trade é basicamente localizado dentro da faixa de 1,5 a 3%. Com isso, os vencedores não tiveram os maiores valores de GHPR, embora não sejam os mais pequenos. O valor extremo GHPR=12,77% nos diz mais uma vez que houve uma anormalidade no trading, e podemos ver que esta conta registrou as maiores flutuações com erro Padrão LR=$9.208,08.
Z-score não nos dá qualquer generalização sobre os primeiros 15 participantes do campeonato, mas os valores de | Z |> 2,0 podem chamar nossa atenção para o histórico de trading a fim de compreendermos a natureza da dependência entre trades na conta. Assim, sabemos que Z=-3,85 para a conta do Rich foi foi praticamente atingido devido à abertura simultânea de três posições. E como estão as coisas com a conta do Idamiani ?
Finalmente, a última coluna na tabela acima, Composto financeiro, também tem uma grande gama de valores de 8 a 50, sendo 50 o valor máximo para este campeonato já que o tamanho máximo de trade permitido é 5,0 lotes, o que é 50 vezes mais do que o dimensão mínima de 0,1 lote. No entanto, curiosamente, este parâmetro não é o maior dos vencedores. Os três valores mais altos são 17,27, 28,79 e 16,54. Os vencedores não utilizaram completamente o tamanho máximo permitido de posição? Sim, utilizaram. A questão é, talvez, que os métodos de MM não influenciaram consideravelmente os riscos de trading cada vez maiores nos tamanhos dos contratos. Esta é uma evidência visível de que a gestão financeira é muito importante para um sistema de trading.
O 15º lugar foi ganho por payday. O EA deste participante não poderia abrir trades de tamanho maior que 1. Lote 0 devido a um pequeno erro no código. E se esse erro não ocorreu e os tamanhos de posição aumentaram 5 vezes, até 5,0 lotes? Então o lucro aumentaria proporcionalmente, de $4.588,90 a $22.944,50? Será que o participante, em seguida, ganharia o segundo lugar ou sofreria um levantamento de crédito irrecuperável devido ao aumento dos riscos? alexgomel estaria em primeiro lugar? O EA dele negociou, também, apenas com trades 1,0-лот. Ou vgc poderia ser o vencedor? O Expert Advisor dele, frequentemente, abriu trades com o tamanho menor que 1,0 lote. Todos os três têm um bom gráfico de balanço suavizado. Como você pode ver, o enredo do campeonato continua mesmo tendo terminado!
Conclusão: Não jogue fora o que você tem de bom
As opiniões divergem. Este artigo fornece algumas abordagens muito gerais para estimativa de estratégias de trading. Pode-se criar muitos mais critérios para estimar resultados de trade. Cada característica, isoladamente, não irá fornecer uma estimativa completa e objetiva, mas em conjunto, podem nos ajudar a evitar a abordagem desequilibrada nesta matéria.
Podemos dizer que podemos submeter a um "interrogatório" qualquer resultado positivo (um lucro obtido em uma seqüência suficiente de trades), a fim de detectar pontos negativos na negociação. Isto significa que todas essas características não caracterizam muito a eficiência da estratégia de trading fornecida como nos informam sobre pontos fracos no trading em que devemos prestar atenção, sem estar satisfeito com apenas um resultado final positivo - o lucro líquido obtido na conta.
Bem, não podemos criar um sistema de trading ideal, cada sistema tem seus benefícios e implicações. O teste de estimativa não é usado para rejeitar uma abordagem de trading dogmaticamente, mas para saber como realizar um maior desenvolvimento dos sistemas de trading e Expert Advisors. A este respeito, os dados estatísticos acumulados durante o Campeonato de Trading Automatizado 2006 serão de grande utilidade para os operadores.
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/1492
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
 Romper o limite do verificador de estratégia em testes de cobertura do EA
Romper o limite do verificador de estratégia em testes de cobertura do EA
 Como cortar um Código de EA para uma vida mais fácil e menos erros
Como cortar um Código de EA para uma vida mais fácil e menos erros
 Modelo Universal do Expert Advisor
Modelo Universal do Expert Advisor
 Verificador no terminal MetaTrader 4: Deve-se saber
Verificador no terminal MetaTrader 4: Deve-se saber
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso