
Mathematik im Trading: Wie man Handelsergebnisse einschätzt
Nassim N. Taleb
Einführung: Mathematik ist die Königin der Wissenschaften
Ein gewisses Maß an mathematischem Hintergrund ist für jeden Trader erforderlich, und diese Aussage braucht keine Beweise. Die Frage ist nur: Wie können wir dieses erforderliche Mindestniveau definieren? Mit dem Wachstum seiner oder ihrer Handelserfahrung, erweitern Trader häufig "eigenhändig" ihren Ausblick, lesen Beiträge in Foren oder in verschiedenen Büchern. Einige Bücher erfordern ein niedrigeres Niveau an mathematischem Hintergrund der Leser, einige, im Gegensatz, inspirieren zum Lernen oder dem Auffrischen des eigenen Wissens in einem Bereich der theoretischer Wissenschaften oder anderer. Wir werden versuchen einige Einschätzungen und deren Interpretationen in diesem einzelnen Artikel zu geben.
Von zwei Übeln das Kleinere wählen
Es gibt mehr Mathematiker auf der Welt als erfolgreiche Trader. Diese Tatsache wird oft als Argument verwendet, bei diesen entgegengesetzten komplexen Berechnungen und Methoden im Trading. Wir können dagegen sagen, dass Trading nicht nur die Fähigkeit Handelsregeln zu entwickeln (analytische Fähigkeiten) ist, sondern außerdem die Fähigkeit diese Regeln zu beachten (Disziplin). Außerdem wurde eine Theorie, welche die Preisgestaltung an den Finanzmärkten genau beschreibt, bis jetzt nicht erstellt (ich denke, sie wird nie erstellt werden). Das Aufstellen der Theorie (Entdeckung der mathematischen Natur) der Finanzmärkte selbst, würde den Tod dieser Märkte bedeuten, was ein unentscheidbares Paradoxon ist, in Bezug auf die Philosophie. Werden wir jedoch vor die Frage gestellt, ob wir an den Markt gehen mit einer nicht ganz zufriedenstellenden mathematischen Beschreibung des Marktes, oder ohne jegliche Beschreibung überhaupt, dann wählen wir das kleinere Übel: Wir wählen die Methode der Prognose von Handelssystemen.
Was ist die Abweichung der Normalverteilung?
Einer der Grundbegriffe in der Wahrscheinlichkeitstheorie ist der Begriff der Normalverteilung (Gaußsche). Warum ist sie so benannt? Es stellte sich heraus, dass viele natürliche Prozesse normal verteilt sind. um genauer zu sein, die meisten natürlichen Prozesse reduzieren, an der Grenze, auf Normalverteilung. Betrachten wir ein einfaches Beispiel. Angenommen wir haben eine gleichmäßige Verteilung im Intervall von 0 bis 100. Gleichmäßige Verteilung bedeutet, dass die Wahrscheinlichkeit des Fallens von jedem Wert auf dem Intervall und die Wahrscheinlichkeit, dass 3,14 (Pi) fallen wird, die gleiche ist wie das Fallen von 77 (meine Lieblingszahl mit zwei Siebenen): Moderne Computer helfen eine ziemlich gute Pseodozufallszahl-Folge zu erzeugen.
Wie können wir Normalverteilung dieser gleichmäßigen Verteilung erhalten? Es stellt sich heraus, dass, wenn wir jedes Mal mehrere zufällige Zahlen (zum Beispiel 5 Zahlen) aus einer einzigartigen Verteilung nehmen und den Mittelwert dieser Zahlen finden (dies wird als 'eine Probe nehmen' bezeichnet), und wenn die Anzahl solcher Proben groß ist, die neu erhaltene Verteilung zu Normal neigen wird. Der zentrale Grenzwertsatz besagt, dass sich die nicht nur auf aus der einzigartigen Verteilung genommenen Proben bezieht, sondern auch auf eine sehr große Klasse anderer Verteilungen. Da die Eigenschaften der Normalverteilung sehr gut untersucht wurden, wird es viel einfacher sie zu analysieren, wenn sie als Prozess mit Normalverteilung dargestellt werden. Jedoch, sehen ist glauben, also können wir die Bestätigung dieses zentralen Grenzwertsatzes mit eine einfachen MQL4 Indikator sehen.
Starten wir diesen Indikator auf jedem Chart mit verschiedenen N (Anzahl der Proben) Werten, sehen wir, dass die empirische Häufigkeitsverteilung glatter und glatter wird.
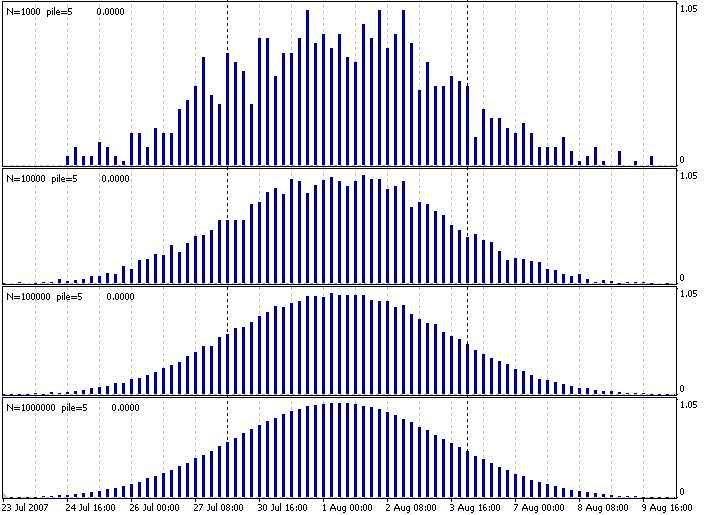
Abb.1. Indikator, der eine Normalverteilung aus einer gleichmäßigen erzeugt.
Hier bedeutet N wie oft wir den Mittelwert von pile=5 gleichmäßig verteilter Zahlen auf dem Intervall 0 bis 100 genommen haben. Wir erhalten vier Diagramme, sehr ähnlich in der Erscheinung. Wenn wir sie irgendwie an der Grenze normalisieren (verbunden mit einem Maßstab), erhalten wir mehrere Umsetzungen der Standard Normalverteilung. Das einzige Haar in der Suppe ist, dass die Kursgestaltung an den Finanzmärkten (genauer Kurs-Schritte und andere Ableitungen von diesen Schritten), allgemein gesprochen, mit in die Normalverteilung passt. Die Wahrscheinlichkeit eines eher seltenen Ereignisses (z.B. das der Kurs um 50% abnimmt) an den Finanzmärkten ist, wenn auch niedrig, dennoch deutlich höher als bei der Normalverteilung. Deshalb sollte man daran denken, wenn man die Risiken auf Grundlage der Normalverteilung einschätzt.
Quantität verwandelt sich in Qualität
Selbst dieses einfache Beispiel der Normalverteilung-Modellierung zeigt, dass die zu verarbeitende Datenmenge viel zählt. Je mehr ursprüngliche Daten es gibt, desto präziser und gültig ist das Ergebnis. Die kleinste Zahl in der Probe wird betrachtet, als habe sie 30 überschritten. Es bedeutet, dass, wenn wir die Ergebnisse von Trades einschätzen wollen (z.B. ein Expert Advisor im Tester), die Anzahl an Trades unter 30 unzureichend ist um statistische Schlussfolgerungen über einige Parameter des Systems zu ziehen. Je mehr Trades wir analysieren, desto geringer ist die Wahrscheinlichkeit, dass diese Trades nur glücklich ausgebrochene Elemente eines ansonsten nicht sehr zuverlässigen Handelssystems sind. Infolgedessen bietet der endgültige Gewinn aus einer Reihe von 150 Trades mehr Gründe zur Umsetzung des Systems in den Betrieb, als ein System, das nur auf 15 Trades eingeschätzt wird.
Mathematische Erwartung und Streuung als Risikoeinschätzung
Die zwei wichtigsten Eigenschaften einer Verteilung sind die mathematische Erwartung (Mittelwert) und die Streuung. Die Standard Normalverteilung hat eine mathematische Erwartung gleich Null. Dabei befindet aich das Verteilzentrum auch bei Null. Flachheit und Steilheit der Normalverteilung sind gekennzeichnet durch das Maß der Ausbreitung eines zufälligen Wertes innerhalb des mathematischen Erwartungsbereichs. Es es die Streuung, die uns zeigt wie Werte sich über die zufälligen Werte mathematischer Erwartung ausbreiten.
Mathematische Erwartungen können auf eine einfache Weise leicht gefunden werden: Für zählbare Reihen werden alle Verteilungswerte summiert, die erhaltene Summe wird geteilt durch die Anzahl an Werten. Zum Beispiel, eine Reihe natürlicher Zahlen ist unendlich, aber zählbar, da jeder Wert mit seinem Index (Order-Nummer) abgeglichen werden kann. Für unzählbare Reihen wird Integration angewendet. Um die mathematische Erwartung einer Reihe von Trades einzuschätzen, summieren wir alle Trade-Ergebnisse und teilen den erhaltenen Betrag durch die Anzahl der Trades. Der erhaltene Wert zeigt das erwartete durchschnittliche Ergebnis von jedem Trade. Wenn die mathematische Erwartung positiv ist, profitieren wir im Durchschnitt. Wenn er negativ ist, verlieren wir im Durchschnitt.
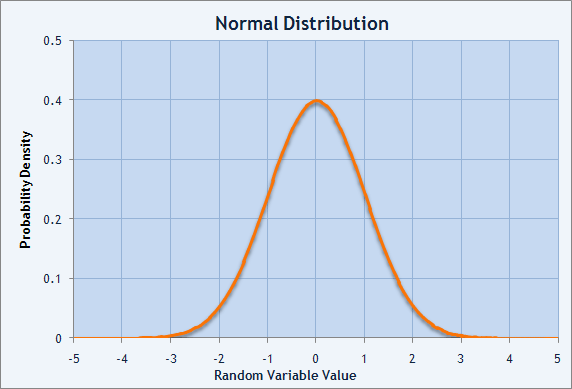
Abb.2. Diagramm der Wahrscheinlichkeitsdichte der Normalverteilung.
Das Maß für die Streuung der Verteilung ist sie Summe der quadrierten Abweichungen des zufälligen Werts von seiner mathematischen Erwartung. Diese Eigenschaft der Verteilung wird Dispersion genannt. Normalerweise wird die mathematische Erwartung für einen zufällig verteilten Wert M(X) genannt. Dann kann Dispersion beschrieben werden als D(X) = M((X-M(X))^2 ). Die Quadratwurzel der Dispersion wird Standardabweichung genannt. Sie wird auch als Sigma (σ) definiert. Es ist eine Normalverteilung mit mathematischer Erwartung gleich Null und Standardabweichung gleich 1, die Normal- oder Gaußsche Verteilung genannt wird.
Je höher der Wert der Standardabweichung ist, desto mehr änderbar ist das Handelskapital, desto höher ist sein Risiko. Wenn die mathematische Erwartung positiv ist (eine profitable Strategie) und gleich $100, und wenn de Standardabweichung gleich $500 ist, riskieren wir eine Summe, die ein Vielfaches größer ist, für jeden verdienten Dollar. Zum Beispiel, wir haben die Ergebnisse von 30 Trades::
|
|
|---|
Um die mathematische Erwartung für die Abfolge von Trades zu finden, summieren wir alle Ergebnisse und teilen dieses durch 30. Wir erhalten den Mittelwert M(X) gleich $4,26. Um die Standardabweichung zu ermitteln, subtrahieren wir den Durchschnitt von jedem Trade-Ergebnis, quadrieren es und finden die Summe der Quadrate. Der erhaltene Wert wird durch 29 geteilt (Anzahl der Trades minus eins). So erhalten wir die Dispersion D gleich 9 353,623. Mit der erzeugten Quadratwurzel der Dispersion erhalten wir die Standardabweichung, Sigma, gleich $96,71.
Die Prüfdaten sind in der folgenden Tabelle angegeben:
| Trade Nummer |
X (Ergebnis) |
X-M(X) (Differenz |
(X-M(X))^2 (Quadrat der Differenz) |
|---|---|---|---|
| 1 | -17.08 | -21.34 | 455.3956 |
| 2 | -41.00 | -45.26 | 2 048.4676 |
| 3 | 147.80 | 143.54 | 20 603.7316 |
| 4 | -159.96 | -164.22 | 26 968.2084 |
| 5 | 216.97 | 212.71 | 45 245.5441 |
| 6 | 98.30 | 94.04 | 8 843.5216 |
| 7 | -87.74 | -92.00 | 8 464.00 |
| 8 | -27.84 | -32.10 | 1 030.41 |
| 9 | 12.34 | 8.08 | 65.2864 |
| 10 | 48.14 | 43.88 | 1 925.4544 |
| 11 | -60.91 | -65.17 | 4 247.1289 |
| 12 | 10.63 | 6.37 | 40.5769 |
| 13 | -125.42 | -129.68 | 16 816.9024 |
| 14 | -27.81 | -32.07 | 1 028.4849 |
| 15 | 88.03 | 83.77 | 7 017.4129 |
| 16 | 32.93 | 28.67 | 821.9689 |
| 17 | 54.82 | 50.56 | 2 556.3136 |
| 18 | -160.10 | -164.36 | 27 014.2096 |
| 19 | -83.37 | -87.63 | 7 679.0169 |
| 20 | 118.40 | 114.14 | 13 027.9396 |
| 21 | 145.65 | 141.39 | 19 991.1321 |
| 22 | 48.44 | 44.18 | 1 951.8724 |
| 23 | 77.39 | 73.13 | 5 347.9969 |
| 24 | 57.48 | 53.22 | 2 832.3684 |
| 25 | 67.75 | 63.49 | 4 030.9801 |
| 26 | -127.10 | -131.36 | 17 255.4496 |
| 27 | -70.18 | -74.44 | 5 541.3136 |
| 28 | -127.61 | -131.87 | 17 389.6969 |
| 29 | 31.31 | 27.05 | 731.7025 |
| 30 | -12.55 | -16.81 | 282.5761 |
Was wir erhalten haben ist die mathematische Erwartung gleich $4,26 und eine Standardabweichung von$96,71. Das ist nicht das beste Verhältnis zwischen Risiko und dem durchschnittlichen Trade. Das folgende Profit Chart bestätigt dies:
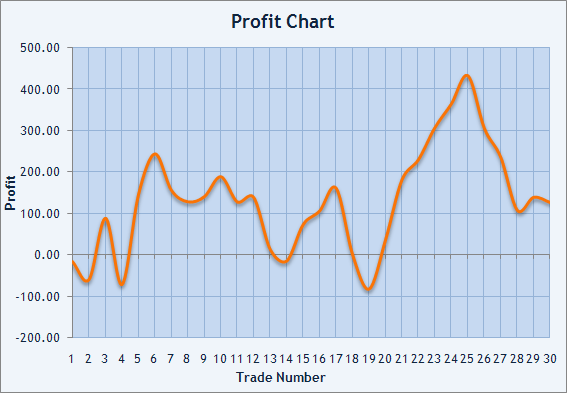
Abb.3. Kontostand-Diagramm für ausgeführte Trades.
Trade ich zufällig? Z-Score
Die Annahme, dass der Gewinn als Ergebnis einer Reihe von Trade zufällig ist, klingt für die meisten Trader hämisch. Wenn er viel Zeit mit der Suche nach einem erfolgreichen Handelssystem verbringt und beobachtet hat, dass das gefundene System bereits einige echte Gewinne in einer eher begrenzten ergeben hat, nimmt der Trader an einen richtigen Ansatz für den Markt gefunden zu haben. Wie kann er oder Sie annehmen, dass all dies nur zufällig war? Das ist ein wenig zu viel, vor allem für einen Anfänger. Dennoch ist es wichtig die Ergebnisse objektiv einzuschätzen. In diesem Fall kommt wieder die Normalverbreitung wieder zur Rettung.
Wir wissen nicht wie das Ergebnis für jeden Trade sein wird. Wir können nur sagen ob wir Profit(+) machen oder Verluste (-) hinnehmen müssen. Gewinne und Verluste wechseln sich bei verschiedenen Handelssystemen auf unterschiedliche Weise ab. Zum Beispiel, wenn der erwartete Gewinn 5 Mal weniger ist als der erwartete Verlust beim Auslösen des Stop Loss, wäre es sinnvoll zu vermuten, dass profitable Trades (+ Trades) Verlust-Trades (- Trades) deutlich überwiegen werden. Z-Score ermöglicht uns einzuschätzen, wie oft profitable Trade sich mit den verlierenden abwechseln.
Z für ein Handelssystem wird mit der folgenden Formel berechnet:
Z=(N*(R-0.5)-P)/((P*(P-N))/(N-1))^(1/2) wobei: |
Eine Reihe ist eine Folge von Pluszeichen gefolgt von anderen (z.B. +++) oder Minuszeichen (z.B. --). R zählt die Anzahl solcher Reihen.

Abb.4. Vergleich von zwei Reihen mit Gewinnen und Verlusten.
In Abb. 4 wird ein Teil der Folge von Gewinnen und Verlusten des Expert Advisors, der den ersten Platz bei der Automated Trading Championship 2006 belegte in blau gezeigt. Der Z-Score von seinem Wettbewerbs-Konto hat einen Wert von -3,85, die Wahrscheinlichkeit von 99,74% ist in Klammern angegeben. Dies bedeutet, dass mit einer Wahrscheinlichkeit von99,74% Trades auf diesem Konto eine positive Abhängigkeit zwischen sich hatten (Z-Score ist negativ): Ein Gewinn wurde von einem Gewinn gefolgt, ein Verlust wurde von einem Verlust gefolgt. Ist dies der Fall? Diejenigen, die sich die Championship angesehen haben erinnern sich wahrscheinlich, dass Roman Rich seinen Expert Advisor MACD platziert hat, der häufig drei Trades in die gleiche Richtung öffnete.
Eine typische Abfolge von positiven und negativen Werten des zufälligen Werts in der Normalverteilung wird in Rot gezeigt. Wir sehen, dass die Folgen sich unterscheiden. Jedoch, wie können wir diesen Unterschied messen? Z-Score beantwortet die Frage: Enthält Ihre Abfolge von Gewinnen und Verlusten mehr oder weniger Streifen (Gewinn oder Verlust Reihen), als Sie wirklich für eine zufällige Abfolge ohne jede Abhängigkeit zwischen den Trades erwarten können? Wenn der Z-Score nah an Null ist, können wir nicht sagen, dass die Trade-Verteilung sich von der Normalverteilung unterscheidet. Der Z-Score einer Handelsabfolge kann uns über mögliche Abhängigkeit zwischen aufeinander folgende Trades informieren.
Die Werte von Z werden auf die gleiche Weise interpretiert wie die Wahrscheinlichkeit der Abweichung von Null eines zufälligen Werts, verteilt nach der Standard Normalverteilung (Durchschnitt=0, Sigma=1). Wenn die Wahrscheinlichkeit des Fallens ein normalverteilter zufälliger Wert innerhalb des Bereichs von ±3σ 99.74% ist, informiert uns das Fallen dieses Werts außerhalb von diesem Intervall mit der gleichen Wahrscheinlichkeit, dass dieser zufällige Wert nicht zu dieser gegebenen Normalverteilung gehört. Deshalb wird die "3-Sigma Regel" wie folgt gelesen: ein normaler zufälliger Wert weicht von seinem Durchschnitt nicht mehr als 3-Sigma Abstand ab.
Zeichen des Z informieren uns über die Art der Abhängigkeit. Plus bedeutet, dass es höchstwahrscheinlich ist, dass der profitable Trade von einem Verlust gefolgt wird. Minus sagt aus, dass der Gewinn von einem Gewinn gefolgt, ein Verlust wieder von einem Verlust gefolgt wird. Eine kleine Tabelle unten illustriert die Art und die die Wahrscheinlichkeit von Abhängigkeiten zwischen Trades, verglichen mit der Normalverteilung.
| Z-Score | Wahrscheinlichkeit der Abhängigkeit, % | Art der Abhängigkeit |
|---|---|---|
| -3 | 99.73 | Positiv |
| -2.9 | 99.63 | Positiv |
| -2.8 | 99.49 | Positiv |
| -2.7 | 99.31 | Positiv |
| -2.6 | 99.07 | Positiv |
| -2.5 | 98.76 | Positiv |
| -2 | 95.45 | Positiv |
| -1.5 | 86.64 | Unbestimmt |
| -1.0 | 68.27 | Unbestimmt |
| 0.0 | 0.00 | Unbestimmt |
| 1.0 | 68.27 | Unbestimmt |
| 1.5 | 86.64 | Unbestimmt |
| 2.0 | 95.45 | Negativ |
| 2.5 | 98.76 | Negativ |
| 2.6 | 99.07 | Negativ |
| 2.7 | 99.31 | Negativ |
| 2.8 | 99.49 | Negativ |
| 2.9 | 99.63 | Negativ |
| 3.0 | 99.73 | Negativ |
Eine positive Abhängigkeit zwischen Trades bedeutet, dass ein Gewinn einen neuen Gewinn verursachen wird, wohingegen ein Verlust einen neuen Verlust verursachen wird. Eine Negative Abhängigkeit bedeutet, dass einem Gewinn ein Verlust folgen wird, und ein Verlust wird von einem Gewinn gefolgt. Die gefundene Abhängigkeit ermöglicht uns die Größen der zu öffnenden Positionen zu regulieren (idealerweise) oder einige von ihnen zu auszulassen und sie nur virtuell zu öffnen, um die Abfolge der Trades zu verfolgen.
Holding Period Returns (HPR)
In seinem Buch, The Mathematics of Money Management, verwendet Ralph Vince den Begriff des HPR (Holding Period Returns). Ein Trade, der mit einem Gewinn von 10% endet hat den HPR=1+0.10=1.10. Ein Trade, der in mit einem Verlust von 10% endet hat den HPR=1-0. 10=0.90. Sie können den Wert des HPR für einen Trade auch erhalten durch Teilen des Kontostand-Werts, nachdem der Trade geschlossen wurde (BalanceClose), durch den Kontostand beim Öffnen des Trades (BalanceOpen). HPR=BalanceClose/BalanceOpen. So wird für jeden Trade ein Ergebnis als Geld-Begriff und ein Ergebnis als HPR ausgedrückt. Dies ermöglicht uns Systeme unabhängig von der Größe des gehandelten Kontrakts zu vergleichen. Einer der in einem solchen Vergleich verwendeten Indizes ist der Arithmetische Mittel, AHPR (average holding period returns).
Um den AHPR zu finden, müssen wir alle HPRs summieren und das Ergebnis durch die Anzahl der Trades teilen. Betrachten wir diese Berechnungen unter Verwendung des obigen Beispiels mit 30 Trades. Angenommen wir beginnen unser Trading mit $500 auf dem Konto. Machen wir eine neue Tabelle:
| Trade Nummer | Kontostand, $ | Ergebnis, $ | Kontostand beim Schließen, $ | HPR |
|---|---|---|---|---|
| 1 | 500.00 | -17.08 | 482.92 | 0.9658 |
| 2 | 482.92 | -41.00 | 441.92 | 0.9151 |
| 3 | 441.92 | 147.8 | 589.72 | 1.3344 |
| 4 | 589.72 | -159.96 | 429.76 | 0.7288 |
| 5 | 429.76 | 216.97 | 646.73 | 1.5049 |
| 6 | 646.73 | 98.30 | 745.03 | 1.1520 |
| 7 | 745.03 | -87.74 | 657.29 | 0.8822 |
| 8 | 657.29 | -27.84 | 629.45 | 0.9576 |
| 9 | 629.45 | 12.34 | 641.79 | 1.0196 |
| 10 | 641.79 | 48.14 | 689.93 | 1.0750 |
| 11 | 689.93 | -60.91 | 629.02 | 0.9117 |
| 12 | 629.02 | 10.63 | 639.65 | 1.0169 |
| 13 | 639.65 | -125.42 | 514.23 | 0.8039 |
| 14 | 514.23 | -27.81 | 486.42 | 0.9459 |
| 15 | 486.42 | 88.03 | 574.45 | 1.1810 |
| 16 | 574.45 | 32.93 | 607.38 | 1.0573 |
| 17 | 607.38 | 54.82 | 662.20 | 1.0903 |
| 18 | 662.20 | -160.10 | 502.10 | 0.7582 |
| 19 | 502.10 | -83.37 | 418.73 | 0.8340 |
| 20 | 418.73 | 118.4 | 537.13 | 1.2828 |
| 21 | 537.13 | 145.65 | 682.78 | 1.2712 |
| 22 | 682.78 | 48.44 | 731.22 | 1.0709 |
| 23 | 731.22 | 77.39 | 808.61 | 1.1058 |
| 24 | 808.61 | 57.48 | 866.09 | 1.0711 |
| 25 | 866.09 | 67.75 | 933.84 | 1.0782 |
| 26 | 933.84 | -127.10 | 806.74 | 0.8639 |
| 27 | 806.74 | -70.18 | 736.56 | 0.9130 |
| 28 | 736.56 | -127.61 | 608.95 | 0.8267 |
| 29 | 608.95 | 31.31 | 640.26 | 1.0514 |
| 30 | 640.26 | -12.55 | 627.71 | 0.9804 |
Der AHPR wird gefunden als arithmetisches Mittel. Er ist glich 1,0217. Mit anderen Worten, wir verdienen durchschnittlich (1.0217-1)*100%=2.17% bei jedem Trade. Ist dies der Fall? Wenn wir 2,17 mit 30 Multiplizieren, dass die Erträge 65,1% ausmachen sollten. Multiplizieren wir den ursprünglichen Betrag von $500 mit 65,1%, erhalten wir $325,50. Gleichzeitig macht der reale Gewinn (627.71-500)/500*100%=25.54%. Also ermöglicht uns dear arithmetische Mittelwert nicht immer ein System richtig einzuschätzen.
Zusammen mit dem arithmetischen Mittelwert, stellt Ralph Vince den geometrischen Mittelwert vor, den wir GHPR (geometric holding period returns) nennen, der praktisch immer weniger ist als der AHPR. Der geometrische Mittelwert ist ein Wachstumsfaktor pro Spiel und wir über die folgende Formel ermittelt:
GHPR=(BalanceClose/BalanceOpen)^(1/N) wobei: |
Das System mit dem größten GHPR wird die höchsten Gewinne erzielen, wenn wir auf der Grundlage der Wiederanlage handeln. Der GHPR unter Eins bedeutet, dass das System Geld verlieren wird, wenn wir auf Grundlage der Wiederanlage traden. Eine gute Illustration des Unterschieds zwischen AHPR und GHPR kann sashken's Kontohistorie sein. Er war lange Zeit der Führende in der Championship. AHPR=9.98% beeindruckt, aber der endgültige GHPR=-27.68% setzt alles in Perspektive.
Sharpe Ratio
Effizienz von Investitionen wird häufig in Bezug auf die Gewinn-Dispersion eingeschätzt. Einer dieser Indizes ist die Sharpe Ratio. Dieser Index, der zeigt wie AHPR zurückging durch den risikofreien Zins (risk-free-Rate - RFR), bezieht sich auf die Standardabweichung (SD) der HPR-Sequenz. Der Wert des RFR wird in der egel gleich zu dem Zinssatz auf die Einzahlung bei der Bank genommen oder dem Zinssatz auf Schatzbriefe. In unserem Beispiel, AHPR=1.0217, SD(HPR)=0.17607, RFR=0.
Sharpe Ratio=(AHPR-(1+RFR))/SD wobei: |
Sharpe Ratio=(1.0217-(1+0))/0.17607=0.0217/0.17607=0.1232. Für Normalverteilung sind über 99% der Zufallswerte innerhalb eines Bereichs von ±3σ (sigma=SD) über den Mittelwert M(X). Daraus folgt, dass ein 3 übersteigender Sharpe Ratio Wert sehr gut ist. In Abb. 5 unten sehen wir, dass, wenn die Handelsergebnisse normal verteilt sind und Sharpe Ratio=3, die Wahrscheinlichkeit eines Verlusts bei unter 1% liegt, der 3-Sigma Regel entsprechend.
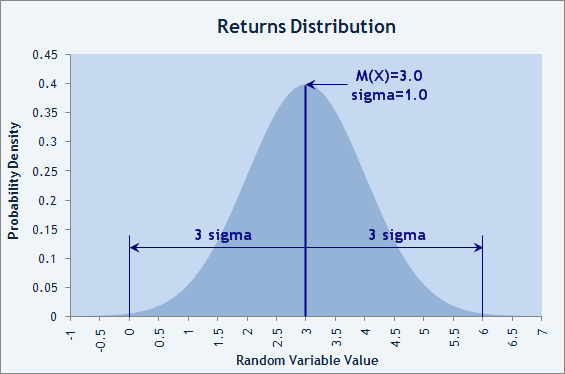
Abb.5. Normalverteilung von Handelsergebnissen mit der Verlust-Wahrscheinlichkeit von weniger als 1%.
Das Konto des Teilnehmers mit dem Namen RobinHood bestätigt dies: sein EA machte 26 Trades bei der Automated Trading Championship 2006 ohne einen Verlust-Trade unter ihnen. Sharpe Ratio=3.07!
Lineare Regression (LR) und Koeffizient der Linearen Korrelation (CLC)
Es gibt noch einen weiteren Weg die Stabilität der Handelsergebnisse einzuschätzen. Sharpe Ratio ermöglicht uns das Risiko einzuschätzen, dem das Kapital ausgesetzt ist. Wenn wir den Wert des Kontostands beim Schließen jon jedem Trade ausblenden, sind wir in der Lage eine gebrochene Linie zu zeichnen. Diese Punkte können mit einer bestimmten geraden Linie verbunden werden, was uns die mittlere Richtung der Kapitalveränderungen zeigen wird. Betrachten wir ein Beispiel dieser Möglichkeit mit dem Kontostand-Diagramm des Expert Advisor Phoenix_4, entwickelt von Hendrick.
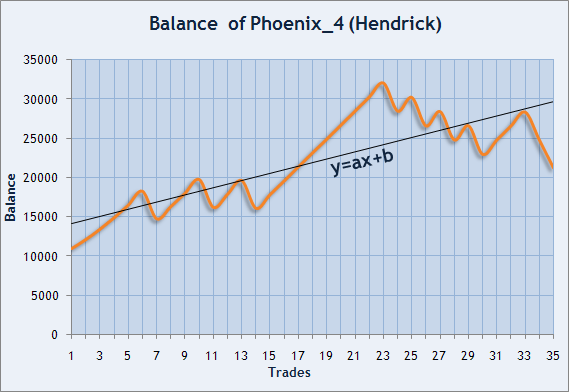
Abb. 6. Kontostand-Diagramm von Hendrick, Teilnehmer bei der Automated Trading Championship 2006.
Wir müssen die Koeffizienten a und b finden, damit diese Linie so nah wie möglich an die Punkte angepasst ist. In unserem Fall ist x die Trade-Nummer, y der Kontostand-Wert beim Schließen des Trades.
|
|
|---|
Koeffizienten einer sich annähernden Geraden werden in der Regel mit der Methode der kleinsten Quadrate (LS Methode - Least Squares Method) gefunden. Angenommen wir haben diese Gerade mit den bekannten Koeffizienten a und b. Für jedes x haben wir zwei Werte: y(x)=a*x+b und balance(x). Abweichung des balance(x) von y(x) wird angegeben als d(x)=y(x)-balance(x). SSD (Summe quadrierter Abweichungen) kann berechnet werden als SD=Summ{d(n)^2}. Das Finden der Geraden mit der LS-Methode bedeutet nach diesen a und b zu suchen, deren SD minimal ist. Die Gerade wird auch als lineare Regression (LR) für die gegebene Sequenz bezeichnet.
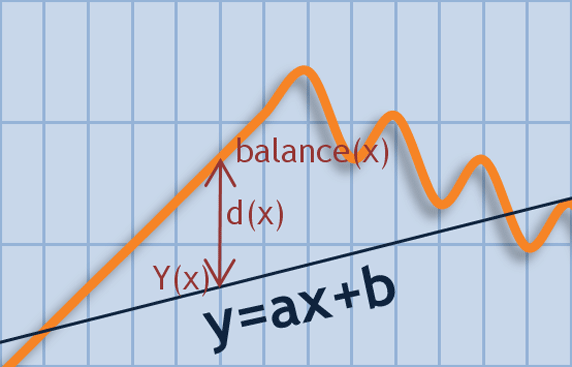
Abb. 7. Kontostand-Wert Abweichung von der Geraden aus y=ax+b
Haben wir die Koeffizienten der Geraden aus y=a*x+b mit der LS-Methode erhalten, können wir die Abweichung des Kontostand-Werts von der gefundenen Geraden in auf den Geldwert bezogen einschätzen. Wenn wir den arithmetischen Mittelwert für die Sequenz d(x) berechnen, werden wir sicher sein, dass M(d(x)) nah an Null ist (um genauer zu sein, gleich Null bis zu einem gewissen Grad der Berechnungsgenauigkeit). Gleichzeitig ist die SSD von SD nicht gleich Null und hat einen bestimmten begrenzten Wert. Die Quadratwurzel von SD/(N-2) zeigt die Ausbreitung von Werten im Kontostand-Diagramm über die Gerade Linie und ermöglicht Handelssysteme bei identischen Werten des ursprünglichen Kontostands einzuschätzen. Wir nennen diesen Parameter LR Standard Error.
Im Folgenden sind die Wertet dieses Parameters für die ersten 15 Konten der Automated Trading Championship 2006:
| # | Login | LR Standard Error, $ | Gewinn, $ |
|---|---|---|---|
| 1 | Rich | 6 582.66 | 25 175.60 |
| 2 | ldamiani | 5 796.32 | 15 628.40 |
| 3 | GODZILLA | 2 275.99 | 11 378.70 |
| 4 | valvk | 3 938.29 | 9 819.40 |
| 5 | Hendrick | 3 687.37 | 9 732.30 |
| 6 | bvpbvp | 9 208.08 | 8 236.00 |
| 7 | Flame | 2 532.58 | 7 676.20 |
| 8 | Berserk | 1 943.72 | 7 383.70 |
| 9 | vgc | 905.10 | 6 801.30 |
| 10 | RobinHood | 109.11 | 5 643.10 |
| 11 | alexgomel | 763.76 | 5 557.50 |
| 12 | LorDen | 1 229.40 | 5 247.90 |
| 13 | systrad5 | 6 239.33 | 5 141.10 |
| 14 | emil | 2 667.76 | 4 658.20 |
| 15 | payday | 1 686.10 | 4 588.90 |
Allerdings, der Grad der Annäherung des Kontostand-Diagramms an eine Geradekann in beidem, Geldwert und absoluter Wert, gemessen werden. Hierzu können wir die Korrelations-Rate verwenden. Die Korrelations-Rate, r, misst den Grad der Korrelation zwischen zwei Sequenzen von Zahlen. Sein Wert kann innerhalb eines Bereichs von - 1 bis +1 liegen. Wenn r=+1 bedeutet dies, das zwei Sequenzen ein identisches Verhalten haben und die Korrelation positiv ist.
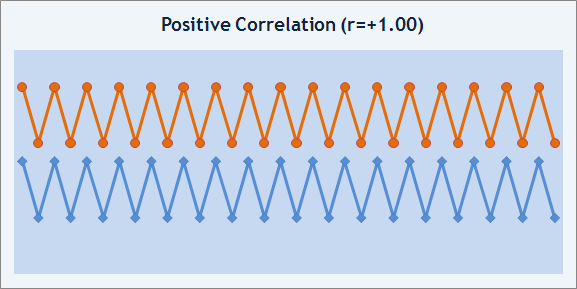
Abb. 8. Beispiel Positive Korrelation.
If r=-1, die zwei Sequenzen ändern sich gegensätzlich, die Korrelation ist negativ.
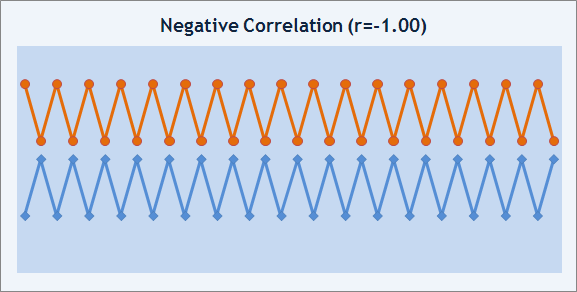
Abb. 9. Beispiel Negative Korrelation.
Wenn r=0 bedeutet dies, dass keine Abhängigkeiten zwischen den Sequenzen gefunden wurden. Es muss betont werden, dass r=0 nichtbedeutet, dass es keine Korrelation zwischen den Sequenzen gibt, es sagt lediglich aus, dass keine Korrelation gefunden wurde. Dass muss beachtet werden. In unserem Fall müssen wir zwei Sequenzen von Zahlen vergleichen: eine Sequenz des Kontostand-Diagramms, die zweite - der entsprechende Punkt aus der Linie der linearen Regression.
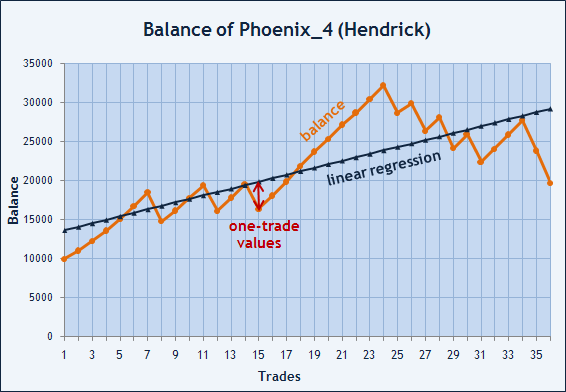
Abb. 10. Werte von Kontostand und Punkten auf linearer Regression.
Die folgende Tabelle stellt die gleichen Daten dar:
|
|
Bezeichnen wir die Kontostand-Werte als X und die Sequenz von Punkten auf der geraden Regressions-Linie als Y. Um den Koeffizienten der linearen Korrelation zwischen den Sequenzen X und Y zu berechnen, ist es zuerst notwendig die Mittelwerte M(X) und M(Y) zu finden. Dann erstellen wir eine neue Sequenz T=(X-M(X))*(Y-M(Y)) und berechnen ihren Mittelwert als M(T)=cov(X, Y)=M((X-M(X))*(Y-M(Y))). Der erhaltene Wert aus cov(X,Y) wird Kovarianz von X und Y genannt und bedeutet mathematische Erwartung des Produkts aus (X-M(X))*(Y-M(Y)). Für unser Beispiel ist der Kovarianz-Wert 21 253 775.08. Bitte beachten Sie, das M(X) und M(Y) gleich sind und jeder den Wert 21 382.26 hat. Es bedeutet, dass der Kontostand Mittelwert und der Durchschnitt der angepassten Geraden gleich sind.
T=(X-M(X))*(Y-M(Y)) M(T)=cov(X,Y)=M((X-M(X))*(Y-M(Y))) wobei: |
Das einzige, was noch gemacht werden muss, ist die Berechnung von Sx und Sy. Um Sx zu berechnen, ermitteln wir die Summe der Werte von (X-M(X))^2, d.h. ermitteln der SSD von X aus seinem Mittelwert. Denken Sie daran, wie wir die Dispersion berechnet haben und den Algorithmus der LS-Methode. Wie Sie sehen, sind sie alle miteinander verwandt. Der ermittelte SSD wird durch die Anzahl der in der Sequenz enthaltenen Zahlen geteilt. - in unserem Fall, 36 (von Null bis 35) - und die Quadratwurzel aus dem Ergebniswert gezogen. Auf diese Weise habe wir den Wert von Sx erhalten. Der Wert von Sy wird auf die gleiche Weise berechnet. In unserem Beispiel, Sx=5839. 098245 und Sy=4610. 181675.
Sx=Summ{(X-M(X))^2}/N
Sy=Summ{(Y-M(Y))^2}/N
r=cov(X,Y)/(Sx* Sy)
wobei: |
Jetzt können wir den Wert des Korrelations-Koeffizienten als r=21 253 775.08/(5839. 098245*4610. 181675)=0.789536583. Dies ist unterhalb von Eins, aber weit von Null. Also können wir sagen, dass das Kontostand-Diagramm mit der Trendlinie als 0,79 bewertet korreliert. Im Vergleich mit anderen Systemen, werden wir allmählich erfahren, wie der Wert des Korrelation-Koeffizient interpretiert wird. Auf der Seite "Reports" der Championship, wird dieser Parameter LR Korrelation genannt. Der einzige gemachte Unterschied um diesen Parameter im Rahmen der Championship zu berechnen ist, dass das Zeichen der LR Korrelation die Handelsrentabilität angibt.
Es handelt sich darum, dass wir den Koeffizienten der Korrelation zwischen dem Kontostand-Diagramm und jeder Geraden berechnen können. Für die Zwecke der Championship wurde er für eine ansteigende Trendlinie berechnet, daher, wenn die LR Korrelation über Null ist, ist das Trading profitabel. Ist sie unter Null, wird es verlieren. Manchmal tritt ein interessanter Effekt auf, wobei das Konto gewinne zeigt, aber die LR-Korrelation negativ ist. Dies kann bedeuten, dass das Trading nicht rentabel ist, trotzdem. Ein Beispiel einer solchen Situation kann bei Aver's gesehen werden. Der Netto Gesamtgewinn beträgt $2.6432, wobei die LR-Korrelation -0,11 ist. Dort ist wahrscheinlich keine Korrelation, in diesem Fall. Es bedeutet, dass wir nicht über die Zukunft des Kontos urteilen können.
MAE und MFE erzählen uns viel
Wir werden oft gewarnt: "Begrenze die Verlust und lass die Gewinne laufen". Mit Blick auf die endgültigen Handelsergebnisse, können wir keine Schlüsse darüber ziehen, ob schützende Stops (Stop Loss) verfügbar sind, oder ob die Gewinn-Fixierung effektiv ist. Wir sehen von der Position nur das Eröffnungsdatum, das Schlussdatum und das endgültige Ergebnis - einen Gewinn oder einen Verlust. Das wäre wie über eine Person zu urteilen, aufgrund ihres Geburts- und Todestages. Ohne Wissen über schwebende Gewinne während der Lebensdauer von jedem Trade und über alle Positionen insgesamt, können wir nicht über die Natur des Handelssystems urteilen. Wie riskant ist es? Wie wurde der Gewinn erreicht? Wurde der Papiergewinn verloren? Antworten auf diese Fragen werden ziemlich gut mit den Parametern MAE (Maximum Adverse Excursion) und MFE (Maximum Favorable Excursion) geliefert.
Jede offene Position (bis sie geschlossen wird) erfährt ständige Ertragsschwankungen. Jeder Trade erreicht seinen maximalen Gewinn und seinen maximalen Verlust, in dem Zeitraum zwischen Öffnen und Schließen. Der MFE zeigt die maximale Kursbewegung in eine günstige Richtung. Entsprechend zeigt der MAE die maximale Kursbewegung in eine ungünstige Richtung. Es wäre logisch beide Indizes in Punkten zu messen. Werden allerding zwei verschiedene Währungspaare gehandelt, müssen wir sie in Geldwert ausdrücken.
Jeder geschlossene Trade entspricht seinem Ergebnis (Return) und zweit Indizes - MFE uns MAE. Wenn ein Trade zu einem Gewinn von $100 führt, MAE -$1000 erreicht, spricht das nicht für den besten Trade. Das Vorhandensein vieler Handelsergebnisse mit Gewinn, aber mit hohen negativen Werten des MAE pro Trade, in formiert uns, dass das System verlierende Positionen einfach "aussitzt". Ein solches Trading wird früher oder später scheitern.
In ähnlicher Weise können uns die Werte des MFE nützliche Informationen zur Verfügung stellen. Wenn eine Position in die richtige Richtung geöffnet wurde, der MFE pro Trade $3000 erreicht hat, aber wurde mit einem Gewinn von $500 geschlossen, können wir sagen, dass es gut wäre das System des nicht festgelegten Gewinnschutz zu überarbeiten. Dies kann ein Trailing Stop sein, den wir dem Kurs hinterher bewegen können, wenn sich letzterer in eine günstige Richtung bewegt. Wenn Short Gewinne systematisch sind, kann das System erheblich verbessert werden. MFE wird uns davon erzählen.
Für eine komfortablere visuelle Analyse, wäre es besser grafische Darstellung der Verteilung der Werte von MFE und MAE zu verwenden. Wenn wir jeden Trade in einem Diagramm anordnen, sehen wie, wie die Ergebnisse zustande gekommen sind. Zum Beispiel, wenn einen weiteren Blick in die "Reports" von RobinHood werfen, der nicht einen Verlust-Trade hatte, werden wir sehen, dass jeder Trade einen Drawdown (MAE) von -$120 bis -$2500 hatte.
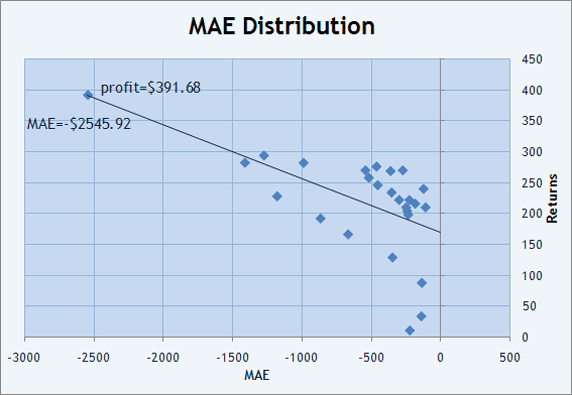
Abb. 11. Trade-Verteilung auf der Ebene von MAExReturns
Außerdem können wir mit der LS-Methode eine gerade Linie ziehen, um die Return x MAE Verteilung anzupassen. In Abb. 11 wird sie in Rot gezeigt und hat eine negative Neigung (die geraden Werte nehmen ab, bei der Bewegung von links nach rechts). Der Parameter Korrelation (Gewinne, MAE)=-0.59 ermöglicht und einzuschätzen, wie nah die Punkte im Diagramm an der geraden Linie verteilt sind. Ein negativer Wert zeigt eine negative Neigung der Anpassungslinie.
Wen Sie die Konten andere Teilnehmer durchsehen, werden Sie feststellen, dass der Korrelation-Koeffizient in der Regel positiv ist. In dem obigen Beispiel sagt uns die abfallende Neigung der Linie, dass es dazu tendiert mehr und mehr Drawdowns zu erhalten, um keine Verlust-Trades zu ermöglichen. Jetzt verstehen wir, welcher Preis für den idealen Parameter-Wert LR-Korrelation =1 bezahlt wurde!
Auf ähnliche Weise können wir ein Diagramm der Erträge und des MFE erstellen, sowie das Ermitteln der Werte von Correlation(Profits, MFE)=0.77 und Correlation(MFE, MAE)=-0.59. Correlation(Profits, MFE) ist positiv und tendiert zu 1 (0.77). Dies informiert uns darüber, dass das System versucht keine lange "aussitzenden" schwebenden Profite zu ermöglichen. Es ist wahrscheinlicher, dass es dem Gewinn nicht möglich ist genug zu wachsen und die Trades durch Take Profit geschlossen werden. Wie Sie sehen können, geben uns die Verteilungen von MFE und MAE eine visuelle Einschätzung und Werte von Correlation(Profits, MFE) und Correlation(Profits, MAE) können uns über die Natur des Handels informieren, auch ohne Charts.
Die Werte von Correlation(MFE, MAE), Correlation(NormalizedProfits, MAE) and Correlation(NormalizedProfits, MFE) werden in den "Reports" der Champioship Teilnehmer als zusätzliche Information angegeben.
Handelsergebnis Normalisierung
Bei der Entwicklung von Handelssystemen verwendet man normalerweise feste Größen für Positionen. Dies ermöglicht eine leichtere Optimierung von System-Parametern, um optimalere in bestimmten Kriterien zu finden. Allerdings, nachdem die Eingaben ermittelt wurden, stellt sich die logische Frage: Welches Sizing-Managemant-System (Money-Management, MM) sollte angewandt werden? Die Größe der geöffneten Positionen bezieht sich direkt auf die Geldmenge auf dem Konto, wodurch es nicht sinnvoll wäre auf einem Konto mit $5.000 auf die gleiche Weise zu handeln, wie auf einem mit $50.000. Darüber hinaus kann ein MM System Positionen öffnen, die nicht direkt proportional sind. Ich meine, eine Position, die auf einem Konto mit $50.000 geöffnet wird muss nicht notwendigerweise 10 Mal größer sein, als auf einem Konto mit $5.000 Einlage.
Positionsgrößen können auch variieren, entsprechend der aktuellen Marktphase, nach den Ergebnissen mehrerer neuer Trade-Analysen, und so weiter. So kann ein angewandtes Money-Management System die ursprüngliche Erscheinung eines Handelssystems wesentlich verändern. Wie können wir den Einfluss des angewendeten Money-Management Systems einschätzen. War es nützlich, oder hat es nur die negativen Seiten von unserem Trading-Ansatz verschlechtert? Wie können wir die Handelsergebnisse auf mehreren Konten mit der gleichen anfänglichen Einzahlungsgröße vergleichen? Eine mögliche Lösung ist die Normalisierung der Handelsergebnisse.
NP=TradeProfit/TradeLots*MinimumLots wobei: |
Die Normalisierung wird wie folgt umgesetzt: Wir teilen jedes Handelsergebnis (Gewinn oder Verlust) durch das Positionsvolumen und multiplizieren dann mit der minimal zulässigen Positionsgröße. Zum Beispiel, Order #4399142 BUY 2,3 Lots USDJPY wurde geschlossen mit einem Gewinn von $4.056,30 + $118,51 (Swaps) = $4.174,71. Das Beispiel wurde von dem Konto GODZILLA (Nikolay Kositsin) entnommen. Teilen wir das Ergebnis durch 2,3 und multiplizieren mit 0,1 (minimale zulässige Positionsgröße), und erhalten einen Gewinn von $4.056,20/2,3 * 0,1 = $176,36 und Swaps $5,15. Dies wäre das Ergebnis für die Order mit 0,1 Lot Größe. Machen wir das gleiche mit allen Trades, erhalten wir die Normalisierten Gewinne (NP - Normalized Profits).
Das erste, worüber wir nachdenken, ist die Ermittlung der Werte von Correlation(NormalizedProfits, MAE) and Correlation(NormalizedProfits, MFE) und vergleichen diesen mit den ursprünglichen Correlation(Profits, MAE) und Correlation(Profits, MFE). Wenn die Differenz zwischen den Parametern deutlich ist, hat die angewandte Methode ds System wahrscheinlich wesentlich geändert. Man sagt, dass die Anwendung eines MM ein profitables System "töten" kann, aber es kann kein verlustbringendes System in ein profitables drehen. Bei der Championship ist das Konto von TMR eine seltene Ausnahme, bei der die Änderung des Correlation(NormalizedProfits, MFE) Wert von 0,23 zu 0,63 es dem Trader ermöglichte in "schwarzen Zahlen zu schließen".
Wie können wir die Aggressivität der Strategie einschätzen?
Wir können noch mehr von normalisierten Trades profitieren, durch die Messung wie die angewandte MM-Methode die Strategie beeinflusst. Es liegt auf der Hand, dass das Erhöhen der Positionsgrößen um das 10-fache, ein endgültiges Ergebnis verursachen wird, dass sich um das 10.fache von dem ursprünglichen unterscheidet. Aber was passiert, wenn wir die Positionsgrößen nicht durch eine gegebene Anzahl ändern, sondern abhängig von den aktuellen Entwicklungen? Erhaltene Ergebnisse von Trust Managing Unternehmen, werden normalerweise nach einem bestimmten Modell verglichen, in der Regel - mit einem Aktien-Index. Der Beta Koeffizient zeigt um wie viele Mal die Konto-Einlage sich ändert, verglichen mit dem Index. Wenn wir normalisierte Trades als Index nehmen, sind wir in der Lage zu wissen, wie viel volatiler die Ergebnisse geworden sind, verglichen mit dem ursprünglichen System (0,1 Lot Trades).
Also, als erstes berechnen wir die Kovarianz - cov(Profits, NormalizedProfits). Dann berechnen wir die Dispersion von normalisierten Trades und benennen die Sequenz der normalisiserten Trades als NP. Dazu werden wir die mathematische Erwartung normalisierter Trades, benannt M(NP), berechnen. M(NP) zeigt das Mittlere Handelsergebnis für normalisierte Trades. Anschließend ermitteln wir die SSD von normalisierten Trades von M(NP), d.h. wir werden (NP-M(NP))^2 summieren. Das erhaltene Ergebnis wird dann geteilt durch die Anzahl an Trades und D(NP) benannt. Dies ist die Dispersion normalisierter Trades. Teilen wir nun die Kovarianz zwischen dem System unter Messen, Gewinne, und dem idealen Index, NormalizedProfits cov(Profits, NormalizedProfits) durch den Index DispersionD(NP). Das Ergebnis ist der Parameter, der es ermöglicht einzuschätzen wie viel Mal volatiler das Kapital ist, als die Ergebnisse der Original-Trades (Trades in der Champioship), verglichen mit normalisierten Trades. Dieser Parameter wird in den "Reports" Money Compounding genannt. Er zeigt in einem gewissen Grad die Handelsaggressivität.
MoneyCompounding=cov(Profits, NP)/D(NP)= M((Profits-M(Profits))*(NP-M(NP)))/M((NP-M(NP))^2) wobei: |
Jetzt können wir die Art und Weise überarbeiten, in der wir die Tabelle der Teilnehmer der Automated Trading Championship 2006 lesen:
| # | Login | LR Standard-Fehler, $ | LR Korrelation | Sharpe | GHPR | Z-Score (%) | Money Compounding | Profit, $ |
|---|---|---|---|---|---|---|---|---|
| 1 | Rich | 6 582.66 | 0.81 | 0.41 | 2.55 | -3.85(99.74) | 17.27 | 25 175.60 |
| 2 | ldamiani | 5 796.32 | 0.64 | 0.21 | 2.89 | -2.47 (98.65) | 28.79 | 15 628.40 |
| 3 | GODZILLA | 2 275.99 | 0.9 | 0.19 | 1.97 | 0.7(51.61) | 16.54 | 11 378.70 |
| 4 | valvk | 3 938.29 | 0.89 | 0.22 | 1.68 | 0.26(20.51) | 40.17 | 9 819.40 |
| 5 | Hendrick | 3 687.37 | 0.79 | 0.24 | 1.96 | 0.97(66.8) | 49.02 | 9 732.30 |
| 6 | bvpbvp | 9 208.08 | 0.58 | 0.43 | 12.77 | 1.2(76.99) | 50.00 | 8 236.00 |
| 7 | Flame | 2 532.58 | 0.75 | 0.36 | 3.87 | -2.07(96.06) | 6.75 | 7 676.20 |
| 8 | Berserk | 1 943.72 | 0.68 | 0.20 | 1.59 | 0.69(50.98) | 17.49 | 7 383.70 |
| 9 | vgc | 905.10 | 0.95 | 0.29 | 1.63 | 0.58(43.13) | 8.06 | 6 801.30 |
| 10 | RobinHood | 109.11 | 1.00 | 3.07 | 1.74 | N/A (N/A) | 41.87 | 5 643.10 |
| 11 | alexgomel | 763.76 | 0.95 | 0.43 | 2.63 | 1.52(87.15) | 10.00 | 5 557.50 |
| 12 | LorDen | 1229.40 | 0.8 | 0.33 | 3.06 | 1.34(81.98) | 49.65 | 5 247.90 |
| 13 | systrad5 | 6 239.33 | 0.66 | 0.27 | 2.47 | -0.9(63.19) | 42.25 | 5 141.10 |
| 14 | emil | 2 667.76 | 0.77 | 0.21 | 1.93 | -1.97(95.12) | 12.75 | 4 658.20 |
| 15 | payday | 1686.10 | 0.75 | 0.16 | 0.88 | 0.46(35.45) | 10.00 | 4 588.90 |
Der LR Standard-Fehler in Sieger-Konten war nicht der kleinste. Gleichzeitig waren die Kontostand-Diagramme der meisten profitablen Expert Advisors ziemlich glatt, da die LR Korrelation Werte nicht weit von 1,0 sind. Die Sharpe Ratio lag im Allgemeinen im Bereich von 0,20 bis 0,40. Der einzige Expert Advisor mit extremer Sharpe Ratio=3,07 stellte sich mit nicht den besten Werten vom MFE und MAE heraus.
Der GHPR pro Trade ist grundsätzlich innerhalb des Bereichs von 1,5 bis 3,0%. Dabei hatte der Gewinner nicht den höchsten Wert des GHPR, aber auch nicht den niedrigsten. Der extreme Wert GHPR=12,77% sagt uns wieder, das es dort eine Anomalie im Handel gab, und wir können sehen, dass dieses Konto die größte Schwankungen erfahren hat mit einem LR Standard-Fehler=$9.208,8.
Der Z-Score gibt uns keine Verallgemeinerungen über die 15 ersten Champioship Teilnehmer, aber Werte von |Z|>2.0 ziehen unsere Aufmerksamkeit auf die Trading-Historie, um die Abhängigkeit zwischen Trades auf dem Konto zu verstehen. Also, wir wissen, dass Z=-3.85 für Rich's Konto praktisch über das gleichzeitige Öffnen von drei Positionen erreicht wurde. Und wie stehen die Dinge mit ldamiani's Konto?
Schließlich hat auch die letzte Spalte in der obigen Tabelle, Money Compounding, einen großen Bereich von 8 bis 50. 50 ist der maximale Wert für diese Championship, da die maximal zulässige Positionsgröße 5,0 Lots war, was 50 Mal mehr ist als die minimale Positionsgröße von 0,1 Lot. Dieser Parameter ist jedoch, seltsamerweise, nicht der höchste bei den Gewinnern. Die Werte der Top Drei sind 17,27, 28,79 und 16,54. Haben die Sieger nicht die maximal zulässige Positionsgröße verwendet? Ja, taten sie. Die Sache ist die, vielleicht, dass die MM Methoden die Handelsrisiken bei der allgemeinen Erhöhung der Kontraktgrößen nicht wesentlich beeinflusst hat. Dies ist ein sichtbarer Beweis dafür, dass Money-Management für das Handelssystem sehr wichtig ist.
Der 15. Platz wurde von payday belegt. Der Es dieses Teilnehmers konnte keine Trades größer als 1,0 Lot öffnen, durch einen kleinen Fehler im Code. Was, wenn dieser Fehler nicht aufgetreten und die Positionsgrößen wären um das 5-fache erhöht worden, bis zu 5,0 Lots? Wäre der Gewinn dann proportional angestiegen, von $4.588,90 auf $22.944,50? Hätte der Teilnehmer dann den zweiten Platz belegt oder hätte er einen unwiederbringlichen Verlust aufgrund der erhöhten Risiken erlitten? Wäre alexgomel auf dem ersten Platz? Sein EA handelte ebenfalls nur mit 1,0 Lot. Oder hätte vgc gewinnen können, dessen Expert Advisor am häufigste Trades von weniger als 1,0 Lot geöffnet hat. Alle drei haben ein gutes glattes Kontostand-Diagramm. Wie sie sehen können, geht die Geschichte der Championship weiter, obwohl sie beendet war!
Fazit: Kippe das Baby nicht mit dem Badewasser aus
Die Meinungen gehen auseinander. Dieser Artikel zeigt einige sehr allgemeine Ansätze zum Einschätzen von Handelsstrategien. Man kann viel mehr Kriterien erstellen, um Handelsergebnisse einzuschätzen. Jedes Merkmal für sich genommen wir keine vollständige und objektive Einschätzung bieten, aber zusammengenommen können sie uns helfen einen schiefen Ansatz in dieser Angelegenheit zu vermeiden.
Wir können sagen, dass wir jedes positive Ergebnis (ein erreichter Gewinn auf eine ausreichende Anzahl von Trades) einem "Kreuzverhör" unterziehen können, um negative Punkte im Trading zu erkennen. Das bedeutet, dass alle diese Eigenschaften die Effizienz einer gegebenen Handelsstrategie nicht so sehr kennzeichnen, wie sie uns über schwache Punkte im Handel informieren, die wir beachten müssen, ohne nur mit einem positiven Endergebnis zufrieden zu sein - dem gewonnenen Netto-Profit auf dem Konto.
Nun, wir können kein ideales Handelssystem erstellen, jedes System hat seine Vorteile und Konsequenzen. Der Einschätzungs-Test wird verwendet um einen Handelsansatz nicht dogmatisch zurückzuweisen, sondern um zu wissen, wie man die weitere Entwicklung von Handelssystemen und Expert Advisors durchführt. In dieser Hinsicht können die gesammelten statistischen Daten der Automated Trading Championship 2006 eine großartige Unterstützung für jeden Trader sein.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/1492
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
 Durchbrechen des Strategietester Limits beim Testen eines Hedge EA
Durchbrechen des Strategietester Limits beim Testen eines Hedge EA
 Wie man einen EA Code Beschneidet für ein Leichteres Leben und Weniger Fehler
Wie man einen EA Code Beschneidet für ein Leichteres Leben und Weniger Fehler
 Universelle Expert Advisor Vorlage
Universelle Expert Advisor Vorlage
 Tester im Terminal MetaTrader 4: Man sollte ihn kennen
Tester im Terminal MetaTrader 4: Man sollte ihn kennen
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.