MetaTrader 4 / Ejemplos
English Русский 中文 Deutsch 日本語 Português
Aplicación de lógica difusa en el trading por medio del MQL4

Aplicación de lógica difusa en el trading por medio del MQL4

MetaTrader 4 — Ejemplos | 1 agosto 2016, 10:56
2 329 0
Alexander Fedosov
Alexander Fedosov

Introducción

El trading de hoy en día no puede imaginarse sin sistemas de automatización, generalmente llamados Asesores Expertos o robots de trading. Pero, si no todos, lamayoría de ellos cuentan con algo claro, el código duro de la estrategia de trading y el sistema de gestión del dinero. Su principal ventaja es un algoritmo rígido que excluye el factor humano. Sin embargo, esta ventaja es también su principal inconveniente de los robots comerciales que carecen de flexibilidad. Independientemente de las condiciones de mercado, un Asesor Experto aplica siempre la misma estrategia comercial con los mismos parámetros estrictamente clasificados. En otras palabras, el sistema siempre actúa rígidamente: tendencia promedio > entrar en el mercado con un lote, fuerte tendencia > entrar en el mercado con dos lotes. ¡¡¡ Sin desvios !!!

A diferencia de un sistema automatizado, los traders humanos piensan en categorías difusas y pueden tener diferentes opiniones sobre las señales de entrada de mercado similares. A menudo son dudosas y se siguen preguntando si la tendencia es moderada o fuerte. Y aunque la tendencia es significativa, ¿es lo suficientemente fuerte como para entrar en dos lotes? Tales categorías difusas pueden ser manejadas por lógica borrosa. La lógica difusa no establece límites rígidos entre las categorías. En cambio, las "desdibuja" haciendo un sistema de trading más flexible y combina la rigidez de un robot de trading con la flexibilidad de una mente humana. El artículo proporciona ejemplos de aplicación del sistema de lógica difusa en el trading por medio del MQL4.


Funciones para los miembros

Lea el artículo "Introducción a la Lógica Difusa" comprender los conceptos generales de la teoría de lógica difusa. También, aprender los fundamentos de la librería FuzzyNet de MQL4, ya que se utiliza para la aplicación de los ejemplos.

Vamos a describir las funciones de pertenencia utilizadas en el artículo.


Función triangular para los miembros

Como su nombre indica, es una función de permanencia triangular. Es una función simple y más frecuentemente utilizada, definida por la siguiente fórmula analítica:

Fórmula de función triangular

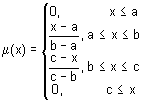
Generalmente se utiliza para especificar los siguientes tipos de incertidumbres: "aproximadamente igual", "valor medio", "encuentra dentro de la gama", "similar al objeto", "se ve como el objeto", etc.. Los parámetros de la función de permanencia triangular generalmente se interpretan como sigue:

  • [a, c] — rango variable;
  • b — valor más probable de la variable.

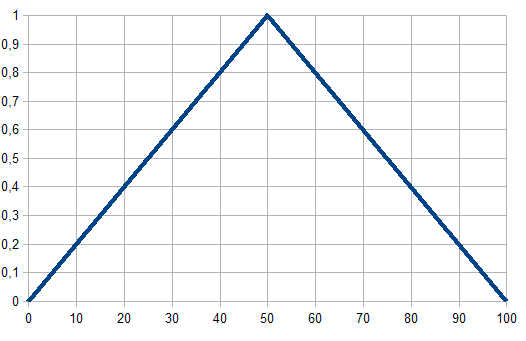
Fig. 1. Función triangular para los miembros


Función de permanencia trapezoidal

La función de permanencia en forma de trapecio definida por la siguiente fórmula:

Función de permanencia trapezoidal

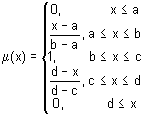
Los parámetros de la función de permanencia trapezoidal se interpretan como sigue:

  • [a, d] – portador conjunto difuso, evaluación pesimista de la variable;
  • [b, c] – núcleo de un conjunto difuso, evaluación optimista de la variable;

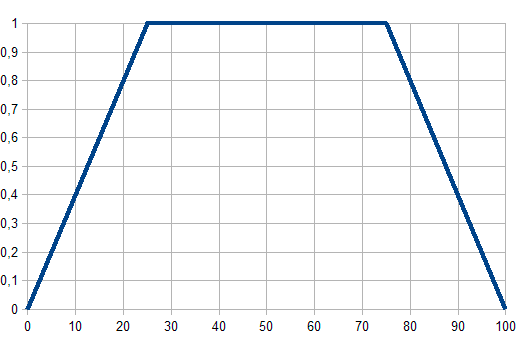
Fig. 2. Función de permanencia trapezoidal


Funciones de pertenencia en forma de campana

La función de permanencia en forma de curva de campana simétrica definida por la fórmula:

Funciones de pertenencia en forma de campana

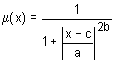
Los valores de parámetro se interpretan como sigue:

  • a – ratio de concentración de función de pertenencia;
  • b – ratio de pendiente de función permanencia;
  • c – coordenadas de punto más alto de la funcion de membresía.

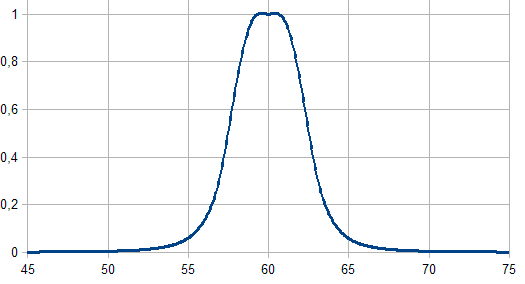
Fig. 3. Funciones de pertenencia en forma de campana


Funciones de pertenencia sigmoidea

La función se calcula usando la siguiente fórmula y aplicada al establecer funciones de membresía monótonas:

Funciones de pertenencia sigmoidea

Sus parámetros deben ser interpretados como sigue:

  • a – ratio de la pendiente de la función de permanencia;
  • c – coordenada de inflexión de la función pertenencia.

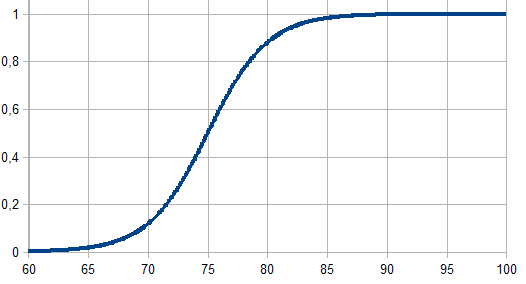
Fig. 4. Funciones de pertenencia sigmoidea


Implementación de un indicador por medio de la librería FuzzyNet de MQL4

Utilizaremos el Average Directional Movement Index (Índice de movimiento direccional promedio) (ADX) como ejemplo. Este es un indicador de tendencia que determina el poder de la tendencia actual (línea verde gruesa). En primer lugar, vamos a definir los criterios del poder de tendencia precisa (Fig. 5):
  • Tendencia débil – la línea verde se encuentra dentro de la gama 30-50. Los valores dentro de esta gama rígidamente definidos se consideran una tendencia débil.
  • Tendencia promedio – la línea verde se encuentra dentro de la gama 50-70 (tendencia promedio).
  • Fuerte tendencia – la línea verde se encuentra por encima de 70 hasta 100 (fuerte tendencia).

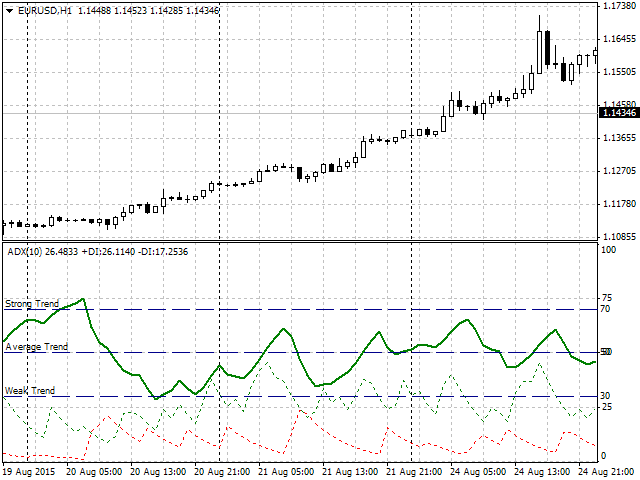
Fig. 5. Operación de ADX y división implementada por una potencia de tendencia

Estas tres categorías rígidamente definidas tienen algunos inconvenientes causados por su lógica de clasificación clara y estricta:

  • El primer inconveniente es la naturaleza subjetiva de la clasificación. De hecho, ¿por qué elegimos 30, 50 y 70 como valores de frontera? ¿Por qué no escogió 25, 50 y 75 o algunos otros? Estas opiniones diversas pueden afectar mucho el funcionamiento del ADX e incluso conducen a resultados diametralmente opuestos de trading.
  • La segunda cuestión es la zona fronteriza de las categorías seleccionadas. Por ejemplo, 50 es la frontera entre tendencia débil y media. Si aplicamos la lógica estricta, tenemos que admitir que 48 y 49 todavía pertenecen a la zona de tendencia débil, mientras que 50 y 51 están en la zona media de la tendencia. Pero, ¿la transición de 49 a 50? En ambos casos (48-49 y 49-50), la diferencia entre los valores es igual a uno. Sin embargo, por alguna razón, este último caso se considera una transición de una categoría a otra.

Así que, ¿cómo puede la lógica difusa resolver estos problemas?

Como ya se mencionó, la lógica borrosa "desenfoca" (fuzzifies) los límites especificados. Se asignan los valores de frontera de categorías rígidamente determinados para ambas categorías a la vez pero con diferentes grados de pertenencia. Una descripción de la muestra en este caso puede verse como sigue: la tendencia actual puede ser descrita como débil (30%), pero probablemente puede ser descrito como promedio (70%). Un trader humano describiría esto como sigue: la tendencia es promedia en lugar de débil. Creo que esta es la principal ventaja de la lógica borrosa. Es flexible y variable cuando ocupan rígidamente los parámetros especificos. He seleccionado las siguientes funciones de pertenencia para nuestro ejemplo con el indicador ADX:

  • La función de pertenencia trapezoidal para la descripción del concepto de tendencia débil.
  • La función de pertenencia en forma de campana para la descripción del concepto de tendencia media.
  • La función sigmoidea para la descripción de concepto de fuerte tendencia.

Sistemas más complejos que contienen numerosas categorías pueden describirse utilizando otras funciones disponibles en la libreria FuzzyNet. Actualmente, la librería contiene más de una docena de funciones. A continuación se muestra la representación gráfica de nuestro ejemplo:


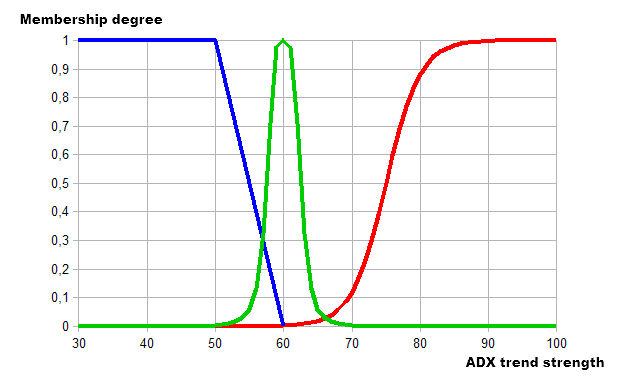
Fig. 6. Describiendo una tendencia utilizando la lógica borrosa

Como podemos ver, el gráfico tiene ahora las áreas con dos categorías de tendencia simultáneamente. La tendencia en la zona de 50-60 es débil y media, mientras que en el 60-70 es media y fuerte. Por lo tanto, hemos definido un término con las funciones de pertenencia predeterminadas para las tres categorías. Ahora que ya tenemos las entradas ADX descritas por las funciones de pertenencia, debemos definir lo que consideramos un resultado de valor de salida y defuzzificación, así como seleccionar un algoritmo de salida lógica fuzzy.

Para nuestro ejemplo, he seleccionado el porcentaje de riesgo de depósito en relación con la variable de fuerza de tendencia difusa inicialmente especificado. En otras palabras, cuanto más fuerte la tendencia, más alto porcentaje del riesgo y depósito aplicadas en el trading. He elegido Mamdani como algoritmo de salida lógica.

Como con la fuerza de la tendencia, vamos a introducir tres categorías distintas según el grado de riesgo:

  • Bajo riesgo – 2-4% del depósito.
  • Riesgo normal (Normal)-4-5%.
  • Alto riesgo (alto) – de 5 al valor máximo del 10% del depósito.

Ahora, vamos a definir categorías de riesgo mediante las funciones de pertenencia:

  • Trapezoidal, de bajo riesgo.
  • Triangular – de riesgo normal.
  • Sigmoideo – de alto riesgo.

Como resultado, obtenemos la siguiente descripción gráfica por medio de lógica difusa:


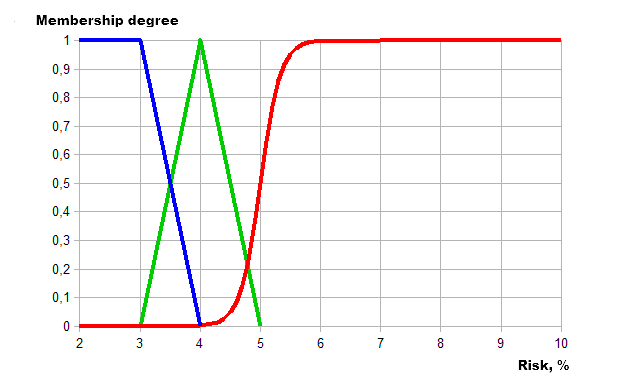
Fig. 7. Que describe un grado de riesgo por medio de la lógica borrosa


Vamos a implementar los datos descritos usando la librería FuzzyNet de MQL4:

//+------------------------------------------------------------------+
//|                                                    ADX_Fuzzy.mq4 |
//|                                                Alexander Fedosov |
//|                           https://www.mql5.com/en/users/alex2356 |
//+------------------------------------------------------------------+
#property copyright "Alexander Fedosov"
#property link      "https://www.mql5.com/en/users/alex2356"
#property version   "1.00"
#property strict
#property indicator_separate_window
#property indicator_buffers 2
#property indicator_color1 Green
#property indicator_color2 Red
#property indicator_minimum 0
#property indicator_maximum 10
//+------------------------------------------------------------------+
//| Conexión de librerías                                            |
//+------------------------------------------------------------------+
#include <Math\FuzzyNet\MamdaniFuzzySystem.mqh>
//--- parámetros de entrada
input string  p1="==== Parameters ====";
input int    visual=100;             // Periodo Visual
input int    adx_period=10;          // Periodo ADX
//---
double Buffer1[],Buffer2[],adx,adx_di_minus,adx_di_plus;
int limit;
//+------------------------------------------------------------------+
//| Función de inicialización del indicador personalizado            |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- indicador de asignación de buffers
   SetIndexStyle(0,DRAW_HISTOGRAM,0,2);
   SetIndexBuffer(0,Buffer1);
   SetIndexEmptyValue(0,0.0);
//---
   SetIndexStyle(1,DRAW_HISTOGRAM,0,2);
   SetIndexBuffer(1,Buffer2);
   SetIndexEmptyValue(1,0.0);
//---
   ArrayResize(Buffer1,visual);
   ArrayResize(Buffer2,visual);
   ArrayInitialize(Buffer1,0.0);
   ArrayInitialize(Buffer2,0.0);
//---
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Función de iteración de indicador personalizado                  |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
  {
   int count_bars=IndicatorCounted();
//---
   if(count_bars<0)
      return(-1);
//---
   if(Bars-1<adx_period)
      return(0);
//---
   for(int i=0; i<visual;i++)
     {
      adx=NormalizeDouble(iADX(_Symbol,PERIOD_CURRENT,adx_period,PRICE_CLOSE,MODE_MAIN,i),_Digits);
      adx_di_plus=NormalizeDouble(iADX(_Symbol,PERIOD_CURRENT,adx_period,PRICE_CLOSE,MODE_PLUSDI,i),_Digits);
      adx_di_minus=NormalizeDouble(iADX(_Symbol,PERIOD_CURRENT,adx_period,PRICE_CLOSE,MODE_MINUSDI,i),_Digits);
      //---
      double r=(adx_di_plus-adx_di_minus);
      if(MathAbs(r)>10 && adx>=30.0)
         if(r>0)
            Buffer1[i]=mamdani(adx);
      else if(r<0)
         Buffer2[i]=mamdani(adx);
     }
   return(rates_total);
  }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
double mamdani(double v)
  {
   double res=0;
//--- Sistema difuso Mamdani  
   MamdaniFuzzySystem *fsRisk=new MamdaniFuzzySystem();
//--- Crear las variables de entrada para el sistema
   FuzzyVariable *fsTrend=new FuzzyVariable("trend",30.0,100.0);
//---
   fsTrend.Terms().Add(new FuzzyTerm("weak", new TrapezoidMembershipFunction(20.0, 30.0, 50.0, 60.0)));
   fsTrend.Terms().Add(new FuzzyTerm("average", new GeneralizedBellShapedMembershipFunction(2.5,2.0,60.0)));
   fsTrend.Terms().Add(new FuzzyTerm("strong",new SigmoidalMembershipFunction(0.4,75.0)));
   fsRisk.Input().Add(fsTrend);
//--- Crear Salida
   FuzzyVariable *fvRisk=new FuzzyVariable("risk",2.0,10.0);
   fvRisk.Terms().Add(new FuzzyTerm("low", new TrapezoidMembershipFunction(1.0, 2.0, 3.0, 4.0)));
   fvRisk.Terms().Add(new FuzzyTerm("normal", new TriangularMembershipFunction(3.0, 4.0, 5.0)));
   fvRisk.Terms().Add(new FuzzyTerm("high", new SigmoidalMembershipFunction(6.0,5.0)));
   fsRisk.Output().Add(fvRisk);
//--- Crear tres reglas difusas Mamdani
   MamdaniFuzzyRule *rule1 = fsRisk.ParseRule("if (trend is weak) then risk is low");
   MamdaniFuzzyRule *rule2 = fsRisk.ParseRule("if (trend is average) then risk is normal");
   MamdaniFuzzyRule *rule3 = fsRisk.ParseRule("if (trend is strong) then risk is high");
//--- Añadir tres reglas difusas Mamdani en el sistema
   fsRisk.Rules().Add(rule1);
   fsRisk.Rules().Add(rule2);
   fsRisk.Rules().Add(rule3);
//--- Configurar valores de entrada
   CList *in=new CList;
   Dictionary_Obj_Double *p_od_in=new Dictionary_Obj_Double;
   p_od_in.SetAll(fsTrend,v);
   in.Add(p_od_in);
//--- Obtener resultado
   CList *result;
   Dictionary_Obj_Double *p_od_out;
   result=fsRisk.Calculate(in);
   p_od_out=result.GetNodeAtIndex(0);
   res=NormalizeDouble(p_od_out.Value(),_Digits);
//---
   delete in;
   delete result;
   delete fsRisk;
   return res;
  }
//+------------------------------------------------------------------+

He desarrollado un indicador de histograma simple visualizando la relación de fuerza del grado/tendencia de riesgo (tendencia bajista verde – tendencia alcista, rojo-). La altura de las barras del histograma muestra un valor numérico de un grado de riesgo a diferentes fuerza de tendencia dentro de los límites descritos anteriormente. Vamos a examinar el código en detalle.

En primer lugar, vamos a definir los dos buffers para los histogramas aplicados, así como su color y rango en el eje vertical de cero riesgo especificado mayor de 10%.

#property indicator_separate_window
#property indicator_buffers 2
#property indicator_color1 Green
#property indicator_color2 Red
#property indicator_minimum 0
#property indicator_maximum 10

A continuación, conecte la librería para la creación de sistemas de acuerdo con el algoritmo Mamdani y agregar variables para visualizar la cantidad de barras a partir de la cero y ajustado al periodo ADX.

//+------------------------------------------------------------------+
//| Conectando librerías FuzzyNet                                    |
//+------------------------------------------------------------------+
#include <Math\FuzzyNet\MamdaniFuzzySystem.mqh>
//--- parámetros de entrada
input string  p1="==== Parameters ====";
input int    visual=100;             // Periodo Visual
input int    adx_period=10;          // Periodo ADX

Al inicializar, deberíamos establecer el indicador en forma de histograma.

//+------------------------------------------------------------------+
//| Función de inicialización del indicador personalizado            |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- indicador de asignación de buffers
   SetIndexStyle(0,DRAW_HISTOGRAM,0,2);
   SetIndexBuffer(0,Buffer1);
   SetIndexEmptyValue(0,0.0);
//---
   SetIndexStyle(1,DRAW_HISTOGRAM,0,2);
   SetIndexBuffer(1,Buffer2);
   SetIndexEmptyValue(1,0.0);
//---
   ArrayResize(Buffer1,visual);
   ArrayResize(Buffer2,visual);
   ArrayInitialize(Buffer1,0.0);
   ArrayInitialize(Buffer2,0.0);
//---
   return(INIT_SUCCEEDED);
  }

En el código principal, definimos las lecturas básicas del indicador ADX. la variable r se utiliza para encontrar la diferencia entre los indicadores de dirección de dos tendencias + DI y -DI. Además, presentamos el filtro de la presencia de tendencia como una diferencia entre los valores absolutos +DI y -DI por encima de 10 y la fuerza de la tendencia principal por encima de 30 (el límite inferior de una tendencia débil). A continuación, vamos a definir una dirección de tendencia basada en el signo de la variable signo r y emplazar la función mamdani() en un valor predeterminado.

int count_bars=IndicatorCounted();
//---
   if(count_bars<0)
      return(-1);
//---
   if(Bars-1<adx_period)
      return(0);
//---
   for(int i=0; i<visual;i++)
     {
      adx=NormalizeDouble(iADX(_Symbol,PERIOD_CURRENT,adx_period,PRICE_CLOSE,MODE_MAIN,i),_Digits);
      adx_di_plus=NormalizeDouble(iADX(_Symbol,PERIOD_CURRENT,adx_period,PRICE_CLOSE,MODE_PLUSDI,i),_Digits);
      adx_di_minus=NormalizeDouble(iADX(_Symbol,PERIOD_CURRENT,adx_period,PRICE_CLOSE,MODE_MINUSDI,i),_Digits);
      //---
      double r=(adx_di_plus-adx_di_minus);
      if(MathAbs(r)>10 && adx>=30.0)
         if(r>0)
            Buffer1[i]=mamdani(adx);
      else if(r<0)
         Buffer2[i]=mamdani(adx);
     }

Descripción de la función Mamdani :

1. Vamos a crear el nuevo sistema del sistema de lógica difusa del tipo Mamdani * fsRisk.

2. Añadir la variable * fsTrend a él con un nombre especificado trend y los valores mínimos y máximos de 30 y 100.

//--- Sistema difuso Mamdani  
   MamdaniFuzzySystem *fsRisk=new MamdaniFuzzySystem();
//--- Crear las variables de entrada para el sistema
   FuzzyVariable *fsTrend=new FuzzyVariable("trend",30.0,100.0);

3. A continuación, se suman los términos difusos descritos anteriormente (Fig. 6) con las funciones de pertenencia para cada categoría.

fsTrend.Terms().Add(new FuzzyTerm("weak", new TrapezoidMembershipFunction(30.0, 40.0, 50.0, 60.0)));
   fsTrend.Terms().Add(new FuzzyTerm("average", new GeneralizedBellShapedMembershipFunction(2.5,2.0,60.0)));
   fsTrend.Terms().Add(new FuzzyTerm("strong",new SigmoidalMembershipFunction(0.4,75.0)));
   fsRisk.Input().Add(fsTrend);

4. Pasar los pasos 2-3 para el valor de salida: crear la variable * fvRisk denominada risk y el mínimo y máximo de los valores de riesgo 2% y 10%.

//--- Crear Salida
   FuzzyVariable *fvRisk=new FuzzyVariable("risk",2.0,10.0);
   fvRisk.Terms().Add(new FuzzyTerm("low", new TriangularMembershipFunction(2.0, 3.0, 4.0)));
   fvRisk.Terms().Add(new FuzzyTerm("normal", new TriangularMembershipFunction(3.0, 4.0, 5.0)));
   fvRisk.Terms().Add(new FuzzyTerm("high", new SigmoidalMembershipFunction(6.0,5.0)));
   fsRisk.Output().Add(fvRisk);

5. Ahora, vamos a crear el sistema de tres reglas borrosas que representa nuestro sistema:

  • Si una tendencia es débil, el riesgo es bajo.
  • Si una tendencia es promedio, el riesgo es normal.
  • Si una tendencia es fuerte, el riesgo es alto.
//--- Crear tres reglas difusas Mamdani
   MamdaniFuzzyRule *rule1 = fsRisk.ParseRule("if (trend is weak) then risk is low");
   MamdaniFuzzyRule *rule2 = fsRisk.ParseRule("if (trend is average) then risk is normal");
   MamdaniFuzzyRule *rule3 = fsRisk.ParseRule("if (trend is strong) then risk is high");

6. Let's add our rules into the system:

//--- Añadir tres reglas difusas Mamdani en el sistema
   fsRisk.Rules().Add(rule1);
   fsRisk.Rules().Add(rule2);
   fsRisk.Rules().Add(rule3);

7. Crear las listas de variables de entrada y de salida y añadir v de entrada en el argumento de la función mamdani . Así, especificadas tanto las variables difusas de entrada y salida del sistema de lógica difusa, se ajusta para toda la función mamdani, mientras que el valor del indicador ADX se utiliza como una entrada.

//--- Configurar valores de entrada
   CList *in=new CList;
   Dictionary_Obj_Double *p_od_in=new Dictionary_Obj_Double;
   p_od_in.SetAll(fsTrend,v);
   in.Add(p_od_in);
//--- Obtener resultado
   CList *result=new CList;
   Dictionary_Obj_Double *p_od_out=new Dictionary_Obj_Double;
   result=fsRisk.Calculate(in);
   p_od_out=result.GetNodeAtIndex(0);
   res=NormalizeDouble(p_od_out.Value(),_Digits);

8. El histograma se basa en el valor de la función resultante de la variable res.

adx=NormalizeDouble(iADX(_Symbol,PERIOD_CURRENT,adx_period,PRICE_CLOSE,MODE_MAIN,i),_Digits);
      adx_di_plus=NormalizeDouble(iADX(_Symbol,PERIOD_CURRENT,adx_period,PRICE_CLOSE,MODE_PLUSDI,i),_Digits);
      adx_di_minus=NormalizeDouble(iADX(_Symbol,PERIOD_CURRENT,adx_period,PRICE_CLOSE,MODE_MINUSDI,i),_Digits);
      //---
      double r=(adx_di_plus-adx_di_minus);
      if(MathAbs(r)>10 && adx>=30.0)
         if(r>0)
            Buffer1[i]=mamdani(adx);
      else if(r<0)
         Buffer2[i]=mamdani(adx);

A continuación se presentan los resultados de operación de indicador visual:

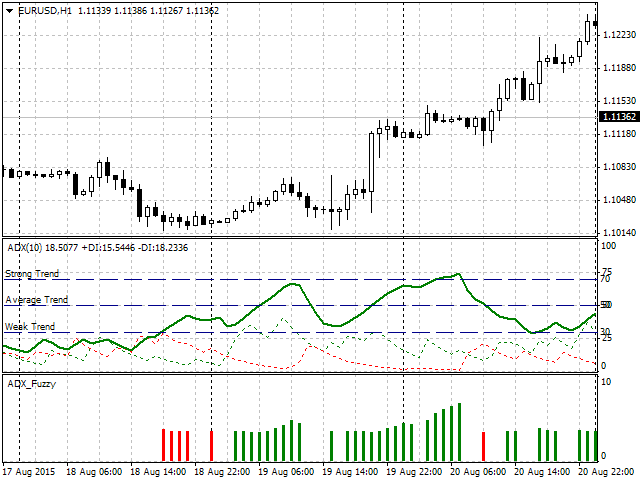
Fig. 8. Funcionamiento del indicador

Como podemos ver, el indicador muestra la presencia de una tendencia utilizando un histograma de color, mientras que la altura de la barra muestra el porcentaje de riesgo del depósito recomendado. La pregunta obvia surge: ¿Cuál sería la diferencia si el indicador se implementa con intervalos claros? Para responder esto, consideremos la siguiente sección en más detalles (Fig. 9). La flecha verde muestra la barra de histograma, mientras que su valor numérico y su fuerza de tendencia ADX aparecen a la izquierda. Como se define anteriormente, si el ADX es superior a 70 se trata de una tendencia fuerte, lo que significa que el valor de riesgo debe exceder el 5%. Como podemos ver claramente en la figura 9, ADX = 69.7923. Así, si aplicamos estrictas reglas, esta es todavía una tendencia promedio y el riesgo no debe exceder el 5%. Sin embargo, es igual a 5.6406, es decir, es mayor.


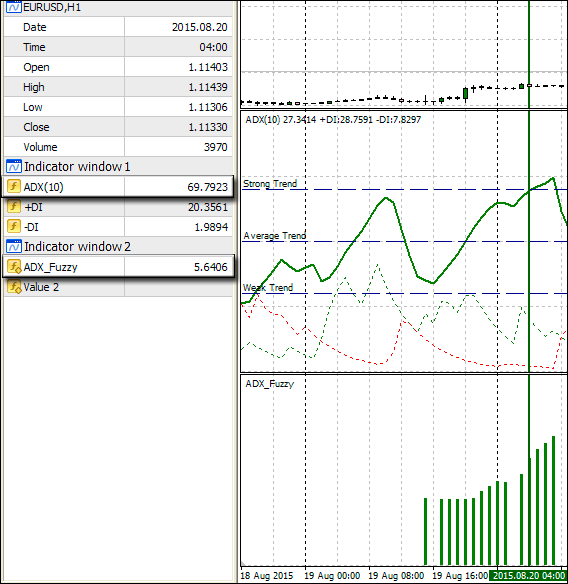
Fig. 9. Mostrando las diferencias entre lógica difusa y estándar

Aquí podemos ver la lógica difusa en la acción. Ha definido que a pesar de que el valor es inferior a 70, la tendencia en la zona es más fuerte que la media. Podemos ver esto examaminando la figura 6. Cuando el valor del eje X muestra 69.7923, la función de permanencia de una tendencia fuerte es mayor que la función de la tendencia promedio. Por lo tanto, nuestro sistema ha ofrecido el valor de riesgo superior al 5%, acercándose a la zona fronteriza entre tendencia media y fuerte de manera más flexible en comparación con el sistema de lógica estricta.


Implementación de un EA por medio de la librería FuzzyNet de MQL4

Aquí quiero mostrar la diferencia en la operación del Asesor Experto en caso de unas condiciones claramente definidas y elementos de lógica difusa. Para hacer la comparación tan bien fundamentada como sea posible, decidí usar el EA de mi otro artículo "Comercio de ideas basada en la velocidad de dirección y movimiento precios", que describe en detalle la idea del robot de trading. Para evitar repeticiones excesivas, utilizo este EA como base con los siguientes cambios:

  • La lógica del EA se basa en la idea de la persistencia del movimiento de precio. Los parámetros de movimiento son descritos por los siguientes indicadores: RSI (indicador de velocidad) y AC (indicador de aceleración). La velocidad y la aceleración se calculan por la indexación de los rangos de los valores de estos indicadores. Ahora, apliquemos la teoría difusa determinada con los valores del índice RSI. Como resultado, los valores RSI se utilizan como entrada, mientras que la salida es un índice de velocidad difusa que no sólo puede tener valores enteros, como 1-4, sinó también 1.3 o 3.85.
  • A su vez, el valor del índice difuso se utiliza como entrada para otro sistema, en el cual la salida es un valor de beneficio. Así, el take profit permanece intacto en el EA inicial.

La idea detrás de la conexión es simple. Si el RSI y el AC son parámetros de movimiento, a continuación a más alta la velocidad, mayor será la persistencia del movimiento y por lo tanto, es razonable colocar un mayor take profit. Si la velocidad de movimiento es baja, debe establecerse un objetivo de beneficio más firme para no incurrir en una regresión o un cambio de tendencia. La figura 10 muestra un diagrama de bloques para una comprensión más clara de la aplicación de lógica difusa en el EA.


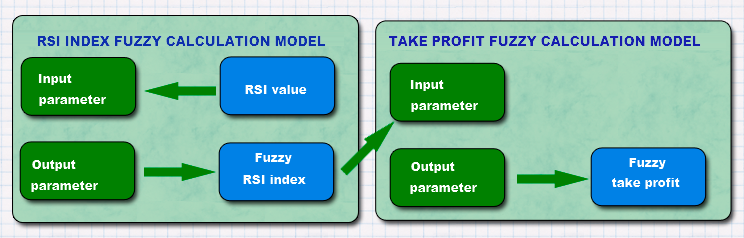
Fig. 10. Aplicación de la lógica difusa en el EA

Como es el caso con el indicador, vamos a describir las funciones de pertenencia para ambos modelos difusos. El primero es un modelo difuso de cálculo del índice RSI donde la entrada es el valor del indicador. Vamos a dividir los valores necesarios en tres categorías:

  • Débil. La primera categoría define la tendencia débil. RSI: 60-70.
  • Promedio. La segunda categoría define la tendencia promedio. RSI: 70-80.
  • Fuerte. La tercera categoría se relaciona con una tendencia fuerte. RSI: 80-85.

Vamos a seleccionar la función de permanencia para describir las categorías especificadas:

  • Débil. La función sigmoidea con la relación de pendiente de -0.75 y de punto de inflexión 67,5.
  • Promedio. La función Gaussiana con la coordenada máxima de 72,5 y el cociente de concentración de 2.2.
  • Fuerte. La función Gaussiana con la coordenada máxima de 80 y la tasa de concentración de 1.4.

La presentación visual es la siguiente:


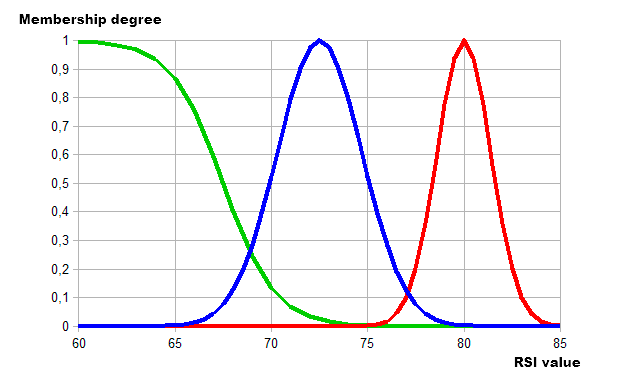
Fig. 11. Utilizando las funciones de pertenencia para describir las categorías de los valores RSI

La salida de este modelo difuso es el índice RSI. Las siguientes categorías y funciones de permanencia se usan para describirlo:

  • Baja. Índice bajo, rango 1-2. La función de permanencia es sigmoidea con la pendiente de -11 y de punto de inflexión 1.5.
  • Normal. Índice promedio, margen de 2-3. La función de pertenencia es el Gaussiano con el punto máximo de la 2 y la tasa de concentración de 0,3.
  • Alta. Alto índice, rango 3-4. La función de pertenencia es el sigmoide, uno con pendiente de 6 y el punto de inflexión 3.

Como resultado, obtenemos la siguiente visualización:


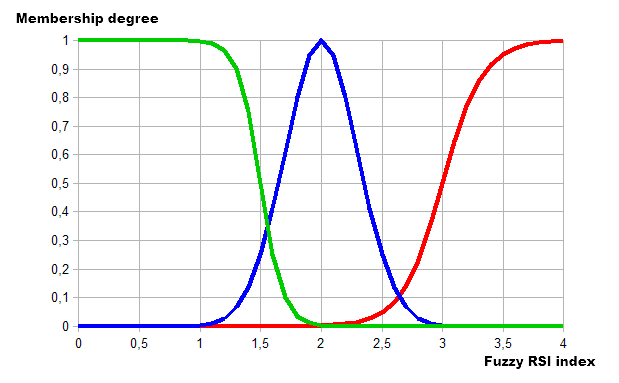
Fig. 12. Utilizando las funciones de pertenencia para describir las categorías de los valores del índice RSI

A continuación vamos a describir el modelo segundo difuso Figura 10 – cáculo del take profit del modelo difuso. Las entradas del modelo ya han sido descritas, así como las salidas del primer modelo (índice difuso de RSI). Aquí se utiliza un valor de take profit como salida. Vamos a definir categorías concisas para él:

  • Mínima. Categoría de mínimo take profit dentro de la gama de 30-40.
  • Media. Categoría de take profit medio dentro del rango de 40-60.
  • Máxima. Categoría de take profit alta dentro del rango de 60-70.

Ahora, vamos a hacer descripciones utilizando las funciones de pertenencia:

  • Mínimq. La función de permanencia es sigmoidea con la pendiente de -0,8 y el punto de inflexión de 37,5.
  • Media. La función de permanencia es la función Gaussiana con la coordenada máxima de 50 y la tasa de concentración de 3.
  • Máxima. La función de permanencia es sigmoidea con la pendiente de 0.8 y de punto de inflexión 62.5.

La aplicación gráfica se ve como sigue:


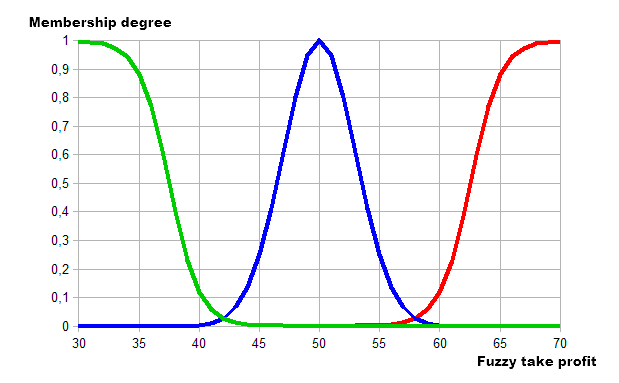
Fig. 13. Utilizando las funciones de pertenencia para describir las categorías de los valores de take profit

Ahora que definen todos los parámetros, es hora de implementar la idea en el robot de trading. Vamos a añadir dos modelos de difusión para sucesivos cálculos de stop loss y take profit en base a lecturas del RSI.

//+------------------------------------------------------------------+
//|                                                       tester.mq4 |
//|                                                Alexander Fedosov |
//|                                                                  |
//+------------------------------------------------------------------+
#property copyright "Alexander Fedosov"
#property strict
#include "trading.mqh" //Librerías de soporte de operaciones de trading
//+------------------------------------------------------------------+
//| Conexión de librerías                                            |
//+------------------------------------------------------------------+
#include <Math\FuzzyNet\MamdaniFuzzySystem.mqh>
//+------------------------------------------------------------------+
//| Parametetros                                                     |
//+------------------------------------------------------------------+
input bool           Lot_perm=false;               // Lotes del balance?
input double         Risk = 2;                     // Riesgo del depósito, %
input double         lt=0.01;                      // Lote
input int            magic=2356;                   // Magic number
input int            period=14;                    // Periodo del indicador RSI
input ENUM_TIMEFRAMES tf=PERIOD_CURRENT;           // timeframe de trabajo
//---
int index_rsi,index_ac;
double tkp,stl;
double rs,mdm;
CTrading tr;
//+------------------------------------------------------------------+
//| Función de inicialización del Experto |
//+------------------------------------------------------------------+
int OnInit()
  {
   tr.Trading(magic,5,lt,Lot_perm,Risk);
   tr.exp_name="Tester Fuzzy Logic";
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Función de cálculo principal |
//+------------------------------------------------------------------+
void OnTick()
  {
//--- comprobar la presencia de órdenes abiertas
   if(!tr.isOpened(magic))
     {
      depth_trend();
      speed_ac();
      rs=tr.ND(iRSI(_Symbol,tf,period,PRICE_CLOSE,0),2);
      //--- comprobación de las condiciones de compra
      if(Buy() && rs<=85.0)
        {
         mdm = mamdani_rsi(rs);
         tkp = MathCeil(mamdani_tp(mdm));
         stl = MathCeil(tkp*0.43);
         if(tr.OpnOrd(OP_BUY,lt,(int)tkp,(int)stl))
            Print("RSI is equal to ",rs," TP is equal to ",tkp," SL is equal to ",stl);
        }
      //--- comprobación de las condiciones de venta
      if(Sell() && rs>=15.0)
        {
         mdm = mamdani_rsi(100-rs);
         tkp = MathCeil(mamdani_tp(mdm));
         stl = MathCeil(tkp*0.43);
         if(tr.OpnOrd(OP_SELL,lt,(int)tkp,(int)stl))
            Print("RSI is equal to ",rs," TP is equal to ",tkp," SL is equal to ",stl);
        }
     }
//--- ¿hay órdenes abiertas?
   if(tr.isOpened(magic))
     {
      //--- comprobar y cerrar órdenes de venta cumplan con las condiciones de cierre
      if(Sell_close())
         tr.ClosePosAll(OP_SELL);
      //--- comprobar y cerrar órdenes de compra que cumplan con las condiciones de cierre
      if(Buy_close())
         tr.ClosePosAll(OP_BUY);
     }
  }
//+---------------------------------------------------------------+
//| Función para determinar la profundidad de la tendencia |
//+---------------------------------------------------------------+
void depth_trend()
  {
//--- definir el índice de entrada de mercado
   double rsi=iRSI(_Symbol,tf,period,PRICE_CLOSE,0);
//---
   index_rsi=0;
   if(rsi>90.0)
      index_rsi=4;
   else if(rsi>80.0)
      index_rsi=3;
   else if(rsi>70.0)
      index_rsi=2;
   else if(rsi>60.0)
      index_rsi=1;
   else if(rsi<10.0)
      index_rsi=-4;
   else if(rsi<20.0)
      index_rsi=-3;
   else if(rsi<30.0)
      index_rsi=-2;
   else if(rsi<40.0)
      index_rsi=-1;
  }
//+----------------------------------------------------------------+
//| Función para determinar la velocidad de tendencia |
//+----------------------------------------------------------------+
void speed_ac()
  {
   double ac[];
   ArrayResize(ac,5);
   ArrayInitialize(ac,0.0);
   for(int i=0; i<5; i++)
      ac[i]=iAC(_Symbol,tf,i);
//---
   index_ac=0;
//--- buy indices
   if(ac[0]>ac[1])
      index_ac=1;
   else if(ac[0]>ac[1] && ac[1]>ac[2])
      index_ac=2;
   else if(ac[0]>ac[1] && ac[1]>ac[2] && ac[2]>ac[3])
      index_ac=3;
   else if(ac[0]>ac[1] && ac[1]>ac[2] && ac[2]>ac[3] && ac[3]>ac[4])
      index_ac=4;
//--- sell indices
   else if(ac[0]<ac[1])
      index_ac=-1;
   else if(ac[0]<ac[1] && ac[1]<ac[2])
      index_ac=-2;
   else if(ac[0]<ac[1] && ac[1]<ac[2] && ac[2]<ac[3])
      index_ac=-3;
   else if(ac[0]<ac[1] && ac[1]<ac[2] && ac[2]<ac[3] && ac[3]<ac[4])
      index_ac=-4;
  }
//+----------------------------------------------------------------+
//| Función para comprobar condiciones de compra                   |
//+----------------------------------------------------------------+
bool Buy()
  {
   return (((index_rsi==2 && index_ac>=1) || (index_rsi==3 && index_ac==1))?true:false);
  }
//+----------------------------------------------------------------+
//| Function for checking sell conditions                          |
//+----------------------------------------------------------------+
bool Sell()
  {
   return (((index_rsi==-2 && index_ac<=-1) || (index_rsi==-3 && index_ac==-1))?true:false);
  }
//+----------------------------------------------------------------+
//| Función para comprobar comprar posición condiciones de cierre  |
//+----------------------------------------------------------------+
bool Buy_close()
  {
   return ((index_rsi>2 && index_ac<0)?true:false);
  }
//+----------------------------------------------------------------+
//| Función de comprobación de las condiciones de cierre de las posiciones de venta |
//+----------------------------------------------------------------+
bool Sell_close()
  {
   return ((index_rsi<-2 && index_ac>0)?true:false);
  }
//+----------------------------------------------------------------+
//| Modelo de cálculo difuso del índice RSI |
//+----------------------------------------------------------------+
double mamdani_rsi(double rsi)
  {
   double res=0;
//--- Sistema difuso Mamdani  
   MamdaniFuzzySystem *fsRSI=new MamdaniFuzzySystem();
//--- crear las entradas para el sistema y definir los términos
   FuzzyVariable *fsTrend=new FuzzyVariable("rsi",60.0,85.0);
//---
   fsTrend.Terms().Add(new FuzzyTerm("weak", new SigmoidalMembershipFunction(-0.75,67.5)));
   fsTrend.Terms().Add(new FuzzyTerm("average", new NormalMembershipFunction(72.5,2.2)));
   fsTrend.Terms().Add(new FuzzyTerm("strong", new NormalMembershipFunction(80.0,1.4)));
   fsRSI.Input().Add(fsTrend);
//--- crear las salidas para el sistema y definir los términos
   FuzzyVariable *fsIndex=new FuzzyVariable("index",1.0,4.0);
   fsIndex.Terms().Add(new FuzzyTerm("low", new SigmoidalMembershipFunction(-11.0,1.5)));
   fsIndex.Terms().Add(new FuzzyTerm("normal", new NormalMembershipFunction(2.0,0.3)));
   fsIndex.Terms().Add(new FuzzyTerm("high", new SigmoidalMembershipFunction(6.0,3.0)));
   fsRSI.Output().Add(fsIndex);
//--- crear reglas difusas y agregarlas al sistema
   MamdaniFuzzyRule *rule1 = fsRSI.ParseRule("if (rsi es débil) then (index es bajo)");
   MamdaniFuzzyRule *rule2 = fsRSI.ParseRule("if (rsi es medio) then (index es normal)");
   MamdaniFuzzyRule *rule3 = fsRSI.ParseRule("if (rsi es fuerte) then (index es alto)");
   fsRSI.Rules().Add(rule1);
   fsRSI.Rules().Add(rule2);
   fsRSI.Rules().Add(rule3);
//--- establecer los valores de entrada
   CList *in=new CList;
   Dictionary_Obj_Double *p_od_in=new Dictionary_Obj_Double;
   p_od_in.SetAll(fsTrend,rsi);
   in.Add(p_od_in);
//--- resultado de salida
   CList *result=new CList;
   Dictionary_Obj_Double *p_od_out=new Dictionary_Obj_Double;
   result=fsRSI.Calculate(in);
   p_od_out=result.GetNodeAtIndex(0);
   res=NormalizeDouble(p_od_out.Value(),_Digits);
//---
   delete in;
   delete result;
   delete fsRSI;
   return res;
  }
//+----------------------------------------------------------------+
//| Modelo difuso del cálculo de índice de take profit             |
//+----------------------------------------------------------------+
double mamdani_tp(double ind_rsi)
  {
   double res=0;
//--- Sistema difuso Mamdani  
   MamdaniFuzzySystem *fsTP=new MamdaniFuzzySystem();
//--- crear las entradas para el sistema y definir los términos
   FuzzyVariable *fsIndex=new FuzzyVariable("index",1.0,4.0);
   fsIndex.Terms().Add(new FuzzyTerm("low", new SigmoidalMembershipFunction(-11.0,1.5)));
   fsIndex.Terms().Add(new FuzzyTerm("normal", new NormalMembershipFunction(2.0,0.3)));
   fsIndex.Terms().Add(new FuzzyTerm("high", new SigmoidalMembershipFunction(6.0,3.0)));
   fsTP.Input().Add(fsIndex);
//--- crear las entradas para el sistema y definir los términos
   FuzzyVariable *fsProfit=new FuzzyVariable("TP",30.0,70.0);
   fsProfit.Terms().Add(new FuzzyTerm("minimal", new SigmoidalMembershipFunction(-0.8,37.5)));
   fsProfit.Terms().Add(new FuzzyTerm("average", new NormalMembershipFunction(50.0,3.0)));
   fsProfit.Terms().Add(new FuzzyTerm("maximal", new SigmoidalMembershipFunction(0.8,62.5)));
   fsTP.Output().Add(fsProfit);
//--- crear reglas difusas y agregarlas al sistema
   MamdaniFuzzyRule *rule1 = fsTP.ParseRule("if (index is low) then (TP is minimal)");
   MamdaniFuzzyRule *rule2 = fsTP.ParseRule("if (index is normal) then (TP is average)");
   MamdaniFuzzyRule *rule3 = fsTP.ParseRule("if (index is high) then (TP is maximal)");
   fsTP.Rules().Add(rule1);
   fsTP.Rules().Add(rule2);
   fsTP.Rules().Add(rule3);
//--- establecer los valores de entrada
   CList *in=new CList;
   Dictionary_Obj_Double *p_od_in=new Dictionary_Obj_Double;
   p_od_in.SetAll(fsIndex,ind_rsi);
   in.Add(p_od_in);
//--- resultado de salida
   CList *result=new CList;
   Dictionary_Obj_Double *p_od_out=new Dictionary_Obj_Double;
   result=fsTP.Calculate(in);
   p_od_out=result.GetNodeAtIndex(0);
   res=NormalizeDouble(p_od_out.Value(),_Digits);
//---
   delete in;
   delete result;
   delete fsTP;
   return res;
  }
//+------------------------------------------------------------------+

Ahora, vamos a examinar los principales cambios que se han hecho a el EA:

  • El cambio más importante es la implementación de los dos modelos difusos como funciones mamdani_rsi y mamdani_tp .
  • Se han eliminado los parámetros de stop loss y take profit. Ahora se calculan utilizando la lógica difusa.
  • Aquí es cómo se aplica este cálculo:
if(OrdersTotal()<1)
     {
      depth_trend();
      speed_ac();
      rs=tr.ND(iRSI(_Symbol,tf,period,PRICE_CLOSE,0),2);
      // ---comprobación de las condiciones de compra
      if(Buy() && rs<=85.0)
        {
         mdm = mamdani_rsi(rs);
         tkp = MathCeil(mamdani_tp(mdm));
         stl = MathCeil(tkp*0.43);
         if(tr.OpnOrd(OP_BUY,lt,tkp,stl))
            Print("RSI is equal to ",rs," TP is equal to ",tkp," SL is equal to ",stl);
        }
      //--- comprobación de las condiciones de venta.
      if(Sell() && rs>=15.0)
        {
         mdm = mamdani_rsi(100-rs);
         tkp = MathCeil(mamdani_tp(mdm));
         stl = MathCeil(tkp*0.43);
         if(tr.OpnOrd(OP_SELL,lt,tkp,stl))
            Print("RSI is equal to ",rs," TP is equal to ",tkp," SL is equal to ",stl);
        }
     }

Si no hay órdenes abiertas con el EA magic, el sistema utiliza las funciones depth_trend() y speed_ac() para el seguimiento de los parámetros de movimiento del mercado. Se realiza una entrada si concuerdan con Buy() o Sell(). Si se cumplen las condiciones, el resultado de la operación del modelo difuso se asigna al parámetro mdm que utiliza el valor actual del RSI como una entrada y un índice difuso como una salida. A su vez, el valor del índice difuso se utiliza como entrada para otro sistema, en el cual la salida es un valor de take profit en puntos. El valor del take profit se asigna a la variable tkp .

La relación de 0.43 es tomada basándose en el valor del take profit máximo de 70 puntos, mientras que el stop loss correspondiente es de 30. En caso de una orden de apertura acertada, nuestro EA muestra también el valor RSI, la orden se abrirá, y se calcula los parámetros de stoo loss y take profit basados en él. Esto se hace meramente para conveniencia de la prueba.

Además, es necesario aclarar lo siguiente:

  1. En el caso de una condición de venta, mamdani_rsi(100-rs) se asigna a mdm. Esto se hace porque se duplican sus rangos y las fronteras en relación con valores extremos del RSI (0 y 100).
  2. Dos condiciones adicionales: en la compra de rs <= 85 y semejantemente al vender rs >= 15. Esto se hace porque al crear las entradas del modelo difuso del cálculo del índice RSI, las fronteras se establecen en 60-85. Por lo tanto, el valor de 15 resulta ser el extremo para vender.

El ejemplo de la operación del EA se muestra en la figura 14. Como podemos ver, los valores de stop loss y take profit se calculan en el caso de diferentes valores RSI.


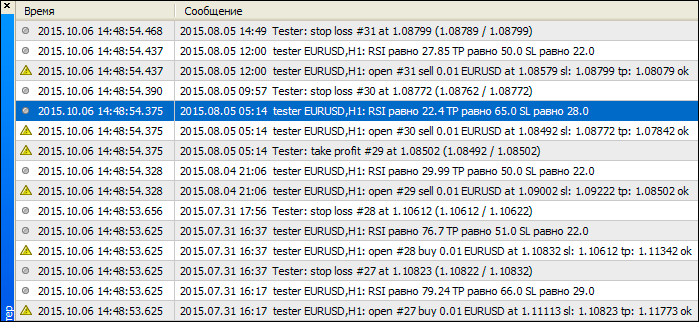
Fig. 14. Resultados de operación del Asesor Experto


Conclusión

En este artículo, hemos examinado las implementaciones de ejemplo de la teoría de configuraciones difusas mediante la librería de FuzzyNet del MQL4. Hemos demostrado que los sistemas basados en la lógica difusa son más flexibles cuando se trata con las cuestiones de estricta categoría, como diferenciación de clasificación o riesgo de la tendencia. El Asesor Experto demostró cómo un sistema basado en lógica difusa analiza una señal de trading mientras aplica su propia estrategia de trading y define el stop loss y take profit adecuados. Creo que los sistemas de trading basados en la lógica difusa son capaces de combinar las mejores cualidades necesarias para un trading exitoso – la disciplina de los robots de trading y la flexibilidad de una mente humana.

Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/2032

Archivos adjuntos |
Descargar ZIP
trading.mqh (42.67 KB)
tester.mq4 (20.49 KB)
adx_fuzzy.mq4 (10.62 KB)
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.

Otros artículos del autor

Pasar a la discusión en el foro de los operadores
Usando archivos de texto para guardar los parámetros de entrada de asesores, indicadores y scripts Usando archivos de texto para guardar los parámetros de entrada de asesores, indicadores y scripts
En el artículo vamos a analizar cuestiones relacionadas con el guaradado de objetos dinámicos, matrices y otras variables en forma de propiedades de asesores, indicadores y scripts en archivos de texto. Estos son un complemento cómodo a la funcionalidad de los recursos estándar propuestos por los lenguajes MQL.
Trabajando con sockets en MQL, o Cómo convertirse en proveedor de señales Trabajando con sockets en MQL, o Cómo convertirse en proveedor de señales
Los sockets... ¿Qué podría existir sin ellos en este mundo de información? Aparecieron por primera vez en 1982 y prácticamente no han cambiado hasta el día de hoy, siguen funcionando para nosotros cada segundo. Son la base de una red, las terminaciones nerviosas del Matrix en el que vivimos.
Expresiones regulares para los traders Expresiones regulares para los traders
Una expresión regular es un lenguaje especial para el manejo de textos mediante la aplicación de una regla especificada, también llamada un regex o regexp para abreviar. En este artículo, vamos a mostrar cómo manejar un informe sobre el trade con la librería RegularExpressions para MQL5 y también demostrar los resultados de optimización después de usarlo.
Interfaces gráficas VIII: Control "Explorador de archivos" (Capítulo 3) Interfaces gráficas VIII: Control "Explorador de archivos" (Capítulo 3)
En los capítulos anteriores de la octava parte de la serie, nuestra librería se ha completado con las clases para la creación de los punteros para el cursor del ratón, calendarios y listas jerárquicas. En este artículo vamos a analizar el control “Explorador de archivos” que también puede utilizarse como parte de la interfaz gráfica de la aplicación MQL.