Discusión sobre el artículo "Características del Wizard MQL5 que debe conocer (Parte 16): Método de componentes principales con vectores propios"
Muy útil saberlo, gracias.
Sin embargo, para la matriz "_m", ¿por qué no iteras el índice "_rates" hasta que "i<=_buffer_size"?
Sebastien Nicolas Paul Boulenc #:
Es muy útil saberlo, gracias.
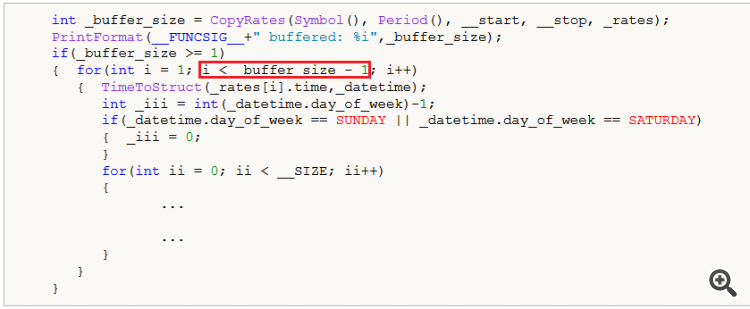
Sin embargo, para la matriz "_m", ¿por qué no iteras el índice "_rates" hasta que "i<=_buffer_size"?
if(_buffer_size >= 2) { for(int i = 1; i <= _buffer_size - 1; i++) { ... } }
Debería haber sido así, pero dado el gran tamaño del buffer, creo que copiamos un año de datos, el efecto de este error era mínimo. Gracias por señalarlo.
Está perdiendo oportunidades comerciales:
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Registro
Entrada
Usted acepta la política del sitio web y las condiciones de uso
Si no tiene cuenta de usuario, regístrese
Artículo publicado Características del Wizard MQL5 que debe conocer (Parte 16): Método de componentes principales con vectores propios:
En este artículo analizaremos el método de componentes principales, una técnica de reducción de la dimensionalidad para el análisis de datos, y cómo podemos aplicar este utilizando valores propios y vectores. Como siempre, intentaremos desarrollar un prototipo de la clase de señales del asesor experto que se pueda utilizar en el Wizard MQL5.
La SVD consigue reducir la dimensionalidad partiendo el conjunto de datos matriciales en tres matrices separadas, una de las cuales, la matriz Σ, definirá las direcciones más importantes de la varianza en los datos. Esta matriz, también conocida como matriz diagonal, contiene valores singulares que representan los valores de varianza a lo largo de cada dirección predeterminada (escrita en otra de las tres matrices, con frecuencia denominada U). Cuanto mayor sea el valor singular, más significativa será la dirección correspondiente para explicar la variabilidad de los datos. Esto hace que la columna U con el valor singular más alto se seleccione como representativa de toda la matriz, reduciendo de hecho la dimensionalidad de la matriz a un único vector.
Por el contrario, el método de las potencias refina iterativamente la estimación del vector tendiendo al vector propio dominante. Este vector propio captará la dirección con los cambios más significativos en los datos y representará la dimensionalidad reducida de la matriz de origen.
Sin embargo, como en este artículo nos centramos en los vectores y valores propios, podemos transformar una matriz n x n en n vectores posibles de tamaño n, asignando a cada uno de estos vectores un valor propio. Este valor propio determinará entonces la elección de un único vector propio para representar mejor la matriz; en este caso, además, un valor más alto indicará de nuevo una mayor correlación positiva para explicar la variabilidad de los datos.
Autor: Stephen Njuki